Magnetovolume effects in manganese nitrides with antiperovskite structure

Abstract

Magnetostructural correlations in antiperovskite manganese nitrides were investigated systematically for stoichiometric and solid solution Mn₃Cu_1−xA_xN (A = Co, Ni, Zn, Ga, Ge, Rh, Pd, Ag, In, Sn or Sb). This class of nitrides is attracting great attention because of their giant negative thermal expansion, which is achieved by doping Ge or Sn into the A site as a relaxant of the sharp volume contraction on heating (spontaneous volume magnetostriction ω_s) because of the magnetovolume effects. The physical background of large ω_s and mechanism of how the volume contraction becomes gradual with temperature are central concerns for the physics and applications of these nitrides. An entire dataset of thermal expansion, crystal structure and magnetization demonstrates that the cubic triangular antiferromagnetic state is crucial for large ω_s. The intimate relationship between ω_s and the magnetic structure is discussed in terms of geometrical frustration related to the Mn₆N octahedron and magnetic stress concept. The results presented herein also show that ω_s depends on the number of d electrons in the A atom, suggesting the important role of the d orbitals of the A atom. Not all the dopants in the A site, but the elements that disturb the cubic triangular antiferromagnetic state, are effective in broadening the volume change. This fact suggests that instability neighboring the phase boundary is related to the broadening. The relation between the gradual volume change and the local structure anomaly is suggested by recent microprobe studies.

Introduction

An antiperovskite compound with the formula M₃AX (M, transitional metal; A, metal or semiconducting element and X, interstitial light element) is a treasury of functionalities. Various beneficial properties including magnetovolume effects [1, 2], magnetostriction [3, 4], magnetocaloric effects [5, 6], magnetoresistance [7, 8], low-temperature coefficient of resistance [9–11], superconductivity [12, 13] and functional mechanical properties [14, 15] have been obtained in antiperovskites. The wide diversity of physical properties of antiperovskites reflects an equally wide range of chemical-bonding interactions consisting of the d orbital in M and the p orbital in X. Intermetallic compounds containing ordered interstitial light elements, as typified by antiperovskites, form a major class of materials that have different physical backgrounds and different parameters from those of oxides. Their value as a reservoir of smart materials becomes still higher.

Among these compounds, antiperovskite manganese nitrides Mn₃AN characterized by their peculiar magnetostructural correlations exhibit giant negative thermal expansion (NTE) [16–19]. The coefficient of linear thermal expansion α is over −30 ppm K⁻¹ for Mn₃AN, which is more than ten times as large as that of the NTE materials known before the discovery of this compound. This gigantic, isotropic and non-hysteretic NTE attracts great interest from practical and fundamental viewpoints. The NTE of the manganese antiperovskites was achieved by broadening the sharp volume contraction upon heating from low-temperature (low-T) large-lattice antiferromagnetic (AF) to high-T small-lattice paramagnetic (PM) phases using partial replacement of constituent elements. Such control of electronic phase change is now a key paradigm for the development of smart materials [20].

The gigantic NTE of Mn₃AN strongly affected NTE research, leading to the discovery of many NTE materials such as Cd(CN)₂·CCl₄ [21], ReO₃ [22], ScF₃ [23], ZnF₂ [24], SrCu₃Fe₄O₁₂ [25], (Bi, La)NiO₃ [26] and La(Fe, Si, Co)₁₃ [27]. Particularly, NTE of SrCu₃Fe₄O₁₂, (Bi, La)NiO₃ and La(Fe, Si, Co)₁₃ is achieved using phase control similar to Mn₃AN. It is noteworthy that α reaches −80 ppm K⁻¹ in (Bi, La)NiO₃. In addition, Ca₂Ru_1−xCr_xO₄ [28] was discovered as one NTE material realized by phase control, in which ordering of orbitals as well as spins is relevant to the NTE [29].

Unresolved problems related to the giant NTE in Mn₃AN are the origin of the large volume change associated with the magnetic phase transition, defined as spontaneous volume magnetostriction ω_s, and the mechanism of how this volume change becomes gradual with T. They reflect the peculiar electronic states of Mn₃AN and the central issues to elucidate the physics of the magnetostructural correlations in this class of nitrides. Furthermore, they are dominant factors for the practical functionalities of NTE. Therefore, understanding them is desired as a scientific basis for improvement and control of NTE properties.

This report describes systematic explorations of the magnetism and the crystal structure for stoichiometric and solid solution Mn₃Cu_1−xA_xN (A = Co, Ni, Zn, Ga, Ge, Rh, Pd, Ag, In, Sn or Sb), including typical NTE compositions. Here, we summarize the compositional requirements for large ω_s and gradual volume change with T, and discuss their physical background.

Experimental procedures

All measurements were taken using sintered polycrystalline samples [30]. First we obtained Mn₃AN using a solid-state reaction. Powders of Mn₂N and pure element A (purity: 99.9% or higher), in total about 2 g, were mixed in a bag filled with nitrogen gas and then sealed in a quartz tube (9 mm diameter and 20 cm long) under vacuum (< 10⁻³ Torr). The sealed quartz tube was heated at 500–760 °C for 40–70 h. To obtain the solid solution, we mixed powders of the stoichiometric antiperovskites in an appropriate molar ratio, pressed it into a pellet and sealed it in a quartz tube under vacuum. The final sintering was conducted at 800 °C for 60 h. The crystal structure was investigated by powder x-ray diffraction (XRD). The nitrogen deficiency δ was confirmed by the method of thermal conductivity detection of the emitted gas. Here, we define δ as the general formula Mn₃AN_1−δ. The results of δ measurements are presented in tables 1, 2, 4 and 5. In the text, we use the notation Mn₃AN for simplicity. The term ‘stoichiometric’ means in this paper that the A site is occupied by a single element, and does not mean δ = 0.

Table 1.

Physical properties of cubic antiperovskite manganese nitrides Mn₃AN_1−δ showing magnetovolume effects.

				Lattice constant (Å)			Fitting parameters
Mn3AN1−δ A	1−δ	TN (K)	Magnetic properties	295 K	400 K	10 K	a0 (Å)	γ	θD (K)	ωs (10−3) 10 K
Co	0.74	252		3.872	3.879	3.867	3.859	2.14	452.0	5.64
Ni	0.87	256		3.888	3.893	3.886	3.875	2.11	525.9	8.18
Zn	0.96	170		3.904	3.913	3.890	3.887	2.57	344.5	20.44
Ga	0.92	288		3.888	3.897	3.898	3.873	2.54	429.2	19.10
Rh	0.75	226		3.930	3.936	3.918	3.916	2.19	419.2	2.07
Pd	0.89	316		3.993	3.997	3.982	3.977	2.42	484.2	3.60
Ag	0.88	276	Weak FM	4.022	4.029	4.013	4.006	2.42	336.8	5.79
In	0.89	366	Weak FM	4.012	4.012	4.000	3.983	2.65	394.8	9.24

Table 2.

Physical properties of antiperovskite manganese nitrides Mn₃AN_1−δ without magnetovolume effects: C, cubic; T₁ and T₄, tetragonal and a∗ represents the cubic root of the pseudo-cubic-cell volume.

Mn3AN1−δ							Lattice constant Å
A	1−δ	T>T∗1	T∗1 (K)	T∗1>T>T∗2	T∗2 (K)	T∗2>T	295 K	10 K
							a=3.907
Cu	0.95	PM, C	143	FM, T−1	−	−	a=3.907	c=3.846
								(a∗=3.887)
							a=5.431	a=5.424
Ge	0.75	PM, C	600	AF, T4	380	FM, T4	c=8.119	c=8.035
							(a∗=3.912)	(a∗=3.895)
Sn	0.76	PM, C	550	AF, C	45	FM, C	a=4.061	a=4.049
							a=4.183	a=4.157
Sb	0.91	PM, C	360	FM, T+1	−	−	c=4.289	c=4.273
							(a∗=4.218)	(a∗=4.195)

Table 4.

Physical properties of Mn₃Cu_0.85A_0.15N_1−δ showing magnetovolume effects: C, cubic and T₁ and T₄, tetragonal.

Mn3Cu0.85A0.15N1−δ							Lattice constant (Å)			ωs (10−3)
A	1−δ	T>T∗1	T∗1 (K)	T∗1>T>T∗2	T∗2 (K)	T∗2>T	295 K	10 K		10 K
Co	0.93	C	152	C	−	−	3.901	a=3.906		8.39
Ni	0.90	C	165	C	50	C(PS)	3.906	a1=3.908	a2=3.888	7.92
Zn	0.90	C	95	T−1	−	−	3.903	a=3.915	c=3.860	2.66
Ga	0.91	C	75	T−1	−	−	3.906	a=3.905	c=3.856	0.38
Ge	0.90	C	105	C	−	−	3.903	a=3.904		12.34
Rh	0.92	C	248	(Not measured)	3.915					7.89
Pd	0.91	C	212	C(PS)	−	−	3.920	a1=3.929	a2=3.903	6.93
Ag	0.94	C	145	C	70	T−1	3.922	a=3.936	c=3.878	1.88
In	0.87	C	100	(Not measured)	3.916					10.99
Sn	0.86	C	95	C	−	−	3.917	a=3.915		9.97

Table 5.

Physical properties of Mn₃Cu_0.5A_0.5N_1−δ showing magnetovolume effects.

Mn3Cu0.5A0.5N1−δ				Lattice constant (Å)			ωs (10−3)
A	1−δ	T∗ (K)	ΔT (K)	295 K	400 K	10 K	10 K
Co	0.88	238	46	3.889	3.896	3.889	10.10
Ni	0.93	232	5	3.901	3.906	3.903	12.03
Zn	0.95	43	<1	3.901	3.910	3.900	12.20
Ga	0.91	140	<1	3.895	3.904	3.899	14.43
Ge	0.86	365	85	3.911	3.911	3.906	14.90
Rh	0.87	292	10	3.934	3.939	3.926	7.82
Pd	0.92	276	30	3.956	3.961	3.953	8.92
Ag	0.91	212	8	3.959	3.967	3.956	9.25
In	0.83	243	5	3.950	3.959	3.948	10.00
Sn	0.86	332	36	3.966	3.967	3.958	11.03

Linear thermal expansion ΔL(T)/L was measured using a strain gage (types KFL and KFH; Kyowa Electronic Instruments Co. Ltd) at temperatures of 4–500 K. This method is simple but requires a material having a known degree of expansion. We used copper (purity: 99.99%) and the corresponding thermal expansion data of pure copper [31, 32]. Measurements of ΔL/L were partly conducted using a laser-interference dilatometer. The T dependence of the lattice constant obtained from XRD data was reported for A = Ni [33], Cu [9], Zn [34], Ga [35] and Ag [36]. Our ΔL/L data for stoichiometric Mn₃AN are in quantitative agreement with the previous XRD data presented above, thereby validating our thermal expansion measurements. Temperature-dependent magnetization M(T) was measured at 5000 Oe using a superconducting quantum interference device magnetometer.

Results

Stoichiometric Mn₃AN

Results for stoichiometric Mn₃AN are presented in tables 1 and 2. The previously reported crystal structure and lattice parameters of the stoichiometric Mn₃AX [2, 9, 33–51] are listed in table 3. The inset of figure 2(b) shows a crystal structure of an antiperovskite M₃AX.

Table 3.

Literature review of lattice constants at ambient temperature for Mn₃AN. Data for carbide counterpart Mn₃AC are also listed for comparison: C, cubic and T₁ and T₄, tetragonal.

Mn3AN
A	Structure	Lattice constant (Å)		References
Al	C	a=3.8545		[48]
Mn	C	a=3.872		[39]
Ni	C	a=3.886		[33]
Cu	C	a=3.906		[37]
		a=3.908		[41]
		a=3.905		[9]
Zn	C	a=3.902		[42]
		a=3.8951		[34]
		a=3.90082		[49]
Ga	C	a=3.888		[39]
		a=3.898		[40]
		a=3.885		[35]
Ge	T4	a=5.422,	c=8.134	[41]
As	T4	a=5.782,	c=8.370	[41]
		a=5.786,	c=8.378	[45]
Rh	C	a=3.9280		[38]
Pd	C	a=3.9796		[38]
Ag	C	a=4.0195		[37]
		a=4.025		[36]
In	C	a=4.0291		[50]
Sn	C	a=4.0585		[38]
		a=4.060		[43]
		a=4.058		[46]
Sb	T+1	a=4.181,	c=4.280	[41]
		a=4.172,	c=4.282	[45]
Pt	C	a=3.9685		[38]
		a=3.972		[44]
Au	C	a=4.0235		[38]
Hg	C	a=4.0720		[38]
Mn3ZnC	C	a=3.930		[2]
Mn3GaC	C	a=3.896		[39]
		a=3.895		[35]
		a=3.894		[2]
Mn3SnC	C	a=3.994		[47]
		a=3.989		[2]
		a=3.984		[51]

Figure 2.

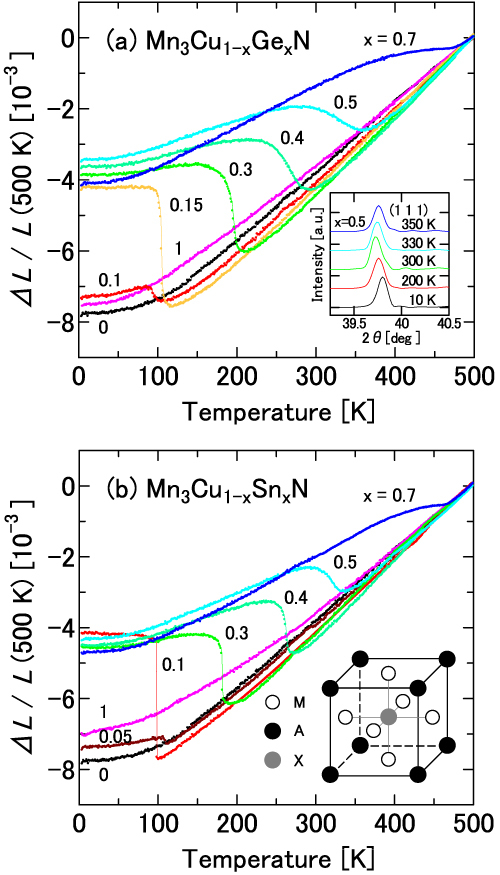
Linear thermal expansion Δ(T)/L of Mn₃Cu_1−xA_xN: A = Ge (a) and Sn (b). The inset in (a) shows the (111) peak of XRD for x = 0.5. The inset in (b) shows the crystal structure of an antiperovskite M₃AX.

Figure 1 displays ΔL/L measured for Mn₃Cu_1−xA_xN for eight dopants A = Co, Ni, Zn, Ga, Rh, Pd, Ag and In. Each of the eight elements forms the stoichiometric Mn₃AN that exhibits magnetovolume effects in the cubic AF ground state. Cadmium, which is also categorized in the same group, is omitted from the present study. Figure 2 displays ΔL/L of typical NTE compounds Mn₃Cu_1−xA_xN with A = Ge and Sn. A comparison with the magnetization M(T) depicted in figure 3 shows that the anomaly temperature in ΔL/L, T∗, corresponds to the magnetic transition temperature (the Curie temperature T_C for the ferromagnetic (FM) transition; the Neel temperature T_N for the AF transition).

Figure 1.

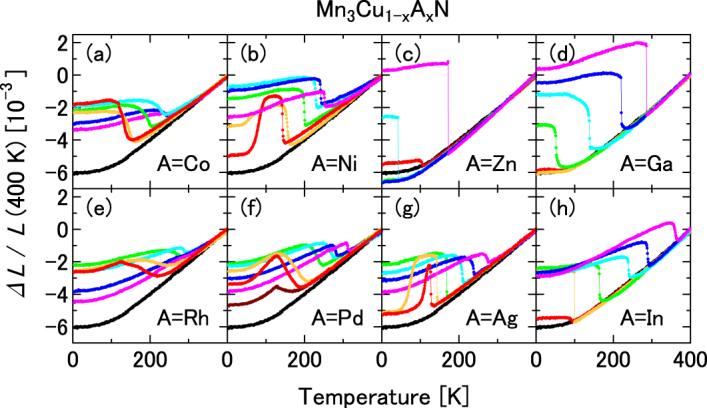
Linear thermal expansion Δ(T)/L of Mn₃Cu_1−xA_xN for x = 0 (black), 0.1 (red), 0.15 (orange), 0.3 (green), 0.5 (light blue), 0.7 (blue) and 1 (magenta): A = Co (a), Ni (b), Zn (c), Ga (d), Rh (e), Pd (f), Ag (g) and In (h).

Figure 3.

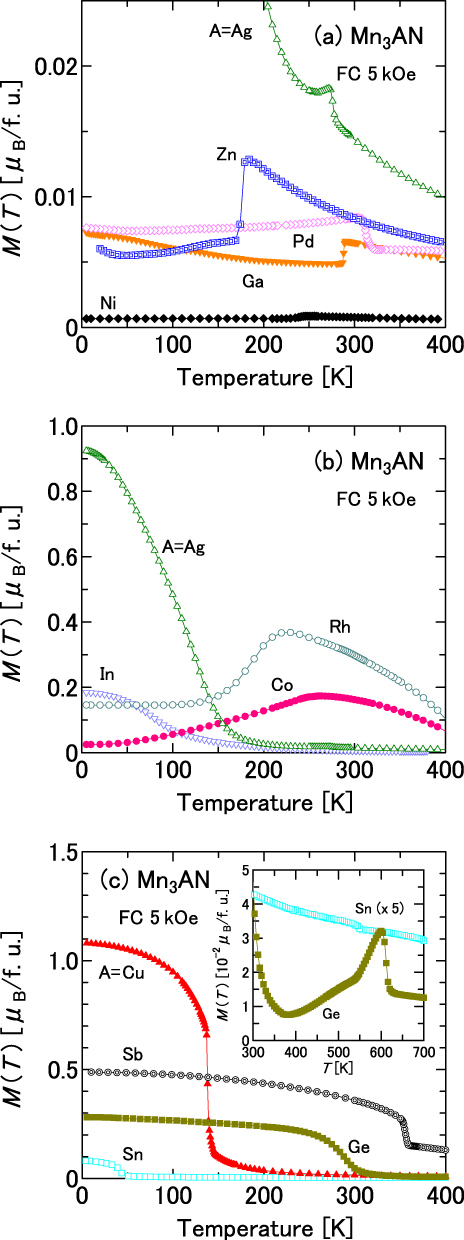
Temperature-dependent magnetization M(T) of stoichiometric Mn₃AN measured during a cooling process in an applied field of 5 kOe: (a) A = Ni, Zn, Ga, Pd and Ag; (b) A = Co, Rh, Ag and In and (c) A = Cu, Ge, Sn and Sb. The inset in (c) shows magnified magnetization for A = Ge and Sn at the high-temperature region of T = 300–700 K.

The PM–FM transition temperature (T∗ = T_C) of Mn₃CuN is 143 K, which is the lowest one among the stoichiometric Mn₃AN. Mn₃CuN exhibits negligibly small magnetovolume effects (figure 4). At T_C, the structural deformation occurs simultaneously from high-T cubic C to low-T tetragonal T⁻₁ (c/a < 1) symmetry. The magnetic unit cell of the FM phase is enlarged two times within the ab plane (, , 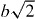c), containing six manganese atoms or magnetic moments; four moments are canceled out within the ab plane, whereas two moments are aligned ferromagnetically. The study of magnetostriction indicates that the magnetic easy axis is the a-axis (ab plane) [3]. A similar ferrimagnetic-like spin configuration is also realized in Mn₃SbN, in which the magnetic unit cell is twice as long as the c-axis (a, b, 2c) [1], but the direction of tetragonal distortion is opposite. That is, T⁺₁ (c/a > 1) [4].

Figure 4.

Linear thermal expansion Δ(T)/L of Mn₃CuN (open circle) and the ideal lattice thermal expansion determined by fitting analysis using equation (1) (red line). The fitting parameters are a₀ = 3.891 Å, θ_D = 320.3 K and γ = 2.33.

The eight stoichiometric cubic Mn₃AN compounds presented in figure 1, respectively, exhibit anomalies in ΔL/L at T∗ and contract upon heating. For quantitative evaluation of the magnetovolume effects, we estimate the magnetic contribution to the volume, i.e. spontaneous volume magnetostriction ω_s, defined as the difference between the hypothetical phononic thermal expansion (ΔL/L)_ph and the measured thermal expansion. As presented in figure 1, ΔL/L of Mn₃Cu_1−xA_xN at the PM phase is apparently universal irrespective of x. Consequently, the hypothetical phononic expansion is determined by extrapolating this envelope using the following equation of the lattice constant a at T due to the anharmonic phonon [52]:

(ϕ, Thacher's approximate function [53]; a₀, the lattice constant at absolute zero temperature; V ₀, the volume of the unit cell at absolute zero temperature; r, the number of atoms in the unit cell; K, the bulk modulus; θ_D, the Debye temperature; γ, the Grüneisen parameter and k_B, the Boltzmann constant). Because the cubic crystal structure is maintained over the T range, we assume that V =a³. Based on the previous results on the Young modulus of the antiperovskites [54], we fixed K at 130 GPa. For an antiperovskite structure, r is five. Consequently, the fitting parameters were reduced to three in the present analysis: a₀, γ and θ_D. The obtained parameters are listed in table 1. The result for Mn₃CuN is portrayed in figure 4. These fitting parameters are physically reasonable because they are comparable to those of typical transition metal-based intermetallic compounds [55–57].

For A = Ni, it might be difficult to define the envelope because ΔL/L in the PM phase varies according to x. If we estimate (ΔL/L)_ph by extrapolating the measured ΔL/L at the PM phase of Mn₃NiN, then we would obtain an unphysically large Debye temperature (a₀ = 3.883 Å, γ = 3.23 and θ_D = 1441 K). However, ΔL/L at the PM phase is apparently universal for x = 0.1–0.5. We estimated (ΔL/L)_ph for Mn₃NiN using this common part of ΔL/L for x = 0.1–0.5, instead of the measured Mn₃NiN data. In this analysis, the fitting parameters are in the reasonable range (a₀ = 3.875 Å, γ = 2.11 and θ_D = 525.9 K). Assuming this (ΔL/L)_ph, ω_s does not disappear even at the PM phase for Mn₃NiN. Empirically, the finite ω_s originates from the rather weak T dependent ΔL/L of Mn₃NiN at the PM phase. This flat ΔL/L is also the origin of an unphysically large θ_D in the fitting analysis of (ΔL/L)_ph. The finite ω_s suggests spin fluctuations at the PM phase [58].

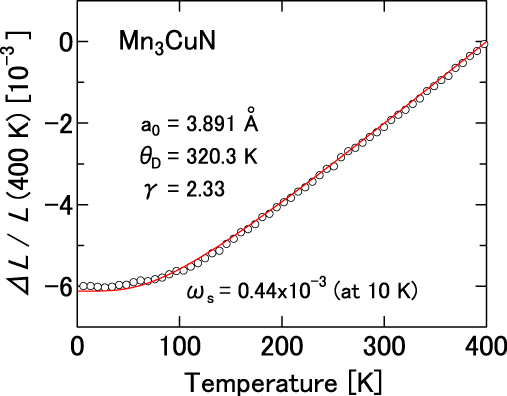
For a cubic system, ω_s is defined as 3[ΔL/L − (ΔL/L)_ph]. The obtained ω_s values are presented in figure 5 and table 1. For Mn₃GeN and Mn₃SnN, we do not obtain finite values of ω_s. We infer that they are zero. Furthermore, for Mn₃CuN (figure 4), ω_s is negligibly small (ω_s is less than 0.44 × 10⁻³). However, slight dopants, typically x ∼ 0.1, produce large ω_s. Therefore, we plot in figure 5 the value for A = Cu_0.85Ge_0.15 and ω_s = 12.59 × 10⁻³, as a potential ω_s of Mn₃CuN (see table 4). The presented result clearly exhibits a good agreement between ω_s and the number of d electrons in the A atom. ω_s is larger for the 3d series than for the 4d series. It increases concomitantly with increasing atomic number in the same series. For Mn₃ZnN and Mn₃GaN, ω_s becomes prominently large, more than twice the size of the second largest group, A = In, Ni or Ag. In previous arguments, the number of valence (outer s and p) electrons in A, n_v, was regarded as the dominant factor for the electronic states, based on the clear relationship between T∗ and n_v [1]. However, ω_s is unrelated to T∗. Therefore, it is unrelated to n_v in the presented results. In terms of the electronic structure, this fact implies that ω_s increases as the d level of the A atom moves away from the Fermi level, suggesting an important role of the d level of the A atom, although it has been disregarded to date.

Figure 5.

Spontaneous volume magnetostriction ω_s for stoichiometric Mn₃AN at 10 K. For A = Cu, the value of Mn₃Cu_0.85Ge_0.15N is shown as a representative value of potential ω_s because Mn₃CuN-based antiperovskites exhibit pronounced ω_s when the cubic triangular AF state is recovered by slight dopants on the A site.

From the viewpoint of n_v, the cubic AF phase showing the magnetovolume effects appears for n_v = 2 and 3. When n_v becomes smaller (n_v = 1: A = Cu) or larger (n_v = 4: A = Ge, Sn; n_v = 5: A = As, Sb), the system undergoes structural deformation, possesses different magnetic structure and does not exhibit magnetovolume effects (table 2). The structural deformation is interpreted as a consequence of the band Jahn–Teller effects. The band filling varies according to n_v. At both ends of small and large n_v its condition is satisfied, i.e. the Fermi level approaches singularity in the density of states [59].

3.2. Solid solution Mn₃Cu_1−xA_xN

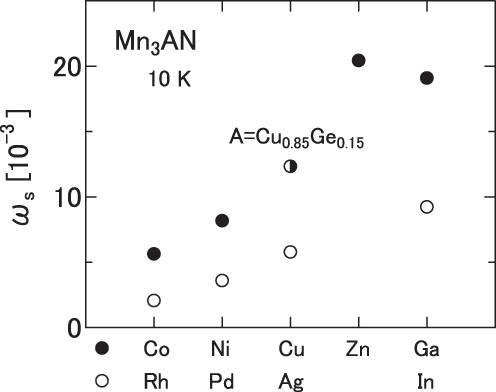
The results are presented in tables 4 (x = 0.15) and 5 (x = 0.5). The giant NTE of the antiperovskites was first discovered in the Mn₃Cu_1−xGe_xN solid solution. Surprisingly, neither end material Mn₃CuN nor Mn₃GeN exhibits magnetovolume effects or NTE. The drastic change in physical properties of Mn₃Cu_1−xGe_xN exemplifies the diverse physical properties of Mn₃AN.

First, we examine the doping effects of two representative dopants: Ge and Sn. The linear thermal expansion and the magnetization are shown, respectively, in figures 2 and 6. Doping effects of Ge and Sn are fundamentally the same. The sequence starting from the low-doping level is the following: (i) Mn₃CuN and slightly doped (x < 0.1) compounds possess the tetragonal FM ground state, (ii) cubic and AF structures are recovered and magnetovolume effects appear (x = 0.1–0.15), (iii) T_N increases concomitantly with increasing x, (iv) the volume change at T_N becomes broader as the doping proceeds and shows the giant NTE (x ∼ 0.5), (v) further doping decreases ω_s and (vi) eventually the phase transition occurs and the crystal structure and the magnetism become the same as those of the end material Mn₃GeN or Mn₃SnN, without showing magnetovolume effects (x ∼ 0.9). For the other eight dopants presented in figure 1, the sequence is similar to that of the Ge- or Sn-doped compounds, except that the cubic AF state with magnetovolume effects survives the doping to the end. The change in T∗ is interpreted as a consequence of the change in n_v by doping. For A = Ni and Ag, the re-entrant behavior was clearly observed for the low-doping region of x = 0.1–0.15. Upon cooling, the volume expands at the onset of the AF state and shrinks at the reentrant (figures 1(b) and (g)).

Figure 6.

Inverse susceptibility χ⁻¹(T) of Mn₃Cu_1−xA_xN measured during a cooling process in an applied field of 5 kOe. A = Ge (a) and Sn (b).

Although the minimum x required for recovery of the cubic AF state varies between 0.1 and 0.3 according to the A dopant, we find a remarkable relation between the recovery of cubic structure and the appearance of magnetovolume effects. This is illustrated nicely in the series of Mn₃Cu_0.85A_0.15N. Temperature-dependent XRD measurements were conducted for all the compounds except for A = Rh and In. Table 4 shows the crystal structure and the lattice parameter determined by the XRD measurements and ω_s estimated using a procedure similar to that of the case of stoichiometric Mn₃AN.

The XRD results at 10 K for Mn₃Cu_0.85A_0.15N are classified into three categories: (i) single-phase cubic (A = Co, Ge and Sn), (ii) tetragonal T⁻₁ (A = Zn, Ga and Ag) and (iii) phase-separated cubic (A = Ni and Pd) states. The XRD patterns are portrayed in figure 7 for A = Ge (a), Ga (b), Ag (c) and Ni (d) as representatives. Here, the contribution from the Kα₂ was subtracted. For A = Ge, the (200) peak keeps a single component down to the lowest temperature, implying the cubic structure over a whole T range. For A = Ga, the (200) peak is a single component at 300 K, but it splits into two parts at 10 K. The intensity ratio of the lower-angle peak to that of the higher-angle one is 2:1. Therefore, the lower and higher peaks are assigned, respectively, to (200) and (002) in the tetragonal notation. The cubic unit cell is deformed into the tetragonal one with the shorter c-axis, namely T⁻₁, which is the same as Mn₃CuN [3, 9]. For A = Ag, the (200) peak keeps a single component down to 100 K, but it splits into two parts at 10 K similar to Mn₃CuN and Mn₃Cu_0.85Ga_0.15N, which indicates that the crystal structure is cubic in the intermediate state (70 < T < 145 K) and it is deformed into T⁻₁ in the ground state (T < 70 K). For A = Ni, the (111) peak splits into two parts. However, this (111) peak does not split by tetragonal deformation in principle. Similar splitting occurs for all XRD peaks for A = Ni and Pd. These profiles are reasonably explained by assuming the co-existence of two cubic phases with different lattice parameters.

Figure 7.

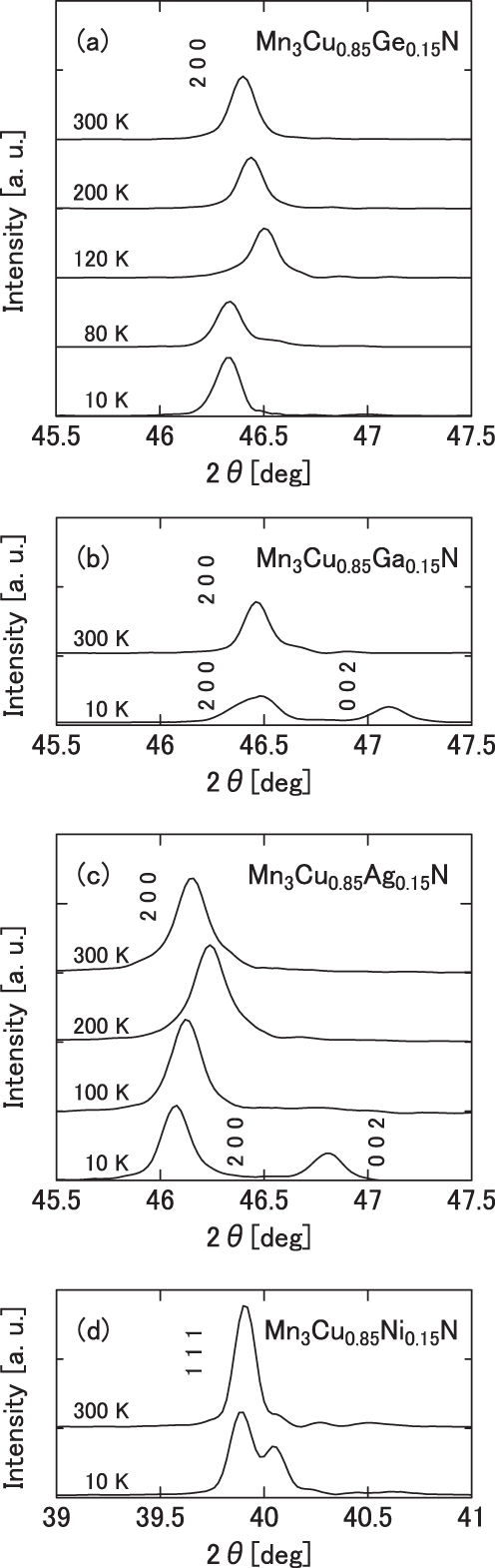
Temperature dependence of XRD profiles of Mn₃Cu_0.85A_0.15N: A = Ge (a), Ga (b), Ag (c) and Ni (d).

Good agreement exists between the cubic crystal symmetry and the large ω_s, as shown in table 4. ω_s is large for (8–10) × 10⁻³, at largest 12.34 × 10⁻³, for cubic compounds including phase-separated ones, although it is at its largest 2.66 × 10⁻³ for A = Zn and becomes much smaller for A = Ga and Ag, where the lattice is tetragonally distorted. For A = Ag, however, ω_s becomes large (10.51 × 10⁻³) in the cubic intermediate state (70 < T < 145 K), although it is small (1.88 × 10⁻³) in the T⁻₁ ground state. The presented result on A = Ga is in agreement with the previous result [43].

Even though 15% doping is small for magnetovolume effects, such as A = Ga or Zn, further doping achieves the cubic AF state showing magnetovolume effects. This is nicely presented in the series of Mn₃Cu_0.5A_0.5N (table 5). The experiments here reveal that all the systems listed in table 5 maintain a cubic structure over the whole T range and possess the AF ordered state. ω_s is (7.82–14.90) × 10⁻³. An important difference is not the magnitude of volume change ω_s, but the temperature window ΔT in which the volume gradually contracts on heating. The broadening of the volume change that causes NTE at room temperature does not appear for all dopants. In this study, broadening is remarkable in the order of A = Ge (ΔT = 85 K), Co (46 K), Sn (36 K) and Pd (30 K). For the other dopants, broadening is limited and the volume change remains sharp. Particularly, ΔT is less than 1 K for A = Zn and Ga. Such a sharp volume change is a characteristic feature of the end materials Mn₃ZnN and Mn₃GaN. The difference in atomic size between Cu and the dopant A is unrelated to the broadening.

Discussion

Physical background of magnetovolume effects

Requisites for large ω_s.

From the results, we might conclude that the cubic crystal structure is a requisite for large ω_s in Mn₃AN. In addition, the AF state, particularly, the triangular (Γ^5g and Γ^4g) magnetic structure, is apparently required for large ω_s. Although the dc magnetization measurements do not provide us with information related to the magnetic structure, this study shows that large ω_s is incompatible with FM states. A comparison between the previous neutron diffraction study and the presented results offers direct evidence for the relation between the triangular AF structure and the large ω_s.

The stoichiometric compounds, Mn₃NiN, Mn₃ZnN and Mn₃GaN, which were confirmed to have the triangular AF configuration by neutron diffraction study [1], exhibit a large ω_s in this study, 8.18 × 10⁻³, 20.44 × 10⁻³ and 19.10 × 10⁻³, respectively. However, for Mn₃RhN, which is confirmed to have a different AF configuration by the neutron study [1], ω_s is small (2.07 × 10⁻³). The neutron study [1] also indicates that the Γ^5g AF structure is realized just below T_N in Mn₃AgN, but the Γ^4g FM component is developed as T decreases. The small ω_s of Mn₃AgN at 10 K (5.79 × 10⁻³) might be partly explained by this mixing of the FM components.

A recent neutron study [60] revealed good agreement between the Γ^5g AF structure and the appearance of ω_s for the solid solution Mn₃Cu_1−xGe_xN. In addition, the Γ^5g AF state with large ω_s of Mn₃GaN is found to be unstable against slight Fe dopants on the Mn site. Moreover, the FM state is induced at lower temperatures [61]. Impressively, the ω_s disappears at the impurity-induced FM state. The detailed magnetic structure is yet to be confirmed.

An exception is Mn₃SnN. An earlier neutron study [1] revealed that it possesses the cubic Γ^5g AF state at 237 < T < 357 K, although no magnetovolume effects are confirmed in previous [46] studies or the present study. It must be considered that Mn₃SnN easily loses nitrogen (1 − δ = 0.76 in this study). The nitrogen deficiency drastically alters the physical properties of this class of nitrides [62]. Indeed, the physical properties of Mn₃SnN studied here differs from those of the previous one [1]: the former undergoes two successive transitions at 550 and 45 K (figure 3(c)), whereas the latter undergoes four transitions at 475, 357, 237 and 186 K.

These arguments enable us to predict the low-T crystal structure of Mn₃Cu_0.85Rh_0.15N and Mn₃Cu_0.85In_0.15N, which were not measured in this study. Rather, the large ω_s, estimated as 7.89 × 10⁻³ and 10.99 × 10⁻³ for the Rh- and In-doped compounds, respectively, predicts the cubic crystal structure for these solid solutions.

Frustration.

An intimate relation between the triangular AF structure and the large ω_s suggests that geometrical frustration plays a role in the magnetovolume effects. An Mn₆N octahedron has three-dimensional geometrical frustration because the nearest-neighbor (Mn–Mn) magnetic interaction J₁ is AF [63]. As a result, non-collinear long-range order such as Γ^5g or Γ^4g AF structure is stabilized, keeping the cubic structure only by a very narrow margin of energy with the assistance of the strong FM next-nearest-neighbor interaction J₂ [40]. The pronounced magnetovolume effects in the cubic triangular AF phase imply that lattice expansion with cubic symmetry brings larger energy gain than removal of degeneracy by lattice deformation. An idea incorporating the frustration into the magnetovolume effects is that the strong frustration might assist lattice contraction at the PM state because the volume contraction increases the bandwidth and hence reduces the electronic energy. This is energetically favorable, although the amplitude of a magnetic moment is decreased, when the short-range magnetic ordering, or spin fluctuation, is suppressed by the strong frustration.

This study produces a result supporting the idea presented above. Figure 8 displays the x dependence of the lattice parameter deduced from XRD and thermal expansion measurements. As presented in figure 8(a), Vegard's law is not fulfilled for Mn₃Cu_1−xGe_xN. The deviation from Vegard's law at 10 K is reasonably ascribed to the large ω_s. At this temperature, the lattice parameter is fairly scaled to ΔL/L. That is, it increases suddenly at x ∼ 0.1 and possesses a broad peak around x = 0.5. Then, it decreases slowly with increasing x. What is important is the deviation from Vegard's law at 500 K, at which the magnetovolume effects cannot affect the lattice parameter. The a − x curve at 500 K has a dip around x = 0.5, in contrast to that at 10 K. Similar deviation from Vegard's law is also observed for Mn₃Cu_1−xSn_xN at 500 K (figure 8(b)), although it is less clear because the atomic size of Sn is much greater than that of Cu. The large ω_s might be partly attributable to the small volume at the PM state because of the frustration. A similar effect might play an important role also for the huge ω_s up to 5% in YMn₂ [64], in which strong frustration is regarded as suppressing spin fluctuations and hence the volume immediately above T_N. We refer to an important difference: T_N of NTE manganese nitrides (∼ 300 K or higher) is much higher than that of YMn₂ (∼ 100 K).

Figure 8.

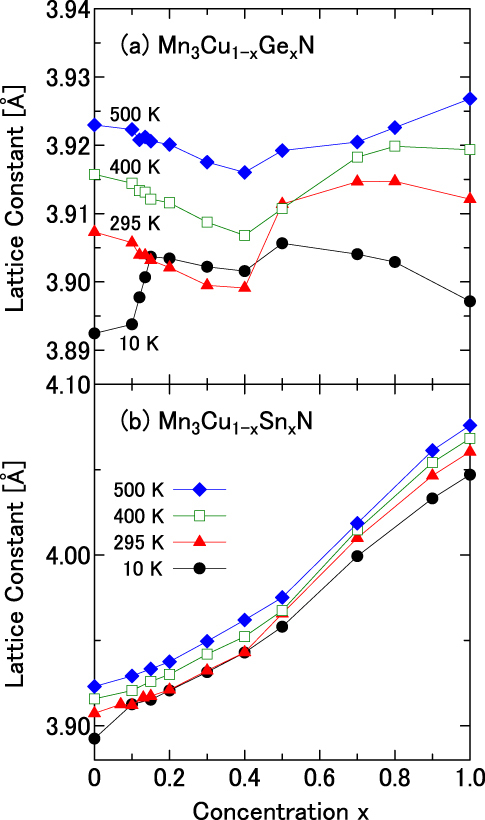
Deviation from Vegard's law in the lattice constant of solid solutions Mn₃Cu_1−xA_xN: A = Ge (a) and Sn (b).

Magnetic structure.

The magnetovolume effect is a change in volume attributable to a variation in the amplitude of the magnetic moment m in a magnetic metal. It was first discovered in Ni–Fe Invar, showing low thermal expansion of α = 0.5 − 1 ppm K⁻¹ below T_C = 500 K [65]. It appears as a huge volume change up to 5% in YMn₂ [64] as described above. A general explanation of NTE caused by the magnetovolume effect is that a larger volume favors the appearance of a magnetic moment in a metal. The electronic theory of solids provides a microscopic picture: an increase in volume suppresses the overlap of electronic orbitals and therefore reduces the electronic bandwidth. Narrowing of the bandwidth can increase the density of states ρ(ε) at Fermi energy ε_F, which favors magnetism. The magnetovolume effect is related directly to a longstanding problem, the origin of magnetism in a metal, and has long been regarded as a fundamental topic of physics³ [66, 67].

Magnetovolume effects are formulated in terms of itinerant-electron magnetism, or the Stoner–Edwards–Wohlfarth concept [68], ascribed to singularity in ρ(ε). In this framework, ω_s is related to the amplitude of the magnetic moment m in a manner: ω_s = C_mvm²/K. Here, C_mv is the magnetovolume coupling constant. In the spin fluctuation theory [69], this relationship is modified as ω_s = C_mv[m² + ξ²]/K (ξ: the amplitude of spin fluctuations). In these frameworks, the physics related to the magnetic structure would be incorporated via the coupling constant C_mv. However, magnetovolume effects related to the magnetic structure are apparently not fully discussed in the framework explained above.

In an itinerant-electron magnet, the magnetic and electronic structures are intimately related. Therefore, ω_s is naively related to the magnetic structure. However, the physics of the electronic structure is too rich to incorporate only through the unique constant C_mv or singularity in ε_F. One attempt to take the physics omitted from the arguments presented above into consideration is the concept of magnetic stress [70]. Magnetic stress is related to the strain tensor 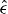derivative of the energy exchange interaction parameter J, which determines the magnetic structure. In fact, J and its strain tensor derivative depend strongly on the origin of the magnetic interactions, and consequently on the distance between the sites. They provide us with information related to the anisotropy or strains. We can also examine volume effects by considering the trace of the stress tensor.

For CrN [70], the nearest-neighbor AF Cr–Cr coupling J₁ is mediated by direct t_2g orbital interactions. The shorter atomic distance enhances overlapping of the orbitals. Therefore, the magnitude of J₁ becomes larger. In that case, the AF nearest-neighbor Cr–Cr bonds tend to decrease, although the FM nearest-neighbor Cr–Cr bonds tend to increase. This scheme explains the observed AF ordering and lattice distortion in CrN at T_N to an excellent degree. Consequently, the magnetostructural correlations of the antiperovskites also might be discussed comprehensively using the magnetic-stress concept.

Mechanism of broadening in volume change

Chemical disorder is not a primary cause for broadening of the volume change. The XRD measurement of typical broadened composition Mn₃Cu_0.5Ge_0.5N (the inset of figure 2(a)) clearly contra-indicates compositional inhomogeneity: the width of the (111) peak does not widen in the operating temperature window of NTE, compared with that above and below it. Moreover, the neutron and NMR measurements [71] reveal that the volume expands as the Γ^5g AF ordered moment gradually develops. Instead, the broadening seems to result from dopants that disturb the cubic triangular AF state because Mn₃GeN and Mn₃SnN have different electronic states from it [72]⁴.

No data presented here contradict the assumption that disturbance to the cubic triangular AF state is relevant to the broadening of the volume change. Because we know the detailed magnetic structure of seven stoichiometric Mn₃AN (A = Ni, Zn, Ga, Ge, Rh, Ag and Sn) [1], we first examine these seven dopants. The ground state of Mn₃AN (A = Ni, Zn, Ga or Ag) was confirmed to be the cubic triangular AF state, showing remarkable magnetovolume effects. Actually, Mn₃AgN is weak FM at low temperatures, but it clearly shows a peak in the M(T) curve (figure 3(a)) and T_N is definable. This weak FM behavior is ascribed to the mixing of the Γ^4g FM component. However, the ground state of Mn₃AN (A = Ge, Rh or Sn) has different magnetic structures from the triangular AF. This study demonstrates that the former four dopants do not induce remarkable broadening of the volume change, although the latter three dopants induce broadening.

Indium also does not induce broadening. For Mn₃InN, we have no information related to the magnetic structure, but this study confirmed that the crystal structure is cubic and the magnetic state is suggested to be weak FM, similar to Mn₃AgN, which are consistent with a recent report [50]. Therefore, Mn₃InN might have the ground state of the triangular AF structure. However, Co and Pd induce broadening of the volume change. Results of this study confirmed that Mn₃CoN and Mn₃PdN have a cubic structure and AF magnetic properties. Although the magnetic structures of Mn₃CoN and Mn₃PdN are yet to be confirmed, this study predicts that they have no triangular AF structure.

For Mn₃Cu_1−xGe_xN and Mn₃Cu_1−xSn_xN, the cubic triangular AF states spread over a large area up to x ∼ 0.9. The volume change is gradual as T from x ∼ 0.4 to this boundary. The broadening of volume change near the phase boundary suggests that a kind of phase instability plays an important role in this broadening. It is interesting and suggestive that Ni–Fe Invar showing anomaly in thermal expansion lies near the fcc–bcc boundary in the Ni–Fe phase diagram [66]. Microscopic probes such as pair-distribution-function analysis of the neutron diffraction [73], x-ray absorption fine structure [74] and electron microscope observation [75] indicate that local structure anomaly is relevant to the broadening of the volume change in the antiperovskites. The relation to phase instability is yet to be explored.

Concluding remarks

We performed systematic explorations of the crystal structure and magnetism of stoichiometric and solid-solution Mn₃Cu_1−xA_xN (A = Co, Ni, Zn, Ga, Ge, Rh, Pd, Ag, In, Sn or Sb), particularly addressing the origin of pronounced spontaneous volume magnetostriction ω_s and the mechanism of broadening of the volume change.

An entire set of linear thermal expansion data enables us to evaluate the magnetic contribution to the thermal expansion, ω_s. The results demonstrate that ω_s depends highly on crystal and magnetic structures. Particularly, the cubic triangular AF state is apparently a prerequisite for large ω_s. In addition, ω_s was found to depend on the number of d electrons in A, suggesting an important role of the d orbitals of the A atom. Based on these results, we discussed the effects of the geometrical frustration related to the Mn₆N octahedron and a concept of magnetic stress.

Not all dopants in the A site, but the elements that disturb the cubic triangular AF state, are effective in broadening the volume change. The results suggest that chemical disorder is not a primary cause for the broadening, but that a kind of instability in structural and/or magnetic states is related to the broadening. As an important issue for future study, we refer to the relation between local structure anomaly and broadening of the volume change.