Skip to main content
PMC home page
Science and Technology of Advanced Materials logoLink to Science and Technology of Advanced Materials
. 2010 Oct 27;11(5):054502. doi: 10.1088/1468-6996/11/5/054502

A study of the synthetic methods and properties of graphenes

C N R Rao 1,2,✉, K S Subrahmanyam 1, H S S Ramakrishna Matte 1, B Abdulhakeem 1, A Govindaraj 1,2, Barun Das 1,2, Prashant Kumar 1, Anupama Ghosh 1,2, Dattatray J Late 1
PMCID: PMC5090618  PMID: 27877359

Abstract

Graphenes with varying number of layers can be synthesized by using different strategies. Thus, single-layer graphene is prepared by micromechanical cleavage, reduction of single-layer graphene oxide, chemical vapor deposition and other methods. Few-layer graphenes are synthesized by conversion of nanodiamond, arc discharge of graphite and other methods. In this article, we briefly overview the various synthetic methods and the surface, magnetic and electrical properties of the produced graphenes. Few-layer graphenes exhibit ferromagnetic features along with antiferromagnetic properties, independent of the method of preparation. Aside from the data on electrical conductivity of graphenes and graphene-polymer composites, we also present the field-effect transistor characteristics of graphenes. Only single-layer reduced graphene oxide exhibits ambipolar properties. The interaction of electron donor and acceptor molecules with few-layer graphene samples is examined in detail.

Keywords: graphenes, surface variations, magnetic properties, electronic properties, field-effect transistor characteristics, preparation methods, charge-transfer, mechanical properties

Introduction

The discovery of the fascinating properties of single-layer graphene (SLG) has generated much interest in the physical and materials sciences [1–4]. Graphene exhibits an ambipolar electric field effect along with ballistic conduction of charge carriers [5], integer quantum Hall effect at room temperature, fractional quantum Hall effect at low temperatures [6–8] and high elasticity [9]. As investigations of single, bi-, tri- and few-layer graphenes (n<10) are being pursued, it is useful to classify graphenes by the number of layers. After the initial studies conducted on SLG prepared by micromechanical cleavage, graphenes containing varying number of layers have been produced using diverse strategies [2, 4, 10]. There are reports on some of the properties of few-layer graphenes, but only a few studies document the changes brought about by the variation in the number of layers. Furthermore, well-defined procedures are still lacking for the synthesis of graphenes with the desired number of layers. In this article, we discuss the methods used to produce graphenes with varying number of layers and then examine their surface, magnetic and electrical properties. The electrical properties pertain to pure graphenes as well as to their composites with polymers. The characteristics of field-effect transistors formed with different graphene samples are also compared.

Graphene is characterized by a variety of techniques. In particular, transmission electron microscopy (TEM) and atomic force microscopy (AFM) are essential for determining the number of layers and other structural features. Among the spectroscopic techniques, Raman scattering is very effective in investigations of graphene. Whereas carbon nanotubes can be characterized with optical absorption and luminescence, Raman spectroscopy is the only optical tool available for structural investigations of graphene, providing information about the quality and number of layers in a given sample. The G-band (around 1580 cm−1) in the Raman spectra is sensitive to doping and other effects. The D-band (around 1340 cm−1), which is a defect-related band, also provides a signature of the quality of the graphene. SLG shows a strong G-band and a very weak D-band, but the D-band strengthens with the increase in the number of layers. The 2D-band (∼2600 cm−1), which appears in both single-layer and few-layer graphenes, is sensitive to both the number of layers and doping. Here, we present data from Raman spectroscopy and other characterization techniques wherever necessary. In the discussion of properties, we compare the features exhibited by graphenes with different number of layers and prepared by different methods.

Synthesis methods

Single-layer graphene

Single-layer graphene is generally prepared by micromechanical cleavage from highly ordered pyrolytic graphite (HOPG) [11]. In this procedure, a layer is peeled off the HOPG crystal with Scotch tape and transferred onto a silicon substrate. A popular chemical method to prepare SLG involves reduction of single-layer graphene oxide (SGO) dispersion in dimethlyformamide (DMF) with hydrazine hydrate [12]. Graphite oxide (GO) [5, 13] readily forms a stable colloidal suspension in water, and the suspension is subjected to ultrasonic treatment (300 W, 35 kHz) to produce SGO. The SGO suspension (0.3 mg ml−1) in a mixture of water and DMF is treated with hydrazine hydrate at 80 °C for 12 h [12]. This yields a black suspension of reduced graphene oxide (RGO) in DMF/H2 O. An additional amount of DMF is then added to stabilize the suspension. The thus prepared single-layer graphene (RGO) differs, however, from the SLG obtained by micromechanical cleavage of graphite or other means by that RGO contains some residual oxygen. Gram quantities of single-layer graphene can be obtained by a solvothermal procedure using sodium and ethanol [14]. Exfoliation of graphite in N-methyl pyrrolidone or surfactant/water solution employing ultrasonication also yields stable SLG dispersions [15, 16].

SLG films are produced on the Si-terminated (0001) face of single-crystal 6H-SiC by the thermal desorption of Si [17–19]. In this procedure, the substrates are subjected to electron bombardment in ultrahigh vacuum at 1000 ° C to remove oxide contaminants and then heated to temperatures ranging from 1250 to 1450 ° C for 1–20 min. The formation of carbon films by cooling Ni foils saturated with carbon at high temperatures was studied by Blakely and co-workers [20–22]. Recently, SLG has been prepared by the decomposition of hydrocarbons on films or sheets of transition metal such as Ni, Cu, Co and Ru [23]. We have employed this method to generate graphene layers on different transition metal substrates by decomposing a variety of hydrocarbons such as methane, ethylene, acetylene and benzene. We found that the number of layers varies with the hydrocarbon and reaction parameters. In our experiments, nickel and cobalt foils with thicknesses of 0.5 and 2 mm, respectively, were used as catalysts. These foils were cut into 5×5 mm2 pieces and polished mechanically, and the chemical vapor deposition (CVD) was carried out by decomposing hydrocarbons at a temperature in the range 800–1000 °C. By employing a nickel foil, CVD was carried out by passing methane (60–70 sccm) or ethylene (4–8 sccm) along with a high flow of hydrogen of about 500 sccm at 1000 ° C for 5–10 min. When using benzene as the hydrocarbon source, benzene vapor diluted with argon and hydrogen was decomposed at 1000 ° C for 5 min. On a cobalt foil, acetylene (4 sccm) and methane (65 sccm) were decomposed at 800 and 1000 ° C, respectively. In all these experiments, the metal foils were cooled gradually after the decomposition. The produced graphene layers were difficult to remove from the metal surface, however, and this is a drawback of the CVD method.

Figure 1 shows high-resolution TEM images of graphene sheets obtained by CVD on a nickel foil. Figures 1(a)–(c) show graphenes obtained by the thermal decomposition of methane and benzene, respectively, on the nickel foil. The insets in figures 1(a) and (c) show selected area electron diffraction (SAED) patterns. Figure 1(b) clearly reveals the edge of the graphene sheet. All these graphene samples exhibit the G-band at 1580 cm−1 and the 2D-band around 2670 cm−1 with a narrow linewidth of 30–40 cm−1. The narrow linewidth and relatively high intensity of the 2D-band confirm that these Raman spectra correspond to 1–2 layer graphenes [23]. In figures 2 and 3, we plot the Raman spectra recorded from different graphene samples produced by CVD. The Raman spectra of graphene grown on nickel by the thermal decomposition of methane, ethylene and benzene, particularly the first two hydrocarbons, show an intense 2D-band, a weaker G-band and hardly any D-band (see figures 2(a) and (b)), and are clearly indicative of SLGs [23]. Figures 3(a) and (b) show the Raman spectra of graphene prepared on cobalt by the thermal decomposition of methane and acetylene, respectively; the spectrum in (b) resembles that of SLG.

Figure 1.

Figure 1.

Open in a new tab

TEM images of graphene prepared by the thermal decomposition of (a, b) methane (70 sccm) and (c) benzene (Ar passed through benzene at a flow rate of 200 sccm), at 1000 ° C on a nickel sheet. Insets in (a) and (c) show electron diffraction patterns from the corresponding graphene sheets.

Figure 2.

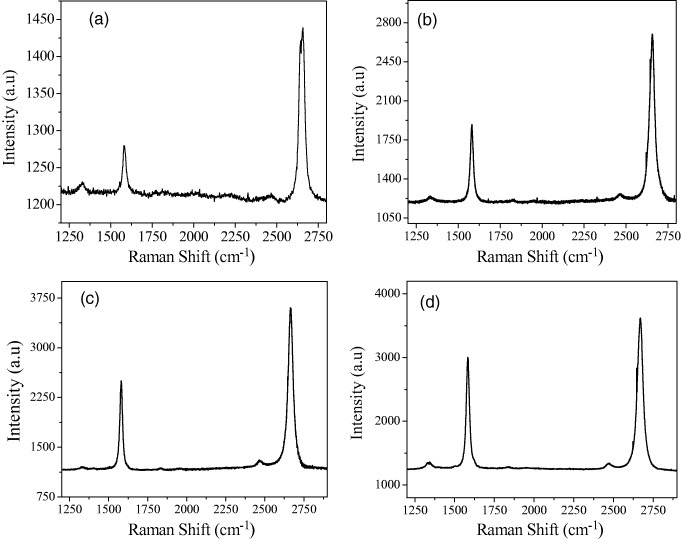
Figure 2.

Open in a new tab

Raman spectra of graphene prepared by the thermal decomposition of hydrocarbons on a nickel sheet: (a) methane (70 sccm) at 1000 ° C, (b) ethylene (4 sccm) at 900 ° C, (c) benzene (argon passed through benzene at a flow rate of 200 sccm) at 1000 ° C, (d) benzene (argon passed through benzene at a flow rate of 400 sccm) at 1000 ° C.

Figure 3.

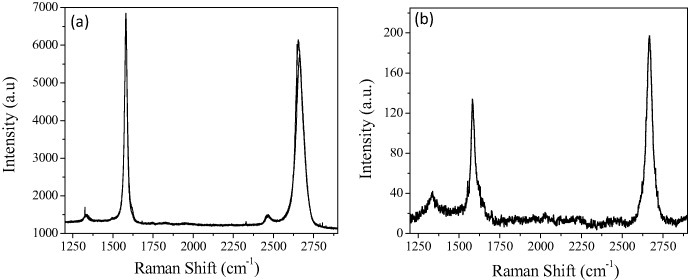
Figure 3.

Open in a new tab

Raman spectra of graphene prepared by the decomposition of (a) methane (64 sccm) at 1000 ° C and (b) acetylene (4 sccm) at 800 ° C on a cobalt sheet.

Few-layer graphene

An important method to prepare few-layer graphene is thermal exfoliation of graphite oxide at high temperatures [13, 24–26]. In this procedure, graphite oxide (0.2 g) is placed in an alumina boat and inserted into a long quartz tube sealed at one end. The sample is purged with Ar for 10 min, and then the tube is quickly inserted into a tube-furnace preheated to 1050 ° C and held in the furnace for 10 min. The graphene obtained by this procedure has few layers and is called exfoliated graphene (EG). Another method of preparing few-layer graphene is by reacting SGO in water with hydrazine hydrate at the refluxing temperature or by microwave treatment (EG-H) [2, 27]. In this method, hydrazine hydrate (1 mM) is added to 100 ml of stable aqueous exfoliated graphene oxide solution (1 mg ml−1) and refluxed for 24 h. The reduced graphite oxide turns black and precipitates at the bottom of the flask. The resulting precipitate is filtered and washed with water and methanol. Instead of hydrazine hydrate, one can also use ethylene glycol as a reducing agent to prepare few-layer graphene (EG-H(G)). In this procedure, the homogeneous mixture of 25 ml of exfoliated graphene oxide and 2 ml of ethylene glycol is placed in a 50 ml Teflon-lined bomb. The sealed autoclave is kept in an oven at 170 ° C for 24 h under autogenous pressure and allowed to gradually cool to room temperature. The product is washed with water and ethanol.

Few-layer graphene can be prepared by heating nanodiamond in an inert or reducing atmosphere (DG) [25, 28] and the effect of temperature on the product has been studied by Enoki and co-workers [28, 29]. We have examined this procedure in detail. We first treated nanodiamond particles by soaking in concentrated HCl to avoid contamination with magnetic impurities. We then heated 100 mg of pristine nanodiamond powder (particle size 4–6 nm, Tokyo Diamond Tools, Japan) placed in a graphite container in a graphite furnace in a helium atmosphere at different temperatures (1650, 1850, 2050 and 2200 ° C) for 1 h. These samples are designated as DG-1650, DG-1850, DG-2050 and DG-2200, respectively, and figure 4 shows their TEM images. Figure 5 shows the histograms of the number of layers and of the lateral dimension of the DG-1650 and DG-2200 samples obtained from AFM data. There is a slight increase in the number of layers and a decrease in lateral dimensions after heating at 2200 ° C. Raman spectra of DG-1650 and DG-2200 samples in figure 6 show the characteristic D-, G- and 2D-bands of graphene at 1340, 1580 and 2680 cm−1, respectively. The D-band is quite intense in the DG samples.

Figure 4.

Figure 4.

Open in a new tab

TEM images of (a) DG-1650, (b) DG-1850, (c) DG-2050 and (d) DG-2200 samples. The sample number indicates the temperature of transformation in ° C.

Figure 5.

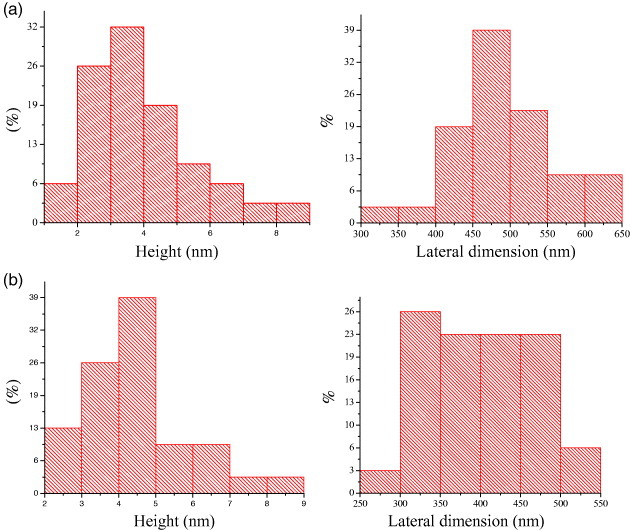
Figure 5.

Open in a new tab

Histograms of height profile and lateral dimensions of (a) DG-1650 and (b) DG-2200 samples obtained from the analysis of AFM images.

Figure 6.

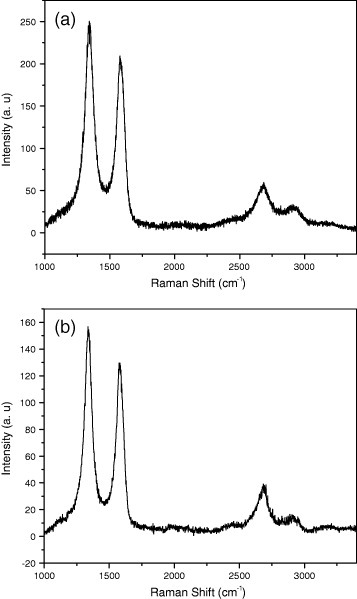
Figure 6.

Open in a new tab

Raman spectra of (a) DG-1600 and (b) DG-2200 samples.

We have discovered that arc evaporation of graphite in the presence of hydrogen yields graphene (HG) with exclusively 2–3 layers, although the flakes are relatively small (100–200 nm) [30]. This process relies on the knowledge that the presence of H2 during the arc discharge terminates the dangling carbon bonds with hydrogen and prevents the formation of closed structures. To prepare HG, direct current arc discharge of graphite evaporation was carried out in a water-cooled stainless steel chamber filled with a mixture of hydrogen and helium in different proportions, without using any catalyst. The partial pressures of H2 and He were H2 (70 torr)-He (500 torr), H2 (100 torr)-He (500 torr), H2 (200 torr)-He (500 torr) and H2 (400 torr)-He (300 torr). In a typical experiment, a graphite rod (Alfa Aesar, 99.999% purity, 6 mm in diameter and 50 mm in length) was used as the anode and another graphite rod (13 mm in diameter and 60 mm in length) was used as the cathode. The discharge current was in the 100–150 A range, with a maximum open-circuit voltage of 60 V [31]. Figure 7 shows typical TEM and AFM images of a produced sample. An important aspect of the arc discharge method is its use in doping graphene with boron or nitrogen [32]. Boron-doped and nitrogen-doped graphenes (B-HG and N-HG) were obtained by carrying out the discharge in the presence of H2+ diborane and H2+ (pyridine or ammonia), respectively. Table 1 summarizes the different methods of graphene synthesis and the number of layers obtained. In spite of the many advances made in the last four years, controlled synthesis with a desired number of layers remains a challenge.

Figure 7.

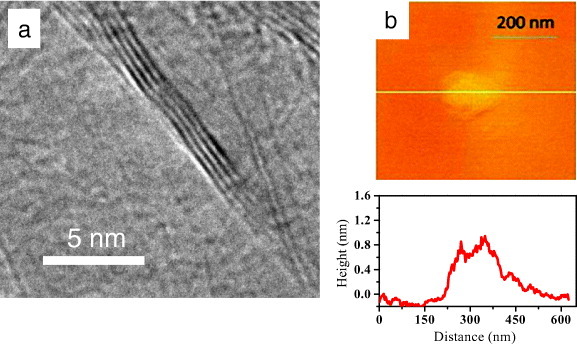
Figure 7.

Open in a new tab

(a) TEM and (b) AFM images of HG material prepared by arc discharge of graphite in hydrogen. (Reproduced with permission from [4] © 2010 American Chemical Society.)

Table 1.

Synthetic methods and the number of layers in graphenes.

Synthetic method No. of layers
Micromechanical cleavage from graphite 1
Solution phase exfoliation of graphite 1
Epitaxial growth 1
Chemical vapor deposition (CVD) 1
Solvothermal synthesis 1
Reduction of single-layer 1
graphene oxide (RGO)
Arc evaporation of graphite in H2 (HG)a 2–3
Thermal exfoliation of graphite oxide (EG) 2–7
Chemical reduction of exfoliated 2–6
graphene oxide (EG-H)
Conversion of nanodiamond (DG) 4–8
Open in a new tab

aNitrogen-doped and boron-doped HG samples (N-HG and B-HG) have been prepared by introducing N- and B-containing molecules in the arc discharge.

Surface properties of few-layer graphenes

Single-layer graphene is theoretically predicted to have a large surface area of 2600 m2 g−1 [33]. We have measured the surface properties of few-layer graphene samples prepared by different methods. The Brunauer, Emmett and Teller (BET) surface area was typically in the range of 270–1550 m2 g−1 , approaching the value of single-layer graphene for some samples [34]. The surface area varies as EG > DG > EG-H > HG. These high surface area samples might enable the storage of hydrogen. Hydrogen storage reaches 3 wt% at 100 bar and 300 K and the uptake varies linearly with the surface area [34]. Theoretical calculations show that SLG can accommodate up to 7.7 wt% hydrogen, whereas bi- and trilayer graphenes can have an uptake of ∼2.7 wt % and that the H2 molecules attach to the graphene surface in an alternating end-on and side-on fashions. The CO2 uptake of few-layer graphenes at 1 atm and 195 K is around 35 wt%. Calculations suggest that SLG can have a maximum uptake of 37.9 wt% CO2 and that the CO2 molecules reside parallel to the graphene surface [34].

Magnetic properties of few-layer graphenes

There were a few studies on the magnetic properties of nanographite particles, which demonstrate the importance of the edge states arising from the nonbonding electrons [35–37]. It was pointed sometime ago that edges in graphene ribbons play a crucial role in determining the electronic structure [35]. Nanographite particles exhibit unusual magnetic properties including spin-glass behavior and magnetic switching phenomena [38–40]. Bilayer graphene is predicted to be ferromagnetic [41]. Hydrogenated nanographite is also predicted to show spontaneous magnetism [42]. The magnetic properties of nanographite were reviewed by Enoki et al [38–40] and the main message is that the edge states and the adsorbed or intercalated species affect the magnetic properties. By carrying out first-principles density functional calculations, Lee et al [43] have shown the existence of a ferromagnetically ordered ground state in the zigzag edges of graphene. Zigzag edges longer than 3–4 repeat units are predicted to be magnetic, irrespective of whether the edges are regular or irregular [44, 45].

We have studied the magnetic properties of different graphene samples. Magnetization measurements were carried out with a vibrating sample magnetometer in a physical property measurement system (PPMS, Quantum Design, San Diego, CA, USA). All the graphene samples show a divergence between the field-cooled (FC) and zero-field-cooled (ZFC) curves, which starts at around 300 K and disappears upon the application of the magnetic field of 1 T (for typical data from EG material see figure 8). The divergence between the FC and ZFC curves in the graphene samples is similar to that in magnetically frustrated systems. The Curie–Weiss temperatures obtained from the high-temperature inverse susceptibility data were negative in all these samples, indicating the presence of antiferromagnetic interactions. Interestingly, we observe well-defined maxima in the magnetization at low temperatures, the maxima becoming prominent in the data recorded at 1 T. Such magnetic anomalies are found when antiferromagnetic correlations compete with ferromagnetic order. It is possible that the data correspond to the coexistence of different types of magnetic states [46]. The ferromagnetic clusters in such a case would not be associated with a well-defined global ferromagnetic transition temperature. This behavior is similar to that of microporous carbon and the members of the rare-earth manganite family with the formula RE1−xAx MnO3 (RE=rare-earth, A=alkaline earth element) [47–50]. Recent theoretical calculations do indeed predict the presence of antiferromagnetic states in the sheets and ferromagnetic states at the edges of graphene [51]. All the graphene samples show magnetic hysteresis at room temperature (figure 9). In DG samples, we observe a systematic decrease in magnetization with increasing preparation temperature. Thus, in DG-1650, the saturation magnetization (Ms), remnant magnetization (Mr) and coercive field (Hc), are 0.04 emu g−1, 0.0015 emu g−1 and 41 Oe, whereas in DG-2200, they are 0.02 emu g−1, 0.001 emu g−1 and 213 Oe, respectively. Among all the samples, HG shows the best hysteretic features with a high value of magnetization, whereas EG and DG-2200 have a high coercive field of 213 Oe at room temperature. Electron paramagnetic resonance investigations revealed a signal with a linewidth of ΔH≈ 0.7–2.9 mT and a g value of 2.006–2.013. The narrow linewidth and the small deviation of g from the free-electron value suggest that the spins are carbon related and do not originate from transition-metal impurities. The magnetic properties depend on the number of layers and the sample area, with small values of both favoring larger magnetization.

Figure 8.

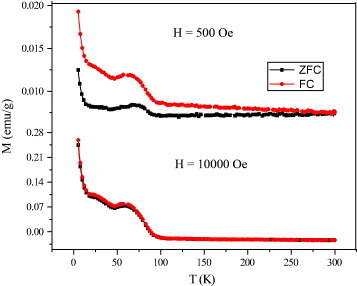
Figure 8.

Open in a new tab

Temperature dependence of magnetization of EG sample at 500 Oe and 1 T. (Reproduced with permission from [46] © 2009 American Chemical Society.)

Figure 9.

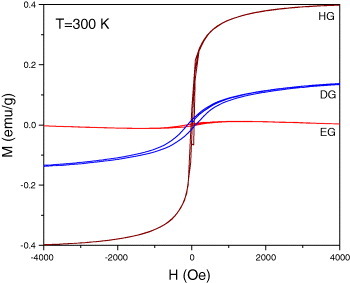
Figure 9.

Open in a new tab

Magnetic hysteresis in EG, DG and HG samples at 300 K. (Reproduced with permission from [46] © 2009 American Chemical Society.)

Even though enough care was taken during the preparation of graphene samples to ensure the absence of magnetic metal impurities, we washed some of the graphene samples with complexing agents. Thus, in the case of EG-H, we washed the graphite oxide solution with 8-hydroxy-quinoline-5-sulfonic acid prior to the reduction. The graphene so obtained is designated as EG-H (W). Figure 10 shows the temperature dependence of magnetization of EG-H (W) measured at 500 Oe. The inset shows the hysteresis loop at room temperature. Clearly, the basic features of the graphene samples described earlier are preserved and thus do not originate from metal contamination. Table 2 lists the values of Ms, Hc and Mr at room temperature and θ p for all the studied materials.

Figure 10.

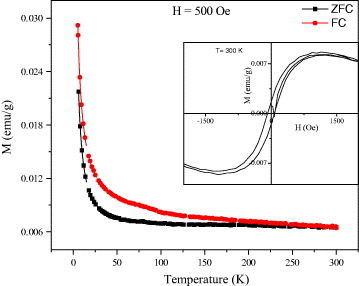
Figure 10.

Open in a new tab

Temperature variation of magnetization of EGH (W) at 500 Oe showing the ZFC and FC data. The inset shows the magnetic hysteresis at 300 K. EGH (W) stands for graphene prepared by exfoliation of graphene oxide followed by hydrazine reduction with prior washing with 8-hydroxy-quinoline-5-sulfonic acid.

Table 2.

Room temperature coercive field (Hc), remnant magnetization (Mr) and saturation magnetization (Ms) of graphene samples the values in parenthesis were obtained at 5 K; (θp) is the Curie–Weiss temperature.

Sample Hc (Oe) Mr (emu g−1) Ms (emu g−1) θp FC (500 Oe)
RGO 185 (78) 0.001 (0.0031) 0.003 (0.71) 106 K
(agglomerate)
EG 139 (213) 0.003 (0.0055) 0.01 (0.07) -1454 K
EG-H 155 (109) 0.001 (0.0063) 0.004 (1.29) -100 K
EG-Ha 145 (214) 0.001 (0.004) 0.002 (0.25) –
EG-H (w)b 80 (96) 0.002 (0.006) 0.009 (1.35) -756 K
DG-1650 41 (136) 0.002 (0.007) 0.04 (0.13) 235 K
DG-2200 200 (213) 0.001 (0.003) 0.002 (0.05) -75 K
HG 23 0.05 (0.036) 0.32 (0.54) -4178 K
Open in a new tab

aReduced with ethylene glycol.

bWashed with 8-hydroxy-quinoline-5-sulfonic acid.

Electrical properties of graphenes

Few-layer graphenes show semiconducting behavior with conductivity increasing upon heating in the 35–300 K range. The conductivity increases sharply from 35 to 85 K but the changes slow down at higher temperatures. Electron scattering can occur in graphenes at ripple sites (usually having a 10 nm periodicity) and defect sites, such as edges and grain boundaries. However, the intraripple flexural vibrations switch in the high-temperature range [52, 53]. In the case of exfoliated graphene with 5–6 layers, which is more rigid and exhibits weaker rippling, the temperature dependence due to the ripples and intraripple flexural vibrations is not appreciable, but the contributions of the edges and grain boundaries are prominent. There is an opening of the band gap in EG with 5–6 layers [54] and, hence, our graphene samples are not metallic but are semiconducting. This behavior is unlike the metallic nature exhibited by the single-layer graphene [27].

Graphene nanoribbons are predicted to be half-metallic if an in-plane, homogeneous electric field is applied across the zigzag edges [55]. Nanoribbon-based field-effect transistors (FETs) were fabricated with an on-off ratio of 107 at room temperature [56], and their properties are comparable to those of carbon nanotube FETs [57]. The saturation velocity of graphene FETs depends on the charge carrier concentration because of the carrier scattering by interfacial phonons in the silica layer [58]. Electrostatic modulation gives rise to transconductances as high as 150 μ S μ m−1 [58].

We have studied the electrical properties of few-layer graphenes prepared by different methods. For electrical measurements, the [100] silicon surface was oxidized at 1000 ° C for a few hours to produce a 300-nm-thick silicon dioxide layer. This SiO2 /Si substrate was coated with a resist (PMMA 950K/ EL9, where PMMA stands for poly(methyl methacrylate)). The substrate was then mounted into the chamber of an electron beam lithographic system (ultrahigh-resolution Raith e-line) equipped with a thermally assisted field-emission gun and a 100×100 mm2 laser interferometer stage. The minimum guaranteed linewidth of the system is 10 nm with a stitching accuracy of 40 nm and an overlay accuracy of 20 nm. The vacuum was 1.6×10−9 mbar at the e-beam gun and 4.7×10−6 mbar in the chamber. The tension used for the electron beam was 10 kV with a 30 μm aperture. The beam current was measured as 0.198 nA using a small Faraday cup. Patterns separated by 70 nm were written on a 100×100 μ m2 electrode pad. After the direct writing of such patterns, platinum metal was coated onto it and the resist was lifted off. A field emission scanning electron microscope (FESEM) attached to the Raith e-beam line was used for imaging the platinum thin-film electrodes with a nanogap. Dispersions of RGO, EG and HG in DMF solvent were then drop cast in between the nanogap separating the platinum electrodes, and the device was heated to 150 ° C to settle the graphene flakes and evaporate the solvent. I–V measurements were carried out with an Agilent RF Probe Station, which has a picoampere resolution.

Electrical conductivity and thermopower of EG graphene were measured with a physical property measurement system (PPMS, Quantum Design, USA) in the temperature range of 10–300 K. For these measurements, rectangular bars (4×10×2 mm) were cold pressed and then contacted in a four-probe configuration using gold-coated copper leads and silver epoxy (Epoxy Technology). For the thermopower measurements, the whole system was brought to equilibrium at a fixed temperature and then one end of the bar was slowly and locally heated while measuring the electromotive force induced between two electrodes.

We have recorded the current–voltage characteristics (I–V) of graphene samples with different number of layers, namely, RGO (1 layer), HG (2–3 layers) and EG (5–6 layers), using platinum electrodes separated by a 70 nm gap on a SiO2 /Si substrate. Figure 11 shows the FESEM images of the blank electrodes and the RGO, HG and EG samples between them, and figure 12 shows the typical I–V characteristics. The current varies at a fixed applied voltage according to the order RGO>HG>EG, reflecting the number of layers. Figures 13(a) and (b) show the temperature variation of the electrical conductivity and thermopower for EG graphene measured in a four-probe configuration. The electrical conductivity increases with temperature revealing the semiconducting nature. Its value at room temperature, approximately 50 Ω −1 cm−1, is much lower than that of a single graphene sheet. The thermopower has a small but positive value (16 μ V K−1 at 300 K), comparable to the values reported in the literature [59] for single-layer pristine graphene, and it increases with increasing temperature.

Figure 11.

Figure 11.

Open in a new tab

FESEM images of a platinum thin-film electrode separated by 70 nm, without any graphene sample (a), and with different graphene samples that were drop cast between the gap, namely, RGO (b), HG (c) and EG (d).

Figure 12.

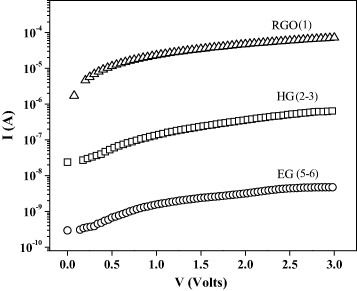
Figure 12.

Open in a new tab

I–V characteristics of RGO, HG and EG samples (the number of layers is shown in parenthesis).

Figure 13.

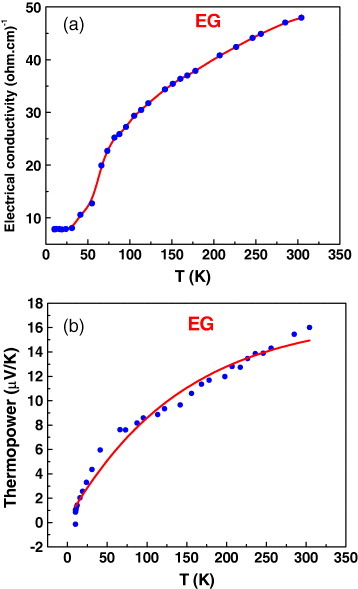
Figure 13.

Open in a new tab

Temperature variations of (a) electrical conductivity and (b) thermopower for an EG sample.

FET characteristics of different graphene samples (EG, EG-H, DG, HG, N-HG and B-HG) were studied in comparison with those of RGO. The ambipolar transfer characteristics of RGO measured at Vds =1 V, sweeping Vgs between −20 and +20 V, show both p- and n-type behaviors (figure 14(a)), while all the other undoped SLGs show n-type behavior with varying mobility, conductance and threshold voltage. FET devices based on boron-doped and nitrogen-doped graphene (B-HG and N-HG) show p- and n-type behaviors, respectively (figures 14(b) and (c)) [60]. Table 3 summarizes the FET characteristics of various types of graphenes. Different factors such as the average number of layers, surface functionality and concentration of defects are responsible for the sample-dependent characteristics. HG with the smallest number of layers exhibits the highest mobility among all the samples.

Figure 14.

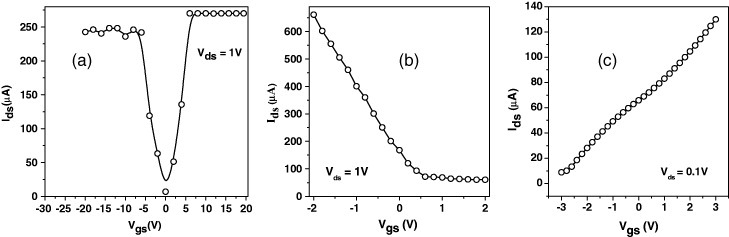
Figure 14.

Open in a new tab

Transfer characteristics (Ids versus Vgs) of FETs based on (a) RGO, (b) B-HG and (c) N-HG. Here, Ids, Vds and Vgs stand for source to drain current, source to drain voltage and gate to source voltage, respectively. (Reproduced with permission from [60] © 2010 Elsevier B. V.)

Table 3.

Characteristics of FETs based on few-layer graphene sample.

Graphene Threshold Transconductance Mobility Subthreshold
FET device Voltage gm (S) μ (cm2 Vs−1) Swing (SS)
Vth (V) V/decade
SGO −4.15 1.15× 10−7 0.3 10.9
0.84 3.28×10−5 μe=87.9 5.45
RGO −0.62 V 3.77×10−5 μh=101.3 5.15
EG −0.17 1.56 × 10−7 0.4 2.1
EG-H −1.72 3.88× 10−7 0.4 9.7
EG-MW 1.0 3.78× 10−6 4.3 4.5
DG −1.49 3.09× 10−4 715 11.5
HG −1.72 9.01× 10−3 10,428 3.0
B-HG 1.06 2.47× 10−4 572 2.9
N-HG −3.1 1.93× 10−5 447 8.37
Open in a new tab

Electrical properties of graphene-polymer composites

Lightweight and tough composites were prepared by incorporating a small amount of graphene in polymers [61]. The composites conduct electricity and can withstand much higher temperatures than the polymers alone [62]. Conventional polymer matrix composites often require large amounts of filler material (∼10 vol%) to achieve the desired properties. In contrast, marked enhancement of properties can be achieved by reinforcing the polymer with a relatively small amount (∼2 vol%) of materials, which are nano sized in at least one dimension. Polymers can be infused with metallic nanoparticles or single-wall or multiwall carbon nanotubes to create materials with superior properties. As compared with carbon nanotubes, graphene seems better suited to produce desired mechanical [62, 63] and electrical characteristics [64], and it is also less toxic. Few-layer graphenes have large surface areas as compared with nanofiller materials such as nanotubes [62], resulting in an increased interaction between the few-layer graphenes and the polymer matrix [63]. We have examined the electrical properties of graphene-polymer composites.

We have prepared PMMA-RGO composites using the following procedure. A DMF dispersion of RGO was mixed with the PMMA solution in DMF and sonicated for 20–30 min. The dispersion was then dried over water in Petri dishes at 35–40 ° C for 2 days. Films thus formed were removed from the Petri dish and dried before grinding them to obtain a fine powder. The PMMA-RGO powder was then used to make pellets for measurements. PMMA-HG composites were prepared using a similar procedure. As-prepared HG dispersed in toluene was added to a PMMA solution in toluene, and then the mixture was sonicated for 20 min. The dispersion was settled over water in Petri dishes at 35–40 ° C for 6–7 h. For the preparation of PVA-EG (PVA=polyvinyl alcohol) composites, PVA was first dissolved in warm water and then heated to 70–80 ° C for a complete dissolution. Acid-functionalized EG was dispersed in distilled water, sonicated for 15 min, then added to the PVA solution and sonicated for further 30 min. The dispersion so obtained was dried in Petri dishes at 35–40 ° C over a period of 3 days. PVA-EG composites containing different weight percentage of acid-functionalized EG were also prepared.

I –V measurements of PMMA-RGO, PMMA-HG pellet and PVA-EG film samples were carried out with a Keithley 6430 meter at room temperature. The conductivities of the polymer composites were calculated from the I–V curve, assuming ohmic behavior between 2 and 3 volts (in most cases, I–V curves were linear in this range). The electrode fabrication process for dielectric measurements was similar to that for conductivity measurements. Dielectric measurements were carried out with an Agilent 4294A impedance analyzer. Capacitance (Cp) was recorded in a frequency range of 100 Hz–1 MHz at an applied AC bias of 0.5 V at room temperature. The dielectric functions of different polymer composites were calculated using the formula k=Ct/ε 0 A, where C is capacitance and A and t are the area and the thickness of the pellets or films, respectively. Electrical conductivity and dielectric function were then plotted against the weight percentage of graphene for the studied composite samples, namely, PMMA-RGO, PMMA-HG and PVA-EG.

Figure 15(a) shows the typical I–V characteristics of PMMA-graphene composites containing single-layer graphene (RGO) and HG (2–3 layers) as a filler material. The I–V curves are ohmic, with the current increasing with the graphene content. The current is slightly higher for PMMA-HG than PMMA-RGO composites. Figure 15(b) shows the variation of electrical conductivity in PMMA-RGO and HG composites. The conductivity increases with increasing graphene content in both composites. The conductivity value is two orders of magnitude higher for PMMA-RGO (10−14 Ω −1 cm−1) compared to PMMA-HG (10−12Ω −1 cm−1) composites, and PVA-EG shows higher conductivity than PMMA-EG and PMMA-HG composites.

Figure 15.

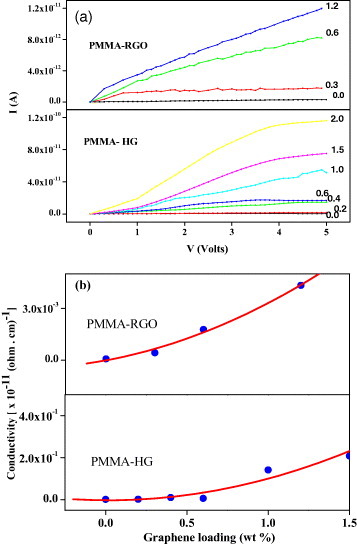
Figure 15.

Open in a new tab

(a) I–V characteristics of PMMA composites with different percentages of RGO and HG. (b) Electrical conductivity as a function of graphene nanofiller loadings (wt%) for PMMA composites with RGO and HG.

Figure 16(a) shows the typical I–V characteristics of PVA-EG composites containing varying weight percentages of EG. Here, the I–V curves are more linear compared to PMMA composites and the current increases with the graphene content. The current is 104–105 times higher for the PVA-EG than PMMA-RGO and HG composites. Figure 14(b) plots the electrical conductivity of PVA-EG composites with varying EG content. The conductivity increases with the graphene content just as in the PMMA composites. We have not found a percolative transition with the increase in graphene content in any studied composite.

Figure 16.

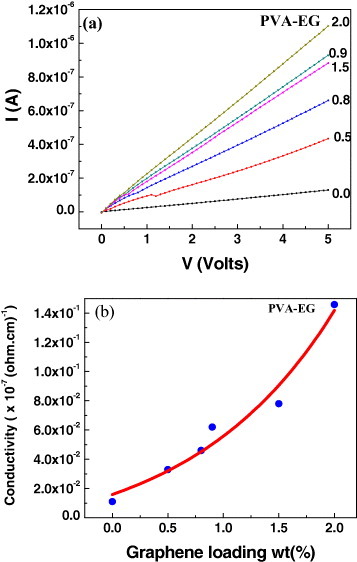
Figure 16.

Open in a new tab

(a) I–V characteristics of PVA-EG graphene composites for various nanofiller loading. (b) Electrical conductivity as a function of graphene nanofiller loadings (wt%) for PVA-EG composites with acid-functionalized EG.

We have also investigated the dielectric properties of PMMA-RGO and PVA-EG composites. Figure 17(a) shows the variation of dielectric function with frequency for PMMA-RGO composites with varying weight percentage of RGO. The dielectric function decreases and then becomes constant with increasing frequency. The variation of the dielectric function of PMMA-RGO composites at 1 MHz with the graphene (RGO) content is shown in figure 17(b). The dielectric function increases from 1 to 4 with increasing RGO content similarly to the electrical conductivity. Figure 18 shows the variation of dielectric function with frequency for PVA-EG composites with different graphene contents. Here too, the dielectric function initially decreases and becomes constant with increasing frequency. The inset in figure 18 shows the variation of dielectric function at 1 MHz with EG content for PVA-EG composites. Here, the dielectric function increases with increasing EG content. Interestingly, the dielectric function values for PVA-EG are 10 times higher than those for the PMMA-RGO composites.

Figure 17.

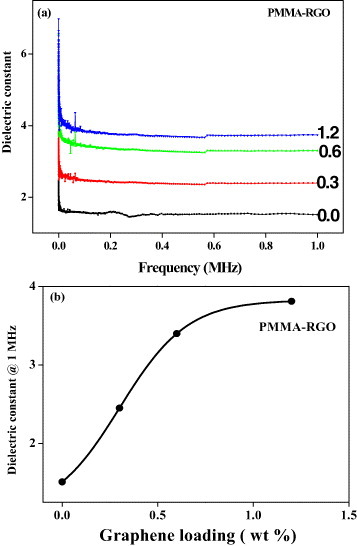
Figure 17.

Open in a new tab

(a) Variation of dielectric function of PMMA-RGO composites with frequency for various nanofiller contents (wt%). (b) Dielectric function (at 1 MHz) as a function of graphene loading (wt%) for PMMA-RGO graphene composites.

Figure 18.

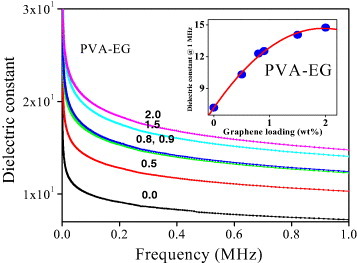
Figure 18.

Open in a new tab

Variation of dielectric function with frequency for PVA-EG graphene composites having various nanofiller contents. The inset shows the dielectric function (at 1 MHz) as a function of loading (wt%) for PVA composites with acid-functionalized EG.

Interaction of few-layer graphenes with electron donor and acceptor molecules

Raman bands of graphene are strongly affected by electron-phonon interactions and, hence, by doping with electrons and holes. It has been found recently, using in situ Raman measurements, that a top-gated SLG transistor can reach doping levels of up to 5×1013 cm−1 [65]. Electron donor and acceptor molecules do affect the positions and widths of the G- and 2D-bands of few-layer graphenes. The changes caused by the interaction of tetrathiafulavalene (TTF) and tetracyanoethylene (TCNE) with few-layer exfoliated graphene are particularly large [66], with the shifts in the G-band of up to 25 cm−1. These strong alterations are ascribed to surface-related phenomena. We have, therefore, investigated the effects of TTF and TCNE on the Raman bands with few-layer graphenes prepared by three different methods and, hence, associated with differences in the surface condition [67].

Figure 19 shows the Raman G-bands of the EG, DG and HG samples and the changes brought about by interaction with TTF and TCNE. The band on the right side of the G-band is defect related and is called G′ or sometimes D′. The G′-band is more prominent in HG than in DG and EG samples. The full width at half maximum (FWHM) of the G-band is the smallest in HG and the largest in EG samples. We have followed the variation in the G-bands of EG, DG and HG material on interaction with different concentrations of TTF and TCNE. All the samples show an increase and a decrease in the G-band frequency on interaction with TCNE and TTF, respectively. Figure 20 reveals the changes in the G-band position of the three graphene samples with varying concentrations of TTF and TCNE. The corresponding shifts in the G-band in the EG, DG and HG samples are 25, 17 and 11 cm−1, respectively, on interaction with 0.1 M TCNE.

Figure 19.

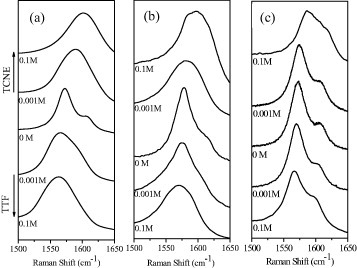
Figure 19.

Open in a new tab

Variation in the Raman G-bands of graphene samples (a) EG, (b) DG and (c) HG, caused by interaction with varying concentrations of TTF and TCNE. (Reproduced with permission from [67] © 2009 Elsevier B. V.)

Figure 20.

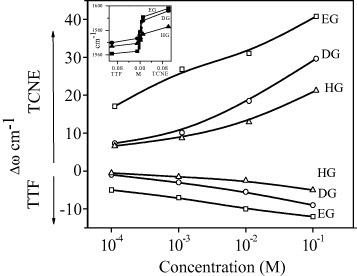
Figure 20.

Open in a new tab

Changes in the G-band position plotted against the logarithm of concentration of TTF or TCNE. The inset shows a linear plot against the concentration. (Reproduced with permission from [67] © 2009 Elsevier B. V.)

The FWHM of the G-band of the three graphenes also varies with the concentration of TTF and TCNE. It generally increases upon interaction with TTF and TCNE, the strongest effect is observed for the EG, and the initial increase is rather sharp. We could obtain reliable data on the changes in the G′-band for HG. The FWHM of the G′-band also increases with increasing concentration of TTF or TCNE.

Figure 21(a) shows the intensity ratio of the 2D- and G-bands, I(2D)/I(G), against the concentrations of TTF and TCNE. The 2D-band intensity decreases with the increase in concentration of either TTF or TCNE, and the initial decrease is sharp. The decrease in intensity is higher for EG and DG than for HG. The intensity of the defect-related D-band also varies with the TTF/TCNE concentration, but in a manner opposite to that of the 2D-band, as shown in figure 21(b). This is because of the different origins of the 2D- and D-bands. The D-band, unlike the 2D-band, couples preferentially to electronic states with the wave vector k such that 2q = k [68], where q is the scattering wave vector. Two scattering events, of which one is an elastic process involving defects and the other is inelastic involving a phonon, occur in the case of the D-band. In contrast, both processes are inelastic and involve phonons for the 2D-band. The I(D)/I(G) ratio increases more markedly for EG and DG than for HG samples, the initial rise being sharp in all cases.

Figure 21.

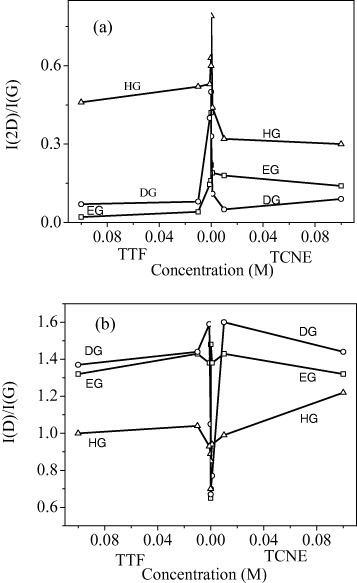
Figure 21.

Open in a new tab

Variation in the (a) 2D/G and (b) D/G intensity ratios with the concentration of TTF and TCNE. (Reproduced with permission from [67] © 2009 Elsevier B. V.)

The variations in the Raman spectra and hence the magnitude of the charge-transfer interaction are the largest for EG and the smallest for HG material. The changes in the bandwidth, intensity and frequency caused by electron donor and acceptor molecules occur sharply, with significant changes at low concentrations. This is probably because of the relatively strong interaction induced by the donor and acceptor molecules of the very first layer compared to the next layers. This study shows the importance of the graphene surface in determining doping effects through molecular charge transfer.

Conclusions

Graphenes with varying number of layers can be prepared using several strategies, but definitive procedures are only available for single-layer graphene. Reduction of single-layer graphene oxide in solution allows easy manipulation and transfer of graphene onto substrates. CVD results in single layers, but they are difficult to remove from the metal surface. Arc discharge of graphite in a hydrogen atmosphere yields graphenes containing 2–3 layers and is suited for doping with boron or nitrogen. It must be noted that there is yet no simple chemical method to produce graphene samples with the desired number of layers. The surface area of graphene depends on the number of layers and the method of preparation, but is generally large (600–1600 m2 g−1). All graphenes seem to be ferromagnetic, independent of the preparation method. The electrical conductivity of graphene decreases with the increasing number of layers and this affects the electrical properties of polymer-graphene composites as well. The electrical conductivity of graphene composites formed with few-layer graphenes increases with increasing graphene content, but shows no percolation, which is characteristic of single-layer graphene. Few-layer graphenes have relatively small thermopower as compared with single-layer graphene; they generally show n-type conduction and field-effect transistors are readily fabricated with them. The best transistor characteristics are exhibited by the graphene prepared by arc discharge of graphite in hydrogen. Few-layer graphenes with the largest surface area interact more strongly with electron-donor and acceptor molecules through molecular charge transfer.

References

  1. Geim A K. and Novoselov K S. Nat. Mater. 2007;6:183. doi: 10.1038/nmat1849. [DOI] [PubMed] [Google Scholar]
  2. Rao C N R, Sood A K, Subrahmanyam K S. and Govindaraj A. Angew. Chem. Int. Ed. 2009;48:7752. doi: 10.1002/anie.200901678. [DOI] [PubMed] [Google Scholar]
  3. Geim A K. Science. 2009;324:1530. doi: 10.1126/science.1158877. [DOI] [PubMed] [Google Scholar]
  4. Rao C N R, Sood A K, Voggu R. and Subrahmanyam K S. J. Phys. Chem. Lett. 2010;1:572. doi: 10.1021/jz9004174. [DOI] [Google Scholar]
  5. Allen M J, Tung V C. and Kaner R B. Chem. Rev. 2009;110:132. doi: 10.1021/cr900070d. [DOI] [PubMed] [Google Scholar]
  6. Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V. and Firsov A A. Nature. 2005;438:197. doi: 10.1038/nature04233. [DOI] [PubMed] [Google Scholar]
  7. Zhang Y, Tan J W, Stormer H L. and Kim P. Nature. 2005;438:201. doi: 10.1038/nature04235. [DOI] [PubMed] [Google Scholar]
  8. Novoselov K S, Jiang Z, Zhang Y, Morozov S V, Stormer H L, Zeitler U, Maan J C, Boebinger G S, Kim P. and Geim A K. Science. 2007;315:1379. doi: 10.1126/science.1137201. [DOI] [PubMed] [Google Scholar]
  9. Lee C, Wei X, Kysar J W. and Hone J. Science. 2008;321:385. doi: 10.1126/science.1157996. [DOI] [PubMed] [Google Scholar]
  10. Dreyer D R, Park S, Bielawski C W. and Ruoff R S. Chem. Soc. Rev. 2010;39:228. doi: 10.1039/b917103g. [DOI] [PubMed] [Google Scholar]
  11. Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V. and Firsov A A. Science. 2004;306:666. doi: 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
  12. Park S, An J, Jung I, Piner R D, An S J, Li X, Velamakanni A. and Ruoff R S. Nano Lett. 2009;9:1593. doi: 10.1021/nl803798y. [DOI] [PubMed] [Google Scholar]
  13. Hummers W. and Offeman R E. J. Am. Chem. Soc. 1958;80:1339. doi: 10.1021/ja01539a017. [DOI] [Google Scholar]
  14. Choucair M, Thordarson P. and Stride J A. Nat. Nanotech. 2009;4:30. doi: 10.1038/nnano.2008.365. [DOI] [PubMed] [Google Scholar]
  15. Hernandez Y.et al2008Nat. Nanotech. 3563. 10.1038/nnano.2008.215 [DOI] [PubMed] [Google Scholar]
  16. Lotya M.et al2009J. Am. Chem. Soc. 1313611. 10.1021/ja807449u [DOI] [PubMed] [Google Scholar]
  17. Berger C. et al 2004. J. Phys. Chem. B 108 19912 10.1021/jp040650f [DOI] [Google Scholar]
  18. Rollings E, Gweon G-H, Zhou S Y, Mun B S, McChesney J L, Hussain B S, Fedorov A V, First P N, de Heer W A. and Lanzara A. J. Phys. Chem. Solids. 2006;67:2172. doi: 10.1016/j.jpcs.2006.05.010. [DOI] [Google Scholar]
  19. Emtsev K V.et al2009Nat. Mater. 8203. 10.1038/nmat2382 [DOI] [PubMed] [Google Scholar]
  20. Shelton J C, Patil H R. and Blakely J M. Surf. Sci. 1974;43:493. doi: 10.1016/0039-6028(74)90272-6. [DOI] [Google Scholar]
  21. Isett L C. and Blakely J M. Surf. Sci. 1976;58:397. doi: 10.1016/0039-6028(76)90478-7. [DOI] [Google Scholar]
  22. Eizenberg M. and Blakely J M. Surf. Sci. 1979;82:228. doi: 10.1016/0039-6028(79)90330-3. [DOI] [Google Scholar]
  23. Reina A, Jia X, Ho J, Nezich D, Son H, Bulovic V, Dresselhaus M S. and Kong J. Nano Lett. 2009;9:30. doi: 10.1021/nl801827v. [DOI] [PubMed] [Google Scholar]
  24. Schniepp H C, Li J-L, McAllister M J, Sai H, Herrera-Alonso M, Adamson D H, Prud'homme R K, Car R, Saville D A and Aksay I A. 2006. J. Phys. Chem. B 110 8535 10.1021/jp060936f [DOI] [PubMed] [Google Scholar]
  25. Subrahmanyam K S, Vivekchand S R C, Govindaraj A. and Rao C N R. J. Mater. Chem. 2008;18:1517. doi: 10.1039/b716536f. [DOI] [Google Scholar]
  26. Staudenmaier L. Ber. Dtsch. Chem. Ges. 1898;31:1481. doi: 10.1002/cber.18980310237. [DOI] [Google Scholar]
  27. Stankovich S, Dikin D A, Piner R D, Kohlhaas K A, Kleinhammes A, Jia Y, Wu Y, Nguyen S T. and Ruoff R S. Carbon. 2007;45:1558. doi: 10.1016/j.carbon.2007.02.034. [DOI] [Google Scholar]
  28. Andersson O E, Prasad B L V, Sato H, Enoki T, Hishiyama Y, Kaburagi Y, Yoshikawa M and Bandow S. 1998. Phys. Rev. B 58 16387 10.1103/PhysRevB.58.16387 [DOI] [Google Scholar]
  29. Prasad B L V, Sato H, Enoki T, Hishiyama Y, Kaburagi Y, Rao A M, Eklund P C, Oshida K and Endo M. 2000. Phys. Rev. B 62 11209 10.1103/PhysRevB.62.11209 [DOI] [Google Scholar]
  30. Subrahmanyam K S, Panchakarla L S, Govindaraj A and Rao C N R. 2009. J. Phys. Chem. C 113 4257 10.1021/jp900791y [DOI] [Google Scholar]
  31. Seshadri R, Govindaraj A, Aiyer H N, Sen R, Subbanna G N, Raju A R. and Rao C N R. Curr. Sci. 1994;66:839. [Google Scholar]
  32. Panchakarla L S, Subrahmanyam K S, Saha S K, Govindaraj A, Krishnamurthy H R, Waghmare U V. and Rao C N R. Adv. Mater. 2009;21:4726. [Google Scholar]
  33. Peigney A, Laurent Ch, Flahaut E, Bacsa R R. and Rousset A. Carbon. 2001;39:507. doi: 10.1016/S0008-6223(00)00155-X. [DOI] [Google Scholar]
  34. Ghosh A, Subrahmanyam K S, Krishna K S, Datta S, Govindaraj A, Pati S K and Rao C N R. 2008. J. Phys. Chem. C 112 15704 10.1021/jp805802w [DOI] [Google Scholar]
  35. Nakada K, Fujita M, Dresselhaus G and Dresselhaus M S. 1996. Phys. Rev. B 54 17954 10.1103/PhysRevB.54.17954 [DOI] [PubMed] [Google Scholar]
  36. Enoki T, Kawatsu N, Shibayama Y, Sato H, Kobori R, Maruyama S. and Kaneko K. Polyhedron. 2001;20:1311. doi: 10.1016/S0277-5387(01)00611-8. [DOI] [Google Scholar]
  37. Wakabayashi K, Fujita M, Ajiki H and Sigrist M. 1999. Phys. Rev. B 59 8271 10.1103/PhysRevB.59.8271 [DOI] [Google Scholar]
  38. Enoki T. and Kobayashi Y. J. Mater. Chem. 2005;15:3999. doi: 10.1039/b500274p. [DOI] [Google Scholar]
  39. Enoki T. and Takai K. Dalton Trans. 2008:3773. doi: 10.1039/b800138n. [DOI] [PubMed] [Google Scholar]
  40. Enoki T, Kobayashi Y. and Fukui K. Int. Rev. Phys. Chem. 2007;26:609. doi: 10.1080/01442350701611991. [DOI] [Google Scholar]
  41. Castro E V, Peres N M R, Stauber T. and Silva N A P. Phys. Rev. Lett. 2008;100:186803. doi: 10.1103/PhysRevLett.100.186803. [DOI] [PubMed] [Google Scholar]
  42. Kusakabe K and Maruyama M. 2003. Phys. Rev. B 67 092406 10.1103/PhysRevB.67.092406 [DOI] [Google Scholar]
  43. Lee H, Son Y W, Park N, Han S W and Yu J J. 2005. Phys. Rev. B 72 1745431 [Google Scholar]
  44. Bhowmick S. and Shenoy V B. J. Chem. Phys. 2008;128:244717. doi: 10.1063/1.2943678. [DOI] [PubMed] [Google Scholar]
  45. Yazyev O V. Phys. Rev. Lett. 2008;101:037203. doi: 10.1103/PhysRevLett.101.037203. [DOI] [PubMed] [Google Scholar]
  46. Matte H S S R, Subrahmanyam K S and Rao C N R. 2009. J. Phys. Chem. C 113 9982 10.1021/jp903397u [DOI] [Google Scholar]
  47. Kopelvich Y, Dasilva R R, Torres J H S and Penicaud A. 2003. Phys. Rev. B 68 092408 10.1103/PhysRevB.68.092408 [DOI] [Google Scholar]
  48. Dho J, Kim W S. and Hur N H. Phys. Rev. Lett. 2002;89:027202. doi: 10.1103/PhysRevLett.89.027202. [DOI] [PubMed] [Google Scholar]
  49. Shenoy V B and Rao C N R. 2008. Phil. Trans. R. Soc. A 63 366. [DOI] [PubMed] [Google Scholar]
  50. Ghosh M, Biswas K, Sundaresan A. and Rao C N R. J. Mater. Chem. 2006;16:106. doi: 10.1039/b511920k. [DOI] [Google Scholar]
  51. Dutta S, Lakshmi S and Pati S K. 2008. Phys. Rev. B 77 073412 10.1103/PhysRevB.77.073412 [DOI] [Google Scholar]
  52. Morozov S V, Novoselov K S, Katsnelson M I, Schedin F, Elias D C, Jaszczak J A. and Geim A K. Phys. Rev. Lett. 2008;100:016602. doi: 10.1103/PhysRevLett.100.016602. [DOI] [PubMed] [Google Scholar]
  53. Katsnelson M I. and Geim A K. Phil. Trans. R. Soc. 2008;366:195. doi: 10.1098/rsta.2007.2157. [DOI] [PubMed] [Google Scholar]
  54. Ritter K A. and Lyding J W. Nanotechnology. 2008;19:015704. doi: 10.1088/0957-4484/19/01/015704. [DOI] [PubMed] [Google Scholar]
  55. Son Y, Cohen M L. and Louie S G. Nature. 2006;444:347. doi: 10.1038/nature05180. [DOI] [PubMed] [Google Scholar]
  56. Li X, Wang X, Zhang L, Lee S. and Dai H. Science. 2008;319:1229. doi: 10.1126/science.1150878. [DOI] [PubMed] [Google Scholar]
  57. Wang X, Ouyang Y, Li X, Wang H, Guo J. and Dai H. Phys. Rev. Lett. 2008;100:206803. doi: 10.1103/PhysRevLett.100.206803. [DOI] [PubMed] [Google Scholar]
  58. Meric I, Han M Y, Young A F, Ozyilmaz B, Kim P. and Shepard K L. Nat. Nanotech. 2008;3:654. doi: 10.1038/nnano.2008.268. [DOI] [PubMed] [Google Scholar]
  59. Zuev Y M, Chang W. and Kim P. Phys. Rev. Lett. 2009;102:096807. doi: 10.1103/PhysRevLett.102.096807. [DOI] [PubMed] [Google Scholar]
  60. Late D J, Ghosh A, Subrahmanyam K S, Panchakarla L S, Krupanidhi S B. and Rao C N R. Solid State Commun. 2010;150:734. doi: 10.1016/j.ssc.2010.01.030. [DOI] [Google Scholar]
  61. Prasad K E, Das B, Maitra U, Ramamurty U. and Rao C N R. Proc. Natl Acad. Sci. USA. 2009;106:13186. doi: 10.1073/pnas.0905844106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Ramanathan T.et al2008Nat. Nanotech. 3327. 10.1038/nnano.2008.96 [DOI] [PubMed] [Google Scholar]
  63. Das B, Prasad K E, Ramamurty U. and Rao C N R. Nanotechnology. 2009;20:125705. doi: 10.1088/0957-4484/20/12/125705. [DOI] [PubMed] [Google Scholar]
  64. Stankovich S, Dikin D A, Dommett G H B, Kohlhaas K M, Zimney E J. and Stach E A. Nature. 2006;442:282. doi: 10.1038/nature04969. [DOI] [PubMed] [Google Scholar]
  65. Das A.et al2008Nat. Nanotech. 3210. 10.1038/nnano.2008.67 [DOI] [Google Scholar]
  66. Voggu R, Das B, Rout C S. and Rao C N R. J. Phys.: Condens. Matter. 2008;20:472204. doi: 10.1088/0953-8984/20/47/472204. [DOI] [Google Scholar]
  67. Subrahmanyam K S, Voggu R, Govindaraj A. and Rao C N R. Chem. Phys. Lett. 2009;472:96. doi: 10.1016/j.cplett.2009.03.003. [DOI] [Google Scholar]
  68. Saito R, Jorio A, Souza Filho A G, Dresselhaus G, Dresselhaus M S. and Pimenta M A. Phys. Rev. Lett. 2002;88:02740. doi: 10.1103/PhysRevLett.88.207401. [DOI] [PubMed] [Google Scholar]

Articles from Science and Technology of Advanced Materials are provided here courtesy of National Institute for Materials Science and Taylor & Francis

RESOURCES