X-ray diffraction as a promising tool to characterize bone nanocomposites

Abstract

To understand the characteristics of bone at the tissue level, the structure, organization and mechanical properties of the underlying levels down to the nanoscale as well as their mutual interactions need to be investigated. Such information would help understand changes in the bone properties including stiffness, strength and toughness and provide ways to assess the aged and diseased bones and the development of next generation of bio-inspired materials. X-ray diffraction techniques have gained increased interest in recent years as useful non-destructive tools for investigating the nanostructure of bone. This review provides an overview on the recent progress in this field and briefly introduces the related experimental approach. The application of x-ray diffraction to elucidating the structural and mechanical properties of mineral crystals in bone is reviewed in terms of characterization of in situ strain, residual stress–strain and crystal orientation.

Introduction

The human skeletal system provides rigidity, support and protection to the body. A healthy skeletal system with adequate strength is essential for the overall health and better quality of life. Fractures in bone, traumatic or pathologic, are most common orthopedic problems. Elderly peoples are prone to a common bone disease, called osteoporosis, which increases a risk of bone fracture. Fractures in bone, even simple, often lead to the degradation in physical and mental health. To prevent and cure them, it is important to have knowledge about the mechanical and material status of bone tissue in the body, such as crack generation and propagation, strength, stiffness, toughness, elastic constants, deformation, stress, strain, etc.

Bone is a unique material possessing structural hierarchy at different length scales. In order to properly understand the mechanical properties of bone at the tissue level, it is necessary to have information about the structure, organization and characteristics of the underlying structural components down to the nanoscale, as well as the interaction between different structural levels. Because of the structural complexity in bone, information on bulk properties mostly reflects the tissue strength, fracture or deformation; however, the underlying origins are not known unless the lower-level structures are investigated. Hence, it remains a major challenge to reveal, non-destructively and non-invasively, how the macroscopic bone characteristics are affected by the microstructural behavior. Such knowledge would help understanding bone tissue and developing next generation of biomaterials, biomimetic designs and bio-inspired nanocomposites for engineering and clinical applications. It would also enable proper assessment of aged and diseased bones for osteoporosis (brittle and porous bone), osteopetrosis (highly dense bone), bone tumors and other deceases which affect the stiffness, strength and toughness of bone [1, 2].

The failure analysis of bone tissue based on fracture mechanics approach has provided various insights on the bulk behavior of bone as what mechanisms lead to development and propagation of cracks and microdamage formation [3–8]. Since the origin of failure mostly lies in the basic structural unit, it is obvious that failures in bone initiate in the basic building component called mineralized collagen fibril, formed by the composition and organization of collagen fibers and mineral crystals at the nanoscale level. With the technological advancements, it has become possible to probe these basic components in bone (collagens and minerals) individually and non-destructively. With the growing interest to the bone nanostructure and its importance in the orthopedic research, x-ray diffraction has become an effective technique capable of non-destructive probing the mechanical and structural integrity of bone constituents. In this article, we review recent advances in the application of x-ray diffraction to bone tissue. After a brief introduction of the structural and mechanical aspects of cortical bone, we present recent experimental approaches of x-ray diffraction techniques to elucidate the mechanical interaction between the macrostructure level at bone tissue size and the nanostructure level at molecular size.

Structure and mechanical properties of cortical bone

Hierarchical structure of cortical bone

Bone is a multifunctional biological tissue possessing a hierarchy of structures at different size scales to perform various mechanical, biological, physiological and chemical functions. The geometry and structure of bone are optimized so as to minimize weight, disperse-bearing stresses at the joints, and sustain external loads in the body. Altogether, bone as a structural component has an ideal combination of properties, namely high stiffness, strength, fracture toughness and low weight [9–11]. These properties of bone are attributed to its unique composite characteristics and complex hierarchical structure from the nanoscale to macroscopic scale. However, there is a lack of understanding how such structural hierarchy and the resulting mechanical properties at different size scales affect the overall mechanical behavior of bone.

Figure 1 shows five levels of hierarchical structure in cortical bone [12]. The macrostructure level is defined as the range from 10 mm to several cm, or the whole bone level. Bone tissue consists of two architectural forms: cortical (compact) bone (80% volume of the total skeleton) and cancellous (trabecular or spongy) bone (20% volume) [3]. Cortical bone of the outer core is mostly solid with only 10% of porous fraction. Cancellous bone is coordinated with a trabecular network inside the cortical core, and is found in the metaphysics of long bones and in vertebral bodies. The mechanical properties of bone at the macroscopic level vary within different regions of the same bone.

Figure 1.

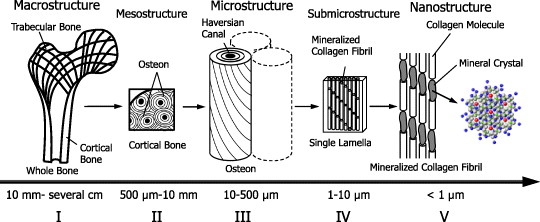
Five levels of hierarchical structure in cortical bone; (I) Macrostructure level (10 mm to several cm), or whole bone level, consisting of cortical and trabecular bone types. (II) Mesostructure level (0.5–10 mm), or cortical bone level. (III) Microstructure level (10–500 μm), single osteon and interstitial lamella level in cortical bone. (IV) Sub-microstructural level, single lamella level (1–10 μm). (V) Nanostructure level (<1 μm), multiphase nanocomposite consisting of an organic phase, an inorganic phase and water.

The next lower level is the mesostructure level (0.5–10 mm), which contains randomly arranged osteons embedded in the interstitial lamella with some resorption cavities.

The microstructure level ranges from 10 to 500 μm and is called the single osteon level or interstitial lamella level. At this level, three different structures are distinguished in cortical bone: osteon, lamellar and woven or plexiform. Osteons are long narrow cylinders consisting of concentric layers of lamellae, which are oriented in different directions surrounding a long hollow Haversian canal. These cylinders are several mm long and 200–300 μm in diameter. In long bones osteons are aligned to the long axis of the bone. Interstitial lamellae, which contain remnants of old osteons, fill spaces between osteons. They have a layered lamellar structure similar to osteons but with a higher degree of mineralization. The next lower level, the sub-microstructure level spanning from one to a few μm are called the single lamella level. Here, mineralized collagen fibrils are oriented in a preferential direction to form a single lamella of thickness 3–7 μm. Lamellae contain ellipsoidal cavities, typically 5–15 μm in cross-section and 25 μm in length.

At the nanostructure level (size less than 1 μm), bone can be considered as a multi-phase nanocomposite consisting of an organic phase (32–44% bone volume), an inorganic phase (33–43% bone volume) and water (15–25% bone volume) [13]. The main element of the organic phase is type I collagen that comprises 90% of the total protein [9]. The inorganic phase consists of nanosized apatite-like mineral crystals, mostly hydroxyapatite (Ca₁₀(PO₄)₆(OH)₂) having a hexagonal lattice structure, and present as plates with an average size of 50×25×3 nm [3]. These mineral crystals are located within the gap-overlap region of staggered patterned collagen fibers and are found to grow with a specific crystalline orientation. The crystallographic c-axis of a mineral crystal coincides with the axis of symmetry parallel to the long dimension of the crystal; it is normal to the (002) lattice plane and has a strong preferred orientation parallel to the long axes of the collagen fibers [14, 15]. The mineral crystals also grow outside the collagen fibers. Together with collagen fibers, these intra- and extra-fibrillar minerals constitute a mineralized fibril structure. The hydroxyapatite crystallites are brittle with low tensile strength, whereas the protein-rich collagen fibers are tough and fairly strong in tension; thus their combination gives bone both high strength and high toughness [16].

Strength of bone

The stiffness and strength of bone are often ascribed to the two-phase composites of bone consisting of apatite minerals and collagen matrix [16, 17]. The mineral phase of bone is stiff and strong but brittle, whereas the collagen phase is soft and highly deformable. The interaction of mineral and collagen in bone is discussed from the concept of a mineral-reinforced collagen matrix, and there is an evidence for a mineral matrix with collagen inclusions [18–22]. The role of water in the overall behavior of bone is also considered important [23]; however, the underlying mechanism is still not clearly understood. The compressive strength of bulk cortical bone in humans is around 170 MPa for the femur, and the elastic compressive modulus is around 17 GPa [24]. Cancellous bone is much weaker, with a strength varying over the bone. Its bulk compressive strengths and elastic modulus are 2.2 and 76 MPa, respectively [24]. Generally, it is useful to consider the variables or parameters that determine the bone material properties as either compositional or organizational [11]. The compositional variables include porosity and mineralization, and the organizational parameters account for structural arrangements in different hierarchies and in different length scales.

Fracture occurrence and propagation in bone are of great interest to the biomechanical and orthopedic researchers. It is generally accepted that bones are well adapted to resist fractures under learned loading conditions of daily activities. Most fractures take place when bone encounters situations beyond their normal situations. The deformation characteristics of bone vary with the loading modes, anisotropy and microcracks developed. The rule of mixtures approach does not provide correct estimate for the elastic properties of bone. The results of data for individual hierarchies, whether at the fibrillar, osteon or tissue levels, do not supply uniformly applicable answers for the whole bone. The presence of mineral crystals within the fibers distinguishes bone from the normal composite structure. The effect of mechanical loading varies for different hierarchical levels of bone and depends on the structure, such as lamella or crystal grains.

Deformation mechanisms in bone

The nanoscale deformation in bone is governed by the two-phase structure of collagen-mineral composites, and has received increased attention (review article [17]). The mineral crystals grow with the crystallographic c-axes parallel to the long axes of collagen fibers [14, 15]. The presence of such mineral crystals within the fibers had inspired many researchers to directly apply the principles of composite theories to bone. With the model of bone as a two-phase composite of mineral-reinforced collagens [18], discussions on the anisotropic properties of bone continued to the range of orientations of bone axes with stress axes [15, 25–27], microstructures [28] or fracture toughness and crack propagation [6, 7, 29]. The geometrical arrangement of mineral particles is also considered to play an important role, as the tensile stress transmitted through the matrix on the composite may be arising from shear [30, 31]. The toughness of bone composites is further said to arise from glue-like sacrificial bonds in the collagen matrix [32–34], where the ability and duration of reforming such bonds after pulling are correlated with the time needed for the bone to recover its toughness.

Attempts of the theoretical analysis of bone tissue mainly consider the traditional rule of mixtures, mineral particles reinforced composite models, homogenization approach, or multiple length scales modeling [21, 30, 35–37]. The experimental validation of these approaches is still lacking. The initial studies assumed bone as a unidirectional reinforced mineral-collagen composite [18, 26, 38]. This model was later modified considering the orientation distribution of mineral crystals [15, 39, 40]. However, unlike fiber-reinforced engineering composites, there are mixed views about the reinforcing component in bone at the nanoscale level. This uncertainty hinders the direct application of existing theories on engineering composites to bone. The possibilities of inter- and intra-phase interaction and underlying shear or debonding phenomena further complicates the issue.

X-ray diffraction

X-ray diffraction is a widely used non-destructive technique for the characterization of structural properties, crystalline phases, texture and orientation pattern, crystal size, crystallinity and perfection. This section provides a brief introduction to the technique, covering the issues relevant to the article.

When a monochromatic beam of x-ray photons falls onto a given specimen, three basic phenomena may result: scattering, absorption and fluorescence. These phenomena form the bases of three important characterization techniques: x-ray diffraction, radiographic analysis and x-ray fluorescence spectrometry, respectively [41]. The regular arrangement of atoms in crystallites constitutes planes (lattice planes) of high electron density. These atomic electrons scatter a monochromatic beam of x-rays, generating diffraction maxima via interference in scattered light. Hence, x-ray diffraction can provide exact information on the spatial relationships between constituent atoms, which can be defined most explicitly in the crystalline substances where the distribution of atoms consists of periodic repetition. This regularity of the atomic arrangement results in the scattered x-rays canceling each other in most directions, and only in certain directions reinforcement will occur [41, 42]. The diffraction of x-rays from a crystal is described by the Bragg's law:

Here λ is the wavelength of x-ray, n is an integer denoting the order of the reflection, θ is one-half the angle between the incident and scattered x-ray beams and d is the inter-planar spacing.

The higher-energy x-rays in the range 12–120 keV (0.10–0.01 nm wavelength) are classified as hard x-rays, while the lower-energy x-rays in the range 0.12–12 keV (10–0.10 nm wavelength) are called soft x-rays. Soft x-rays can be produced in a laboratory system using an x-ray tube, whereas hard x-rays are selected from synchrotron radiation generated by particle accelerators. Depending on the penetration depth required and type of study, both types of x-ray sources are widely applied. X-rays are considered to behave either as waves or particles, and are treated as waves in x-ray diffraction. Interaction of waves with spatially uncoordinated atoms and ordered atoms is called scattering and diffraction, respectively. The development of two-dimensional detectors, such as imaging plate (IP) and charge coupled device (CCD), resulted in a rapid progress in the techniques and widening of application areas of x-ray diffraction.

X-ray diffraction analysis has been extensively employed in the study of biological systems, especially in the geometrical description of their molecular components. The importance of x-ray diffraction analysis in the study of mineralized tissue is also known to some extent. De Jong [43] was the first to apply x-ray diffraction to bone and establish the mineral phase of bone tissue as hydroxyapatite. In addition to the revelation about the nature of the bone mineral phase, the method has played an important role in interpreting the structure of the principal protein component of bone, collagens. X-ray diffraction patterns of pure hydroxyapatite and bone minerals are compared in figure 2 [44]. The different peaks represent diffraction from lattice planes of the crystals. The periodic arrangement of atoms in mineral crystals and periodicity of the gap-overlap region in collagen fibers provide the effective use of x-ray diffraction for the study of bone nanostructure [45–47]. Characterization of the structure and deformation of mineral crystals and collagen fibers under load is possible in wide and small-angle regimes, respectively. Because of their non-destructive and non-invasive properties, x-rays are widely used to study crystalline materials, but are rarely applied to biological tissue like bone. Despite a long history of attempts on the ultrastructural characterization of bone [14, 15, 41, 43, 45, 48–52], there are only few reports on the change in lattice parameters with simultaneous loading of bone specimens, which is discussed in the following section.

Figure 2.

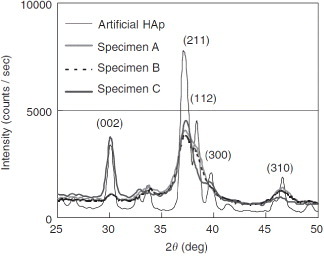
X-ray diffraction patterns of cortical specimens, harvested from bovine femoral shaft along the axial (A), circumferential (B) and radial (C) directions, are compared with the pattern of artificial hydroxyapatite crystals. The low crystallinity and the effect of orientation can be observed in bone patterns. (Reprinted with permission from [44] © 2006 Elsevier Ltd.)

X-ray diffraction techniques for in-situ studies of structure and deformation of bone

In-situ strain measurement

X-ray diffraction is widely used to determine the in situ strains in a material, where the crystalline planes are considered as strain gauges. The measurement of lattice strains and their relation to stresses follow from the classical theory of elasticity. In a polycrystalline sample, x-rays are diffracted by a family of crystallographic planes, forming series of diffraction cones. These cones appear as circular intensity rings in the transmitted diffracted beams, known as Debye rings; they are recorded with a two-dimensional detector placed normal to the incident beam (figure 3). Application of stress changes the interplanar distance, resulting in the distortion of these Debye rings at the detector. The amount of distortion in the direction of applied stress gives the estimate of lattice strain. The schematic of strain measurement using a loading device is shown in figure 3(a). Using the Bragg's law (equation (1)), the interplanar spacing (d) and corresponding lattice strain can be estimated from the deformation of a particular Debye ring along the considered direction as follows:

Figure 3.

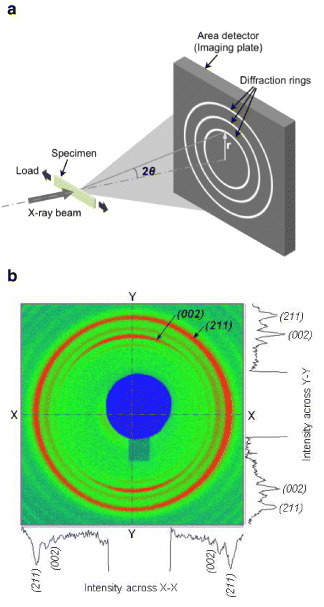
(a) Schematic of x-ray diffraction experiment in transmission mode using the area detector. (b) Two-dimensional diffraction pattern recorded in the detector. The intensity rings represent diffractions from different lattice planes of the crystal.

Here, the sub-script ‘0’ indicates values at unloaded (initial) state.

The x-ray diffraction pattern of a crystalline phase contains most information about its structure. Peaks representing the lattice planes are observed depending on the distribution, crystallinity and alignment of the crystals. A number of mathematical functions can be used to fit the experimental diffracted intensity profile near the peaks, such as Gaussian, Lorentzian, Voigt, Pseudo-Voigt, Pearson, Rietveld refinement, etc [41, 42, 53, 54]. These functions work well for the perfect and pure crystalline structures, where the diffraction peaks are sharp and distinct. However, the mineral particles in bone are several forms of apatite (mostly hydroxyapatite) having lower crystallinity [55, 56]. Therefore, while diffraction profiles of bone mineral crystals have characteristics close to the apatite crystals, they lack distinct peaks (figures 2 and 4(a)).

Figure 4.

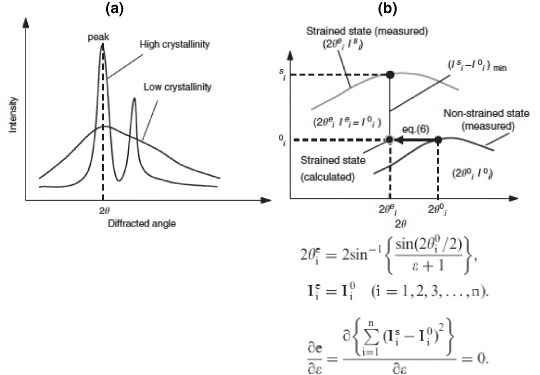
(a) An illustration of x-ray diffraction profiles showing that materials with high crystallinity have sharper peaks compared to low-crystallinity materials. The profile of mineral crystals in bone tissue is broad mainly because of low crystallinity. (b) Profile-shift method: the strained state point is estimated from non-strained state profile and compared to the strain state profile. Differences between the estimated and measured points on the strained state profile were used for strain evaluation. (Reprinted with permission from [44] © 2006 Elsevier Ltd.)

The quantification of shift in diffraction peaks, which results from deformation of lattice spacing due to load, is critical for strain estimation. When there is preferred orientation of the crystals and the region of interest is aligned to that direction, it is preferable to consider the lattice plane corresponding to that direction. For instance, a (00 l) plane representing the c-axis (longitudinal) orientation of the crystals is widely used in the case of hexagonal crystal system like bone to analyze the deformation and orientation characteristics [14]. However, if the crystals are randomly oriented, the region of interest is not aligned to the preferred orientation, or the x-ray exposure is too short, the diffracted intensity becomes weak and the diffraction profile may lack distinct peaks. In such situations, it is advantageous to consider a lattice plane providing regular distribution in all orientation directions irrespective of the preferred orientation (like (211) plane). Specific to the application to bone, Fujisaki et al [44] proposed a novel method of quantifying the shift in diffraction profile using the integrated shifts in the segment of the profile to measure the change in lattice spacing of apatite crystals. Figure 4(b) illustrates this approach, called segmental-shift method, and is presented in detail in [44]. This approach was demonstrated to provide higher degree of accuracy of measurement both in the case of linear detector (scintillation counter, figure 5(b)) [44, 57] and area detector (figures 5(a) and (b)) [58] compared to other widely used approaches [41, 53].

Figure 5.

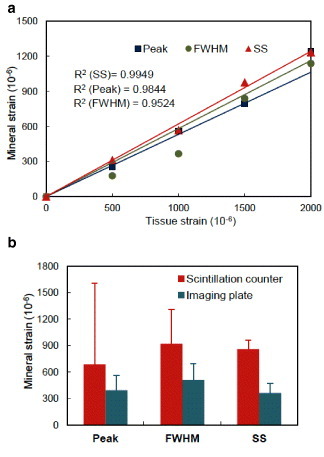
(a) Correlation between applied tissue strain and measured mineral strain. Segmental-shift approach for bone tissue [44] gives closer relationship having lower R² value. (b) Comparison of mineral strain along loading direction with the previous results using scintillation counter [44] at applied strain of 0.001. A similar standard error range in the case of imaging plate was observed by the segmental-shift (SS) method. Lower standard errors were obtained in the case of imaging plate for all the three approaches (n=5). (Plotted with permission from [58] © 2006 Elsevier Ltd.)

Deformation of mineral crystals

The studies on the deformation of bone at the tissue level are extensive and well documented. The application of x-ray diffraction to the study of deformation of bone at the nanoscale level was initiated by Sasaki and co-workers [59, 60], Tadano and co-workers [61, 62] and Fratzl et al and [17, 49]. With the progress in synchrotron x-ray diffraction in recent years, interests are growing in this area with some notable experimental outcomes. Followed by the work of Borsato and Sasaki [59] who estimated stress concentration in bone minerals, the work by Almer and Stock [63] provided some additional insights on the deformation of mineral crystals and its measurements using x-ray diffraction techniques. This study well documented the applicable advantages of x-ray diffraction from fundamentals on lattice deformation, texture and profile broadening. The measurements were facilitated by the introduction of area detector, which allows direct observation of strain evolution of the mineral crystals in all orientations under different external loads (figure 6) [58, 63]. Further to this, a simultaneous quantification of the mechanical properties of bone mineral and collagen fibers become possible using the diffraction patterns in wide-angle and small-angle scattering regimes [46, 47, 64]. The nonlinearity in both the mineral and collagen strains were observed after the yield point in these reports, exhibiting significantly higher applied strains compared to the individual strains in mineral and collagen. However, difference in deformation behavior before and after yielding was observed, when using different loading modes. These studies reported different values of strain in collagen and minerals compared to the applied strain 000; however, the results are difficult to compare because they were obtained on different species under different loading modes. Dong et al [64] used an alternative loading protocol to a continuously loaded case [46, 47], where the samples went through relaxation stages after every loading stage before proceeding to the next strain level. These studies provided novel insights on bone deformation at the nanoscale level.

Figure 6.

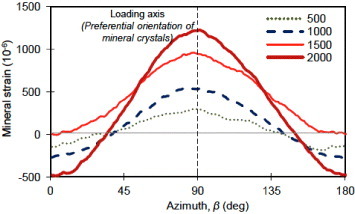
Distribution of mineral strain along the azimuthal directions derived from the segmental-shift approach. Crystal strain along different orientation can be visualized using the area detector (IP) under different applied loads. Loading axis is along the preferential orientation of mineral crystals. The zero-strain line separates tensile and compressive regions. (Reprinted with permission from [58] © 2008 Elsevier Ltd.)

On the basis of simultaneous observation of tissue, fibrillar and mineral strains, Gupta et al [47] suggested the existence of significant interfibrillar shear or sliding based on the previously proposed model [30]. Dong et al [64] speculated on the importance of mineral crystals and collagen fibers oriented off-axis to the loading direction, the shear deformation of which might contribute to the bulk yielding of bone. The orientation of mineral crystals and their volume fraction distribution could be other important factors governing the nanoscale deformation behavior. Considering the deformation of different lattice planes (i.e. crystallites lattice alignment), it was found that mineral strains and elastic moduli vary from plane to plane [46, 57]. This result suggested the anisotropy and orientation distribution of mineral crystals might be crucial in the overall average deformation. The role of orientation distribution determining the structural anisotropy at the nanoscale level was further clarified by loading the specimens having different orientations of mineral crystals (figure 7) [65]. This example illustrates the important ability of x-ray diffraction technique to reveal local deformations. The differences in the local deformation of mineral crystals along different orthogonal planes (or directions) were also observed in trabecular bone [66, 67]. It is also informative to evaluate the local deformation of mineral crystals (and collagen fibers) in identical samples under different bulk loadings and the same environmental conditions to address the discrepancy discussed earlier [46, 47, 64]. A preliminary study comparing the tension and compression loading modes reported different mineral crystals behaviors. In addition to strains, other factors like diffraction profile broadening were also considered to see how defects in the crystals might evolve upon loading [63, 65]. Combing all these factors obtained through x-ray diffraction techniques, it might become possible to clarify the issues related to the local and bulk behavior in bone and their interrelationship.

Figure 7.

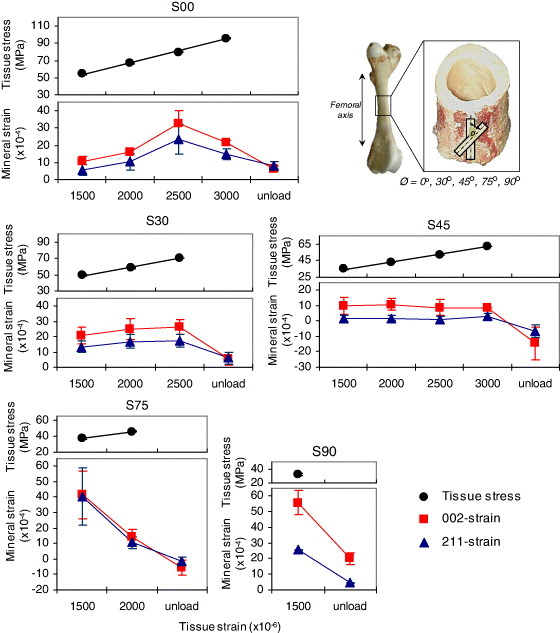
Tissue stresses and mineral strains plotted for different applied strains and structural anisotropy cases. The straight lines for the tissue stresses represent linear fits (within R²=0.99). The figure presents variations in the deformation characteristics of mineral crystals. The error bars represent standard deviations for different trial combinations. (Plots reprinted with permission from [65] © 2009 Elsevier Ltd.)

Residual stress–strain measurement

Another useful application of x-ray diffraction is estimation of residual stress–strain in materials. Residual stress–strain is defined as the stress–strain that remains in a material when external forces acting on it have been removed. The existence of residual stress–strain in engineering structures has high importance and generates both positive and negative effects. Using diffraction principles, change in the interplanar spacing can be calculated to provide strain of the surface layer, and knowing the elastic constants of the material used, the residual stress can then be determined. In general, during the measurement of surface strains, plane stress conditions are assumed to exist, and only two principal stresses lying within the plane of the surface are used, neglecting the stress normal to the surface. Hence, from the theory of elasticity, the basic equation relating lattice spacing d to stress is [53, 54]:

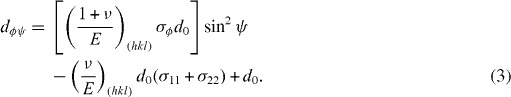Here, ψ is the inclination angle between the normal direction of the specimen surface and the diffracting lattice plane, φ is the azimuthal angle in the surface plane relatively to some chosen direction, ν is Poisson's ratio, E is Young's modulus, and σ₁₁ and σ₂₂ are stress components.

In a typical stress determination, the lattice parameter d is calculated for more than two sample orientations ψ and plotted against sin²ψ. From the slope of linear fit, the corresponding stress is obtained without requiring the knowledge of lattice spacing d₀ in the unstressed state. Application of this method, known as the sin²ψ technique, with the two-dimensional detector requires extraction of one-dimensional profile. The width of a particular Debye ring has been shown to yield similar relationship with sin²ψ as that of lattice spacing d [68]. But the advantage of using two-dimensional detector is that multiple d-spacing values can be obtained by extracting one-dimensional profiles along different azimuthal directions from a single diffraction pattern. From another approach, a direct relationship between the diffraction data around the whole Debye ring and the lattice strain tensors can be obtained by combining the elastic theory and Bragg's relation for any sample and detector orientation [69]. The information from sample orientation, diffraction cone orientation and diffraction cone distortion allows the determination of stress or strain.

The concept of residual stress–strain does not have long history for biological tissues [61, 62, 70, 71]. Also in the case of bone, during remodeling process the old tissue is replaced by the new tissue with the construction of osteons [72]. Since the new tissue is generated under in vivo loading as a non-deformed state, an indeterminate structure may be generated as a result of differences in the deformation of the old and new phases. Further, the mechanical properties (e.g. elastic modulus) are also different in these phases [73, 74]. Because of such nonuniform structures in bone tissue, residual stress–strain may remain in the replaced region even without external forces being applied. Tadano and co-workers initiated efforts to estimate residual stress–strain in cortical bone [61, 62]. Among a very few applications with bone, researchers have successfully applied x-ray diffraction to quantify residual stresses at the bone surface: Tadano and Okoshi [75] reported the existence of residual stress in rabbit tibiofibula and Todoh et al [62] measured the anisotropic residual stress in bovine femoral shaft. Site-specific residual strain characteristics in relation with the mineral crystals orientation were studied [76], and the effect of hydration–dehydration on generating residual stress in bone was reported in [46]. The sin²ψ method illustrated in figure 8 was applied to estimate residual stresses in bovine femur [77] and rabbit extremities [78]. From the distribution of residual stress in the rabbit limb bones (figure 9), tensile residual stresses were observed at every position. Furthermore, the hindlimb bones were found to possess the tensile residual stress 1.4 times higher than that in the forelimb bones. In the femur, the residual stress at the anterior position was observed to be larger than at the posterior position, while in the tibia the stress at the posterior position was larger than at the anterior position. In the forelimb bones, the residual stress at the anterior positions was larger than at the posterior positions.

Figure 8.

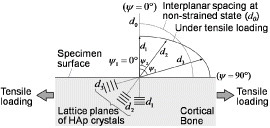
An illustration of residual stress–strain measurement using the sin²ψ method. When bone tissue deforms, the interplanar spacing d of the mineral crystals in the tissue changes. The angle of inclination ψ is defined as the angle between the normal direction of the specimen surface and the diffracted lattice plane. The interplanar spacing in lattice planes under tensile stress is larger in the ψ=90° than in ψ=0° direction. The relation between d and ψ is affected by the stress intensity. (Reprinted with permission from [77] © 2010 ASME.)

Figure 9.

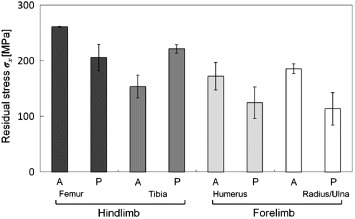
Distribution of residual stresses in rabbit limb bones: femur, tibia/fibula, humerus and radius/ulna. ‘A’ and ‘P’ indicate the anterior and posterior positions in each limb bone, respectively. (Reprinted with permission from [78] © 2009 Elsevier Ltd.)

The relationship between residual stress and density of osteons on the respective sites has also been studied [78]. The photographs in figure 10(a) show areas in rabbit hind limb bones which were characterized by x-ray measurements [78]. Numbers of osteons were counted to establish the osteon population densities (OPD), which were calculated in the cortical surface region at the indicated areas. In the femur, there were more osteons in the anterior position than the posterior positions. The residual stresses were correlated with the OPD; hence, the mechanism of residual stress occurrence would affect the microstructure of osteons. Further, using high-energy synchrotron radiation (SPring-8, Japan), the residual stress was detected from the surface to deep depths, and the distribution along the depth to 10 mm of a bovine femoral diaphysis was observed [79].

Figure 10.

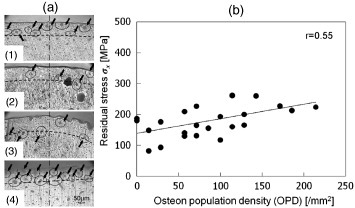
(a) Microscopic images showing the x-ray measurement positions in the hindlimb bones: (1) anterior in the femur, (2) posterior in the femur, (3) anterior in the tibia and (4) posterior in the tibia of the same limb. The top part of the images shows the outer side of the diaphysis. The dashed lines show a depth from the surface of about 100 μm, and the black arrows indicate osteons. (b) Relationship between the residual stress and the OPD in the rabbit limb bones. The correlation is positive (r=0.55, P<0.01). (Reprinted with permission from [78] © 2010 Elsevier Ltd.)

Thus, the knowledge about residual stress–strain in bone, related with mineral crystals distribution and osteon density, might play an important role in the biomechanical aspects of bone healing and remodeling.

Orientation of mineral crystals

The transmitted intensity patterns obtained with a two-dimensional area detector in an x-ray diffraction imaging system provides much more information about the sample including the knowledge about texture variation. Because of the preferred orientation of the crystals, the intensity along the diffracted rings becomes uneven and arc-like. As explained in previous sections, the (002) lattice plane has sharper reflection compared to other planes and provides an estimate of the preferential direction, i.e. the alignment of crystallites within the examined area (figure 3(b)). The diffracted intensity pattern from the polycrystalline aggregates hence can be useful in characterizing the spatial arrangement and orientation of the crystals. X-ray pole figure analysis is a popular tool in the texture characterization [14, 80–82] and the orientation patterns of collagen fibers in bone are well documented [83–88]. The texture analysis of mineral crystals using x-ray pole figure reveals that the mineral crystals are oriented not only parallel to the long axis of bone but also in other directions [80, 82], and that the orientations of mineralized fibrils form a spiral around the central axis, exhibiting varying orientation angles in different lamellae [81, 89]. The application of micro-focus beam enabled localized mapping of bone mineral crystals [90]. By mapping the preferred orientation of mineral crystals around bovine femoral hole, the site-specific characteristics of crystals orientation have been revealed [76, 91]. While the mineral crystals are generally expected to align to the long bone axis, the alignment was deteriorating when approaching the foramen region, becoming tangential at the edge of the hole (figure 11(a)) [76]. The crystals make a tailored structure around the foramen following the hole geometry. Comparing the orientation tendency of apatite crystals between the site of femoral foramen (where axial loading is prevalent) and vertebral foramen (where irregular loading is expected), it is clear that the mineral organization is highly influenced by the load experienced by the site. However, these crystals also play a major role in protecting the internal body structures by reinforcing them. Using the intensity variation of the 002 reflection in the two-dimensional diffraction pattern, a simplified way was proposed to quantify the effective amount of mineral crystals along any reference direction [65, 76]. The distribution function of crystals was presented in terms of degree of orientation (DO) by a mathematical expression, which describes the extent of orientation of the crystals in terms of 〈cos²α〉 with respect to a reference direction [92]:

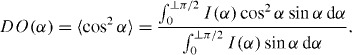Figure 11.

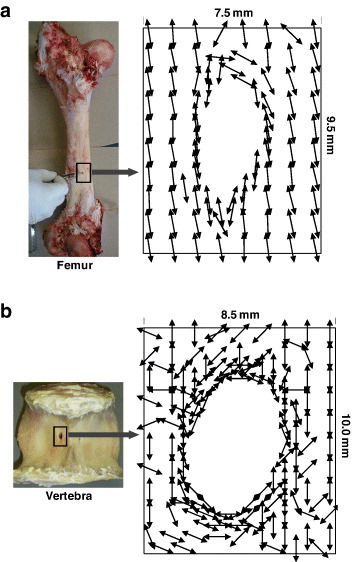
Mapping of the preferential orientation direction of crystallites around the foramen determined from the 002 reflection. (a) Femoral foramen case: the crystals are diverted around the edge according to the geometry of the hole; they are oriented along the bone axis away from the hole. (b) Vertebral foramen case: the crystals make tailored structure around the edge of the hole similar to femoral foramen, but have random orientation away from the hole. (Replotted with permission from [76] © 2008 Elsevier Ltd.)

Here, I(α) is the radial integrated intensity along azimuthal directions and α is the angle with reference to any direction considered. The DO approaches 1 (0) if the orientation direction is parallel (perpendicular) to the reference direction. This parameter had been used to determine the degree of compliance and stiffness in bone samples and analyze corresponding mechanical characteristics—to address the site-specific adaptation [76] and deformation dependent on structural anisotropy [65].

Summary

The combination of two different components in bone, a stretchable fibrous protein and a brittle mineral phase, results in a very strong and tough material. The synthesis and functions of such material have been of wide interest to the scientific community. With the increasing attention to bone nanocomposites, various investigations have been performed to reveal the characteristics of their organic and inorganic components. It has further become apparent that the bone mineral density alone does not determine the strength of bone as a whole [1, 2, 93, 94]. In addition to the mineral density, there are other characteristics associated with mineral crystals including their shape, size, perfection, orientation, etc, which might have direct impact on the mechanical properties of bulk bone tissue. The information from the basic structural unit of bone, i.e. mineral-collagen composite would provide a better understanding of the bulk behavior and fragility of the tissue. In this regard, x-ray diffraction has proved to be an effective technique to examine the structural and mechanical characteristic of bone mineral and provide reliable experimental data. This technique has enabled the understanding of the existence and state of residual stress–strain within bone, which can be directly related to the remodeling and adaptation phenomena in bone. This knowledge provides a way to expedite the bone formation and healing processes. Furthermore, the idea about mineral crystals and their organization helps understand the structural integrity in bone and the overall tissue characteristics. Such information is helpful in deducing the mechanical model of bone considering anisotropy and heterogeneity.

In addition to bone, x-ray diffraction technique has also been useful to investigate the structure and mechanical properties of dentin [95, 96]. However, recent studies have questioned the non-perturbing character of x-rays and discussed a possible effect of high-energy x-ray doses on the mechanical properties of bone [97, 98]. Furthermore, in spite of several advantages of high-energy x-ray sources, they are often confined to basic science laboratories and have limited application in clinical studies. Aiming at bringing novel technologies to clinical practice and providing remedies on bone tissue related problems, several studies have emphasized the use of low-energy x-ray sources (see works cited in this article, mostly by Tadano and co-workers). There is still a lot to be achieved; however, recent progress in this field has provided new hopes for future diffraction studies to be used as an effective non-destructive technique and reveal new aspects of bone nanocomposites.