Multi-scale learning based segmentation of glands in digital colonrectal pathology images

Abstract

Digital histopathological images provide detailed spatial information of the tissue at micrometer resolution. Among the available contents in the pathology images, meso-scale information, such as the gland morphology, texture, and distribution, are useful diagnostic features. In this work, focusing on the colon-rectal cancer tissue samples, we propose a multi-scale learning based segmentation scheme for the glands in the colon-rectal digital pathology slides. The algorithm learns the gland and non-gland textures from a set of training images in various scales through a sparse dictionary representation. After the learning step, the dictionaries are used collectively to perform the classification and segmentation for the new image.

1. DESCRIPTION OF PURPOSE

Digital histopathological images provide detailed spatial information of the tissue at micrometer resolution.¹ Among the available contents in the pathology images, meso-scale information, such as the gland morphology, texture, and distribution, are useful diagnostic features.

Researchers in^2–6 design gland and nuclei segmentation algorithms that aid in determining the grading and/or sub-typing of the prostate, breast, and brain cancers. Gland morphology is studied in.^7–9 In gland extraction, one common assumption is that the contours of the glands appear as conic curves in 2D imaging planes.^{10, 11} While this may be a satisfying assumption for normal tissue, for the malignant tissue, however, such a morphological prior does not hold.

In this work, focusing on colon-rectal cancer tissue samples, we propose a multi-scale learning based segmentation scheme for the glands in the colon-rectal digital pathology slides. The algorithm learns the gland and non-gland textures from a set of training images in various scales through a sparse dictionary representation, regardless of the tissue type (benign vs malignant). After the learning step, the dictionaries are used collectively to perform the classification and segmentation for the new image.

2. METHOD

In,¹² a sparse dictionary approach is employed for extracting texture features from the foreground and background, for the purpose of interactive segmentation. In digital pathology images, it is noted that certain images features can be captured in a multi-scale fashion. As a result, we extend the sparse dictionary representation based segmentation into a multi-scale framework.

Specifically, denote the training images as

$$I_i:{ℝ}^2\to {ℝ}^3,i=1,\dots ,N$$ (1)

Their corresponding ground truth segmentations are

$$L_i:{ℝ}^2\to \{0,1\}$$ (2)

where 1 indicates the gland region. Then, M₀ image patches of the size m × m are sampled, with replacement and overlapping, from the training images.¹³ A 3-channel RGB patch is denoted as

$$\begin{array}{r}{g}_i,t_i\in {ℝ}^{m\times m\times 3}\\ \text{with}i=1,\dots ,M_0\end{array}$$ (3)

where g_i is from gland region and t_i is non-gland. Such a sample-with-replacement strategy successfully enlarges the sample set and reduces the estimation variance. All the patches are grouped into two categories: gland and non-gland. Denote the patch list of the gland tissue as

$$G_0=\{g_i\in {ℝ}^{3m^2};i=1,\dots ,M_0\}$$ (4)

and the non-gland tissue has the list

$$T_0=\{t_i\in {ℝ}^{3m^2};i=1,\dots ,M_0\}$$ (5)

Here, we slightly abuse the notation such that g_i, t_i ∈ ℝ^3m2 are vectors.

With the two lists of patches (vectors), the K-SVD algorithm is used to learn the underlining structure of the texture space as in Algorithm 1¹⁴

Algorithm 1.

K-SVD Dictionary Construction

1:	Initialize $D_0^g$ (T0 resp.)
2:	repeat
3:	Find sparse coefficients Γ (γi’s) using any pursuit algorithm.
4:	for j = 1, …, d0, update fj, the j-th column of $D_0^g$ (T0 resp.), by the following process do
5:	Find the group of vectors that use this atom: ζj:= {i : 1 ≤ i ≤ d0, γi(j) ≠ 0}
6:	Compute $E_j:=Q-{\sum }_{i\ne j}{\mathit{f}}_i{\mathrm{\Gamma }}_T^i$ where ${\mathrm{\Gamma }}_T^i$ is the i-th row of Γ
7:	Extract the i-th columns in Ej, where i ∈ ζj, to form $E_j^R$
8:	Apply SVD to get $E_j^R=U\mathrm{\Delta }V$
9:	fj is updated with the first column of U
10:	The non-zeros elements in ${\mathrm{\Gamma }}_T^j$ is updated with the first column of V × Δ(1, 1)
11:	end for
12:	until Convergence criteria is met

The over-complete basis for G₀ (T₀ resp.) is denoted as

$$\begin{array}{r}{D}_0^g\in {ℝ}^{3m^2\times d_0},D_0^t\in {ℝ}^{3m^2\times d_0}\\ \text{with}{d}_0\gg 3m^2\end{array}$$ (6)

Such a dictionary construction is performed in the highest (native) resolution of the image. In order to better capture the texture information at various scales, wavelet decomposition is performed on the I_i’s, and the learning is performed at each decomposition level. More explicitly, let the original image be at level 0, then level i ≥ 1 is the 2ⁱ down-sampled version of the original image. In all the levels, the same patch size is used for learning. Equivalently, the same patch will cover bigger tissue region and therefore capture larger scale information of the image texture. The dictionaries (gland and non-gland) in the i-th level are denoted as $D_i^g$ and $D_i^t$, with i ≥ 0.

After the gland and non-gland dictionaries at all levels have been constructed, we perform classification on the patches in the given image to be segmented. The classification is also performed in a multi-scale fashion, which is detailed as follows.

At the original resolution, given a new image patch g : ℝ^m×m → ℝ³, by slightly abuse of notation, we also consider g as a 3m² dimensional vector. Then, we compute the sparse coefficient η of g, with respect to the dictionary $D_0^g$.

$$\begin{array}{r}\underset{\mathit{\eta }}{min}{\Vert g-D_0^g·\mathit{\eta }\Vert }_2\le \epsilon \\ \text{s.t.}{\Vert \mathit{\eta }\Vert }_0\le k\end{array}$$ (7)

where k is the sparsity constraint. The reconstruction error is defined as

$$e_0^g:={\Vert g-D_0^g·\mathit{\eta }\Vert }_2$$ (8)

This problem is solved by the Orthogonal Matching Pursuit (OMP) method.¹⁵ Similarly, the sparse coefficient ξ of g under the dictionary $D_0^t$ is also computed as:

$$\begin{array}{r}\underset{\mathit{\xi }}{min}{\Vert g-D_0^t·\mathit{\xi }\Vert }_2\le \epsilon \\ \text{s.t.}{\Vert \mathit{\xi }\Vert }_0\le k\end{array}$$ (9)

The reconstruction error is defined as:

$$e_0^t:={\Vert g-D_0^t·\mathit{\xi }\Vert }_2$$ (10)

Moreover, we define

$$e_0:=e_0^g-e_0^t$$ (11)

It is noted that the errors $e_0^g$ and $e_0^t$ indicate how well (or how bad) the new image patch can be reconstructed from information learned from the gland and non-gland region. Hence, the higher the e₀ is, the more this patch is considered as the non-gland region and vice versa. Furthermore, for each pixel (x, y) ∈ Ω, a patch p(x, y) is extracted as the sub-region of I defined on [x, x + m] × [y, y + m]. Following the procedure above, we compute the image e₀(x, y) accordingly. A probability map P₀(x, y) for the gland region is defined as

$$P_0(x,y)=\frac{1}{1+exp(-e_0(x,y))}$$ (12)

Such procedure is performed for all the scales and a series of probability maps P_i(x, y) with i = 0, 1, …, L are constructed. Note that each P_i(x, y) is reconstructed to the original scale (with all detail coefficients set to 0) and is therefore of the same size as P₀. Finally, define

$$P(x,y)=\underset{l=0}{\overset{L}{max}}{P}_l(x,y)$$ (13)

as the maximum response along the scale dimension. The final probability is threshold at 0.5 for the final mask of gland region.

3. EXPERIMENTS AND RESULTS

80 images are extracted from The Cancer Genome Atlas (TCGA) colon-rectal digital pathology diagnosis images. The resolution is 0.5μm/pixel. The image sizes are all 1024×1024 pixels.

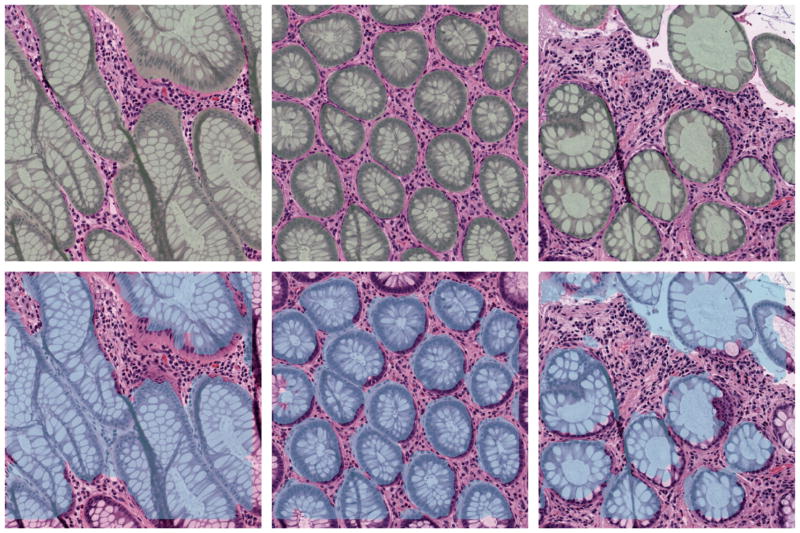
Three randomly picked results are shown in Figure 1. The top row shows the image with the shading indicating the manual segmentation. The corresponding panel below shows the proposed automatic segmentation results.

Figure 1.

Segmentation on three benign tissues patches.

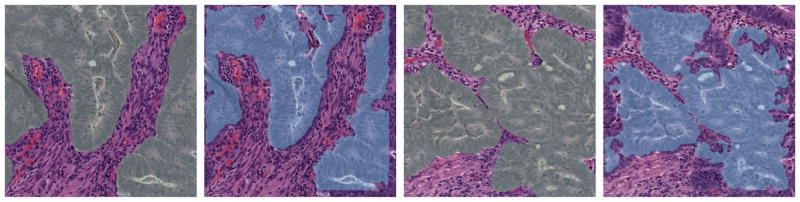
In addition to the benign tissue, the algorithm also performs consistently on malignant tissue, as shown in Figure 2. Here two cases are shown from left to the right: The first/third are the manual segmentation and the second/forth are the algorithm outputs.

Figure 2.

Segmentation on two malignant tissues patches.

Quantitatively, a leave-one-out scheme is performed for testing. Specifically, the 79 images and their manual segmentations are used for learning. The learned model is then applied on the left-out image. The Dice coefficient is measured for all the 80 cases and a mean of 0.81 accuracy (0.056 standard deviation) is achieved. Moreover, the Hausdorff distance is measured and a mean of 70μm (10.0μm standard deviation) is achieved.

4. CONCLUSION AND FUTURE RESEARCH DIRECTIONS

In this work, we propose a multi-scale learning based segmentation scheme for the glands in the colon-rectal digital pathology slides. The algorithm learns the gland and non-gland textures from a set of training images in various scales through a sparse dictionary representation. After the learning, the dictionaries are used collectively to perform the classification and segmentation for the new image.

More recently, the deep neural network (DNN) framework is becoming more and more widely adopted, including for the task of gland segmentation.^{16, 17} The DNN framework has the advantage that minimal manually curated features are needed for the classification process. The proposed framework utilizes the sparse dictionary for the learning and feature extraction. However, the signal sparse reconstruction based on dictionary is a linear combination. DNN harnesses the hierarchical nonlinear transformation and may result in better performance. The ongoing research include combining the manually designed features with the DNN based features, for a better overall performance.

The work has not been submitted for publication or presentation elsewhere.