Modeling the Co-Development of Correlated Processes with Longitudinal and Cross-Construct Effects

Abstract

Conceptualizations of developmental trends are driven by the particular method used to analyze the period of change of interest. Various techniques exist to analyze developmental data, including: individual growth curve analysis in both observed and latent frameworks, cross-lagged regression to assess interrelations among variables, and multilevel frameworks that consider time as nested within individual. In this paper, we report on findings from a latent change score analysis of oral reading fluency and reading comprehension data from a longitudinal sample of approximately 16,000 students from first to fourth grade. Results highlight the utility of latent change score models compared to alternative specifications of linear and non-linear quadratic latent growth models, as well as implications for modeling change with correlated traits.

Measuring change over time is not only ubiquitous to developmental research, it is essential. A scan of the developmental literature demonstrates that a plethora of models are available to researchers, yet McArdle (2009) rightly notes that all “repeated measures analyses should start with the question, ‘What is your model for change?’” (p. 601). The answer to this question is predicated on several facets of one’s data, including: the number of data waves in the study, whether the scale of measurement is discrete or continuous, and the nature of distributional characteristics of the scores. When the number of data waves is three, the class of longitudinal models is maximally restricted to linear growth models. With more available time points comes the ability to model curvilinear trends--with the caveat that the increased complexity of nonlinear models based on more time points often also requires more individuals. The scale of measurement for the data impacts the type of model that can be used to estimate one’s developmental trajectory; for example, ordinal data have more restrictive conditions for the identification of growth models than interval data (Hishinuma, Chang, McArdle, & Hamagami, 2012; O’Connell, Logan, Pentimonti, & McCoach, 2013). Though ordinal data are less frequently observed with fluency outcomes, the number of time points and the nature of the distributions of scores are particularly germane to conversations about appropriate models for fluency change.

When extended to longitudinal data, reduced between-time correlations may impact developmental relations such that a mean trajectory for a sample may not best capture change over time. Linear latent growth models include an estimate of average change via the slope, yet it is possible that the mean obfuscates differential change which may occur between two points of time within the period when longitudinal data were collected. It is plausible that in the presence of floor or ceiling effects, change between the first two time points for longitudinal data may significantly differ from change between two later points. The focus of this paper is to introduce the reader to a relatively new latent variable technique, latent change score (hereafter referred to as LCS) modeling (McArdle, 2009), which can be applied to longitudinal data. LCS models differ from traditional individual growth curve analysis. The LCS model estimates trajectories based on an average, latent slope across all time points as well as multiple latent change scores that represent the change between two succeeding time points. The individual linear growth curve model, which is more familiar to developmental psychologists, only estimates a single latent slope. A distinct advantage of the LCS model is that by estimating both an average slope and latent change, one is theoretically able to use latent change scores as a source of understanding individual differences in a more nuanced manner than is allowed by individual growth curve analysis (Grimm, An, McArdle, Zonderman, & Resnick, 2012).

Developmental Contexts

Utilizing LCS modeling to estimate change trajectories for important psychological and educational outcomes has the potential for yielding more theoretically interesting findings about how individuals change. For example, Ahmed, Wagner, and Lopez (2014) used LCS to understand relations between reading and writing from first to fourth grade. The authors noted that the literature was conflicted pertaining to whether the relation between the constructs was uni- or bi-directional and used LCS to test whether cross-lag effects on change scores between constructs were stronger for the uni-directional or bi-directional specifications. Results pointed to a uni-directional model providing the best fit. In a study of the influence of race and divorce on change in child behavior problems (Malone et al., 2004), LCS models revealed that divorce had a greater influence on boy’s change in externalizing behavior problems in middle school but not in elementary school. The magnitude of the effect of divorce was more readily observed by modeling its relation via the latent change score compared to its effect on the average slope factor. Lastly, Moon and Hofferth (2016) used LCS models to test the relation between parental involvement and child effort with growth in reading and math skills for immigrant children. The LCS model was chosen in order to examine specific effects of covariates at different change points over the course of kindergarten to fifth grade. Among the findings reported by the authors, it was observed that parental involvement in kindergarten had a stronger association with change in reading for boys from kindergarten to first grade compared to change from first to third grade, and that involvement in first grade had a greater association with change from first to third than it did on change from third to fifth grade.

Such studies represent a sample of applications of LCS in the literature (see Hawley, Zuroff, Ho, & Blatt, 2006; Hertzog, Dix, Hultsch, & MacDonald; and Quinn, Wagner, Petscher, & Lopez, 2015 for examples related to depression outcomes, memory outcomes, and reading outcomes, respectively), each of which identify how covariates or parallel, developmental changes can be more comprehensively studied using the LCS model for simultaneously measuring average, latent growth across all time points and latent change between two time points of development. Despite the emerging applications of LCS models across various disciplines, a relatively small literature base exists on unpacking the latent change model specification, the potential advantages it may hold in modeling compared to other statistical models for developmental analysis, and highlighting how to use the results for understanding individual growth and sources of influence on change.

In this paper we present the conceptual and mathematical underpinnings of LCS models, how such models compare and contrast with other applications of latent growth/direct effects models, and illustrate how they may be used to model individual differences in change over time using data pertaining to the development of reading comprehension and oral reading fluency. Applying the LCS to these constructs helps to unpack the developmental relations for a few reasons. Although oral reading fluency is a critical skill to develop related to reading comprehension, prior research has demonstrated that floor effects in fluency in the beginning years of reading instruction are common (e.g. Catts et al., 2009) and that the technical adequacy of scores requires further study (Petscher, Cummings, Biancarosa, & Fien, 2013). Thus, estimating oral reading fluency trajectories, even with non-linear models, may mask nuanced trends in both the developmental and individual differences aspects of the model due to the impact of measurement error. Reading comprehension, like other developmentally important outcomes, is a complex skill, influenced by multiple constructs and skills (Kim, Wagner, & Foster, 2011). Oral reading fluency is an excellent predictor of reading comprehension, especially in the early elementary years (Kim, Wagner, & Foster, 2011). Estimating the LCS model to examine the developmental, bidirectional effects of oral reading fluency and reading comprehension, as well as comparing it to other latent growth model specifications, serves a potentially useful example by which to understand the benefits and deficiencies of various longitudinal model specifications.

Perspectives on Growth Models

When presented with longitudinal data, two broad frameworks emerge as conventional methodologies for individual growth curve modeling, namely, multilevel regression and latent variable analysis. Many studies use one of these two approaches, yet as long as the same assumptions are met, the models will yield identical results (Hox, 2000). This observation is due to the fact that the terminology of growth models (e.g., random effects growth models, hierarchical linear growth models, latent growth, mixed effects growth models) muddies the point that the model specification and estimation are often the same (Mehta & Neale, 2005). For example, a multilevel, linear growth model is typically expressed as:

$$\begin{array}{l}{Y}_{ti}={\pi }_{0i}+{\pi }_{1i}(X_{ti})+e_{ti}\\ {\pi }_{0i}={\beta }_{00}+r_{0i}\\ {\pi }_{1i}={\beta }_{10}+r_{1i}\end{array}$$ Eq. 1

where Y_ti is the observed score for student i at time t on measure y, π_0i and π_1i represent the initial status and slope, respectively, for which β₀₀ and β₁₀ are the means corresponding to the status and slope. X_ti represents time and is coded in a manner to reflect the measurement occasions (e.g., 0, 1, 2 for three time points centered at time 1, or −2, −1, 0 for centering at time 3). The r_0i and r_1i coefficients are random effects associated with the initial status and slope parameters, and e_ti is the measurement-level residual. In a similar vein, consider the specification of the same linear growth model expressed in a latent variable framework:

$$\begin{array}{l}{Y}_{ti}={\lambda }_{0t}{\eta }_{0i}+{\lambda }_{1t}{\eta }_{1i}+{\epsilon }_{ti}\\ {\eta }_{0i}={\nu }_0+{\zeta }_{0i}\\ {\eta }_{1i}={\nu }_1+{\zeta }_{1i}.\end{array}$$ Eq. 2

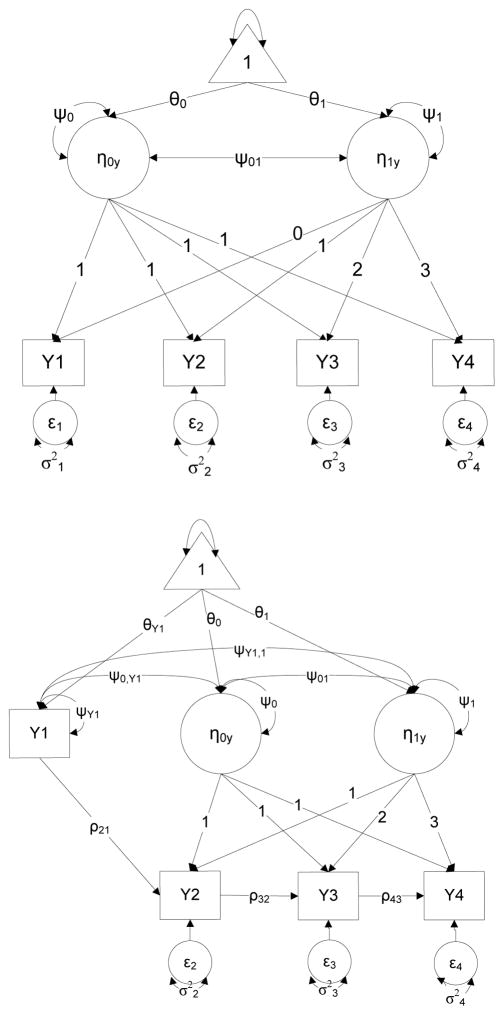
The structures of the multilevel and latent variable equations are nearly identical. The initial status and slope parameters, means, and random effects in the latent framework are characterized with η, ν, and ζ, instead of being represented by the π, β, and r components, as in Equation 1; X_ti from the multilevel regression is replaced by λ_1t. Although λ_1t represents factor loadings, it is coded in the same manner as X_ti from the multilevel regression (e.g., 0, 1, 2 for three time points centered at time 1). λ_0t in the latent variable model represents factor loadings for the intercept, which are constrained to 1 for each of the time points in a model. As noted previously, identical results may be obtained using either the multilevel regression or latent growth curve approach (Stoel, van Den Wittenboer, & Hox, 2004). Equation 2 may be expressed as a measurement model (i.e., Figure 1, top), which includes latent intercept and slope factors (η_0y and η_1y), each of which are indicated by four measurement occasions (Y1–Y4), which in turn are associated with a residual error (ε₁ − ε₄). The intercept and slope factors have associated means (θ₀ and θ₁, respectively), variances (ψ₀ and ψ₁, respectively), and a covariance (ψ₀₁,). This type of model is useful for answering a number of questions pertaining to change over time such as: What is the average rate of change in a measured domain for a sample of individuals? To what extent do individuals within a sample differ in their rate of change? What is the relation between initial status and change over time?

Figure 1.

Sample latent linear growth model (top) and autoregressive latent trajectory model (bottom). η_0y = latent intercept, η_1y = latent slope, ψ₀ = latent intercept variance, ψ₁ = slope variance, ψ_xy = latent covariances, θ₀ = latent intercept mean, θ₁ = latent slope mean, ε_1–4 = observed score residuals, ${\sigma }_{1-4}^2=\text{residual}\text{variances}$..

Although such questions are readily addressed by either multilevel regression or latent variable modeling approaches, a number of limitations exist pertaining to traditional multilevel regression as implemented in many conventional software packages. Structural modeling (i.e., direct and indirect effects) and multivariate longitudinal analysis (e.g., parallel process growth models) are often difficult to directly model in a multilevel regression framework. A latent variable approach allows for such models to be fit as it overcomes the restrictive univariate framework of multilevel regression (Muthén, 2004). An additional strength of latent variable modeling is that multiple constructs may be simultaneously modeled, and each construct may be represented as either continuous or categorical factors. Despite such advantages, individual growth curve analyses and direct/indirect effects modeling have generally been viewed as mutually exclusive approaches to analyzing longitudinal data. That is, although it is possible to model longitudinal data with direct and indirect-effects based structural equation models, or separately, to estimate individual growth curves, few models exist which allow for the simultaneous specification of both for a univariate outcome.

The Latent Change Score Model

Given such limitations, the LCS model (McArdle, 2009; McArdle & Hamagami, 2001; McArdle & Nesselroade, 1994) was developed as one method to combine direct/indirect effects modeling and individual growth curve analysis. Although traditional latent growth curve and multilevel regression analyses are useful in yielding average estimates of change over time, they are frequently limited in that direct/indirect effects cannot be simultaneously modeled with growth for a univariate outcome (i.e., one frequently models either growth or direct/indirect effects) nor can growth be segmented into piecewise “chunks” of change in order to evaluate unique effects of average growth or change. In many aspects of developmental research it is quite plausible that students may change more or less during particular segments of measured growth. When students differentially change, whether due to immediate intensive interventions, measurement sensitivity to skills development, or individual student factors, average estimates of growth may be insufficient for characterizing the nature of the data.

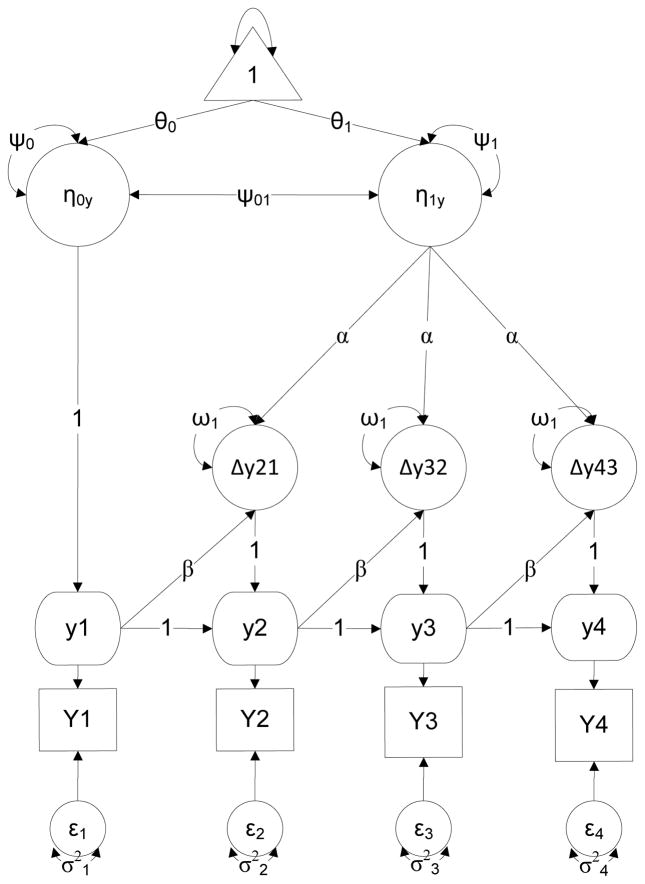
The LCS model is sensitive to such types of developmental change; consider the general structure of a univariate LCS model in Figure 2. Before providing model equations and explication of the underlying components to the model, it is first useful to picture the representation of the LCS model and understand the path and latent components. Similar to the latent linear growth model in Figure 1, there are latent factors for intercept and slope (η_0y and η_1y), observed measures with unique effects for the four time points (Y1–Y4 and ε₁ − ε₄), as well as means (θ₀ and θ₁), variances (ψ₀ and ψ₁), and, and a covariance (ψ₀₁). The unique components of the LCS model include latent factors for the observed measures at each time point (y1–y4), autoregressive effects for the time-specific latent factors (e.g., y2 on y1), latent change score factors (Δy21, Δy32, and Δy43) with associated loadings (α), and proportional change effects (β). To decompose the elements of Figure 2, we first evaluate the direct effects portion of the model, which includes the relations among, for example, the latent constructs of y1, y2, and Δy21. An underlying mechanism of the LCS model lies in its origins in classical test theory, namely, that one’s observed score at a time point (Y_ti) is modeled as a function of an unknown latent true score (y_ti) and a unique score for the individual (e_ti), expressed as:

$$Y_{ti}=y_{ti}+e_{ti}.$$

Figure 2.

Sample univariate dual change score model. η_0y = latent intercept, η_1y = latent slope, ψ₀ = latent intercept variance, ψ₁ = slope variance, ψ₀₁ = latent covariance, θ₀= latent intercept mean, θ₁ = latent slope mean, ε_1–4 = observed score residuals, ${\sigma }_{1-4}^2=\text{residual}\text{variances}$, α = mean constant change, β = auto-proportion coefficient, ω₁= change score variances, Δy_t = latent change scores, y1–y4 factor variances not included in figure.

In Figure 2, Y_ti is represented by the observed scores Y1–Y4, y_ti is expressed via the latent factors y1–y4, and e_ti are the errors ε₁ − ε₄. A simple difference score between two observed time points (ΔY_i) is calculated as the difference between a one time point (Y_ti) and performance at an earlier time point (Y_(t−1)i):

$$\mathrm{\Delta }{Y}_{ti}=Y_{ti}-Y_{(t-1)i}.$$

This observed score equation can be extended to a latent variable model by substituting y_ti for Y_ti:

$$\mathrm{\Delta }{y}_{ti}=y_{ti}-y_{(t-1)i}$$ Eq. 3

which could be rearranged to solve for y_ti instead of the difference score

$$y_{ti}=y_{(t-1)i}+\mathrm{\Delta }{y}_{ti}.$$ Eq. 4

The re-expression of Equation 3 as Equation 4 states that a latent score y for individual i at time t (i.e., y_ti) is comprised of a latent score from a previous time point (y_(t−1)i), and the amount of change that occurs between the two points (Δy_ti). Equation 4 can be viewed in the model of Figure 2 via the latent change score. For example, y_ti could be representative of y2 which is the latent construct at time 2 indicated by observed measure Y2. This latent variable is shown as being the sum of the latent variable y1 (i.e., y_(t−1)i) as well as Δy21, that is the latent change between y2 and y1 (i.e., Δy_ti). Note that the LCS of Δy21 is not directly measured, whereas y1 and y2 are directly measured by Y1 and Y2. Two constraints are included among the relations of these three latent constructs. The first constraint fixes the effect of y1 on y2 at 1.0, and the second constraint has the effect of the change score Δy21 on y2 constrained at 1. Such constraints serve to identify the model as well as allow for the estimation of the LCS mean and variance. Further, with the constraints, the latent change score is characterized as the portion of the y2 score that is not equal to y1 (McArdle and Nesselroade, 1994).

The proportional change effect of β designates the effect of y1 on Δy21 and characterizes the relation between initial status and change for a selected interval of change. When the mean constant change is positive, a positive β coefficient indicates that when accounting for constant change (i.e., latent slope) in the model, individuals with higher scores at y1 changed more between y1 and y2 compared to individuals with lower y1 scores. Conversely, a negative β coefficient when the mean constant change is positive is reflective of individuals with lower y1 scores experiencing greater change between y1 and y2, compared to higher ability individuals at y1. In this way, the β coefficient from Figure 2 represents the direct/indirect effects portion of the univariate LCS model. In a different light, the proportional change parameters can also be conceptualized as the non-linear portion of a latent growth model. A negative value for β indicates, when accounting for constant change (i.e., latent slope) in the model, deceleration in growth relative to the previous time point, whereby a positive value for β indicates acceleration in growth relative to the previous time point. In instances where the mean constant change is negative, individuals can change less in the presence of a positive β. Such interpretational nuances of the LCS parameters underscore the need both for caution when evaluating any individual resulting coefficient and for empirically testing whether β is leading to more or less change based on higher individual scores relative to mean constant change.

The mean constant change portion of the LCS model in Figure 2 is based on the change score loadings associated with the latent slope factor (i.e., α). Note that, different from Figure 1, the latent slope factor η_1y is not indicated by the observed measures but rather by the individual latent change scores. Subsequently, the growth portion of the LCS model is estimated with:

$$y_{ti}={\eta }_0+\mathrm{\sum }(\mathrm{\Delta }{y}_{ti}).$$ Eq. 5

Eqs. 4 and 5 share similarities in that both include an initial status component, y_(t−1)i in Eq. 4 and η₀ in Eq. 5, and both include change scores. The primary difference between the two specifications is that Eq. 5 generalizes the form of Eq. 4 so that the intercept η₀ denotes the individuals’ initial status based on centering (much like η_0i in the latent growth model, Eq. 2), and Σ(Δy_ti) represents the summed LCSs up to time t (Grimm, 2012). Within Figure 2, the three LCSs load on η_1y with α.

When both the growth and direct/indirect effects portions of α and β are estimated in the LCS model, it is referred to as a dual change score model; dual in the sense that both constant change (i.e., average change across the change scores) via the α coefficients and proportional change via the β coefficients are simultaneously estimated. When a dual change score model is specified, Eq. 3 is extended to:

$$\mathrm{\Delta }{y}_{ti}=\alpha \ast {\eta }_1+\beta \ast y_{(t-1)i},$$ Eq. 6

and states that LCS Δy at time t for individual i is estimated as a function of the average latent change slope (α * η₁, where α = 1), plus the proportional change (β * y_(t−1)i). It should be noted that even within Eq. 6 it is possible to solely estimate either constant change or proportional change given one’s research interests. Should a primary research question be associated with constant change over time, the β coefficients in Eq. 6 can be fixed to 0. This reduces the dual change model from Eq. 6 to what is termed a constant change model and is estimated with:

$$\mathrm{\Delta }{y}_{ti}=\alpha \ast {\eta }_1.$$

When this occurs, the result of a LCS constant change model will be identical to the latent linear growth curve model in Figure 1. Conversely, when only the proportional change component of the dual change score model is of interest, the α coefficients are fixed to 0, as are the mean and the variance of the latent slope. In this instance, Eq. 4 reduces to:

$$\mathrm{\Delta }{y}_{ti}=\beta \ast y_{(t-1)i}.$$

An alternative approach to the univariate LCS in modeling both autoregressive effects and constant change is known as the autoregressive latent trajectory model (ALT; Figure 1; Bollen & Curran, 2004). Similar to a more traditional latent growth curve model, the ALT specification includes latent intercept and slope factors, and similar to the LCS model, the ALT model includes direct effects between an earlier and a later observation. A few primary distinctions and similarities between the ALT and LCS specifications are worth noting. First, the ALT model is more similar to a basic latent growth curve in the average slope portion of the model. Note that both models in Figure 1 estimate growth as a function of the observed measures. Second, the ALT and LCS models both include autoregressive effects in the model. The ALT does this via the direct paths between time points (ρ) whereas the LCS estimates the autoregressive effects via the β parameter. The differences between ALT and LCS can be viewed in how data at the first time point is treated. In the LCS model of Figure 2, Y1 is viewed as an observed variable indicating the latent variable y1. Moreover, latent variable y1 serves an indicator of the latent intercept η_0y, maintains direct effects on y2 and the change score Δy21, and also informs the slope factor η_1y through its influence on Δy21. In the ALT model of Figure 1, Y1 has a direct effect on Y2 but does not directly inform either the latent intercept or slope factors. Rather, it is specified as covarying with latent intercept and slopes (i.e., η_0y and η_1y).

Latent Change Score Multivariate Considerations

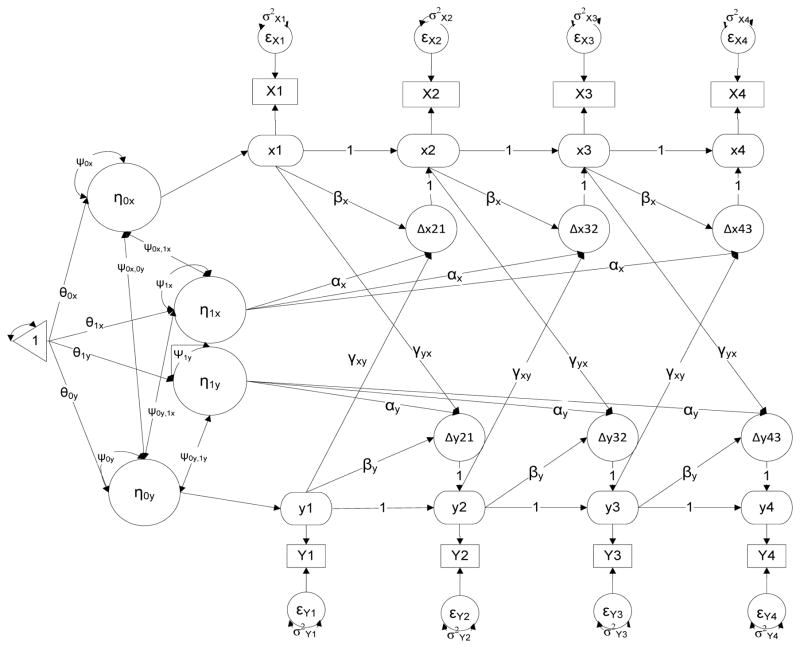
The univariate specification of the LCS model from Figure 2 and Eq. 6 can be extended to simultaneously model multiple outcomes. Although one outcome of early literacy skills, such as vocabulary (Quinn et al., 2015) could be modeled in the univariate LCS framework, data on multivariate developmental data such as vocabulary and reading comprehension can be fit in a bivariate LCS model. Figure 3 presents the basic specification for the bivariate dual change score model that was used in this study. The primary difference between it and the univariate specification is the inclusion of coupling or cross-lag effects (i.e., γ_yx and γ_xy). The coupling effect in the bivariate LCS equations extends Eq. 6 to:

$$\begin{array}{l}\mathrm{\Delta }{y}_{ti}={\alpha }_y\ast {\eta }_{1y}+{\beta }_y\ast y_{(t-1)i}+{\gamma }_{yx}{x}_{(t-1)i}\text{and}\\ \mathrm{\Delta }{x}_{ti}={\alpha }_x\ast {\eta }_{1x}+{\beta }_x\ast x_{(t-1)i}+{\gamma }_{xy}{y}_{(t-1)i}.\end{array}$$ Eq. 7

Figure 3.

Sample bivariate dual change score model. η₀ = latent intercept, η₁ = latent slope, ψ₀ = latent intercept variance, ψ₁=slope variance, ψ_0,0;0,1, = latent covariances among factors, θ₀ = latent intercept mean, θ₁ = latent slope mean, ε_1–4 = observed score residuals, ${\sigma }_{1-4}^2=\text{residual}\text{variances}$, α = mean constant change, β = auto-proportion effect, γ= coupling effect, Δx_t,y_t = latent change scores, x1–x4 and y1–y4 factor variances not included in figure.

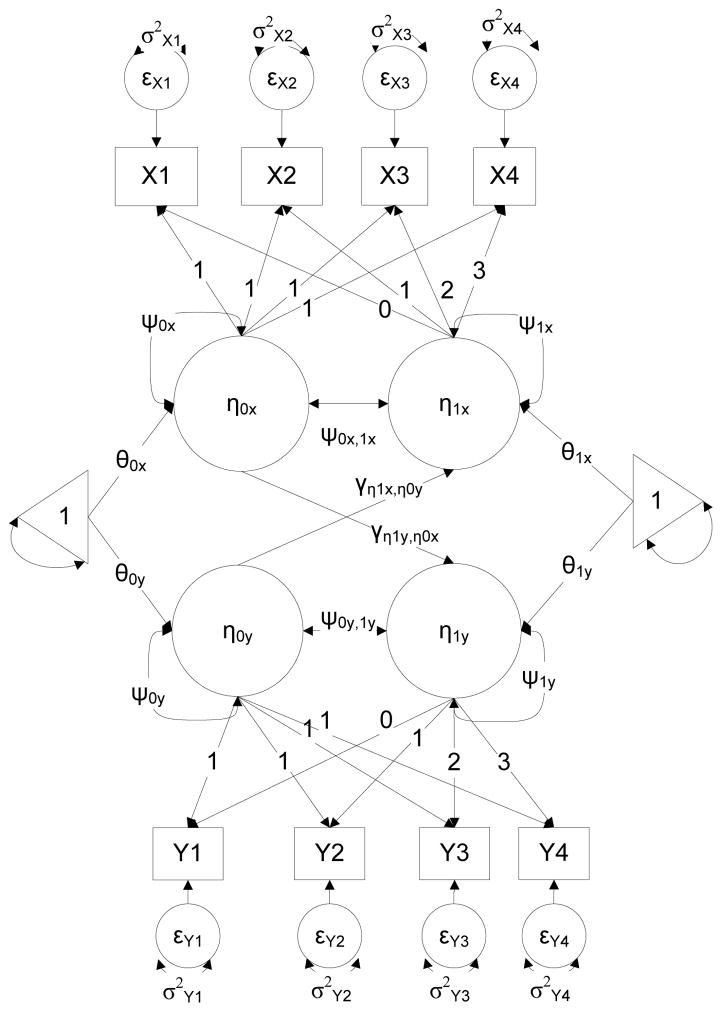
As with the univariate LCS model in Eq. 6, Eq. 7 includes subscripts for the constant and proportional change coefficients that are specific to the outcome for which the LCS is estimated. Further, the insertion of the coupling effect (e.g., γ_yx) denotes the influence of one of the outcomes from a previous time point (e.g., x1 in Figure 3) on a change score for the other outcome (i.e., Δy21). The flexibility of the bivariate model is that it can extend to more than two outcomes and the limitations to the generalization of this model include sample size and one’s computing power. Just as in the univariate context, a bivariate LCS model is flexible such that the constant change, proportional change, or coupling effects may be freed for estimation or fixed based upon the primary question of interest. An ancillary consideration when fitting the multivariate model is the extent to which this offers improvement above other SEMs which model growth and direct effects. Similar to the univariate example, whereby latent growth curve, LCS, and ALT models are available, the multivariate context presents with other possible SEMs. For example, Figure 4 shows a parallel process SEM. This specification allows for individual growth models to be fit to separate processes, such as vocabulary and reading comprehension, but also to test the direct effect of intercepts on one outcome (e.g., the intercept η_0x) on the slope for another outcome (i.e., η_1y).

Figure 4.

Sample parallel process structural equation model. η₀ = latent intercept, η₁ = latent slope, ψ₀ = latent intercept variance, ψ₁ =slope variance, ψ_0,0;0,1, = latent covariances among factors, θ₀ = latent intercept mean, θ₁ = latent slope mean, ε_1–4 = observed score residuals, ${\sigma }_{1-4}^2=\text{residual}\text{variances}$, γ = latent variable regressions.

Univariate and multivariate model building for the latent growth, ALT, and LCS models are quite flexible so that one may evaluate nested versions of univariate or bivariate outcomes, and test the extent to which constrained or freed α, β, and γ parameters result in the most parsimonious but well-fitting model applied to the data. As with most latent variable models, criterion-based fit indices such as the comparative fit index (CFI), Tucker-Lewis index (TLI), root mean square error of approximation (RMSEA), and standardized root mean residual (SRMR) may be used to evaluate fit. Further, AIC and BIC indices can be used for instances where tested models are not nested.

Present Study – Applied Example

To build a better understanding of how these models may be specified and evaluated to describe change over time, we illustrate the differential fit of various latent change score models (i.e., constant change, proportional change, and dual change score models) along with linear and non-linear (i.e., quadratic) latent growth curve models, ALT models (for univariate analysis), and the parallel process SEM (for the multivariate analysis).

As a segue to the model testing and explication, we note the following. First, conventional approaches to growth curve models, specifically multilevel software, frequently assume that the residual variances of the observed variables are constrained to be equal, thereby sufficing the assumption of homoscedasticity. More recent evaluation of this assumption in the latent variable framework has suggested that such a constraint does not contribute much to the understanding of important model estimates, including latent factor means and variances, yet it does contribute to substantial misfit and estimation of the variances and covariances of the model (see Grimm & Widaman, 2010). Second, the application of LCS models across various studies (e.g., Reynolds & Turek, 2012) constrains the auto-proportion effects to be equal over time. Researchers often do this from a theoretical standpoint, where it is assumed that the dynamic relation for the developmental phenomena does not change over the developmental period. Although this constraint can be useful, one could also empirically test whether the auto-proportion effect is the same across all measured time points. Thus, in the context of the present application, four dual change score models were tested to evaluate differential constraints on the proportional change coefficients and freed/fixed error variances: 1) constrained error variances and auto-proportions; 2) freed error variances and constrained auto-proportions; 3) constrained error variance and freed auto-proportions; and 4) freed error variances and auto-proportions.

Method

Participants

Data for the following set of examples were obtained from the Progress Monitoring and Reporting Network at the Florida Center for Reading Research. Participants in this study were a longitudinal cohort that was followed from first to fourth grades. Individuals were assessed four times a year on the Dynamic Indicators of Basic Early Literacy Skills (DIBELS; Good, Kaminski, Smith, Laimon, & Dill, 2001) assessments as part of Florida’s assessment system during the federal Reading First initiative which occurred from 2003–2009, and were also administered the Stanford Achievement Test – 10^th Edition (SAT-10; Harcourt Brace, 2003). The present data were comprised of 16,074 second-grade students who had available data on the DIBELS oral reading fluency (ORF) assessment and the SAT-10 at the end of each academic year (i.e. approximately April of each year). No data were missing on the oral reading fluency assessment, as these data were required of all students during the Reading First initiative. SAT-10 administration was not required in grades 1 and 2, but was required in grades 3 and 4. As such, in grade 1 data were missing for 34% of students, compared to 20% in grade 2, and 1.7% in grades 3 and 4. The data for SAT-10 in grades 1 and 2 were evaluated for patterns of missingness and it was determined they were missing at random. Subsequently, multiple imputation was conducted with methods outlined by Lang & Little (2014).

Measures

DIBELS Oral Reading Fluency (ORF; Good, Kaminski, Smith, Laimon, & Dill, 2001)

DIBELS ORF is a measure that assesses oral reading rate and accuracy in grade-level connected text. This standardized, individually administered test was designed to identify students who may need additional instructional support in reading and to monitor progress toward instructional goals. During a given administration of ORF, students are asked to read three previously unseen passages out loud consecutively, for 1 minute per passage. Students are given the prompt to “be sure to do your best reading” (Good et al., 2001, p. 30). Between the administration of each passage, students are given a break, in which the assessor simply reads the directions again before the task resumes. Words omitted, substituted, and hesitations of more than 3 seconds are scored as errors, although errors that are self-corrected within 3 seconds are scored as correct. Errors are noted by the assessor, and the score produced is the number of words correctly read per minute (wcpm). Research has demonstrated adequate to strong predictive validity of DIBELS ORF for reading comprehension outcomes (r = .65 to .80; Petscher & Kim, 2011; Roehrig, Petscher, Nettles, Hudson, & Torgesen, 2008).

Stanford Achievement Test- 10^th edition (SAT-10; Harcourt Brace, 2003)

The SAT-10 is a standardized test of reading comprehension which may be administered in a group format. This assessment was given by classroom teachers as part of Reading First and was scored by the test publisher. Students were required to respond to 54 multiple choice questions assessing critical analysis, initial understanding, interpretation, and usage of reading strategies for informational and literary text. Reliability for the SAT-10 for a nationally representative sample was .88. Construct and criterion validity with other assessments of reading comprehension have been evaluated in multiple studies (Harcourt Brace, 2003).

Procedure¹

Most commonly used software packages, such as Mplus and R, maintain flexibility to estimate LCS models (i.e., RAMpath in R; Zhiyong, McArdle, Hamagami, & Grimm, 2013). For the present illustrations, all statistical models were run in Mplus and graphs were generated via R. The goal of this illustration is to highlight the LCS model as well as its comparison to various specifications of other latent growth curve models. The sequence of univariate model tests applied to both ORF and SAT-10 were: 1) a linear latent growth curve model using a fixed loading structure [i.e., time coded as 0, 1, 2, 3] and constrained errors; 2) a linear latent growth curve model using a fixed loading structure [i.e., time coded as 0, 1, 2, 3] and unconstrained errors; 3) a linear latent growth model with a freed loading structure [i.e., time coded as 0, *, *, 1, where * denotes freed estimation at time-points 2 and 3] and with correlated errors; 4) a linear latent growth model with a freed loading structure [i.e., time coded as 0, *, *, 1, where * denotes freed estimation at time-points 2 and 3] and with uncorrelated errors; 5) a non-linear, quadratic growth model with constrained errors; 6) a non-linear, quadratic growth model with unconstrained errors; 7) a proportional change LCS model; 8) a constant change LCS model; 9) an autoregressive latent trajectory model; and 10–13) a dual change score model with differentially constrained/unconstrained errors and auto-proportion coefficients (see Table 2 for specifications). Following the univariate models, a set of multivariate models were then estimated to compare alternatives to a bivariate dual change LCS model, including: 1) a parallel process growth model with a fixed loading structure, 2) a parallel process growth model with a freed loading structure, and 3) a parallel process SEM with intercepts [centered at time 1] predicting cross-construct slopes. From the larger sample we randomly selected ten students in order to highlight differences in the observed and estimated trends across selected models.

Table 2.

Model fit for differential specifications of growth models.

Outcome	Model	χ2	df	CFI	TLI	BIC	RMSEA	LB	UB	Δχ2	Δdf	p
ORF	Linear constrained error	24085	8	.65	.73	590964	.433	.428	.738
	Linear unconstrained error	19479	5	.71	.66	586377	.492	.486	.498
	Freed loading constrained error	1039	6	.98	.98	567930	.103	.098	.109
	Freed loading unconstrained error	203	3	.99	.99	567114	.064	.057	.072
	Quadratic constrained error a	4048	4	.94	.91	570953	.251	.244	.257	20037	4	<.001
	Proportional Change	32802	10	.52	.71	599667	.452	.448	.456
	Constant Change	24085	8	.65	.73	590964	.433	.428	.738
	Autoregressive LT	12353	7	.82	.84	579538	.331	.326	.336
	Dual Change 1	1628	7	.98	.98	568513	.120	.115	.125
	Dual Change 2	677	4	.99	.99	567581	.102	.096	.109	951	3	<.001c
	Dual Change 3	745	5	.99	.99	567643	.096	.090	.102	883	2	<.001d
	Dual Change 4	42	2	.99	.99	566959	.035	.026	.045	1586	5	<.001e
SAT-10	Linear constrained error	112718	8	.74	.81	613468	.295	.291	.300
	Linear unconstrained error	9369	5	.79	.74	611639	.341	.336	.347
	Freed loading constrained error	681	6	.99	.99	602944	.084	.078	.089
	Freed loading unconstrained error	310	3	.99	.99	602593	.08	.072	.087
	Quadratic constrained error b	2470	4	.94	.92	604747	.196	.189	.202	110248	4	<.001
	Proportional Change	15211	10	.65	.79	617449	.308	.303	.312
	Constant Change	112718	8	.74	.81	613468	.295	.291	0.3
	Autoregressive LT	14765	7	.66	.71	617022	.362	.357	.367
	Dual Change 1	1255	7	.97	.98	603511	.105	.100	.110
	Dual Change 2	919	4	.98	.97	603196	.119	.113	.126	336	3	<.001c
	Dual Change 3	476	5	.99	.99	602746	.077	.071	.082	779	2	<.001d
	Dual Change 4	61	2	.99	.99	602350	.043	.034	.052	858	1	<.001e

Note. Dual Change 1 = Constrained error variances and auto-proportion, Dual Change 2 = Freed error variances and constrained auto-proportions, Dual Change 3 = Constrained error variances and freed auto-proportion, Dual Change 4 = Freed error variances and auto-proportion.

^aA non-linear model for SAT-10 was estimated with freed error variances but resulted in a non-positive definite and model non-convergence.

^bA non-linear model for ORF was estimated with unconstrained error variances but resulted in worse model fit compared to constrained error variances.

^ccomparison made to constant change model,

^dcomparison made to dual change 1,

^ecomparison made to dual change 2

The CFI, TLI, and RMSEA were used to compare the models. CFI and TLI values of at least .95 are considered acceptable, and RMSEA up to .10 also provide evidence of acceptable model fit. Between-model comparisons were made by using either a χ² difference test when models were nested or using the sample-sized adjusted BIC to evaluate model parsimony when models were non-nested. Raftery (1995) demonstrated that between-model BIC differences between 10 and 100 are sufficient to indicate a practically important difference in model fit.

Results

Descriptive Statistics

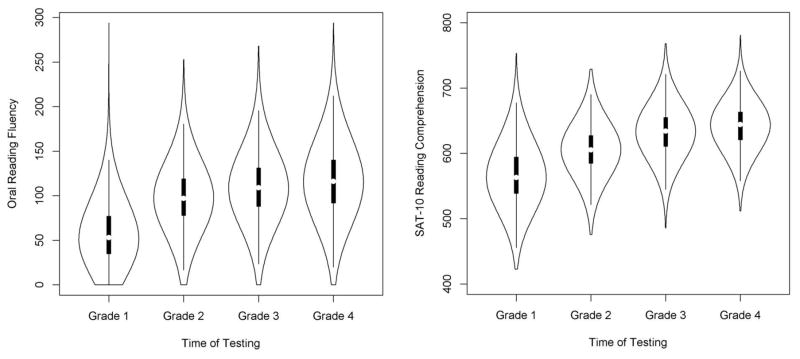
Sample statistics for the oral reading fluency and reading comprehension measures across the four time points are provided in Table 1. Both measures demonstrated relatively normal score distributions, yet some skew and kurtosis existed for the ORF measures. Graphing the descriptive statistics as violin plots (Figure 5) better displays the statistical summary from Table 1, where it may be observed that ORF was more likely to include scores further from the mean compared to the SAT-10. Violin plots are a useful mechanism for simultaneously evaluating the distribution of scores and the interquartile range of scores. The plots for both measures highlight that average performances increased across the four testing periods.

Table 1.

Descriptive statistics for oral reading fluency (ORF) and reading comprehension (SAT-10).

	Minimum	Maximum	Mean	SD	Skew	Kurtosis
Grade 1 ORF	0	294	58.07	31.67	.80	.87
Grade 2 ORF	0	253	98.18	33.33	.07	.63
Grade 3 ORF	0	268	109.39	33.52	.14	.74
Grade 4 ORF	0	294	116.98	36.31	.13	.38
Grade 1 SAT-10	423	753	566.53	42.84	.17	−.08
Grade 2 SAT-10	476	729	605.37	36.46	−.04	.32
Grade 3 SAT-10	486	768	632.80	35.83	−.03	.23
Grade 4 SAT-10	512	781	641.38	32.49	−.18	.03

Note. ORF = DIBELS Oral Reading Fluency, SAT-10 = Stanford Achievement Test.

Figure 5.

Violin plots for ORF (left) and SAT-10 (right).

Growth Models

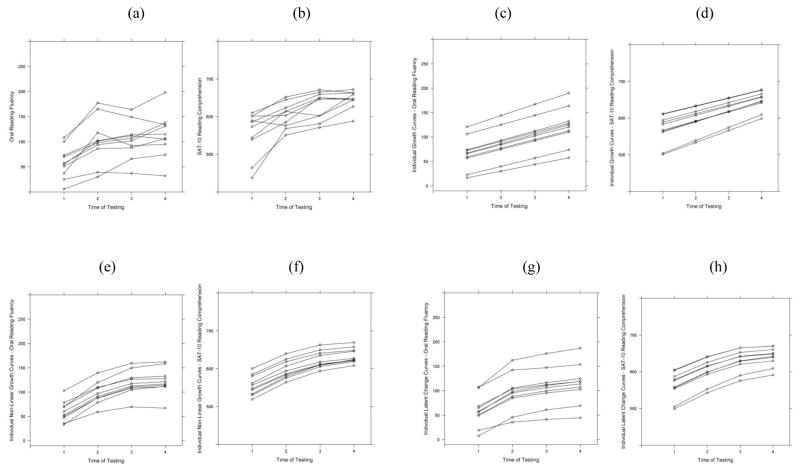
Prior to fitting the growth models, it was of interest to plot the raw data to evaluate whether the scores for each of the measures demonstrated a linear or curvilinear trend. Ten students were randomly selected and their plotted scores for ORF and SAT-10 are presented in Figures 6a and 6b. Both within and across the measures it is clear that individual differences in trends exist. Although some of the randomly selected students demonstrated a linear growth pattern, most individuals’ growth could be characterized as non-linear. Individual differences across the time points were larger for ORF compared to SAT-10, with several students demonstrating a drop off in performance between the third and fourth time points. Such differences in the sample plots suggested it may be valuable to test a curvilinear growth model in addition to the linear latent growth and LCS models.

Figure 6.

Observed (a/b), Linear (c/d), Non-Linear (e/f), and Latent Change (g/h) individual growth for ORF/SAT-10 for n=10 selected students.

Model comparison

In Table 2, results are presented for the fit of the latent growth model for ORF and SAT-10. As can be seen for both the SAT-10 and ORF outcomes, neither the linear model with constrained or unconstrained errors, nor the quadratic growth models provided acceptable fit to the data. Although the quadratic model with constrained errors fit statistically better than the linear model with constrained errors for SAT-10 [Δχ²(4) = 110,248, p < .001] and ORF [Δχ²(4) = 20,037, p < .001), the CFI, TLI, and RMSEA failed to meet typically accepted thresholds for model fit. The proportional change and constant change LCS models did not improve upon model fit compared to either the linear or quadratic growth models, nor did the ALT provide acceptable fit to the data. Conversely, the freed loading linear growth models and the dual change LCS models provided excellent fit to the data. Relative fit for the first dual change score model (i.e., constrained auto-proportion and error variances; dual change 1; BIC = 603511) showed a marked improvement compared to either the linear growth model with unconstrained errors (BIC = 611639) or the non-linear growth model (BIC = 604747). This observation was replicated for ORF as well, whereby the dual change 1 model (BIC = 568513) fit better than the linear, constrained errors (BIC = 586377) and non-linear specifications (BIC = 570953). Not only did the dual change 1 model provide improved relative fit compared to linear or quadratic specifications, the criterion fit for this model was also acceptable for SAT-10 [χ²(1255, N=16,074) = 7, CFI = .97, TLI = .98, RMSEA = .105 (95% CI = .100, .110)] and ORF [χ²(1625, N=16,074) = 7, CFI = .98, TLI = .98, RMSEA = .120 (95% CI = .115, .125)]. Alternative specifications of the dual change score model yielded additional improved fit. The freed error variance-constrained auto-proportion model (i.e., dual change 2) and the constrained auto-proportion freed error variance model (i.e., dual change 3) provided better fit than the fully constrained dual-change model (p < .001; Table 2). When both error variances and auto-proportion parameters were freed for estimation (i.e., dual change 4), this model provided the best fit to the data and fit significantly better than the other three dual change model specifications. Note that although the freed loading specifications of the linear growth model provided better fit to the data compared to most models, the dual change 4 model still provided the best relative fit compared to the freed loading growth model with unconstrained errors for both ORF (ΔBIC = 155) and SAT-10 (ΔBIC = 33).

Resulting model coefficients for each of the tested models are reported in Table 3. Despite dual change 4 for both outcomes demonstrating the best relative fit, dual change model 3 was selected for the explication of coefficients, as this configuration conforms to more traditional growth modeling (i.e., fixed residual variances). As will be shown later, little difference is observed in the estimated latent change scores using either dual change 3 or 4.

Table 3.

Model coefficient results for univariate model specifications.

Parameter	Linear	Non-linear	Proportional	Constant	DC1	DC2	DC3	DC4
ORF Fixed
Intercept	67.46	59.33	72.58	67.46	58.33	58.08	58.20	58.07
Linear Slope	18.79	43.19	-	18.79	75.56	77.33	68.26	80.99
Non-Linear Slope	-	−8.13	-	-	-	-	-	-
Proportional Change	-	-	-	-	-	-	-	-
D1->T1	-	-	0.19	-	−0.63	−0.66	−0.49	−0.70
D2->T2	-	-	0.19	-	−0.63	−0.66	−0.58	−0.71
D3->T3	-	-	0.19	-	−0.63	−0.66	−0.55	−0.67
ORF Random
Intercept	773.68	866.28	485.29	773.68	874.92	992.82	850.97	1042.72
Linear Slope	11.69	104.05	-	11.69	453.61	478.33	357.12	534.61
Non-Linear Slope	-	2.48	-	-	-	-	-	-
Error variance G1	288.58	151.39	363.6	288.58	144.42	9.93	139.27	0*
Error variance G2	288.58	151.39	363.6	288.58	144.42	148.26	139.27	151.38
Error variance G3	288.58	151.39	363.6	288.58	144.42	100.95	139.27	97.73
Error variance G4	288.58	151.39	363.6	288.58	144.42	206.53	139.27	200.55
SAT-10 Fixed
Intercept	573.72	566.53	574.92	573.72	566.03	566.03	566.52	566.52
Linear Slope	25.2	42.4	-	25.2	297.26	294.50	361.39	38.09
Non-Linear Slope	-	−3.56	-	-	-	-	-	-
Proportional Change	-	-	-	-	-	-	-	-
D1->T1	-	-	-	-	−0.45	−0.45	−0.57	.002
D2->T2	-	-	-	-	−0.45	−0.45	−0.55	−.018
D3->T3	-	-	-	-	−0.45	−0.45	−0.56	−.047
SAT-10 Random
Intercept	1307.45	1512.14	821.38	1307.45	1505.75	1423.66	1544.50	1252.12
Linear Slope	26.59	390.72	-	26.59	173.42	169.53	268.67	36.25
Non-Linear Slope	-	18.1	-	-	-	-	-	-
Error variance G1	440.37	323.17	510.89	440.37	311.15	434.51	301.89	558.91
Error variance G2	440.37	323.17	510.89	440.37	311.15	320.15	301.89	282.84
Error variance G3	440.37	323.17	510.89	440.37	311.15	317.53	301.89	304.71
Error variance G4	440.37	323.17	510.89	440.37	311.15	251.37	301.89	228.49

Note. Linear = linear latent growth model; Non-linear = non-linear latent growth model; Proportional = proportional change model; Constant = constant change model; DC1 = Constrained error variances and auto-proportion; DC2 = Freed error variances and constrained auto-proportions, DC3 = Constrained error variances and freed auto-proportion; DC4= Freed error variances and auto-proportion; D1->T1 = proportional change coefficient of the first difference score on time 1; D2->T2 = proportional change coefficient of the second difference score on time 2; D3->T3 = proportional change coefficient of the third difference score on time 3.

^*Error variance was fixed at 0 due to a negative residual variance.

For ORF, results of model 3 showed a mean intercept, or the average initial starting values at time one, of 58.20 wcpm and an average yearly constant slope of 68.26 wcpm. This mean slope factor is not interpreted in the same way as the slope factor in the linear growth models where growth is viewed as the average amount of expected increase in the outcome between time-points. Instead, the mean in a latent change model is interpreted as the average unique effect that contributed to the estimated LCS above the proportional change coefficients. In this model, the proportional coefficients were β = −0.49 (p <.001) for the effect of time 1 ORF on the change score between times 1 and 2, β = −0.58 (p <.001) for the effect of time 2 on the second change score, and β = −0.55 (p <.001) for the effect of time 3 on the third change score. A negative proportional change value between time points in the presence of a positive linear slope provides two interpretations: 1) when accounting for average ORF change of 68.26 wcpm, individuals with lower ORF scores on the previous occasion changed more than individuals with higher ORF scores, and 2) change in ORF ability slightly decelerated over time.

Similarly for SAT-10, dual change model 3 coefficients will be explicated. An initial mean score of 566.52 was estimated along with an average yearly slope mean of 361.39. As stated previously, this slope mean must be interpreted with caution and in combination with the proportional change parameters. The proportional change coefficients for SAT-10 were approximately equal with β = −0.57 (p <.001) for the effect of time 1 SAT-10 on the change score between times 1 and 2, β = −0.55 (p <.001) for the effect of time 2 on the second change score, and β = −0.56 (p <.001) for the effect of time 3 on the third change score. Note that even though dual change model 3 fit significantly better than dual change models 1 and 2 which had constrained auto-proportion estimates, the coefficients in model 3 were only marginally different from each other for the freed auto-proportion coefficient. Such a phenomenon occurs with large sample sizes whereby incremental model fit may suggest a better fitting model with little difference in the magnitude of parameter estimates.

Estimating individual latent change scores

Resulting coefficients from the ORF and SAT-10 LCS models can subsequently be used to create individual predicted LCSs using Eq. 6. The LCSs for ORF would then be estimated with:

$$\begin{array}{l}\mathrm{\Delta }\text{ORF}{[t]}_{21i}=68.26+-0.49\ast {\text{ORF}}_{1i}\\ \mathrm{\Delta }\text{ORF}{[t]}_{32i}=68.26+-0.58\ast {\text{ORF}}_{2i}\\ \mathrm{\Delta }\text{ORF}{[t]}_{43i}=68.26+-0.55\ast {\text{ORF}}_{3i}.\end{array}$$

The ORF models show that from the first time point to the second, the predicted LCS simultaneously increased by 68.26 points and decreased proportionally by 0.49 points relative to the time 1 ORF score. Similarly, while the ORF scores increased by the constant of 68.26 points for the other two change scores, the proportion decrease changed from 0.49 points to 0.58 and 0.55 for the second and third change scores, respectively. The individual LCSs for SAT-10 would be constructed with:

$$\begin{array}{l}\mathrm{\Delta }\text{SAT}-10{[t]}_{21i}=361.39+-0.57\ast \text{SAT}{10}_{1i}\\ \mathrm{\Delta }\text{SAT}-10{[t]}_{32i}=361.39+-0.55\ast \text{SAT}{10}_{2i}\\ \mathrm{\Delta }\text{SAT}-10{[t]}_{43i}=361.39+-0.56\ast \text{SAT}{10}_{3i}.\end{array}$$

The SAT-10 results show that across the assessment periods, students increased their reading comprehension scores additively by 361.39 points, but decreased proportionally depending on when change was estimated.

The relation between the mean slope and the auto-proportion in the individual LCS models may be tricky to grasp at first, but when related to descriptive means can be seen more clearly. Suppose we take a student whose ORF performance at each time point was at the mean reported in Table 1; their estimated LCSs for each occasion would be:

$$\begin{array}{l}\mathrm{\Delta }\text{ORF}{[t]}_{21i}:39.81=68.26+-0.49\ast 58.07\\ \mathrm{\Delta }\text{ORF}{[t]}_{32i}:11.32=68.26+-0.58\ast 98.18\\ \mathrm{\Delta }\text{ORF}{[t]}_{43i}:8.10=68.26+-0.55\ast \mathrm{109.39.}\end{array}$$

Note that if one were to estimate the LCSs using the coefficients from dual change model 4 instead of dual change model 3, the estimated change scores would have been ΔORF[t]_21i = 40.34, ΔORF[t]_32i = 11.28, and ΔORF[t]_43i = 7.70, all of which closely approximate the values from dual change model 3. The predicted LCSs from dual change model 3 indicate that the greatest change in ORF was made between times 1 and 2 (i.e., 39.81 between grade 1 and grade 2), whereas the least amount change of 8.10 occurred between grades 3 and 4. Notice how the average calculated change score from grade 1 to grade 2 of 39.81 is very close to the difference of the grade 1 and grade 2 observed means from Table 1 (i.e., 98.18 – 58.07 = 40.11), as are the other estimated change scores related to the difference in observed means.

With the individual change scores estimated, an individual growth trajectory can be constructed from the predicted LCSs. In this example, with an estimated grade 1 ORF score of 58.07, at grade 2 it would be the grade 1 value plus the estimated ΔORF[t]_21i (i.e., 58.07 + 39.81 = 97.88). At grade 3, the estimated ORF score is 97.88 + 11.32 = 109.20, and at grade 4 the estimated ORF score is 109.20 + 8.10 = 117.30. Again, notice how in each case the estimated ORF score using latent change produces a value that very closely approximates the mean scores from Table 1. Because our illustration used mean performance this is within expectation, but demonstrates that the average growth and auto-proportion coefficients work in conjunction with each other to produce estimated latent scores that can be used to construct an individual trajectory. In the same way, if we use the mean SAT-10 score at each time point, the estimated LCSs are:

$$\begin{array}{l}\mathrm{\Delta }\text{SAT}-10{[t]}_{21i}:44.17=361.39+-0.57\ast 566.53\\ \mathrm{\Delta }\text{SAT}-10{[t]}_{32i}:28.44=361.39+-0.55\ast 605.37\\ \mathrm{\Delta }\text{SAT}-10{[t]}_{43i}:7.02=361.39+-0.56\ast \mathrm{632.80.}\end{array}$$

If the model coefficients from dual change 4 were used, the estimated change scores would be: ΔSAT − 10[t]_21i = 42.39, ΔSAT − 10[t]_32i = 27.19, and ΔSAT − 10[t]_43i = 7.08. Similar to the ORF example, students changed the most between the first two time points (44.17) and the least between the last two time points (7.02). The SAT-10 estimated LCSs, used in a similar manner as in the ORF example, show that the estimated grade 1 through grade 4 scores would be: 566.53 at grade 1, 610.70 at grade 2 (566.53 + 44.17), 639.14 at grade 3 (610.70 + 28.44), and 646.16 at grade 4 (639.14 + 7.02). Notice again that these estimated scores closely correspond to the observed means in Table 1.

Just as estimated scores from the LCS can be done at each time point, they may also be plotted. Grouped individual linear latent trajectories and the latent change score trajectories for the random sample of students on ORF and SAT-10 are plotted in Figure 6e and 6f. As seen in Figure 6c, the results of the ORF latent growth model do not capture the acceleration/deceleration in growth over time in ORF as is captured in Figure 6e or 6g via the latent change or quadratic growth plots. This sudden deceleration of growth is based on the decreasing LCSs just estimated in the example (39.81, 11.32, and 8.10, respectively). The same pattern is seen for the SAT-10 data, whereby Figure 6d does not capture the acceleration/deceleration in growth captured through the LCSs in Figure 6f (44.17, 28.44, and 7.02, respectively).

Bivariate dual change scores

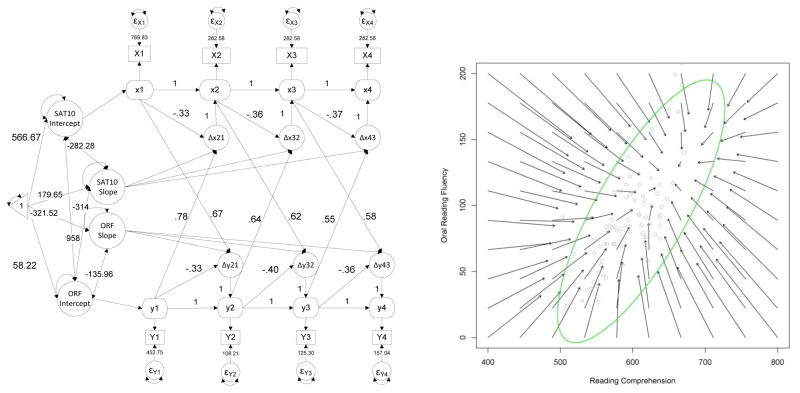
The final model illustration of the LCS models is the bivariate specification that incorporates lag or coupling effects on the change scores. Prior to estimating the bivariate dual change model, a parallel process non-linear growth model with a quadratic term was estimated to serve as the baseline comparison. This model estimated the growth of ORF and SAT-10, as well as the covariances across intercepts and linear/quadratic slopes of both measures. Resulting fit for this model was moderately acceptable criteria [χ² (14, N = 16,074) = 4,808, CFI = .96, TLI =.93, RMSEA = .146 (95% CI = .143, .149), BIC = 1,153,023]. When changing the model to include structural paths from the intercepts to cross-construct slopes, the model fit declined [χ² (18, N = 16,074) = 5,211, CFI = .96, TLI =.94, RMSEA = .134 (95% CI = .131, .137), BIC = 1,153,402]². Conversely, the bivariate LCS model provided good fit to the data based on criterion indices [χ²(15, N = 16,074) =1,441, CFI = .99, TLI = .98, RMSEA = .077 (95% CI = .074, .080)], and the BIC (1,149,652) was lower compared to the non-linear, parallel process SEM [ΔBIC = 3,750)]. Resulting parameters for the bivariate LCS model are provided in Figure 7.

Figure 7.

Bivariate dual change score model (left) and vector plot results (right) for ORF and SAT-10.

Similar to the univariate dual change models, the estimated parameters included means for the latent intercepts (58.22 and 566.67 for ORF and SAT-10) and slopes (−321.52 and 179.65 for ORF and SAT-10) as well as the variances, covariances, and proportional change coefficients. The inclusion of coupling effects of ORF on SAT-10 change, as well as SAT-10 on ORF change, demonstrated the differential contributions each makes to the estimated LCSs. Model coefficients from Figure 7 can be inserted into Eq. 7 to create the estimated scores for ORF and SAT-10 as:

$$\begin{array}{c}\mathrm{\Delta }\text{ORF}{[t]}_{21i}=-321.52-0.33\ast {\text{ORF}}_{1i}+0.67\ast \text{SAT}{10}_{1i}\\ \mathrm{\Delta }\text{ORF}{[t]}_{32i}=-321.52-0.40\ast {\text{ORF}}_{2i}+0.62\ast \text{SAT}{10}_{2i}\\ \mathrm{\Delta }\text{ORF}{[t]}_{43i}=-321.52-0.36\ast {\text{ORF}}_{3i}+0.58\ast \text{SAT}{10}_{3i}\\ \text{and}\\ \mathrm{\Delta }\text{SAT}-10{[t]}_{21i}=179.65-0.33\ast \text{SAT}{10}_{1i}+0.78\ast {\text{ORF}}_{1i}\\ \mathrm{\Delta }\text{SAT}-10{[t]}_{32i}=179.65-0.36\ast \text{SAT}{10}_{2i}+0.64\ast {\text{ORF}}_{2i}\\ \mathrm{\Delta }\text{SAT}-10{[t]}_{43i}=179.65-0.37\ast \text{SAT}{10}_{3i}+0.55\ast {\text{ORF}}_{3i}.\end{array}$$

From these equations several important implications can be seen. When considering ORF, note that the average slope coefficient was negative (i.e., −321.52). This phenomenon speaks to the nature of change scores; that is, one must account for all the individual components predicting the change score coefficient when considering an estimation of individual change scores. For example, taking the mean ORF and SAT-10 score at grade 1 (i.e., 58.07 and 566.53, respectively) and substituting into the ΔORF[t]_21i equation gives an estimated latent change score of:

$$38.56=-321.52-0.33\ast 58.07+0.67\ast 566.$$

As such, an individual who is average with regards to both ORF and SAT-10 in grade 1 is estimated to change approximately 39 wcpm between grade 1 and grade 2 for their oral reading fluency. In the same way, the mean grade 1 ORF and SAT-10 scores can be substituted into the equation for ΔSAT − 10[t]_21i:

$$37.99=179.65-0.33\ast 566.53+0.78\ast 58.07,$$

indicating that students with average grade 1 ORF and SAT-10 scores are expected to change 37.99 points in their SAT-10 scores from grade 1 to grade 2. Both of these estimated latent change scores mapped well onto their descriptive counterparts from Table 1, whereby the mean difference between grade 1 and grade 2 ORF was 40.11 points (compared to expected, estimated change of 38.56), and the mean SAT-10 difference between grade 1 and 2 was 38.84 points (compared to the expected, estimated change of 37.99 points).

When considering the individual model parameters, the auto-proportion coefficients for ORF and SAT-10 only slightly varied in its strength to the change score over time, ranging from −.33 to −.40 for ORF and −.33 to −.37 for SAT-10 when accounting for the other variables in the model. The positive coupling coefficient for ORF to SAT-10 and for SAT-10 to ORF indicated the presence of a strong leading indicator effect. Herein lies a strength of the LCS model compared to parallel process models; typically, growth models would not easily allow for the testing of coupling effects for specific change components in the model. Within Figure 7, it can be seen that the influence of ORF in grade 1 (i.e., y1) on SAT-10 change between grades 1 and 2 (Δx21; .78) is slightly stronger compared to the association between ORF in grade 3 (i.e., y3) and SAT-10 change between grades 3 and 4 (Δx43; .55). The unique, simultaneous estimation of the coupling and auto-proportion effects allows for a potentially greater understanding of individual differences in change that would be obfuscated by using a growth model that averages the change over all times points.

A limitation of the bivariate LCS models is that constructing individual growth curves poses a particular challenge because each outcome is directly influenced by the other. Subsequently, a more comprehensive way to view the joint, estimated trajectories of ORF and SAT-10 is through a vector field plot (Figure 7, right). The arrows represent the initial values of each ORF-SAT-10 combination, and the direction of the arrow shows the type of expected change to occur from the initial status combinations in the vector field. For example, arrows in the upper left-hand portion of the figure reflect those individuals who start with relatively high ORF scores and low SAT-10 scores. Most of the arrows in this section of the graph point downward and to the right, indicating that the expected scores are such that ORF scores decrease over time but SAT-10 scores increase over time. Conversely, scores toward the lower, left portion of the graph have arrows which are low in both ORF and SAT-10 and point upward, indicating that students increase in both ORF and SAT-10. Thus, the vector field is useful for identifying individuals who may be growing in both scores over time, growing only based on one outcome, or those with an expected decrease in both, such as individuals in the upper right hand portion of the graph. A particular nuance of the vector field plots is that they contain the joint expectation of growth across the distribution of both scores, which may be somewhat misleading in that it could suggest as many students are decreasing in their expected trajectories as those who are increasing. A useful mechanism to evaluate where the concentration of student joint development in skills occurs is to overlay a scatterplot for a random selection of individuals in the sample, as well as a 95% density ellipse. The density of the scatter can better facilitate which of the arrows in the vector field reflect actual observed performance. Based on the inclusion of these two elements, it can be observed that most students were in the lower middle or lower left hand portions of the figure, which is reflective of those students who have expected positive growth in both ORF and SAT-10 scores from first to fourth grades.

Discussion

The goal of this article was to introduce the reader to latent change score modeling and highlight its complexities and the information it yields in the context of traditional latent growth models. Modeling individual trajectories in educational research presents several complex issues that have previously been evaluated using either structural or dynamic modeling. Each has its set of distinct advantages and disadvantages, yet the strengths of both may be combined in the LCS model. Such a framework enables one to understand the nature of change for a given assessment, as well as the determinants of such change (McArdle & Grimm, 2013).

A distinct advantage of using the LCS model with developmental data is that it allows one to disaggregate growth into multiple change scores, which can be useful in isolating where a student is likely to change the most. The model coefficients from Figure 5a highlight that the direct/indirect effect portions of the model are useful in understanding the effects on change. The auto-proportion coefficient for both SAT-10 (−.33, −.36, −.37) and ORF were negative (−.33, −.40, −.36), suggesting that when accounting for the average growth rate, individuals who start low change more. The positive and significant coupling effects for both SAT-10 to ORF (.67, .62, .58) and ORF to SAT-10 (.78, .64, .55) demonstrate the tendency for students with higher scores at previous time points on one skill to change more positively over time on the other. This potential Matthew Effect (Stanovich, 1986), whereby “the rich get richer and the poor get poorer,” shows an increasing gap in higher performing and lower performing students over time. This would not have been captured in traditional growth models to the same extent as LCS models.

Moreover, not only are the dynamic growth and direct/indirect effect portions of the model useful to understanding change, but the coupling effects may assist in identifying which predictors yield the most useful information about change. In the current illustration it was found that prior ORF performance was a strong, positive predictor of change in SAT-10 in addition to the strong, negative effect of the SAT-10 auto-proportion coefficient. This finding, in line with previous studies showing the large effect of fluency on reading comprehension (e.g., Kim, Wagner, & Foster, 2011), may assist in yielding new understanding about reciprocal causation when predicting individual differences in fluency type outcomes. At the same time, it is worth noting that the interpretation of model coefficients requires more focus compared to traditional growth curve models. Because the LCS model includes latent slope and auto-proportion effects, the interpretation of each is in reference to the other. As such, the LCS model can be viewed similarly to a non-linear, quadratic latent growth model such that it is necessary to account for multiple parameters in the model when attempting to understand change over time. Just as the non-linear model requires a first-order derivative of growth to estimate instantaneous change (Raudenbush & Bryk, 2002), so does the LCS model require a “plug-and-chug” in the vein of Eq. 6 and 7 to obtain the full benefit of interpreting model results.

Model Considerations

In the present design, the LCS model was selected based on both traditional criterion and relative fit indices, as well as for theoretical reasons. It is worth noting at this point that when evaluating Table 2, both the dual change and the freed loading models provided acceptable fit to the SAT-10 and ORF outcomes. An implication of this finding is that just as the differential constraints on auto-proportion and error variances led to better or worse fit in the dual-change LCS models, so does differential treatment of loadings and error variances in other model specifications lead to better fitting models. The difference in fit between the linear and freed loading model sets, both constrained and unconstrained error conditions, was due to how the loadings themselves were treated (i.e., fixed in the linear model and estimated in the freed loading model). The difference between the proportional change and constant change models also lies in what portions of the model were fixed and freed (i.e., constant change was fixed in the proportional change model, and proportional change was fixed in the constant change model).

Within the LCS applications here, the selection of using dual change 4 versus dual change 3 for both SAT-10 and ORF was guided by achieving the best model fit compared to other specifications. When comparing linear, non-linear, auto-regressive, latent change, and other longitudinal models and selecting the “most appropriate” model, one should do well to look beyond just fit, as a good-fitting model can be achieved based on combinations of relaxing or restricting model constraints. As many of the models tested are nested versions of each other, it is important to study the connection each model has with each other to understand the common and unique aspects each one provides when understanding developmental trends.

Extensions and Limitations

The univariate and bivariate examples both illustrated how the LCS model can be applied to data when there is one measured variable per construct at each measurement occasion. Researchers frequently have access to multiple measures of a given construct such as multiple passages for ORF, which allows a common factor to be estimated as a function of the shared variance across the individual passages. McArdle and Prindle (2008) used a common-factor LCS model to evaluate the impact of cognition training on the elderly. Similarly, Calhoon and Petscher (2013) used a common-factor LCS model to test the impact of different reading interventions for middle and high school students, and Quinn et al. (2015) used a common-factor LCS model to examine the bidirectional influences between vocabulary knowledge and reading comprehension. A notable difference between the examples presented here and the common-factor LCS model is that there is a strict requirement for invariance of the factor loadings across the measurement occasions (McArdle & Hamagami, 1998). As with many longitudinal applications of structural equation modeling (SEM) using common factors, strict invariance is often not tenable (Millsap, 2012), with many models meeting requirements for partial measurement invariance; thus it is important that one carefully evaluates the invariance of the loadings prior to proceeding with a common-factor LCS model.

Further, previous changes predicting future changes can be estimated in these models, whereby the change scores can be considered leading indicators of levels of or change in another variable. This adds an additional component to the change score equations above, whereby a new predictive component comprises the change score. Grimm et al., (2012) consider this the changes-to-changes portion of the model, whereby recent changes can be used to predict subsequent changes. The ϕ coefficient is introduced as an autoregressive component of the latent change score, and changes-to-changes pathways are added to the equations with the ξ coefficient (Grimm et al., 2012, p. 279) to add an additional predictive component. These are not without limitations, though, as one is limited by computing power and sample size. Additionally, Grimm et al. (2012) mention the increased difficulty in interpreting the system of change by adding in more components to the change scores, often resulting in impractical growth curves given the theories regarding the construct(s) of interest.

Additional aspects of the LCS model that may be useful for researchers working with fluency data are multiple-group, multilevel, and multivariate change models. As with many SEMs, questions about invariance of means, variances, and loadings are of interest when one has collected data where multiple groups are involved. Several studies have used the multiple group approach to evaluate how different auto-proportion and coupling effects differ between males and females (McArdle & Grimm, 2013), as well as whether an intervention had a different effect in the treatment or control groups (Calhoon & Petscher, 2013; McArdle & Prindle, 2008). We note that while the focus on this paper has made comparisons to several models, it is by no means comprehensive, and other growth specifications (e.g., piecewise, freed-loading) could be compared. It is also important that in prospective planning for using the LCS, one is sensitive to sample-size planning and potentially use Monte Carlo simulation.

Because fluency and comprehension data may often retain distributional properties which may restrict individual differences (e.g., Catts et al., 2008), or more appropriately, may mask differences from estimated means effects, growth models may be inefficient in capturing the developmental nature of change. The LCS model demonstrated equal or better model fit to the data compared to other models that are appropriate for longitudinal data, and displayed predicted individual growth curves from the change scores which were not too dissimilar from the observed fluency and comprehension scores or the predicted non-linear individual growth curves. At the same time, it should be noted that a transformation of the observed measures could also have improved model fit of the latent growth model. The flexibility to fit dual change, constant change, or proportional change models allows for researchers with longitudinal data to potentially obtain a richer understanding of change over time and it is our hope that these models, which are gaining great flexibility in software such as Mplus and R, will allow users to better study individual differences over time.