bcl::Cluster : A method for clustering biological molecules coupled with visualization in the Pymol Molecular Graphics System

Abstract

Clustering algorithms are used as data analysis tools in a wide variety of applications in Biology. Clustering has become especially important in protein structure prediction and virtual high throughput screening methods. In protein structure prediction, clustering is used to structure the conformational space of thousands of protein models. In virtual high throughput screening, databases with millions of drug-like molecules are organized by structural similarity, e.g. common scaffolds. The tree-like dendrogram structure obtained from hierarchical clustering can provide a qualitative overview of the results, which is important for focusing detailed analysis. However, in practice it is difficult to relate specific components of the dendrogram directly back to the objects of which it is comprised and to display all desired information within the two dimensions of the dendrogram. The current work presents a hierarchical agglomerative clustering method termed bcl::Cluster. bcl::Cluster utilizes the Pymol Molecular Graphics System to graphically depict dendrograms in three dimensions. This allows simultaneous display of relevant biological molecules as well as additional information about the clusters and the members comprising them.

I. Introduction

Hierarchical clustering is the procedure of iteratively grouping similar objects together, and a cluster is constituted by this group of similar objects [1]. A distance measure is necessary to calculate the similarity between two objects. The purpose of clustering is to facilitate the identification of data patterns or classification of objects. Clustering methods are used in a wide variety of scientific applications and several different clustering algorithms can be applied to a dataset (for recent reviews of clustering methods see [2, 3]).

In particular, clustering is utilized in de novo protein structure prediction in order to aid in the selection of native-like models [4, 5]. Theoretically, the native protein structure resides in the global energy minimum and can be identified unambiguously as the point of lowest free energy in the conformational space. However, vastness of the conformational space requires evaluation of millions of protein models to generate some that are “native-like”, i.e. reasonably similar in structure to the native conformation; typically a root mean square distance (RMSD) of backbone atoms smaller 7.5 Å. Such models have a score significantly higher than the native conformation. Further, the scoring functions used in protein structure prediction to estimate protein free energy are designed for fast evaluation of models. Stabilizing interactions within the protein model are not evaluated at atomic detail which reduces accuracy. In result, some non-native conformations will achieve scores similar to the native-like conformations.

Clustering is used to overcome this limitation [6]. Although the depth of the energy minimum in which the native conformation resides is reduced, the width of the energy funnel is less affected. Therefore, upon clustering predicted models according to structural similarity as measured by the RMSD, large clusters have an increased likelihood to contain native-like conformations. Global Distance Test (GDT) [7] and distance matrices [8] are alternative distance measures used in the process.

Clustering is also used in the analysis of libraries of small, often drug-like, molecules. Often millions of such molecules are included in (virtual) high-throughput screening or generated by structure generators [9–11]. Clustering structures the chemical space and identifies, for example, sets of similar compounds that share a common biological activity [12, 13]. Similarity measures compare the configuration of small molecules either based on the largest common substructure [14] or based on a vector of descriptors, so-called fingerprints [15–17]. The Tanimoto [18] coefficient is a popular similarity measure (for review see [19]).

The focus of the current work is to introduce a hierarchical agglomerative clustering method (bcl::Cluster). The goal of bcl::Cluster is to facilitate the clustering and analysis of biological molecules such as proteins and ligands by allowing visualization of the molecules within the context of the dendrogram. bcl::Cluster uses the Pymol Molecular Graphics System (Pymol) [20] to display the dendrogram and the biomolecules.

II. Methods

bcl::Cluster is implemented as a part of the BioChemical Library, an in-house developed, object oriented, C++ programming library. The code has been developed with flexibility and extensibility as a priority. Key aspects of the method are elaborated on below.

A. Input

bcl::Cluster relies upon pre-calculated pair-wise distances between objects in order to perform clustering. As input formats, bcl::Cluster reads data in the format of a distance matrix or a pair-wise list of distances, where the objects to be clustered are represented by an identifier. Both input formats are independent of the actual type of object that is being clustered. Therefore, although the graphical output of the method is tailored to biological molecules, bcl::Cluster is generally applicable. The separation of the calculation of distances between individual objects and the clustering algorithm allows bcl::Cluster the flexibility to work with any numerical distance measure for any type of object. The bcl library is used to compute a variety of similarity measures such as GDT [7], longest continuous segment [7], MaxSub [21], average distance matrix error [8], RMSD [22], RMSD100 [23], largest common substructure [24], and the Tanimoto coefficient [18].

B. Distance measures

bcl::Cluster allows the use of similarity or dissimilarity distance measures for clustering. In the case of a similarity distance measure, objects with a greater distance value are more similar. An example of such a measure would be the Tanimoto coefficient frequently used to calculate the similarity of small molecules [18]. A dissimilarity distance measure is one where objects with a smaller distance value are more similar. The RMSD value between two proteins is an example of a dissimilarity distance measure [25].

C. Clustering Algorithm

bcl::Cluster uses a hierarchical agglomerative clustering algorithm [26]. Each individual object starts out in a cluster containing only that object. The method continues to iteratively combine the most similar cluster pairs until only a single cluster remains.

The similarity, or linkage, between two clusters can be calculated in several ways in bcl::Cluster. Average linkage between two clusters is calculated as the average pair-wise distance between all objects in two clusters. Single linkage between two clusters is calculated as the distance of the most similar pair of objects between the two clusters. Complete linkage between two clusters is calculated as value of the most dissimilar pair of objects between the two clusters. Lastly, total linkage is calculated similarly to average linkage but also considers pair-wise distances within the two clusters when calculating the average distance. This differs from average linkage which only considers pair-wise distances between clusters.

D. Clustering Cutoff

For practical applications, it is typically not necessary to compute the entire hierarchy of cluster agglomerations. For example, in the case of clustering protein models, clustering can be stopped once linkage values are reached where combining two clusters would produce a cluster encompassing proteins of different topology, i.e. at a RMSD of approximately 7.5 Å. By allowing the user to limit the extent of clustering, the time and memory requirements of bcl::Cluster can be reduced.

E. Pre-clustering

As mentioned in the description of the clustering algorithm, a hierarchy of clusters is obtained by iteratively combining pairs of clusters until only a single cluster remains that contains all previous clusters. Reducing the number of iterations that are needed until all clusters are combined will reduce the number of linkage values that need to be calculated and increase the speed of the clustering algorithm. To this end, bcl::Cluster offers the ability to perform a “pre-clustering” step before the hierarchical clustering takes place. The pre-clustering step consists of a single pass through all objects where objects that are within a defined similarity are automatically combined to form a cluster. As the clusters are formed during the single iteration through all objects, an object will be added to a cluster if it is within the predefined similarity cutoff of any object within the cluster. In this manner, the pre-clustering step is using single linkage. After pre-clustering, agglomerative clustering proceeds as normal albeit some initial clusters will already contain multiple objects.

F. Pymol Visualization

The Python programming language can be used to interface with Pymol in a scriptable manner. Python scripts can be written which perform calculations based on data extracted directly from Pymol and perform functions within Pymol. In addition, Pymol allows simple shapes such as spheres and cylinders as well as text to be generated. These generated objects are termed compiled graphics objects, CGOs. bcl::Cluster takes advantage of these features. After clustering is complete, bcl::Cluster generates a Python script which will create the dendrogram and load any molecules for display in Pymol.

III. Results

A set of protein models and a set of small molecules with distance matrices are used to demonstrate bcl::Cluster. Up to 1000 protein models are used, with an RMSD matrix containing values ranging from 0.0 Å to 18.8 Å. Five small molecules are used with a randomly filled distance matrix assumed to be a similarity measure. The values range from 0.2 to 1.0.

A. Pymol Dendrogram Output

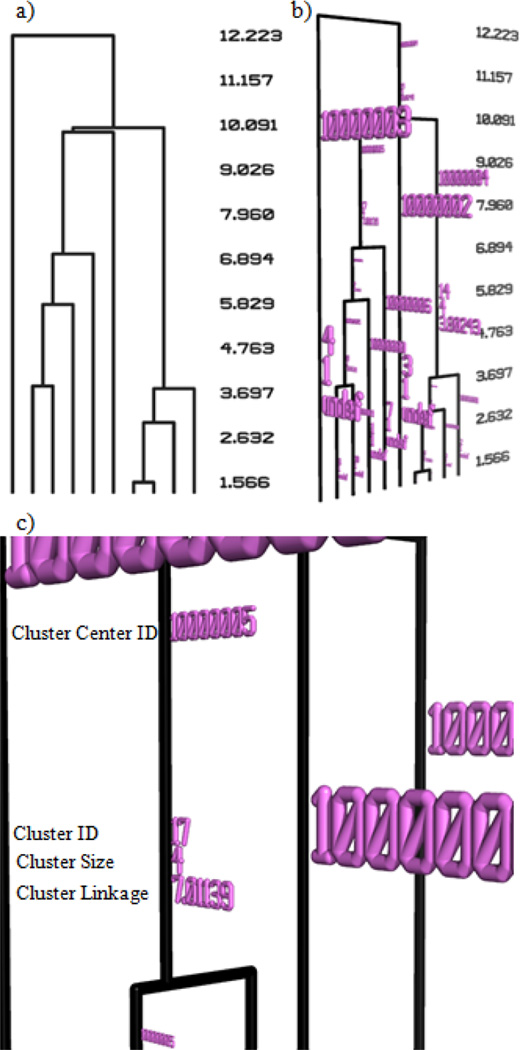
In Pymol, the dendrogram is displayed in conjunction with additional text information. The scale of linkages is shown on the right side of the dendrogram (Fig. 1(a)). In addition, information about each cluster can be displayed in front of the dendrogram (Fig. 1(b)). The information contains in order from top to bottom along the cluster (Fig. 1(c)): a.) the identifier for the object which is the center of the cluster, where the center object is calculated as the object with the smallest average distance to all other objects in the cluster; b.) a unique identification number for the cluster which can be used as a guide to find the cluster in text files created by bcl::Cluster; c.) the size of the cluster in terms of the number of objects that are contained within the cluster; d.) the linkage of the cluster.

Figure 1.

Dendrograms and cluster information generated using Pymol from the output of bcl::Cluster. (a) Simple display of a dendrogram. The numbers at right denote linkage levels of clusters. (b) Clusters within dendrograms can be labeled with information about each cluster. Displaying the dendrogram in Pymol allows the user to dynamically adjust the view. (c) A zoomed-in view of a specific cluster with the information about the cluster labeled.

B. Cluster Color Gradient

Visualization of the dendrogram in Pymol provides additional opportunities to aid in the analysis of clustering beyond directly viewing the biological molecules. Pymol allows the colors of CGOs to be specified. In bcl::Cluster, the individual clusters in the dendrogram can be colored according to a gradient indicative of some numerical descriptor. For example, the color of a cluster can indicate how similar the members of the cluster are to the native protein structure (Fig. 2(a)).

Figure 2.

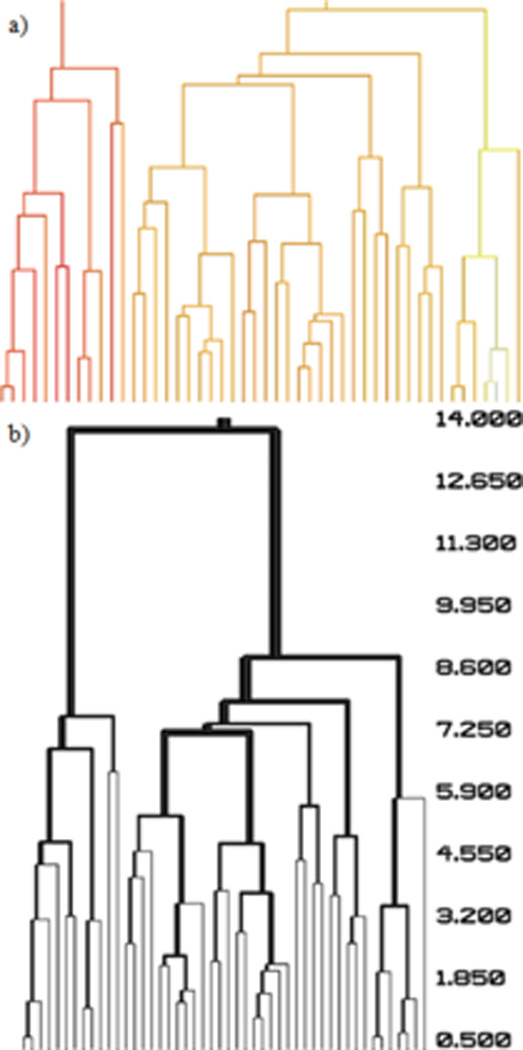
The flexibility in generating dendrograms in Pymol allows the dendrogram itself to contain more information than just the cluster hierarchy. (a) Clusters of the dendrogram are color coded according to the average RMSD to an experimental structure of cluster members. The color scheme goes from red (very similar to experimental structure) to yellow to white (less similar to experimental strucdture). (b) Clusters in the dendrogram are scaled in size according to the number of members contained within the cluster. Clusters are scaled by 3.0*sqrt(number of members - 1).

C. Cluster Radius

When defining the cylinder CGOs that comprise the dendrogram in Pymol, the desired radius is specified. bcl::Cluster can vary the radius of the cylinders according to the number of objects that are within the cluster corresponding to a cylinder (Fig. 2(b)). Scaling the visual size of a cluster with the number of members allows the user to quickly determine which clusters in the dendrogram contain the largest number of members.

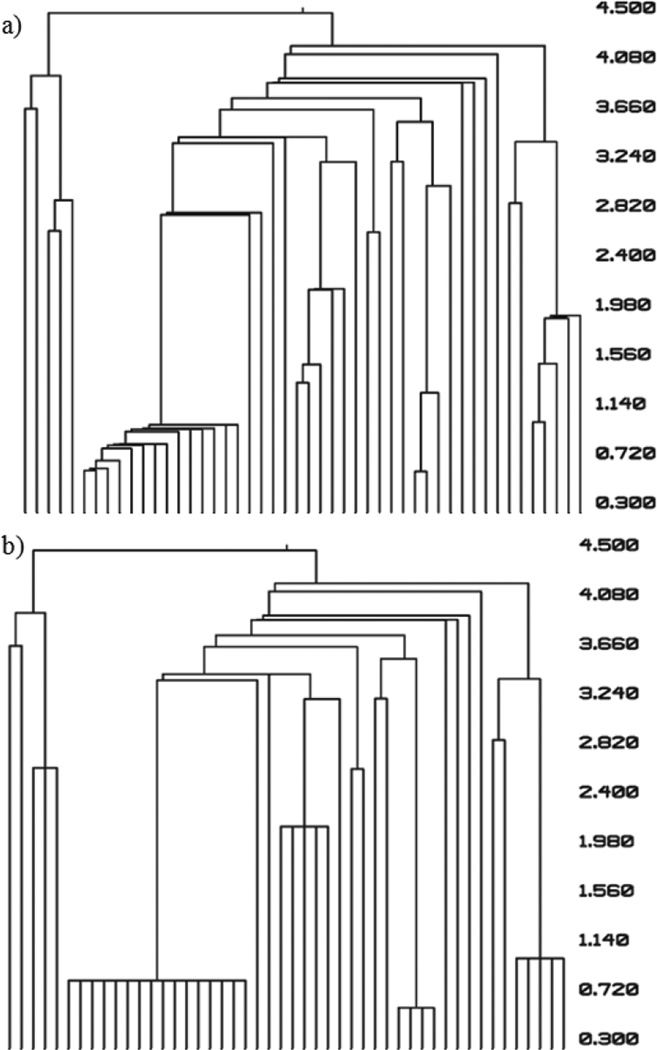
D. Pre-clustering Procedure

The pre-clustering procedure allows similar objects to be grouped into a cluster prior to hierarchical clustering (Fig. 3). Selecting an appropriate value for the distance threshold for combining objects allows pre-clustering to take place without affecting the upper regions of the dendrogram. In a test case using 1000 proteins with a pre-clustering threshold set so the effect is similar to that seen in Fig. 3, clustering is finished 20% faster.

Figure 3.

Comparison of the clustering results (a) without pre-clustering and (b) with pre-clustering. In a set of 50 protein models, a pre-clustering threshold of 3.0

Å RMDS was used to create clusters of the most similar models before hierarchical clustering was performed. The dendrogram that is obtained with the added pre-clustering step shows several models were initially clustered together.

As hierarchical clustering progresses, the differences between (a) and (b) diminish. Pre-clustering is performed in a single pass through all the objects being clustered, and it therefore reduces the number of iterations that must take place during the hierarchical clustering step.

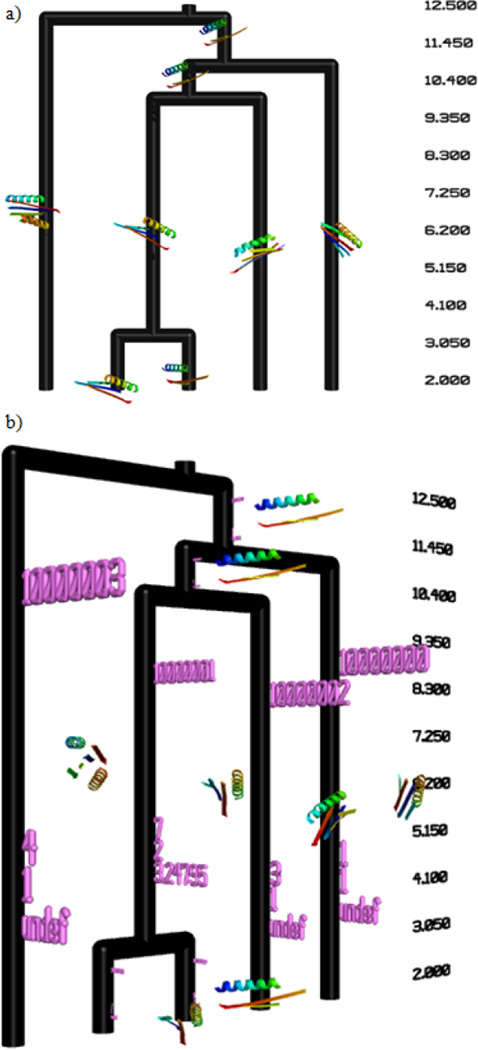
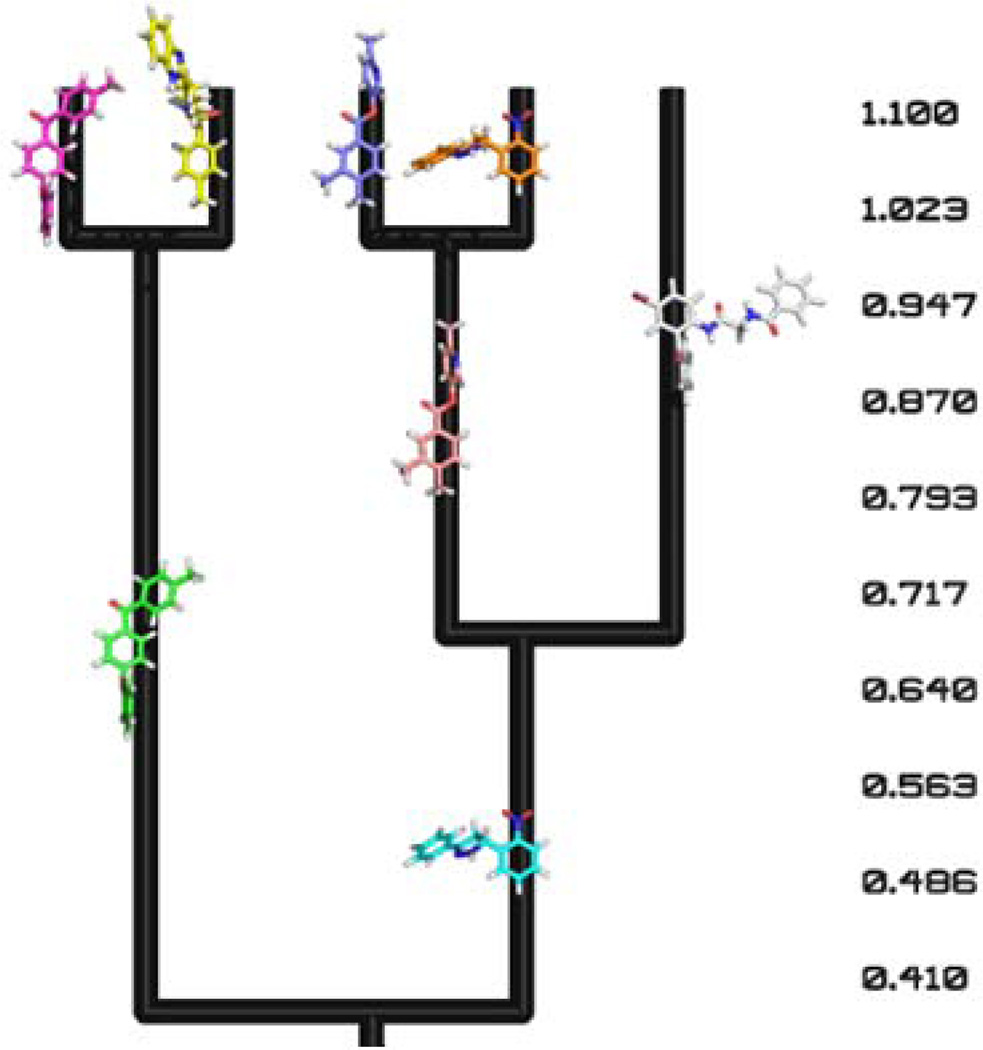
E. Display of Biological Molecules

For every cluster, the biological molecule which is the center of the cluster is displayed as a representative of that cluster (Fig. 4(a) and Fig. 5). The additional cluster information previously described can be shown along with the biological molecules (Fig. 4(b)) but is easily hidden in the Pymol environment if desired. In Fig. 5, the small molecule distance measurement is assumed to be a similarity measure, so larger distance values indicate a higher similarity between objects. As a result, the dendrogram is inverted compared to when a similarity measurement is used, as in the case of the protein model dendrogram (Fig. 4).

Figure 4.

Display of clustered proteins directly within the context of the dendrogram. The protein which is the center of the cluster is displayed as the representeative. (a) Simple view of the dendrogram with cluster center protein structures displayed. (b) Additional information about each cluster can also be displayed in conjunction with the protein structures. The cluster center id (see Fig. 1(c)) indicates the coordinate file from which the structure is created.

Figure 5.

Clustered small molecules displayed within the resulting dendrogram. Here the distances used were similarity measures such as the Tanimoto coefficient.

F. Text Output

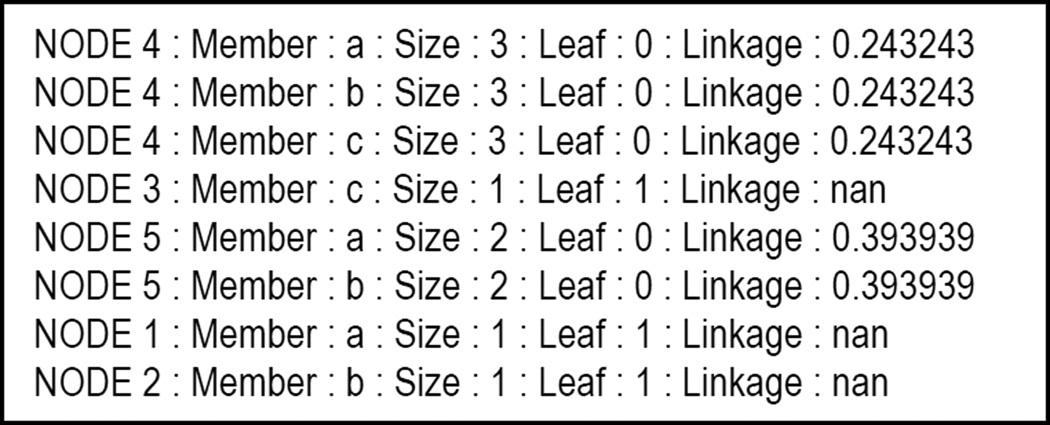
In addition to the Python script for displaying the dendrogram in Pymol, bcl::Cluster outputs information about the dendrogram in text format to facilitate quantitative analysis. Every member of every cluster is listed on a separate line with additional information (Fig. 6).

Figure 6.

Sample text output from a dendrogram created from three objects (a, b, and c). Each member of each cluster is listed on a separate line. The cluster identification and linkage is given for each member. Also, whether or not the node is at the base of the dendrogram (Leaf) is indicated by a boolean (one for true, zero for false). Linkages for clusters of only one member are undefined

IV. Discussion

This work describes the bcl::Cluster clustering method which has been developed to allow straight forward analysis of clustering of biological molecules. Pymol provides the graphical interface which displays the dendrogram resulting from the hierarchical agglomerative algorithm of bcl::Cluster. Using Pymol allows other information to be displayed to the user in addition to the dendrogram such as the actual molecular structures of the objects being clustered, cluster sizes, and color coding according to some other numerical descriptor. The user can then quickly focus on the areas of interest in the dendrogram.

One of the advantages of using Pymol is that the display of the clustering results is dynamic. The user can perform any function of Pymol while viewing the results such as zooming, translating, and hiding certain objects. When looking at large, complex dendrograms, this functionality makes it easier to view the results as compared to if the dendrogram was displayed as a static picture. However, one limitation of bcl::Cluster is the computational power needed to display a complex dendrogram and many proteins or ligands in real time in Pymol. This limitation can be partially overcome by hiding objects within the Pymol environment, but with very large datasets the dendrogram alone will grow to be the limiting factor in what can be displayed. However, the bcl::Cluster text output provides the information needed to analyze clustering results for datasets too large to view in Pymol.

The object oriented nature of the bcl::Cluster code allows additional functionality to be easily added in the future. One extension would be to add other clustering algorithms. Additional formats for inputting distance values or outputting results can also be added. The application is available from the bcl::Commons website (http://bclcommons.vueinnovations.com/).