Abstract
High-density SNP screening of panels of inbred mouse strains has been proposed as a method to accelerate the identification of genes associated with complex biomedical phenotypes. To evaluate the potential of these studies, a more detailed understanding of the fine structure of sequence variation across inbred mouse strains is needed. Here, we use high-density oligonucleotide arrays to discover an extremely dense set of SNPs in 13 classical and two wild-derived inbred strains in five genomic intervals totaling 4.6 Mb of DNA sequence, and then analyze the segmental haplotype structure defined by these high-density SNPs. This analysis reveals segments ranging from 12 to 608 kb in length within which the inbred strains have a simple and distinct phylogenetic relationship with typically two or three clades accounting for the 13 classical strains examined. The phylogenetic relationships among strains change abruptly and unpredictably from segment to segment, and are distinct in each of the five genomic regions examined. The data suggest that at least 12 strains would need to be resequenced for exhaustive SNP discovery in every region of the mouse genome, that ∼97% of the variation among inbred strains is ancestral (between clades) and ∼3% private (within clades), and provides critical insights into the proposed use of panels of inbred strains to identify genes underlying quantitative trait loci.
Most of the classical inbred mouse strains commonly used in biomedical research descend from the colonies of a single mouse breeder, Abbie Lathrop of Granby, Massachusetts, in the early 20th century (Silver 1995; Beck et al. 2000). These colonies were largely derived from European “fancy” mice (derivatives of the domesticus subspecies of Mus musculus) and East Asian “fancy” mice (derivatives of castaneus, molossinus, and musculus subspecies). It has long been recognized that because of this unique man-made bottleneck, the genomes of these inbred strains originate from a mixed but very limited pool of founders from the various subspecies (Bonhomme 1987). Recent studies using low-pass shotgun sequence and SNP genotyping data have shown that the genomes of commonly used inbred mouse strains are a recognizable mosaic of discrete segments derived from two or three sources (primarily the domesticus and musculus subspecies) and that when the sequences of any two strains are compared, long 1–2-Mb segments of either extremely high (∼40 SNPs per 10 kb) or extremely low (∼0.5 SNPs per 10 kb) variation are observed (Wade et al. 2002; Wiltshire et al. 2003). Here, we use a high-density SNP collection derived from near complete resequencing data to explore the detailed structure of these patterns across a wider array of mouse strains. With these data, we examine the phylogenetic relationships of inbred strains within segmental blocks and how those relationships change from segment to segment and genomic region to region. This enables us to much more precisely characterize the patterns of genetic variation among classical inbred strains and determine the relative contributions of strain-specific and shared ancestral variation in the mouse genome.
RESULTS
SNP Discovery and Validation
SNPs were discovered by resequencing 13 well-characterized classical inbred strains (129X1/SvJ, A/J, A/HeJ, AKR/J, BALB/cByJ, BALB/cJ, C3H/HeJ, C57BL/6J, B10.D2-Hc0 H2d H2-T18c/oSnJ [subsequently referred to as B10.D2-H2d], DBA/2J, MRL/MpJ, NZB/BlNJ, and NZW/LacJ), which were selected based solely on the fact that they are among the most commonly used strains, and two wild-derived inbred strains, Mus musculus castaneus (CAST/EiJ) and Mus musculus spretus (SPRET/EiJ). Mouse DNA sequences from five genomic intervals (NT_027761, NT_026540, NT_029829, NT_014989, MM11_Cytokine interval) ranging in length from 617,309 to 1,559,426 bp and in total comprising 4,596,781 bp were masked for repetitive sequences and the resulting 3,002,233 bp (63%) of unique sequence was assayed for variation with high-density oligonucleotide arrays. The genomic DNA of the 15 inbred mouse strains was amplified by long-range PCR (LR-PCR). We designed 439 primer pairs to generate LR-PCR products ranging from 5 to 12 kb in length covering the five genomic intervals. For each inbred strain, the LR-PCR products were pooled and hybridized to the high-density array as a single reaction. SNPs were detected as altered hybridization with a pattern recognition algorithm (Fodor et al. 1991; Chee et al. 1996; Patil et al. 2001). In total, we identified 18,366 SNPs in the 15 inbred strains, or one SNP per 157 bp tiled (Table 1). Of these, 4065 were observed as polymorphic among the 13 inbred classical strains (one SNP per 711 bp tiled) and 14,301 were observed as polymorphic only when the CAST/EiJ and SPRET/EiJ strains were included. These polymorphism rates (number of SNPs per base pair) are proportional to but considerably lower than those observed previously among inbred classical strains and between wild-derived inbred strains and classical inbred strains (Lindblad-Toh et al. 2000).
Table 1.
Characterization of the Phylogenetic Segments
| All 15 strains
|
13 lab strains
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Segment | Start | End | Length | Tiled bases | % tiled | SNPs | bp/SNP | SNPs | bp/SNP |
| A. NT_027761 | |||||||||
| 1 | 4775 | 60,623 | 55,848 | 39,942 | 72 | 178 | 224 | 27 | 1479 |
| 2 | 60,624 | 96,289 | 35,665 | 29,995 | 84 | 261 | 115 | 44 | 682 |
| 3 | 96,290 | 154,178 | 57,888 | 49,967 | 86 | 325 | 153 | 14 | 3569 |
| 4 | 154,179 | 167,379 | 13,200 | 9983 | 76 | 78 | 128 | 11 | 908 |
| 5 | 167,380 | 328,404 | 161,024 | 109,918 | 68 | 1070 | 103 | 453 | 243 |
| 6 | 328,405 | 546,803 | 218,398 | 169,859 | 78 | 1330 | 128 | 163 | 1042 |
| 7 | 546,804 | 561,088 | 14,284 | 9988 | 70 | 77 | 130 | 10 | 999 |
| 8 | 561,089 | 672,407 | 111,318 | 86,567 | 78 | 533 | 162 | 10 | 8657 |
| Entire contig | 667,625 | 506,219 | 76 | 3852 | 131 | 732 | 692 | ||
| B. NT_026540 | |||||||||
| 1 | 25 | 41,753 | 41,728 | 29,953 | 72 | 258 | 116 | 77 | 389 |
| 2 | 41,754 | 55,130 | 13,376 | 10,012 | 75 | 96 | 103 | 18 | 556 |
| 3 | 55,131 | 259,782 | 204,651 | 159,826 | 78 | 1282 | 125 | 333 | 480 |
| 4 | 259,783 | 314,496 | 54,713 | 39,967 | 73 | 280 | 142 | 59 | 677 |
| 5 | 314,497 | 343,919 | 29,422 | 9,986 | 34 | 95 | 105 | 22 | 454 |
| 6 | 343,920 | 438,863 | 94,943 | 79,952 | 84 | 666 | 120 | 182 | 439 |
| 7 | 438,864 | 452,944 | 14,080 | 9987 | 71 | 53 | 188 | 22 | 454 |
| 8 | 452,945 | 480,192 | 27,247 | 19,997 | 73 | 146 | 137 | 45 | 444 |
| 9 | 480,193 | 506,047 | 25,854 | 19,978 | 77 | 141 | 142 | 76 | 263 |
| 10 | 506,048 | 532,543 | 26,495 | 19,975 | 75 | 79 | 253 | 28 | 713 |
| 11 | 532,544 | 561,215 | 28,671 | 19,994 | 70 | 100 | 198 | 22 | 909 |
| 12 | 561,216 | 585,089 | 23,873 | 19,984 | 84 | 82 | 244 | 12 | 1665 |
| 13 | 585,090 | 617,308 | 32,218 | 29,539 | 92 | 84 | 352 | 17 | 1738 |
| Entire contig | 617,271 | 469,150 | 76 | 3362 | 140 | 913 | 514 | ||
| C. NT_029829 | |||||||||
| 1 | 1221 | 411,323 | 410,102 | 259,556 | 63 | 1165 | 223 | 196 | 1324 |
| 2 | 411,324 | 589,223 | 177,899 | 109,808 | 62 | 564 | 195 | 84 | 1307 |
| 3 | 589,224 | 1,197,358 | 608,134 | 409,304 | 67 | 1886 | 217 | 39 | 10,495 |
| 4 | 1,197,359 | 1,266,511 | 69,152 | 39,921 | 58 | 257 | 155 | 50 | 798 |
| 5 | 1,266,512 | 1,300,811 | 34,299 | 19,953 | 58 | 151 | 132 | 26 | 767 |
| 6 | 1,300,812 | 1,316,392 | 15,580 | 9978 | 64 | 78 | 128 | 18 | 554 |
| 7 | 1,316,393 | 1,558,180 | 241,787 | 154,033 | 64 | 784 | 196 | 85 | 1812 |
| Entire contig | 1,556,953 | 1,002,553 | 64 | 4885 | 205 | 498 | 2013 | ||
| D. Cytokine interval | |||||||||
| 1 | 4290 | 41,519 | 37,229 | 29,961 | 80 | 104 | 288 | 45 | 666 |
| 2 | 41,520 | 71,794 | 30,274 | 19,956 | 66 | 93 | 215 | 46 | 434 |
| 3 | 71,795 | 168,876 | 97,081 | 64,490 | 66 | 80 | 806 | 13 | 4961 |
| 4 | 168,877 | 367,752 | 198,875 | 139,833 | 70 | 1062 | 132 | 449 | 311 |
| 5 | 367,753 | 453,442 | 85,689 | 59,923 | 70 | 328 | 183 | 87 | 689 |
| 6 | 453,443 | 469,695 | 16,252 | 9,983 | 61 | 80 | 125 | 39 | 256 |
| 7 | 469,696 | 496,748 | 27,052 | 19,966 | 74 | 149 | 134 | 63 | 317 |
| 8 | 496,749 | 597,137 | 100,388 | 69,920 | 70 | 255 | 274 | 130 | 538 |
| 9 | 597,138 | 609,095 | 11,957 | 9992 | 84 | 31 | 322 | 11 | 908 |
| 10 | 609,096 | 663,488 | 54,392 | 39,992 | 74 | 179 | 223 | 94 | 425 |
| 11 | 663,489 | 704,386 | 40,897 | 29,996 | 73 | 133 | 226 | 54 | 555 |
| 12 | 704,387 | 734,769 | 30,382 | 19,968 | 66 | 116 | 172 | 67 | 298 |
| 13 | 734,770 | 795,947 | 61,177 | 49,975 | 82 | 335 | 149 | 169 | 296 |
| 14 | 795,948 | 917,066 | 121,118 | 98,423 | 81 | 544 | 181 | 211 | 466 |
| Entire contig | 912,763 | 662,378 | 73 | 3489 | 190 | 1478 | 448 | ||
| E. NT_014989 | |||||||||
| 1 | 70 | 123,575 | 123,505 | 29,942 | 24 | 222 | 135 | 32 | 936 |
| 2 | 123,576 | 358,931 | 235,355 | 109,949 | 47 | 788 | 140 | 22 | 4998 |
| 3 | 358,932 | 502,615 | 143,683 | 69,952 | 49 | 511 | 137 | 63 | 1110 |
| 4 | 502,616 | 540,102 | 37,486 | 30,003 | 80 | 388 | 77 | 165 | 182 |
| 5 | 540,103 | 552,618 | 12,515 | 9993 | 80 | 129 | 77 | 57 | 175 |
| 6 | 552,619 | 567,174 | 14,555 | 9993 | 69 | 102 | 98 | 38 | 263 |
| 7 | 567,175 | 649,219 | 82,044 | 29,977 | 37 | 230 | 130 | 60 | 500 |
| 8 | 649,220 | 821,887 | 172,667 | 71,558 | 41 | 408 | 175 | 7 | 10,223 |
| Entire contig | 821,810 | 361,367 | 44 | 2778 | 130 | 444 | 814 | ||
For each of the five contigs, the start nucleotide, end nucleotide, and length in base pairs of the phylogenetic segments are given. The number of unique base pairs synthesized onto the water (Tiled bases) and the percentage that this represents are indicated for each segment. The number of variable sites identified within each segment (SNPs) from all 15 strains (All 15 strains) and the SNP frequency (bp/SNP) calculated as the number of unique base pairs identified divided by the number of SNPs are given. The number of SNPs identified in each segmental block from the 13 classical strains (13 lab strains) excluding Mus. mus castaneus and Mus. spretus and the corresponding SNP frequencies are also given. Sequences at the beginning and end of each contig were not included in the analysis, and thus the indicated contig lengths and number of tiled bases is different from that stated in the Methods section.
To assess the reliability of our SNP detection algorithm, 78 singleton SNPs (detected in only one of the 15 strains) and 22 common SNPs (both alleles seen in more than one strain) were dideoxy-sequenced. The overall rate of validation was 98%, with 97% (76 out of 78) of the singletons and 100% of the nonsingletons (22/22) confirmed. To achieve this low false-positive rate of 2%, we required stringent thresholds for SNP detection (Fodor et al. 1991; Chee et al. 1996; Patil et al. 2001) on the high-density arrays, with an estimated false-negative rate of 53% based on previously published results using the same approach to identify human polymorphisms (Patil et al. 2001).
Identification of Ancestral Segment Boundaries in Classical Inbred Strains
We first used the high-density SNP data to determine the segmental structure of variation in classical inbred strains over extended contiguous genomic regions. To examine regional polymorphism rates between pairs of strains, the five contiguous sequences were divided into bins of 10,000 nucleotides. For each pairwise comparison, a tally of sequence differences was made for each bin and these tallies were used as input to a hidden Markov model (Wade et al. 2002), that defined regions as ancestrally identical (low SNP rate) or ancestrally divergent (high SNP rate). Across all 78 pairs of classical inbred strains, the ancestrally identical and divergent segments were determined to have average polymorphism rates of one SNP per 27 kb and one SNP per 750 bp, respectively. Considering the 53% false-negative detection rate and the rate of missing data at discovered polymorphic sites (15%), the one SNP observed per 750 bp suggests a true underlying SNP rate of 1 per 287 bp in diverged regions, consistent with the estimates in Wade et al. (2002). Ancestry breakpoints within these genomic regions were defined as locations at which any of the 78 strain-to-strain comparisons displayed a transition from either ancestral sequence identity (low SNP rate) to sequence divergence (high SNP rate) or vice versa. The intervals between these breakpoints could thus be considered segments in which each strain had a single unbroken ancestral haplotype, and the raw sequence data for these segments were then subjected to phylogenetic analysis.
Phylogenic Relationships Among Inbred Strains
Phylogenetic analysis of segments of consistent ancestry was performed using the 13 inbred classical strains along with two wild-derived strains that serve as outgroups, CAST/EiJ and SPRET/EiJ. All genotyped SNPs in the 15 strains were used to estimate genetic distances using the Kimura 2-parameter model (Kimura 1980), and from these distances, phylogenetic trees were built (Felsenstein 1989).
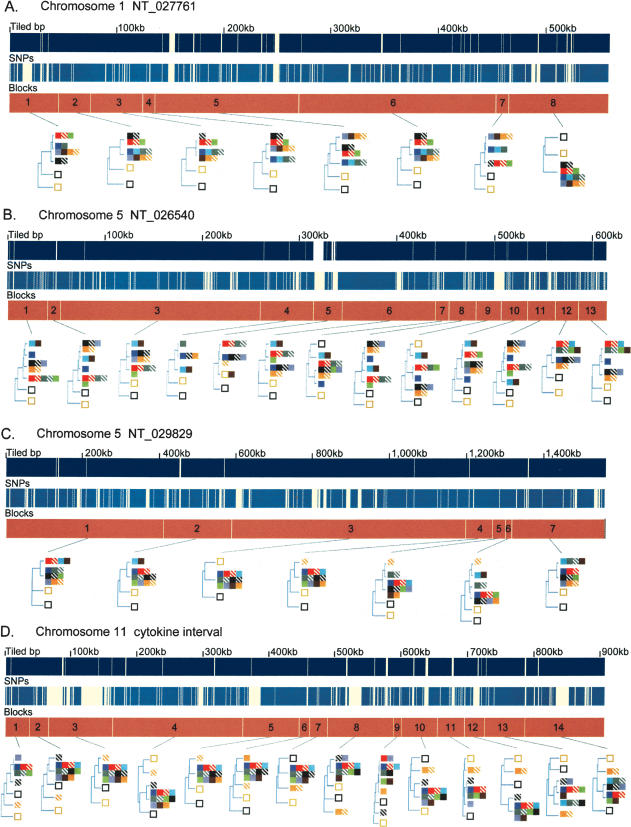
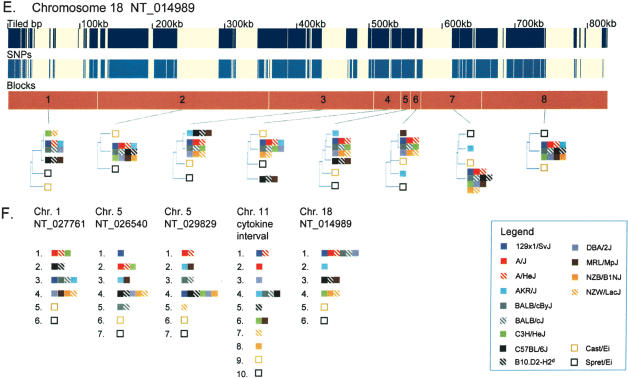
Figure 1 shows the locations of the segmental blocks identified in the five contig sequences and the phylogenetic relationships among the 15 strains within each block. A total of 50 segmental blocks averaging 92 kb in length, and ranging from 12 to 608 kb, were identified across the five genomic intervals (Table 1). For each segmental block, pairs of strains with phylogenetic distances representing less than one SNP per 10,000 nucleotides were considered ancestrally identical and collapsed into a single clade. After collapsing, the vast majority (∼97%) of the variable sites identified among the 13 inbred classical strains could be described as ancestral differences between the clades in the 50 segmental blocks (i.e., all strains within a clade share the identical genotype), whereas the small remainder (∼3%) describe differences between strains in the same clade. Excluding two sets of pairs expected to be nearly identical (A/J ∼ A/HeJ, and BALB/cJ ∼ BALB/cByJ), 53% of the pairwise comparisons within the 50 segmental blocks were defined as ancestrally identical by phylogeny and 47% were defined as divergent, underscoring the limited sequence diversity of the classical inbred lines at any one location in the genome.
Figure 1.
Phylogenetic relationships of the 13 inbred classical strains and the two wild-derived strains. (A–E) For each of the five sequence contigs, the phylogenetic relationships within adjacent segments are shown. (Top and middle panels) The locations of unique sequences represented on the high-density arrays and identified SNPs, respectively. (Third panel) The segmental block locations (numbered), the boundaries of which were determined by analyzing transition points between high SNP and low SNP blocks for all 78 pairwise sequence comparisons of the 13 inbred classical strains. The phylogenetic relationships of the 15 inbred mouse strains (color-coded squares), determined using the Kimura 2-parameter model, are shown for each segment. For the wild-derived inbred strains, CAST/EiJ and SPRET/EiJ, uneven amounts of missing data may affect the relative branch lengths of these outgroups in some trees as a result of unbalanced loss of CAST or SPRET specific polymorphisms. (F) For the five sequence contigs, classical inbred strains that were in the same phylogenetic group for every segment in the contig are shown together. Missing SNP data are ignored for this analysis. Related strains are depicted as solid and hatched squares of the same color (A/J and A/HeJ, BALB/cByJ and BALB/cJ, C57BL/6J and B10.D2-H2d, NZB/B1NJ and NZW/LacJ).
The relative distances of the clades defined by the 15 inbred strains in each segmental block are depicted in phylogenetic trees (Fig. 1). The 13 inbred classical strains have a limited number of phylogenetic patterns with typically two to three branches (minimum 1, maximum 5) across the 50 segmental blocks. The breaks in phylogenetic continuity between adjacent segmental blocks can often be attributed to a single historical recombination event in the formation of the classical inbred lines with one strain changing positions or a small number of strains (most likely sharing the same ancestral recombinant chromosome) changing positions in tandem. Frequently, the pairs of more closely related strains (A/J ∼ A/HeJ, BALB/cByJ ∼ BALB/cJ, C57BL/6J ∼ B10.D2-H2d, NZB/B1NJ ∼ NZW/LacJ) are cladistically identical across the entire genomic region. However, even highly related strains (A/J ∼ A/HeJ) do not share all haplotype patterns in common (Fig. 1D, see block 9). As expected, in most segments, the 13 classical inbred strains are more related to each other than to the two wild-derived inbred strains. However, as shown in Figure 1B (blocks 5 and 9), there are exceptions to this rule in which some classical strains are more related to one of the wild-derived strains than they are to other classical strains, underscoring the variability of the regional phylogenetic relationships and that, rather than true outgroups, wild-derived strains such as CAST/Ei represent ancestral populations beyond the domesticus and musculus subspecies that have probably made small contributions to the classical strains.
Of the 390 possible pairwise comparisons across entire genomic intervals [(13 × 12)/2 = 78 pairs per contig × 5 contigs], 78 (20%) have continuous ancestral sequence identity (i.e., occur in the same clade in every block), 29 (7%) have continuous sequence divergence (i.e., strains occur in a different clade in every block), and 283 (73%) alternate between ancestral identity and divergence (Fig. 1F). Given an average genomic interval length of 900 kb, the proportion of pairs of strains carrying continuous identity over an entire contig suggests an average ancestral segment length of 1.4 Mb in any single individual assuming that ancestral breakpoints occur randomly. However, the nature of the distribution of ancestral sequence identity and divergence for the 78 strain-to-strain comparisons differs among the five genomic intervals. Three of the five contigs (NT_027761, NT_029829, and NT_014989) contain regions where all inbred strains appear to share the same ancestral haplotype in at least one block (Fig. 1A,C,E). Such blocks are characterized by having many tiled bases but few variable sites, and the variable sites are not ancestrally derived. Although such regions have been frequently described as “SNP deserts,” there is no specific evidence that they are anything other than sampling artifacts (i.e., each strain examined having an origin in the same ancestral subspecies by chance because the founding pool is so limited). In contrast, contig NT_026540 and the Cytokine interval (Fig. 1B,D) contain no blocks in which all strains appear to be ancestrally identical.
Number of Strains Required for SNP Discovery in the Mouse Genome
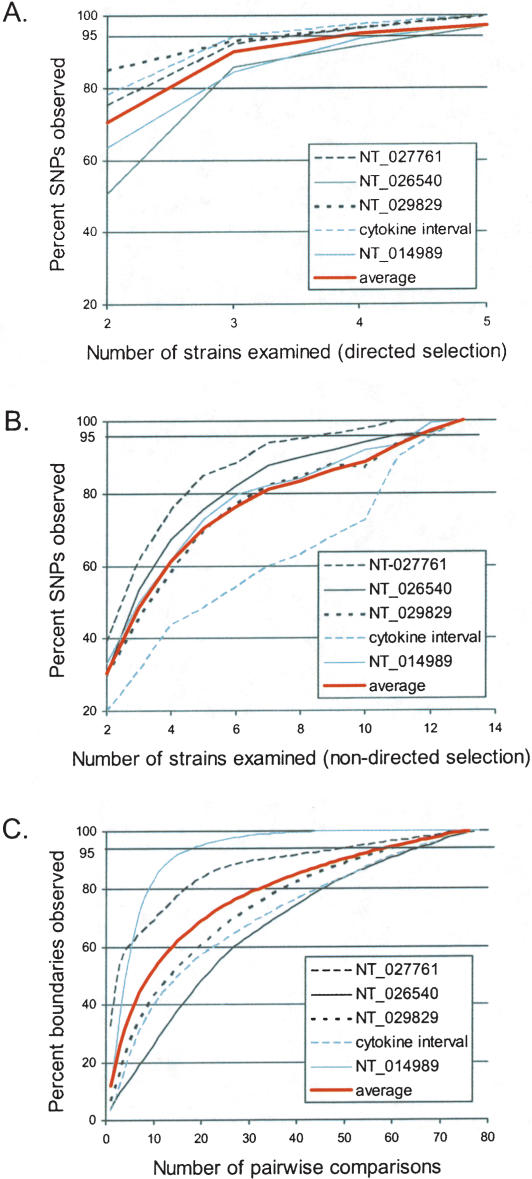
To estimate the number of strains required for thorough SNP discovery in the mouse genome, we determined the minimum number of inbred classical strains required to capture >95% of the variable sites observed in the data set. When a directed selection method based on the calculated divergence of the strains across the entire contig was used, each of the five genomic regions had a different set of inbred classical strains selected, and on average only four optimally selected inbred lines were required to capture >95% of the variable sites observed (Fig. 2A). These results demonstrate that for any given region in the mouse genome only a small number of classical inbred lines would be required to observe the majority of the variation. However, the set of classical inbred lines that provides this information varies from region to region, and thus a significantly larger set of strains will need to be used for more comprehensive SNP discovery in the mouse genome. When the strains were randomly selected for this analysis, the average number of classical inbred lines needed to capture 95% of the observed variation was 12, although one contig (NT_027761) required only nine classical inbred lines, and one contig (NT_026540) required only 11 classical inbred lines (Fig. 2B). These results suggest that for thorough SNP discovery in the mouse genome, at least 12 (and likely more) classical inbred lines will need to be examined. In a second analysis, we determined the minimum number of pairwise comparisons between classical inbred strains required to capture >95% of the segmental block boundaries (Fig. 2C). On average, the random sampling of 63 pairs of strains (which is the equivalent to resequencing 12 individual strains) was required. These results further support the idea that a significant number of inbred classical strains will need be examined to create comprehensive genomic resources for mouse genetics.
Figure 2.
The number of strains required to capture >95% of the observed variation was calculated both by determining how many of the 13 inbred classical strains were needed to detect >95% of the SNPs (A,B) and by determining how many of the 78 pairwise comparisons of the inbred classical strains were needed to observe >95% of the segmental block boundaries (C). (A,B) The percent of SNPs observed versus the number of inbred classical strains examined was determined for each contig individually as well as the average across all five contigs. (A) Directed selection of strains based on their level of divergence (based on the Kimura 2-parameter distance), starting with the most divergent. (B) The selection of inbred strains was random (nondirected selection), with the process being repeated 100 times, and the average results for each contig and across all five contigs shown. (C) The percent of segmental boundaries observed versus the number of inbred classical pairwise comparisons examined is shown for each contig individually as well as the average across all five contigs. Intervals containing relatively few segmental blocks, such as NT_014989, require fewer pairs of strains, and intervals containing an above-average number of segmental blocks, such as NT_026540, require more pairs of strains.
DISCUSSION
We have used the extensive resequencing of 15 strains of mice across five megabase-sized genomic regions to explore questions of keen interest to mouse genetics: the balance between common ancestral and rare private polymorphism in classical inbred strains, the extent of ancestral haplotypes, and the local phylogenetic relationships among classical inbred strains. The landscape of variation across panels of classical inbred strains has important implications for the design and interpretation of murine haplotype maps, for their potential utility in positional cloning, and for the rational design of subsequent murine resequencing projects. Most significantly, we find that the phylogenetic relationships among the classical inbred strains examined have an extremely simple local structure. Within segmental blocks, which in this data set range in size from 12 to 608 kb, all 13 classical inbred lines can be described with a phylogeny containing typically just two or three clades that represent significantly diverged ancestral haplotypes. As previously described (Wade et al. 2002), in most cases these clades will represent the contributions of different ancestral subspecies of M. musculus (most often domesticus and musculus) but in some cases could also represent multiple diverged sequences from the same subspecies. These phylogenetic relationships change abruptly and unpredictably between neighboring segmental blocks (so-called ancestry breaks), likely in most cases the result of historical recombination events that occurred during the formation of the classical inbred lines. Importantly, differences between the clades comprise 97% of the variable sites discovered in this experiment, whereas the much rarer remainder is made up of private, often strain-specific variation, which, given the very recent coancestry of these strains, may often represent rare sites that were polymorphic among closely related sequences from the same subspecies that made up the founders of the classical inbred strains. These data are consistent with the historical description of the creation of the inbred classical strains through the interbreeding of mice derived from mixtures of isolated derivatives of M. musculus domesticus, M. musculus musculus, and to a lesser extent, Mus musculus molossinus and Mus musculus castaneus.
SNP-based “association-style” scans (in the context of positionally cloning established QTLs and perhaps de novo genome screens for genetically simpler phenotypes) across panels of classical inbred strains appear poised to become an important tool for identifying genes underlying complex phenotypes such as obesity, cancer, aging, hypertension, diabetes, and senescence in mice. To perform SNP-based association studies, a genome-wide fine-structure map of the sequence variation among commonly used classical inbred mouse strains is needed. Our findings indicate that to accurately determine this segmental phylogenetic structure, at least 12 randomly selected classical inbred lines would have to be thoroughly examined for variation to discover an adequate set of SNPs covering all areas of the genome. Theoretical calculations based on the observation that >50% of the genome in any pairwise comparison of strains appears identical would suggest a similar figure. Indeed, existing sequencing done in addition to the completed C57BL/6J genome sequence, both in the public domain (strains 129/SvImJ, C3H/HeJ, and BALB/cByJ) and at Celera (strains 129/S1, 129/X1, A/J, and DBA2/J), show that although most of the genome contains a high density of discovered polymorphisms, there are several long regions with few or no SNPs discovered as a result of the chance sharing of the same ancestral haplotype by all strains examined thus far. Analysis of additional classical inbred strains will complete the identification of a minimum set of SNPs needed to distinguish the phylogenetic clades in each segment. On average, one to three SNPs per segment should be sufficient to distinguish between the different phylogenetic patterns. Based on the identification of 50 segmental blocks in 4.6 Mb when 13 classical inbred lines are studied, we might expect to find at least 25,000 phylogenetically distinct segments across an entire 2.5-Gb genome. Thus, the genotyping of ∼50,000 pattern-defining SNPs in a large panel of classical inbred lines should allow for the determination of the phylogenetic relationships among the most commonly used strains for each segment in the mouse genome. These data would then allow for panels of classical inbred mouse strains to be used to rapidly positionally identify genes associated with complex traits.
The data analysis also suggests an obvious synergy between the “haplotype map” constructed from those 50,000 SNPs and the deeper resequencing desired to capture a complete set of SNPs and to catalog more exhaustively coding and other putatively functional variation. The haplotype patterns inferred from SNP mapping of unsequenced strains will often be grouped into local clades with one or more strains that have been sequenced. In these cases, we will be able to approximately infer the complete sequence of the unsequenced strain in that region based on the shared haplotype. However, haplotype structure inferred from SNP mapping over a larger panel of strains will also identify strains that carry unique patterns in specific regions that may warrant resequencing. Thus, if one uses prior knowledge of the local phylogenetic relationships among strains, there would be a significant gain in efficiency of resequencing to capture the complete set of functional SNPs in the mouse genome.
METHODS
Inbred Mouse Strains
Genomic DNA was obtained from The Jackson Laboratory (Bar Harbor, Maine) for the following 13 classical inbred mouse strains, 129X1/SvJ (Jackson Laboratory stock 000691), A/J (stock 000646), A/HeJ (stock 000645), AKR/J (000648), BALB/cByJ (stock 001026), BALB/cJ (stock 000651), C3H/HeJ (stock 000659), C57BL/6J (stock 000664), B10.D2-Hc0 H2d H2-T18c/oSnJ (stock 000461) [referred to as B10.D2-H2d], DBA/2J (stock 000671), MRL/MpJ (stock 000486), NZB/BlNJ (stock 000684), and NZW/LacJ (stock 001058), and the two wild-derived inbred strains, CAST/EiJ (stock 000928), and SPRET/EiJ (stock 001146). B10.D2-H2d is a congenic strain that carries the H2d haplotype from DBA/2J following six generations of backcrossing to C57BL/10Sn.
High-Density Oligonucleotide Array Design
The following contig sequences were selected from the NCBI mouse sequence database: Chr1 NT_027761.2 (from NCBI dated 1/29/2002, 673,299 bp), Chr5 NT_026540.2 (1/29/2002, 617,309 bp), Chr5 NT_029829.1 (1/29/2002, 1,559,426 bp), and Chr18 NT_014989.4 (1/29/2002, 828,142 bp). Chr11 (MM11_Cytokine interval, 918,605 bp) was assembled as previously reported (Dubchak et al. 2000). In all, 4,596,781 bp of genomic sequence from the five intervals was masked for repetitive sequence using RepeatMasker (http://ftp.genome.washington.edu/RM/RepeatMasker.html; A.F.A. Smit and P. Green, unpubl.), and the resulting 3,002,233 bp of unique sequence was used to design a high-density oligonucleotide array for SNP detection (Fodor et al. 1991; Chee et al. 1996; Patil et al. 2001). The array was designed such that each base of the reference sequence was interrogated by eight 25-nt oligonucleotides synthesized and attached to a glass surface.
SNP Detection
A total of 439 LR-PCR reactions were designed to amplify the five intervals represented on the arrays with an average size of 10.5 kb per amplicon. LR-PCR was performed using DNA from each of the 15 strains as previously described (Patil et al. 2001). The PCR products for each strain were combined into one tube, concentrated by Centricon-30 column purification (Millipore), fragmented with DNase I (Roche), biotinylated using terminal deoxytransferase (Roche), and hybridized to the high-density oligonucleotide arrays (Affymetrix Inc.) for 16 H at 50°C (Patil et al. 2001). Following hybridization, the arrays were stained with Phycoerythrin-conjugated-Streptavidin, washed at high stringency, and scanned. SNPs were detected based on altered hybridization patterns as previously described (Wang et al. 1998; Lindblad-Toh et al. 2000; Patil et al. 2001). The 18,366 SNPs identified in this study are part of a larger set of SNPs (ss20399387–ss20418279) that have been submitted to the NCBI dbSNP database.
SNP Validation
To estimate the SNP false-positive rate, we randomly selected 78 singleton SNPs (those present in only one strain) and 22 common SNPs (those present in at least two strains) for validation by dideoxy sequencing. The SNP loci were amplified using the same LR-PCR primers as for SNP detection, and sequenced using locus-specific primers on an ABI377 Sequencer (Applied Biosystems).
Identification of Segmental Block Boundaries in Inbred Classical Strains
For each of the five sequence contigs, the nonrepetitive sequences synthesized on the high-density arrays were divided into bins of 10,000 nt. Because repetitive elements were not counted, the bins frequently spanned >10,000 contiguous nucleotides. The last bin on each contig was allowed to be smaller. The position of the start nucleotide, end nucleotide, and the number of SNPs observed in each bin was recorded.
All pairs of DNA sequences from the 13 classical inbred strains were compared to discover clear points of transition from low SNP rate to high SNP rate. SNP rates from each 10,000-nt bin were analyzed by a hidden Markov model (HMM) fitted for a two-state model of low SNP rate and high SNP rate using the forward–backward algorithm (Wade et al. 2002). The HMM was used to assign the probability of the bin being in a state of divergence between the pair of strains analyzed. Observation probabilities were assigned based on the observed SNP rate in each bin, with missing observations at variable sites counted as one-half for this purpose only. All 78 pairwise comparisons among the 13 inbred classical strains were individually analyzed using the HMM algorithm. Block boundaries of continuous sequence similarity or divergence for each of the 78 pairwise comparisons were determined by the distances between the start nucleotide of the first bin and the end nucleotide of the last bin where consecutive bins met “low” or “high” SNP rate criteria, respectively. Starting values were derived from the results using this model as described in Wade et al. (2002).
All 78 pairs of comparisons were examined, and any point at which a pair of strains displayed a probable transition from low to high SNP rate or vice versa was defined as an ancestral breakpoint. The segments between these ancestral breakpoints were defined as the blocks for which phylogenetic analysis of the raw sequence data were later performed. In some cases, missing data resulted in either artifactual or misplaced boundaries. After the phylogenetic analysis of each distinct block, adjacent blocks with the identical phylogenetic tree relating all strains were merged and reanalyzed.
Given an average genomic interval length of 900 kb, the proportion of pairs of strains carrying continuous identity over an entire contig suggests an average ancestral segment length among classical inbred strains of 1.5 Mb when breakpoints occur at random according to a Poisson distribution. This estimate is derived from the fact that there is at most a two-thirds probability that two strains share identity at any point and that we observe 20% of strain pairs showing complete identity across an average of 900 kb, which suggests a mean rate of transition of 1.2 per 900 kb (1 per 750 kb), because 0.67 exp(–1.2) ∼ 0.20. Because an ancestral transition in either one of the pair of strains will generate a transition from identity to divergence, on average an ancestral segment will be 1.5 Mb in length.
Haplotype Phylogeny
After the segmental block boundaries were established, the individual SNP sequences of all 15 strains within these intervals were analyzed to assess their phylogenetic relationships. If the sequences within a segmental block contained six or more SNPs and all 15 inbred strains had >70% of the SNPs in the block successfully genotyped, then these nucleotide sequences were written to a multisequence file in Phylip format (Felsenstein 1989), and phylogenetic distances were calculated using a custom script with the Kimura 2-parameter model (Kimura 1980) assuming a transition–transversion ratio of 2.0. For each segmental block, transition–transversion rates were calculated between pairs of strains from the observed SNPs and the number of base pairs represented on the array. The output was a two-dimensional matrix of genetic distances between strains determined from the ratio of the between-pair nucleotide substitution rate (substitutions per base examined) to the total nucleotide substitution rate within the segment adjusted for the transition–transversion ratio. Because the actual phylogenetic distances among different mice were quite small by normal phylogenetic standards, the distances were magnified 1000-fold to prevent rounding errors. The strains with distances less than one SNP per 10,000 nt examined were collapsed into groups (haplotypes) by averaging the individual distances first in columns and then in rows of the matrix. The original matrix was then redrawn to reflect haplotype × haplotype pattern distances. An outcall was made to the “kitsch” module of Phylip (Felsenstein 1989). The “treefile” of haplotypes produced by this call was captured and dynamically drawn to an image file for each segmental block.
Number of Strains Required to Capture >95% of the Available Variation
To determine the number of inbred classical strains required to identify >95% of the observed SNPs, we compared two inbred classical strains, recorded the number of SNPs identified, then added one more inbred classical strain to the mix, recorded the number of SNPs identified between the three strains, and continued adding strains one at a time to the analysis until >95% of the SNPs had been accounted for. The selection of inbred strains for addition was performed using both nondirected and directed methods. Nondirected selection, in which classical inbred strains were randomly selected, was replicated 100 times, and the results were averaged for each of the five sequence contigs. Directed selection was performed on the basis of divergence (based on the Kimura 2-parameter distance), with the most divergent strains selected first, followed by the next most divergent, and so on. We also determined the minimum number of pairwise comparisons required to capture >95% of the segmental block boundaries by randomly sampling results from the hidden Markov model files. We determined the number of boundaries identified between two inbred classical strains, and then added randomly selected pairwise comparisons of inbred classical strains to the mix for analysis until >95% of the haplotype block boundaries were found. This was replicated 1000 times for each of the five contigs, and the average number of pairwise comparisons required to capture >95% of the boundaries was recorded.
Acknowledgments
We thank Erica Beilharz for assistance with manuscript preparation, Geoff Nilsen and Wade Barrett for designing the high-density arrays and assistance with data analysis, and Preeti Jain for assistance with DNA sample preparation and hybridization of the high-density oligonucleotide arrays. We thank Kerstin Lindblad-Toh, Andrew Kirby, and Itsik Pe'er for helpful discussions.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.2627804.
Footnotes
[The 18,366 SNPs identified in this study are part of a larger set of SNPs (ss20399387–ss20418279) that have been submitted to the NCBI dbSNP database.]
References
- Beck, J.A., Lloyd, S., Hafezparast, M., Lennon-Pierce, M., Eppig, J.T., Festing, M.F., and Fisher, E.M. 2000. Genealogies of mouse inbred strains. Nat. Genet. 24: 23–25. [DOI] [PubMed] [Google Scholar]
- Bonhomme, F., Guenet, J.-L., Dod, B., Moriwaki, K., and Bulfield, G. 1987. The polyphyletic origin of laboratory inbred mice and their rate of evolution. J. Linn. Soc. 30: 51–58. [Google Scholar]
- Chee, M., Yang, R., Hubbell, E., Berno, A., Huang, X.C., Stern, D., Winkler, J., Lockhart, D.J., Morris, M.S., and Fodor, S.P. 1996. Accessing genetic information with high-density DNA arrays. Science 274: 610–614. [DOI] [PubMed] [Google Scholar]
- Dubchak, I., Brudno, M., Loots, G.G., Pachter, L., Mayor, C., Rubin, E.M., and Frazer, K.A. 2000. Active conservation of noncoding sequences revealed by three-way species comparisons. Genome Res. 10: 1304–1306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein, J. 1989. PHYLIP—Phylogeny Inference Package (Version 3.2). Cladistics 5: 164–166. [Google Scholar]
- Fodor, S.P., Read, J.L., Pirrung, M.C., Stryer, L., Lu, A.T., and Solas, D. 1991. Light-directed, spatially addressable parallel chemical synthesis. Science 251: 767–773. [DOI] [PubMed] [Google Scholar]
- Kimura, M. 1980. A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. J. Mol. Evol. 16: 111–120. [DOI] [PubMed] [Google Scholar]
- Lindblad-Toh, K., Winchester, E., Daly, M.J., Wang, D.G., Hirschhorn, J.N., Laviolette, J.P., Ardlie, K., Reich, D.E., Robinson, E., Sklar, P., et al. 2000. Large-scale discovery and genotyping of single-nucleotide polymorphisms in the mouse. Nat. Genet. 24: 381–386. [DOI] [PubMed] [Google Scholar]
- Patil, N., Berno, A.J., Hinds, D.A., Barrett, W.A., Doshi, J.M., Hacker, C.R., Kautzer, C.R., Lee, D.H., Marjoribanks, C., McDonough, D.P., et al. 2001. Blocks of limited haplotype diversity revealed by high-resolution scanning of human chromosome 21. Science 294: 1719–1723. [DOI] [PubMed] [Google Scholar]
- Silver, L.M. 1995. Mouse genetics. Oxford University Press, New York.
- Wade, C.M., Kulbokas III, E.J., Kirby, A.W., Zody, M.C., Mullikin, J.C., Lander, E.S., Lindblad-Toh, K., and Daly, M.J. 2002. The mosaic structure of variation in the laboratory mouse genome. Nature 420: 574–578. [DOI] [PubMed] [Google Scholar]
- Wang, D.G., Fan, J.B., Siao, C.J., Berno, A., Young, P., Sapolsky, R., Ghandour, G., Perkins, N., Winchester, E., Spencer, J., et al. 1998. Large-scale identification, mapping, and genotyping of single-nucleotide polymorphisms in the human genome. Science 280: 1077–1082. [DOI] [PubMed] [Google Scholar]
- Wiltshire, T., Pletcher, M.T., Batalov, S., Barnes, S.W., Tarantino, L.M., Cooke, M.P., Wu, H., Smylie, K., Santrosyan, A., Copeland, N.G., et al. 2003. Genome-wide single-nucleotide polymorphism analysis defines haplotype patterns in mouse. Proc. Natl. Acad. Sci. 100: 3380–3385. [DOI] [PMC free article] [PubMed] [Google Scholar]
WEB SITE REFERENCES
- http://ftp.genome.washington.edu/RM/RepeatMasker.html; RepeatMasker.