Indel-Based Evolutionary Distance and Mouse–Human Divergence

Abstract

We propose a method for estimating the evolutionary distance between DNA sequences in terms of insertions and deletions (indels), defined as the per site number of indels accumulated in the course of divergence of the two sequences. We derive a maximal likelihood estimate of this distance from differences between lengths of orthologous introns or other segments of sequences delimited by conservative markers. When indels accumulate, lengths of orthologous introns diverge only slightly slower than linearly, because long indels occur with substantial frequencies. Thus, saturation is not a major obstacle for estimating indel-based evolutionary distance. For introns of medium lengths, our method recovers the known evolutionary distance between rat and mouse, 0.014 indels per site, with good precision. We estimate that mouse–human divergence exceeds rat–mouse divergence by a factor of 4, so that mouse–human evolutionary distance in terms of selectively neutral indels is 0.056. Because in mammals, indels are ∼14 times less frequent than nucleotide substitutions, mouse–human evolutionary distance in terms of selectively neutral substitutions is ∼0.8.

Evolutionary distance (ED) between two homologous DNA sequences is defined as the per nucleotide site number of mutations that have been fixed in the course of evolution of the sequences from their last common ancestor. For not-too-tightly related sequences, ED exceeds their dissimilarity (DS), the per site number of differences between the properly aligned sequences. This happens because several mutations can affect the same site. Different methods of inferring the number of such multiple hits from the observed DS often produce rather different estimates of ED (see Li 1997; Nei and Kumar 2000). For example, figures for Ks, the number of substitutions per synonymous site, range from 0.45 (Makalowski and Boguski 1998) to 0.60 (Waterston et al. 2002; Rat Genome Sequencing Project Consortium 2004), 0.65 (Cooper et al. 2004), 0.73 (Castresana 2002), and 0.74–0.80 (Smith and Eyre-Walker 2003; Table 1) for the evolutionary path between mouse and human.

Table 1.

Summary of Notations

L1,L2	lengths of two orthologous timer sequences
Δ = L1-L2	difference of lengths of timer sequences
δ	length of an individual indel
I	fraction of insertions among all indels
A	fraction of indels which occurred in the first of the two lineages
a	probability that an indel increases Δ
p(δ)	distribution of δ of all indels
Pi(δ), Pd(δ)	distributions of length of insertions and of deletions
p+(δ), p-(-δ)	distributions of indels with only positive and only negative values of δ
pm(δ), ph(δ)	distribution of indel length in muroids and in primates
k	number of indels on the path between two timer sequences
fk(Δ)	distribution of Δ between two timer sequences with a certain k
T	number of generations of independent evolution of timer sequences
b	per nucleotide site per generation probability of an indel fixation
q = bT	average per site number of accumulated indels
u(k)	probability of a timer of length L accumulating k indels, under a given q
Ii(q)	likelihood function for the i-th timer sequence
I(q)	likelihood function for a set of timer sequences
q^	maximal likelihood estimate of q

ED is usually estimated on the basis of single nucleotide substitutions. Then, each site serves as an independent timer, which is advantageous when only short sequences are available. However, substitution-based ED also has two substantial limitations.

First, as DS at single-site timers can assume only two states (match or mismatch), it rapidly reaches saturation when ED increases. In the simplest case of equally frequent nucleotides and no selective constraint, DS approaches 0.75 and ED is almost impossible to estimate when the number of hits per timer exceeds two or three (see Li 1997; Nei and Kumar 2000). Thus, ED between even moderately distant species can be determined only for slowly evolving non-neutral sequences. The rate of evolution of sequences affected by selection depends not only on the mutation rate, but also on the population size and the mode and strength of selection.

Second, even when the number of hits per neutral site is below one or two, so that recovering ED from DS may be feasible, selectively neutral sequences often cannot be used, due to their unreliable alignments. Even for placental mammals from different orders, accumulated insertions and deletions often make it impossible to establish homology of individual sites within introns and other noncoding sequences (Shabalina et al. 2001). Thus, ED can be estimated only for sites that are embedded into conservative sequences, such as synonymous coding sites. However, synonymous sites are not entirely free from selective constraint (Hellman et al. 2003).

Thus, it may be preferable to estimate ED on the basis of length-difference mutations, insertions, and deletions (indels). Then, a timer is the segment of the sequence delimited by unambiguous markers, for example, an intron flanked by conservative exons. Availability of large-scale sequence data makes such long timers acceptable. If homologous timer sequences are similar enough to allow their unambiguous alignments, the indel-based ED between them must be close to their indel-based DS, the number of gaps in their alignment over its length. Recently, methods of phylogenetic reconstruction based on individually recognizable indels become available (see Sanchis et al. 2001). However, indel-based ED between more distant, unalignable timer sequences must be estimated from the differences between their lengths.

Indel-based ED is less prone to saturation than substitution-based ED, due to two factors. First, lengths of two homologous segments of DNA can diverge almost without a limit. Second, as indels are less common than substitutions, even distant sequences can be compared without encountering too many hits.

This study is concerned with estimating indel-based ED between unalignable timer sequences. We derive a maximal likelihood estimate of indel-based ED, test it by recovering the known ED between rat and mouse, and apply it to estimate ED between mouse and human.

METHODS

First, let us assume that we know the distribution p(δ) of the length δ of individual indels that occurred in a timer sequence (e.g., an intron) in the course of evolution of a pair of species (e.g., mouse and human) from their last common ancestor (Table 1 presents the notations). We arbitrarily assign one (mouse) sequence to be the first, and the other (human) the second. The lengths of these timer sequences are L₁ and L₂, respectively, and Δ = L₁–L₂. Then, an indel of positive length makes the mouse sequence longer than the human sequence, and vice versa. Usually, we cannot tell a deletion in the murine lineage from an insertion of the same length in the human lineage. Thus, an indel of a positive (negative) length was either an insertion into murine (human) lineage or a deletion from human (murine) lineage.

If different indels are fixed independently, the distribution f_k(Δ) of length difference between two timer sequences such that k indels have been fixed on the evolutionary path connecting them is related to p(δ) through successive convolutions [with f₁(Δ) = p(δ)]:

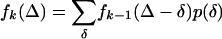(1)

We need to recover k, the per timer number of indels, from the observed Δ. To simultaneously use information on many timers, each with its own value of Δ, we adopt the following model. Let us assume that the per nucleotide site per generation probability b of an indel fixation is the same for all timers, and that the path connecting the two species consisted of T generations. Then, the probability of a timer of length L accumulating k indels has Poisson distribution

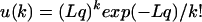(2)

where q = bT is the average per site number of fixed indels, that is, the sought indel-based ED. We will estimate this common parameter q from all of the timers simultaneously. The length of a timer L, which, in fact, changes in the course of its evolution, is approximately assumed to be (L₁ + L₂)/2.

Because there are no a priori restrictions on k, the likelihood function for q for the i-th timer with length difference Δ_i is

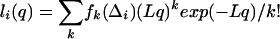(3)

For a set of many independent timers,

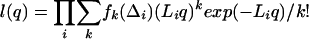(4)

The value of q which maximizes l(q), q^, is the maximal likelihood estimate of q for this set.

Now, let us address the problem of estimating p(δ). Of course, we cannot directly ascertain p(δ) for mouse and human or any other pair of species too distant for unambiguous alignments of timer sequences (and if alignments are reliable, there is no need to estimate q). However, we can ascertain two analogous small-scale distributions, p_m(δ) and p_h(δ), for the compared distant species and their corresponding sufficiently close relatives, for example, rat for mouse and Old World monkeys (OWM, family Cercopithecidae) for human, and try to infer large-scale p(δ) from them. In the simplest case of an invariant mode of indel accumulation, p(δ) and both the small-scale distributions would be identical. This is likely, although not guaranteed, if p_m(δ) and p_h(δ) are similar enough. In the opposite extreme case of an arbitrarily varying mode of indel accumulation, there is no obvious way to estimate p(δ). Finally, there may be intermediate situations where p(δ), although not identical to p_m(δ) and p_h(δ), still can be estimated.

We will consider probably the most realistic among such intermediate situations. It is easy to see that

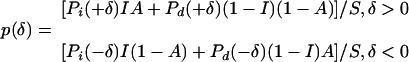(5)

where I is the fraction of insertions among all indels, A is the fraction of all indels that occurred in the first (murine) lineage (A depends on relative generation times and per generation indel rates in the two lineages), P_i(δ) (P_d(δ)) is the probability that an insertion (deletion) has the length δ, and S is a normalizing constant. We will assume that P_i(δ) and P_d(δ) are the same for all the three distributions and consider the consequences of changes in A and I. We will also assume that P_i(δ) = P_d(δ) = P(δ), that is, that distributions of length of insertions and of deletions coincide. If so, the shapes of the branches of p(δ), that is, the distributions corresponding to only positive or only negative values of δ, p₊(δ) and p_–(–δ), are always the same and coincide with P(δ), and the probability that an indel has positive length is given by:

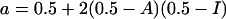(6)

Thus, with I = 0.5 or A = 0.5, p(δ) is always symmetric. Otherwise, the areas under the positive and negative branches of p(δ), a, and 1 – a, become unequal.

We will ascertain P(δ) from the small-scale distributions p_m(δ) or p_h(δ) and then seek p(δ) as

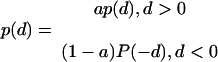(7)

The asymmetry parameter a will be estimated from the relationship of differences between the lengths of timer sequences and absolute values of these differences.

We identified 8817 of triplets of mouse, rat, and human orthologous protein-coding genes, using the standard reciprocal best hit approach (Tatusov et al. 1997). These genes contain 37,110 triples of orthologous introns. Using OWEN (Ogurtsov et al. 2002), we produced pairwise alignments of orthologous introns. Rat–mouse alignments are essentially unambiguous. In contrast, mouse–human and rat–human alignments are mostly unreliable. Also, we identified 255 pairs of orthologous genes in human and Old World monkeys, and created 1747 unambiguous alignments of their orthologous introns.

RESULTS

Figure 1 presents data on distributions of lengths of individual indels within alignments of orthologous introns. Figure 1A displays p_m(δ) and p_h(δ). Area under the positive branch, a, is 0.46 (605,079 indels of positive lengths vs. 715,175 indels of negative lengths) in p_m(δ) and 0.48 (12,866 vs. 13,801) in p_h(δ), reflecting the fact that gaps in the first of the aligned sequences (rat or human) are slightly more common than in the second sequence (mouse or OWM).

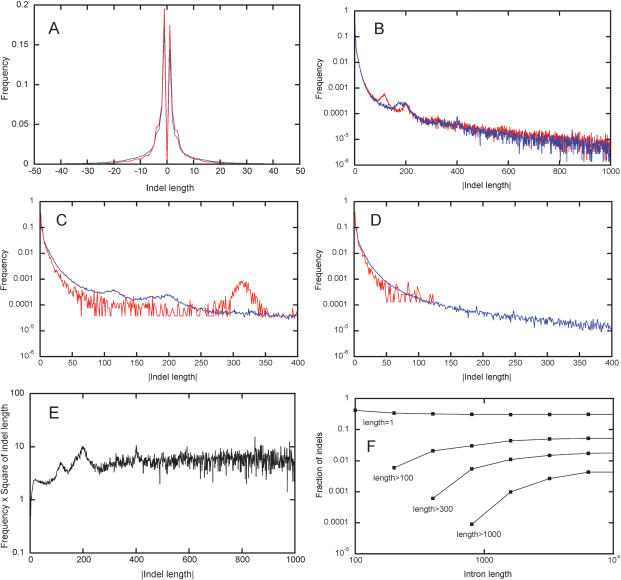
Figure 1.

Lengths of individual indels. p_m(δ) and p_h(δ), distributions of lengths of all indels in all alignments (A) of rat–mouse (blue line) and human–OWM (red line) intron pairs. p₊(δ) and p_–(–δ), distributions of the absolute value of length of indels of only positive lengths (red line) and only negative lengths (blue line) in all rat–mouse alignments (B). P(δ) = (p₊(δ) + p_–(–δ))/2, the averaged distribution of the absolute value of length of indels with positive and negative lengths in all rat–mouse (blue line) and human–OWM (red line) alignments (C). The same as the previous figure, but indels were recorded only in those parts of alignments where neither of the two sequences was masked by RepeatMasker (D). P(δ) in all rat–mouse alignments, multiplied by δ²(E). Properties of distributions P(δ) obtained for rat–mouse pairs of introns with the following average lengths: 0–100, 100–200, 200–400,..., 6400–12800. For each distribution, fractions of indels of length 1 and of indels longer than 100, 300, and 1000 nucleotides are shown (F).

Shapes of the positive and negative branches are nearly identical in both p_m(δ) (Fig. 1B; elevated frequencies of indels of lengths ∼100 and ∼200 are due to insertions of B1 and B2 SINEs) and p_h(δ) (data not reported). The shape of the branches is also very similar between p_m(δ) and p_h(δ) (Fig. 1C; elevated frequencies of indels of lengths ∼320 in human–OWM alignments are due to insertions of Alu SINEs). The shapes of these branches computed only for those parts of rat–mouse and human–OWM alignments where neither of the two sequences is masked by RepeatMasker, are similar (Fig. 1D), and the total number of gaps that are due to insertion of recognizable transposable elements is <3%. Although short indels are slightly more frequent in p_h(δ) than in p_m(δ), in both distributions the median indel length is 3. The average length of an indel is not a good parameter because when δ → ∞, P(δ) declines as δ^–2 (Fig. 1E), and all its moments diverge. Alignments of introns of different lengths yield different P(δ) (Fig. 1F). Not surprisingly, long indels are more common within longer introns.

To estimate mouse–human indel-based ED, we calculate p(δ) (eq. 7) on the basis of rat–mouse data, which are better than human–OWM data, due to a much larger sample size. Several values of a and several distributions P(δ), ascertained as (p₊(δ) + p_–(–δ))/2 for rat–mouse intron pairs with different average lengths, will be used.

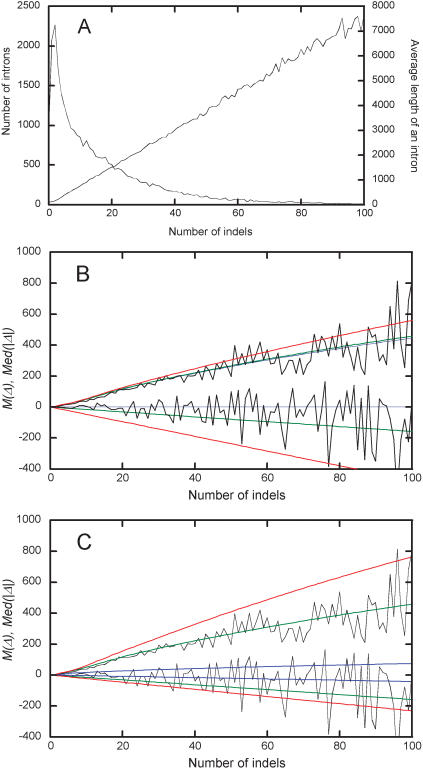
Figure 2 shows how properties of intron pairs depend on k. Such data exist only for rat–mouse (and human–OWM) pairs. The average intron length increases linearly with k (Fig. 2A). Figure 2, B and C compare the data on the mean length difference and median absolute value of length difference between orthologous introns, M(Δ) and Med(|Δ|), in all rat–mouse intron pairs to theoretical predictions (equation 1). Declining a leads to a decline in M(Δ) (obviously, M(Δ) = 0 with a = 0.5) and also slightly increases Med(|Δ|) (Fig. 2B). Under the correct rat–mouse a = 0.46, using P(δ) obtained from introns of intermediate lengths only (>80% of all rat–mouse pairs of introns have average lengths between 150 and 2500) leads to the best agreement with all the data. Using P(δ) obtained from short introns underestimates divergence after k steps, as indels in such introns are shorter, and vice versa (Fig. 2C).

Figure 2.

Data on rat–mouse pairs of orthologous introns with different numbers of accumulated indels, k. Numbers and average length L of intron pairs (A). Data on M(Δ) (decreasing lines) and Med(|Δ|) (increasing lines) in all intron alignments (rugged lines) compared with theoretical predictions (equation 1; smooth lines) obtained with a = 0.5 (blue lines), 0.46 (green lines), and 0.38 (red lines) under P(δ) (equation 7) for intron pairs with the average lengths between 150 and 2500 (B), or with P(δ) for intron pairs of average lengths >150 (blue lines), between 150 and 2500 (green lines), and <2500 (red lines) under a = 0.46 (C).

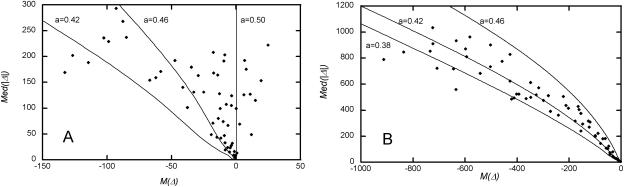
Figure 3 presents properties of intron pairs as functions of L. In rat–mouse intron pairs, M(Δ) and Med(|Δ|) depend on L almost exactly as on k, which is to be expected, as L is a good proxy for k. Probably, the same is also true for mouse–human intron pairs. Figure 4 shows how a can be estimated from the relationship between M(Δ) and Med(|Δ|). In the course of mouse–human divergence a was ∼0.42.

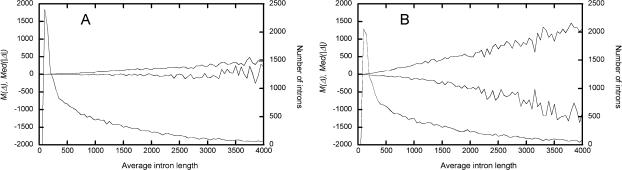
Figure 3.

Properties of intron pairs as functions of their average length, L. Numbers of introns with different values of L (in bins of size 50), and the corresponding M(Δ) (decreasing lines) and Med(|Δ|) (increasing lines) are shown for rat–mouse (A) and mouse–human (B) intron pairs.

Figure 4.

The relationship between M(Δ) and Med(|Δ|) in intron pairs with different L (as in Fig. 3) in rat–mouse (A) and mouse–human (B) intron pairs, compared with theoretical predictions (equation 1), obtained under P(δ) calculated for intron pairs of with 150 < L < 2500 and several values of a.

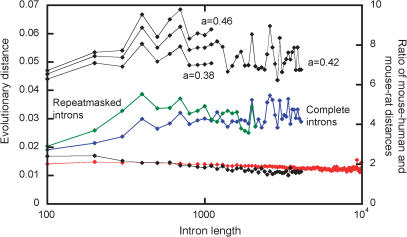
Figure 5 shows estimates of q between rat and mouse and between mouse and human, together with actual values of q between rat and mouse. Using the correct value of a, 0.46, leads to the best estimate of rat–mouse ED. Using smaller a underestimates q (because the same number of indels leads, on average, to a large divergence of intron lengths), and vice versa (data not reported). Thus, we assume that for mouse and human, where q cannot be observed directly, its best estimate is also obtained under the correct value of a = 0.42.

Figure 5.

Indel-based evolutionary distance q for intron pairs of different average lengths L (in bins of size 100, data points are shown at the top boundaries of bins; for each bin, its own P(δ) was used). For rat and mouse, actual data (red line) and the maximal likelihood estimate of q (black line, a = 0.46) are shown. For mouse and human, estimates of q under a = 0.46, 0.42, and 0.38 are shown. The blue line shows the ratio of mouse–human over rat–mouse estimates of q. The green line shows the same ratio, computed for only those parts of mouse and human intron sequences that are not masked by RepeatMasker, on the basis of P(δ), calculated from repeat-free parts of rat–mouse alignments.

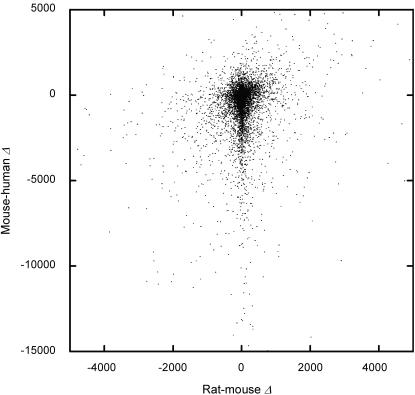
Figure 6 compares rat–mouse and mouse–human divergence of lengths of orthologous introns.

Figure 6.

Length differences between rat and mouse introns, and between mouse and human introns that belong to the same rat–mouse–human triplet of orthologous introns.

DISCUSSION

Our results demonstrate that q, the indel-based ED, can be estimated from length differences between orthologous timer sequences. Figure 1A and shows that p_m(δ) and p_h(δ) are close to each other (very similar data have been obtained previously; Britten 2002; Silva and Kondrashov 2002; Britten et al. 2003). These distributions deviate from symmetry mostly due to a ≠ 0.5, as the shapes of their positive and negative branches are almost the same (Fig. 1B). Thus, p_m(δ) or p_h(δ) can be described by equation 7 with P(δ) = (p₊(δ) + p_–(–δ))/2 and a = 0.46 or 0.48, respectively.

Rigorously speaking, any observed distribution of gap lengths is a convolution of the distribution of length of individual indels, because multiple indels can occur on top of each other. However, as rat and mouse and, in particular, human and OWM, are close enough to each other, ascertaining p_m(δ) and p_h(δ) through the distribution of the length of gaps in the corresponding alignments cannot lead to substantial errors.

We will assume that P(δ) in the course of mouse–human divergence was close to that in the course of divergence within rodents and within primates (Fig. 1C,D,E). Of course, we cannot rule out that during early mammalian radiation, long indels were much more common (or rare) than recently. Masking those repeats that are recognizable within rat–mouse and human–OWM alignments reduces the proportion of long indels (Fig. 1C,D). Because P(δ) is slightly different for introns of different lengths (Fig. 1F), better estimates of q can be obtained if such introns are treated separately.

Data on rat–mouse intron pairs show that the number of accumulated indels k is proportional to the average intron length L (Fig. 2A). Thus, the per site density of indels q is almost independent of intron length. For rat and mouse, q = 0.014. When k increases, both M(Δ) and Med(|Δ|) change as predicted by equation 1, as long as the correct a and P(δ) are used in equation 7 (Fig. 2B,C). Thus, within an intron, indels accumulate approximately independently of each other. Because murine and human introns usually cannot be aligned, there could be no analogous data for this pair of species. However, it is plausible that in mouse–human intron pairs, q is also independent of L.

The key property of timer lengths evolution is evident from Figure 2, B and C. When k increases, lengths of orthologous introns diverge only slightly slower than linearly. As a result, saturation, a major obstacle to estimating substitution-based ED, is much less of a problem in the case of indel-based ED. Two extreme cases elucidate this pattern. On the one hand, if all indels were of length 1, and indels of positive and negative lengths were equally frequent (a = 0.5), Med(|Δ|), as well as the expected difference between the numbers of indels of positive and negative length, would increase slowly, only as a 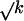(Feller 1968). On the other hand, if all indels were of positive (or of negative) length (a = 1.0 or a = 0.0), Med(|Δ|) would increase linearly with k, as an indel always increases |Δ|. In our data, Med(|Δ|) increases almost as fast as linearly, despite a ≈ 0.5. This happens because P(δ) declines only rather slowly with δ (Fig. 1E), so that long individual indels, although rare, do occur. Thus, a large value of |Δ| is usually reached, not due to accumulation of many short indels, but because of one or several long indels. The probability of occurrence of long, rare indels increases linearly with k.

Two facts are obvious if we compare the patterns in divergence of lengths within rat–mouse and mouse–human intron pairs (Fig. 3). First, for pairs with the same L, Med(|Δ|) is approximately four times higher between mouse and human. Second, M(Δ) in mouse–human pairs declines much faster with L, indicating that in the course of mouse–human divergence, a was substantially below 0.46 (its rat–mouse value). Comparing the observed relationship between M(Δ) and Med(|Δ|) with those predicted by equation 1 under various values of a, we conclude that mouse–human a is ∼0.42 (Fig. 4).

Data on mammalian evolution (Springer et al. 2003) and mutation (Waterson et al. 2002; Kondrashov 2003) imply the same value of a. Applicability of equation 7 suggests that asymmetry of p(δ) is due to unequal rates of insertions and deletions and unequal lengths of the murine and human lineages (equation 6). If the fraction of mutations fixed within the human lineage from all of those fixed in the course of mouse–human divergence is 1/3 (i.e., if the human lineage is two times shorter than murine lineage, Springer et al. 2003) and deletions in mammals are three times more common than insertions (Waterson et al. 2002; Kondrashov 2003), equation 6 predicts a = 0.42.

Indel-based ED between rat and mouse is 0.014 (Fig. 5). Slight decline of q with L may be due to its underestimation in long introns, whose alignments often contain long gaps, as additional indels cannot be recorded within such gaps.

Maximal likelihood estimate of q recovers its real values for rat and mouse with good precision (Fig. 5). In long introns, q is slightly underestimated because Med(|Δ|) in such introns is ∼5%–10% below what it would be if indels were distributed independently (data not reported), probably due to selection against very long introns. Overestimation of q in very short introns also appear to be due to selection on intron length, in this case, against too-short introns (a mammalian intron cannot be shorter than 50). This selection reduces the variance of the distribution of k among intron pairs (the fractions of alignments of introns of length ∼100 with two or three gaps are higher, and of those with 0 or ≥4 gaps are lower than the corresponding terms of Poisson distribution with the same mean; data not reported). Consequently, the fraction of intron pairs of exactly the same length is ∼25% smaller than if indels occurred independently, which leads to overestimation of q. Estimates of q for very long introns fluctuate, due to relatively small numbers of such introns (Fig. 3).

Thus, the best estimates of q are obtained for introns of lengths 300–1500, where accumulation of indels is closest to independent. Within this range, the average q between mouse and human is 0.056, that is, four times higher than between rat and mouse (Fig. 5). Simple considerations support this estimate. Med(|Δ|) is four times larger for mouse and human than for rat and mouse (Figs. 3, 6). Thus, one can expect the ratio of the corresponding q's to be slightly above four, because Med(|Δ|) increases slower than linearly with k (Fig. 2B,C). This would be the case if mouse–human a were 0.46 (Fig. 5). However, mouse–human a = 0.42 deviates from 0.5 more than in rat–mouse a = 0.46 and, because under more deviating values of a, Med(|Δ|) increases faster with k, the ratio of q's should be below four. These two effects approximately cancel each other, and the ratio of q's is close the ratio of median divergences of absolute values of intron lengths.

Perhaps mouse–human ED estimated for completely neutral indels would be slightly above 0.056, as stabilizing selection must slow down the divergence of intron lengths. This is certainly the case for very short introns (Fig. 5). However, Med(|Δ|) in mouse–human intron pairs is only ∼20% of the average intron length (Fig. 3B), so that the impact of selection is probably not large for introns longer than ∼300 nucleotides.

Insertions of transposable elements is a distinct, important mechanism of accumulation of indels that is probably less homogeneous over evolutionary times than other mechanisms (Waterson et al. 2002). Thus, it is interesting to estimate indel-based ED, which is independent of this process. For this purpose, we used p(δ) obtained only from those parts of rat–mouse alignments where neither of the sequences is masked by RepeatMasker. This p(δ) was then applied to only those parts of rat, mouse, and human introns that were not masked. This procedure led to a ∼10% increase of rat–mouse q, because ignoring long inserted sequences of transposable element origin increases the density of the most common, short indels. Maximal likelihood estimate of rat–mouse q recovers its real values with the same precision as when no sequences were masked (data not reported). In contrast, masking repeats increases the estimated ratio of mouse–human q over rat–mouse q by ∼20%, from four to almost five (Fig. 5).

We believe that masking transposable elements causes overestimation of mouse–human divergence. Some elements inserted early in the mammalian radiation changed beyond recognition (Waterson et al. 2002) and are not detected by RepeatMasker. Such elements still contribute to the length difference between orthologous mouse and human introns, even when all masked sequences are ignored. In contrast, RepeatMasker must recognize almost all transposable elements inserted after rat–mouse (or human–OWM) divergence, so that p(δ) obtained from masked rat–mouse alignments does not reflect any indels caused by transposition. Naturally, using this p(δ) leads to overestimated mouse–human q, as insertions of transposable elements produce longer indels than other insertions and deletions (Fig. 1C,D).

Therefore, which ED, substitution-based or indel-based, should be calculated for a pair of species? Obviously, if the species are so close that even their neutral sequences can be aligned, both measures can be used, and substitution-based ED is preferable, as it requires less data. In the opposite extreme case of very distant species, ED can only be estimated from non-neutral sequences. Traditionally, this is done on the basis of substitutions, and using indels, although feasible, would require analysis different from presented here. However, there appears to be a substantial range of moderate distances between species for which only indel-based ED can be estimated for neutral sequences. Mouse and human are close to the lower boundary of this range; if they were approximately two times more similar than they are, their introns would be alignable. The upper boundary of this range is currently unknown and the possibility of indel-based estimate of ED between, for example, Fugu and mammals is worth studying.

Both indel-based and substitution-based estimates of ED are vulnerable to changes in the parameters of the underlying process. The distribution of the length of individual indels did not stay exactly invariant (Fig. 1). However, relative rates of nucleotide substitutions of different types also change in the course of evolution (Duret et al. 2002; Arndt et al. 2003; Rat Genome Sequencing Project Consortium 2004). The most believable conclusions can be reached when both methods produce similar estimates.

Indel-based and substitution-based ED's can be converted into each other, as long as we know the indel/substitution ratio R among fixed mutations. Within primates, R = 1/13 for noncoding sequences (Silva and Kondrashov 2002; Britten et al. 2003; and our data), and a lower R = 1/25 in coding sequences is due to elevated substitution rate because of high prevalence of mutable CpG context (Kondrashov 2003). For rat–mouse alignments used here, R = 1/15. Thus, assuming R = 1/14 in the course of mouse–human divergence, we conclude that for neutral sequences substitution-based ED between these species is ∼0.8. This figure is very slightly above maximal likelihood (Yang 1997) estimates of mouse–human Ks, 0.73 (Castresana 2002) and 0.74–0.80 (Smith and Eyre-Walker 2003), perhaps implying weak selective constraint at synonymous sites (Hellman et al. 2003).

Thus, if we could construct the correct alignment of human and mouse selectively neutral sequences, we would see ∼50% of matches at homologous sites, and 5.6 gaps per every 100 nucleotides. Because 25% of these gaps are longer than 10 nucleotides, a substantial fraction of sites in one sequence has no homolog in the other (Britten 2002; Britten et al. 2003). This is similar to what is observed when one attempts to align murine and human introns (Shabalina et al. 2001), although sometimes they appear even more dissimilar.

Knowing the evolutionary distance between murine and human neutral sequences is essential for identifying selectively constrained regions. Quantitative analysis is necessary to determine whether such regions cover >10% (Shabalina et al. 2001), ∼5% (Cooper et al. 2004), or only 2% (Waterson et al. 2002) of mammalian noncoding sequences.