Elucidation of Gene Interaction Networks Through Time-Lagged Correlation Analysis of Transcriptional Data

Abstract

The photosynthetic cyanobacterium Synechocystis sp. strain PCC 6803 uses a complex genetic program to control its physiological response to alternating light conditions. To study this regulatory program time-series experiments were conducted by exposing Synechocystis sp. to serial perturbations in light intensity. In each experiment whole-genome DNA microarrays were used to monitor gene transcription in 20-min intervals over 8- and 16-h periods. The data was analyzed using time-lagged correlation analysis, which identifies genetic interaction networks by constructing correlations between time-shifted transcription profiles with different levels of statistical confidence. These networks allow inference of putative cause-effect relationships among the organism's genes. Using light intensity as our initial input signal, we identified six groups of genes whose time-lagged profiles possessed significant correlation, or anti-correlation, with the light intensity. We expanded this network by using the average profile from each group of genes as a seed, and searching for other genes whose time-lagged profiles possessed significant correlation, or anti-correlation, with the group's average profile. The final network comprised 50 different groups containing 259 genes. Several of these gene groups possess known light-stimulated gene clusters, such as Synechocystis sp. photosystems I and II and carbon dioxide fixation pathways, while others represent novel findings in this work.

The DNA microarray has become an established tool for the parallel monitoring of gene expression profiles. Most common experimental design strategies observe static gene expression differences between conditions, such as disease versus nondisease case comparisons. While such experiments generate information for diagnostic applications, they are not well suited for uncovering the roles of these genes in the larger context of cellular regulation.

Dynamic transcriptional data allow the formation of gene clusters with similar temporal expression profiles. The various forms of clustering (Eisen et al. 1998; Alter et al. 2000; Holter et al. 2000) employed to date have produced valuable information, including potential gene relationships and the identity of transcription factor binding motifs. These methods, however, are limited in their ability to infer causality or directional relationships between genes. The results of clustering algorithms often yield relations such as “gene A is a good predictor of gene B,” which is an equivalent statement to “gene B is a good predictor of gene A.” Neither Bayesian networks (Friedman et al. 2000), nor information theory-based approaches (Somogyi and Fuhrman 1997) have made use of the sequential nature of time-series data in current applications. Conversely, when enough time points are available to prevent over fitting the data and find statistically significant correlations, a discovery method to uncover potential causal relationships among genes may be attempted. Directionality can be added to these probabilistic networks by determining the temporal order in which gene expression patterns are affected in a sequence.

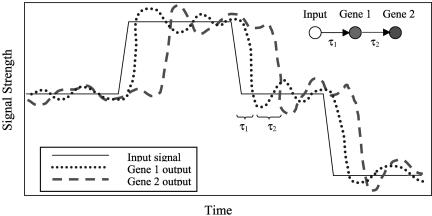
Consider Figure 1 in which an input signal, such as light intensity, affects the transcription of a pair of genes through a cascade from gene 1 to gene 2. In an experiment that only measures static gene expression values at each input signal intensity, the best conclusion that might be drawn from such data is that the genes are somehow related. On the other hand, if dynamic experiments are conducted that allow the observation of delayed responses, then it is possible to extract additional information from these measurements pointing to potential directionality.

Figure 1.

Idealized gene expression experimental results, where measurable time lags τ₁ and τ₂ are indicative of the underlying cascade of biochemical reactions which lead to the input signal's effect on the genes.

A relatively complete picture of transcriptional regulatory behavior should be possible by probing the transcriptional dynamics of carefully designed experiments covering a wide range of conditions. Dynamic experiments that sequentially vary external parameters offer insights into how cellular physiology depends on changing environmental conditions. Time-lagged correlation analysis is one method that can be applied to infer putative causal relationships between system perturbations and system responses.

Linear Pearson correlations have been used to identify genes that are coexpressed or antiexpressed for clustering purposes (D'Haeseleer et al. 1998; Kuruvilla et al. 2002). Time-lagged correlations extend this technique by determining the best correlations among profiles shifted in time. For a transcription profile represented by a series of n measurements taken at equally spaced time points, the correlation between genes i and j with a time lag, τ, is R(τ) = (r_ij(τ)), defined by

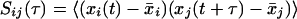(1)

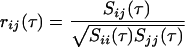(2)

where x_i(t) denotes the expression of gene i at time t, x̄_i is the expression value of gene i averaged across all time points, and the angled brackets represent the inner product between the time-shifted profiles. The matrix of lagged correlations R(τ) can be used to rank the correlation and anticorrelation between genes through conversion to a Euclidean distance metric, d_ij:

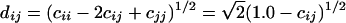(3)

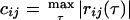(4)

where, c_ij is the maximum absolute value of the correlation between two genes with a time lag τ. If the value of τ that gives the maximum correlation is 0, then the two genes are best correlated with no time lag. The matrix D = (d_ij) describes the correlation between two genes, i and j, in terms of “distance” by making genes that are least correlated (for any τ) the “farthest” apart (Arkin and Ross 1995). Thus by transforming the correlation matrix, R, into a distance matrix, D, we are able to include highly anticorrelated genes, in addition to correlated genes, in the network. By finding genes that are closely related and then examining the corresponding value of τ, an underlying network of potential cause and effect relationships can be elucidated. Some caution is needed to ensure genes with high correlation have been chosen using enough data points to give statistical significance, otherwise all of the τ values used will merely overfit the data. Such errors may be obvious if values for τ are unreasonably long from a biological standpoint.

Arkin, Shen, and Ross (1997) previously used time-lagged correlations to “reconstruct” the reaction network of central carbon metabolism by placing eight major enzymes and 14 chemical components into a continuous stirred tank reactor and inducing dynamic concentration shifts of the chemical species. Concentrations of the major chemical species were measured throughout the experiment, while the input concentrations of citrate and adenosine monophosphate (AMP) were periodically adjusted to keep the system away from steady-state. Using time-lagged correlations to analyze the output data, these authors were able to recreate most of the features from the original pathway; however, some of the interactions were not recovered in the reconstruction attempt. For example the inhibitory impact of citrate on the conversion of fructose-6-phosphate (F6P) to fructose 1,6-bisphosphate (F16BP) was not included. Furthermore, species that are not controlled or measured cannot be placed in the network. Despite these drawbacks, this example showed that even when the specific method of interaction is unknown or unmeasured, useful information could be inferred about the overall structure of a network from forced dynamic experiments.

By sequencing the Synechocystis genome (Kaneko et al. 1996), it is now possible to begin investigating the systemic properties of the organism. As a model system, increasing interest in the cyanobacterium Synechocystis PCC6803 has focused on the organism's ability to synthesize various chemicals such as polyhydroxyalkanoate (PHA) biopolymers. Coupled with the cyanobacterium's CO₂ fixation ability, Synechocystis represents a potentially useful biocatalyst for the conversion of CO₂ gas emissions into value-added materials. On the other hand, the organism suffers from a relatively slow growth rate and low PHA yields, which create economic hurdles that must be overcome before its implementation in commercial processes. Understanding, and subsequently improving, network properties may help alleviate these obstacles, enabling the carbon-fixing and product forming potential of Synechocystis to be exploited for industrial purposes.

In this work we identified a network of putative directional interactions between cascades of genes by using time-lagged correlation analysis. This network relates the changing light input signal to dynamic gene transcription data obtained using full genome DNA microarrays (Schmitt Jr. and Stephanopoulos 2003) in cultures of the cyanobacterium Synechocystis PCC6803. Perturbations in light intensity are easy to implement experimentally and have minimal diffusional time lag. Synechocystis is particularly well-suited to this type of regulatory analysis because the expression levels of many genes change over a period of 24 h in response to environmental light changes (Hihara et al. 2001; Gill et al. 2002).

RESULTS

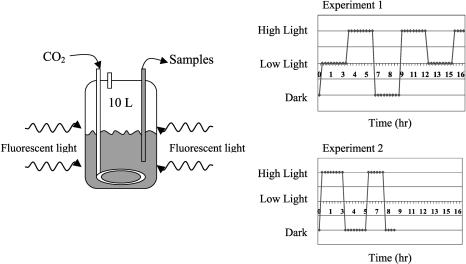
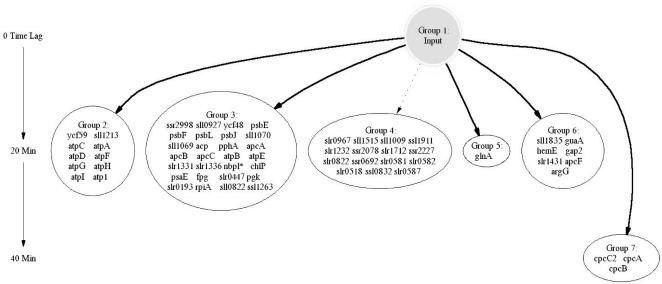
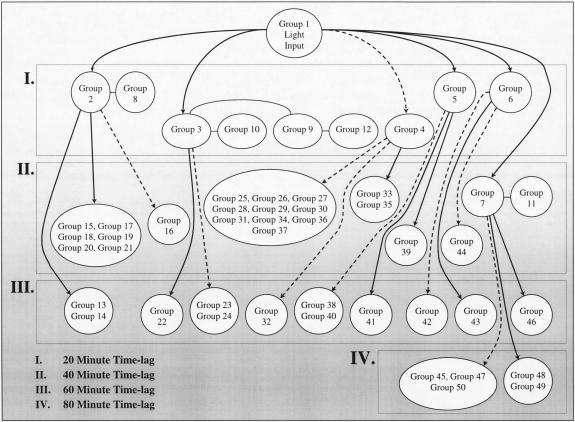
In the first experiment the culture was exposed to a series of three-step changes in light intensity ranging from 0 to 16 to 90 μmol/m²/s, as shown in Figure 2. Forty-seven of the fifty samples from this experiment were successfully hybridized to DNA microarrays and provided sufficient signal intensities for further analysis. Two iterations of the time-lagged correlation implementation algorithm were applied to this data. Figure 3 shows 64 genes that were divided among six groups with high correlation directly to the input signal (|R| > 0.7 for at least one member of the group), while Figure 4 shows the expansion of this original set to 50 groups comprising 259 genes, using an additional iteration of the algorithm. Both time-lagged correlations (bold arrows) and time-lagged anticorrelations (dotted arrows) are shown, along with zero-lagged correlations (straight lines). Note that genes correlated with no lag to other genes need not necessarily belong in the same group, as they do not show the same degree of correlation with other clusters in the diagram. It is possible that further experiments will confirm their inclusion into a single group, or suggest the elimination of one or both of the two groups.

Figure 2.

Experimental set-up and light intensity profiles for both experiments.

Figure 3.

Simplified time-lagged correlation network from Synechocystis sp. PCC6803. The arrows indicate close correlation (|R| > 0.70) between groups, and the corresponding numbers indicate the time lag relative to the input. The network is derived from data from Experiment 1. Dashed lines indicate inverse correlation.

Figure 4.

Simplified time-lagged correlation network, second iteration. The genes contained within each group are given in Table 3.

The annotated genes that respond to the input light signal in a time-lag “wave” are listed in Table 1. Among the transcripts in Table 1, many encode proteins found in the Synechocystis photosystem complexes. For example, genes associated with photosystem I (such as psaE or psaK) and photosystem II (such as psbEFLJ) seem to become activated at several different time lags relative to the light intensity. Interestingly, this analysis also found both ycf3 and ycf48 having transcriptional expression coordinated with light exposure with the minimum time lag of 20 min. It has been suggested that these genes contribute to either assembly or stability of photosystem I (Wilde et al. 2001) and II (Meurer et al. 1998). The fast response at the transcriptional level of ycf3 and ycf48 to changing light conditions is consistent with these hypotheses. Additionally, Table 1 lists many of the subunits for ATP synthase (such as atpCADFGHI1), which are best correlated with the light intensity at the smallest measurable time lag of 20 min. At least one subunit for the cytochrome complex (petG) was also identified.

Table 1.

The Expression Intervals at Which Some Characterized Genes Are Correlated (Directly or Indirectly) to the Experimental Light Intensity

20-min time lag
accB, efp	acp	apcA, B, C	apcE, F, G
atpBE	bioB	atpC, A, D	atpF, G, H
atpl, 1	chlP	clpP	trpB, E
psaD	ycf58	cpcG1	crtQ-2
cupB	ctpA	rbcL, X, S	fus
fpg	psaE	tufA	dnaK
glyA	gap2	glnA	gpx1
guaA	gyrB	hemB, E	icd
ilvC	murC	nbp1	ndhH
nirA	pacS	petH	pgk
ppa	pphA	ycf48	psbE, F, L
psbJ, K	purD	rfbFGC	rfbE
rpl19, 36	rps11, 13	rpoC1	rps1a, 20
secDF	serA	sigA	thiC
valS	ycf23, 3, 59	sll0822	sll0842
sll0843	sll0927	sll1009	sll1069
sll1070	sll1130	sll1213	sll1234
sll1515	sll1665	sll1835	sll1921
sll1945	sll1951	slr0193	slr0447
slr0483	slr0484	slr0518	slr0581
slr0582	slr0587	slr0654	slr0752
slr0773	slr0776	slr0822	slr0967
slr0981	slr0982	slr1020	slr1050
slr1051	slr1052	slr1062	slr1063
slr1105	slr1160	slr1176	slr1177
slr1232	slr1237	slr1276	slr1277
slr1331	slr1336	slr1349	slr1363
slr1431	slr1462	slr1464	slr1535
slr1616	slr1617	slr1618	slr1619
slr1623	slr1624	slr1712	slr1770
slr1855	slr2002	slr2025	slr2046
slr2047	slr2048	slr2052	ssl0832
ss1263	ssl1911	ssl2245	ssr0692
ssr2078	ssr2227	ssr2998
40-min time lag
ccmK	gap1	glnB	hemD
cpcA, B, C2	cpcC1, D	natE	nblA1
ndbB	ndhD1	psaC	ndhJ
petF, G	pppA	psaL, I, F	psaJ, K
psbI, X	ribF	rpl21, 27	rps15
rps21, r	serS	sodB	sll0062
sll0063	sll0064	sll0085	sll0086
sll0096	sll0103	sll0135	sll0163
sll0264	sll0350	sll1268	sll1343
sll1386	sll1712	sll1721	sll1837
sll1979	slr0038	slr0039	slr0073
slr0082	slr0232	slr0294	slr0476
slr0765	slr0784	slr0821	slr0886
slr0921	slr1282	slr1338	slr1406
slr1821	slr1926	ssl0242	ssl0294
ssl1046	ssl2009	ssl2874	ssr1480
ssr1528	ssr2130
60-min time lag
hspA	psbB, M	slr0709	slr0816
slr0907	slr0915	slr1066	slr1068
slr1070	slr1071	slr1072	slr1073
slr1396	slr1410	slr1964	slr2010
ssl1792
80-min time lag
hisD	ycf46	pxcA	rpl24
slr2115	ssl1045	ycf46

Genes separated by commas indicate that they are located adjacent to one another in the genome.

Other genes that are known to be light-regulated, such as apcF, apcE, and apcABC (Gill et al. 2002) also fall into groups with other highly correlated genes. These allophycocyanin genes all possess a time lag of 20 min, while several phycocyanin genes, such as cpcABC2C1D, have a greater time lag (Table 1; note that cpcC1 was filtered from the original analysis due to low expression ratios, but is in fact well correlated with the other genes listed). Given that the allophycocyanin units make up the core of the phycobilisome structure, while the phycocyanin genes make up the rod-like projections from this core, a model of sequential activation seems plausible and agrees with the transcription of the allophycocyanin genes preceding that of the phycocyanin genes. Furthermore, cpcG1, found at the earliest measured time lag, links the phycocyanin rods to the core allopycocyanin proteins of the phycobilisome (Bryant et al. 1990).

As reported in earlier studies (Watson and Tabita 1996; Hihara et al. 2001; Gill et al. 2002), the sub-units of the carbondioxide fixation complex rubisco (rbcL, rbcS, and the potential chaperone protein rbcX) are shown to be highly correlated with light intensity at the transcriptional level. Other findings, including a homolog of the carbon dioxide concentration unit ccmK (Watson and Tabita 1996), as well as a handful of genes related to metabolism (icd, gap2, etc.), are also cataloged in Table 1.

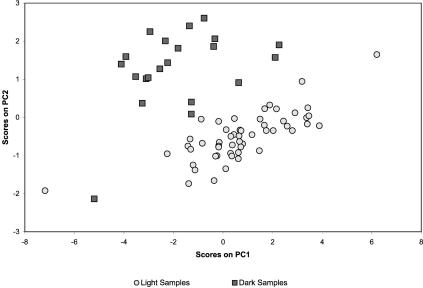
In addition to validating the response of known light sensitive genes, some information concerning the roles, and potential interactions, of putative genes can be derived from our analysis. Genes slr0581 and slr0582, were inversely correlated to the light intensity. A homology search using BLAST on these open reading frames (ORFs) suggests no strong homologies with known proteins, so assigning a functional role is difficult. However, slr0582 has at least some similarity with putative binding factors, and therefore may play a role in the transcription of genes regulated as a response to light. Furthermore, slr0581, which had a sufficiently strong signal at every time point to be included in the Principle Component Analysis (Raychaudhuri et al. 2000), has one of the larger loading coefficients determining the shape of Figure 5. This pair of adjacent genes, with operon-like coexpression and a high correlation to light-regulated genes in Synechocystis, requires further study to determine their actual function, but testable hypotheses can be formulated from our work.

Figure 5.

Two-dimensional mean-centered Principle Components Analysis of all 74 time points, using only the 113 genes.

Although we used levels of R large enough to minimize the chance of randomly observing highly correlated genes, a second experiment, with a different input light signal (see Fig. 2) was conducted to test the correlations observed in the first experiment. Results for the genes shown in Figure 3 are shown in Table 2. Most of these genes have similar correlations with the input signal in both experiments. Exceptions that have different values between the experiments, could then be used to “prune” or adjust the networks shown in Figures 3 and 4. Consider, for example, the cpc genes found in Group 7, which seem to correlate less well in the second experiment. Although the correlation is still significant at this level for a time lag of two units (40 min), we also observe a nearly equal correlation at a lag of three units (60 min), and further experiments are required to accurately plot these genes within the network. However, unless exceedingly low correlation is observed, such connections cannot reasonably be rejected with only this data, and testing the correlations using complementary techniques would be highly beneficial.

Table 2.

The Maximum “R” Values and Corresponding Time Lags for Those Groups Directly Correlated With Light Intensity in Figure 3

	Expt 1		Expt 2
Gene	R_value	lag	R_value
ycf59	0.7076	-1	0.8459
sll1213	0.6528	-1	0.6282
atpC	0.7104	-2	0.6834
	0.6954	-1	0.5538
atpA	0.7621	-1	0.7062
atpD	0.7656	-1	0.6996
atpF	0.7887	-1	0.7376
atpG	0.7923	-1	0.7986
atpH	0.7515	-1	0.726
atpI	0.7174	-1	0.7129
atp1	0.6957	-1	0.6956
ssr2998	0.7368	-1	0.5498
sll0927	0.7577	-1	0.7832
ycf48	0.6153	-1	0.617
psbE	0.773	-1	0.8076
psbF	0.6935	-1	0.7679
psbL	0.7051	-1	0.7225
psbj	0.6534	-3	0.4751
	0.6454	-1	0.4812
sll1070	0.7236	-1	0.5628
sll1069	0.6787	-1	0.5806
acp	0.7625	-1	0.734
pphA	0.737	-1	0.3616
apcA	0.7081	-1	0.7729
apcB	0.7122	-2	0.7714
	0.7101	-1	0.7686
apcC	0.7757	-1	0.7301
atpB	0.6959	-1	0.7359
atpE	0.7519	-1	0.7067
slr1331	0.6175	-1	0.5313
slr1336	0.7095	-1	0.4099
nbpl	0.7482	-1	0.6761
chlP	0.792	-1	0.8206
psaE	0.7258	-1	0.626
fpg	0.5831	-1	0.4718
slr0447	0.7872	-1	0.7425
pgk	0.7521	-1	0.7304
slr0193	0.7216	-1	0.6682
rpiA	0.6194	-1	0.4247
sll0822	0.7776	-1	0.7791
ssl1263	0.7031	-1	0.7185
slr0967	-0.8524	-1	-0.8587
sll1515	-0.7392	-1	-0.8205
sll1009	-0.7878	-1	-0.273
ssl1911	-0.7832	-1	-0.8907
slr1232	-0.7922	-1	-0.8773
ssr2078	-0.7062	-1	-0.7272
slr1712	-0.7016	-1	-0.6647
ssr2227	-0.8571	-1	-0.9117
slr0822	-0.7292	-1	-0.7255
ssr0692	-0.7791	-1	-0.8701
slr0581	-0.7666	-1	-0.5221
slr0582	-0.6686	-1	-0.4439
slr0518	-0.7619	-1	-0.9146
ssl0832	-0.7446	-1	-0.9486
slr0587	-0.7757	-1	-0.8677
glnA	0.0744	-1	0.7902
sll1835	0.7433	-1	0.7475
guaA	0.706	-1	0.6698
hemE	0.7058	-1	0.6841
gap2	0.8028	-1	0.7914
slr1431	0.7106	-1	0.7032
apcF	0.7222	-1	0.7767
argG	0.7397	-1	0.7682
cpcC2	0.6376	-2	0.2069
cpcA	0.7095	-2	0.4941
cpcB	0.7299	-2	0.593

Genes with similar “R” values at different time-lags were placed in Figure 3 by consensus of the group, and the corresponding “R” values are also listed.

Having conducted two sets of experiments under different input light profiles, the consistency of the measured transcriptional profiles was investigated. One way to do so is by projecting the transcriptional state of the cells in a reduced dimensional space, defined by coordinates that are linear combinations of the gene expression data. In such a space we anticipate that cellular samples taken under similar experimental conditions will cluster together. Principal components analysis (PCA) was used as an unsupervised data visualization tool to test whether cells exposed to the same environmental conditions in different experiments clustered together in the space defined using the first two principle components (Misra et al. 2002) of the combined data sets.

Only genes with expression values for all 74 samples, from both experiments, were considered in the PCA analysis. For these 113 genes, the two largest principle components account for approximately 68.7% of the variance. Figure 5 shows the 74 samples in a space defined by the two principal components. It can be seen that samples obtained during the “dark” conditions (with a time lag of 20 min) reside in an area distinct from those obtained during either of the light conditions in both experiments, with the exception of a single, easily identified outlier point from the second experiment. Not surprisingly, examination of the gene loadings (Misra et al. 2002) used to create Figure 5 shows that many of the genes in the networks of Figures 3 and 4 are key to this distinction (data not shown).

To further substantiate the results of the analysis two sets of simulations were conducted. In the first set of simulations we reanalyzed the data set using only half the data points. Thus instead of having 47 data points at 20-min intervals, we used 24 data points at 40-min intervals. Genes that possessed a maximum correlation value at a time lag of 20 min in the original data (47 time points) set fell into either the 0- or 40-min time-lagged group when 40-min sampling intervals were used. Likewise, genes that possessed a maximum correlation value at a time lag of 60 min in the original data set were placed in either the 40 or 80 min group. Although some additional genes now pass the |R| > 0.70 threshold and enter the analysis, none of the genes that were identified using all 47 time points are eliminated from the analysis when only 24 time points are used. Thus as more time points are used, only the strongest correlations emerge in the analysis. In the second set of simulations we tested the statistical significance of our correlations. To do this we created 10 million sets of random data in the same format as the original data set (47 time points) and found only two samples that had a correlation value of |R| > 0.70for τ between –40 and 40 min. For uncorrelated data, |R| follows a t-distribution with N – 2 degrees of freedom. In this case N = 47, thus the probability of |R| > 0.70 by chance is ≪0.0001. This indicates that it is extremely unlikely to observe the correlations identified in this analysis by chance alone.

The three design criteria that need to be considered in planning similar dynamic experiments are the frequency of sampling, the properties of the induced perturbations, and the dynamics of gene transcription. These factors interact with one another and should be optimized to address a specific condition. In these experiments we wanted to study the transcriptional dynamics of Synechocystis sp. in response to light perturbations. Because changes in light intensity can be introduced instantaneously, we were not limited by diffusional effects that may slow the response, or create varying time lags dependent upon the magnitude of the induced change. The induction and relaxation times of gene transcription also need to be considered in selecting the sampling frequency. Because changes in gene transcription have been observed over 2- to 6-h periods (Hirahara et al. 2001; Gill et al. 2002), a 20-min sampling was deemed sufficient to provide a high enough resolution to accurately assess system responses on this time scale. We note that we cannot accurately resolve higher frequency oscillatory reactions or discrete changes in transcription that respond in less than 20 min, either directly to the change in light or indirectly to environmental or other gene regulatory changes affected by the light. In these cases, if the sampling frequency is not an even multiple of the response period, or if the overall response is transient over the length of the perturbation, poor correlations may be obtained (false-negatives), or high correlations to the wrong stimuli (false-positives). Additionally, more complex analyses meant to uncover multi-gene interactions occurring within these experiments are certainly possible. Information-theory approaches (D'Haeseleer et al. 1998) could be adapted to include time-lag components to search for such relationships, but practical implementation of such an algorithm requires substantial additional effort and is outside of the scope of this project.

DISCUSSION

We have conducted two time-series DNA microarray experiments, one with 47 measurements (of 50 time points) taken over 17 h, and another of 27 measurements taken over 9 h. Both of these experiments share the same sampling interval (20 min) and are taken from single, homogeneous (well-stirred) cultures. These experiments are especially unique because of the application of an instantaneous forcing environmental input, the intensity of the incident light to the system. Compared to earlier time-series experiments with DNA microarrays (Chu et al. 1998; Spellman et al. 1998; Iyer et al. 1999; Hihara et al. 2001; Gill et al. 2002), these experiments possess a much higher, and evenly spaced, sampling frequency. These experimental parameters were specifically designed to enable the use of time-lagged correlations that could identify directional transcriptional relationships on a 20-min time scale.

Time-lagged correlations (Arkin and Ross 1995) provide a reasonable method for extracting potential relationships within the genetic network, and we have detailed our adjustments for practical implementation to such large data sets that contain significant obscuring error. For the time-interval studied, these correlations manifest themselves as “waves” of expression in Synechocystis sp. lagged at different intervals from the changing light intensity. Larger intervals would have allowed, for the same number of experiments, study of a longer cycle of transcriptional events, with loss of resolution between time-scales (i.e., a 40-min sampling period cannot distinguish between 20-, 40-, and 60-min lag times). Similarly, for greater resolution into the ordering of transcriptional events, smaller time-scales than those attempted here may be tried, with the accompanying increase in required arrays.

Although a substantial effort is required to plan and perform this type of experiment, an enormous amount of information is obtained. This information enables the construction of genetic networks using the system's identification technique of time-lagged correlations. The directionality of the resulting networks provides more information than clustering alone, and therefore allows the researcher to generate hypotheses based on the system structure. Additionally, it is important to consider similarly expressed genes as potential regulon members. Regulons are sets of coregulated genes with common promoter regions differing from operons in that they are not necessarily sequentially oriented in the genome. To this end, genes with the same time-lagged correlation may be considered as good regulon candidates.

The 50 groups containing 259 genes uncovered by this analysis technique (Table 1) contained genes that are known to have light-induced regulation, as well as unannotated genes, whose functions have yet to be completely assessed. The former group, containing genes such as apcF, apcE, and apcABC, demonstrate the reliability of the technique, while the latter group can help formulate testable hypotheses for a gene's function. This suggests that dynamic studies of transcriptional behavior with significant numbers of time-points can play a key role in understanding cellular regulation. As other measurements such as protein and metabolite data become available at similar scales and frequencies as DNA microarray data, then time-lagged correlation studies should allow for the creation of hypothetical networks similar to Figures 3 and 4 that will contain greater degrees of mechanistic information. Such approaches will hold new insights into the regulation of Synechocystis and may contribute to its utilization for carbon fixation at a practical scale.

METHODS

Time-Lagged Correlation Methodology

To analyze DNA microarray data using time-lagged correlations, some adjustments were made to the method described by Arkin et al. (Arkin and Ross 1995; Arkin et al. 1997). Because we are interested in the transcriptional response to a single perturbation in the experimental system, the input light intensity profile was used as a “seed” in the search for genes with correlated time-lagged expression profiles. This seed profile consists of the autoscaled light intensity values at each time point. It is the initial profile to which the autoscaled dynamic gene transcription profiles are compared to determine their level of correlation in the first iteration of the algorithm. The following steps were then used to perform the network reconstruction effort.

Step 1: Filter Low-Signal Genes and Cluster Potential Operon Members

Some microarray genes (or features) may not exhibit significant expression levels under the conditions investigated. Such genes unnecessarily complicate the computations and are easily removed by the application of filters requiring not only significant expression levels but also significant changes in expression. Genes that did not have an experimental signal intensity significantly above the background variation for at least half of the time points in a given experiment were excluded from further consideration. Also, all genes without a significant expression change (defined as a twofold increase or decrease) for at least one time-point were eliminated from further analysis. In these experiments the filters typically eliminated approximately 25% of the microarray features from further consideration.

Because the Synechocystis genome has been sequenced, additional information is available about each gene's chromosomal location and relative ordering within the genome (http://www.kazusa.or.jp/cyano/). This information, along with the experimental expression data, may suggest the existence of operons, or coexpressed sets of genes due to a common upstream promoter system. In this algorithm, instead of traditional clustering (Dillon and Goldstein 1984; Kamimura 1997; Eisen et al. 1998; Heyer et al. 1999; Tamayo et al. 1999; Zhu and Zhang 2000), genes that are located adjacent to one another in the genome were analyzed for correlation of expression with zero time-lag. Those that correlated, |R(τ)| > 0.7, were grouped into clusters. The average autoscaled profile of the gene cluster was calculated to represent the entire group of adjacent genes.

Step 2: Correlate Gene Expression Profiles With the Input Signal

After applying the filters in Step 1, all genes and gene clusters were subsequently analyzed for their time-lagged correlation with the input signal. In subsequent iterations, the network can be expanded by substituting the gene groups from Step 3 for the input signal used in this step.

Recall that the correlation of equations 1 and 2 comparing the input signal in the first iteration (or the average profile of a gene cluster in subsequent iterations), i, to gene j best identifies relationships of the type

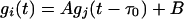(5)

Substituting this relationship into the correlation equations shows that a maximum S_ij value will occur at τ = –τ₀. At this point S_ij = A · σ_j, where σ_j is the variance of, which g_j corresponds to r_ij = 1. Because gene expression is affected by a variety of variables, some of which are not accounted for, the resulting pair-wise-correlations will often be less than unity. This suggests that key genes will possess strong but imperfect correlation with the input signal. By lowering the threshold values for r_ij from unity, such imperfect correlations with appropriate time lags can be captured. All genes having at least one r(τ) value greater than the preselected cutoff of |R| > 0.7, were set aside for further consideration. In this way, a set of “first-order” interactions was obtained in a computational time increasing linearly with the number of genes included.

Using simulations, we found that the determination of time-lags and correlations is highly dependent on perturbations in the experimental conditions that lead to measurable changes in gene transcription. This has also been noted by Arkin and Ross (1995) who suggest continuous perturbation of the system away from steady-state to discover the underlying system structure. Thus, all experiments in our studies were conducted under dynamic conditions, with the data collected at homogenously spaced sampling intervals.

Step 3: Assemble Groups Containing Retained Genes From Step 2

In this step, the retained genes were sorted by their time-lag correlations with the input signal—all genes that best correlated with lags of one interval were put into one category, lags of two intervals into a second category, etc. After grouping the genes according to their time-lags, a nearest-neighbor (Dillon and Goldstein 1984) clustering scheme was implemented within each group using correlation with no time-lag zero as the definition of similarity. In other words, each gene was compared to all other genes within each group, and the highest correlated genes were assembled into sub-groups. This procedure was repeated until the correlation between groups fell below the preselected cutoff value, |R| > 0.7 (as in Step 2). In this way we partition the original time-lagged groups into subgroups based on clustering. The difference between these subgroups is at least as strong as the differences between the correlated and uncorrelated genes found in Step 2.

Step 4: Expand the Network by Repeating Steps 2 and 3

Each of the discovered groups can be used as a “seed” node in the same way the input signal (i.e., light intensity) was used in Step 2 to expand the network. In general, the correlation threshold could be selected to either encourage inclusion of genes into the network or promote exclusion and focus on “core” interactions. If the cutoff is chosen too low, however, the network could expand to include thousands of genes. For our studies, more stringent cutoffs at a value of 0.7 were used to limit the size of the resulting networks.

Step 5: Create a Graphical Representation of the Network

For small data sets the interaction network may be analyzed and visualized manually; however, for larger systems this process needs to be automated. The Graphviz program from ATT Research Labs (http://www.research.att.com/sw/tools/graphviz/) was adapted for this purpose. This program has been optimized using heuristics to minimize cross-over events between edges in order to create easily interpreted output figures. For our purposes, the output of our analysis software (written in MatLab) has been written into simple text code that is reinterpreted to create jpeg images. MatLab functions for automating the creation of such files from time-lagged correlation analysis have been written for this purpose and are available from the author, along with the data sets (http://web.mit.edu/cheme/gnswebpage/index.shtml) and time-lagged correlation algorithm files.

Experimental Conditions

Synechocystis can grow on a variety of carbon sources including glucose or CO₂. For all of the studies conducted here, cells were grown solely on dissolved CO₂ as . Other medium requirements, such as a source of nitrogen and salts, were provided using BG-11 medium (Sigma), designed specifically to satisfy the nutritional needs of freshwater cyanobacteria. All cultures were grown in an incubator at 30°C under fluorescent light. Light intensity in the incubator was determined to be approximately 6900 LUX, or a photosynthetic photon flux (PPF) of about 90 μmol/m²/s at the surface of a culture. This flux is expected to drop significantly inside of the cultures due to shielding by the outermost cells; therefore all cultures were continuously shaken or stirred to ensure homogeneity of light exposure.

Seed cultures were used to inoculate intermediate cultures, which fed the reactor vessel. Seed cultures were grown in 250-ml flasks with cotton and gauze caps and contained 100 ml of H₂O that was heat sterilized. Concentrated (50X) BG-11 medium (2 ml) and 0.38 M Na₂CO₃ (300 μl) were added to the cooled (30°C maximum) flasks. Intermediate cultures used to inoculate the larger reactor vessels were grown in 1-L flasks with 300 ml of H₂O. Concentrated (50X) BG-11 (6 ml) and 0.38M Na₂CO₃ (300 μl) were added to the flasks, along with sterile-filtered 1 M HEPES (6 ml) to create an environment similar to the sparged reactor vessel (see below). Approximately 10 ml from a 250-ml seed culture in late-exponential or stationary phase was used for inoculation of the intermediate cultures. Intermediate cultures were grown to mid-exponential phase (A₇₃₀ ∼ 1.0, approximately 4 days) before inoculating the large reactors.

The layout of the sparged-gas vessel is shown in Figure 2. Six liters of H₂O was autoclaved in the 10-L reactor vessel with a large stir-bar placed in the center of the gas-sparging ring. Since CO₂ was bubbled through this reactor, no Na₂CO₃ was added, only BG-11 media (120 ml). Dissolved CO₂ gas in the form of (H⁺)() increases the acidity of the culture, drastically inhibiting growth. To counteract this, 1M HEPES (120 ml) was added as a pH buffer (pKa = 7.31 at 37°C). The CO₂ source gas (1–3% CO₂, ∼16% O₂, balance N₂) flowed through a sterile tubing plastic ring sparger filter into a at a rate of about 150ml/min. Sparged gas escaped through a pressure release valve at the top of the vessel. A final tube, extending deep into the liquid culture, was sealed with a quick-release and used for sampling.

All experiments were conducted as described in Schmitt Jr. and Stephanopoulos (2003). The experimental setup and light intensity profiles are shown in Figure 2. To ensure that the cells never reached a steady state, the input intensity of light was changed every 3 h for the first experiment. The three light intensities shown correspond to 0, 16, and 90 μmol/m²/s photosynthetic photon flux (PPF). Culture samples were taken in tubes containing 10% of a phenol (5%) and ethanol (95%) mixture and immediately chilled, but not frozen, in liquid nitrogen. These samples were centrifuged at 5000 × g for 5 min at 2°C, and the resulting pellets were stored at –80°C until isolating the RNA.

To isolate the RNA, pellets were resuspended and processed according to the Qiaquick (Qiagen) RNA extraction kit, with the additional step of grinding the cell pellets in a bead mill for 4 min to break the Synechocystis' outer cell wall. Typical yields were 10–50 μg of RNA for 50-ml tubes of samples, which is enough to run between one and four microarrays.

Full-length cDNA microarrays (provided by DuPont Co. comprising 3078 unique cDNA sequences were used. These were shipped dry in 384 well (16 × 24) plates (Genetix), resuspended with 5 μl of 50% (vol.) DMSO in H₂O, and stored at –80°C until printing. Arrays were printed on a MicroGrid II quill pin microarrayer (BioRobotics) at 35–45% relative humidity at room temperature on Corning Gap slides. Sixteen quill pins were used to print with a 0.29 pitch (290 μm spacing) between features. The features were printed in 16 grids, each containing 15 rows and 15 columns of cDNA features. While printing, each pin was blotted three times on each of four spare slides to remove excess liquid from the quills. Then printing was performed at one tap/slide for each of 104 slides. This entire procedure was repeated on the bottom half of each slide. The printing procedure took about 20 h to print the entire cDNA library in duplicate on 104 slides. Slides were then crosslinked in batches of 18 slides using a Stratalinker (Stratagene) set to the “Autocrosslink” option at 1200 μJ, and were stored in the dark until use.

All RNA samples were processed into labeled cDNA, hybridized to arrays, and scanned as described in Schmitt Jr. and Stephanopoulos (2003). To summarize the results of that paper, data from this experiment was used to build AutoRegressive with eXogeneous input (ARX; Wei 1990; Schmitt Jr. and Stephanopoulos 2003) models to predict the transcriptional outcome of various potential follow-up experiments. The profile selected as most likely to contain discriminating information was used as the input light signal for the second experiment, also shown in Figure 2. Details of this experimental design procedure are also contained in Schmitt Jr. and Stephanopoulos (2003).

Microarray quality, sample processing, and data filters were analyzed in aggregate by hybridizing six samples from cultures grown in parallel and labeled with different dyes to three microarrays. On average, the expression ratio of 8.8% genes differed by greater than 1.75, while only 5.1% of genes differed by more than twofold, consistent with other cDNA microarray experiments. Based on these results, genes were deemed to be differentially expressed if they exhibited an expression ratio of two-fold or greater with respect to the control. A compilation of all duplicate spots within slides gave a within-slide coefficient of variation of 0.18.

Table 3.

Gene Groups for the Network of Figure 4.