Abstract
To understand the relationship between enhancer DNA sequence and quantitative gene expression, thermodynamics-driven mathematical models of transcription are often employed. These “sequence-to-expression” models can describe an incomplete or even incorrect set of regulatory relationships if parameter space is not searched systematically. Here, we focus on an enhancer of the Drosophila gene ind and demonstrate how a systematic search of parameter space can reveal a more comprehensive picture of a gene’s regulatory mechanisms, resolve outstanding ambiguities, and suggest testable hypotheses. We describe an approach that generates an ensemble of ind models; all are technically acceptable solutions to the sequence-to-expression problem in light of wild-type data; some represent mechanistically distinct hypotheses about the regulation of ind. This ensemble can be restricted to biologically plausible models using requirements gleaned from in vivo perturbation experiments. Biologically plausible models make unique predictions about how specific ind enhancer sequences effect ind expression; we validate these predictions in vivo through experiments using transgenic Drosophila embryos.
Introduction
Transcription factors (TFs) work in concert with other DNA-binding molecules to regulate gene expression. These molecules act as inputs at enhancers, distinct genomic regions that contain binding sites for TFs and can regulate the transcription of target genes (Shlyueva et al., 2014).. Maintaining a quantitative relationship between input and transcriptional output is key to the precise patterning of gene expression. Accordingly, as the levels of inputs vary across different cell types, the enhancer-controlled levels of gene expression (also termed as the “readout” of the enhancer) also vary (Yanez-Cuna et al., 2013). These relationships are a direct function of the enhancer’s DNA sequence. However, a detailed understanding of how enhancer sequence effects a gene’s expression level remains elusive (Yanez-Cuna et al., 2013). Such understanding may be achieved by interrogating a mathematical model that explains the available experimental results about the gene both qualitatively and quantitatively, suggests experiments to improve upon the current model, and is capable of predicting the gene’s expression pattern upon cis- or trans- perturbations. Here, we refer to such models here as “sequence-to-expression” models, and show how they can form the basis of a systematic, unbiased enquiry into gene regulation by multiple TFs.
A common paradigm of sequence-to-expression modeling is based on equilibrium thermodynamics (Shea and Ackers, 1985). This approach models the rate of transcription initiation based on quantitative descriptions of variable site affinities (“motifs”) (Stormo, 2000) and expression levels of TFs. Because they can incorporate the DNA sequence-dependent characteristics of TF binding, sequence-to-expression thermodynamic models of this genre are arguably more realistic than thermodynamic models where all TF binding sites are assumed to have the same affinity (Cohen et al., 2014; Fakhouri et al., 2010; Papatsenko and Levine, 2008; Zinzen and Papatsenko, 2007) or only classified as “strong” vs. “weak” (Bintu et al., 2005; Gertz et al., 2009; Parker et al., 2011; White et al., 2012). We previously reported one such sequence-to-expression model called GEMSTAT, and used it for modeling ~40 enhancers involved in anterior-posterior patterning during early embryonic development of Drosophila (He et al., 2010).
Sequence-to-expression models like GEMSTAT face a significant challenge. They are formulated using one to three free parameters that are specific to each TF, and other parameters that represent TF-TF interactions and basal activity at the promoter. Because a typical enhancer is controlled by a handful of TFs, even simple models may have a considerable number of free parameters. Most of these parameters have not been determined experimentally. Instead, they are estimated by numerical algorithms that operate within a defined parameter space to identify parameter values whose predictions are optimal fits to the data. Importantly, these fits are not necessarily unique. Since the models are typically overdetermined given experimental data, a given model may make different predictions that are consistent with available data at distinct parameter settings.
It is entirely possible that there are multiple optima within the parameter space for a given enhancer. Some related studies have indeed found widely different parameter assignments to fit a data set (Dresch et al., 2010; Granek and Clarke, 2005; Zinzen and Papatsenko, 2007), yet the standard practice is to report one or at most a few best models that result after iterative improvements upon initial random guesses (He et al., 2010; Janssens et al., 2006; Kim et al., 2013; Parker et al., 2011; Segal et al., 2008). An alternative approach, however, can be taken. For example, several papers on multi-parameter models for systems biology and climatology (Gutenkunst et al., 2007; Tebaldi and Knutti, 2007) have demonstrated that different parameter sets can fit the same data. In such cases, the different optima may represent distinct, mutually exclusive hypotheses about underlying mechanisms. A systematic interrogation of a gene’s sequence-to-expression model must consider all such hypotheses and distinguish between them. Some related studies have indeed found widely different parameter assignments to fit a data set (Dresch et al., 2010; Granek and Clarke, 2005; Zinzen and Papatsenko, 2007), yet the standard practice is to report one or at most a few best models that result after iterative improvements upon initial random guesses (He et al., 2010; Janssens et al., 2006; Kim et al., 2013; Parker et al., 2011; Segal et al., 2008).
This suggests that if one is to understand the relationship between enhancer sequence and quantitative gene expression in an unbiased way, one should go beyond the common practice of seeking the single best fitting model. Instead, one could explore the entire parameter space for models that agree with data.
Here, we take this approach and perform a systematic exploration of the parameter space of the GEMSTAT model for a specific developmental gene, intermediate neuroblasts defective (ind), in D. melanogaster. Beginning with a qualitative understanding of its likely regulators, we adopt an ensemble modeling approach (Brown et al., 2004; Kuepfer et al., 2007; Swigon, 2013; Toni et al., 2009; Villaverde et al., 2014; von Dassow et al., 2000) to learn all quantitative models consistent with wild-type expression data, then use a visualization tool that we introduce here to recognize the distinct mechanistic hypotheses they represent. Next, we ask how additional perturbation experiments reported in the literature refine the ensemble of models, and eliminate mechanistic explanations that are inconsistent with these additional data. The surviving ensemble of models, despite representing distinct hypotheses about regulation, can make unambiguous predictions about ind’s response to specific perturbations. We verify these predictions experimentally. Using this approach iteratively we can narrow down the ensemble of consistent models and refine our understanding of the gene’s cis-regulatory logic. In total, we outline a “strong inference” approach (Platt, 1964) that systematically eliminates various mechanistic explanations to the data, within the context of a pre-determined qualitative model, and also suggests the additional experiments necessary to further refine our mechanistic understanding.
Results
A model of transcriptional regulation by sequence-specific transcription factors and their interplay with signaling molecules
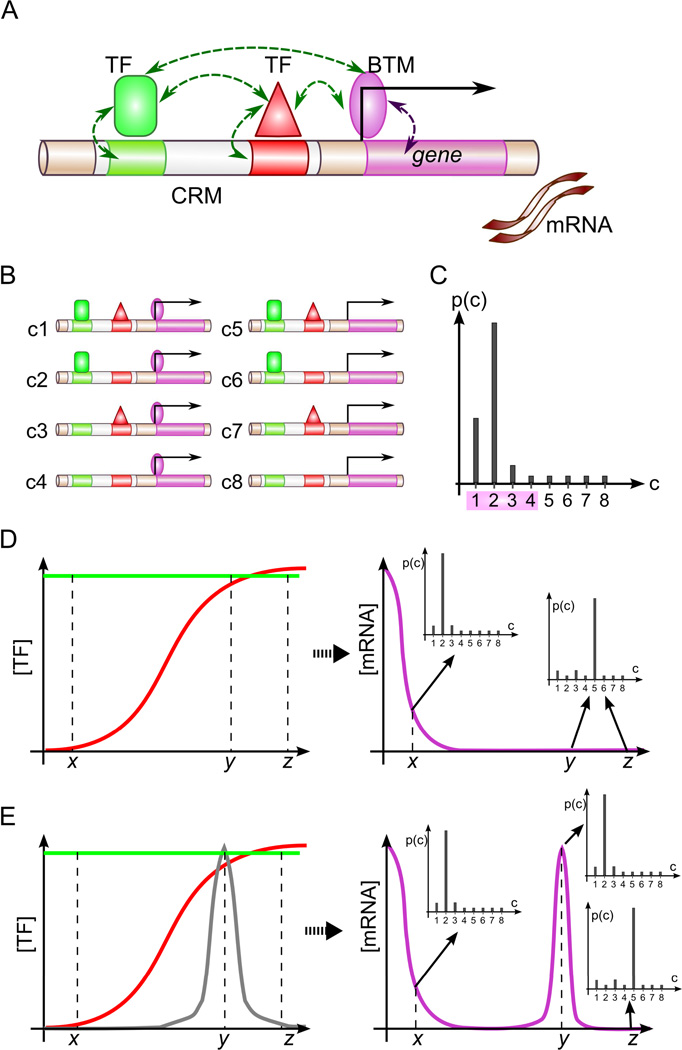
We modified GEMSTAT (He et al., 2010), a sequence-to-expression model, to study how TFs bound to the ind enhancer may regulate the gene’s expression. We outline the main assumptions and components of the model here; see Experimental Procedures and Supporting Online Information for details of model formulation. GEMSTAT is founded on a theory of combinatorial gene regulation first proposed by Shea and Ackers (Shea and Ackers, 1985). The model considers the system of TF molecules and their cognate sites in the enhancer, as well as the basal transcriptional machinery (BTM) and its binding to the promoter, and uses a minimal set of parameters to model the interactions among TFs, BTM and DNA (Figure 1A). All interactions are assumed to happen in thermodynamic equilibrium, which is assumed to be reached much more rapidly than the time scale at which the transcription machinery is activated and begins producing mRNA. Under these assumptions, the transcription initiation rate, and hence the equilibrium level of mRNA transcription, is proportional to the fractional occupancy of the BTM at the promoter. GEMSTAT computes this fractional occupancy by considering all possible configurations of DNA-bound TFs and BTM (Figure 1B) and summing the probability of configurations where the BTM is promoter-bound (Figure 1C). The equilibrium probability of each configuration is computed based on the Boltzmann distribution. As TF concentrations change across cell types, the probability of bound BTM configurations also changes, reflecting the variation of expression levels due to the change in regulator concentration (Figure 1D).
Figure 1.
Overview of GEMSTAT model. (A) GEMSTAT models the expression readout of an enhancer from the strength of TF-DNA and TF-BTM interactions in thermodynamic equilibrium and (B) considers all possible configurations of bound TFs and the BTM to compute the equilibrium probability of BTM occupancy at promoter (C). Shown is a hypothetical probability distribution for the configurations shown in B; probability of BTM occupancy is computed from configurations c1—c4. (D) GEMSTAT’s predictions change as TF concentrations change across different conditions. Shown is the profile of mRNA levels (magenta) resulting from a uniformly expressed activator (green) and a graded repressor (red); horizontal axis: different spatial locations. Also shown is how the equilibrium probability distributions change with changes in TF concentrations. (E) A molecular species (gray) that can attenuate the DNA-binding affinity of a repressor may increase the mRNA level of the gene shown in D.
An important distinction of the GEMSTAT model from several other thermodynamics-based models – as we mentioned in the Introduction – is its ability to account for varying affinities of a TF’s binding sites, by relating mutations from the optimal or “consensus” site to corresponding changes in binding energy. For this, GEMSTAT implements Berg and von Hippel’s theory of protein-DNA interaction energetics (Berg and von Hippel, 1987), using the TF’s position weight matrix (Stormo, 2000) to predict the “mismatch energy” relative to the consensus site (Supporting Online Information).
Our modification of GEMSTAT in this work allows for modulation of a TF’s DNA binding affinity depending on the concentration of some other molecular species, which in our case (next section) was the dual phosphorylated extracellular signal-regulated kinase (dpERK). We modeled a recently proposed “de-repression” mechanism whereby the kinase attenuates a repressor TF’s DNA-binding affinity, resulting in higher expression levels of the regulated gene at higher levels of the kinase (Figure 1E). This allows us to model how a non DNA-binding regulatory input may shape the expression pattern of a target gene by interacting with the gene’s enhancer.
A model of transcriptional regulation of the ind gene
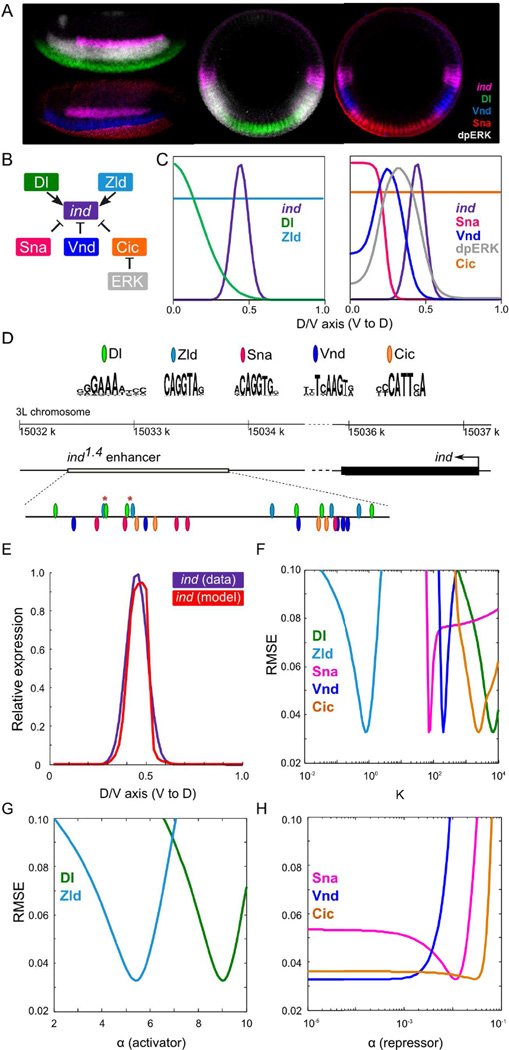
We used GEMSTAT to study the details of regulation of ind, a dorsoventral (D/V) patterning gene in Drosophila. The neuroectodermal expression pattern of this gene and an enhancer driving this expression have been characterized previously (Stathopoulos and Levine, 2005; Weiss et al., 1998). Prior works have also revealed or suggested identities of its major regulatory inputs, and reported several genetic perturbations and the resulting changes in ind expression. Our main goals were to infer mechanistic details of the combinatorial action of these regulators, to test if these details are consistent with observations made under various perturbations of the system, and to make testable predictions about additional perturbations. We list below our assumptions about how these inputs regulate ind expression (Figure 2A—C).
Dl directly activates ind (Hong et al., 2008), while Sna and Vnd are its direct repressors (Cowden and Levine, 2003; McDonald et al., 1998; Weiss et al., 1998).
Zld activates ind (Nien et al., 2011), but the mechanism may be either direct (similar to Dl) or indirect, or a combination of both. To model the indirect mechanism, we considered Zld and Dl to exhibit cooperative DNA binding at closely located binding sites, based on our observation of proximally located binding sites for the two TFs (Figure 2D, Supporting Online Information, Figure S1A), and on reports of a similar mechanism in the sog enhancer (Foo et al., 2014; Liberman and Stathopoulos, 2009). We note that Dl-Zld cooperativity can also act as a surrogate for chromatin-mediated effect of Zld on Dl activation, as suggested in (Cheng et al., 2013; Foo et al., 2014; Sun et al., 2015).
Cic is a repressor of ind. Mutation of Cic sites in the ind enhancer results in a dorsal expansion of ind expression (Ajuria et al., 2011; Lim et al., 2013). However, Cic has a spatially uniform nuclear concentration during the pre-gastrulation stage, suggesting that an additional input that localizes Cic’s activity domain must be considered when modeling Cic-mediated repression of ind. Spatially restricted signaling may provide this input, presumably by relieving Cic-driven repression of ind. In particular, ERK phosphorylates Cic (Astigarraga et al., 2007) and this has been proposed to influence Cic activity by impeding its DNA binding (Dissanayake et al., 2011; Lim et al., 2013), leading to ind de-repression in a specific domain along the D/V axis. This is the mechanism we chose to implement here, though other mechanisms have also been proposed (Grimm et al., 2012). We obtained a D/V profile of dual-phosphorylated ERK (dpERK) from (Lim et al., 2013) and used it as a proxy for ERK activity. To model this effect, we modified GEMSTAT so that the energy of Cic-DNA binding is increased (binding affinity is reduced) to an extent proportional to dpERK concentration (Experimental Procedures).
Figure 2.
Inputs to the model and an example of predicted ind expression from a wild-type model. (A) Lateral (left) and D/V cross-sections (right) of blastoderm stage Drosophila embryos. Embryos were stained with ind mRNA (magenta) and its four non-uniform regulators, Dl (green), Vnd (blue), Sna (red), and dpERK (gray). (B) Assumed relationships between ind and its regulators. (C) Expression profiles of ind and its regulators along D/V axis. (D) PWMs of the regulators and locations of computationally identified sites for TF binding. Asterisks mark the pairs of closely located Dl-Zld sites. (E) (i) Predicted ind expression (red) from a model optimized on wild-type data (purple). (ii – iv) Sensitivity plots for a model: panels show the RMSE scores of the model as the corresponding parameter’s value is varied within its range, keeping other parameters fixed at their optimized values. For brevity, the vertical axis is limited at RMSE = 0.10.
To capture the above qualitative features, GEMSTAT uses 13 free parameters: two per TF representing its DNA-binding and activation/repression potency (denoted by K and α, respectively), one for Dl-Zld cooperativity (denoted by ω), one representing basal transcriptional activity (denoted by qBTM), and one representing the attenuation of Cic’s DNA-binding energy by dpERK (denoted by CicATT). The free parameters of the model were optimized to fit the wild-type D/V expression profile of ind, and prediction from the trained model was found to be in excellent agreement with this wild-type pattern and also to be sensitive with respect to most of the parameters (Figure 2E), indicating that the model is flexible enough to capture the combinatorial effect of the assumed regulators in driving ind expression. Notably, model training failed completely when we did not incorporate ERK-Cic interplay (data not shown), providing quantitative evidence in favor of this mechanism. However, this exercise also raised questions about the validity and utility of the trained model, such as: 1) Can the model correctly predict the effect of cis- and trans- perturbations to the system? 2) Does the trained model provide a unique quantitative explanation of ind regulation consistent with the data? 3) If not, what are all possible quantitative explanations of these data, what do they predict about various perturbations, and how can we narrow them down to the true underlying mechanism? We address these questions in the following sections.
Systematic exploration of parameter space provides an ensemble of distinct mechanistic hypotheses consistent with the wild-type data
In Figure 2E, we presented the prediction of a single model, i.e., one particular setting of parameter values, that accurately fits wild-type ind expression. Any assignment of values to the 13 free parameters of the model corresponds to a predicted readout of the ind enhancer, which can be scored against the wild-type ind pattern using a “goodness-of-fit” function. Any high-scoring parameter assignment represents a plausible mechanistic description of ind regulation; it provides insights into the relative strengths of various regulatory inputs, and makes predictions about the effects of different cis- and trans-perturbations.
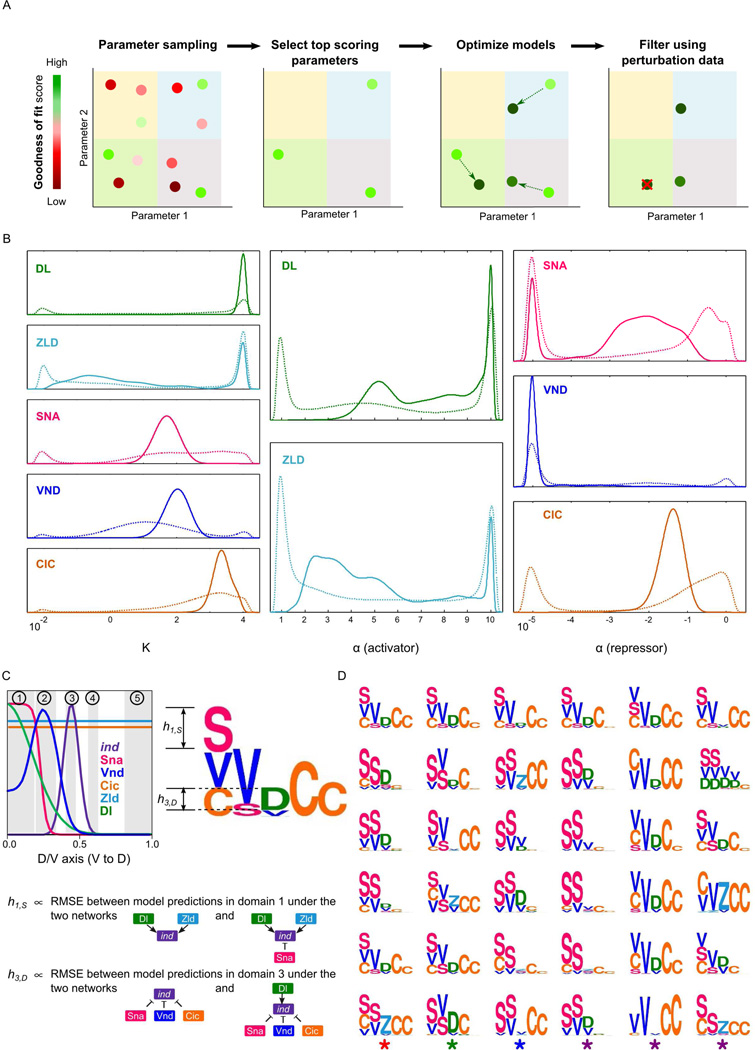
Given any initialization of parameter values, the GEMSTAT program systematically and iteratively modifies those values and reports a locally optimal parameter setting that maximizes the goodness-of-fit. However, there may exist many other parameter assignments that are as good or nearly as good in terms of their agreement with data, and examining the one optimal assignment reported by GEMSTAT may provide a skewed view of plausible models (Kirk et al., 2013). We therefore modified the GEMSTAT program to perform a comprehensive exploration of the multi-dimensional parameter space, with the goal of constructing a complete map of plausible quantitative models. To this end, we first generated a large number of 13-dimensional vectors (parameter assignments) as follows (Figure 3A; Supporting Online Information). We partitioned each parameter’s range into halves, which gave us 213 compartments of the parameter space. From each compartment, we sampled 1000 parameter vectors and scored them for their goodness-of-fit to data. Next we sorted these 1000 × 213 parameter vectors based on their scores and for each parameter vector with a score among the top 2% of unique scores in this sorted list, we optimized the GEMSTAT model using that vector as initial estimate of model parameters. The resulting collection of optimized models can predict ind expression accurately in wild-type condition (Figure S1B), with little dispersion in their predictions (maximum difference with the mean is < 0.07 at any position along the D/V axis). We call this collection of models (~21000 in total) the “wild-type ensemble”. We note that an alternate strategy to compute such an ensemble would be to sample from the parameter space using Monte Carlo based techniques (Toni et al., 2009). However, there are major challenges associated with these methods – e.g., slow convergence to the stationary distribution and consequently less control over the coverage of the parameter space, the need for pre-computing an ensemble of models that covers the parameter space (Toni et al., 2009), etc. – which motivated us to choose the exhaustive strategy described above.
Figure 3.
Construction and visualization of model ensembles. (A) Left to right: sampling of parameter vectors, scoring, model optimization initiated from each parameter vector which scored above the threshold (the resulting set of optimized models is the “wild-type ensemble”), and filtering of wild type models according to their accuracy in predicting the effects of various perturbations. The remaining models (not crossed-out) constitute the “filtered ensemble”. (B) Marginal densities of parameters of the wild-type and the filtered ensemble models (dashed and solid lines, respectively). (C) The motif for a model shows how it utilizes each TF to regulate ind in five domains along D/V axis. Each domain corresponds either to the peak expression domain of ind (domain 3) or a TF (domains 1 and 2: peak expression domains of Sna and Vnd, respectively), or to a domain where the effect on ind expression is known for a specific site-mutagenesis experiment (domains 4 and 5: results known for Cic site mutagenesis). Columns in a motif correspond to domains, symbols denote the regulator TFs, and the height of a symbol in a column represents the contribution of that TF in the corresponding region: if a TF f is an activator then its height in a column represents the root-mean-squared-error (RMSE) between model-predicted ind expression profiles in the corresponding domain when there is no activator and when f is the only activator in the model. Similarly, the height of a repressor f is computed from the conditions when there is no repressor and when f is the only repressor in the model. (D) Representative motifs of the 36 clusters computed from the wild-type ensemble models.
The ~21,000 models of the wild-type ensemble spanned widely different compartments of the parameter space (652 out of 213 ≈ 8000), and the marginal densities of individual parameters showed high variance and multimodality (Figure 3B). This suggested the existence of many distinct parameterizations that explain the wild-type data equally well, and we asked if this meant that many distinct mechanistic hypotheses explain the data on ind regulation. To this end, we summarized the models as motifs that visually depict how a particular model utilizes each TF to regulate ind in five key spatial domains along the D/V axis (Figure 3C; see the legend). Columns in a motif correspond to domains, symbols denote the regulator TFs, and the height of a symbol in a column represents the contribution of that TF in the corresponding region.
Hierarchical k-medoids clustering of the motifs for the wild type ensemble revealed at least 36 distinct sets of mechanistic hypotheses (motifs) that are supported by the wild-type data (Figure 3D). As an example of how these hypotheses differ, we marked three motifs in the bottom row with asterisks, that suggest three distinct mechanisms of activating ind in its peak domain of expression (third column in the motif): (i) Zld is the dominant activator of ind while Dl does not have an important role to that end (marked with red *), (ii) Dl is the dominant activator of ind while Zld does not play a strong role in activating ind (marked with green *), and (iii) neither of Dl and Zld alone, but only their synergistic interaction is the dominant input toward activating ind (marked with blue *). Clearly, a number of different quantitative models are consistent with wild type data, raising the concern that some of these may yield incorrect predictions under perturbation conditions, and prompting us to ask how additional experiments can refine the wild-type ensemble.
Data from perturbation experiments narrow down the range of plausible models
Wild-type data may not have sufficient information to constrain a multi-parameter model such that it captures the precise extent of each TF’s effect on the target gene. To further constrain the values of model parameters, we examined how well models in the ensemble predict the effects of the following genetic perturbations for which we have data from the literature.
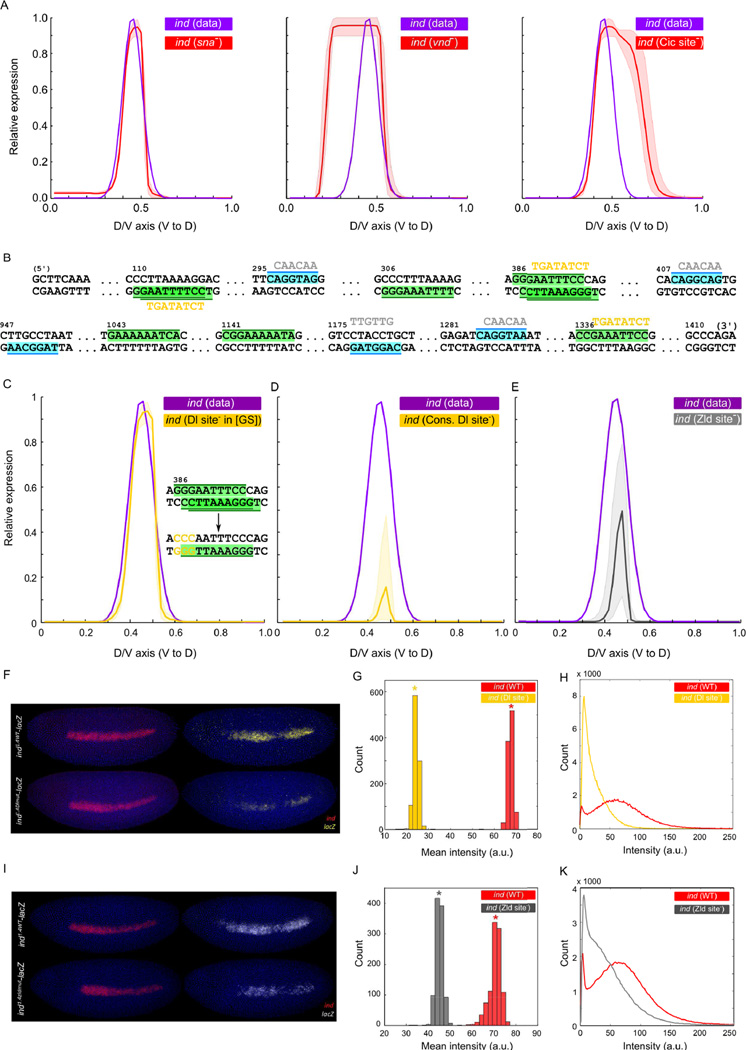
Mutation of sna: the ind expression domain remains essentially unaltered in sna mutants. vnd expression is de-repressed in these embryos and expands ventrally such that ind stays repressed in the endogenous domain of sna expression (Figure S2A).
Mutation of vnd: the ind expression domain expands ventrally, yet does not encroach into the mesoderm region, in vnd mutants (McDonald et al., 1998; Weiss et al., 1998).
Mutation of Cic binding sites in the ind enhancer: the readout of the ind enhancer expands dorsally, to an extent that matches the spatial domain of the Dl protein, upon mutating two particular Cic sites in the enhancer (Lim et al., 2013).
These are the only perturbations reported in the literature that manifest direct effects on ind expression. We used each model to predict ind expression upon knocking down a TF, by setting the DNA-binding parameter of the respective TF to zero. Additionally, when simulating sna knockdown, we replaced the spatial patterns of vnd and egfr with their altered patterns in sna mutants (Figure S2B–C). To predict the effect of mutating a site, we discarded the site from our set of annotated TF binding sites in the ind enhancer (Experimental Procedures). In evaluating models on perturbation data we focused on carefully selected domains along the D/V axis which, we reasoned, should provide adequate information about the accuracy of model predictions (Experimental Procedures).
For each of the ~21,000 models in the wild-type ensemble, we evaluated its predictions on perturbation data and discarded every model that failed to correctly predict the known effects. We found ~2100 models whose predictions are accurate in both wild-type and in the three perturbation conditions (Figure 4A). We call these models the “filtered ensemble”. Parameters of these models were found to be far more constrained than those of the initial ensemble, falling into 42 of the 213 compartments in the parameter space, whereas the wild-type ensemble models span 652 compartments. (Also compare the solid to the dotted curves in Figure 3B, which shows marginal distributions of parameters). Considering perturbation data in this manner greatly narrowed down the possible explanations of ind regulation, with the only surviving mechanistic hypotheses being those shown as motifs in the first row of Figure 3D. Whereas models in the wild-type ensemble could explain ind regulation without one of our three assumed repressors (the three motifs marked with purple asterisks in the bottom row of Figure 3D), the filtered ensemble unambiguously supports the need for all three repressors: Sna and Vnd repress ind in the mesoderm and the neuroectoderm domains, and Cic plays a role in defining the dorsal border of ind. This filtering step also removed from the wild type ensemble those models that implied a very weak activating input from Dl (low KDL, αDL; dotted lines in panels labeled ‘DL’, Figure 3B). Such models overestimate the activating role of Zld, and thus over-predict the expression level of ind in the dorsal-ectoderm upon Cic site mutagenesis, leading to their exclusion from the filtered ensemble.
Figure 4.
Predictions of the filtered ensemble and their experimental validations. (A) Predictions of filtered ensemble under perturbed conditions; left to right: mutation of sna, vnd, and two Cic sites in the ind enhancer. Shown are the mean (red) and the range (shaded red area around the curve) of ensemble-predictions. Plots in C, D, and E follow the same semantics. (B) Computationally identified sites for Dl (green) and Zld (cyan) in ind enhancer. Yellow and gray sequences show mutations to disrupt Dl and Zld sites, respectively. (C) Filtered ensemble models do not predict any significant change in ind expression upon the mutations reported in (Garcia and Stathopoulos, 2011); but (D) predict that ind expression nearly abolishes upon removing the additional sites for Dl. (E) Filtered ensemble models predict ~50% reduction in ind expression upon mutating Zld sites in ind enhancer. (F) The ind enhancer was used to drive expression that recapitulates the endogenous ind expression (ind1.4WT-lacZ) and Dl sites in the enhancer were mutated (ind1.4Dlmut-lacZ). Embryos were co-stained with ind (red) and lacZ (yellow). (G) Histograms of mean intensity values computed from bootstrapped profiles; asterisks mark bootstrapped mean values. (H) Smoothed histograms from wild-type and mutant lacZ profiles (each created from 20 profiles (one per embryo) on 256 bins (one per intensity value)). (I) Zld sites in the enhancer were mutated (ind1.4zldmut-lacZ). Embryos were co-stained with ind (red) and lacZ (white). (J), (K): plots analogous to (G), (H).
Predicting the effect of mutating activator binding sites
An important aspect of the utility of any modeling approach is its ability to make testable predictions. Here we show how we utilized our filtered ensemble to predict the effects of Dl and Zld in activating ind and how we validated those predictions experimentally.
ind expression is known to be abolished in Dl mutants (von Ohlen and Doe, 2000) and to become weaker in Zld mutants (Nien et al., 2011). However, both Dl and Zld are also implicated in regulating several direct regulators of ind, e.g., sna, vnd, rho, and egfr (Hong et al., 2008; Nien et al., 2011), hence their genetic effects comprise a combination of direct and indirect influences. To accurately characterize the direct activating roles of Dl and Zld one needs to mutate their binding sites in the ind enhancer. To this end, we focused here on the computationally identified binding sites for Dl and Zld in the ind enhancer (Figure 4B; Experimental Procedures).
To our knowledge, the only prior experimental study that examines direct effects of Dl on ind is that of Garcia and Stathopoulos (Garcia and Stathopoulos, 2011), who mutated a Dl binding site in the ind enhancer and found no significant change in ind expression – leading them to speculate that Dl only partially supports ind activation. Predictions from our filtered ensemble for the particular mutation performed by Garcia and Stathopoulos agree with their report (Figure 4C). The filtered ensemble also predicts, unambiguously, that removal of all Dl sites should abolish ind expression (Figure S2D) – suggesting a dominant role of Dl in activating ind. (This also means that Zld alone cannot activate the gene.) We confirmed this prediction experimental ly in transgenic embryos through mutating three evolutionarily conserved sites of Dl in the ind enhancer (Figure 4B, Figure S2E). In particular, we mutated the above three sites to a sequence which is both shorter than the known Dl binding site and has a very low affinity score based on the position weight matrix of Dl. We also confirmed computationally that these mutations do not create any new site for the TFs considered in our model. The reporter sequences containing the mutated Dl sites were then integrated at the same chromosomal location, which allowed us to make direct comparisons of their expression levels (Experimental Procedures). Our filtered ensemble predicts that ind expression will reduce by 60–100% (mean 85%) of its wild-type level upon this perturbation (Figure 4D). The experiment showed ~65% reduction in peak ind expression which validates the model prediction and supports a dominant role of Dl in ind activation (Figure 4F–H, also see Supporting Online Information, Figure S3). This investigation illustrates that an ensemble of models can make unambiguous predictions despite large variations in individual parameters, as has been previously argued more generally for multi-parameter ODE-based models (Gutenkunst et al., 2007). Our investigation is also significant in that it correctly predicts a major effect of Dl site mutagenesis in one experiment and no effect in a different mutagenesis experiment (Garcia and Stathopoulos, 2011) for the same transcription factor (Fig 4C, D). It is extremely difficult to make such nuanced predictions based on qualitative reasoning alone.
The filtered ensemble predicts that Zld-induced activation is necessary for wild-type ind expression; specifically, that ind expression should reduce, on average, to ~50% of its peak wild-type level upon mutating the four strongest Zld binding sites (out of five sites) in the ind enhancer (Figure 4E). We tested this prediction, and noted that ind expression is indeed reduced in transgenic embryos where Zld sites were mutated (Figure 4I–K, also see Supporting Online Information, Figure S3), to about half of the endogenous levels. The expression of ind in these embryos is considerably more variable than its endogenous expression, leading us to speculate whether the apparent reduction in expression level is due to increased noise (i.e., ind has bimodal expression, at a basal level and at a level comparable to its endogenous peak level) or due to an overall reduction in expression level within the nuclei where ind is expressed. We find further analyses support the latter proposition (Figure 4K).
Thus, the filtered ensemble reveals Dl as the dominant activator of ind, while also demonstrating an important activating role for Zld. There remain uncertainties in parameter values in the ensemble (Figure 3B), and these uncertainties can in some cases translate to ambiguous predictions for specific perturbations. We revisit this point in Discussion, where we show how the modeling framework suggests the most informative experiments to perform in order to resolve such ambiguities.
Models in the filtered ensemble explain ind regulation in other Drosophilids
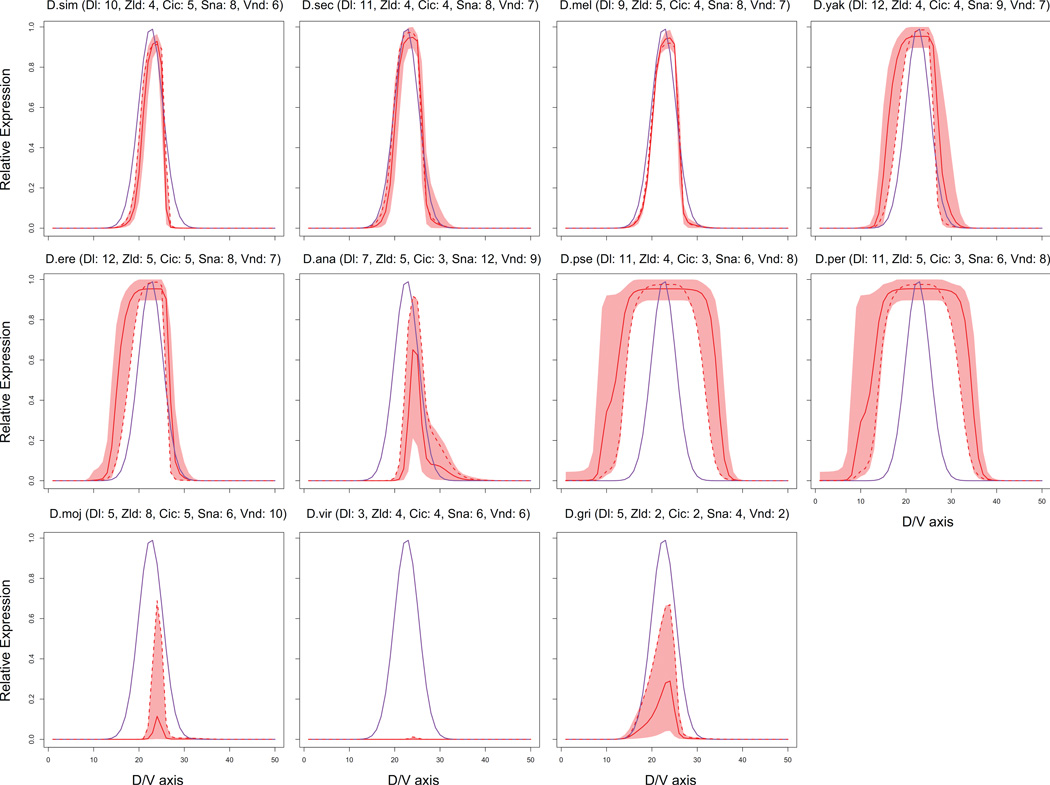
One potential issue with the filtered ensemble models is that they might be ‘overfit’ to the specific number and arrangement of TF binding sites in the D.melanogaster ind enhancer, as opposed to capturing a more general logic. If this were the case, we would expect the filtered ensemble of models to contain features that are specific to D. melanogaster and not conserved across Drosophilids. We asked whether our filtered ensemble models of the D.melanogaster ind enhancer can explain features found in the orthologous ind enhancers of ten other Drosophilids species. As shown in Figure 5, for orthologs in the species related closely to D.melanogaster, the filtered ensemble models predict readouts that are very similar to the ind expression pattern in D.mel. For the orthologs from the more distantly related species, e.g., D.grimshawii, the filtered ensemble includes some models that are able to predict the expression domain with reasonable accuracy, and also models whose predictions deviate substantially from the ind pattern. (The exception to this was the ortholog in D.vir, which shows very poor sequence conservation with the D.melanogaster ind enhancer; see Figure S1.) Our observation suggests that the filtered ensemble, despite being trained on several perturbation experiments in addition to wild-type data, has sufficient diversity of models to capture the logic of orthologous ind enhancers.
Figure 5.
Predictions of the filtered ensemble models for the orthologs of the D.mel ind enhancer in ten other Drosophilids. See the legend of Figure S1 for the details of how the orthologs were extracted. Semantics of the plots are the same as that of Figure 4A. We also show in parentheses the number of TF binding sites in each ortholog. Additionally, the dotted red curve for each ortholog shows the best prediction of a filtered ensemble model for the corresponding ortholog. The goodness of a model prediction for a given ortholog is defined as the sum of squared error between the model prediction and ind expression data in D.mel.
Discussion
Recent technological advances allow the rapid generation of hypotheses about a biological system. Because biological problems are often under-constrained, the challenge becomes reconciling different hypotheses about the same system. Multi-parameter computational models are one way to unify diverse hypotheses into a comprehensive description of one system. However, with more parameters comes the burden of estimating those parameters and addressing parameter uncertainty (Gutenkunst et al., 2007). Ensemble modeling is a powerful solution to this problem, with demonstrated success in the context of signal transduction networks, protein folding and climate change, among others.
A major contribution of our work is the rigorous demonstration of how ensemble modeling may benefit a complex, multi-parameter model of transcriptional cis-regulation by refining its parameter estimates in a systematic and unbiased manner. Notably, integrating perturbation data into our analysis did not refine parameter estimates to precise points. However, it did lead to rejection of a large fraction of models from the wild-type ensemble, for example, models where Sna (or Vnd) alone can explain the ventral repression of ind. This illustrates why “learning” in biological systems should not be defined only as reduction of a mechanistic parameter to a point estimate; reducing the acceptable ranges of a mechanistic parameter, or of a combination of parameters, can be equally valuable. Moreover, such modeling can help us comprehend the disparate experimental evidence pertaining to regulation of the ind gene in Drosophila.
What insights does our filtered ensemble provide about ind regulation? First, the ensemble establishes a dominant, direct role of Dl in activating ind, and contradicts the previous observations that suggested a minor function of Dl in this context. We note that, since a direct activating role of Dl was an assumption of the model, the predictive value of our model is more in its ability to identify that ind cannot be induced in the absence of Dl sites and that removal of a particular subset of Dl sites leads to strongly reduced ind expression. Our experimental data on Dl site mutagenesis is therefore not only conforming to our assumption, but also to a quantitative prediction. Second, the ensemble emphasizes an important role of Zld in expressing ind. Recent work (Foo et al., 2014; Li et al., 2014; Sun et al., 2015) proposes that Zld functions primarily as a chromatin remodeler for these genes rather than imparting a direct activating input. However, such a direct role for Zld has been implicated previously (Hamm et al., 2015; ten Bosch et al., 2006). Our filtered ensemble models comprise two classes where one class of models suggests only an indirect activating role (possibly through chromatin remodeling) for Zld, while the other class suggests an additional direct activating input from Zld is necessary. As such, our current modeling cannot explain unambiguously how Zld activates ind. However, the filtered ensemble suggests an experiment that can disambiguate the mechanism. For this, we considered model predictions in spatial domains where Zld is the only regulator of ind. A non-basal level of ind expression under such a condition will imply the existence of a direct activating input from Zld, whereas basal levels will imply a lack thereof and signify Zld’s role as a facilitator of the DNA binding of Dl (Supporting Online Information). One such setup is available in the dorsal-ectoderm region upon mutating all Cic sites: this leaves Zld as the sole regulator in that region, and as summarized in Figure S4, predicted ind expression upon Cic site mutation shows large uncertainty in the dorsal-ectoderm region. Likewise, the filtered ensemble motifs (Figure 3D) exhibit maximum disagreement in the fifth column, i.e., in predicting the effect of Cic site mutation in the dorsal-ectoderm region. We therefore propose mutation of all Cic sites as an experiment that can disambiguate Zld’s mode of function. This is an illustration of how ensemble - based modeling can provide guidance about the most informative experiments to perform next.
An important assumption in this study was that a post-translational modification of Cic by ERK may inhibit DNA-binding of Cic and de-repress ind in a manner that depends on ERK’s spatial distribution. Without such an assumption of a localized de-repression of ind from the repressive effect of Cic, we were unable to fit any model with reasonable accuracy. While ERK-mediated de-repression of ind from Cic has experimental evidence (Ajuria et al., 2011; Lim et al., 2013), our assumption may not be the only mechanistic explanation to this phenomenon. Alternative hypotheses about spatially localized modifications in the influence of CIC on transcription initiation or on activator recruitment are also plausible. Notably, these alternative hypotheses do not rely on attenuation of Cic’s DNA binding, but on the potency of Cic’s interaction with transcription initiation machinery or with other TFs. One can also imagine a scenario where ERK activates some yet-unknown non-repressive TF that competes with Cic to bind DNA. Ascertaining any such mechanism is a subject for future studies.
One might ask if modeling a larger data set (i.e., multiple enhancers) could make the conventional approach of computing one or a few optimal models as effective as our ensemble approach in terms of eliminating incorrect mechanistic explanations. It is important to note that, the conventional approach attempts to discover models consistent with the entire data set. However, when relevant TFs and mechanisms of their functions are not well understood, a systematic ensemble approach for individual enhancers could provide insights that the one or few optimal models for the entire data set would have missed. For example, when trying to fit the enhancers of ind and sog simultaneously (data not shown), we consistently discovered models that do not use a direct activating input from Zld, presumably because the assumed inputs do not include a dorsal repressor for sog. Given that our understanding about the regulators of sog and the mechanism of Zld-mediated gene activation is still unclear (Supporting Online Information), simply rejecting a direct activating input from Zld, as one would if one were taking a more conventional approach, would produce a biased working hypothesis and opportunities for follow-up experiments could be missed. A systematic ensemble approach can thus improve sequence to expression models by identifying mechanistic hypotheses that are consistent with the entire data set and also those that conform to different subsets of the data, and thereby specifying the experiments for follow-up.
Experimental Procedures
The GEMSTAT model
To estimate the probability that TFs bound to an enhancer regulates the expression of a target gene, GEMSTAT considers the “statistical weight” Zc of each configuration c in the ensemble of all possible configurations of occupied and unoccupied TF-binding sites and the promoter. Detailed formulation of Zc and the algorithm to compute probability of mRNA expression from Zc are given in Supporting Online Information; here we mention the parameters that define Zc. For a given site S, the binding of a TF f at S contributes a statistical weight of qf,S = Kf,S [f] to Zc. Here Kf,S is the equilibrium constant of the DNA-binding reaction between f and S, and [f] is the concentration of f. Let denote the strongest binding site of f and denote the association constant of TF-DNA binding between f and . We re-write Kf,S as , where β is the Boltzmann constant and ΔEf,S denotes the “mismatch energy” of the site S relative to for f. The concentration [f] is in arbitrary units and can be re-written as v[f]rel where [f]rel is the concentration of f relative to some unknown reference value v. Therefore,
where and v are unknown quantities. We take their product as a free parameter and refer to it as the “DNA-binding parameter” for f. In addition to the qf,S terms, Zc includes the following multiplicative terms: (i) ωf1,f2 for each instance of two interacting TFs f1 and f2 bound in configuration c, (ii) αf for each instance of a TF f bound to one of its cognate sites and when c is a BTM-bound configuration, and (iii) qBTM whenever c is a BTM-bound configuration.
Filtering models based on perturbation data
Qualitative effects on the ind expression pattern upon various perturbations were mentioned in Results; we discard every model that fails to meet the following quantitative criteria in predicting those effects.
Upon Sna knock-out, a model should predict the mean probability of ind expression in the ventral-most 20% of the D/V axis to be low (≤ 0.05 times of the probability of ind expression at its peak domain).
Upon Vnd knock-out, a model should predict the mean probability of ind expression at locations of peak Vnd expression (at least 80% of its maximum concentration level) to be high (mean probability of expression ≥ 0.80).
Upon mutation of two (out of four) Cic binding sites, a model should predict ind expression to expand dorsally (mean probability of expression ≥ 0.80 at the location where wild-type ind expression is half-maximal at its dorsal boundary) and to remain low (≤ 0.05 times of the probability of ind expression at its peak domain) in the dorsal-most 20% of the D/V axis.
Model optimization
GEMSTAT optimizes the “root mean squared error” (RMSE) function in course of parameter estimation. At location i along the D/V axis, let Di and Mi denote the ind expression level and model-predicted readout of the ind enhancer, respectively. Assuming there are n data points, the RMSE for the predicted expression pattern is: , where β is a free parameter as used in standard least square estimation. We constrain β ≤ 2 since allowing β to assume arbitrary values may scale up and assign good RMSE scores to very low expression levels, even as low as one may expect from randomly generated sequences—a problematic issue for sequence to expression models (He et al., 2012). Several other sequence to expression models also constrained the value of β in optimizing RMSE (Kazemian et al., 2010; Kim et al., 2013; Segal et al., 2008). GEMSTAT uses the Nelder-Mead Simplex and the quasi-Newton Gradient Descent algorithms to optimize RMSE.
In vivo methods and quantitative analysis of imaging data
Embryo imaging and extraction of fluorescence intensity of mRNA expression and TF concentrations are described in the Supplemental Experimental Procedures. Likewise, procedures for co-staining ind and LacZ in embryos are also described in the Supplemental Experimental Procedures.
Supplementary Material
Acknowledgments
NSF Grant EFRI 1136913; MICINN Grant BFU2011-23611; NIH Grant R01 5R01GM114341.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author Contributions
Conceptualization, MAHS, SS, SYS; Methodology, MAHS; Software, MAHS; Formal Analysis, MAHS; Investigation, MAHS, BL, NS; Resources, MAHS, BL, NS; Data Curation, MAHS, BL, NS; Writing – Original Draft, MAHS, SS; Writing – Review and Editing, All authors; Visualization, MAHS; Supervision, SS, SYS, GJ; Funding Acquisition, SS, SYS, CR, HL, GJ.
References
- Ajuria L, Nieva C, Winkler C, Kuo D, Samper N, Andreu MJ, Helman A, Gonzalez-Crespo S, Paroush Z, Courey AJ, et al. Capicua DNA-binding sites are general response elements for RTK signaling in Drosophila. Development. 2011;138:915–924. doi: 10.1242/dev.057729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Astigarraga S, Grossman R, Diaz-Delfin J, Caelles C, Paroush Z, Jimenez G. A MAPK docking site is critical for downregulation of Capicua by Torso and EGFR RTK signaling. The EMBO journal. 2007;26:668–677. doi: 10.1038/sj.emboj.7601532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg OG, von Hippel PH. Selection of DNA binding sites by regulatory proteins. Statistical - mechanical theory and application to operators and promoters. Journal of molecular biology. 1987;193:723–750. doi: 10.1016/0022-2836(87)90354-8. [DOI] [PubMed] [Google Scholar]
- Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, Phillips R. Transcriptional regulation by the numbers: models. Current opinion in genetics & development. 2005;15:116–124. doi: 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown KS, Hill CC, Calero GA, Myers CR, Lee KH, Sethna JP, Cerione RA. The statistical mechanics of complex signaling networks: nerve growth factor signaling. Physical biology. 2004;1:184–195. doi: 10.1088/1478-3967/1/3/006. [DOI] [PubMed] [Google Scholar]
- Cheng Q, Kazemian M, Pham H, Blatti C, Celniker SE, Wolfe SA, Brodsky MH, Sinha S. Computational Identification of Diverse Mechanisms Underlying Transcription Factor-DNA Occupancy. PLoS genetics. 2013;9:e1003571. doi: 10.1371/journal.pgen.1003571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen M, Page KM, Perez-Carrasco R, Barnes CP, Briscoe J. A theoretical framework for the regulation of Shh morphogen-controlled gene expression. Development. 2014;141:3868–3878. doi: 10.1242/dev.112573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowden J, Levine M. Ventral dominance governs sequential patterns of gene expression across the dorsal-ventral axis of the neuroectoderm in the Drosophila embryo. Developmental biology. 2003;262:335–349. doi: 10.1016/s0012-1606(03)00395-6. [DOI] [PubMed] [Google Scholar]
- Dissanayake K, Toth R, Blakey J, Olsson O, Campbell DG, Prescott AR, MacKintosh C. ERK/p90(RSK)/14-3-3 signalling has an impact on expression of PEA3 Ets transcription factors via the transcriptional repressor capicua. The Biochemical journal. 2011;433:515–525. doi: 10.1042/BJ20101562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dresch JM, Liu X, Arnosti DN, Ay Z. Thermodynamic modeling of t ranscription: sensitivity analysis differentiates biological mechanism from mathematical model-induced effects. BMC systems biology. 2010;4:142. doi: 10.1186/1752-0509-4-142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fakhouri WD, Ay A, Sayal R, Dresch J, Dayringer E, Arnosti DN. Deciphering a transcriptional regulatory code: modeling short-range repression in the Drosophila embryo. Molecular systems biology. 2010;6:341. doi: 10.1038/msb.2009.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foo SM, Sun Y, Lim B, Ziukaite R, O'Brien K, Nien CY, Kirov N, Shvartsman SY, Rushlow CA. Zelda potentiates morphogen activity by increasing chromatin accessibility. Current biology : CB. 2014;24:1341–1346. doi: 10.1016/j.cub.2014.04.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia M, Stathopoulos A. Lateral gene expression in Drosophila early embryos is supported by Grainyhead-mediated activation and tiers of dorsally-localized repression. PloS one. 2011;6:e29172. doi: 10.1371/journal.pone.0029172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gertz J, Siggia ED, Cohen BA. Analysis of combinatorial cis-regulation in synthetic and genomic promoters. Nature. 2009;457:215–218. doi: 10.1038/nature07521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granek JA, Clarke ND. Explicit equilibrium modeling of transcription-factor binding and gene regulation. Genome biology. 2005;6:R87. doi: 10.1186/gb-2005-6-10-r87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimm O, Sanchez Zini V, Kim Y, Casanova J, Shvartsman SY, Wieschaus E. Torso RTK controls Capicua degradation by changing its subcellular localization. Development. 2012;139:3962–3968. doi: 10.1242/dev.084327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutenkunst RN, Waterfall JJ, Casey FP, Brown KS, Myers CR, Sethna JP. Universally sloppy parameter sensitivities in systems biology models. PLoS computational biology. 2007;3:1871–1878. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamm DC, Bondra ER, Harrison MM. Transcriptional activation is a conserved feature of the early embryonic factor Zelda that requires a cluster of four zinc fingers for DNA binding and a low-complexity activation domain. The Journal of biological chemistry. 2015;290:3508–3518. doi: 10.1074/jbc.M114.602292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X, Duque TS, Sinha S. Evolutionary origins of transcription factor binding site clusters. Molecular biology and evolution. 2012;29:1059–1070. doi: 10.1093/molbev/msr277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X, Samee MA, Blatti C, Sinha S. Thermodynamics-based models of transcriptional regulation by enhancers: the roles of synergistic activation, cooperative binding and short-range repression. PLoS computational biology. 2010;6 doi: 10.1371/journal.pcbi.1000935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong JW, Hendrix DA, Papatsenko D, Levine MS. How the Dorsal gradient works: insights from postgenome technologies. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:20072–20076. doi: 10.1073/pnas.0806476105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janssens H, Hou S, Jaeger J, Kim AR, Myasnikova E, Sharp D, Reinitz J. Quantitative and predictive model of transcriptional control of the Drosophila melanogaster even skipped gene. Nature genetics. 2006;38:1159–1165. doi: 10.1038/ng1886. [DOI] [PubMed] [Google Scholar]
- Kazemian M, Blatti C, Richards A, McCutchan M, Wakabayashi-Ito N, Hammonds AS, Celniker SE, Kumar S, Wolfe SA, Brodsky MH, et al. Quantitative analysis of the Drosophila segmentation regulatory network using pattern generating potentials. PLoS biology. 2010;8 doi: 10.1371/journal.pbio.1000456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim AR, Martinez C, Ionides J, Ramos AF, Ludwig MZ, Ogawa N, Sharp DH, Reinitz J. Rearrangements of 2.5 kilobases of noncoding DNA from the Drosophila even-skipped locus define predictive rules of genomic cis-regulatory logic. PLoS genetics. 2013;9:e1003243. doi: 10.1371/journal.pgen.1003243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirk P, Thorne T, Stumpf MP. Model selection in systems and synthetic biology. Current opinion in biotechnology. 2013;24:767–774. doi: 10.1016/j.copbio.2013.03.012. [DOI] [PubMed] [Google Scholar]
- Kuepfer L, Peter M, Sauer U, Stelling J. Ensemble modeling for analysis of cell signaling dynamics. Nature biotechnology. 2007;25:1001–1006. doi: 10.1038/nbt1330. [DOI] [PubMed] [Google Scholar]
- Li XY, Harrison MM, Villalta JE, Kaplan T, Eisen MB. Establishment of regions of genomic activity during the Drosophila maternal to zygotic transition. eLife. 2014;3 doi: 10.7554/eLife.03737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liberman LM, Stathopoulos A. Design flexibility in cis-regulatory control of gene expression: synthetic and comparative evidence. Developmental biology. 2009;327:578–589. doi: 10.1016/j.ydbio.2008.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim B, Samper N, Lu H, Rushlow C, Jimenez G, Shvartsman SY. Kinetics of gene derepression by ERK signaling. Proceedings of the National Academy of Sciences of the United States of America. 2013;110:10330–10335. doi: 10.1073/pnas.1303635110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDonald JA, Holbrook S, Isshiki T, Weiss J, Doe CQ, Mellerick DM. Dorsoventral patterning in the Drosophila central nervous system: the vnd homeobox gene specifies ventral column identity. Genes & development. 1998;12:3603–3612. doi: 10.1101/gad.12.22.3603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myasnikova E, Samsonova M, Kosman D, Reinitz J. Removal of background signal from in situ data on the expression of segmentation genes in Drosophila. Development genes and evolution. 2005;215:320–326. doi: 10.1007/s00427-005-0472-2. [DOI] [PubMed] [Google Scholar]
- Nien CY, Liang HL, Butcher S, Sun Y, Fu S, Gocha T, Kirov N, Manak JR, Rushlow C. Temporal coordination of gene networks by Zelda in the early Drosophila embryo. PLoS genetics. 2011;7:e1002339. doi: 10.1371/journal.pgen.1002339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papatsenko D, Levine MS. Dual regulation by the Hunchback gradient in the Drosophila embryo. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:2901–2906. doi: 10.1073/pnas.0711941105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker DS, White MA, Ramos AI, Cohen BA, Barolo S. The cis-regulatory logic of Hedgehog gradient responses: key roles for gli binding affinity, competition, and cooperativity. Science signaling. 2011;4:ra38. doi: 10.1126/scisignal.2002077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Platt JR. Strong Inference: Certain systematic methods of scientific thinking may produce much more rapid progress than others. Science. 1964;146:347–353. doi: 10.1126/science.146.3642.347. [DOI] [PubMed] [Google Scholar]
- Rasband WS. ImageJ. Bethesda, Maryland, USA: National Institutes of Health; 1997–2014. ( http://imagej.nih.gov/ij/) [Google Scholar]
- Segal E, Raveh-Sadka T, Schroeder M, Unnerstall U, Gaul U. Predicting expression patterns from regulatory sequence in Drosophila segmentation. Nature. 2008;451:535–540. doi: 10.1038/nature06496. [DOI] [PubMed] [Google Scholar]
- Shea MA, Ackers GK. The OR control system of bacteriophage lambda. A physical - chemical model for gene regulation. Journal of molecular biology. 1985;181:211–230. doi: 10.1016/0022-2836(85)90086-5. [DOI] [PubMed] [Google Scholar]
- Shlyueva D, Stampfel G, Stark A. Transcriptional enhancers: from properties to genome-wide predictions. Nature reviews Genetics. 2014;15:272–286. doi: 10.1038/nrg3682. [DOI] [PubMed] [Google Scholar]
- Stathopoulos A, Levine M. Localized repressors delineate the neurogenic ectoderm in the early Drosophila embryo. Developmental biology. 2005;280:482–493. doi: 10.1016/j.ydbio.2005.02.003. [DOI] [PubMed] [Google Scholar]
- Stormo GD. DNA binding sites: representation and discovery. Bioinformatics. 2000;16:16–23. doi: 10.1093/bioinformatics/16.1.16. [DOI] [PubMed] [Google Scholar]
- Sun Y, Nien CY, Chen K, Liu HY, Johnston J, Zeitlinger J, Rushlow C. Zelda overcomes the high intrinsic nucleosome barrier at enhancers during Drosophila zygotic genome activation. Genome research. 2015;25:1703–1714. doi: 10.1101/gr.192542.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swigon D. Ensemble Modeling of Biological Systems. In: Antoniouk A, Melnik R, editors. De Gruyter Series in Mathematics and Life Sciences 1. Berlin: De Gruyter; 2013. pp. 19–42. [Google Scholar]
- Tebaldi C, Knutti R. The use of the multi-model ensemble in probabilistic climate projections. Philos T R Soc A. 2007;365:2053–2075. doi: 10.1098/rsta.2007.2076. [DOI] [PubMed] [Google Scholar]
- ten Bosch JR, Benavides JA, Cline TW. The TAGteam DNA motif controls the timing of Drosophila pre-blastoderm transcription. Development. 2006;133:1967–1977. doi: 10.1242/dev.02373. [DOI] [PubMed] [Google Scholar]
- Toni T, Welch D, Strelkowa N, Ipsen A, Stumpf MP. Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. Journal of the Royal Society, Interface / the Royal Society. 2009;6:187–202. doi: 10.1098/rsif.2008.0172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villaverde A, Bongard S, Mauch K, Müller D, Balsa-Canto E, Schmid J, Banga J. High-Confidence Predictions in Systems Biology Dynamic Models. In: Saez-Rodriguez J, Rocha MP, Fdez-Riverola F, De Paz Santana JF, editors. 8th International Conference on Practical Applications of Computational Biology & Bioinformatics (PACBB 2014) Springer International Publishing; 2014. pp. 161–171. [Google Scholar]
- von Dassow G, Meir E, Munro EM, Odell GM. The segment polarity network is a robust developmental module. Nature. 2000;406:188–192. doi: 10.1038/35018085. [DOI] [PubMed] [Google Scholar]
- von Ohlen T, Doe CQ. Convergence of dorsal, dpp, and egfr signaling pathways subdivides the drosophila neuroectoderm into three dorsal-ventral columns. Developmental biology. 2000;224:362–372. doi: 10.1006/dbio.2000.9789. [DOI] [PubMed] [Google Scholar]
- Weiss JB, Von Ohlen T, Mellerick DM, Dressler G, Doe CQ, Scott MP. Dorsoventral patterning in the Drosophila central nervous system: the intermediate neuroblasts defective homeobox gene specifies intermediate column identity. Genes & development. 1998;12:3591–3602. doi: 10.1101/gad.12.22.3591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White MA, Parker DS, Barolo S, Cohen BA. A model of spatially restricted transcription in opposing gradients of activators and repressors. Molecular systems biology. 2012;8:614. doi: 10.1038/msb.2012.48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yanez-Cuna JO, Kvon EZ, Stark A. Deciphering the transcriptional cis-regulatory code. Trends in genetics : TIG. 2013;29:11–22. doi: 10.1016/j.tig.2012.09.007. [DOI] [PubMed] [Google Scholar]
- Zinzen RP, Papatsenko D. Enhancer responses to similarly distributed antagonistic gradients in development. PLoS computational biology. 2007;3:e84. doi: 10.1371/journal.pcbi.0030084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zinzen RP, Senger K, Levine M, Papatsenko D. Computational models for neurogenic gene expression in the Drosophila embryo. Current biology : CB. 2006;16:1358–1365. doi: 10.1016/j.cub.2006.05.044. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.