Glycated Hemoglobin, Plasma Glucose, and Erythrocyte Aging

Abstract

Background:

The relationship between HbA1c and blood glucose averages has been characterized many times, yet, a unifying, mechanistic description is still lacking.

Methods:

We calculated the level of HbA1c from plasma glucose averages based solely on the in vivo rate of hemoglobin glycation, and the different turnover rates for erythrocytes of different ages. These calculations were then compared to the measured change of HbA1c due to changes in mean blood glucose (MBG), to complex models in the literature, and our own experiments.

Results:

Analysis of data on erythrocyte ageing patterns revealed that 2 separate RBC turnover mechanisms seem to be present. We calculated the mean red blood cell (RBC) life span within individuals to lie between 60 and 95 days. Comparison of expected HbA1c levels to data taken from continuous glucose monitors and finger-stick MBG yielded good agreement (r = .87, P < .0001). Experiments on the change with time of HbA1c induced by a change of MBG were in excellent agreement with our calculations (r = .98, P < .0001).

Conclusions:

RBC turnover seems to be dominated by a constant rate of cell loss, and a mechanism that targets cells of a specific age. Average RBC life span is 80 ± 10.9 days. Of HbA1c change toward treatment goal value, 50% is reached in about 30 days. Many factors contribute to the ratio of glycated hemoglobin, yet we can make accurate estimations considering only the in vivo glycation constant, MBG, and the age distribution of erythrocytes.

Glycated HbA has stood as a clinical marker of long term glycemic control for well over 4 decades, and remained for the past 20 years, alongside fasting glucose, as the golden standard for diabetes control.^1-6

The status of this clinical assay has motivated much research, particularly about its relationship with blood glucose levels, and its reaction time to changes in their mean values.^3,7-17 Many of these studies have focused on finding an empirical relationship between HbA1c ratios and mean blood glucose concentration. It is clear that there is such a relationship, but there is certainly no agreement as to a single algebraic form for it.^16,18 Recently, models have been proposed to infer this form,^3,6,14 and have collectively incorporated fine details of hemoglobin glycation and turnover, such as the contribution from reticulocyte glycation in bone marrow, the rate of dissociation of glucose from hemoglobin, the effect of high glucose concentrations on RBC life span, etc. Yet, in each case, the main components are always the in vivo glycation rate of hemoglobin, and some model of erythrocyte life cycle.

The mechanism of hemoglobin glycation, especially at the amino-terminal of the β subunits, has been extensively studied and many experiments have been designed to calculate its reaction rate.^19-22 On the other hand, and despite numerous efforts,^23-25 not until recently has detailed data on human erythrocyte turnover cycles been made available.²⁶

In our study, we analyze the experiments on biotinylated RBCs from Cohen et al²⁶ and incorporate our findings to a straightforward method to calculate the percentage of HbA1c from a steady-state mean blood glucose value.

Research Design and Methods

Erythrocyte Survival

We extracted data on day to day, in vivo survival of biotinylated RBCs from Cohen et al²⁶ using a MATLAB script developed by our group (version 8.6.0, R2015b; MathWorks Inc, Natick, MA, USA). The digitized survival curves, shown in the third figure in the source publication, belong to 6 diabetic patients and 6 nondiabetic controls. From the survival curves we can infer the proportion of RBCs of a specific age to the total, the mean RBC age, the average RBC life span, etc (mathematical details in Appendix A). While Cohen et al used a cubic function to characterize these curves, we found that a restricted quadratic form (ax²+bx+1) fitted the data well in every case (R² > .99). A randomly chosen example is shown in Figure 1.

Figure 1.

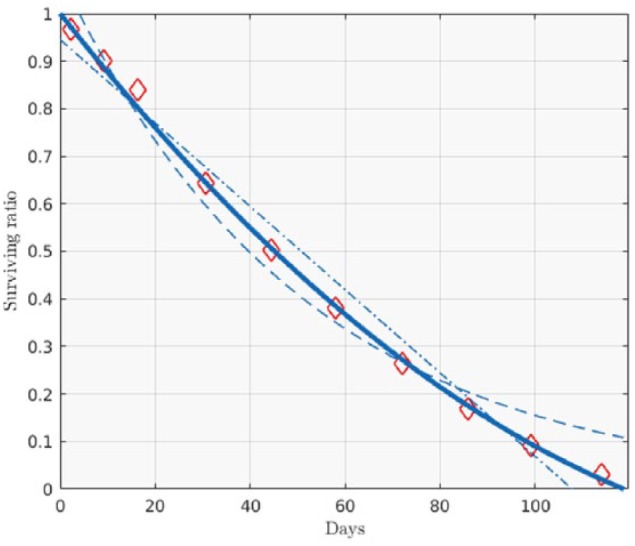
Example of biotinylated RBC survival curve (data from Cohen et al²⁶). Diamonds are biotynilated RBC survival ratios. The following fits are shown: a constrained quadratic ($f\left(t\right)=a{t}^2+bt+1$R² = .998, solid line), linear (homogeneous life-span model, R² = .979, dot-dashed line), and exponential (random death model, R² = .976, dashed line).

HbA Glycation

Knowing the general shape of RBC survival curves we can calculate the total HbA1c using an experimental estimate of the in vivo glycation rate of hemoglobin (here we use the constant 7.75×10^-6(mMol×h)^-1 reported by Mortensen et al²¹). To do so, we first calculate the proportion of glycated to non glycated HbA molecules within RBCs 1 day old, which is roughly the product of glucose concentration and the daily rate of glycation per Mol glucose. We then calculate the same proportion for erythrocytes that are 2 days old; this is equal to the proportion of HbA1c in RBCs 1 day old, plus a contribution given by the probability that a (nonglycated) HbA molecule within a 1-day-old RBC is glycated by the second day, all multiplied by a factor equal to the probability that an erythrocyte age 1 day survives 24 hours. We then iterate this process to calculate the contribution to total HbA1c from RBCs of every age, and obtain the total HbA1c ratio by adding each contribution (see Appendix B for details). It should be noted that although such first order kinetics have been used extensively before,^3,27 coupling it with a nontrivial treatment of RBC clearance from empirical data makes the design novel. It would seem, also, that what Tahara and Shima called the “Weight Function” in their seminal work,³ was an indirect measurement of RBC survival.

Mean Blood Glucose and HbA1c Ratio

To test the accuracy of our method of calculating HbA1c to total HbA we used 4 sets of data: our own, previously published data of continuous glucose monitor (CGM) readings and HbA1c in 45 patients with chronic pancreatitis and 9 healthy volunteers,²⁸ a set extracted from a study on 22 diabetic patients and 3 healthy controls,¹⁶ a larger, CGM-based study,¹⁷ and a large set (>600) of self-measured blood glucose and HbA1c percentages extracted from Kovatchev et al.¹⁰

Variation in time of HbA1c

With a minor variation of the procedure described above to calculate the ratio of glycated to total hemoglobin, we can estimate the rate of change of HbA1c due to a sudden change in mean blood glucose levels. Tahara et al³ describe such situation on a series of trials in which 9 patients were monitored closely after hospitalization for diabetes treatment. We used their data for validation of our estimations on the time course of HbA1c. In addition, we compared our output to a similar scenario modeled by Osterman-Golkar et al.¹⁴

Results

In many of the previous models of MBG and HbA1c, a daily turnover of only the oldest fraction of RBCs has been used,^1,3,14 the so called homogeneous life-span model.²⁹ The patent curvature of the erythrocyte survival function suggests a different approach and has important clinical consequences. Mainly, it contradicts the seemingly prevalent notion of a homogeneous RBC life span of about 120 days;^4,30 while the interindividual average survival of the most longevous RBCs (maximum erythrocyte life span, MEL) is indeed about 120 days (116.6 ± 12.7 days), the biotinylated RBC measurements we analyzed yielded an average erythrocyte life span (AEL) of 80 ± 10.9 days. This means that in addition the well documented senescence-mediated clearance,^31,32 contributions to RBC turnover from non age-related mechanisms should be included in calculating HbA1c ratios. Figure 1 shows an example of an experimental survival curve, our quadratic fit, a linear fit (homogeneous life-span model), and an exponential fit (random death model). The average age of circulating erythrocytes was 49 ± 6 days.

Unlike a general quadratic, a 2-parameter constrained form like the one we chose is not expected to be a de facto improvement over a linear function, which was our case for every fit. We further found that the 2 parameters, a and b, which describe each curve were not independent (the exponential fit a = αe^-βx yielded R² = .98). Therefore, survival curves of human erythrocytes can be characterized by a single parameter. In the following we use MEL to completely characterize an individual’s RBC turnover.

Self-measured, finger-stick MBG has 2 main inherent difficulties: the bias introduced by periodic rather than random measurements, and the inability of the subject to perform measurements during sleep. The former problem was addressed by Kovatchev et al.¹⁰ To assess possible biases from the latter, we compared separate CGM averages for awake and sleep periods on our healthy volunteers. In most cases the difference between averages was significant (10 of 11, ANOVA at α = 0.05), though it was not systematic (greater during sleep in only 7 out of 10 ), and only 1 presented a difference of more than 10 mg/dL (0.56 mMol). We then decided to append finger-stick measurements to CGM data.

We calculated 1-day moving averages of our CGM data (not shown) to confirm the plausibility of considering a 24 hour glycemic steady-state for our calculations.

In Figure 2 we plot the experimental HbA1c-MBG pairs alongside our estimations of HbA1c for a human with MEL = 90, 117, and 140 days. The curve belonging to the mean MEL (117 days) agrees with the overall data position (r = .87, P < .0001), while the enveloping curves (MEL = 90 and 140 days, the 2 extreme MEL values reported in Cohen et al 2008²⁶) spread toward the greater glucose density ranges, also in agreement with the experiments’ heteroscedasticity (a Kolmogorov-Smirnov test failed to reject the hypothesis that the data were standard Gaussian when normalized to a mean of MEL = 117 d, and spread of MEL = 134 d). It should be noted that experimental points in the higher MBG ranges group slightly closer to the lower (MEL = 90 d) estimate. This fact constitutes a nod to the sentiment that hyperglycemia reduces erythrocyte life span,^18,25,29 though biotinylated RBC experiments failed to confirm such a notion.^6,26 This inability of the biotinilated RBC experiments to resolve a difference between nondiabetic and diabetic RBC life spans does not allow us to treat these 2 cases separately. A likely consequence of this is the fact that the predicted variability of HbA1c in the nondiabetic cohort is slightly higher than the one reported in the literature (9.9% vs. 8.1%).

Figure 2.

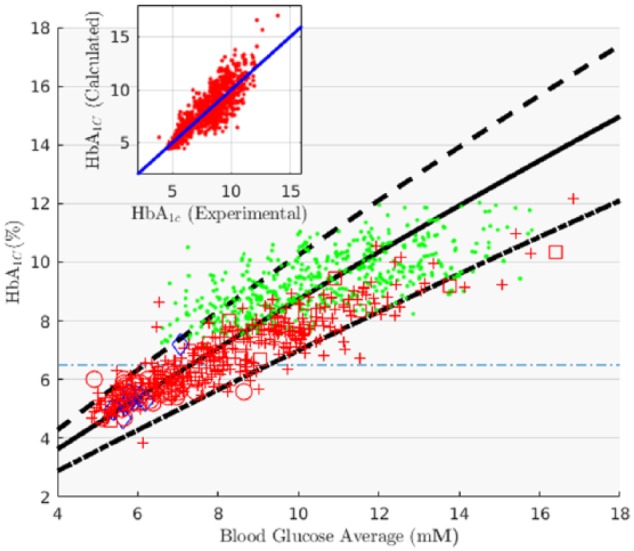
Calculated and experimental values of HbA1c % vs MBG (chronic pancreatitis patients from Beltrán del Río et al,²⁸ circles; Healthy volunteers from Beltrán del Río et al,²⁸ diamonds; diabetes mellitus from Kovatchev et al,¹⁰ dots; diabetes mellitus from Nathan et al,¹⁷ crosses; diabetes mellitus from Nathan et al,¹⁶ squares). The 3 predictions correspond to different values of erythrocyte life spans: MEL = 117d, solid line; MEL = 140d, dashed line; MEL = 97d, dot-dashed line. The inset shows the correlation between experimental and expected HbA1c values (MEL = 117d) of all combined data (dots in inset).

We calculated the expected change in time of HbA1c after a stepwise decrease in blood sugar average for 3 cases: a median MEL of 117 days, and 2 extreme cases MEL = 140 and 97 days. We normalized these calculations to percentage change and compared them to the equivalent experiment described in Tahara and Shima.³ The fit yielded quite good agreement: (r = .98, P < .0001), see Figure 3. Also, the HbA1c half-life we predicted (31 days) is consistent with values reported by Osterman-Golkar and Vesper, and Tahara and Shima.^3,14 Finally, we found that equivalent calculations using a much more complicated model, shown in the fifth graph in Osterman-Golkar et al,¹⁴ are not only consistent but completely overlap our estimates (not shown, R² > .999, P < .0001).

Figure 3.

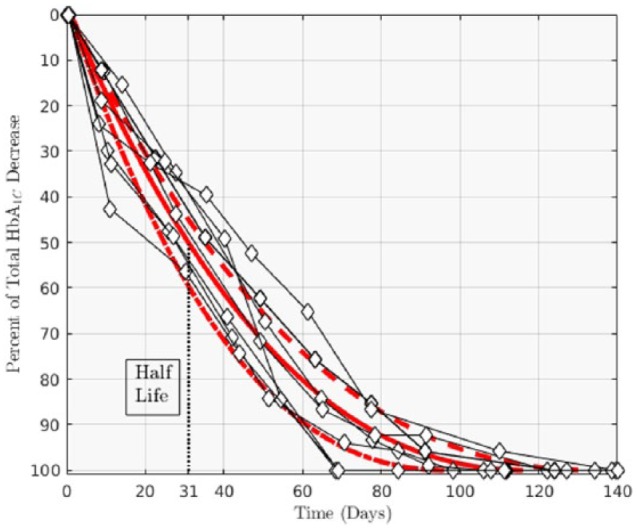
Rate for change of HbA1c % after a stepwise change in MBG. The 3 estimates correspond to calculations based on different erythrocyte life spans: MEL = 117d, solid line; MEL = 140d, dashed line; MEL = 97d, dot-dashed line. Data in diamonds are measurements from Tahara and Shima.³

Conclusions

The analysis done on RBC survival curves from Cohen et al²⁶ suggests an average erythrocyte circulation time of 80 ± 11 days. It was found that in the population examined, a single parameter (MEL, AEL, etc ) was enough to fully characterize an individuals’ RBC turnover. The shape of the survival functions speaks of 2 main mechanisms for RBC turnover: a constant, seemingly random loss (not dependent on RBC age), and a sudden, senescence-mediated cutoff around a definite age. From our calculations we inferred that only about 38 ± 9.6% of erythrocytes survive to reach this active clearance age. The small sample (N = 12) reported in Cohen et al,²⁶ is substantial enough for us to conclude that erythrocyte survival is more complex than what the commonly used homogeneous life span model describes, but not to draw a detailed picture of the distribution of RBC life spans in the general population, less so in smaller cohorts of clinical relevance. Our estimations provided an accurate and parsimonious portrayal of HbA1c dynamics through a mechanistic approach, rather than the more common linear descriptions in the literature.¹⁸ The method presented inherently incorporates a mean and a spread, from which we inferred a maximum RBC life span average and standard deviation of 117 ± 12 days. Measurements yielded an HbA1c half-life between 25 and 35 days, and 50 to 70 days to reach 80% of an HbA1c goal value.

Appendix A

Erythrocyte Turnover Analysis

From a survival curve S(t) we obtain the RBC age density function ϱ(t), through the relationship:

$$S\left(t\right)=\underset{t}{\overset{\infty }{{\displaystyle \int }}}\rho \left(\xi \right)d\xi ,$$

under the assumption of steady erythropoiesis. Average RBC age per individual is therefore:

$$RBCAge={{\displaystyle \int }}^{}\xi \rho \left(\xi \right)d\xi$$

For quadratic S(t) we inferred:

$$\varrho \left(t\right)=\{\begin{array}{c}-at+b,t\le MEL\\ 0,t>MEL\end{array}.$$

AEL is calculated through the life span probability density:

$$\lambda \left(t\right)=\frac{1-\beta }{MEL}+\beta \delta \left(t-MEL\right)$$

where β = ϱ(MEL)/ϱ(0) is the probability that an erythrocyte survives until maximum life span, and δ is a Dirac density function.

Appendix B

HbA1c Estimation

To calculate HbA1c we used a simple Markov model: if ${\rho }_1$ is the ratio of RBCs aged i to RBCs aged 1, and ${\rho }_1=1$, then the probability that an RBC survives day j is $p_j={\rho }_{j+1}/{\rho }_j$. The contribution to HbA1c percentage by erythrocytes aged 1 day is ${\alpha }_1={\rho }_1\gamma \sigma$ where γ is the per-day, per Mol, in vivo glycation rate, and σ is the MBG concentration. The contribution to HbA1c from RBCs aged j days is then: ${\alpha }_j=p_{j-1}\left({\alpha }_{j-1}+\gamma \sigma \left({\rho }_{j-1}-{\alpha }_{j-1}\right)\right)$, the contribution of already glycated hemoglobin molecules in surviving erythrocytes plus the contribution from newly formed HbA1c. Total ratio is then calculated with:

$$Hb{A}_{1C}=\frac{{{\displaystyle \sum }}_i^{MEL}{\alpha }_i}{{{\displaystyle \sum }}_i^{MEL}{\rho }_i}\cdot 100$$