The influence of curvature on three-dimensional mineralized matrix formation under static and perfused conditions: an in vitro bioreactor model

Abstract

Bone remodelling is the continuous turnover of bone by resorption and formation. It is controlled by interstitial fluid flow sensed by osteocytes. The refilling of bone resorption sites has been shown to be curvature driven. In vitro, curvature influences tissue growth and cytoskeletal arrangements under static and perfused conditions. Nevertheless, this has only been demonstrated for non-mineralized tissue in limited three-dimensional volumes. This study aims at investigating the influence of three different channel curvatures (S, −2.00 mm⁻¹; M, −1.33 mm⁻¹; L, −0.67 mm⁻¹) on mineralized tissue formation in three dimensions under static and perfused conditions. The ingrowth of mineralized tissue into the channels was dependent on curvature and was higher under perfusion (M and S channels). L channels were not closed in any group compared with partially (static) or fully (perfused) closed M and S channels. Mineralized tissue morphology was cortical-like in static samples and trabecular-like in perfused samples. Our results suggest that the three-dimensional in vitro model presented is not only able to reveal effects of curvature on mineralized tissue formation, but may be used as an in vitro model for critical size defects in trabecular or cortical bone.

1. Background

Bone remodelling describes the process of continuous turnover of bone tissue by bone resorption and bone formation in the adult skeleton, which also allows bones to adapt their structure to changes in long-term mechanical loading [1,2]. The refilling of bone resorption sites with mineralized tissue in vivo is most probably curvature driven [3,4]. In cortical bone, bone resorption is performed by osteoclasts excavating cylindrical tunnels, which are subsequently refilled with osteoid and a central blood vessel ultimately forming a Haversian canal. In trabecular bone, osteoclasts form semicircular resorption pits that can be seen as hemi-osteons that are later refilled with osteoid produced by osteoblasts [5]. Bone remodelling always leads to transient local changes of surface geometry of bone tissue [3,4]. In trabecular bone, it has been shown that average curvature is close to zero, implying a strong control of cellular behaviour and cell response to changes in tissue geometry [3]. This phenomenon can be explained by the fact that, on curved surfaces, cells are bent and experience tensile forces. Cells aim to reduce these forces by contracting their cytoskeleton, which subsequently leads to a flattening of the tissue surface. This has been attributed to the fact that cellular growth is not only controlled by biological signalling pathways but also by mechanical control mechanisms [6,7].

The predominant mechanical loading condition in remodelling processes is believed to be the interstitial fluid flow in the lacuno-canalicular network. Interstitial fluid flow is driven by deformations of the bone matrix and sensed by osteocytes that are also known to orchestrate the process of bone remodelling [8]. In vitro, mechanical loading of cells with fluid flow using perfusion bioreactors has been performed frequently to investigate the effects of fluid flow on bone tissue engineering cultures [9]. Perfusion has been shown to increase levels of osteogenic markers and mineralized tissue formation of different cell types [10,11]. Local fluid flow velocity in scaffolds is strongly influenced by scaffold pore size and increases with decreasing pore size if porosity is kept constant [12]. The curvature of a perfectly spherical pore is indirectly proportional to the pore size (1/radius) and therefore directly relates to the fluid flow velocity in the pore. The bigger the radius of a pore, the smaller is the curvature and the flow velocity in the pore compared with a pore with a small radius at a given flow rate. Endothelial cells cultured on curved surfaces showed cytoskeletal changes when compared with cells cultured on flat surfaces [13]. The changes observed were significantly enhanced when cells were additionally exposed to perfusion, while cells cultured on flat surfaces remained the same even when perfusion was applied. Taken together, these observations lead to the assumption that in vitro mineralization under perfused conditions is also influenced by curvature, but, to date, similar experiments using bone cells have not been realized to our knowledge.

Essential work investigating the influence of curvature on non-mineralized tissue growth in static cultures was performed by Rumpler, Woesz and co-workers [14]. They evaluated the local growth rate of non-mineralized tissue formed by osteoblasts on hydroxyapatite (HA) scaffolds of 2 mm height in response to different channel shapes (triangular, square, hexagonal and circular) and channel sizes (perimeters of 3.14 mm, 4.71 mm and 6.28 mm). They quantified projected tissue area and visualized the cytoskeleton using confocal scanning microscopy. Tissue thickness, defined as the layer thickness of tissue growing on the channel wall, has been shown to be affected by local curvature and channel size. Increasing curvature and decreasing channel size led to higher tissue thickness. The total amount of tissue formed was dependent on the channel perimeter and was proportional to the local curvature. Other studies have also shown that the tissue growth rate was highly dependent on curvature [6,7,15]. Curvature sign was also found to be important, showing decreasing tissue growth from concave (negative curvature) to convex (positive curvature) to flat (zero curvature) surfaces [6,15–17]. The formation of mineralized tissue on different bioceramic materials has been shown to be controlled by the size of cavities introduced to the scaffold's surface compared with no mineralized tissue formation on the planar surfaces of the scaffolds [18].

The above-mentioned in vitro studies focused on non-mineralized extracellular matrix (ECM) formation only [6,7,14,15], or the formation of mineralization was initiated by soaking the scaffold material in simulated body fluid, which does not reflect cell-mediated mineralization [18]. Despite the fact that three-dimensional scaffolds have been used to investigate the influence of curvature on tissue growth, analyses were performed using confocal microscopy limited to a penetration depth of about 500 µm [6,7,14,15,17,19]. To evaluate tissue growth along the whole height of the channels, it would have been necessary to cut the samples into thinner slices by destroying the samples, making them unavailable for longitudinal monitoring of tissue growth.

In addition to the limited penetration depth of confocal microscopy, measurements of projected tissue area imply homogeneous tissue growth along the height of the channel. This seems very unlikely, because the curvature of a channel is defined by the two principal curvatures in the horizontal and vertical directions (see [15] for detailed calculation) and the highest tissue growth is therefore expected at half the channel height. A three-dimensional computational model of curvature-driven growth was derived from [6] to estimate tissue formation in three dimensions. Unfortunately, this model did not contain any biology, e.g. completely ignoring the influence of growth factors and other biochemical signals [17].

Alternatively, micro-computed tomography (µCT) is a non-invasive and non-destructive imaging technique [20] that has been used to investigate the three-dimensional structure of mineralized biological specimens in vivo, in vitro and in situ [21–23]. It has been shown that it is possible to longitudinally monitor mineralized tissue formation of cells seeded on scaffolds over several weeks [24].

The aim of this study was to investigate the influence of three different channel curvatures on mineralized tissue formation in three dimensions under static and perfused conditions. To quantify the influence of curvature on mineralized tissue formation, µCT online monitoring was applied to calculate static quantitative measures such as mineralized tissue volume fraction (BV/TV) [25] and dynamic quantitative measures such as mineralized tissue formation rate (BFR), mineral apposition rate (MAR) and mineralizing surface (MS) [21]. We hypothesized that: (i) mineralized tissue formation is driven by curvature, (ii) mineralized tissue formation is dependent on the channel depth showing the highest value at half the channel height, and (iii) mechanical loading by perfusion has a synergistic effect with curvature leading to higher mineralized tissue formation under perfused conditions compared with static conditions.

2. Material and methods

2.1. Materials

Dulbecco's modified Eagle's medium (DMEM), fetal bovine serum (FBS; order number 10270-06), penicillin–streptomycin–fungizone (P/S/F), non-essential amino acids (NEAA), basic fibroblast growth factor (bFGF), β-glycerolphosphate (βGP), ascorbic acid (AA) and dexamethasone (Dex) were from Gibco (Zug, Switzerland). Hexafluoroisopropanol (HFIP) was from Fluorochem Ltd (Hadfield, UK). Lithium bromide (LiBr) was from Thermo Fisher Scientific (Reinach, Switzerland) and methanol (MeOH) from Merck (Zug, Switzerland). All other substances were purchased from Sigma (Buchs, Switzerland) and were of analytical grade. Silkworm cocoons were kindly supplied by Trudel Silk Inc. (Zurich, Switzerland).

2.2. Scaffold production

Silk fibroin (SF) scaffolds have been produced as described in [26]. In short, Bombyx mori silkworm cocoons were degummed by boiling twice for 1 h in 0.02 M Na₂CO₃ and washed with ultrapure water (UPW). After drying, the silk was dissolved in a 9 M LiBr solution and dialysed for 36 h against UPW (Slide-A-Lyzer 3.5 K MWCO; Thermo Fisher Scientific, Waltham, MA, USA). After freezing at −80°C overnight, the solution was lyophilized for 5 complete days. The lyophilized silk was dissolved in HFIP, resulting in a 17% (w/v) solution which was subsequently added to 2.5 g sodium chloride crystals of 300–400 µm granule diameter. β-sheet formation was induced by immersing the silk–salt blocks into 90% MeOH for 30 min and subsequent drying overnight [27]. Before leaching for 2 days in UPW, scaffolds were cut to a height of 3 mm using a precision saw (Isomet low-speed saw; Buehler, Bluff, IL, USA). The scaffold discs were punched to an outer diameter of 9 mm with the help of a cork borer. Channels and pin holes were punched using biopsy punches of 3 mm, 1.5 mm and 1 mm in diameter (Kai medical, Solingen, Germany) with the help of a custom-made metal guide to ensure reproducible positioning of the channels within the scaffold volume. The curvatures of the channels were chosen according to [14], leading to relative curvatures of + 50% (S) and −50% (L) with respect to the curvature of the M channel (figure 1d). Owing to the silk's similar density to the density of the culture medium, scaffolds are not visible in µCT scans. Two pins have been used for scaffold orientation in both bioreactor types and for scaffold fixation in static bioreactors. Scaffolds were sterilized by steam autoclaving in phosphate-buffered saline at 121°C, 1 bar for 20 min.

Figure 1.

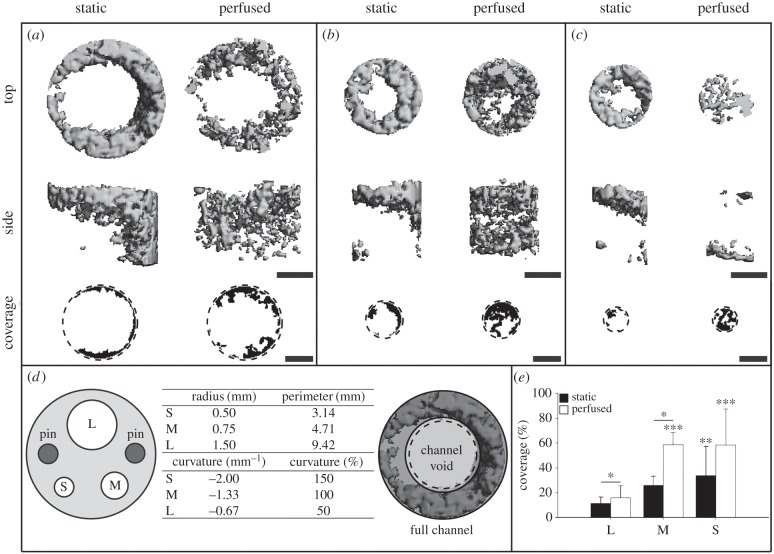
Three-dimensional images of mineralized tissue formed in the full channel with the corresponding coverage in the channel void for (a) L channels, (b) M channels and (c) S channels. (d) Schematic illustration of the scaffold geometry with the three different channel sizes and the two pin holes (left). Radii, perimeters, curvatures and relative curvatures of all channels (middle). Schematic representation of the two volumes (full channel and channel void) used for the evaluation of mineralized tissue formation in the channel (right). (e) Coverage of channel void. Scale bar, 1 mm. *p ≤ 0.05. **p ≤ 0.05. ***p ≤ 0.01. ** and *** indicate statistical significances between different curvatures within the same bioreactor type.

2.3. Cell study

Human mesenchymal stem cells (hMSCs) (Lonza, Walkersville, MD, USA) were isolated from bone marrow aspirate and characterized as described before [28]. P3 hMSCs were expanded for 7 days in expansion medium (DMEM, 10% FBS, 1% P/S/F, 1% NEAA and 1 ng ml⁻¹ bFGF) and re-suspended in control medium (DMEM, 10% FBS, 1% P/S/F) at a concentration of 5 million cells per 50 µl. Scaffolds (n = 20) were seeded by pipetting 5 million cells on top of each scaffold. After incubation in a 12-well plate under standard cell culturing conditions (37°C, 5% CO₂) for 90 min, half of the scaffolds (n = 10) were moved into static bioreactors and supplied with 6 ml osteogenic medium (control medium, 10 mM βGP, 50 µg ml⁻¹ AA, 100 nM Dex), which was completely exchanged three times a week. The other half of the scaffolds were supplied with 1 ml control medium and incubated for 24 h to ensure proper cell attachment, before the scaffolds were moved into perfusion bioreactors the next day. Perfusion bioreactors were provided with 18 ml osteogenic medium to avoid air inclusions in the perfusion system. A third of the medium was exchanged three times a week. In the bioreactor setting applied, it is not possible to completely remove the full medium volume within the perfusion system. Based on the assumption that AA, βGP and Dex are steadily degraded the medium was replaced by triple concentrated osteogenic medium (control medium, 30 mM βGP, 150 µg ml⁻¹ AA, 300 nM Dex) to keep the concentration of osteogenic factors within the full volume (18 ml) constant. A continuous flow rate of 12 ml min⁻¹ was set at the pump.

2.4. Micro-computed tomography monitoring

The deposition of three-dimensional mineralized tissue was monitored as described earlier [23] by weekly µCT scans starting at day 7 of the cell culture. All bioreactors were scanned in a µCT scanner at 36 µm resolution (µCT 40; SCANCO Medical AG, Brüttisellen, Switzerland). The energy level was set to 45 kVp and the intensity to 177 µA. An integration time of 200 ms and twofold frame averaging was applied. To reduce noise the reconstructed images were Gaussian filtered with a filter width of 1.2 and a support of 1. Mineralized tissue was segmented at a grey-scale value of 135 (corresponding to a density of 64.9 mg HA cm⁻³) and unconnected particles smaller than 20 voxels were removed. Three-dimensional volumes were evaluated for BV/TV as described earlier for bone [20,25].

For final evaluation, all scaffolds exhibiting a BV/TV lower than 1% at day 42 of the cell culture were excluded. Owing to biological variation, the onset of mineralized tissue formation was not equal in all bioreactors, which has been shown in previous studies monitoring mineralized tissue formation in bioreactors [23]. We accounted for this variation by introducing a threshold value that corresponded to the median BV/TV value of the whole scaffold observed at day 14 of the cell culture (day 14 equalled the first scan time point where mineralized tissue formation was observed). The day when the BV/TV of a single bioreactor exceeded the threshold value was defined as time point 0 (t0). After passing the threshold, each bioreactor was maintained in culture for an additional four weeks, leading to a total of five evaluated scan time points for each bioreactor (t0, t1, t2, t3, t4). All evaluations were based on these time points.

2.5. Mineralized tissue formation: whole scaffold

Mineralized tissue formation in the whole scaffold was determined by fitting a cylindrical mask to the outer scaffold borders. The volume of the fixation pins was determined from day 7 scans and subsequently subtracted from BV for later time points. Site-specific variations in vertical distribution of mineralized tissue in the whole scaffold were evaluated by regionalizing the whole volume height into 10 regions and nine overlapping regions (figure 2d). For each region, BV/TV was quantified and a morphometrical profile was generated.

Figure 2.

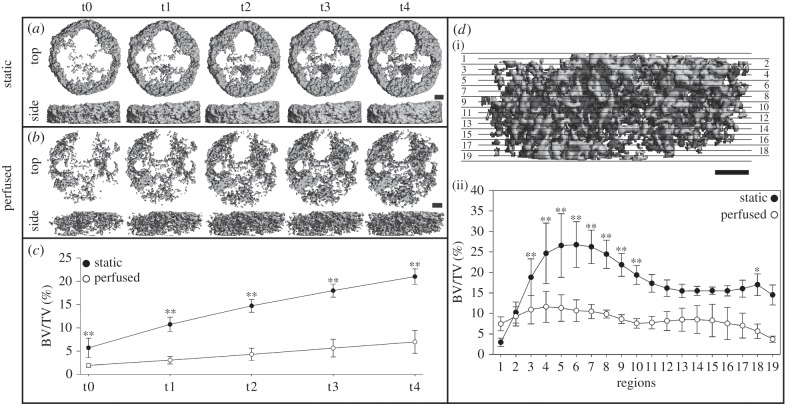
Three-dimensional images of mineralized tissue formed in the whole scaffold under: (a) static conditions and (b) perfused conditions. (c) Mineralized tissue volume fraction (BV/TV) of the whole scaffold. (d) Schematic illustration of regionalization of the whole scaffold into 10 regions and nine overlapping regions (i) and the corresponding morphometrical profile (ii). Scale bar, 1 mm. *p ≤ 0.05. **p ≤ 0.01.

2.6. Mineralized tissue formation: channels

Mineralized tissue formation in the three channels was evaluated based on two different volumes of interest: (i) the channel void volume and (ii) the channel volume including an adjacent ring volume consisting of the SF scaffold (figure 1d). These volumes are referred to as the ‘channel void’ and ‘full channel’. The diameter of the channel void was set to 90% of the real channel diameter to exclude potential effects of the scaffold–channel interface (S, 0.9 mm; M, 1.35 mm; L, 2.7 mm). The diameter of the full channel was set to the real channel diameter plus 1 mm (S, 2 mm; M, 2.5 mm; L, 4 mm). This volume was chosen in order to investigate the influence of curvature on mineralized tissue formation in the SF scaffold close to the channel. The mineralized tissue in the channel void was projected in the top–bottom direction, creating a pseudo-radiograph to calculate coverage in analogy to [29]. Briefly, a pseudo-X-ray was generated by projecting the three-dimensional µCT data in the top to bottom direction in one image. Coverage was used to quantify the ingrowth of mineralized tissue into the channel. The effect of curvature on the dynamic mineralized tissue formation parameters was investigated using a technique that has been used to quantify dynamic bone morphometric parameters in vivo [21,30]. Briefly, dynamic mineralized tissue formation parameters were determined by registering µCT scans of t2 and t4. Based on the registered µCT scans, sites that were present at t2 only have been considered as resorbed mineralized tissue (coloured blue; figure 3a–c,g–i), sites present at t4 only have been considered as newly formed mineralized tissue (coloured orange; figure 3a–c,g–i) and sites present at both t2 and t4 have been considered as quiescent mineralized tissue (coloured grey; figure 3a–c,g–i). The registered µCT scans were further evaluated for the calculation of dynamic mineralized tissue morphometric parameters, namely BFR, MAR and MS (see [21] for a detailed description of the parameter calculation). BFR is defined as the formed BV per existing BV per day as a percentage (%/day), MS is defined as the percentage of formed mineralized BS per total existing BS (%), and MAR is defined as the mean thickness of formed BV per day in micrometres (µm d⁻¹) in accordance with [21]. Dynamic parameters have been determined for the channel void (figure 3d–f) as well as for the full channel (figure 3j–l).

Figure 3.

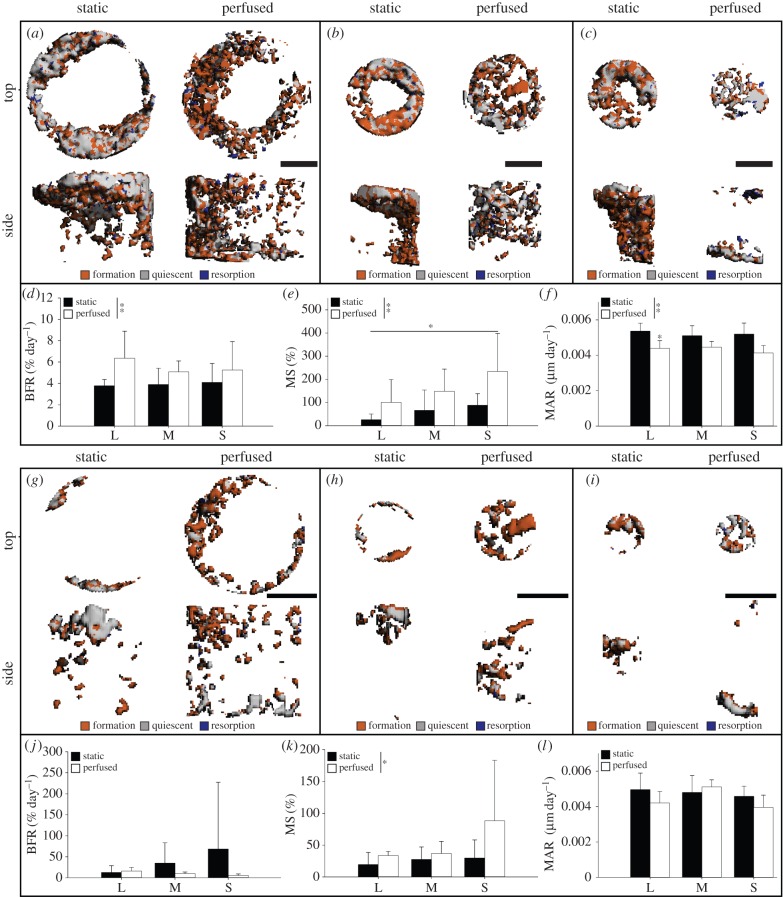
Three-dimensional images of registered scans of time point 2 and time point 4 showing newly formed (orange), quiescent (grey) and resorbed (blue) mineralized tissue for L channels (a,g), M channels (b,h), and S channels (c,i) in the full channel and the channel void, respectively. Dynamic mineralized tissue morphometric parameters for the full channel and the channel void are depicted as (d,j) mineralized tissue formation rate (BFR), (e,k) mineralizing surface (MS) and (f,l) mineral apposition rate (MAR). Scale bar, 1 mm. *p ≤ 0.05. **p ≤ 0.01. (Online version in colour.)

2.7. Histology

At the end of the study scaffolds were fixed in 10% (v/v) neutral buffered formalin over night at 4°C. After embedding in paraffin, scaffolds were cut to a thickness of 10 µm either into horizontal cross-sections through the top, middle and bottom of the scaffold or into vertical cross-sections through all channel sizes. To visualize cell nuclei and ECM, haematoxylin and eosin (H&E) staining was performed. Sirius Red staining was performed to visualize collagen. Von Kossa staining was performed to visualize the phosphate groups of the mineralized tissue [31].

2.8. Statistics

All statistical evaluations were performed using IBM SPSS Statistics 20 (SPSS Inc., Chicago, IL, USA). Comparisons of more than two means were done by repeated-measures analysis of variance (ANOVA) or ANOVA followed by post hoc testing with Bonferroni corrected significance levels. Data are presented as means ± s.d. and were considered statistically significant at p ≤ 0.05 and highly statistically significant at p ≤ 0.01. Figures show upper median samples (based on BV/TV values of the whole scaffold).

3. Results

3.1. Mineralized tissue formation: whole scaffold

Three-dimensional images showed substantial mineralized tissue formation in the static (figure 2a) and the perfused (figure 2b) group. L channels were clearly visible in both groups. M channels of the static group were clearly visible. S channels and the M channel of the perfused group were less visible especially at late time points (t3 and t4) due to the channels filling up with mineralized tissue over time. BV/TV of the static group was significantly higher than BV/TV of the perfused group for all time points (p ≤ 0.01). BV/TV of the static group increased from 5.70% ± 2.09% at t0 to 21.04% ± 1.65% at t4, whereas BV/TV of the perfused group increased from 1.94% ± 0.40 at t0 up to 6.97% ± 2.47% at t4 (figure 2c). Mineralized tissue formed in the static group was mostly located at the top and on the edge of the scaffold, whereas mineralized tissue formed in the perfused group was distributed more homogeneously throughout the whole scaffold volume. The morphometrical profile showed a regional dependence of BV/TV (p ≤ 0.01; figure 2d). The static group showed an increased BV/TV value in the upper regions (regions 3–10) compared with the perfused group. The mineralized tissue of the static group was unevenly distributed along the scaffold height. More mineralized tissue was found in the upper regions (regions 3–7), where a higher BV/TV value was observed compared with at least three other regions (p ≤ 0.05; significances not indicated in the figure). In the perfused group, BV/TV was identical among all regions. These results confirm that the distribution of mineralized tissue in the scaffold is highly dependent on the loading condition applied.

3.2. Mineralized tissue formation: channels

Three-dimensional images of mineralized tissue in the full channel (=channel volume plus an adjacent ring volume consisting of the SF scaffold) showed that the all channels in the static group and the L channels in the perfused group were not completely filled with mineralized tissue (figure 1a–c). In the perfused group, the M channels were almost closed (figure 1b). The S channels were completely closed in both groups (figure 1c). Even more pronounced than for the whole scaffold, the mineralized tissue in the static group was mostly located at the top of the scaffold and not in the centre. Mineralized tissue in the perfused group was distributed throughout the whole scaffold height. The coverage, representing tissue ingrowth into the channel void (=void volume of the channel with the diameter set to 90% of the real channel diameter), confirmed the results observed in three-dimensional images (figure 1a–c). Curvature had a significant influence on coverage (p ≤ 0.01; figure 1e). The coverage in the perfused group was higher in L (p ≤ 0.01) and M (p ≤ 0.05) channels than the coverage in the L and M channels of the static group. The static group showed a higher coverage in S channels than in L channels (p ≤ 0.05), whereas the perfused group showed a higher coverage in S and M channels than in L channels (p ≤ 0.01).

Three-dimensional images of registered scans from t2 and t4 revealed newly formed mineralized tissue (orange; figure 3a–c,g–i), quiescent mineralized tissue (grey; figure 3a–c,g–i) and very little resorbed mineralized tissue (blue; figure 3a–c,g–i). The resorbed mineralized tissue was neglected for further evaluation, because there were no cells present that could have resorbed the tissue and resorption was therefore considered to be an artefact of the µCT. In the full channel, BFR was dependent on the loading condition applied (p ≤ 0.01), but there were no differences observed between the different curvatures (figure 3d). The loading condition (p ≤ 0.01) and the curvature (p ≤ 0.05) influenced the MS, but no differences were observed among the different curvatures or loading conditions (figure 3e). MAR was influenced by the loading condition (p ≤ 0.01) and was lower for L channels in the perfused group (p ≤ 0.05; figure 3f). In the channel void, no significant differences were observed for BFR and MAR (figure 3j,l). MS was influenced by the loading condition (p ≤ 0.05), but no differences were observed for curvature (figure 3k).

3.3. Histology

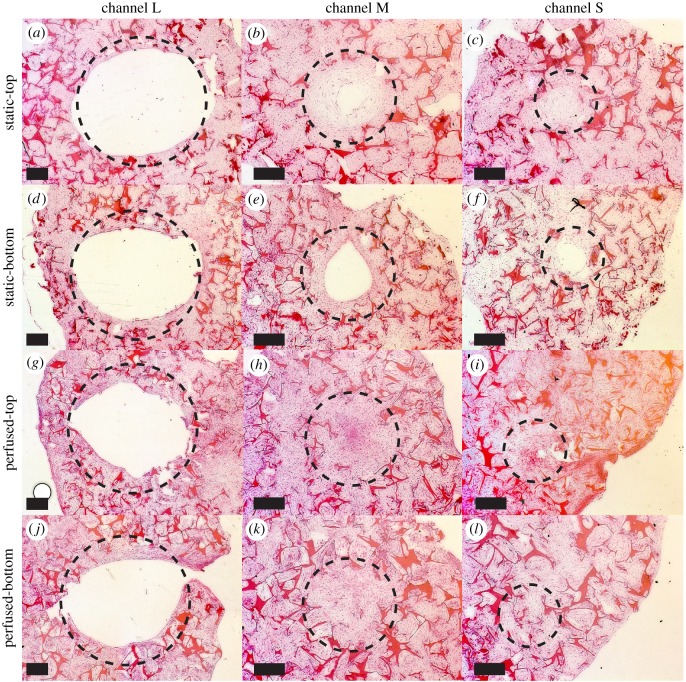
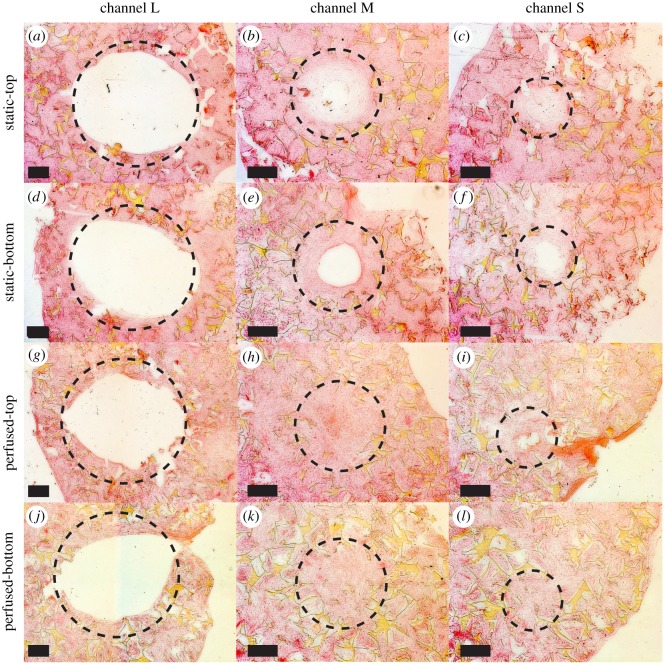
H&E staining revealed that cells were able to penetrate into the pores of the whole scaffold volume independent of the group (data not shown). Horizontal scaffold cross-sections stained with H&E revealed no ECM ingrowth in L channels for both loading conditions at neither the top nor the bottom of the scaffold (figure 4a,d,g,j). In the static group, ECM ingrowth was observed in M and S channels. M channels were almost closed at the top and less closed at the bottom of the scaffold (figure 4b,e). S channels were completely closed at the top, but not completely closed at the bottom of the scaffold (figure 4c,f). In the perfused group, M and S channels were completely closed independent of the location in the scaffold (figure 4h,i,k,l). The more uniform ECM distribution along the height of the scaffold in the perfused group was in agreement with the distribution of mineralized tissue observed with µCT. Similar patterns were observed for horizontal scaffold cross-sections stained with Sirius Red (figure 5). Collagenous matrix was present in the static and the perfused group. Vertical scaffold cross-sections through S channels confirmed the results observed for horizontal cross-sections (figure 6). In the static group, S channels were closed by collagen in the upper half of the scaffold only (figure 6a), whereas in the perfused group S channels were completely filled (figure 6b). Again, collagen staining was positive for both conditions following the same patterns as observed for H&E staining (figure 6c,d). Von Kossa staining had to be excluded from histological analysis because the tissue was washed away during staining of the static samples.

Figure 4.

Horizontal scaffold cross-sections stained with haematoxylin and eosin. The dashed line circles represent the real diameter of the channels (L, 3 mm; M, 1.5 mm; S, 1 mm). (a–c) L, M and S channels of scaffolds cultured under static conditions at the top of the scaffold. (d–f) L, M and S channels of scaffolds cultured under static conditions at the bottom of the scaffold. (g–i) L, M and S channels of scaffolds cultured under perfused conditions at the top of the scaffold. (j–l) L, M and S channels of scaffolds cultured under perfused conditions at the bottom of the scaffold. Cells are located within channels and the pores of the scaffold. Scale bar, 500 µm. (Online version in colour.)

Figure 5.

Horizontal scaffold cross-sections stained with Sirius Red. The dashed line circles represent the real diameter of the channels (L, 3 mm; M, 1.5 mm; S, 1 mm). (a–c) L, M and S channels of scaffolds cultured under static conditions at the top of the scaffold. (d–f) L, M and S channels of scaffolds cultured under static conditions at the bottom of the scaffold. (g–i) L, M and S channels of scaffolds cultured under perfused conditions at the top of the scaffold. (j–l) L, M and S channels of scaffolds cultured under perfused conditions at the bottom of the scaffold. Cells are located within channels and the pores of the scaffold. Scale bar, 500 µm. (Online version in colour.)

Figure 6.

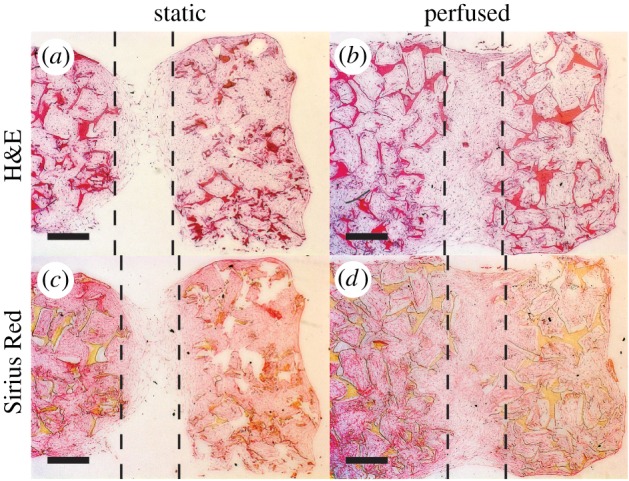
Vertical scaffold cross-sections stained with haematoxylin and eosin (H&E) (a,b) and Sirius Red (c,d). The dashed lines represent the width of the S channel (1 mm). Cells are located within channels and the pores of the scaffold. Scale bar, 500 µm. (Online version in colour.)

4. Discussion

The process of bone remodelling constantly leads to transient changes of bone surface geometry [1,2]. It was shown that there exists an intimate correlation between geometrical changes and cellular behaviour in vivo [3]. Different experimental studies have shown that curvature influences tissue growth under static and perfused conditions in vitro [6,13–15,19]. Nevertheless, these studies focused on non-mineralized ECM formation only and evaluations of tissue growth were performed in limited three-dimensional volumes. The study presented herein investigates the influence of three different channel curvatures on three-dimensional mineralized tissue formation under static and perfused conditions. Scaffolds with three channels corresponding to three different curvatures (S, −2.00 mm⁻¹; M, −1.33 mm⁻¹; L, −0.67 mm⁻¹) were produced (figure 1d). Three-dimensional mineralized tissue formation was investigated using µCT monitoring in the whole scaffold (including all channels; figure 2) and two different sub-volumes: (i) the ‘channel void’ and the ‘full channel’ (figures 1 and 3).

The mineralized tissue formation in the channels was clearly driven by curvature (figure 1a–c,e). The ingrowth of mineralized tissue into the channel void, as represented by coverage, was directly dependent on curvature. As hypothesized, mineralized tissue formation was increased with increasing curvature, as reported for non-mineralized ECM previously [6,14,15,19]. A limitation of this study is the lack of a cell-free control group. It is known that SF is able to mineralize when immersed into solutions mimicking extracellular fluid [32,33]. We have shown that spontaneous mineralization of the SF scaffold was prevented when the scaffold was seeded with cells [34]. Based on these results, we assume that spontaneous mineralization can also be excluded for this experiment, but with the techniques used for the evaluation of the mineralized tissue (µCT, histology: Von Kossa staining) it was not possible to distinguish between spontaneous or cell-mediated mineralized tissue formation.

The closing of the channels with ECM was in agreement with the mineralized tissue formation observed by µCT. The presence of collagen formation was confirmed by Sirius Red staining (figures 5 and 6). Collagen formation followed the same pattern as observed for mineralized ECM, which is in accordance with similar observations just recently published [7]. In vivo, the formation of mineralized tissue is a sequential process, initiated by the formation of a three-dimensional collagen framework followed by mineralized tissue deposition [35,36]. Unfortunately, this could not be confirmed by Von Kossa staining because the sections of the static samples were washed away during the staining process. We assume that this happened due to the high amount of mineralized tissue in the static group. The tissue needs to be decalcified to perform a proper staining, which of course makes no sense if the mineralized tissue needs to be visualized. All other stains were performed on non-decalcified sections, due to differences in the staining protocols. Based on the results observed by histology, curvature is thought to increase ECM and collagen production at first, which subsequently leads to increased deposition of mineralized tissue. The presence of collagen could therefore be evidence for future mineralized tissue formation locations. This might be an indication that curvature influences ECM formation directly and mineralized tissue formation indirectly via increased ECM and collagen formation. A limitation of this study is that collagen cannot be visualized with µCT due to its low density and had to be determined by histology, which is a destructive technique. Nevertheless, the evaluation of several sequential µCT scans in combination with computational simulations could lead to a predictive model revealing potential sites for newly mineralized tissue formation.

The mineralized tissue formation was expected to depend on the depth of the channel. According to simulations of curvature-driven growth in three-dimensional cylindrical channels, the highest mineralized tissue growth was predicted at half the channel height and the final shape of the tissue formed should resemble a catenoid (a surface that is generated by rotating a U-shaped curve formed by a rope about its horizontal axis, here the inner wall of the channel) [15,17]. The shape of the mineralized tissue in the channel void of all channels was inhomogeneous and did not show a catenoid pattern under either static or perfused conditions (figure 1a–c). This implies that the mineralized tissue growth inside a cylindrical channel does not follow the pattern predicted by the simulation [17]. Furthermore, the simulation was performed under static conditions only and is therefore not able to explain mineralized tissue formation in perfused cultures.

Culture conditions affected the amount, spatial distribution, tissue ingrowth and morphology of the mineralized tissue formed in the whole scaffold as well as in the channel void and full channel.

The BV/TV in the whole scaffold was always higher in the static group (figure 2c). This may be attributed to non-optimal loading conditions. Some studies have shown that perfusion may increase mineralized matrix formation of cells in vitro, but cell proliferation rather than differentiation or even apoptosis was also reported [37,38]. The chosen perfusion culture conditions might not have been optimal to enhance mineralized tissue formation. Nevertheless, while the total amount of mineralized tissue is important for bone regeneration, it is of minor relevance to investigate the effects of loading on the morphology and spatial distribution of the mineralized tissue formed.

The spatial distribution of mineralized tissue was vastly improved by perfusion. In the static group, the mineralized tissue was located at the top and on the edge of the scaffold (figure 2a,d). It is known that, in static cultures, cells tend to concentrate on the outer scaffold surface due to poor nutrient and waste exchange at the centre of the scaffold [39]. This is still a major issue in bone tissue engineering and several studies have tried to solve this problem using dynamic bioreactors [40]. It may be hypothesized that the cells were not able to migrate into the scaffold volume or that the cells could have died in the middle of the scaffold [41]. These assumptions were disproved by histological data showing cells throughout the whole scaffold volume (figures 4–6). The enhanced tissue distribution in the perfused group might be due to improved nutrient and waste exchange within the scaffold, giving rise to a more advantageous environment for the cells to produce mineralized tissue. In addition, the mechanical stimulation by perfusion could have provoked mineralized tissue formation inside the scaffold volume.

Tissue ingrowth into the channels did not lead to closed L channels in either the static or the perfused group. Similar patterns were observed in M and S channels, but with higher tissue ingrowth into the channel void as represented by increasing coverage with decreasing channel size (figure 1e). It is interesting to note that, with this model, we were able to imitate critical size bone defects. A critical size defect is the smallest size tissue defect that will not heal completely over the lifetime of an animal [42]. The L channel clearly represents a defect that does not heal while the M channel shows delayed healing compared with the S channel. Indeed, this might be an indication that the healing of bone defects in vivo is curvature dependent and if the curvature is too low the defect does not heal. The model presented might even allow for scaffold material testing. The channels could be filled with different biomaterials to investigate their effect on bone regeneration in a simulated defect in vitro.

Compared with static conditions, it was expected that perfusion would enhance mineralized tissue deposition because of a synergistic effect with higher curvature, due to enhanced cytoskeletal changes observed in endothelial cells after the application of fluid flow [13]. This synergistic effect could not be shown and, therefore, cytoskeletal changes might not be beneficial to increase the mineralized tissue formation by hMSCs. This cannot be confirmed but neither can it be excluded with this experiment because cytoskeletal changes were not examined. The investigation of cytoskeletal changes requires destructive techniques and would therefore not have been feasible to perform longitudinally during the experiment. Investigating cytoskeletal changes should be considered at dedicated time points in future experiments to study the influence of perfusion and curvature on mineralized matrix production with respect to morphology and orientation of hMSCs. Another reason for less mineralized tissue deposition within channels could be an impairment of the mechanical stability of the formed tissue due to the fluid flow applied. Only recently, it has been shown that impaired mechanical stability of ECM leads to deteriorated tissue organization and decreased tissue growth and reduces the ability of cells to assemble collagen fibres [7]. As a consequence, tissue organization and cytoskeletal changes need to be investigated further for our scaffold model especially by evaluating cytoskeletal differences of cells within the scaffold volume or the channel volume.

In addition to tissue ingrowth, the culture conditions influenced the morphology of the mineralized tissue in and close to the channels (figure 1a–c). Under static conditions, the mineralized tissue was more solid, resembling cortical bone. In the perfused group, the mineralized tissue was more porous, resembling trabecular bone. As for the whole scaffold, the difference in tissue distribution is most probably attributable to the differences in nutrient and waste transport or the mechanical stimulation by perfusion within the scaffold. Based on these morphological differences, the channels of our scaffold closely resemble cranial (cortical) and trabecular bone defects, respectively, for static and perfused conditions. Under static conditions, the ingrowth of mineralized tissue into the channels followed the same pattern as that observed for cranial defect healing in vivo [43]. Critical size cranial defects have been defined for mice as 5 mm or rats as 8 mm round defects [44]. Adult human cranial defects do not heal spontaneously; thus, any clinically significant defect is a critical defect [45]. From a mechanical point of view, the static condition represents a cranial defect more than the perfused condition, because skull bones normally experience minimal stresses or strains [46]. From a structural point of view, static conditions could be used to simulate cortical defects and perfused conditions for trabecular defects. It is important to keep in mind that the differences observed for tissue ingrowth or morphology between the static and the perfusion group could also be introduced by the unalterable different protocols used for medium change. It is possible that in the perfusion group osteogenic factors accumulated over time, due to the fact that only one-third of the full culture medium volume was exchanged by triple concentrated osteogenic medium. The higher concentration of osteogenic factors could lead to increased osteogenic differentiation and thus to increased mineralized tissue formation. In the experiment, this was not confirmed. On the contrary, mineralized tissue formation in the perfusion group was significantly lower than that in the static group (figure 2c).

Dynamic mineralized tissue morphometric parameters have been little influenced by curvature or culture conditions (figure 3d–f,j–l). Some non-significant trends could be observed for the full channel though (figure 3d–f), but no trends could be observed for the channel void (figure 3j–l). Based on these results, it may be assumed that the curvature also affects mineralized tissue formation in the SF scaffold in close proximity to the channel. For non-mineralized tissue, it was shown that the ECM formation rate is curvature dependent [6,15], but BFR did not follow this behaviour. The higher tissue ingrowth with increasing curvature can therefore not be explained by higher BFR, but is most probably attributable to an increased MS. The evaluation of dynamic mineralized tissue morphometric parameters confirmed that the surface area of the channel did not have an influence on cell proliferation or differentiation. There are reasons to presume that the quantitative µCT data should be normalized by the surface area of the channels. Normalizing the µCT data to the surface areas of the channels led to bigger differences between the different channels: the bigger the channel the smaller the mineralized volume and vice versa (data not shown). The influence of surface area on cell proliferation or differentiation would also have been reflected by dynamic parameters, e.g. a higher BFR with decreasing curvature, which could not be shown (figure 3d,j). In vivo mechanical loading has been shown to increase BFR and MS [21]. A similar effect was anticipated for this study to increase the rate of tissue repair. It may be assumed that the in vitro model described was not able to reproduce the effects observed in vivo, because it reflects a simplification of the in vivo situation. For example, other cell types such as osteoclasts, which play an important role in bone remodelling, growth factors or optimal loading conditions are lacking. Parameters, such as mineralized tissue formation or morphology, can be thoroughly evaluated while others, such as mineralized tissue resorption, are not evident. Nevertheless, this model can be used as a powerful tool to predict mineralized tissue formation of various biomaterials under different mechanical loading conditions in relation to the curvature of the defect present.

5. Conclusion

In conclusion, the results of this study demonstrate the influence of curvature on mineralized tissue formation in three dimensions. Mineralized tissue formation was dependent on curvature, which was represented by an increased coverage of S and M channels compared with L channels. The amount of mineralized matrix formation was not dependent on the depth of the channel and was not increased by perfusion bioreactor culture. Nevertheless, mineralized tissue morphology was influenced by the culture condition (static, perfused), with more solid, cortical-like morphology under static conditions or more porous, trabecular-like morphology under perfused conditions. Taken together, with the in vitro model described, cylindrical bone defects of trabecular or cortical bone with or without scaffold material could be simulated in vitro prior to conducting in vivo experiments, possibly leading to a reduced number of animal experiments. Additionally, the knowledge gained about curvature-driven mineralized tissue formation could be applied to specifically design scaffold morphologies for bone tissue engineering or in vivo bone regeneration.

Ethics

All experiments were conducted according to Swiss federal law on research on humans (chapter 2, paragraph 3).

Authors' contributions

J.R.V. carried out sequence alignments, designed and coordinated the study, carried out the laboratory work, performed data analysis, carried out the statistical analyses and drafted the manuscript. R.M. helped carry out sequence alignments, participated in the design of the study and revised the manuscript thoroughly and critically. S.H. participated in carrying out sequence alignments, helped to design the study and revised the manuscript thoroughly and critically. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

This project has been funded by the European Union's Seventh Framework Programme (FP/2007-2013) under grant agreement no. 262948 (Biodesign).