Synchronization and collective swimming patterns in fish (Hemigrammus bleheri)

Abstract

In this work, we address the case of red nose tetra fish Hemigrammus bleheri swimming in groups in a uniform flow, giving special attention to the basic interactions and cooperative swimming of a single pair of fish. We first bring evidence of synchronization of the two fish, where the swimming modes are dominated by ‘out-phase’ and ‘in-phase’ configurations. We show that the transition to this synchronization state is correlated with the swimming speed (i.e. the flow rate), and thus with the magnitude of the hydrodynamic pressure generated by the fish body during each swimming cycle. From a careful spatio-temporal analysis corresponding to those synchronized modes, we characterize the distances between the two individuals in a pair in the basic schooling pattern. We test the conclusions of the analysis of fish pairs with a second set of experiments using groups of three fish. By identifying the typical spatial configurations, we explain how the nearest neighbour interactions constitute the building blocks of collective fish swimming.

1. Introduction

Collective behaviours of living animals in nature have recently been the focus of a pluridisciplinary research effort, from biologists and neuroscientists to physicists and applied mathematicians [1,2]. Complex social interactions are hidden behind the motions and reactions of aggregates of individuals, leading to different levels of cohesive organization, which depend on each species' needs and ways of living. Fish schools are archetypes of these kind of cohesive social systems and they have been discussed for several decades [3,4]. Except from social life, benefits from swimming in groups are, for instance, a way to reduce risk from potential predators or to optimize food prospection [4,5]. Schooling is also often evoked from an energy perspective [3,6,7] where the spatial organization of individuals within the swimming group is said to optimize hydrodynamic interactions resulting in a global power saving for the school. In any case, the formation and organization of a group is built on local cooperation between individuals, which is achieved by relying on different sensory systems such as vision or the flow sensing lateral line [8]. The specific characteristics of the subsystem composed of the interactions of an individual and its nearest neighbours are thus the building blocks from which large and complex social groups are developed.

However, if strong efforts have been made by improving models, simulations and observations, the exact comprehension of the formation of swimming groups still need new insights. One of the main shortcomings is the lack of convergence between observations, assumptions and conclusions. For instance, real schooling data can be found in the literature from biologists, reporting tridimensional and unsteady behaviours for different configurations [8,9], which might be considered far from the ideal two-dimensional and energy-based approaches of physicists [6].

In this work, we propose to study the basic mechanisms underlying the formation of a school combining a physical approach and observations of fish. This work focuses specifically on the most simple subsystem of cooperation between individuals, namely the schooling of a fish pair. We aim here at characterizing the transfer of information within the duet mainly using fluid dynamics considerations and direct visualizations of swimming fish. We show that, even for such a simple configuration, the schooling pattern formed by the fish pair already presents certain repeatable features. In particular, we highlight a phenomenon of phase synchronization and elementary pattern formation between swimmers, which are observed to keep the distance to nearest neighbours constant and to prefer an energetically favourable synchronization pattern. Then, based on the two-fish observations, we analyse the behaviour of fish trios and also present an opening account of it.

2. Results

A set-up was especially designed for the collective swimming of red nose tetra fish Hemigrammus bleheri (see Material and methods section). It consists of a shallow water tunnel (2 cm depth) in order to instigate swimming of neighbouring individuals in the same plane; the two other dimensions of the tunnel are 20 × 15 cm (figure 10), sufficiently large compared with the typical size of the fish (approx. 4 cm long × 0.7 cm width). Water flow rates used in this work range from 4 to 22 l min⁻¹, corresponding to swimming velocities of 2.7–15 cm s^–1. For each test, the fish quickly start swimming at the flow velocity imposed in the water tunnel, i.e. they stay in a stationary position in the laboratory frame as can be seen from figure 1a—see also electronic supplementary material, video S1. The swimming velocity U is thus the average flow velocity based on the cross-sectional area of the test section and it can be set precisely by controlling the flow rate through the test section. The fish kinematics are recovered from top-view visualizations, giving the spatio-temporal evolution y(x, t) (for details, see Material and methods section and figure 10).

Figure 10.

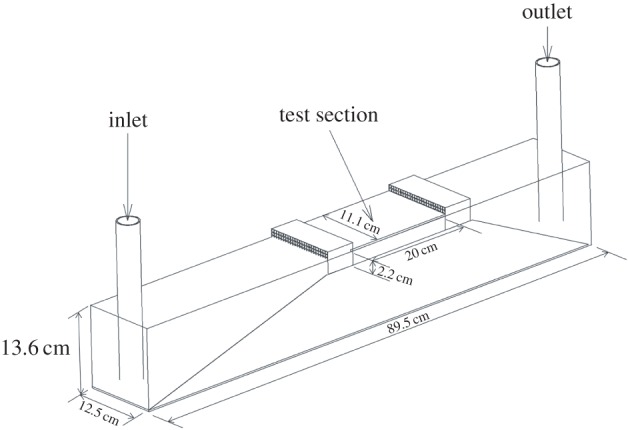
Schematic diagram of the swimming channel. An external pump drives the flow, which is directed toward the test section after a convergent ramp and through a honeycomb section to minimize swirling motions.

Figure 1.

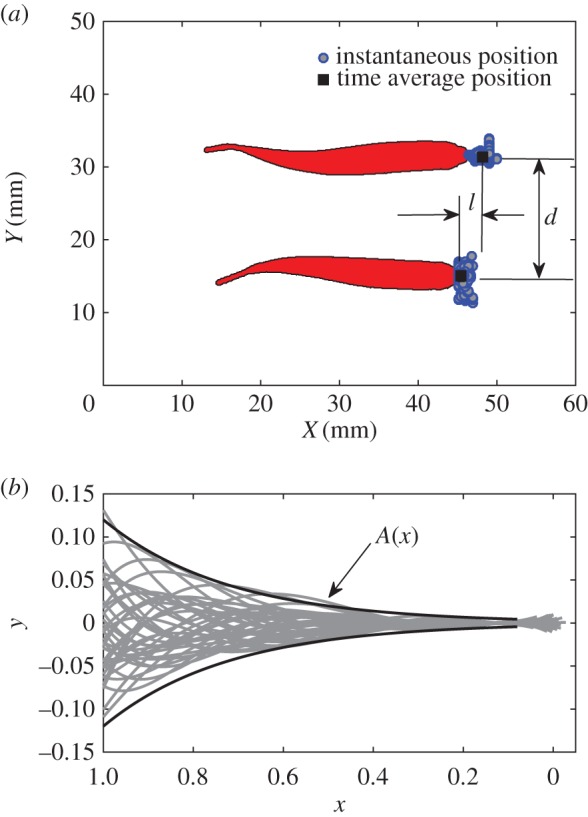
(a) Example of top visualization of two swimming fish. The school pattern is defined by the two characteristic length scales d and l, representing the distance to the nearest neighbour(s) and the shift between leading and following individuals, respectively. (b) Superimposed instantaneous swimming kinematics (middle lines) extracted from the visualization. The black lines are the spatial envelop fitted with the analytical function A(x) = A_r exp α(x − 1) [10]. The head of the fish is located on the right, the tip of the caudal fin on the left.

2.1. Two-fish experiment

We study the statistics of the kinematics of the fish over a population. For the two-fish configuration, 14 different individuals (seven pairs) were studied. For each pair, experiments were performed for 10 different swimming velocities. Neither of the individuals in a pair was repeated in any other pair.

From these data, we first address global quantities of the collective swimming of two fish, namely, the evolution of the beating frequency f and amplitude A, the phase velocity v_ϕ of the bending wave that characterizes the body deformation kinematics, and the evolution of the pattern chosen by the fish to swim together, as a function of the swimming velocity. For a tandem configuration, the swimming pattern is fully described by the two distances d and l as illustrated in figure 1. The results are displayed in figure 2 and correspond to averaged quantities over the seven different pairs of fish.

Figure 2.

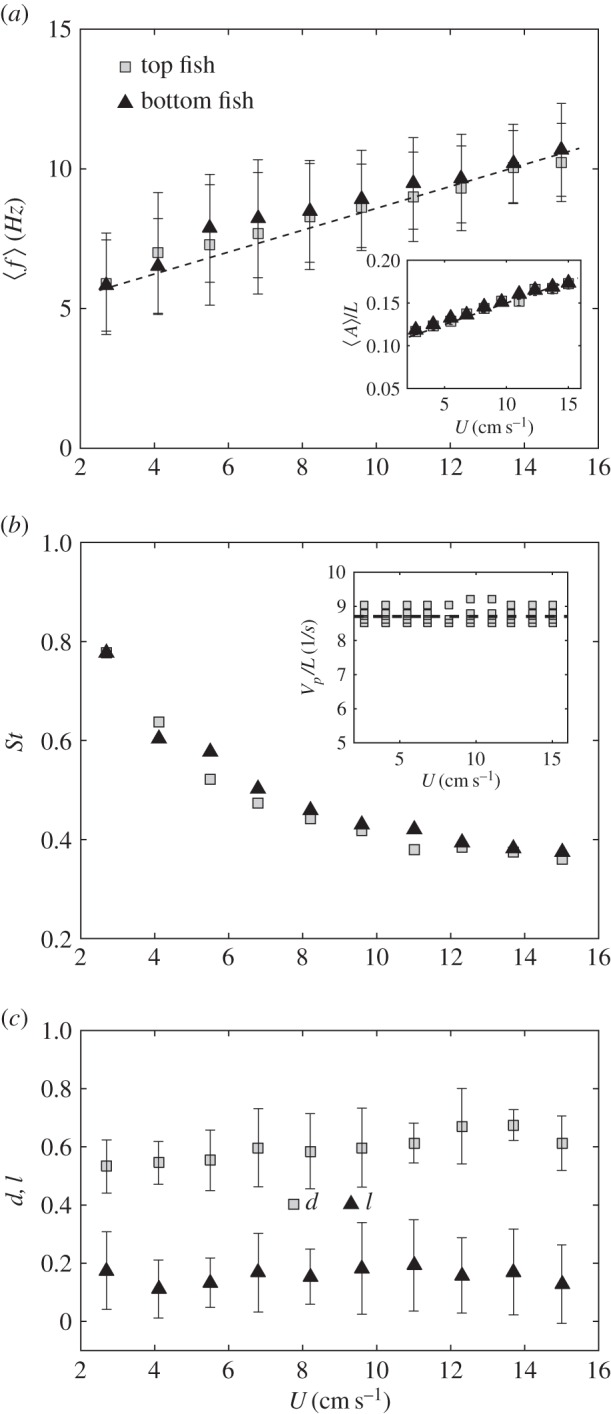
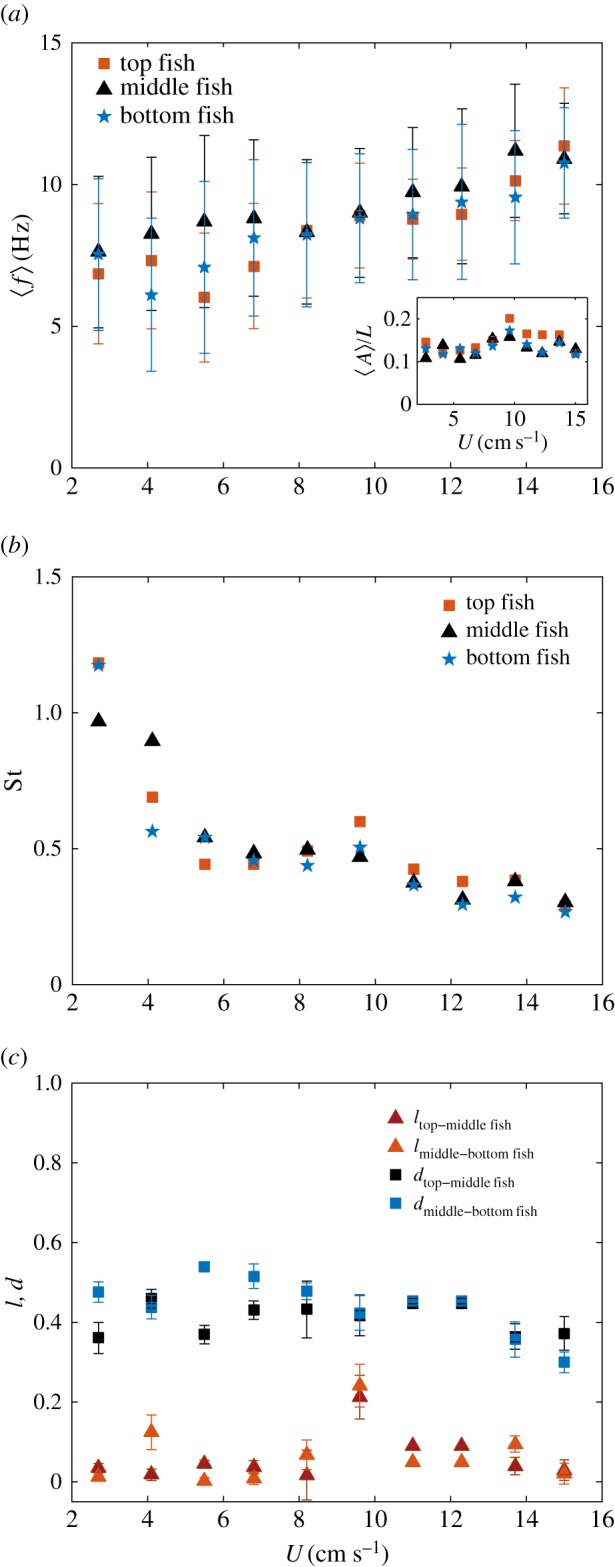
(a) Averaged beating frequency, f, and amplitude, A, (inset) for both top and bottom fish as a function of the swimming velocity averaged over the seven pairs studied. As can be seen here, fish frequencies are very close to each other and evolve linearly with U. L is the fish body length. (b) Strouhal number 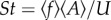and phase velocity v_ϕ (inset) as a function of the swimming speed U. (c) Typical lengths l and d defining the swimming pattern of a tandem of individuals as a function of the swimming speed. Again, the values are averaged over the seven pairs studied. The results show a constant value for both lengths, setting in average, a single spatial ordering for the tandem.

A few conclusions can be readily drawn from these first observations. First about the kinematics, we see that the frequencies of the top and bottom fish (figure 2a), respectively, are on average very close to each other and evolve linearly with the flow rate. There is of course a large scattering around the average values (up to 30% represented by the error bars on the data), resulting from several experimental sources of uncertainty such as the selected pair or the size of the fish. In the inset of figure 2a, the amplitude evolution as a function of the swimming velocity is also shown. In the same manner, the phase velocity v_ϕ (inset figure 2b) appears to converge to a constant value, for all fish and all swimming velocities (again with a large scattering due the heterogeneity of the population). This is not surprising because v_ϕ is directly related to the elasticity modulus of the fish (see also [11]). In figure 2b, we plot the Strouhal number, defined in the usual way as the ratio of the flapping characteristic velocity Af and the swimming speed U. It can be readily seen that as the swimming velocity increases the Strouhal number tends to lower values, in the range of those corresponding to efficient swimming [12].

2.1.1. Spatial pattern

The most notable observation from these data concerns the swimming pattern (or spatial arrangement) chosen by the tandem. This pattern is fully described by the two characteristics l and d, as described in figure 1. As can be observed in figure 2c, the parameters of the swimming pattern stay statistically constant over the large range of swimming velocities tested here; fish seem to choose a stable configuration independent of their gait. The distance d, which can be referred to as the distance to the nearest neighbour (NN) is here measured around 0.5–0.6 fish body lengths. This value is consistent with observations that have been made on schooling fish with strong cohesion (as the red nose tetra fish) [13].

2.1.2. Synchronization

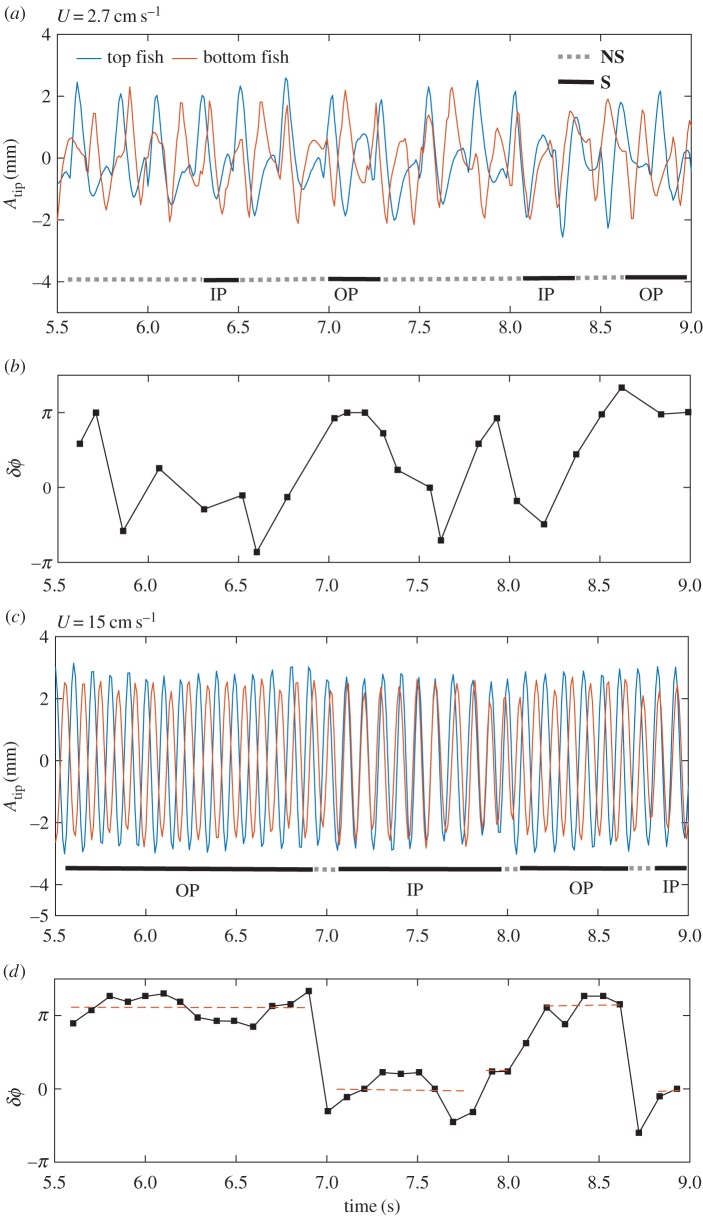
The two cases shown in figure 3 are the two synchronization modes considered: in-phase (IP, figure 3b) and out-of-phase (OP, figure 3a). To define synchronization in a fish pair, we compared the tracks of the tail tips of the two fish using the tail beating of one fish as a reference—the top fish in the representation of figure 1a. For each tail flapping cycle of the reference fish, the signal of the neighbouring fish was analysed defining a phase difference signal δ_ϕ with one measurement point every cycle. Figure 4a,c correspond, respectively, to the tail beat signals of a pair at slow (2.7 cm s^–1) and fast (15 cm s^–1) swimming velocities, while figure 4b,d correspond to the instantaneous phase difference between the tail beat signals of the top and bottom fish. The instantaneous phase can thus be defined as 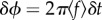, where δt is the time difference between two nearest peaks in the two tail beat signals. To build the histograms in figure 5, we counted one synchronized state (S) for each full flapping cycle in which the two fish were observed to perform IP or OP swimming. In any other configuration, partially synchronized or fully desynchronized, the cycle was counted as non-synchronized (NS). IP or OP were defined, respectively, when the instantaneous phase difference is 0 ± π/4 and π ± π/4. From figure 4a,b, we can clearly see that at low speed there is basically no synchronized swimming except for a few cycles. On the contrary, when the fish are forced to swim faster synchronized states are preferred, as shown in figure 4c,d.

Figure 3.

The two different states of synchronization observed for a pair of swimming H. bleheri. The OP state corresponds to a configuration where both fish swim out-of-phase (a), the IP state to a configuration where both fish swim in-phase (b); see also electronic supplementary material, video S2.

Figure 4.

Two typical caudal fin tip kinematics for, respectively, slow (2.7 cm s⁻¹, (a)) and fast (15 cm s⁻¹, (c)) swimming velocities. Top and bottom fish are represented by blue and red lines, respectively. Phase difference plot for swimming velocities 2.7 cm s⁻¹, (b) and 15 cm s⁻¹, (d), respectively.

Figure 5.

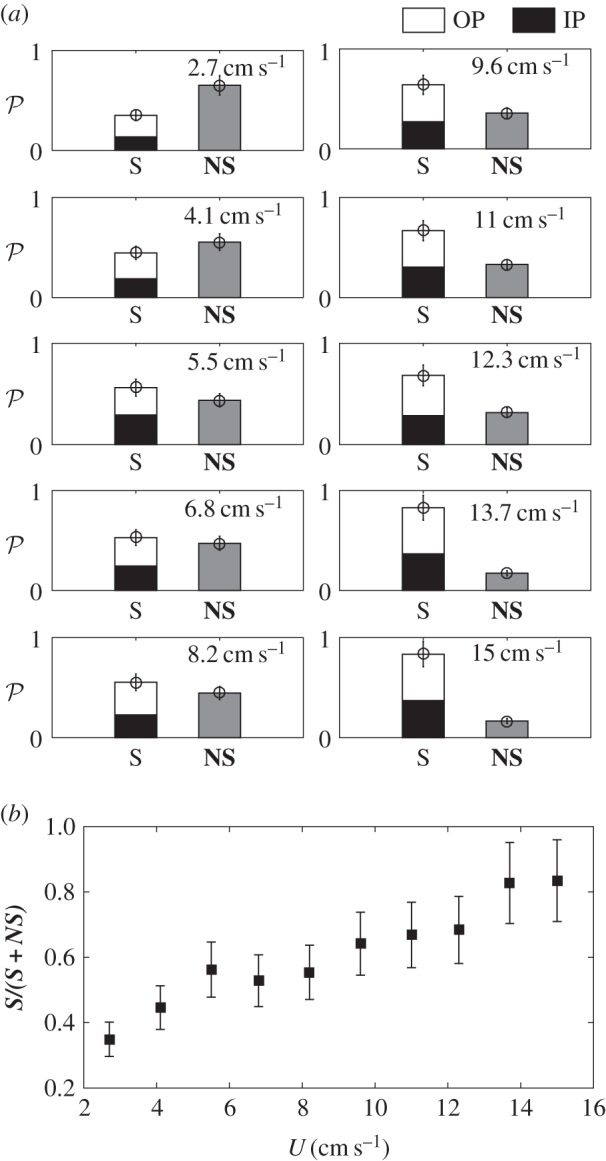
(a) Cumulated probability histograms of synchronization over seven different fish pairs at different flow velocities. In each frame, the left bar represents the percentage of time where the fish were synchronized (S), in phase (black fill) or out of phase (white fill), over a 10 s recording of the swimming kinematics. The right bar is the time spent out of synchronization (NS). The time series were analysed using the flapping frequency of one fish as the time base so that fish were considered synchronized at a given time only if they spent the full flapping period synchronized. (b) Plot showing the cumulative probability of synchronized state as a function of swimming speed.

Figure 5 shows the cumulated statistics (averaged over the seven different pairs of fish) of the synchronized states as a function of the swimming velocity. The evolution here is straightforward: for relatively slow swimming velocity, the fish spend most of their time swimming independently in a NS state (figure 4a). This tendency changes with increasing swimming velocity where more and more S states are observed in the distribution to get, by contrast, for fast velocities, to an almost fully synchronized state over the period of observation (which represents more than 80 tail beating cycles). The transition from independent to collective swimming is here clearly observed to be based on the gait of the fish, which strengthens the importance of the interactions between individuals. This synchronization process recalls, for instance, the mechanisms of interpersonal coordination of side-by-side human walking [14–16], where it was shown that the rate of synchronization was statistically correlated with the strength of sensory feedback mechanisms. And of course synchronization is a widely observed phenomenon in collective motion (see e.g. the recent study by Yuan et al. [17] on the synchronization of swimming Caenorhabditis elegans). It is worth noticing that the fish pair, when synchronized, favours the anti-phase state (OP). This point will be discussed further below.

2.2. Three-fish experiment

We conducted another set of experiments for seven groups of three fish in the same swimming conditions. The results are displayed in figures 6–8. Figure 6 shows the patterns observed over the whole range of swimming speeds, summarizing the geometric parameters of the shoaling pattern. The top row shows the three most probable observed patterns, the last case shown in figure 6d represents 16% of the observations for three fish schooling in this work.

Figure 6.

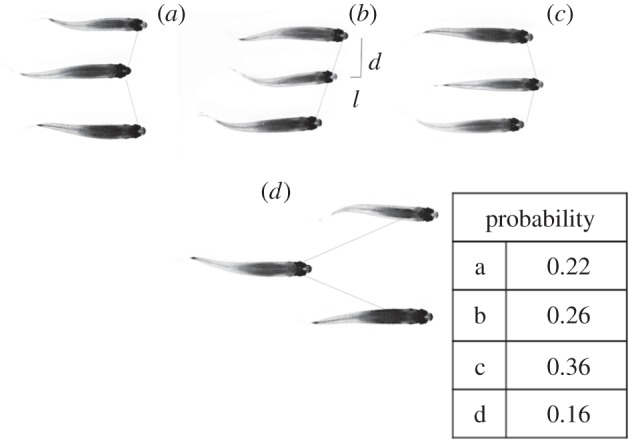
Illustration of the three most probable swimming patterns for a three fish group of H. bleheri. Distances and angles between neighbours are kept constant. (a) Two aligned fish are leading the pattern on the sides and the middle fish lies in the back. (b) One fish is leading the pattern on the side, the two other fish are shifted respectively from the other. (c) One fish is leading in the middle of the pattern, two aligned fish follow in the back. (d) Occasionally observed schooling pattern evoking the diamond-like arrangement described in [6], two aligned fish are leading the pattern on the sides. This time the third fish is evolving in the wakes of the two firsts, changing the global organization of the swimming pattern.

Figure 8.

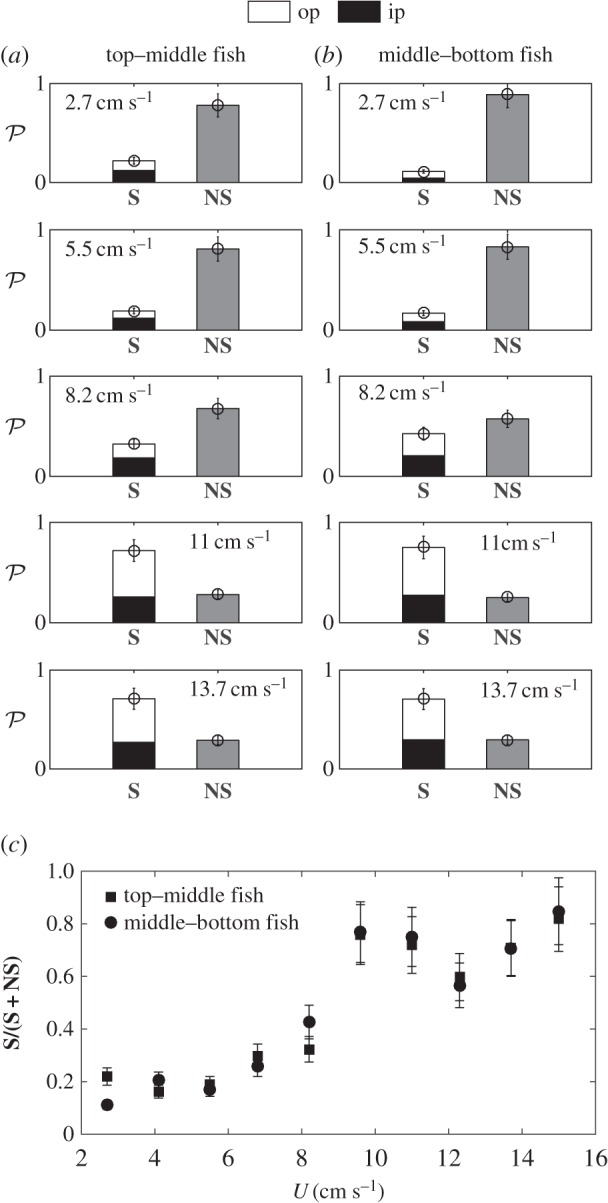
(a,b) Cumulated probability histograms of synchronization over seven different fish trios at different flow velocities. In each frame, the left bar represents the percentage of time where the fish were synchronized (S), in phase (black fill) or out of phase (white fill), over a 10 s recording of the swimming kinematics. The right bar is the time spent out of synchronization (NS). (c) Plot showing the cumulative probability of a synchronized state between top and middle fish (squares) and middle and bottom fish (circles), as a function of swimming speed.

3. Discussion

Some physical arguments can be put forward in order to understand the basic interactions behind the schooling mechanism. The first concerns the synchronization process as a direct consequence of the sensitivity of each individual to hydrodynamic pressure, through the lateral line. This lateral system has been shown to play an important role in the cohesive behaviour of swimming fish [8], and more particularly in a population of H. bleheri [18]. Together with vision, sensitivity to pressure fluctuations is thus the principal mode of interaction between neighbours in the present experiments. To a first approximation, the flow around a swimming fish can be described considering a two dimensional elongated waving plate evolving in a potential flow [19,20]. In that case, the local pressure on the body of the fish can be explicitly calculated for a prescribed kinematics. Here, the kinematics can be easily determined from the middle-line extracted from the visualizations. Following [10], we consider that the amplitude distribution of the swimmer is given by A(x) = A_r exp α(x − 1), where A_r is the amplitude of the displacement at the tail tip of the swimmer and α represents the growth rate of the local amplitude along the body (i.e. the head to tail amplitude ratio). This specific kinematics favours the contribution of the tail to the propulsion with respect to the head of the fish. Using Bernoulli's equation (see [10] and references therein for details), the pressure fluctuation p(x) can be written

3.1

;where 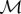is the added mass coefficient defined as the product of the fluid density ρ_f and the fish section 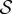[10]; the dot and prime symbols stand for time and spatial derivatives, respectively. Thus, for a fish kinematics given by y(x, t) = A(x) expω(x/v_ϕ − t), where ω = 2πf, we have

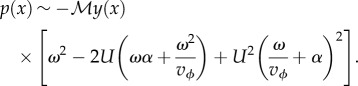3.2

;

Finally, considering that ω ∼ U (figure 2a), it follows that the magnitude of the pressure signal becomes greater with increasing frequency and that it gradually increases from head to tail. An example of the pressure field generated using the kinematics of the moving midline for y(x, t) is shown in figure 9.

Figure 9.

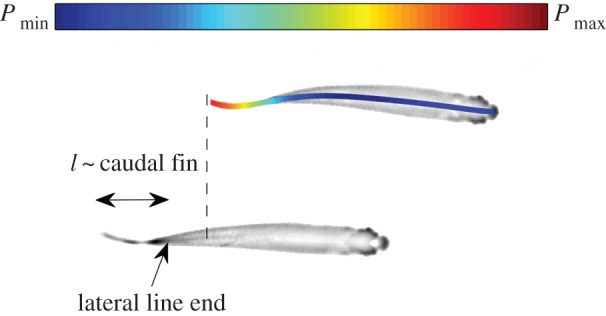
The pressure field produced by the undulating midline calculated using equation (3.2) is shown in colour for the top fish, illustrating that the maximum of pressure fluctuations occurs before the end of the lateral line of the neighbouring fish (at the root of the caudal fin) because of the pattern chosen by the fish pair.

Now, as shown in figure 2c, fish keep a constant separating distance d while swimming, for the whole range of flow speeds studied. This means that, referring to the above scaling for the pressure, the intensity of the interaction between individuals grows drastically with swimming velocity. Assuming that each swimming fish behaves as an independent oscillator, coupled to its neighbours by sensory feedback mechanisms (the feedback being here ensured by the lateral line), synchronization thus takes place when the coupling mechanism constituted by the fluid pressure signal generated between the two individuals is sufficiently strong. This is consistent with models of synchronization of non-correlated and noisy oscillators that have been extensively studied in the literature [21–23]. It can be also seen from figure 4a,c that the tail beat signals at high swimming speeds are periodic and smooth when compared with those at low swimming speeds, which is another indication of the strong coupling of the two synchronous swimmers.

High swimming speed gaits are thus characterized by synchronized states in the side-by-side fish pair configuration. As evoked above, in this regime, the anti-phase pattern (OP) is favoured with respect to the opposite IP mode. These two swimming modes have been studied recently both experimentally [24,25] and numerically [7] in the context of collective swimming of fish-like robots. The main conclusion of those works was that anti-phase swimming is an energy-saving mode for the swimmers. This conclusion was based on the generated wake difference (i.e. the energy dissipation rate) between both configurations. The OP mode, because of its mirror-symmetry between the two swimmers, was found to limit flow velocity fluctuations produced by the tail, hence improving efficiency. Transposed to real fish, the side-by-side configuration should benefit from the same effect. More specifically, the OP mode might be a collective strategy for fish swimming out of their usual gaits as, for instance, in the case of high velocity imposed in this experiment. This conjecture is strengthened by the trend of the Strouhal number displayed in figure 2b, which reaches its lowest values (indicating more efficient swimming) specifically in the regime of synchronization. These observations suggest an adaptation of the gait for efficiency purposes.

The other feature of the basic pattern in the two-fish experiments is the gap length l. As shown in figure 2c, this distance remains statistically constant for all pairs and swimming speeds studied, fixing, with d, the geometric pattern for the two fish. The existence of this gap can be understood by the need to maintain a good transfer of information within the fish pair. As evoked above, H. bleheri use the lateral line to sense the presence of their nearest neighbours. This lateral line, for most species and in particular for H. bleheri and other Hemigrammus species, is located all along the sides of the fish but does not penetrate in the caudal fin [18,26–28]. The zone near the caudal fin is however the region where pressure fluctuations are focused, due to the specific swimming kinematics. In the case of a side-by-side configuration, a perfect alignment of the two fish will not give an optimal configuration as the strongest produced pressure would be placed in face of an inert zone in terms of sensing. A small shift, roughly of the typical size of the caudal fin (measured at 0.16 ± 0.01 body length for the 14 fish), could nevertheless overcome this problem and give a more efficient communication between the two fish. Results plotted in figure 2c show shift distances l of the order of magnitude of the length of the caudal fin, which strengthens the above statement. This consistent shift in the side-by-side configuration establishes a leader–follower hierarchy in the pair. Although beyond the reach of what could be observed in the present experiments, it would be interesting to see if this hierarchy is respected over long periods of swimming.

In the light of the previous observations, assuming that highly shoaling fish hold the distance to their nearest neighbours [8,18], the spatio-temporal pattern seems to be imposed by the transfer of pressure information from one individual to the other. An isolated pair of swimming H. bleheri is then characterized by a side-by-side pattern, shifted to install an efficient transfer between the pressure source (the swimming fish) and the sensor (through the lateral line). Cases of high-speed swimming are characterized by phase synchronization states (IP and OP states) which are not statistically equiprobable; in those specific regimes demanding high energy resources, the anti-phase synchronization is favoured for its efficient nature.

The previous conclusions are of course to be put into perspective for larger populations of fish, and the goal of the experiments with three fish, that we have performed so far, was to test how the results from the two-fish experiment could scale up. The three patterns figure 6a–c can be directly derived from the two-fish interactions as they represent the possible combinations keeping l and d constant for the three fish. Those observations are quantitatively reported in figure 7. Also, synchronization states still hold for the three-fish arrangement. Statistics are displayed in figure 8 and bring strictly the same conclusion as for the side-by-side configuration of figure 2, giving strength to the basic one-to-one interactions illustrated between two fish.

Figure 7.

(a) Averaged beating frequency for the three fish (top, middle, bottom) as a function of the swimming velocity averaged over the seven trios of individuals studied, and amplitude in the inset. As for the two-fish case, respective frequencies are very close to each other and evolve linearly with U. (b) Strouhal number for the three fish (top, middle, bottom) as a function of the swimming velocity. (c) Typical distance to the nearest neighbour and shift lengths l defining the swimming pattern of the trio of individuals as a function of the swimming speed. Again, the values are averaged over the seven pairs studied.

There is, however, a notable difference between the two and three fish configurations. In addition to the preferred pattern illustrated in figure 6a–c, the trio chooses sometimes the organization exemplified in figure 6d. This organization recalls the basic subsystem of the so-called ‘diamond shape’ evoked in the pioneer work of Weihs [6]. Here, the fish in the middle lies in the wakes of the two leaders in the front, breaking the previously observed organization of the swimming pattern. This last spatial configuration is still statistically infrequent to be considered as an alternative swimming strategy in itself. It is however, noteworthy that even if this pattern is occasional, it seems stable over time.

4. Concluding remarks

Previous studies have revealed the network of visual interactions in fish a group [29,30] and its importance for the information transfer within the group. Here, we extend the analysis of inter-individual interactions to bio-mechanical mechanisms. The distance between nearest neighbours d is constant and probably maintained by visual contact. We observed in this work a persistent shift l in the other length scale that defines the basic spatial pattern between neighbouring fish, as well as a synchronization state of the caudal fins oscillations. We argument that while the pattern geometry facilitates information transfer between neighbours, the observed synchronization can be explained from an energy efficiency perspective. Indeed, the synchronization increases with swimming speed, corresponding to a range of Strouhal numbers of efficient gaits. Further works, in the continuity of the present one, will be dedicated to study groups with larger numbers of swimmers to put into perspective the basic interactions shown here in a more complex network.

5. Material and methods

5.1. Swimming tunnel

A shallow water tunnel with a test section of 2.2 cm depth and a swimming area of 20 × 15 cm (figure 10) was used for the experiments. The flow rate Q can be varied from 4 to 22 l min^–1, resulting in an average velocity U = Q/S, where S is the cross-section, in the range between 2.7 cm s^–1 and 15 cm s^–1. The laminar boundary layer thickness is estimated to be of ≈7 mm at the lowest speed to ≈3 mm at the highest speed. The corresponding Reynolds numbers are between 1000 (2.7 cm s^–1) and 6000 (15 cm s^–1). The fish spontaneously place themselves to swim in a region of ≈8 mm in the middle of the channel.

5.2. Animals and housing

Hemigrammus bleheri, also known as red nose tetra fish (approx. 3.5–4 cm long × 0.5–0.6 cm width), were procured from a local aquarium supplier (anthias.fr, France). The fish were fed five to six times a week with commercial flake food. The fish were reared in a 60 l tank with controlled water at a temperature between 26 and 27°C.

5.3. Experimental procedure

Before starting each run, the fish were transferred with a hand net from the rearing tank to the test section of the channel without any flow. The fish were left idle for around 1 h in the channel without any flow to habituate. Each of the swimming experiments was carried out for 10 s. After each experiment with a pair, the fish were allowed to relax for over 20–30 min in the channel without flow. After a complete set of experiments (i.e. 10 observations for 10 different velocities), each pair was transferred to another tank. Also, none of the individuals was repeated in any another pair.

5.4. Visualization

Fish kinematics were recovered from top-view visualizations at 100 fps. Middle lines for each fish were extracted at each time using a Matlab® routine; thus for each fish we obtained its full spatio-temporal evolution y(x, t) (figure 1). For each image, the background was subtracted from the image to obtain the silhouette. The boundary points on each side of the fish and the head were identified for each fish. Finally, the midline was extracted, equidistant from the lateral boundaries of each fish.

Ethics

The experiments performed in this study were conducted under the authorization of the Buffon Ethical Committee (registered to the French National Ethical Committee for Animal Experiments no. 40) after submission to the state ethical board for animal experiments.

Authors' contributions

I.A. performed the experiments. I.A., R.G.-D. and B.T. analysed the data. B.C. and J.H. helped in the design of the experiment and the fish handling protocol. B.T. drafted the first version of the manuscript. I.A., R.G.-D. and B.T. wrote the paper and all authors participated in discussing and approving the final version of the paper. R.G.-D. and B.T. conceived and directed the project.

Funding

I.A. was funded by a PhD fellowship from the Sorbonne Paris City College of Doctoral Schools. J.H. and B.C. were supported by European Union Information and Communication Technologies project ASSISIbf, FP7-ICT-FET-601074.

Competing interests

We declare we have no competing interests.