Spatial evolutionary epidemiology of spreading epidemics

Abstract

Most spatial models of host–parasite interactions either neglect the possibility of pathogen evolution or consider that this process is slow enough for epidemiological dynamics to reach an equilibrium on a fast timescale. Here, we propose a novel approach to jointly model the epidemiological and evolutionary dynamics of spatially structured host and pathogen populations. Starting from a multi-strain epidemiological model, we use a combination of spatial moment equations and quantitative genetics to analyse the dynamics of mean transmission and virulence in the population. A key insight of our approach is that, even in the absence of long-term evolutionary consequences, spatial structure can affect the short-term evolution of pathogens because of the build-up of spatial differentiation in mean virulence. We show that spatial differentiation is driven by a balance between epidemiological and genetic effects, and this quantity is related to the effect of kin competition discussed in previous studies of parasite evolution in spatially structured host populations. Our analysis can be used to understand and predict the transient evolutionary dynamics of pathogens and the emergence of spatial patterns of phenotypic variation.

1. Introduction

Theoretical epidemiology has produced a comprehensive theoretical framework to understand and predict the epidemiological dynamics of pathogens [1–4]. To improve these predictions it is often necessary to explicitly describe the evolution of pathogens [5] but simultaneously taking into account this evolution and the complex spatio-temporal dynamics of epidemics is a major theoretical challenge. Several studies, however, indicate that spatial structure can have a huge impact on the evolution of pathogens. First, most theoretical studies focus on the long-term consequences of spatial structure on pathogen evolution using the adaptive dynamics framework [6–12]. These theoretical studies predict that, in a broad range of scenarios, lower migration selects for lower pathogen virulence (reviewed in [13,14]). Several experimental studies using microbial systems support this prediction [15–17]. Second, recent attempts have been made to model pathogen evolution in spatially spreading epidemics [18–22]. These studies show that selection at the frontline of the epidemics is very different than near an endemic equilibrium. In particular, more transmissible pathogens are selected for at the front of the epidemics. Interestingly, these models generate new predictions that are testable in field studies. In particular, these models highlight the build-up of phenotypic variation between the front and the rear of a spreading epidemic. In accord with these theoretical results, recent field studies report the existence of patterns of phenotypic differentiation between pathogens sampled at the front or at the epicentre of epidemics [19,23–25].

In this article, we model the joint epidemiological and evolutionary dynamics of spatially structured host–parasite interactions. Earlier attempts to study evolution in spatially spreading epidemics relied mostly on simulation studies or on partial differential equations [18–22], with limited connections to classical models of life-history evolution and quantitative genetics. Here, we extend the evolutionary epidemiology approach to take into account the spatial dynamics of epidemics in discrete space. Following Day & Gandon [26,27], we start from a multi-strain epidemiological model. Evolutionary dynamics are modelled by writing equations for the dynamics of the mean life-history traits of interest (such as transmission or virulence). This allows epidemiological and evolutionary dynamics to be followed simultaneously. However, in a spatially structured population, we need to account for the fact that the average trait in a given region of space need not coincide with the average trait in the total population. Using spatial moment equations [28–30], we derive equations for the dynamics of the local as well as global mean traits in the parasite population. We illustrate the value of our approach using a biological scenario where the coupled epidemiological and evolutionary dynamics lead to transient phenomena that cannot be described by standard invasion analyses.

2. A multi-strain epi-evolutionary model

(a). Life cycle

We consider a large population of hosts infected by N pathogen strains. Hosts are assumed to live on a regular network of sites, where each site can harbour at most one individual and is connected to n other sites. A host infected with strain i can transmit the disease to a neighbouring susceptible host at rate 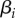. Hosts have a baseline mortality rate d and when they are infected by parasite strain i they have an additional mortality 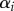(virulence). Host can also reproduce to empty sites, but we leave the details of host demography open for now, as the results in this section do not depend on the assumptions on host dispersal and fecundity, provided there is no vertical transmission of the parasite. Finally, we assume that a parasite of type i can mutate to parasite type j at rate 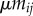, with .

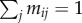Our aim is to track the epidemiological and evolutionary dynamics of the population. To follow epidemiological dynamics, we focus on the total densities of susceptible and infected hosts, which are 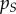and 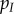, respectively. The density of infected hosts, 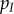is the sum of the densities of each strain, that is 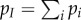, where 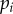is the density of hosts infected by strain i. To follow evolutionary dynamics, we track the frequency of parasite strain i, which is defined as 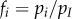, and of mean parasite traits . Table 1 collects the main notations used throughout the article. We refer the reader to the electronic supplementary material for more details on the analysis.

Table 1.

Main symbols and notation used.

	notation	description
life cycle	N	number of parasite strains
	d	baseline mortality rate
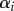		virulence of strain i
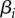		transmission of strain i
	μ	mutation rate
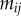		probability to mutate from strain i to strain j
epidemiology		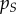global density of susceptible hosts
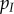		global density of infected hosts
		global density of hosts infected by strain i
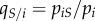		local density of susceptible hosts experienced by an average host infected by strain i
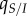		local density of susceptible hosts experienced by an average infected host
		local density of sites in state X experienced by an average site in state Y
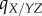		local density of sites in state X experienced by the Y site of a YZ pair
evolution		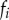frequency of strain i
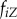		frequency of strain i among all hosts connected to an individual in state Z
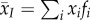		global mean of trait x
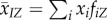		mean of trait x among all hosts connected to an individual in state Z
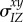		covariance between traits x and y among all hosts connected to an individual in state Z
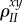		covariance between traits x and y among two neighbouring infected individuals
network	n	number of neighbours
		1/n

(b). Epidemiology

With the above life cycle, the dynamics of the density of strain i, 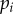, can be written as follows:

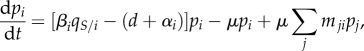2.1

where 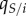is the average proportion (or local density) of susceptible hosts among the neighbours of a host infected by parasite strain i.

Summing over all types i yields the dynamics of the global density of infected hosts,

2.2

which can be understood as follows. First, the total density of infected hosts will decrease at a rate proportional to the mean mortality rate in the population, 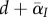, where 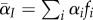is the average virulence in the population. Second, the average transmission rate is given by 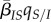, where 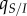is the average density of susceptible hosts experienced by an infected host and 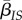denotes the mean transmission rate in infected individuals connected to at least one susceptible host (i.e. in hosts that can effectively transmit the disease).

To compute 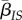, we need to consider the densities 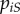of pairs between a susceptible host and a host infected by parasite strain i. Note that we have 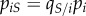. The total density of susceptible–infected pairs is 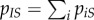, and the frequency of strain i among infected individuals in contact with a susceptible host is 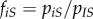. This allows us to compute 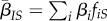. We can similarly define other global and local mean traits, such as 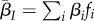and .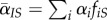

(c). Evolution

For a given parasite trait x (such as transmission or virulence), we are interested in the change over time of the mean value of x, which is 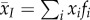. Following Day & Gandon [27], the dynamics of 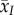is

2.3

The first term represents the effect of selection as the covariance between the trait, 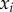, and the per capita growth rate of parasite strain i,

2.4

The second term represents the effect of mutation bias, which is proportional to the difference between the mean trait, 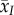, and the mean value of trait x among all new ‘mutations’, 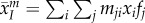[26,27]. Plugging equation (2.4) into equation (2.3), we obtain the following equation for the dynamics of mean virulence and transmission (see electronic supplementary material for details):

2.5

Equation (2.5) allows us to identify three main forces driving the dynamics of the mean traits. First, the effect of natural selection on mean virulence and transmission is described by the product of the genetic (co)variance matrix G with the selection gradient 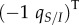. This is analogous to classical quantitative genetics models. However, in a spatially structured population, the genetic covariance matrix needs to be computed at the relevant spatial scale. In our model, we have

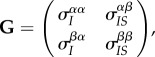2.6

where is the global (co)variance between traits x and α in the population, whereas is the local (co)variance between traits x and β in an infected individual that has at least one susceptible neighbour. Similarly, the selection gradient depends on the local density of susceptible hosts, .

The second term in equation (2.5) is the product of the average transmission rate, 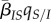, times the difference between the local and global mean traits, 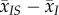. In a well-mixed population, this difference is zero and this term vanishes. Hence, this is a purely spatial effect that reflects the fact that, in spatially structured epidemics, virulence or transmission may be locally higher or lower than in the population as a whole.

Finally, the third term in equation (2.5) is the effect of mutation bias. In the following we assume, for simplicity, that mutations are uniformly distributed 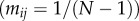. Whether or not this mutation process yields a mutation bias depends on the distribution of strain frequencies.

In a well-mixed population, we have 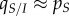, 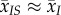and 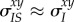. Thus, the genetic (co)variance matrix takes the same form as in classical non-spatial models, and equation (2.5) collapses to

2.7

which is exactly eq. (2.5) in [27]. Equation (2.7) describes the change of the first moment of the trait distributions (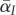 and 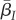) as a function of the second-order genetic moments (the variances 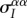and 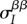and covariances and 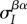). By contrast, equation (2.5) takes one further step by describing the change in the global means in terms of both local and global first- and second-order moments.

3. Application: short-term virulence evolution during an epidemic

In order to better illustrate the value of our approach, we make two simplifying assumptions. First, using the standard assumption of a transmission–virulence trade-off [31], we focus on the change on mean virulence which, from equation (2.5), is given by

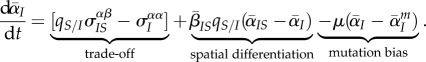3.1

Second, we assume that host fecundity is so large that dead individuals are immediately replaced by a new susceptible host. Consequently, we can neglect host demography and consider that all sites are occupied by one host, which can be either susceptible or infected. In other words, the density of the host population remains constant while the prevalence of the infection varies throughout the epidemic. This corresponds to a spatial version of the classical SIS epidemiological model [32].

(a). Case study

We will now reveal the main insights gained by our approach using a specific biological scenario. Following the analysis of Griette et al. [20], we consider the invasion dynamics of two parasite strains: a wild-type strain and a virulent strain with higher transmission and virulence, but with a lower than the wild-type strain. Mutation occurs between the two strains. Starting from a small inoculum at the centre of a lattice of susceptible hosts, we will use stochastic simulations of the underlying individual-based model to track the joint epidemiological and evolutionary changes over the course of the epidemic. Furthermore, we contrast two scenarios (figure 1). The first scenario assumes global parasite dispersal: infected individuals may transmit the disease to a random susceptible individual in the population. The second scenario assumes local dispersal: infected individuals may transmit the disease to a random susceptible neighbour. Under the global-dispersal scenario, the system is expected to quickly converge to the behaviour of a non-spatial model.

Figure 1.

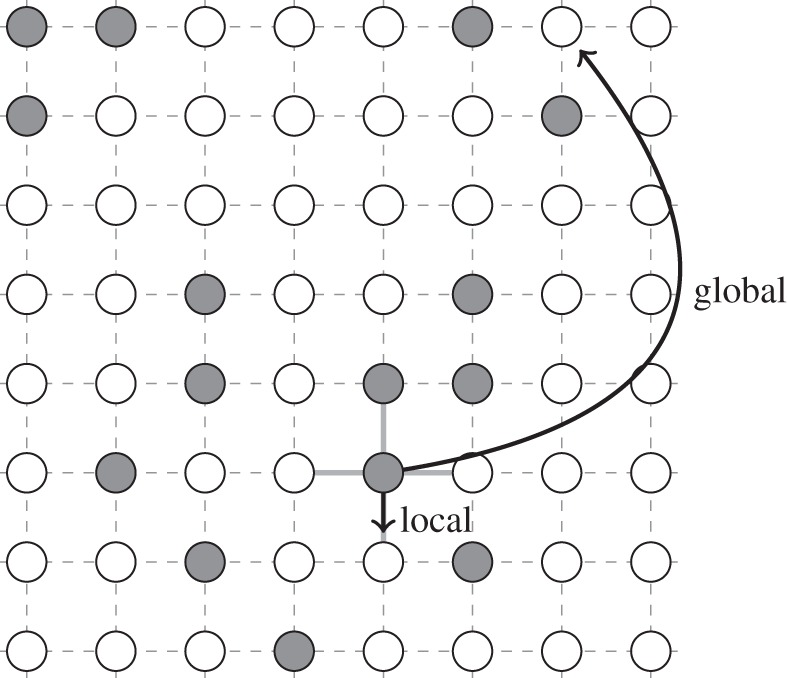
In our simulations, infected hosts may either transmit the disease locally to a susceptible neighbour or globally to a random susceptible individual. Each site can be occupied by a susceptible (white circle) or infected (grey circle) host.

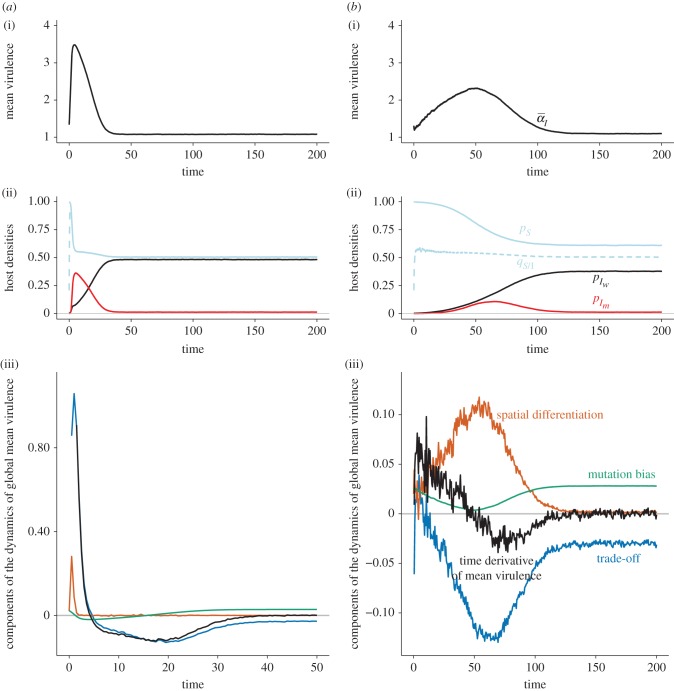
In figure 2a(i),b(i), we show that the virulent strain is transiently favoured by selection before being wiped out, a result previously shown by Day & Gandon [27]. At the endemic equilibrium, the mutant strain persists due to a mutation-selection balance. This is expected from classical, non-spatial theory, which predicts that the strain with the higher 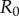(i.e. the wild-type strain) is expected to win the competition. Our simulations show that parasite dispersal does not affect this ultimate outcome. However, parasite dispersal does have an effect on the transient dynamics of the two strains during the epidemic phase. First, the overall dynamics is much slower when dispersal is local than in a well-mixed population. Second, the epidemic produced by the virulent strain lasts longer but is of lower amplitude when dispersal is local than when it is global. As a consequence, while under global dispersal a sharp peak in mean virulence is observed shortly after the start of the epidemic, local dispersal allows mean virulence to persist at an intermediate level for a longer time.

Figure 2.

Two strains w and m compete on a 100 × 100 triangular lattice (n = 6) with periodic boundary conditions. Initially, all sites are occupied by susceptible hosts, except for 37 infected hosts in the centre of the lattice. The initial frequency of mutants is 0.1. Mutation occurs between types at rate 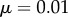, and we have and 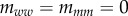. Strain w has traits 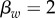, , 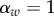which corresponds to 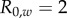. Strain m has traits , , 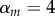which corresponds to 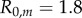. Dispersal is global in (a) and local in (b). (i)–(ii) Show the dynamics of mean virulence and the densities of each type of host (S in light blue, in dotted blue, 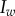in black, 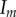in red). (a)(iii) and (b)(iii) Show the components of the Price equation (equation (3.1)) for the change in mean virulence: trade-off effect (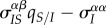, in blue), spatial differentiation effect (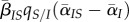, in orange), mutation bias (in green) and the sum of the previous three components (in black). The average of 100 runs of the stochastic process is plotted in all figures. Note that the timescale is different in (a)(iii).

How can we understand these markedly different transient dynamics? In the lower panels of figure 2, we plot the different components of equation (3.1) (trade-off, spatial differentiation, mutation bias). Under global parasite dispersal (figure 2a), the difference between local and global mean virulence, captured by the second term of equation (3.1) (in orange), quickly converges to zero. As a result, the change in mean virulence is solely governed by the balance between mutation bias (in green) and the trade-off effect 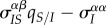(in blue). In the first phase of the epidemics, infected hosts have access to many susceptible hosts and the strain with the higher per capita growth rate (i.e. the virulent strain) is favoured. This is reflected by the positive value of 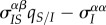(in blue). The frequency of the virulent strain then shoots up, and as the frequencies of each strain get closer, the bias in mutation is eroded. At this point, the supply of susceptible hosts is close to its equilibrium value and the virulent strain becomes counter-selected.

When parasite dispersal is local (figure 2a), the availability of susceptible hosts is lower (because 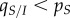) and, as a result, the trade-off effect is much weaker and actually tends to drag the mean virulence downwards (in blue). At the same time, a difference between local and global mean traits () rapidly builds up (in orange). Equation (3.1) shows that this differentiation pulls the mean virulence upwards. The balance between the trade-off, competition and mutation terms allows the virulent strain to be maintained in the population at intermediate frequencies for a longer time compared with well-mixed populations. The virulent strain can only be transiently favoured due to virulence being higher in hosts that can actually transmit the disease, as captured by the term.

In electronic supplementary material, figure S1, we show that as the number of neighbours increases, the dynamics of the spatial epidemic get closer to those observed under global dispersal. This is expected because both an increase in the number of contacts and an increased dispersal tend to decrease spatial structure.

(b). Dynamics of spatial differentiation

Equation (2.5) shows that, in spatially structured epidemics, selection is affected by the difference between local and global mean traits . To better understand how this spatial differentiation builds up under local parasite dispersal, we derive in the electronic supplementary material the following dynamical equation:

3.2a

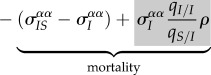3.2b

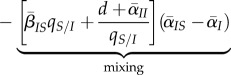3.2c

3.2d

The latter equation is valid in the limit of high host fecundity (see the electronic supplementary material for a more general treatment). In addition, we neglect for simplicity some higher-order terms that depend on another measure of spatial differentiation, 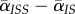. This corresponds to the classical pair approximation [28,30].

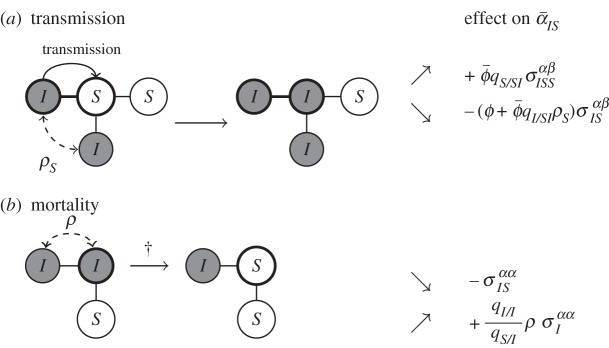
Equations (3.2a–d) show that the dynamics of differentiation is driven by four different forces.

• — First (3.2a), selection on transmission may be heterogeneous in space. Typically, at the front of the epidemic, the availability of a higher number of susceptible hosts selects for higher transmission and, because of the genetic covariance between transmission and virulence, it also selects for higher virulence. This effect may be eroded by the relatedness between pathogens separated by a susceptible host (highlighted in grey, see the electronic supplementary material for a full expression of 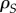). As explained in figure 3a, in a ISI configuration a transmission event destroys two IS pairs and may thus impact the spread of a focal strain if the competing strain (two sites away) is related to the focal strain. This effect will tend to limit differentiation.

• — Second (3.2b), the classical cost of virulence is expected to affect differentiation if the amount of variation for this trait varies between pairs IS and I. The amount of relatedness ρ between parasites in neighbouring sites may also affect differentiation because when an infected host dies in a pair II it creates a new IS (figure 3b). This effect will tend to increase differentiation. See the electronic supplementary material for a full expression of ρ.

• — Third (3.2c), transition between IS and II states, and vice versa, via transmission and mortality will generally tend to mix the trait values between these different types of pairs and will decrease differentiation.

• — Fourth (3.2d), in our model mutation generates a bias towards low frequency strains that tend to homogenize the distribution of strains between different types of pairs. This is also an effect that limits differentiation.

Figure 3.

Effect of transmission or mortality events on the mean virulence in IS pairs (see equation (S11) in the electronic supplementary material). (a) The effect of transmission within a focal IS pair (thick circles) on the mean virulence in IS pairs, 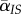. The new infection will create on average 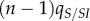new IS pairs, and the resulting increase in local mean virulence is quantified by the covariance 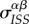. On the other hand, the infection event will destroy existing IS pairs, and this will reduce the local mean virulence: the loss of the focal IS pair will reduce 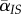by a factor 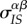, but the focal susceptible neighbours also have 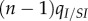infected neighbours, which tend to have the same trait as the transmitting individual with probability 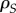. (b) The effect of the death of a focal individual (thick circle) on the mean virulence 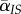. This mortality event destroys a IS pair and, therefore, causes a reduction in mean local virulence, quantified by the variance 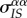, but also creates a new IS pair, which will cause an increase in 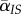quantified by the genetic covariance (or relatedness) between the two infected individuals, which is 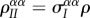. The ratio 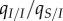quantifies the conversion of II pairs to IS pairs. Note that in equation (3.3), we assume that initially, the local covariances and variances are close to the global ones, in contrast with equations (3.2a–d).

(c). The start of an epidemic

If the epidemic starts from a random spatial configuration of strains, we may neglect the initial differentiation of the different moments of the trait distributions (mean, variance and covariance). This greatly simplifies the equation for the dynamics of spatial differentiation , which can be written as follows:

3.3

This equation highlights the two forces that are initially driving the build-up of spatial differentiation. First, the build-up of differentiation is driven by the quantity 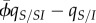which is expected to be high in the early stage of a spreading epidemic. The abundance of SSI triplets at the frontline of epidemics generates differentiation because selection for transmission is particularly high at the tip of the front [20]. Second, relatedness between strains located one or two sites away can also affect differentiation in this model. Simulations indicate that the positive effect of relatedness ρ acting on mortality outweighs the negative effect of relatedness acting on transmission (electronic supplementary material, figure S1). Hence, both forces select for higher virulence in the pairs IS.

The build-up of spatial differentiation can be visualized by showing the mean virulence at different locations across several realizations of the process (figure 4); the hosts infected by the virulent strain (darker shades of red) tend to be located at the front of the epidemic compared with those infected by the milder strain (lighter shades of red). As the frequency of the virulent strain increases, this spatial differentiation becomes more pronounced.

Figure 4.

Snapshots of the lattice at different time points. Each snapshot represents the average of 100 runs for the same scenario as in figure 2b. For each time point, each site is coloured in grey if the host is uninfected in all runs, or in red if it has been infected in at least one run. The mean virulence among runs where the focal site is occupied by an infected individual is shown, and colour-coded using various shades of red (higher levels of red indicate higher virulence). See electronic supplementary material, figure S2, for snapshots of the epidemic under global dispersal. (a) t = 0, (b) t = 10, (c) t = 20, (d) t = 50, (e) t = 70 and (f) t = 150.

(d). Reaching the endemic equilibrium

The build-up of differentiation during the initial phase of the epidemic ultimately feeds back on the dynamics of the difference between local and global traits (equations (3.2a–d)). In the end, this results in an equilibrium level of differentiation that results from the balance between selection and mutation. This equilibrium differentiation can be calculated from equations (3.2a–d), and simplified by noting that at equilibrium in the SIS model, we have 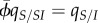[33]. Thus, under pair approximation [28,30], we have . For convenience, we calculate the equilibrium differentiation scaled by the variance, 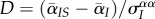. We obtain:

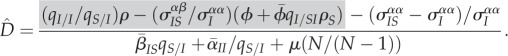3.4

Hence, at equilibrium, spatial differentiation is solely determined by the amount of local and global variation, 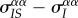, and by the indirect effect of genetic structure. In our example, the frequency of the virulent strain will tend to be higher in IS pairs than globally, so we have 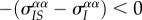. By contrast, the indirect genetic effect will tend to be positive. The balance between these two forces determines the equilibrium level of spatial differentiation.

(e). The role of host demography

So far, we have assumed that host fecundity is infinite, so that all sites on the lattice are occupied by either a susceptible or an infected individual. Relaxing the assumption of large fecundity has two main consequences: first, we need to consider the interplay between epidemiological and demographical dynamics; second, we need to account for the possibility that infected hosts may have empty sites (o) in their neighbourhood. Although equations (2.1)–(2.7) and (3.1) remain valid, the dynamics of is different from equations (3.2a–d) and now depends on the dynamics of another measure of spatial differentiation, . In the electronic supplementary material, we show how equations for the joint dynamics of and can be derived. A key difference is that the effect of the relatedness coefficient ρ vanishes from the dynamics of , but affects instead the dynamics of . This can be understood by noting that, when host fecundity is finite, a mortality event in an II pair creates an Io pair, and not an IS pair as in the SIS life cycle.

4. The weak-selection limit

Up to now, we have made no assumption on the strength of selection. However, if we further assume that selection is weak, we can use a quasi-equilibrium argument to simplify the dynamics of mean traits. In this section, we show that this allows us to recover previous expressions obtained by standard invasion analysis techniques [12] and to make long-term predictions on evolutionarily stable (ES) virulence.

We first consider equation (3.1). Assuming low mutation rates, we can drop the mutation bias term. If we further assume that selection is weak (i.e. the variance in the population is small), we can rewrite equation (3.1) as

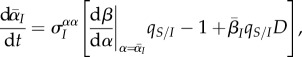4.1

where 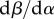is the trade-off between transmission and virulence, and D is the difference between local and global virulence, scaled by the global variance. In the electronic supplementary material, we show that the variable D is a fast variable, in the sense that, under weak selection, D changes on a fast timescale compared with 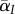. We can, therefore, use a quasi-equilibrium assumption to compute the value of D.

(a). SIS model

In the electronic supplementary material, we show that, in the limit of large host fecundity, the change in mean virulence under weak selection is given by

4.2

4.3

is the selection gradient in the well-mixed population. Equation (4.2) reveals that potential evolutionary endpoints are given by 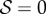. We, therefore, recover the marginal value theorem and the result that selection will tend to maximize the 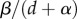ratio. The only effect of spatial structure is to slow down the convergence to the ESS. Equation (4.2) shows that the intensity of selection is decreased at a rate proportional to the relatedness measure ρ, which is now calculated in a neutral population at equilibrium. Hence, using our formalism, we can recover the exact expression for the selection gradient derived in [12,34] using standard invasion analysis techniques.

(b). oSI model

In the electronic supplementary material, we further show that, when host fecundity is finite, the change in mean virulence can be written under weak selection as

4.4

where

4.5

Both and are positive functions of genetic and epidemiological structure (see the electronic supplementary material).

Equation (4.4) has the same form and interpretation as equation (4.2), but the expression of 𝒮 shows that host demography causes a deviation from the marginal value theorem, which is quantified by the factor 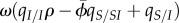. Because ω is proportional to the local density 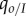, it vanishes in the limit of high host fecundity, and we recover the result of the SIS model. However, when ω is non-zero, equation (4.4) shows that the ES virulence will no longer coincide with the prediction of non-spatial theory. In particular, under a concave-down trade-off between transmission and virulence, we recover the result of Lion & Boots [12] that ES virulence will be lower than predicted by non-spatial theory if genetic relatedness, measured by 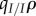, is greater than a threshold solely determined by epidemiological structure ().

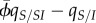5. Discussion

We present a novel theoretical framework to study the evolutionary epidemiology of spatially structured host–parasite interactions. This framework allows us to study both the short-term and the long-term evolution of parasite life-history traits. Using a specific biological scenario, we show that, even when spatial structure has little effect on the long-term dynamics, it can have important effects on the transient evolutionary dynamics during an epidemic. First, epidemiological dynamics is slower when infections are local because of the lower availability of susceptible hosts. Second, transient evolutionary dynamics are affected by the interplay between spatial structuring and epidemiological feedbacks. The transient increase of the virulent and more transmissible strain during the epidemic has a lower amplitude but a longer duration in the spatially structured habitat. Our analysis shows that a key driver of this dynamics is the build-up of a spatial differentiation during the initial phase of the epidemic: virulence tends to be higher among infected hosts with a higher density of susceptible neighbours. In an expanding epidemic this leads to phenotypic differentiation between the front and the rear of the epidemic.

Our approach is an extension of the evolutionary epidemiology framework introduced in [26,35,36], which bridges the gap between quantitative genetics and epidemiology. This theoretical framework provides a way of tracking the transient dynamics of the mean life-history traits in the population as a function of epidemiological densities and genetic covariances between traits. When infections are long-range, the change in mean trait depends only on the genetic (co)variance matrix between traits, on the density of susceptible hosts and on the effect of mutation [26,36]. Our analysis shows that spatial structure has two main consequences. First, the relevant genetic (co)variance matrix depends on the dispersal kernel of parasites. If infections are local, we need to consider both global and local covariances between traits. Similarly, the selective effect of transmission is weighted by the local density of susceptible hosts, , rather than the global density 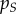. Second, spatial structure introduces a new selective force that is proportional to the phenotypic differentiation, , which measures the difference between global and local mean traits. Recent theoretical studies have also highlighted the build-up of spatial patterns of phenotypic variation during epidemics [18–20]. In particular, Osnas et al. [19] present a Price equation formulation of their result that is very similar to our description of pathogen evolution (cf. equation (3.1) with their eqn (4.2)). Indeed, it is interesting to note that spatial differentiation is akin to the effect of migration in the multi-habitat version of the Price equation discussed in [19,26]. This term also takes the form of a difference in the mean trait values in each habitat. In our model, however, the ‘habitats’ are emergent properties of the dynamics, rather than extrinsic properties of the environment. However, none of these earlier theoretical studies explicitly track the dynamics of differentiation. By contrast, our analytical framework allows us to tease apart the forces driving the build-up of this differentiation. In a similar way, in multi-locus models of pathogen evolution the indirect effect of linkage disequilibrium on selection is a consequence of the non-random distribution of genetic variability between loci [37]. In other words, the genetic covariance between loci is analogous to the spatial differentiation between habitats. All these structured models highlight the importance of the distribution of phenotypic variation across different units of population structure to understand the evolution of average phenotypic traits.

We show that the dynamics of phenotypic differentiation (i.e. ) depends on generalized coefficients of relatedness (the ρ and 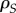coefficients) and on selection (through the covariance terms). Starting from an initial random configuration, a difference between local and global mean virulence builds up as a result of the availability of susceptible hosts in an expanding epidemic (measured as 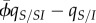). Genetic structure tends to reduce both the transmission benefit (because competition for susceptible hosts tends to take place between related parasites) and the cost of virulence (because death creates new opportunities for the transmission of related parasites). Because the scales of these processes are different, different relatedness coefficients are needed to quantify the effect of genetic structure.

In our model, under the simplifying assumptions of low mutation rates and weak selection, we use a quasi-equilibrium approximation of spatial differentiation. This quasi-equilibrium captures the influence of kin competition between parasites and allows us to recover previous long-term predictions derived from classical invasion analyses [7,12,14]. When host population size is fixed, relatedness erodes the transmission benefit and the cost of virulence with equal weight. As a result, only the rate of evolution is affected by relatedness and the ES virulence is the same as in the non-spatial model [12,34]. By contrast, when host population size depends on host fecundity, we recover the analytical expression for the selection gradient of [12] and show that the predicted ES virulence will, in general, deviate from the non-spatial prediction. We show in the electronic supplementary material that this requires us to track two measures of spatial differentiation, and . Hence, extending our approach to even more complex life cycles (e.g. with recovered or vaccinated hosts) is feasible, provided we track the dynamics of other measures of phenotypic differentiation between different types of pairs of sites. Such extensions of our method would also allow us to take into account more realistic biological scenarios, such as age, class or environmental heterogeneity (e.g. vaccination, see [36,38]).

Because it allows us to shed light on the effect of genetic structure, our approach differs from previous works based on partial differential equations [18–20,39]. Indeed, models based on partial differential equations assume implicitly that local population sizes are very large. As a result, there is no local drift and relatedness coefficients tend to zero. These models thus neglect the impact of kin competition. By contrast, our framework considers finite local population sizes and, therefore, allows us to take into account genetic structure in the population through generalized coefficients of relatedness. On the other hand, a major advantage of reaction–diffusion models over our theoretical framework is that they allow the computation of the speed of the invasion wave [20]. Although attempts have been made to compute invasion speed using spatial moment equations (e.g. [40]), a systematic method to handle this in multi-strain epidemics on networks remains to be developed.

A limitation of our approach is that the dynamics of the first moments of the distribution of traits depends on other moments that need to be computed over the distribution of strains in various spatial configurations. As typical of spatially extended systems, we are faced with an infinite hierarchy of moments, and these equations do not form a closed system. Nevertheless, we show that these equations can be used to understand the results of simulations of the spatial stochastic process of which they represent the expected trajectory. For instance, equation (3.1) is an exact description of the dynamics of mean virulence. However, it depends on the dynamics of spatial differentiation described by equations (3.2a–d), which is an approximation of the full dynamics obtained by neglecting some higher-order terms (as in the standard pair approximation [28,30]). However, equations (3.1) and (3.2a–d) can be used to gain analytical insight without exactly solving the dynamical system.

Throughout this study, we assumed that each site is connected to a constant number of sites. However, empirical contact networks for infectious diseases are typically characterized by variation in the number of contacts per host [41,42]. Theoretical studies have shown that the existence of ‘superspreaders’ could have important consequences on the evolution and epidemiology of infectious diseases [10,42,43]. Although the definition of an invasion front on such contact networks is not as straightforward as on a lattice, it is still possible to measure the phenotypic differentiation between virulence in hosts that have a susceptible contact and mean virulence in the population as a whole. Furthermore, wave-like propagation fronts can be obtained on complex heterogeneous networks by replacing geographical distance by a measure of effective distance [44]. A tentative prediction from the current study would be that, during an epidemic, virulence in the most recently infected individuals would tend to be higher than the mean virulence.

Other realistic features of infectious diseases have also been shown to interplay in non-trivial ways with pathogen evolution in spatially structured populations. First, although theoretical studies typically assume that disease events are exponentially distributed, the introduction of a constant duration of infection leads to selection for maximal outbreak frequency [45,46] Second, empirical data show a diversity of parasite disersal kernels [47,48]. Little is currently known on how these different dispersal distributions affect the evolution of pathogen traits. Although we focus on two extreme cases of parasite dispersal (global versus local dispersal), a potential extension of our framework would be to consider more realistic dispersal kernels combining local and global-dispersal events (see, e.g. [7,12,14] for a review) or even study the joint evolution of dispersal with other pathogen life-history traits (e.g. [19]).

A major aim of evolutionary epidemiology theory is to make short-term predictions in a realistic spatially structured environment [5]. The current framework helps identify quantitative variables required to generate such predictions. In particular, the present study highlights the importance of phenotypic differentiation. It is interesting to note that several empirical studies in different pathosystems support the existence of similar patterns of phenotypic variation in spreading epidemics. For instance, Mondet et al. [25] observed that the virus affecting honeybee colonies in New Zealand are often more virulent at the front of the spreading epidemic. Similarly, Phillips & Puschendorf [24] discuss some evidence that Batrachochytrium dendrobatidis (Bd), a pathogenic fungus known to be a major driver of the recent decline of many amphibian populations around the world, may also induce more virulence at the front line of the epidemics. Empirical studies measuring phenotypic differentiation across space in spreading epidemics remain, however, very limited. We believe the accumulation of data on the spatial distribution of genetic and phenotypic variation of pathogens is key to provide the information needed to generate accurate predictions on the epidemiology and evolution of infectious diseases. In this respect, we hope our work will guide future experimental and empirical studies on the evolution of pathogens in spatially structured environments.

Authors' contributions

S.G. and S.L. designed the study, analysed the model and wrote the manuscript. S.L. performed the simulations.

Competing interests

We have no competing interests.

Funding

We received no funding for this study.