The evolution of recombination rates in finite populations during ecological speciation

Abstract

Recombination can impede ecological speciation with gene flow by mixing locally adapted genotypes with maladapted migrant genotypes from a divergent population. In such a scenario, suppression of recombination can be selectively favoured. However, in finite populations evolving under the influence of random genetic drift, recombination can also facilitate adaptation by reducing Hill–Robertson interference between loci under selection. In this case, increased recombination rates can be favoured. Although these two major effects on recombination have been studied individually, their joint effect on ecological speciation with gene flow remains unexplored. Using a mathematical model, we investigated the evolution of recombination rates in two finite populations that exchange migrants while adapting to contrasting environments. Our results indicate a two-step dynamic where increased recombination is first favoured (in response to the Hill–Robertson effect), and then disfavoured, as the cost of recombining locally with maladapted migrant genotypes increases over time (the maladaptive gene flow effect). In larger populations, a stronger initial benefit for recombination was observed, whereas high migration rates intensify the long-term cost of recombination. These dynamics may have important implications for our understanding of the conditions that facilitate incipient speciation with gene flow and the evolution of recombination in finite populations.

1. Introduction

Ecological speciation is the evolution of reproductive isolation between populations adapting to contrasting environments [1–5]. Gene flow is a major impediment to this as it allows maladapted migrant alleles to infiltrate the local population [5–8]. A major factor determining the extent to which migrant alleles penetrate a population is recombination [9–11]. During ecological speciation with gene flow co-adapted gene complexes break down in recombined hybrids, resulting in chromosomes comprised of both adaptive and maladaptive alleles. Natural selection is not able to efficiently remove these maladaptive alleles because they are ‘hidden’ between adaptive alleles on the chromosome. As a result, alleles conferring local adaptation are expected to accumulate in regions of reduced recombination, such as population-specific chromosomal inversions [12–15].

The presence of maladaptive gene flow between populations is predicted to favour the suppression of recombination within populations (reviewed in [16]). Mathematical models aimed at understanding the evolution of sex demonstrate that a modifier allele reducing the recombination rate between selected loci (the modifier approach [17]) is generally favoured in the presence of maladaptive gene flow [18–20]. This can be interpreted as a mechanism of reinforcement [7,16] because reduced recombination rates will promote the genetic clustering of diverging populations. Similarly, models investigating the origin of species have shown that inversions that capture locally beneficial alleles should also be favoured by natural selection and thus spread within a population [14,21].

Empirical support for these theoretical predictions has only recently accumulated. For example, two host races of the North American apple maggot (Rhagoletis pomonella) diverged following the spread of a chromosomal inversion due to natural selection in one host race [22,23]. Additional evidence comes from the Drosophila genus where closely related sympatric species are more often genetically separated by inversions than their allopatric relatives [24]. More broadly, chromosomal inversions have been implicated in many cases of divergence with gene flow, including sunflowers [25], monkeyflowers [26] and wild rabbits [27]. The capturing of adaptive loci in genomic regions of reduced recombination may be one mechanism that triggers the speciation process [12]. Overall, both theoretical and empirical data indicate that recombination antagonizes speciation, and that there is selection for mechanisms suppressing recombination in the presence of maladaptive gene flow that facilitate both the origin and maintenance of species.

Nevertheless, mechanisms increasing the rate of recombination can also be favoured in local populations adapting to new environments, as a consequence of Hill–Robertson interference [28,29]. This causes selection at one locus to reduce the efficacy of natural selection at another linked locus. This interference relies on stochastic processes (drift and mutation) operating in finite populations and hence is absent in idealized, infinitely large populations [28,29]. Linked modifier alleles that increase recombination between the selected loci will reduce Hill–Robertson interference and can spread through genetic hitchhiking [30–35]. A number of evolution experiments have demonstrated an advantage for sexual reproduction in adapting populations implicating variants of the Hill–Robertson effect as a cause [36–40], but definite evidence is still lacking.

Recombination thus would appear to have contrasting effects during ecological speciation with gene flow: on the one hand, recombination reduces Hill–Robertson interference and may therefore accelerate local adaptation, but on the other hand, recombination homogenizes diverging populations and thereby reduces local adaptation. As a consequence, modifier alleles that increase recombination rates can be favoured during local adaptation because of the Hill–Robertson effect [30–35], but disfavoured because of the maladaptive gene flow effect [18–20]. However, to date these two effects have only been investigated in isolation. A better understanding of the relative contribution and timing of these mechanisms when operating jointly may afford new insights into how recombination rate evolution can affect the early stages of ecological speciation with gene flow [16].

Here, we investigate a mathematical model of two finite populations exchanging migrants while adapting to two contrasting environments. We are interested in the spread of modifier alleles that affect the recombination rate between the loci under direct selection. Specifically, we ask whether the Hill–Robertson effect prevents the evolution of recombination suppression during the early stages of ecological speciation with gene flow. As expected, our model shows that migration selects for reduced recombination whereas finite population sizes can produce selection for increased recombination. However, these two effects operate at different times: selection for recombination through the Hill–Robertson effect is pronounced during the early phase of adaptation, whereas selection against recombination through the maladaptive gene flow effect predominates once the two populations have diverged. Our results suggest that depending on the migration rate and size of the populations, recombination rate evolution may affect both the early and late stages of ecological speciation.

2. Material and methods

(a). The genetic setting

We consider two populations of haploid organisms experiencing contrasting selection pressures while still connected by migration. Within a population, individuals have two biallelic loci (A and B), with a different allele favoured in each environment (A and B in population 1, a and b in population 2). In addition, a biallelic modifier locus M alters the recombination rate between A and B, without being directly affected by selection [17,20,41]. The loci are arranged in the order MAB. The resulting genotype frequencies (p_i and q_i in populations 1 and 2, where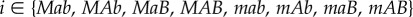) were predicted each generation through a series of five recursion equations corresponding to migration, selection, mutation, recombination and random genetic drift. All parameters and variables of the model are summarized in table 1.

Table 1.

The notation of parameters and variables used in this model. Unless otherwise stated all parameters apply to the A and B locus.

parameter	description	standard values
m	migration rate	0.01
s	selection coefficient	0.05
μ	mutation rate	1 × 10−5
rM	recombination rate determined by M allele	0.0005
rm	recombination rate determined by m allele	0.005
ρ	recombination rate between M and A locus	0
N	population size	100 000

variable	description
pi	genotype frequencies in population 1a
qi	genotype frequencies in population 2a

^aThe subscript i takes values .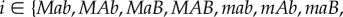

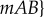(b). Migration, selection and mutation steps

The migration step follows the classic two-island model where each generation a fraction m of individuals are replaced by migrants from the other equally sized population

2.1a

and

2.1b

After migrating, the genotype frequencies are selected in the local environment according to their fitness values (w_i) in the respective population

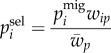2.2a

and

2.2b

Here, the average population fitness is 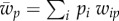in population 1, and 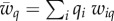in population 2. For fitness values, we assume that beneficial alleles confer a fitness of 1 + s relative to a fitness of 1 in genotypes with the other allele, where s is the selection coefficient in both populations. The genotype fitness is calculated by multiplying the values of its composite alleles (i.e. we assume that there is no epistasis).

The mutation step is a two-locus extension of the single-locus reversible mutation model. We assume that the loci A and B mutate at the same rate μ. Furthermore, to eliminate any effects not attributable to recombination, the modifier locus is assumed not to mutate. Thus, the genotype frequencies after mutation are

2.3a

and

2.3b

Here, the subscripts 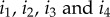refer to different genotypes; with i₁ being the focal genotype, i₄ the genotype that differs at both the A and B loci, and i₂ and i₃ being the genotypes one mutation step away at the A or B locus. For example, when i = MAB, we have .

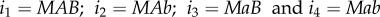(c). Recombination step

The effects of recombination were calculated each generation according to a mating table of the outcomes of all possible crosses, assuming there is random mating between all genotypes. Three different recombination rates are required to cover every potential cross: r_M, r_m and ρ. The parameters r_M and r_m determine recombination rates between the A and B locus, depending on the allelic state at the M locus. Recombination takes place during a brief period of diploidy immediately following syngamy. We assume additive effects of the M and m alleles so that for example, the recombination rate in Mm heterozygotes is equal to r_M + r_m. ρ is the recombination rate between M and A.

Recombination is incorporated into the model through an 8 × 8 × 8 tensor T, whose elements T_jki give the fraction of offspring i that are generated from a cross between parents j and k (see [17] for a full derivation of a similar tensor). The genotype frequencies after recombination were then calculated by the sum of all possible parental genotype frequencies multiplied by their corresponding element in the tensor

2.4a

and

2.4b

(d). Random genetic drift

Random genetic drift was incorporated into the model by randomly sampling variants from a multinomial distribution. Specifically, we assume that the genotype abundances after drift follow a multinomial distribution with parameters (genotype frequencies before drift, corresponding to probabilities of drawing these genotypes from an infinitely large pool of juveniles), and population size N (number of samples drawn). These genotype abundances are then normalized by N to yield the genotype frequencies after drift. Removing this drift step from the model allowed us to compare our full model with a deterministic model that does not involve the Hill–Robertson effect (as studied in [18,20]).

(e). Computation and analysis

Recursion equations were solved numerically using the Mathematica 10 software package (Wolfram Research, Inc., Champaign, Illinois, USA). All simulations started with both modifier alleles in equal frequency and with the a and b alleles fixed in both populations (i.e. 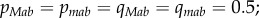all other frequencies are equal to zero). This corresponds to a situation where population 2 is already fully adapted and a new habitat is colonized by population 1. Moreover, equal modifier allele frequencies correspond to standing genetic variation in recombination rates, a situation frequently reported in natural populations [42–45]. Simulations were run for 10 000 generations with 2000 replicate runs. Throughout, only results for population 1 are presented, as population 2 was treated as an ancestral gene pool.

3. Results

To put our work into context, we first briefly summarize previously derived analytical results for two infinitely large populations connected by migration and subject to divergent selection at two loci. Pylkov et al. [18] provided approximations for both the equilibrium allele frequencies and linkage disequilibrium (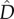) under the resulting migration–selection balance. Using our notation and ignoring mutation, those approximations read

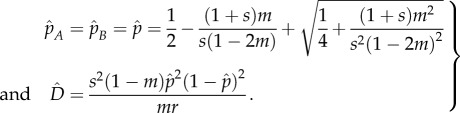3.1

Note that 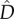will always be positive, meaning there will be disproportionately many extreme genotypes (AB and ab) relative to intermediate ones (aB and Ab). Moreover, is inversely proportional to r and is maximized at intermediate values of m. This is because with higher migration rates the allele frequencies in the two populations become increasingly similar. These approximations assume loose linkage between the loci and hence are in reasonable agreement with our simulation results, only for high recombination rates (not shown). We were able to derive an exact solution for the migration–selection balance accounting for arbitrary linkage, but the resulting formulae are long and uninformative and therefore not given here (Mathematica notebook available upon request).

Both Pylkov et al. [18] and Lenormand & Otto [20] also derived an approximation for the strength of selection acting on a rare modifier allele m that increases recombination, entering a population at migration–selection balance. Again using our notation, this approximation can be expressed as

3.2

As both 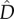and the other two factors in this equation are positive there is always selection against a modifier increasing recombination rates, and the strength of this selection is directly proportional to . We will now explore how the ‘maladaptive gene flow effect’ quantified by these approximations interacts with the Hill–Robertson effect in our full, stochastic model.

We first performed simulations of our model for fixed recombination rates (no modifier). These simulations provided evidence for both the Hill–Robertson effect and the maladaptive gene flow effect (figure 1). In particular, using our standard set of parameters (table 1), we observed a faster spread of the optimal AB genotype with recombination; as predicted by the Hill–Robertson effect, this was only seen in finite populations. However, recombination also led to a lower equilibrium frequency of the AB genotype, as predicted by the maladaptive gene flow effect (figure 1). A stronger maladaptive gene flow effect occurred when either the migration rate was increased or the strength of selection was decreased (electronic supplementary material, figure S1b,c). By contrast, altering the mutation rate (electronic supplementary material, figure S1d) or the population size (electronic supplementary material, figure S1e,f) only affected the speed of adaptation and the magnitude of the Hill–Robertson effect.

Figure 1.

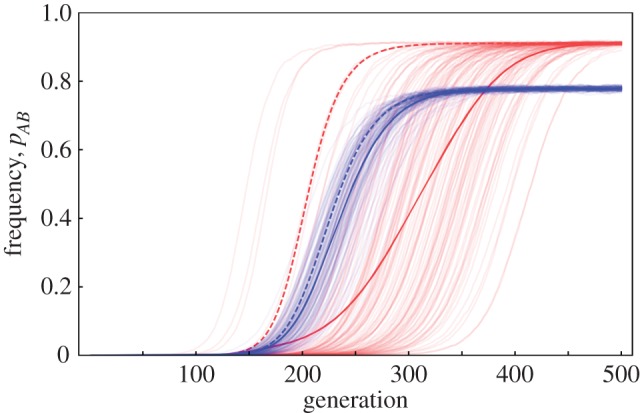
Change in the frequency of the fittest genotype AB in the presence and absence of recombination. Starting from the standard conditions (table 1), the genotype frequency of AB was tracked for 500 generations. The red lines represent simulations without recombination (r = 0), and the blue lines simulations with r = 0.1. The dashed lines are the deterministic model results (N = ∞). The faded lines are 2000 individual simulation runs with the solid line being the mean of all runs. See electronic supplementary material, figure S1 for similar dynamics with different parameters.

We next investigated the full model including the modifier locus. Based on our initial simulations, we expected both selection for and against the M allele which reduces recombination. Indeed, simulations with our standard parameter set demonstrated that on average, the frequency of M declined initially, but then rose almost to fixation in the long term (electronic supplementary material, figure S2). To investigate the generality of this effect, we performed extensive simulations varying all six parameters of our model. The dynamics of each simulation were summarized by focusing on the range of the frequency of M for each set of parameters (figure 2). Increases to the population size N led to a more pronounced reduction in the minimum frequency of M, indicating that selection for recombination through the Hill–Robertson effect becomes stronger for N up to 10⁶ (figure 2a). On the other hand, the maximum frequency of M also increased with increasing N, reflecting more efficient selection for M through the maladaptive gene flow effect. We also observed that the Hill–Robertson effect was most notable when the migration rate was low and the selection pressure was strong, corresponding to the lowest frequencies of M (figure 2b,c).

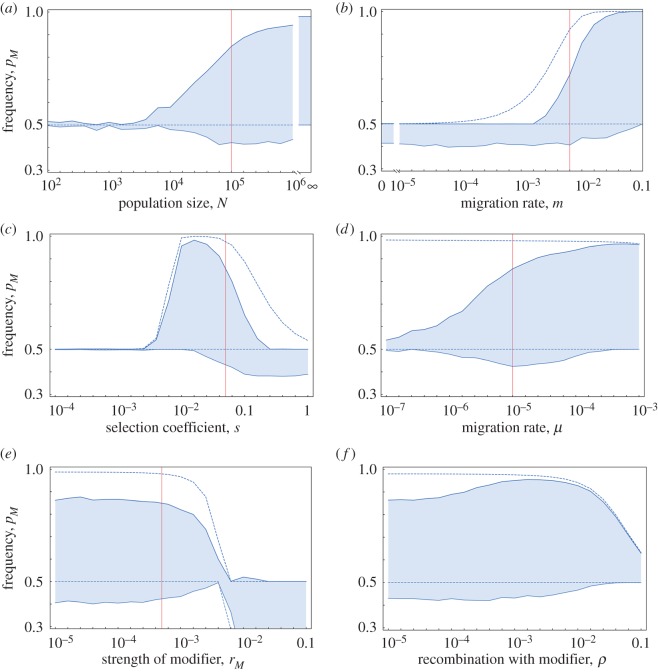
Figure 2.

The range of the modifier frequency of the M allele for different parameters. Each panel shows the maximum and minimum frequency of the modifier through time, averaged across 2000 replicate simulations (solid lines; shading represents the range). In each panel (except panel (a)), the deterministic results from simulations that run without genetic drift (N = ∞) are shown as dashed lines. The vertical lines are the standard values for the focal parameter (table 1); note that because of the logarithmic scale, the standard value of ρ = 0 could not be indicated in panel (f). (Online version in colour.)

The maladaptive gene flow effect was maximized at high migration rates, as recombination needs to be suppressed to prevent the populations rapidly homogenizing (figure 2b). Intriguingly, the maladaptive gene flow effect was maximized under intermediately strong selection, as weaker selection permits maladaptive alleles to persist in the population with little impact on the recombination modifier, while stronger selection would rapidly sweep maladaptive genes out of the population limiting the opportunities for recombining them onto resident backgrounds (i.e. pre-zygotic extrinsic reproductive isolation [3]).

The Hill–Robertson effect was maximized at intermediate mutation rates, as shown by the minimum frequency of M (figure 2d). This is because either mutations arise too rarely in the population to segregate simultaneously, or mutations arise too frequently rapidly producing double mutants and never creating linkage disequilibrium. By contrast, the maximum frequency of M increased with mutation rate (figure 2d), presumably because the migration–selection balance was reached more rapidly. The degree to which the M allele reduced recombination only had minor effects on the range of frequencies (figure 2e; values of r_M < r_m). When r_M > r_m, M enhanced recombination compared to m, leading to a reversal of selection through the Hill–Robertson and maladaptive gene flow effects. However, in line with Barton [46], selection for increased recombination became much weaker when the recombination rate was initially high (see right-hand side of figure 2e). Finally, as the genetic distance increased between the M and A locus (ρ), indirect selection on the modifier through both the Hill–Robertson and the maladaptive gene flow effect was weakened ([20,35] figure 2f; see also [46]).

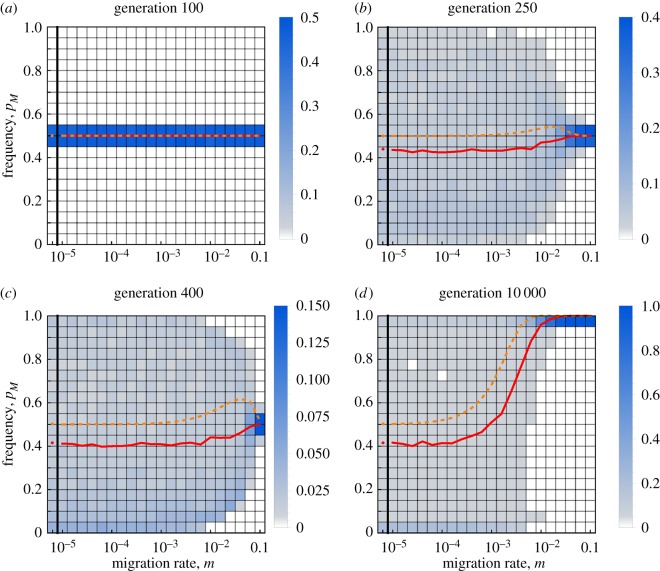
Although the range of the frequency of the M allele is informative about the relative strength of the Hill–Robertson and the maladaptive gene flow effect, it tells us nothing about the relative timing of these two effects. Therefore, we investigated the frequency of M at four explanatory time points over a range of values for the migration rate and population size (figure 3; electronic supplementary material, figure S3). Starting from equal frequencies, the first 100 generations were governed by random genetic drift (figure 3a), with reduced variance in the frequency of M in larger populations (electronic supplementary material, figure S3a). The variance in this frequency expanded by the 250th generation (roughly around the time when the AB genotype arose, which varies between simulation runs). This time also corresponded to the earliest evidence for a Hill–Robertson effect, except in the presence of frequent gene flow (figure 3b). The Hill–Robertson effect became strongest roughly by the time the AB genotype reached equilibrium (figure 3c). Once at equilibrium, selection for recombination suppression through the maladaptive gene flow effect became dominant, resulting in an increased frequency of M with stronger migration rates (figure 3d).

Figure 3.

Distribution of the frequency of a modifier allele M reducing recombination over a range of migration values at four time points. The charts show the frequencies of the modifier p_M at four different time points that describe the evolution of recombination. The y-axis of each chart is split up into 20 equally sized bins (horizontal lines) covering all frequencies from 0 to 1, in increments of 0.05. The shading of each cell indicates the fraction of runs, out of 2000 replicates, that the modifier frequency was in that bin at any given migration rate (see legend). The left-most value for migration rate (left of the thick vertical line) represents m = 0. The solid red line shows the mean of all replicates for a given migration rate, and the dashed orange line indicates the result of the deterministic simulation (N = ∞).

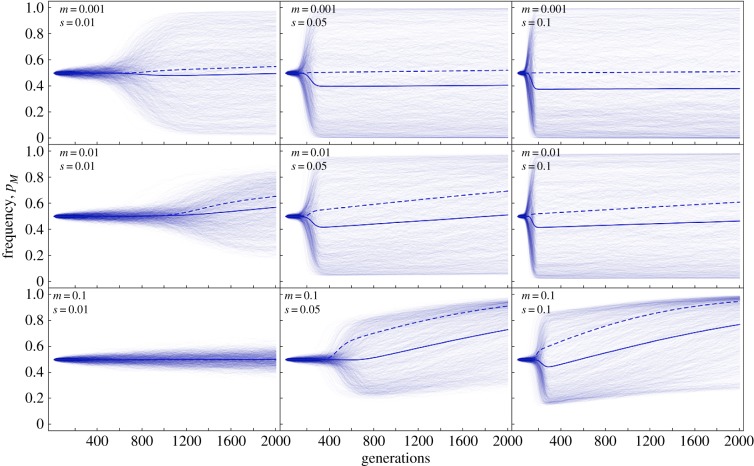
To explore the combined effects of two key parameters of our model, the migration rate and selection coefficient, we performed additional simulations for nine combinations of these parameters (figure 4). These simulations clearly show the limits of the maladaptive gene flow effect, as the rapid suppression of recombination only evolved when both m and s were high. This is because when m was high but s was not, allele frequencies in the two populations became very similar and the populations were close to linkage equilibrium, reducing selection for recombination suppression (see also the discussion of equations (3.1) and (3.2)). Conversely, when m was low but s was high, the few maladaptive migrant alleles that entered a population were very efficiently purged so that again there was only little linkage disequilibrium and hence selection for recombination suppression. In combination, the maladaptive gene flow effect can therefore be strongest at intermediate migration rates or selection coefficients when the other parameter is kept fixed (compare plots in left column or plots in middle row in figure 4). By contrast, early selection for increased recombination through the Hill–Robertson effect became stronger with increasing selection, but was diminished with increasing migration rates because this produces an earlier and stronger maladaptive gene flow effect.

Figure 4.

Changes in the frequency of a modifier allele M reducing recombination depending on the strength of migration and selection. Simulations were run using three different migration rates (rows) and three different selection coefficients (columns); other parameters were maintained at standard conditions (table 1). The faded lines show 1000 replicate runs for each simulation, with the solid line showing the average and the dashed line the deterministic result (N = ∞). (Online version in colour.)

4. Discussion

It has long been recognized that recombination antagonizes adaptive divergence and speciation with gene flow [9–11]. This is because recombination homogenizes migrant and resident genotypes that have diverged by natural selection. Theoretical studies of speciation with gene flow have often found that natural selection favours the spread of suppressors of recombination (e.g. chromosomal inversions and modifier alleles; reviewed in [16]) due to maladaptive gene flow [14,15,18–21]. However, these studies have ignored the stochastic processes that operate in finite populations and that are known to produce selection for increased recombination via the Hill–Robertson effect [29–32,35,47]. Here, we have investigated the interplay between these two effects and demonstrated that the Hill–Robertson effect favours increased recombination between adaptive loci during the early stages of adaptive divergence, whereas the maladaptive gene flow effect leads to suppression of recombination after populations have diverged.

Our results caution against the view that suppressors of recombination will always spread in the presence of maladaptive gene flow. Although in our two-locus model selection for increased recombination is only transitory, the magnitude of the Hill–Robertson effect is expected to increase with a larger number of loci under selection [30,31,33,47]. We would also expect the duration of the Hill–Robertson effect to be extended relative to the maladaptive gene flow effect if there is ongoing selection acting on many loci. In addition, even after the population has reached a fitness peak, selection for increased recombination may continue as a consequence of the mutation–selection balance [33]. Finally, selection for the suppression of recombination can be opposed or even reversed if there is negative epistasis between the selected loci [20]. More generally, the evolution of supressed recombination during the early stages of ecological speciation with gene flow depends on a number of factors including not only genetic architecture (e.g. number of loci and epistatic interactions) and migration rate, but also mutation rate and population size. Whether or not the initial conditions that favour the evolution of reproductive isolation between locally adapted populations in the face of gene flow are common in nature remains an empirical problem.

The strength of the Hill–Robertson and the maladaptive gene flow effect as well as the timing of the transition between these effects was determined by the parameters we used. We selected our standard parameters so that both effects were observed, including complete linkage between the modifier locus and the loci under selection (as figure 2f indicates, this does not seem to be crucial though as long as linkage is reasonably tight). Relatively large populations and strong selection were required for increased recombination rates to evolve under the Hill–Robertson effect, whereas strong migration and selection were necessary for recombination suppression to evolve under the maladaptive gene flow effect. We expect that both of these conditions should be met in many systems. In particular, in hybrid zones between populations with large effective population size recombination suppression should evolve readily. For example, Helianthus sunflowers and Drosophila species that occur in sympatry are often separated by chromosomal inversions [24,25] and strong selection [48,49]. These taxa also frequently have N_e values above one million [48,50,51] and are experiencing, or have experienced, extensive gene flow [50,52,53]. Across other systems, regions of suppressed recombination also separate hybridizing species or locally adapted populations [54–56], but whether these regions evolved during speciation with gene flow or are ancestral genomic landscapes (e.g. [57]) remains to be determined (see [22] for a more detailed discussion).

If populations exposed to maladaptive gene flow can establish suppressed recombination, then it is possible that they might also continue to diverge, becoming new species. However, the specific conditions for continued divergence can be restrictive. For example, Flaxman et al. [58] found that recombination suppression aids speciation when selection is weak but migration is high, presumably because selection effects acting upon each locus are extended to larger regions of the genome [59]. In our model, the recombination rate itself evolves and the levels of migration and selection that lead to its suppression appear to partially differ from those favouring divergence in these speciation models. For instance, under moderate selection and strong migration, the modifier of recombination did not spread. However, when s and m were both high and of similar magnitude, the modifiers of recombination spread easily (figure 4). This disjunction between models might suggest that cases of speciation with gene flow where migration is stronger than selection might be unlikely because the required recombination landscape is difficult to evolve in the first place. Conversely, cases of speciation with gene flow where selection is strong are likely to proceed without the suppression of recombination, although recombination suppression is nonetheless expected to evolve. We therefore speculate that the evolution of suppressed recombination might not be required in some cases, but nonetheless will be a signature of speciation with gene flow. This is because the most favourable conditions for speciation with gene flow are also the most favourable conditions for the spread of modifier alleles that suppress recombination (i.e. when selection is strong). Overall, cases of sympatric and parapatric speciation might require strong selection, and they will generally be characterized by coldspots of recombination.

A number of studies have also investigated the reduction of recombination by chromosomal inversions during speciation with gene flow [14,21,22,24,25,27]. For instance, Kirkpatrick & Barton [14] showed that a chromosomal inversion would spread when it captures loci under divergent selection, as an inversion will prevent hybridization with maladapted migrants. Such an inversion and the modifier model we used in this study are similar, except for one key difference: inversions only prevent recombination in heterokaryotypes. As a consequence, shuffling between resident and migrant alleles is prevented but shuffling of different resident alleles can still occur. Therefore, we would expect the extent to which the Hill–Robertson effect opposes the maladaptive gene flow effect to be reduced, making an inversion a powerful mechanism that simultaneously allows efficient local adaptation and limits maladaptive gene flow between populations during speciation with gene flow. In addition, populations separated by fixed chromosomal inversions might be able to diverge further during secondary contact even if gene flow was very high and selection was weak. As noted by Flaxman et al. [58], these are the conditions where recombination suppression has the greatest contribution to speciation driven by divergent natural selection.

In order to isolate the specific effects on recombination modifiers caused by gene flow as opposed to population size, we intentionally kept our model as simple as possible. Future models should consider a larger number of loci and integrate additional factors that are not part of our model. These could include different types of recombination modifiers (local versus global allelic modifiers and also chromosomal rearrangements), epistasis, diploidy and multiple populations with variable spatial selection and migration rates. It would also be interesting to construct models that explore the interplay between selection on recombination rates and other mechanisms of reinforcement such as selection for assortative mating or migration rate in response to maladaptive gene flow [7,16].

In conclusion, our model indicates that the dynamics of recombination rate evolution during adaptive divergence are governed not only by deterministic evolutionary forces such as selection and migration, but also by stochastic forces such as random genetic drift and mutation. Much of the theoretical literature on adaptive speciation with gene flow has overlooked the interplay between these forces, and consequently often saw recombination as a hindrance to adaptive divergence and speciation. The fact that the benefits of recombination in finite populations are well established within the research community studying the evolution of sex highlights the need of increased dialogue between these fields.

Authors' contribution

J.R. and J.E. created the model and ran simulations. All authors planned the study and wrote the manuscript. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

This research was supported by an Australian Research Council Discovery grant no. (DP140103774) to J.E. and D.O.-B.