Abstract
Theories for the evolution of sex rarely include facultatively sexual reproduction. Sexual harassment by males is an underappreciated factor: it should at first sight increase the relative advantage of asexual reproduction by increasing the cost of sex. However, if the same females can perform either sexual or asexual life cycles, then females trying to reproduce asexually may not escape harassment. If resisting male harassment is costly, it might be beneficial for a female to accept a mating and undertake a sexual life cycle rather than ‘insist’ on an asexual one. We investigate the effects of sexual harassment on the maintenance of sex under different population densities. Our model shows that resisting matings pays off at low population densities, which leads to the complete extinction of males, and thus to the evolution of completely asexual populations. Facultative sex persists in a narrow range of slightly higher densities. At high densities, selection favours giving up resisting male mating attempts and thus sexual reproduction takes over. These interactions between the outcomes of sexual conflict and population density suggest an explanation for the rarity of facultative sex and also patterns of geographical parthenogenesis, where marginal environments with potentially low densities are associated with asexuality.
Keywords: male harassment, female resistance, positive feedback, parthenogenesis, facultative sex, maintenance of sex
1. Background
Sex is considered paradoxical because of several known costs of sexual compared to asexual reproduction. These costs include time and energy spent while mating or finding a partner and—in those cases where sex implies a male–female polymorphism—the demographic costs of producing males [1]. Thus, everything else being equal, parthenogenetic females should outcompete sexual lineages because they avoid paying such costs.
Males can also have additional direct negative effects on female fitness, which adds to the twofold cost of producing males [2]. One example of such a negative effect is sexual harassment by males. Males of many species harass females to achieve copulation [3]. Females that try to resist such harassment suffer fecundity or survival costs in a wide range of systems [4–6]. For example, female guppies move to habitats of higher predation risk to avoid male harassment [7]. Density often plays a role: in high-density feral sheep populations, female mortality peaks in summer—despite high resource availability—due to male harassment [8]. In damselflies, Cordero [9] has shown that at high densities more matings were forced compared with low-density populations, and that at extreme population density harassment by males can hinder oviposition.
If switching to asexual reproduction is an option, harassment by males should at first sight increase its relative advantage, as the cost of sex is increased. However, this assumes that only sexual females suffer the costs of harassment. This is not necessarily the case [10], reflecting the general principle that any evaluation of the cost of sex should be specific regarding whether one is comparing the performance of asexual and sexual females within a single population, or growth rates of separate lineages [1]. If males harass females irrespective of their type and the competition of reproductive types occurs within a population, then parthenogenetic lineages might not manage to escape the costs of such male harassment. It has even been suggested that males should disproportionately target parthenogenetic females with their harassment to maintain sex in a ‘spiteful’ way [10], but see [11] for problems with this argument.
That male behaviour can have a strong effect on the likelihood of observing sexual reproduction becomes arguably more plausible in the case of facultative sex, where the same organism can perform either sexual or asexual life cycles [12]. Which one is employed at any given time can depend on environmental conditions, competition and also—interestingly for our topic—on the availability of males. It is increasingly understood that facultative sex is more than an oddity: rather, it is a fundamental feature of ‘early’ sex, i.e. that of microbial eukaryotes [13]. Facultative sex also occurs in multicellular organisms as diverse as Daphnia [14], aphids [15], Coleoptera [16], stick insects [17], rotifers [18], and many plants [19]. Theoretically, facultative sex appears to be a superior solution to either asexuality or obligate sex: it offers much of the genetic advantages of sexual reproduction (e.g. increasing genetic diversity, avoidance of clonal interference, purging deleterious mutations) with a dramatic reduction of the frequency with which costs have to be paid [20], see also [21].
Facultative sex, whenever it associates with a male–female polymorphism, has the interesting feature that male fitness improves if as many females as possible undergo sexual life cycles, but this is not necessarily the case for females [22]. This offers the possibility of an interesting demographic feedback because of three interacting factors. First, male harassment, if costly enough, might make it beneficial for a female to accept opting for a sexual life cycle over an asexual one (this is akin to the argument of ‘convenience polyandry’ [23], according to which females might accept costly multiple matings, if the costs of resisting would be higher still). Second, the fitness consequences depend on how often females encounter males. Third, asexual reproduction typically does not produce males. It is also clear that there is potential for the total population density to impact the outcome: in sparse populations, encounters between potential mates happen less often. Sexual conflict and asymmetric evolution of sexual harassment between sexual and parthenogenetic lineages have been considered previously [10,11], but there is limited theoretical work on this evolutionary process regarding the maintenance of sex.
Recent theoretical work has focused on the coevolution of male harassment and females' ability to resist it or its consequences. Kawatsu [24] has highlighted the possibility that parthenogens encounter males less often than sexual females. As a consequence, asexuals are hypothesized to suffer higher costs when they subsequently encounter males, because they lack as much coevolutionary experience with males as sexual females have in their evolutionary past [24]. This can prevent invasions by parthenogens and lead to separate distributions of sexual and parthenogenetic lineages [24]. Further work has refined these ideas with considerations where the same female can reproduce asexually or sexually depending on an interaction of her resistance and male coerciveness [22], including an exploration of the indirect sons' effect where females that resist males less, and consequently reproduce sexually more often, may benefit by producing more coercive (and thus more successful) males [25].
Our aim here is to extend previous theory by an explicit look at the role of population density. Feedbacks between population density and sexually antagonistic male–female interactions could play a role in explaining patterns of geographical parthenogenesis, i.e. the finding that the absence of males, as a derived trait, is often associated with marginal environments that are potentially of low population density [26]. In plants, this is often considered to support ideas of reproductive assurance when mate availability is low [27,28]. Here, we highlight the flipside of the coin: male encounters can be harmful, yet resisting them might only pay off sufficiently for females if mate encounters are not too frequent in the first place. If they are frequent, ‘mating for convenience’ becomes the favoured option, an argument similar to that of ‘convenience polyandry’, where females mate multiple times to avoid the costs of coercive behaviour by males [23]. The frequency of mate encounters depends not only on population density as a whole, but also on how often (other) females produce males, which in turn depends on the population-wide rates of sexual versus asexual reproduction.
This idea leads to an intriguing possibility of positive feedback in the following sense: in relatively sparse populations, females encounter males at a low rate and female resistance might be selectively favoured as it allows females to remain virgin for longer (a state in which parthenogenetic reproduction is possible, given a facultatively sexual species). Assuming that parthenogenesis produces female-only offspring, the effect of longer virginity is to reduce male densities relative to female densities in the next generation, which makes resisting females even more successful at avoiding males. Thus, from low enough initial population densities, such feedback might lead to the extinction of males and the population has become de facto asexual. By contrast, in denser populations resistance might not pay off to begin with, as the high male encounter rate makes it futile for females to resist; if non-resisting types then take over, the end result is a de facto sexually reproducing species as the time spent as a virgin remains very low.
2. Material and methods
(a). Model description
Our model considers a species in which females are, at least ancestrally, capable of both asexual and sexual reproduction. Virgins reproduce asexually, producing only female offspring. After mating, females reproduce sexually and produce male and female offspring at a 1 : 1 ratio. Males are assumed capable of forcing females to mate with them, but with their efficiency depending on female resistance. After a successful mating, a female reproduces sexually for the rest of her life. In the population, there are four types of individuals with haploid genetics. Females express a resistance allele such that r females never resist a male mating attempt, while R females are partially successful with their resistance attempts and are thus likely to remain asexual for longer. The strength of the resistance is denoted θ, such that resisting females only mate with every θth male on average (i.e. their mating rate is obtained by dividing the non-resisters' mating rate by θ). When θ = 1, R and r females behave in the same way. Values for θ < 1 are biologically not relevant and thus not considered in our model. Each male carries a copy of the r or the R allele but these are not expressed. The total density of the population, D, is the total number of males, M, plus the total number of females, F, in the population.
We consider discrete generations, but we model within-season dynamics in continuous time. Females and males continually enter the population while the season lasts; we thus do not model any seasonal fluctuations of females or males arriving or dying, which we justify by the fact that the availability of r versus R carrying males should not be seasonally dependent for females if these alleles are not expressed in males. Females' death rate needs to be explicitly modelled, however, as we need to contrast the lifespans of r and R females as well as quantify the proportion of it that is spent in a virgin state. We assume that females produce eggs at a continuous rate while alive. Each female may go through one transition from being unmated (a virgin) to being mated, and the rate at which the transition happens depends both on male density M (mate encounters per female occur at a rate that is proportional to the total density of males; we assume a proportionality constant of 1) and the female's strength of resistance behaviour θ (see the electronic supplementary material, table S1, for model parameters). For each generation, we derive the expected number of eggs produced by virgins and non-virgins and the genotypes of these eggs, which then determines the frequencies of r and R males and females in the next generation.
(b). Analytical calculations
To derive the number of eggs of each type produced, we first derive the expected lifespans as virgins and non-virgins for each type of female. Each female begins her life as a virgin, and this state can end either by mating or by death. As a null model for mate encounter rates one can take the ‘ideal gas approximation’ [29], according to which a density of F females and M males leads to FM mate encounters per time unit. Here, our scaling of densities and time units are chosen such that a density F = M = 1 will lead to one observed mate encounter per time unit. As this time unit is also the mean lifespan of a non-resisting female (see below), F = M = 1 is a density where females only meet on average one potential mate in a lifetime; most natural populations probably occur at higher densities, which we also consider.
Doubling the density of both males and females will, in the null model of ‘ideal gas’ type, lead to a twofold per capita rate for individuals of either sex, or a fourfold observed number of mate encounters in the population as a whole. There are also situations where the kinetics of encounters follows other exponents than suggested above; for example, if encounters take time to complete, then the per capita encounter rate grows less than linearly (also expressable as the total number of encounters growing subquadratically [30]). We model this with an exponent β, presenting results based on the null model (β = 1) in the main text and results for β≠1 in the electronic supplementary material.
We assume that resisting a male is costly, thus the mortality of resisting females is modelled as
whereas non-resisting females have a mortality of μr = 1 (as for these females θ is replaced by 1), which implies an expected lifespan of 1 unit of time. α is a parameter for the strength of the costs of resisting a male. Since 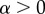 and
and 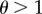 , resisting females are assumed to have shorter lifespans (below 1) than non-resisting females. The excess mortality term increases linearly with the number of mate encounters
, resisting females are assumed to have shorter lifespans (below 1) than non-resisting females. The excess mortality term increases linearly with the number of mate encounters 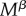 , as more frequent encounters imply that the female needs to activate her resistance behaviours more often.
, as more frequent encounters imply that the female needs to activate her resistance behaviours more often.
Our computations take advantage of the fact that if two events happen at a rate υ and μ and either can end the state that an individual finds itself in, then the expected time the individual spends in this state is 1/(υ + μ). Virginity can end by mating or death. The rate of mating is 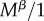 for r females, as they mate with every male they encounter, and
for r females, as they mate with every male they encounter, and 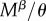 for R females. The expected time a resisting (R) female stays virgin, denoted
for R females. The expected time a resisting (R) female stays virgin, denoted 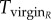 , is impacted by her mating rate
, is impacted by her mating rate 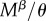 as well as her mortality
as well as her mortality 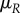 :
:
For non-resisting females, the equivalent expression is
The expected time spent as a non-virgin female is calculated as the probability that mating rather than death ends a female's virgin time (as dead virgins never contribute to non-virgin time), multiplied by the expected time alive after the first mating. Again, we take advantage of mathematical knowledge that if two event types ‘compete’ to end a state and they occur at rates υ and μ, then the probability of υ being the ending transition is υ/(υ + μ). Thus, the expected time after mating becomes
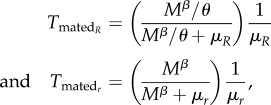 |
for the two female types. Note here, that the expected time females of either type spend in a certain state can be calculated, even if their frequency in the population is negligibly low.
(c). Population dynamics
We assume that egg production occurs at a constant rate, thus egg production per generation is proportional to the time females spend in each of these states. Note that sexual females of either genotype can produce r as well as R eggs, because the sire of their offspring may be of either genotype. During the times of virginity, however, each type of female produces only its own genotype.
With a given initial genotype frequency and an initial sex ratio, we can now calculate 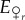 , the number of female eggs that are r in the next generation: these are all the eggs produced by r females while being virgin, half the offspring (i.e. all the females) from an r × r mating, a quarter of the offspring (half of all the females) from an r × R mating where the second letter denotes the male, and a quarter of the offspring from an R × r mating:
, the number of female eggs that are r in the next generation: these are all the eggs produced by r females while being virgin, half the offspring (i.e. all the females) from an r × r mating, a quarter of the offspring (half of all the females) from an r × R mating where the second letter denotes the male, and a quarter of the offspring from an R × r mating:
Here, ρ refers to the proportion of R males among the potential sires. As we assume no life history or behavioural differences between male genotypes, this proportion is simply
The same way the number of R female eggs produced can be calculated:
Males are only produced when the females have already mated. The number of male r eggs that are produced are calculated as the sum of r males produced by r females and r males that are produced by R females:
and similarly for the number of R male eggs that are produced:
When no males are present there are no changes in the composition of the population as r females can only produce r females, R females can only produce R females, and there are no lifespan differences between r and R females if there are no males harassing them.
The above equations complete the description of the within-generation dynamics. At the end of every generation, the equations above give the new genotype frequencies. We then normalize them to sum up to the assumed population density, D, which allows us to track the genetic changes under a variety of low- or high-density scenarios. To see how the dynamics change when population densities change, we tracked the within-generation dynamics starting with a given genotype frequency, for different population densities D. Simulations were initiated with half of the population being male, but the proportion quickly changes as a result of male production in the first generation.
3. Results
Although all populations in all generations are technically facultatively sexual, they can become functionally sexual (if the virginity period of females remains very short) or functionally asexual (if males go extinct). It is also possible that the population remains in a state where virgin females perform a significant fraction of reproduction, but not all of it. In principle, there are six possible outcomes: males and females of one type (either r or R) survive, only females of either type persist, females of both types coexist, or males and females of both types coexist. The realized outcome is dependent on the population density, the initial frequency of the resistant type, and the strength and the costs of resistance. We will first present results from isolated population densities that show the dynamics over several generations and then summarize the evolutionary stable outcomes over a density continuum. The code to produce the simulations is provided in the electronic supplementary material.
(a). At high or intermediate densities, males can exist with either acceptance or resistance behaviours having become fixed in females
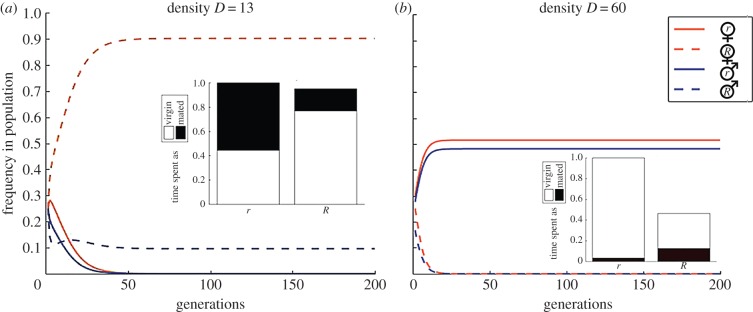
At high to intermediate population densities, the results are independent of the initial frequency of the resistant type in the population. At intermediate density, the resistant R genotype becomes fixed, and resistant males and females persist in the population (figure 1a). Here r goes extinct, because at these densities the male encounter rate is high enough that r females—who do not resist mating attempts—bear the demographic cost of producing males for a larger proportion of their lives (figure 1a). R females have higher mortality, but they spend more of their shorter lives in the virgin state, which as a whole can lead to a significant improvement in the number of daughters produced in a lifetime. As the benefits of reproducing asexually outweigh the lifespan cost of resisting mating attempts, R females outcompete r females. Although the r allele is driven to extinction, males are not. This is because R females also have some expected duration of sexual reproduction as long as resistance is not assumed to be perfect (our example uses θ = 5), thus a small proportion of R males are continually being produced. As a whole, facultative sex can persist indefinitely in populations of intermediate densities (figure 1a).
Figure 1.
The frequency of each type in the population over 200 generations at two densities (a) D = 13 and (b) D = 60. The embedded barplots show the expected lifespans of R and r females and the proportions that they spend in the virgin state at the given population densities at equilibrium. Other parameters: θ = 5, α = 0.01, β = 1, and the initial frequency of R is 0.5. (Online version in colour.)
When the population density is much higher, females of either type spend most of their lifetime reproducing sexually. R females cannot delay mating for long, but they also continually suffer the costs of attempting to resist, resulting in a significant shortening of their lifespan compared with r females (figure 1b). These fitness costs lead to the extinction of the R allele (figure 1b); the phenotypic outcome is that females no longer try to resist male mating attempts. When females reproduce mainly sexually (each female's initial period of virginity remains brief), the male densities become high, and this further shortens the virginity period. Given that we assume that females produce a 1 : 1 sex ratio after mating, we find that the sex ratio of a dense population that is monomorphic for the r allele evolves to be close to 1 (figure 1b). The stable evolutionary endpoints in figure 1 are independent of the initial genotype frequencies (the figures use an initial frequency of 0.5 for R).
(b). At intermediate or low densities, initial frequencies can matter
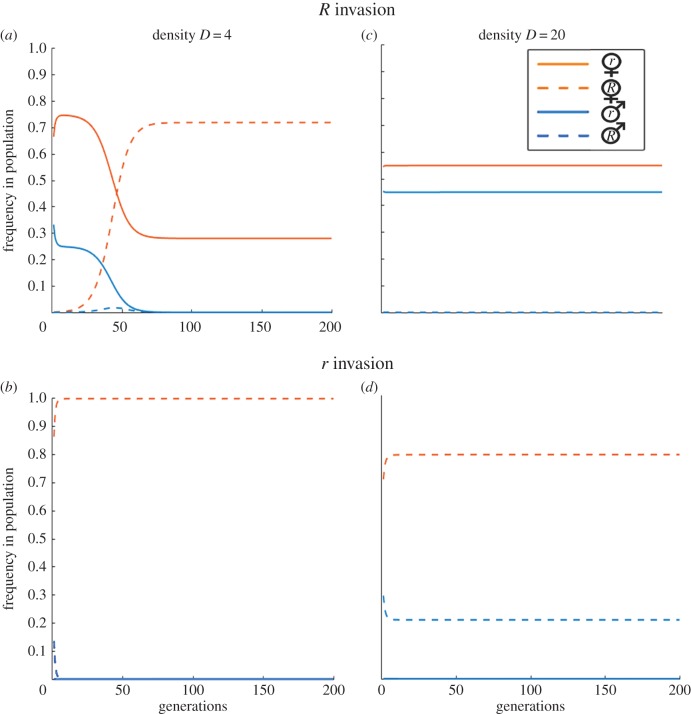
In between the cases of fixation of either r or R, as described above, there is a region of density values, where the initial frequency of R females determines the outcome. When the initial frequency of R is low (denoted ‘R invasion’), the dynamics lead to the persistence of r males and females and the R genotype goes extinct (figure 2c). Starting from a high initial frequency of R (denoted ‘r invasion’), however, leads to the opposite case where the invasion of r fails, and R males and females persist at equilibrium (figure 2d; see also the electronic supplementary material, figure S3).
Figure 2.
The impact of initial frequency on the evolution of resistance and the demographic consequences. The composition of the population is shown for 200 generations at densities D = 4 (a,b) and D = 20 (c,d), starting from an initial frequency of R of either 0.001 (a,c) or 0.999 (b,d). Other parameters: θ = 5, α = 0.01, β = 1. (Online version in colour.)
The initial frequency also influences the outcome at the low end of population densities. Low densities lead to low mate encounter rates, thus females of either type (r or R) remain virgin for most of their lifetime and consequently reproduce mostly asexually. Few males are produced, which again promotes asexual reproduction by prolonging the likely time a female spends in the virgin state; this is a quick demographic process that makes males go rapidly extinct. Once males are extinct, resistance has become a neutral trait as the absence of males means females never express their resistance alleles. In other words, genotypes r and R no longer impose mortality differences and both lead to completely asexual reproduction; they are subsequently only subject to genetic drift (which we do not model explicitly). In this process, the type of female that persists in the population—or whether there is coexistence subject to drift of both types—is dependent on the initial frequency of the R and r individuals (figure 2a,b).
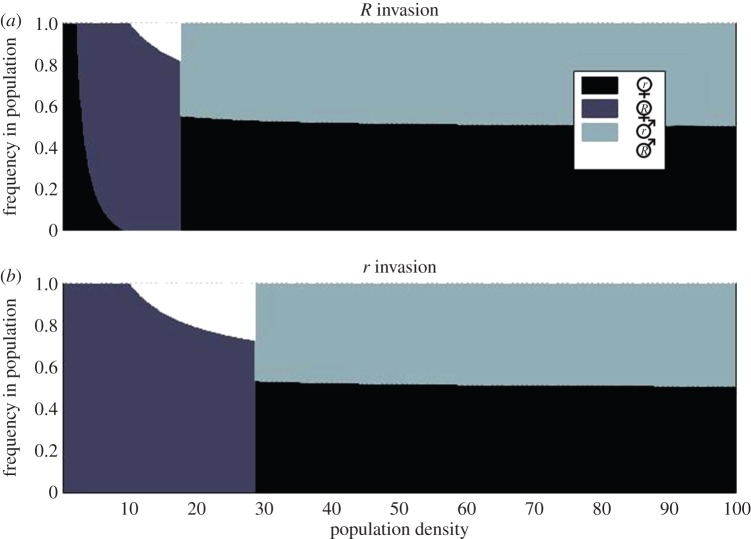
At a very low population density, a genotype's initial frequency is correlated with its frequency at the point where males have become extinct. But at a somewhat higher population density, the production of males persists as an outcome of relatively frequent successful mating attempts by males of the parental generation; this means R is continually selected for and can become fixed even from a very low starting frequency (figure 3a).
Figure 3.
The population composition as a function of population density at stable evolutionary endpoints, (a) for an initial frequency of R individuals of 0.001 and (b) for an initial frequency of R individuals of 0.999. Other parameters: θ = 5, α = 0.01, β = 1. (Online version in colour.)
(c). From no males to facultative sex to a de facto sexually reproducing population
The generality of the results above can be shown with a continuum of densities (figure 3). At very low densities, males go extinct and resistance becomes a neutral trait, with the outcome simply depending on the initial frequencies in the population (densities below 10 in figure 3). At somewhat higher densities (above 10 in our example), males can persist, which means that there is always a difference in how r and R females gain fitness. Females that mate bear the demographic costs of producing males. R females remain virgin for longer than r females, and thus avoid these costs for longer; but they also pay costs of resisting, the magnitude of which depends on the frequency of males in the population. If the total density remains low (and thus mate encounters remain relatively infrequent), resisting pays off and r disappears, but since resisting cannot make a female avoid all matings, males persist.
When R is fixed, male abundance increases with increasing population density, and this case (from density 10 onwards in figure 3) is the endpoint for a greater range of densities if resistance was initially common (figure 3b) than if it was initially rare (figure 3a). This outcome is eventually replaced by a de facto sexually reproducing population, with all females accepting sexual cycles as soon as they encounter males (r fixed), when densities are high enough (figure 3, right side of either panel). The higher the proportion of r individuals in the starting population, the lower is the density at which point the transition to a complete r population happens. At what density it pays for females to accept a sexual life cycle and from which density upwards males can exist, is also dependent on the strength of resistance θ and the costs of resistance α, but the qualitative pattern remains unchanged (i.e. high-density promotes sexual reproduction) for alternative values and random combinations of these parameters (see the electronic supplementary material, figures S1–S4).
Variations in other parameters, such as β (electronic supplementary material, figure S5), the initial frequency of the R allele (electronic supplementary material, figure S3), or the initial sex ratio (electronic supplementary material, figure S6), have only minor effects. Of these effects, the most interesting one is that when β is low, the density range that permits facultative sex becomes larger (electronic supplementary material, figure S5). Note that low β introduces a nonlinearity that makes both high and low densities ‘resemble’ intermediate densities in terms of the mate encounter rate. The biological interpretation is that all else being equal, prolonged mate encounters make facultative sex evolve more easily.
Once sexual reproduction is the norm, the sex ratio approaches 1 : 1 (right end of figure 3 and electronic supplementary material, figure S4); the sex ratio change with population density is nonlinear (figure 3 and electronic supplementary material, figure S4). Note that we predict mild deviations from 1 : 1 at the low density end of de facto sexuality, and these deviations disappear as we move to the right along the density axis. This occurs because our model still allows for virgins to reproduce for the short amount of time that they spend before their first mate encounter.
Our model can also be used to ask what happens if costs of resistance disappear. In this case, resistance pays off as soon as there are any males in the population. Thus, at low densities, non-resistant females can persist, but at densities that permit males to exist, resistance becomes fixed, also at high population densities. Males can also persist given that a finite θ does not prevent all matings (electronic supplementary material, figure S7).
We also asked what happens if matings do not involve sexual harassment (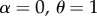 ). In this case, only the initial frequency determines which genotype persists. Male extinction in the main model occurs because of a positive feedback where scarcity of mate encounters leads to the low production of males, which further reduces mate encounter rates until no males are produced. While strong female resistance widens the range of densities where males go extinct, a narrow range of ‘self-extinguishing’ male demography (due to the same demographic feedback) persists even if there is no effective resistance by females (electronic supplementary material, figure S8).
). In this case, only the initial frequency determines which genotype persists. Male extinction in the main model occurs because of a positive feedback where scarcity of mate encounters leads to the low production of males, which further reduces mate encounter rates until no males are produced. While strong female resistance widens the range of densities where males go extinct, a narrow range of ‘self-extinguishing’ male demography (due to the same demographic feedback) persists even if there is no effective resistance by females (electronic supplementary material, figure S8).
4. Discussion
Our model investigates sexual conflict of a profound kind: males can only achieve reproductive success via mating, whereas females in principle have the option to reproduce without the aid of males. This leads to a conflict of interest between males and females, as for the latter, not mating is often desirable. The expected consequence is that it takes effort for females to resist male mating attempts, and here we show a rich set of dynamic outcomes that depend strongly on population density.
Whether or not females evolve to accept ‘mating for convenience’ can lead to the maintenance of facultative sex at intermediate densities, to complete asexuality at low densities, or to de facto sexuality at high densities. Our model thus extends the argument of ‘convenience polyandry’ [23,31] to a situation where the choice is not between mating once or multiple times, but between mating at all (once or multiple times) or reproducing parthenogenetically.
A high population density combined with male harassment leads to the promotion of sexual reproduction and thus the production of males, even when females can resist such harassment. At very low population densities, there is strong enough positive feedback between a female-biased adult sex ratio and the realized time each female spends as a virgin, that males become extinct (at a low enough population density this can happen even when females do not resist matings, see the electronic supplementary material, figure S8). Despite the potential for a sexual cycle to still exist, the observed population would thereafter only perform asexual cycles.
When switching to sex is costly, female resistance to mating can maintain parthenogenetic reproduction, as long as the costs of resistance are outweighed by the benefits of asexual reproduction [32]. In the Australian spiny leaf stick insects, for example, switching from asexual to sexual reproduction imposes fitness costs for the female [17]. Such costs of switching to sexual reproduction and the relatively low costs of resistance at low population densities can promote conditions that favour the evolution of parthenogenesis. Note that even though we do not predict that virgin parthenogenesis followed by sexual cycles of mated females should be a common finding (it becomes easily replaced by other options), the important assumption is that there is potential for life histories to be shaped by this option. This appears possible, e.g. in the form of tychoparthenogenesis, which is the rare hatching of unfertilized eggs in a wide range of normally sexual invertebrates [33].
At what densities accepting a mating becomes the favoured option from females depends on the strength and the costs of resistance and on the initial frequency of the resistant type in the population. This is a typical feature of models with positive feedback [34]: history matters, and in our case this principle manifests itself as phylogenetic inertia at low to intermediate population densities. It is difficult for an r population to invade one in which R is established (and vice versa). Future work could usefully investigate if this difficulty still persists if resistance was a continuous rather than a discrete trait (see below for further discussion of model limitations).
Sex in most organisms appears obligate, even though facultative sex appears to offer an adaptive solution that maintains most of the benefits while minimizing the costs. Our model suggests a partial solution to this puzzle: as long as males exist, it is in their interest to keep females sexual, and if they possess means to achieve this outcome, it may be too costly for females to resist. Our model therefore produces a large parameter region (at sufficient population densities) where sex predominates. We have not explicitly modelled any subsequent evolutionary phase where a functionally sexual population turns obligately sexual. However, it is conceivable that the ability to perform an asexual life cycle could be lost in high-density populations, if females rarely manage to express this option. Thus, obligate sex could have evolved from facultative sex as a consequence of sexual conflict.
Studies of mate rejection in facultatively sexual organisms are rare [17,35], and it is difficult at present to find studies that would track life events of females living at different densities (there is an understandable tendency for researchers in general to favour studying organisms in locations where they are common). Our model assumes that male harassment is a bigger problem for females at high density; evidence for this is mainly available for obligate sexual species [6,9,36]. Another interesting empirical pattern is that tychoparthenogenesis—the rare development of unfertilized eggs in an otherwise sexually reproducing species—becomes common at low densities in Timema stick-insects [33]; without this capacity, the evolution and maintenance of parthenogenesis at low densities would obviously not be possible.
Our model has limitations: resisting females were assumed to all have the same strength of resistance θ. We therefore allow for trait evolution in the sense that the ratio from resisting to non-resisting females evolves, but do not include the possibility of continuous trait variation of θ. Letting θ evolve would require specifying how costs of resistance depend on the value of θ; further work could usefully consider the possibility of antagonistic coevolution between female and male behaviours, as higher θ might select for male counter adaptations.
We also did not consider any feedbacks between the proportion of parthenogenetic females in the population and the population density D. In reality, a higher proportion of parthenogenetic reproduction might lead to more efficient population growth. We have not included such feedbacks, because mate encounter rates in our model depend on adult density (at carrying capacity), which is a different population dynamic concept from the growth rate; to predict the latter purely based on the former is impossible without knowing how density regulation operates in any given species. That said, it is important to keep in mind that empirical testing of our evolutionary predictions regarding the relationship between parthenogenesis and population density could be complicated if males first disappear because density is low, and parthenogenetic females subsequently reach high densities. The dynamics of mating is especially important to understand when there is spatial variation (not yet included in our present model), which could take the form of an invasion front or stochastic metapopulation dynamics. If it is possible that females over time reach higher densities when they can complete development without competing with male conspecifics, we can envisage an interesting ‘double whammy’ that makes maintaining males difficult as a whole: populations might then consist of regions where males are absent and regions where they are present. In the regions where males are present, densities are simultaneously lowered (as less parthenogenesis means less population growth)—and low densities operate against male persistence, as we have shown. If the selective mosaic, however, also contains high-density patches where males are present, the outcome is less clear and might also depend on whether males or females disperse more.
Another interesting result of our model is that facultative sex is maintained at a wider range of densities if mate encounter rates increase less than linearly with mate availability (low β); at very high β the zone for facultative sex disappears. It would be intriguing to combine these findings with spatial dynamics, because of the point made in [30] that spatial clustering may lead to a smaller than linear increase of mating rates.
Finally, we did not consider any sex ratio adjustment [22] or a partial fertilization of the eggs in the model. We assumed that after a female mated, all subsequent eggs are fertilized and offspring are produced at a 1 : 1 sex ratio. It has been shown that sex ratio evolution in female-biased populations can increase the reproductive success of males and thus compensate for the cost of producing them and favour obligate sex [22]. On the other hand, the possibility of sex ratio adjustment could also lead to a lower fertilization rate of the eggs for resistant females and even facilitate the extinction of males at lower densities.
Our findings also suggest that an interaction between male harassment and population density might contribute to our understanding of geographical parthenogenesis, an often documented pattern where asexual lineages appear to occupy marginal niches, with potentially low densities, compared with their sexual counterparts. One explanation for the pattern of geographical parthenogenesis is that asexual lineages are superior colonizers because they do not suffer from mate limitation [37]; see [28] for this and alternative hypotheses. This is an interesting idea: it, too, features positive feedback, with the rarity of fertilization opportunities selecting for improved ability to reproduce without males, which further penalizes females who cannot do so (see [33] for a discussion in the context of tychoparthenogenesis, i.e. the spontaneous development and hatching of unfertilized eggs in otherwise sexual organisms).
While these ideas and our model are not mutually exclusive, our model suggests that sexual harassment and female resistance at different population densities can lead to, or help maintain, geographical parthenogenesis, either independently or acting together with differences in colonization ability. In this scenario, a sexual species with some ability for parthenogenesis would first disperse to higher latitudes or altitudes. Thereafter different population densities in these habitats lead to the extinction or maintenance of males. If asexual types accompany the colonization process, the process will operate faster, if we assume that co-occurrence of asexual and sexual females reduces the local density of males at each point along the colonization route. Future work could therefore usefully investigate how mate limitation and sexual conflict operate together at niche margins versus elsewhere within a species' range.
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Acknowledgements
We are grateful to Tanja Schwander and her group for stimulating discussions. Here we also want to thank three anonymous reviewers for helpful comments.
Authors' contributions
H.K. conceptualized the study; N.G. and H.K. performed methodology and analysis and writing of the manuscript; both authors gave final approval for publication.
Competing interests
We have no competing interests.
Funding
This study was funded by the Finnish Academy (via the Finnish Center of Excellence for Biological Interactions) and the University of Zurich.
References
- 1.Lehtonen J, Jennions MD, Kokko H. 2012. The many costs of sex. Trends Ecol. Evol. 27, 172–178. ( 10.1016/j.tree.2011.09.016) [DOI] [PubMed] [Google Scholar]
- 2.Kokko H, Rankin DJ. 2007. Do males matter? The role of males in population dynamics. Oikos 116, 335–348. ( 10.1111/j.0030-1299.2007.15451.x) [DOI] [Google Scholar]
- 3.Rowe L, Arnqvist G, Sih A, Krupa J. 1994. Sexual conflict and the evolutionary ecology of mating patterns: water striders as a model system. Trends Ecol. Evol. 9, 289–293. ( 10.1016/0169-5347(94)90032-9) [DOI] [PubMed] [Google Scholar]
- 4.Shine R, O'Connor D, Mason RT. 2000. Sexual conflict in the snake den. Behav. Ecol. Sociobiol. 48, 392–401. ( 10.1007/s002650000255) [DOI] [Google Scholar]
- 5.Rönn J, Katvala M, Arnqvist G. 2006. The costs of mating and egg production in Callosobruchus seed beetles. Anim. Behav. 72, 335–342. ( 10.1016/j.anbehav.2005.10.024) [DOI] [Google Scholar]
- 6.Gosden TP, Svensson EI. 2009. Density-dependent male mating harassment, female resistance, and male mimicry. Am. Nat. 173, 709–721. ( 10.1086/598491) [DOI] [PubMed] [Google Scholar]
- 7.Darden SK, Croft DP. 2008. Male harassment drives females to alter habitat use and leads to segregation of the sexes. Biol. Lett. 4, 449–451. ( 10.1098/rsbl.2008.0308) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Réale D, Boussès P, Chapuis J-L. 1996. Female-biased mortality induced by male sexual harassment in a feral sheep population. Can. J. Zool. 74, 1812–1818. ( 10.1139/z96-202) [DOI] [Google Scholar]
- 9.Rivera AC, Andrés JA. 2002. Male coercion and convenience polyandry in a calopterygid damselfly. J. Insect Sci. 2, 14 ( 10.1093/jis/2.1.14) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dagg JL. 2006. Could sex be maintained through harmful males? Oikos 112, 232–235. ( 10.1111/j.0030-1299.2006.14196.x) [DOI] [Google Scholar]
- 11.Rankin DJ. 2008. Can punishment maintain sex? Oikos 117, 173–176. ( 10.1111/j.2007.0030-1299.16271.x) [DOI] [Google Scholar]
- 12.Hartfield M. 2016. Evolutionary genetic consequences of facultative sex and outcrossing. J. Evol. Biol. 29, 5–22. ( 10.1111/jeb.12770) [DOI] [PubMed] [Google Scholar]
- 13.Speijer D, Lukeš J, Eliáš M. 2015. Sex is a ubiquitous, ancient, and inherent attribute of eukaryotic life. Proc. Natl Acad. Sci. USA 112, 8827–8834. ( 10.1073/pnas.1501725112) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Decaestecker E, De Meester L, Mergeay J. 2009. Cyclical parthenogenesis in daphnia: sexual versus asexual reproduction. In Lost sex (eds Schön I, Martens K, Dijk P), pp. 295–316. Dordrecht, The Netherlands: Springer. [Google Scholar]
- 15.Simon J-C, Rispe C, Sunnucks P. 2002. Ecology and evolution of sex in aphids. Trends Ecol. Evol. 17, 34–39. ( 10.1016/S0169-5347(01)02331-X) [DOI] [Google Scholar]
- 16.Pollock DA, Normark BB. 2002. The life cycle of Micromalthus debilis (Coleoptera: Archostemata: Micromalthidae): historical review and evolutionary perspective. J. Zool. Syst. Evol. Res. 40, 105–112. ( 10.1046/j.1439-0469.2002.00183.x) [DOI] [Google Scholar]
- 17.Burke NW, Crean AJ, Bonduriansky R. 2015. The role of sexual conflict in the evolution of facultative parthenogenesis: a study on the spiny leaf stick insect. Anim. Behav. 101, 117–127. ( 10.1016/j.anbehav.2014.12.017) [DOI] [Google Scholar]
- 18.Aparici E, Carmona MJ, Serra M. 1998. Sex allocation in haplodiploid cyclical parthenogens with density-dependent proportion of males. Am. Nat. 152, 652–657. ( 10.1086/286196) [DOI] [PubMed] [Google Scholar]
- 19.Bengtsson & Ceplitis. 2000. The balance between sexual and asexual reproduction in plants living in variable environments. J. Evol. Biol. 13, 415–422. ( 10.1046/j.1420-9101.2000.00187.x) [DOI] [Google Scholar]
- 20.D'Souza TG, Michiels NK. 2010. The costs and benefits of occasional sex: theoretical predictions and a case study. J. Hered. 101(Suppl 1), S34–S41. ( 10.1093/jhered/esq005) [DOI] [PubMed] [Google Scholar]
- 21.Green RF, Noakes DLG. 1995. Is a little bit of sex as good as a lot? J. Theor. Biol. 174, 87–96. ( 10.1006/jtbi.1995.0081) [DOI] [Google Scholar]
- 22.Kawatsu K. 2013. Sexual conflict over the maintenance of sex: effects of sexually antagonistic coevolution for reproductive isolation of parthenogenesis. PLoS ONE 8, e58141 ( 10.1371/journal.pone.0058141) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Griffiths AM, Jacoby DMP, Casane D, McHugh M, Croft DP, Genner MJ, Sims DW. 2012. First analysis of multiple paternity in an oviparous shark, the small-spotted catshark (Scyliorhinus canicula L.). J. Hered. 103, 166–173. ( 10.1093/jhered/esr112) [DOI] [PubMed] [Google Scholar]
- 24.Kawatsu K. 2013. Sexually antagonistic coevolution for sexual harassment can act as a barrier to further invasions by parthenogenesis. Am. Nat. 181, 223–234. ( 10.1086/668832) [DOI] [PubMed] [Google Scholar]
- 25.Kawatsu K. 2015. Breaking the parthenogenesis fertilization barrier: direct and indirect selection pressures promote male fertilization of parthenogenetic females. Evol. Ecol. 29, 49–61. ( 10.1007/s10682-014-9749-0) [DOI] [Google Scholar]
- 26.Tilquin A, Kokko H. 2016. What does the geography of parthenogenesis teach us about sex? Phil. Trans. R. Soc. B 371, 20150538 ( 10.1098/rstb.2015.0538) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Cosendai A-C, Wagner J, Ladinig U, Rosche C, Hörandl E. 2013. Geographical parthenogenesis and population genetic structure in the alpine species Ranunculus kuepferi (Ranunculaceae). Heredity 110, 560–569. ( 10.1038/hdy.2013.1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hörandl E. 2009. Geographical parthenogenesis: opportunities for asexuality. In Lost sex (eds Schön I, Martens K, Dijk P), pp. 161–186. Dordrecht, The Netherlands: Springer. [Google Scholar]
- 29.Hutchinson JMC, Waser PM. 2007. Use, misuse and extensions of ‘ideal gas’ models of animal encounter. Biol. Rev. Camb. Philos. Soc. 82, 335–359. ( 10.1111/j.1469-185X.2007.00014.x) [DOI] [PubMed] [Google Scholar]
- 30.Nicolis SC, Theraulaz G, Deneubourg JL. 2005. The effect of aggregates on interaction rate in ant colonies. Anim. Behav. 69, 535–540. ( 10.1016/j.anbehav.2004.06.007) [DOI] [Google Scholar]
- 31.Lee PLM, Hays GC. 2004. Polyandry in a marine turtle: females make the best of a bad job. Proc. Natl Acad. Sci. USA 101, 6530–6535. ( 10.1073/pnas.0307982101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Arnqvist G, Rowe L. 2013. Sexual conflict. Princeton, NJ: Princeton University Press. [Google Scholar]
- 33.Schwander T, Vuilleumier S, Dubman J, Crespi BJ. 2010. Positive feedback in the transition from sexual reproduction to parthenogenesis. Proc. R. Soc. B 277, 1435–1442. ( 10.1098/rspb.2009.2113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lehtonen J, Kokko H. 2012. Positive feedback and alternative stable states in inbreeding, cooperation, sex roles and other evolutionary processes. Phil. Trans. R. Soc. B 367, 211–221. ( 10.1098/rstb.2011.0177) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schmit O, Fukova I, Vandekerkhove J, Michalakis Y, Matzke-Karasz R, Rossetti G, Martens K, Mesquita-Joanes F. 2013. Mate recognition as a reproductive barrier in sexual and parthenogenetic Eucypris virens (Crustacea, Ostracoda). Anim. Behav. 85, 977–985. ( 10.1016/j.anbehav.2013.02.021) [DOI] [Google Scholar]
- 36.Magurran AE, Seghers BH. 1994. A cost of sexual harassment in the guppy, Poecilia reticulata. Proc. R. Soc. Lond. B 258, 89–92. ( 10.1098/rspb.1994.0147) [DOI] [Google Scholar]
- 37.Baker HG. 1965. Characteristics and modes of origin of weeds. In The genetics of colonizing species (eds Baker HG, Stebbins GL), pp. 147–186. Academic Press, New York: USA. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.