Abstract
The adsorption of water on bimetallic PtRu/Pt(111) surface alloys has been studied based on periodic density functional theory calculations including dispersion corrections. The Ru atoms of the PtRu surface alloy interact more strongly with water than Pt atoms, as far as both single water molecules and ice-like hexagonal structures are concerned. Within the surface alloy layer, the lateral ligand effect reducing the local reactivity of the surface atoms with increasing Ru content is more dominant than the opposing geometric effect due to the tensile strain. The structural preference for the Ru atoms also prevails at room temperature, as ab initio molecular dynamics simulations show.
Keywords: water, bimetallic surface alloys, density functional theory calculations
1. Introduction
There is an ongoing search for better catalysts in heterogeneous and electro-catalysis with improved activity and selectivity [1–3]. Nanostructured bimetallic catalysts offer the possibility to modify their composition, structure and arrangement in order to prepare a catalyst material with the desired properties [4–7]. To do this in a rational way requires an understanding of the underlying principles governing the activity of a bimetallic catalyst.
In electrocatalysis, the desired reactions typically occur at the interface between the electrode and the aqueous electrolyte. The particular structure of water at the metal electrode surface can be crucial as the water molecules interact with the reacting species [8–11]. The presence of water on metal surfaces is also interesting with respect to corrosion [12]. In addition, metal–water interfaces are of fundamental interest as they represent the boundary between an ordered and a disordered phase. This importance has motivated a multitude of experimental [13,14] and theoretical [15–22] studies addressing the structure of metal–water interfaces. As far as closed-packed hexagonal metal electrodes are concerned, ab initio molecular dynamics simulations indicate that at room temperature water does not remain in an ice-like hexagonal structure but rather becomes disordered, in particular, with respect to the orientation of the water molecules [18].
However, these studies have typically concentrated on water layers on pure elemental metal surfaces; only a few studies have been concerned with the adsorption of water on metal alloys [23–25]. In particular, we are not aware of any theoretical study that addresses the geometry of water layers on ordered surface alloys. Hence it is not clear yet whether the structure of an underlying surface alloy is also imposed on adsorbed water layers.
Using periodic density functional theory (DFT) calculations, we have systematically studied the structure of a water layer on a PtRu/Pt(111) surface for varying compositions of the PtRu surface alloy. The PtRu system is of strong interest in electrocatalysis because of its superior properties as a fuel cell catalyst material [26–29]. We have analysed both the adsorption of water monomers as well as the preferential arrangement of ice-like hexagonal water layers on PtRu/Pt(111) surface alloys as a function of the composition of the surface alloy. At room temperature, water layers on flat metal surfaces are typically no longer crystalline, but rather disordered [15,18,21,30]. Therefore, we have also performed ab initio molecular dynamics (AIMD) simulations at a temperature of 300 K in order to assess the thermal stability of the water layers on PtRu/Pt(111) surface alloys.
2. Computational details
Periodic DFT calculations have been performed using the Vienna ab initio software package (VASP) [31]. The electronic cores are described by the projector augmented wave (PAW) method [32] and the electronic one-particle states in the water–metal calculations have been expanded up to 400 eV using a plane wave basis set. In order to describe the water–water and also the water–metal interaction appropriately, it has turned out to be crucial to take dispersion interactions into account [33,34]. Hybrid functionals are not appropriate for metals [35]; hence typically the generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) functional [36] or its revised RPBE version [37] is used. However, PBE leads to an overstructuring of water [38], even if dispersion corrections are taken into account [39]. Yet, in a series of papers it has been shown that the RPBE functional together with the D3 dispersion correction [40] and so-called zero (D3/zero) damping functions [41] yields a rather satisfactory description of the properties of water–metal interfaces [10,34], bulk liquid water [34,42], and even water clusters and ice crystals [42]. Therefore, we have employed in this study the RPBE-D3 scheme. However, as the D3 dispersion correction scheme does not correctly describe the screening of the dispersion interaction within the bulk metal [34,43], in the pairwise summation only the uppermost metal layer is included.
The metal electrodes were modelled by five-layer slabs. The top three layers of the slabs have been fully relaxed, while the bottom two layers have been fixed at their bulk positions. Ordered surface alloys have been considered with a Ru content of 0, 1/3, 2/3 and 1 in a geometry using a k-point sampling of 9×9×1 to replace the integration over the first Brillouin zone. The ab initio molecular dynamics (AIMD) simulations have been performed in a surface unit cell employing 5×5×1 k-points. A vacuum region of at least 15 Å was chosen, depending on the number of water layers. The AIMD simulations were performed with the Verlet algorithm using a time step of 1 fs within the microcanonical ensemble considering two water layers. This corresponds to a rather thin film. Recent AIMD simulations of a water film on Pt(111) have revealed that at this particular electrode the water layers assume a bulk liquid-like structure from the third layer on [42]. On the other hand, it was previously shown that two water layers at close-packed metal electrodes are sufficient to reproduce basic properties of adsorbed water layers [18]. In order to limit the still high computational cost of AIMD simulations, we have therefore chosen to take into account only two layers of water.
3. Results and discussion
Single water molecules adsorb on close-packed metal surfaces typically through their oxygen atom at a top position in a flat configuration with the hydrogen atoms almost at the same height as the oxygen atom [17,44]. This is also the case for isolated water molecules at a coverage of adsorbed on PtRu/Pt(111) surface alloys, as illustrated for a Pt2Ru1/Pt(111) surface alloy in figure 1. As shown in this figure, the water monomer preferentially adsorbs on the Ru atom of the PtRu surface alloy. This can be understood by the higher reactivity of Ru compared with Pt because the d-band is closer to being half-filled.
Figure 1.
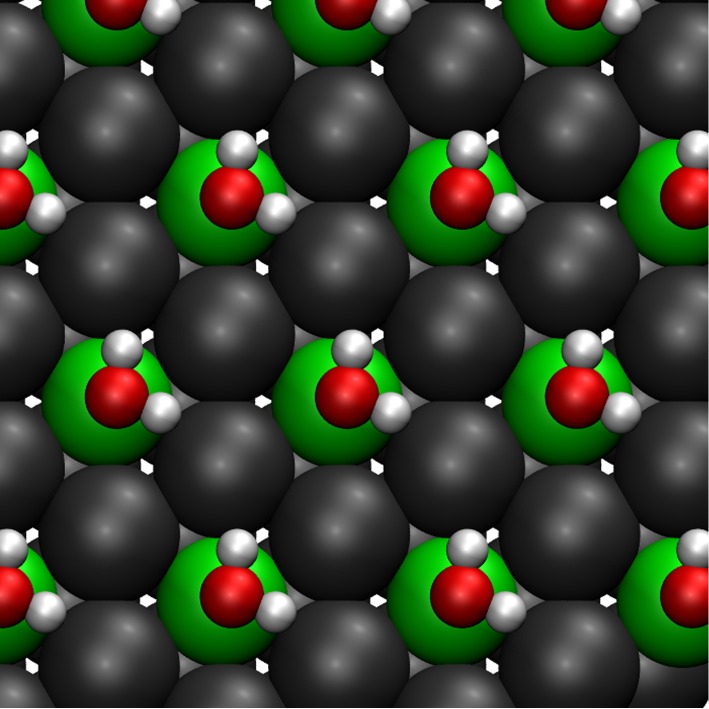
Energy minimum structure of water molecules adsorbed at a coverage of 1/3 on a Pt2Ru1/Pt(111) surface alloy. The Ru atoms are green, the Pt atoms dark grey.
However, in a surface alloy, the different size and interaction strength of the metallic species influence the reactivity of the components. When a more reactive and smaller metal atom such as Ru is added to a Pt system that is less reactive and has a larger lattice constant, there are typically two competing effects [6,45] that can be understood in a simple bond-order like concept, but also within the d-band model [46] which states that adsorption on a particular metal atoms becomes the weaker, the lower the local d-band centre is.
Replacing Pt by the smaller Ru can be regarded as introducing tensile strain. This geometric effect reduces the overlap between the electronic states of adjacent atoms which makes them more strongly interacting with adsorbates. On the other hand, Ru is more reactive than Pt due to the fact that its d-band is less filled, but still more than half-filled. This lateral ligand effect causes a stronger interaction between adjacent atoms which makes them less strongly interacting with adsorbates. In fact, there are surface alloys such as PtAu/Pt(111) where these two opposing effects for the local reactivity cancel, leading to ontop adsorption energies that are independent of the alloy composition [47].
The adsorption energies and geometries of water monomers at a coverage of on the considered PtRu surface alloys are listed in table 1 together with the local d-band centres without adsorbates. The table confirms that the Ru sites are energetically much more favourable. For example, on the Pt2Ru1/Pt(111) surface alloy, the water monomers binds 368 meV stronger on the Ru sites (Eads=−0.730 eV) than on the Pt sites (Eads=−0.362 eV). The stronger binding to the Ru site is also associated with a shorter distance of the oxygen atom of the water molecule to the underlying metal atom. In addition, the O–H bond of the water molecules on the Ru sites is slightly elongated indicating a somewhat weaker O–H bond. As far as the trend in the water adsorption energies as a function of alloy composition is concerned, both on the Pt sites as well as on the Ru sites the water binding becomes weaker with increasing Ru content. According to the discussion given above, this indicates that the lateral ligand effect within the surface alloy is stronger than the tensile strain effect. With respect to the Pt and Ru sites, this trend is also reflected in the corresponding downshift of the local d-band centre that are given in table 1. Note that for CO and O2 adsorption on pseudomorphic Pt/Ru overlayer systems, the ligand effect has also been found to be slightly stronger than the geometric strain effect [27,48]; however, for the Pt/Ru overlayer systems both effects lead to a reduction in the binding energies of adsorbates.
Table 1.
Adsorption energies Eads and geometries of water monomers adsorbed with at a coverage of 1/3 on PtRu/Pt(111) surface alloys. In addition, the local metal d-band centres εd of the adsorption sites without adsorbates are given with respect to the Fermi energy.
| PtRu/Pt(111) | site | εd (eV) | Eads (eV) | dM−O (Å) | dO−H (Å) |
|---|---|---|---|---|---|
| Pt(111) | Pt | −2.36 | −0.395 | 2.615 | 0.980 |
| Pt2Ru1/Pt | Pt | −2.38 | −0.362 | 2.744 | 0.979 |
| Pt1Ru2/Pt | Pt | −2.60 | −0.199 | 2.935 | 0.976 |
| Pt2Ru1/Pt | Ru | −1.49 | −0.730 | 2.295 | 0.985 |
| Pt1Ru2/Pt | Ru | −1.58 | −0.663 | 2.314 | 0.986 |
| Ru/Pt | Ru | −1.90 | −0.554 | 2.328 | 0.985 |
Next, we focus on the most favourable hexagonal ice-like structures on the PtRu/Pt(111) surface alloys. The corresponding adsorption energies and geometries are given in table 2. For the Pt2Ru1/Pt(111) and Pt1Ru2/Pt(111) there are several arrangements of the ice-like layer possible. In the hexagonal ice-like layers, every second water molecule is bound to the metal substrate via its oxygen atom in an adsorption configuration similar to the one of the water monomer. However, in order to complete the hydrogen-bonded network, the other water molecule is typically arranged in either an H-up or H-down configuration with the hydrogen pointed away or towards the metal substrate, respectively [17,18].
Table 2.
Adsorption energies Eads per water molecule of ice-like structures adsorbed with at a coverage of 2/3 on PtRu/Pt(111) surface alloys. dM−O denotes the distance of the oxygen atoms of the water molecule directly bound to the surface alloys.
| PtRu/Pt(111) | site | Eads (eV) | dM−O (Å) |
|---|---|---|---|
| Pt(111) | Pt | −0.606 | 2.636 |
| Pt2Ru1/Pt | Pt | −0.596 | 2.811 |
| Pt2Ru1/Pt | Ru, Pt | −0.732 | 2.303 |
| Pt1Ru2/Pt | Ru, Pt | −0.680 | 2.327 |
| Pt1Ru2/Pt | Ru | −0.643 | 2.365 |
| Ru/Pt | Ru | −0.599 | 2.353 |
The water binding preference for the Ru sites is reflected in the most favourable ice-like structure on the Pt2Ru1/Pt(111) surface alloy that is illustrated in figure 2a. The water molecule bound through its oxygen atom to the metal substrate is located above the Ru site, whereas the second water molecule is in the H-down configuration. This is the most stable geometry among all considered ice-like structures because of the favourable Ru–O interaction. The ice-like structure with all the water molecules above the Pt sites is 138 meV per water molecule less stable.
Figure 2.
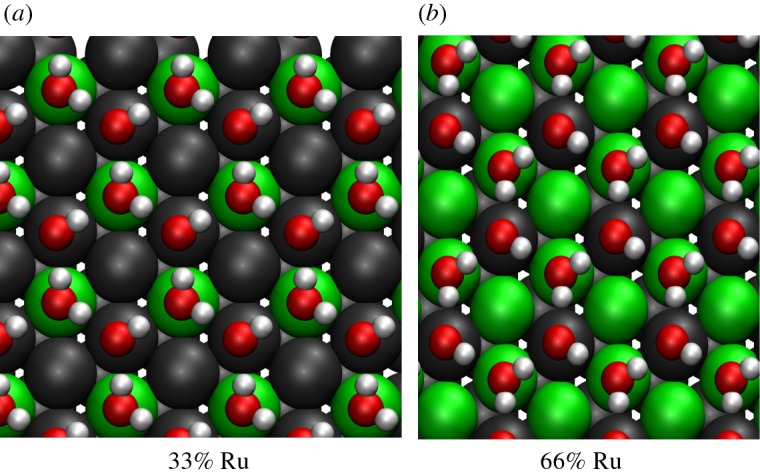
Energy minimum structure of an ice-like hexagonal layer at a water coverage of 2/3 on Pt2Ru1/Pt(111) (a) and on Pt1Ru2/Pt(111) (b). The Ru atoms are green, the Pt atoms dark grey.
On the Pt1Ru2/Pt(111) surface alloy, all water molecules can be situated above Ru sites. Interestingly enough, it is 37 meV per water molecule more stable to have the oxygen-bounded water molecules above the Ru site, but the H-down water molecules above the Pt sites (figure 2b). Apparently, the water–water binding is stronger when the other water molecules are above the less strongly interacting Pt sites [21]. Still, the adsorption is weaker than on Pt2Ru1/Pt(111) although the same local adsorption geometries are realized. Obviously, it is again the ligand effect that reduces the water-binding energy. The distance of the oxygen atoms of the water molecules directly bound to the metal substrate again reflects the stability of the water layers.
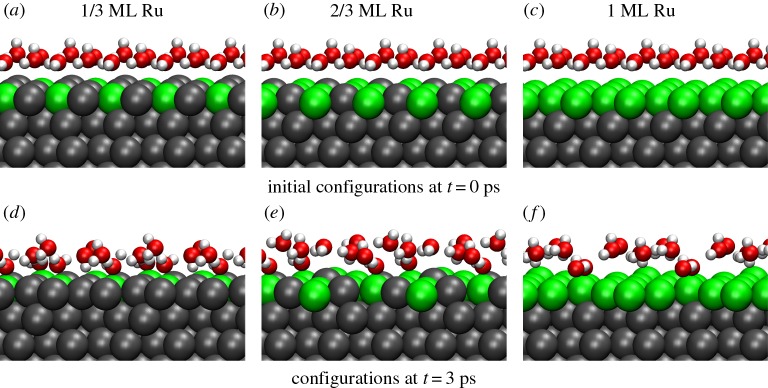
In order to assess the thermal stability of the water layer structures at room temperature on the PtRu surface alloys, AIMD simulations at a temperature of 300 K were performed for two water layers within a geometry. The AIMD simulations were initially started using the energy minimum configuration and a thermalization period of 1 ps. For the two-layer water systems, now the H-up structure is the more stable one in the first layer, as illustrated in figure 3a–c. Note that in the pictures the second water layer has been omitted for the sake of clarity. After the thermalization time, a production run of 3 ps was performed. This is admittedly a rather short run time, but it turns out to be sufficient to derive trends in the stability of the water layers. In fact, the distributions derived from the 3 ps run on pure Pt(111) compare favourably with the corresponding distributions derived from a 10 ps run [30].
Figure 3.
Top view of the structure of the lower water layer of a two-layer water system on PtRu/Pt(111) surface alloys for different Ru contents. (a–c) Energy minimum structures; (d–f) snapshots of AIMD simulations at 300 K after a run time of 3 ps. (g–h) Trajectories of the oxygen atoms of the water molecules along the AIMD run.
Snapshots of the water structure after 3 ps are illustrated in a top view in figure 3d–f. In addition, the trajectories of the oxygen atoms of the water molecules along the AIMD runs are plotted in figure 3g–i illustrating their displacement due to the thermal motion. On the Pt2Ru1/Pt(111) surface alloy, the hexagonal water structure is no longer intact (figure 3d). One of the hexagonal rings is broken at two positions. The water molecules above the Ru sites still stay at these sites, however, their orientation becomes disordered. On the Pt1Ru2 surface alloy, the water molecules still remain at the Ru sites, i.e. there is still a hexagonal structure persisting (figure 3e). Apparently, the less favourable Pt sites keep the water molecules in the ring-like geometry that is preset by the arrangement of the Ru atoms in the surface alloy. On the pure Ru layer on top of the Pt(111) crystal, there is no restoring force that keeps the water molecules in an ice-like structure. Consequently, the hexagonal arrangement is dissolved, in agreement with previous similar AIMD simulations with a 10 ps run time [18]. Instead, pentagons are formed which have been identified as stable structural water motifs on other metal surfaces [49].
The distribution of the distance of the oxygen atoms of the water molecules in the first layer from the PtRu surface alloys is plotted in figure 4. At the pure Pt surface, there is basically one peak at about 3.2 Å, as already found for the same system in 10 ps AIMD simulations [30]. Interestingly enough, for the Ru-containing surface alloys, additional peaks evolve at about 1.8–2.0 Å. Recall that this distance is smaller than the distance between the oxygen atom of an adsorbed water monomer and the metal surfaces, as listed in table 1. The largest additional peak appears for the Pt2Ru1/Pt(111) surface alloy which exhibits the strongest Ru–water interaction (table 1)
Figure 4.
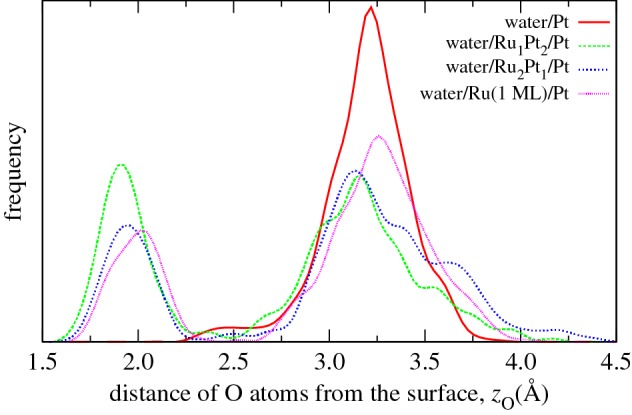
Distribution of the distance of the oxygen atoms of the water molecules in the first layer from the PtRu surface alloys along the AIMD simulations.
In order to identify the water species causing this additional peak, we show in figure 5 side views of the water structures that were shown in a top view in figure 3. A comparison of figures 3 and 5 reveals that the peaks at short oxygen distances are due to water molecules that are to a certain extent detached from the hydrogen-bonded water network structure and bind through their oxygen atom to the metal surface but with their hydrogen atoms pointing away from the surface.
Figure 5.
Side view of the lower water layer of the water structures shown in figure 3. (a–c) Energy minimum structures and (d–f) snapshots of AIMD simulations at 300 K after a run time of 3 ps.
4. Conclusion
Periodic electronic structure calculations based on DFT calculations have been performed in order to identify the structure of water layers on PtRu/Pt(111) surface alloys. Upon increasing the Ru content in the surface alloy, the local reactivity of the metal atoms decreases due to the ligand effect. Still the Ru sites are more attractive towards water adsorption than the Pt sites. This is also reflected in the energetically favourable structure of adsorbed ice-like layers. At room temperature, the ice-like hexagonal structure does not persist, as ab initio molecular dynamics simulations indicate. As an exception, the Pt1Ru2/Pt(111) surface alloy that exhibits a hexagonal pattern seems to stabilize the hexagonal water structure as it provides a hexagonal template of more strongly interacting Ru atoms in the surface alloy. These results indicate that a patterning of a surface alloy can impose a preference for a particular structure on adsorbed water layers.
Acknowledgements
Useful discussions with Dr Sung Sakong, Ulm University, are gratefully acknowledged.
Data accessibility
The crucial data obtained in this work are provided in tables 1 and 2.
Authors' contributions
J.M.F. performed most of the calculations for the static water configurations and the AIMD simulations on the bimetallic surface alloys. D.M. did calculations for additional water structures. T.R. ran the AIMD simulations on clean Pt(111) and carried out the statistical analysis of the trajectories. A.G. initiated and supervised the work and wrote the manuscript.
Competing interests
We declare we have no competing interests.
Funding
This research has been supported by the German Research Foundation (DFG) through contract GR 1503/21-1 and by the Baden-Württemberg Foundation through the project CT-4 ‘ORR-Scale’ within the program ‘Clean Tech’. Computer time has been provided by the bwHPC initiative and the bwHPC-C5 project funded by the Baden–Württemberg government (MWK) and the German Research Foundation (DFG) and by the bwGRiD project of the Federal State of Baden–Württemberg/Germany.
References
- 1.Schlögl R. 1998. Combinatorial chemistry in heterogeneous catalysis: a new scientific approach or the ‘king's new clothes?’ Angew. Chem. Int. Ed. 37, 2333–2336. (doi:10.1002/(SICI)1521-3773(19980918)37:17<2333::AID-ANIE2333>3.0.CO;2-JView) [DOI] [PubMed] [Google Scholar]
- 2.Okamoto Y. 2004. Finding optimum compositions of catalysts using ab initio calculations and data mining. Chem. Phys. Lett. 395, 279–284. (doi:10.1016/j.cplett.2004.07.097) [Google Scholar]
- 3.Schlögl R. 2010. The role of chemistry in the energy challenge. ChemSusChem 3, 209–222. (doi:10.1002/cssc.200900183) [DOI] [PubMed] [Google Scholar]
- 4.Greeley J, Mavrikakis M. 2004. Alloy catalysts designed from first principles. Nat. Mater. 3, 810–815. (doi:10.1038/nmat1223) [DOI] [PubMed] [Google Scholar]
- 5.Groß A. 2006. Reactivity of bimetallic systems studied from first principles. Topics Catal. 37, 29–39. (doi:10.1007/s11244-006-0005-x) [Google Scholar]
- 6.Sakong S, Mosch C, Groß A. 2007. CO adsorption on Cu-Pd alloy surfaces: ligand versus ensemble effects. Phys. Chem. Chem. Phys. 9, 2216–2225. (doi:10.1039/B615547B) [DOI] [PubMed] [Google Scholar]
- 7.Groß A. 2009. Tailoring the reactivity of bimetallic overlayer and surface alloy systems. J. Phys. Condens. Matter 21, 084205 (doi:10.1088/0953-8984/21/8/084205) [DOI] [PubMed] [Google Scholar]
- 8.Roudgar A, Groß A. 2005. Water bilayer on the Pd/Au(111) overlayer system: coadsorption and electric field effects. Chem. Phys. Lett. 409, 157–162. (doi:10.1016/j.cplett.2005.04.103) [Google Scholar]
- 9.Jinnouchi R, Kodama K, Morimoto Y. 2014. DFT calculations on H, OH and o adsorbate formations on Pt(111) and Pt(332) electrodes. J. Electroanal. Chem. 716, 31–44. (doi:10.1016/j.jelechem.2013.09.031) [Google Scholar]
- 10.Sakong S, Naderian M, Mathew K, Hennig RG, Groß A. 2015. Density functional theory study of the electrochemical interface between a Pt electrode and an aqueous electrolyte using an implicit solvent method. J. Chem. Phys. 142, 234107 (doi:10.1063/1.4922615) [DOI] [PubMed] [Google Scholar]
- 11.Sakong S, Groß A. 2016. The importance of the electrochemical environment in the electro-oxidation of methanol on Pt(111). ACS Catal. 6, 5575–5586. (doi:10.1021/acscatal.6b00931) [Google Scholar]
- 12.Todorova M, Neugebauer J. 2014. Extending the concept of defect chemistry from semiconductor physics to electrochemistry. Phys. Rev. Appl. 1, 014001 (doi:10.1103/PhysRevApplied.1.014001) [Google Scholar]
- 13.Henderson MA. 2002. The interaction of water with solid surfaces: fundamental aspects revisited. Surf. Sci. Rep. 46, 1–308. (doi:10.1016/S0167-5729(01)00020-6) [Google Scholar]
- 14.Hodgson A, Haq S. 2009. Water adsorption and the wetting of metal surfaces. Surf. Sci. Rep. 64, 381–451. (doi:10.1016/j.surfrep.2009.07.001) [Google Scholar]
- 15.Izvekov S, Voth GA. 2001. Ab initio molecular dynamics simulation of the Ag(111)-water interface. J. Chem. Phys. 115, 7196 (doi:10.1063/1.1403438) [DOI] [PubMed] [Google Scholar]
- 16.Feibelman PJ. 2002. Partial dissociation of water on Ru(0001). Science 295, 99–102. (doi:10.1126/science.1065483) [DOI] [PubMed] [Google Scholar]
- 17.Michaelides A. 2006. Density functional theory simulations of water-metal interfaces: waltzing waters, a novel 2D ice phase, and more. Appl. Phys. A 85, 415–425. (doi:10.1007/s00339-006-3695-9) [Google Scholar]
- 18.Schnur S, Groß A. 2009. Properties of metal-water interfaces studied from first principles. New J. Phys. 11, 125003 (doi:10.1088/1367-2630/11/12/125003) [Google Scholar]
- 19.Lin X, Groß A. 2012. First-principles study of the water structure on flat and stepped gold surfaces. Surf. Sci. 606, 886–891. (doi:10.1016/j.susc.2011.12.015) [Google Scholar]
- 20.Carrasco J, Hodgson A, Michaelides A. 2012. A molecular perspective of water at metal interfaces. Nat. Mater. 11, 667–674. (doi:10.1038/nmat3354) [DOI] [PubMed] [Google Scholar]
- 21.Groß A, Gossenberger F, Lin X, Naderian M, Sakong S, Roman T. 2014. Water structures at metal electrodes studied by ab initio molecular dynamics simulations. J. Electrochem. Soc. 161, E3015–E3020. (doi:10.1149/2.003408jes) [Google Scholar]
- 22.Gillan MJ, Alfe D, Michaelides A. 2016. Perspective: how good is DFT for water? J. Chem. Phys. 144, 130901 (doi:10.1063/1.4944633) [DOI] [PubMed] [Google Scholar]
- 23.McBride F, Darling GR, Pussi K, Lucas CA, Gründer Y, Darlington M, Brownrigg A, Hodgson A. 2013. The influence of water and hydroxyl on a bimetallic (R30° Sn/Pt surface alloy. J. Phys. Chem. C 117, 4032–4039. (doi:10.1021/jp3112342) [Google Scholar]
- 24.Robinson AM, Montemore MM, Tenney SA, Sutter P, Medlin JW. 2013. Interactions of hydrogen, CO, oxygen, and water with molybdenum-modified Pt(111). J. Phys. Chem. C 117, 26 716–26 724. (doi:10.1021/jp410563s) [Google Scholar]
- 25.Herrmann S, Stamatakis M, Andriotis AN, Mpourmpakis G. 2014. Adsorption behavior of noble metal clusters and their alloys. J. Comput. Theor. Nanosci. 11, 511–520. (doi:10.1166/jctn.2014.3387) [Google Scholar]
- 26.Zhang JL, Vukmirovic MB, Sasaki K, Nilekar AU, Mavrikakis M, Adzic RR. 2005. Mixed-metal Pt monolayer electrocatalysts for enhanced oxygen reduction kinetics. J. Am. Chem. Soc. 127, 12480–12481. (doi:10.1021/ja053695i) [DOI] [PubMed] [Google Scholar]
- 27.Lischka M, Mosch C, Groß A. 2007. Tuning catalytic properties of bimetallic surfaces: oxygen adsorption on pseudomorphic Pt/Ru overlayers. Electrochim. Acta 52, 2219–2228. (doi:10.1016/j.electacta.2006.03.113) [Google Scholar]
- 28.Brimaud S, Jusys Z, Behm RJ. 2014. Shape-selected nanocrystals for in situ spectro-electrochemistry studies on structurally well defined surfaces under controlled electrolyte transport: a combined in situ ATR-FTIR/online DEMS investigation of CO electrooxidation on Pt. Beilstein J. Nanotechnol. 5, 735–746. (doi:10.3762/bjnano.5.86) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Engstfeld A, Klein J, Brimaud S, Behm R. 2015. Electrochemical stability and restructuring and its impact on the electro-oxidation of CO:Pt modified Ru(0001) electrodes. Surf. Sci. 631, 248–257. (doi:10.1016/j.susc.2014.05.022) [Google Scholar]
- 30.Roman T, Groß A. 2013. Structure of water layers on hydrogen-covered Pt electrodes. Catal. Today 202, 183–190. (doi:10.1016/j.cattod.2012.06.001) [Google Scholar]
- 31.Kresse G, Furthmüller J. 1996. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11 169–11 186. (doi:10.1103/PhysRevB.54.11169) [DOI] [PubMed] [Google Scholar]
- 32.Blöchl PE. 1994. Projector augmented-wave method. Phys. Rev. B 50, 17953 (doi:10.1103/PhysRevB.50.17953) [DOI] [PubMed] [Google Scholar]
- 33.Carrasco J, Santra B, Klimĕ J, Michaelides A. 2011. To wet or not to wet? dispersion forces tip the balance for water ice on metals. Phys. Rev. Lett. 106, 026101 (doi:10.1103/PhysRevLett.106.026101) [DOI] [PubMed] [Google Scholar]
- 34.Tonigold K, Groß A. 2012. Dispersive interactions in water bilayers at metallic surfaces: a comparison of the PBE and RPBE functional including semi-empirical dispersion corrections. J. Comput. Chem. 33, 695–701. (doi:10.1002/jcc.22900) [DOI] [PubMed] [Google Scholar]
- 35.Paier J, Marsman M, Kresse G. 2007. Why does the B3LYP hybrid functional fail for metals? J. Chem. Phys. 127, 024103 (doi:10.1063/1.2747249) [DOI] [PubMed] [Google Scholar]
- 36.Perdew JP, Burke K, Ernzerhof M. 1996. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. (doi:10.1103/PhysRevLett.77.3865) [DOI] [PubMed] [Google Scholar]
- 37.Hammer B, Hansen LB, Nørskov JK. 1999. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 59, 7413–7421. (doi:10.1103/PhysRevB.59.7413) [Google Scholar]
- 38.Lin I-C, Seitsonen AP, Tavernelli I, Rothlisberger U. 2012. Structure and dynamics of liquid water from ab initio molecular dynamics–comparison of BLYP, PBE, and revPBE density functionals with and without van der Waals corrections. J. Chem. Theory Comput. 8, 3902–3910. (doi:10.1021/ct3001848) [DOI] [PubMed] [Google Scholar]
- 39.Forster-Tonigold K, Groß A. 2014. Dispersion corrected RPBE studies of liquid water. J. Chem. Phys. 141, 064501 (doi:10.1063/1.4892400) [DOI] [PubMed] [Google Scholar]
- 40.Grimme S, Antony J, Ehrlich S, Krieg H. 2010. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132, 154104 (doi:10.1063/1.3382344) [DOI] [PubMed] [Google Scholar]
- 41.Grimme S, Hansen A, Brandenburg JG, Bannwarth C. 2016. Dispersion-corrected mean-field electronic structure methods. Chem. Rev. 116, 5105–5154. (doi:10.1021/acs.chemrev.5b00533) [DOI] [PubMed] [Google Scholar]
- 42.Sakong S, Forster-Tonigold K, Groß A. 2016. The structure of water at a Pt(111) electrode and the potential of zero charge studied from first principles. J. Chem. Phys. 144, 194701 (doi:10.1063/1.4948638) [DOI] [PubMed] [Google Scholar]
- 43.Mercurio G, et al. 2010. Structure and energetics of azobenzene on Ag(111): benchmarking semiempirical dispersion correction approaches. Phys. Rev. Lett. 104, 036102 (doi:10.1103/PhysRevLett.104.036102) [DOI] [PubMed] [Google Scholar]
- 44.Lin X, Evers F, Groß A. 2016. First-principles study of the structure of water layers on flat and stepped Pb electrodes. Beilstein J. Nanotechnol. 7, 533–543. (doi:10.3762/bjnano.7.47) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mancera LA, Behm RJ, Groß A. 2013. Structure and local reactivity of PdAg/Pd(111) surface alloys. Phys. Chem. Chem. Phys. 15, 1497–1508. (doi:10.1039/C2CP42914D) [DOI] [PubMed] [Google Scholar]
- 46.Hammer B, Nørskov JK. 1995. Electronic factors determining the reactivity of metal surfaces. Surf. Sci. 343, 211–220. (doi:10.1016/0039-6028(96)80007-0) [Google Scholar]
- 47.Gohda Y, Groß A. 2007. Structure-reactivity relationship for bimetallic electrodes: Pt overlayers and PtAu surface alloys on Au(111). J. Electroanal. Chem. 607, 47–53. (doi:10.1016/j.jelechem.2006.10.015) [Google Scholar]
- 48.Schlapka A, Lischka M, Groß A, Käsberger U, Jakob P. 2003. Surface strain versus substrate interaction in heteroepitaxial metal layers: Pt on Ru(001). Phys. Rev. Lett. 91, 016101 (doi:10.1103/PhysRevLett.91.016101) [DOI] [PubMed] [Google Scholar]
- 49.Revilla-Lopez G, Lopez N. 2014. A unified study for water adsorption on metals: meaningful models from structural motifs. Phys. Chem. Chem. Phys. 16, 18 933–18 940. (doi:10.1039/C4CP02508C) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The crucial data obtained in this work are provided in tables 1 and 2.