Abstract
The purpose of this study was to develop realistic phantom models of the intracellular environment of metastatic breast tumour and naïve brain, and using these models determine an analysis metric for quantification of CEST MRI data that is sensitive to only labile proton exchange rate and concentration. The ability of the optimal metric to quantify pH differences in the phantoms was also evaluated.
Novel phantom models were produced, by adding perchloric acid extracts of either metastatic mouse breast carcinoma cells or healthy mouse brain to bovine serum albumin. The phantom model was validated using 1H NMR spectroscopy, then utilized to determine the sensitivity of CEST MRI to changes in pH, labile proton concentration, T 1 time and T 2 time; six different CEST MRI analysis metrics (MTRasym, APT*, MTRRex, AREX and CESTR* with and without T 1/T 2 compensation) were compared.
The new phantom models were highly representative of the in vivo intracellular environment of both tumour and brain tissue. Of the analysis methods compared, CESTR* with T 1 and T 2 time compensation was optimally specific to changes in the CEST effect (i.e. minimal contamination from T 1 or T 2 variation). In phantoms with identical protein concentrations, pH differences between phantoms could be quantified with a mean accuracy of 0.6 pH units.
We propose that CESTR* with T 1 and T 2 time compensation is the optimal analysis method for these phantoms. Analysis of CEST MRI data with T 1/T 2 time compensated CESTR* is reproducible between phantoms, and its application in vivo may resolve the intracellular alkalosis associated with breast cancer brain metastases without the need for exogenous contrast agents.
Keywords: brain, CEST, metastases, MRI, pH
Abbreviations used
- APT*
three‐offset amide proton transfer metric
- AREX
apparent relaxation due to exchange metric
- BayCEST
Bayesian chemical exchange saturation fitting algorithm
- BSA
bovine serum albumin
- CEST
chemical exchange saturation transfer
- CESTR*
chemical exchange saturation transfer ratio metric
- EPI
echo planar imaging
- MTRasym
magnetisation transfer asymmetry metric
- MTRRex
magnetisation transfer ratio relaxation due to exchange metric
- NOE
nuclear Overhauser enhancement
- PCA
perchloric acid
- ppm
parts per million
- qCEST
quantitative CEST
1. INTRODUCTION
Chemical exchange saturation transfer (CEST) is an MRI contrast mechanism that measures changes in signal from water protons owing to their association with other biomolecules and metabolites, particularly via exchange of protons with hydrolysable functional groups such as amides and amines.1, 2 CEST MRI has the potential to make non‐invasive measurements of pH,3 inform on areas of infiltrating tumour,4 differentiate tumour from radiation necrosis,5 and provide information concerning the conformation of proteins.6 Since the pH of tissues is highly regulated, and numerous pathologies interfere with this regulation, the application of CEST MRI to generate pH maps in vivo has received significant research interest recently.7
There is a clear need to develop a reliable, non‐invasive method of measuring tumour pH in vivo. One hallmark of cancerous tumours is their dysfunctional regulation of pH,8 leading to an acidotic extracellular space and slight alkalosis in the intracellular space.9 This change in pH has consequences for the efficacy of various treatments for tumours, and measurement of tumour pH may be useful in stratification of patients based on their expected responsiveness to particular therapies. In particular, brain metastasis, or secondary tumour spread to the brain, represents a major clinical problem, with poor prognosis and few therapeutic options. The development of better methods for interrogating the tumour microenvironment and targeting therapy may greatly enhance our ability to treat these tumours.
It is widely recognized that CEST is sensitive to more than just pH, which has led to various studies offering different explanations for the source of CEST contrast seen in tumours. Some studies claim that an increased protein concentration in tumour cells generates contrast between tumour and surrounding tissue.10, 11 However, others have measured insignificantly different protein concentration between rodent brain and implanted tumour, and suggest that the contrast is a result of T 1 contamination of the signal.12 In addition, evidence suggests that the pH and labile proton concentration are difficult to separate from CEST measurements.13 Despite this difficulty, a metric that is not contaminated by relaxation time changes and only depends on the relevant physiological parameters is needed before the potential of using CEST MRI for pH measurement in tumours can be assessed.
To develop such a metric, previous studies have used simple phantoms with a single exchanging pool of protons.13, 14 These phantoms allow useful insights into the CEST MRI signal source, but do not adequately represent the complex in vivo intracellular biomolecular environment. Methods such as quantitative CEST (qCEST)14 and the Omega plot15 have been used in these phantoms to successfully quantify labile proton exchange rate and concentration independently. However, these methods require many Z spectra to be acquired with varying saturation parameters, which is impractical in a clinical environment. The apparent relaxation due to exchange (AREX) metric has also been proposed to correct for contamination of CEST effects by T 1 relaxation of water,12, 16, 17, 18 but this method has not been validated in physiologically relevant phantoms.
The aims of this study, therefore, were the following: (i) to develop novel phantom models from cellular extracts that are representative of the in vivo intracellular environment of both normal brain and brain metastases; (ii) to use these phantoms to determine the sensitivity of the CEST MRI signal as measured by a number of different analysis metrics to changes in pH, labile proton concentration, T 1 and T 2; (iii) to identify an optimally specific analysis metric for quantification of CEST MRI data and (iv) to evaluate the ability of the optimal metric to quantify pH differences in these phantoms.
2. METHODS
2.1. Phantom preparation
Phantoms were prepared to represent the intracellular environment of naïve mouse brain and in vitro cultured 4T1‐GFP mouse metastatic breast carcinoma cells. The 4T1‐GFP cell line is commonly used as a mouse model of metastatic breast cancer, including studies of metastatic spread to the brain.19 It is an appropriate tumour model here as previous measurements of human breast cancers have displayed intracellular alkalosis.20 For the mouse brain phantoms, female BALB/c mice aged 6–8 weeks (n = 6) were terminally anaesthetized with sodium pentobarbital and transcardially perfused with 20 mL heparinized saline. Subsequently, the brains were removed, frozen in liquid nitrogen and stored at −80°C until further use. For the 4T1‐GFP cell phantoms, cells were cultured in Dulbecco's modified Eagle medium and passaged every second day to grow a sufficient number of cells.
Perchloric acid (PCA) extracts of either naïve brain or 4T1‐GFP cells were prepared. Briefly, either naïve mouse brains (n = 6) or a pellet of 4T1‐GFP cells (8 g) were homogenized and coated with 0.1 M HCl in methanol in a dry ice bath. Subsequently, the mixture was warmed to wet ice bath temperature, 0.02 M HCl and 3 M PCA added to the homogenizer and the precipitated protein sedimented by centrifugation (4800 g, 20 min, 4°C). The supernatant was neutralized to pH ~ 7 with KOH and the precipitated potassium perchlorate sedimented by centrifugation (4800 g, 20 min, 4°C). The supernatant was lyophilized. All volumes of solutions added were scaled to the weight of starting material to match metabolite concentration to their in vivo/intracellular values.
The lyophilized samples were divided into 26 equal fractions and added to bovine serum albumin (BSA) to produce phantoms representative of the intracellular environment of either naïve brain or 4T1‐GFP tumour cells. The pH (6.0–7.6, n = 6), BSA content (4–16% w/v, n = 7), T 1 time (0.3–1.7 s, n = 7) and T 2 time (29–140 ms, n = 6) of each phantom was serially varied for a total of 52 phantoms (n = 26 for each cell type). T 1 and T 2 relaxation times were varied by addition of gadolinium‐DTPA (Omniscan, GE Healthcare) and iron nanoparticles (25–30 nm diameter), respectively. Where pH and BSA content were not varied, the phantoms were pH 7.4 with a BSA concentration of 8% w/v. BSA has been used in previous studies as a protein representative of the in vivo protein pool, and 8% w/v is a reasonable assumption of the protein content of the rodent brain.21, 22 The BSA was not cross‐linked to avoid macromolecular magnetization transfer effects being introduced, and the phantom pH was titrated after addition of BSA.
2.2. Validation of tissue/cell extract phantoms
The validity of the PCA extract supplemented with BSA model as a reasonable representation of the intracellular environment of brain/tumour cells in vivo was confirmed using high‐resolution NMR spectroscopy. One‐dimensional 1H spectra with WATERGATE solvent suppression were acquired (see Section 2.3) from samples of PCA‐extracted naïve mouse brain, in vitro cultured 4T1‐GFP cells, and subcutaneous 4T1‐GFP tumours. The subcutaneous tumours were grown by injecting 5 × 105 4T1‐GFP cells in 100 μL PBS subcutaneously into female BALB/c mice aged 6–8 weeks (n = 6). Tumours were allowed to grow until 10 mm geometric mean diameter, at which point the mice were terminally anaesthetized with sodium pentobarbital and transcardially perfused with 20 mL heparinized saline. The tumours were then isolated from the surrounding skin and fat, frozen in liquid nitrogen and stored at −80°C until further use.
Additional spectra were obtained from the lysate of in vitro cultured 4T1‐GFP cells and the respective phantom model (PCA‐extracted in vitro cultured 4T1‐GFP cells supplemented with 8% w/v BSA). For the PCA extracts, the lyophilized samples were dissolved in pH 7.4 potassium phosphate buffer (1 M) to provide suitable buffering capability over the range required for this study. The cell lysate sample was produced by suspending 4T1‐GFP cells in NP‐40 lysis buffer (2.74 mL 1 M NaCl, 2 mL 200 mM pH 7 Tris HCl, 80 μL 0.5 M EDTA, 200 μL NP‐40, 4.98 mL dH2O) and sedimenting the precipitated cellular membranes by centrifugation (21 000 g, 20 min, 4°C). All samples were prepared to a final volume of 600 μL with 5% D2O.
In addition, samples of 8% w/v BSA in potassium phosphate buffer (1 M, pH 7.4) were supplemented with varying concentrations of PCA‐extracted in vitro cultured 4T1‐GFP cells (1×, 1.5× and 2× metabolite concentration) to confirm that the presence of metabolites from the PCA‐extracted cells in the sample influences the measured CEST spectrum.
2.3. Solution NMR experiments
Proton spectra were acquired using a vertical bore 600 MHz (14.1 T) spectrometer (Agilent Technologies, Santa Clara, CA, USA) using a WATERGATE sequence with a relaxation delay of 2 s, an acquisition time of 2 s and 128 transients per free induction decay recorded. The carrier was centred on water (4.7 ppm) with a sweep width of 9551 Hz. Spectra were processed using NMRPipe.23
2.4. MRI experiments
All MRI experiments were performed using a horizontal bore 400 MHz (9.4 T) spectrometer (Agilent Technologies) with a volume transmit–receive coil (internal diameter 40 mm, RAPID Biomedical, Rimpar, Germany). Shimming was performed prior to each experiment to minimize the B 0 field inhomogeneity. CEST images were acquired of 26 phantoms simultaneously using a saturation scheme of 300 Gaussian pulses of 26 ms duration and 180° flip angle each (50% duty cycle, equivalent continuous wave saturation power 0.8 μT) at 85 saturation frequencies spaced equally between ±10 ppm, followed by an eight‐shot spin‐echo echo planar imaging (EPI) readout. Additional images were acquired following saturation at ±100 ppm for normalization; field of view 38 mm × 38 mm, matrix size 32 × 32, slice thickness 2 mm, echo time (T E) 8.22 ms and repetition time (T R) 7.85 s. Total scan time for each set of phantoms was 3 h 6 min.
In addition to CEST imaging, the T 1 and T 2 relaxation times of each phantom were measured using inversion recovery (T R = 10 s, T E = 8.22 ms, inversion time (T I) varied in nine steps from 13.14 ms to 8 s, signals fitted to M z = M 0(1–2 exp(−T I/T 1)) and spin echo (T R = 10 s, T E varied in 10 steps from 30 ms to 160 ms, signals fitted to M z = M 0 exp(−T E/T 2) experiments, respectively. In both cases eight‐shot spin‐echo EPI readout was used to acquire images.
2.5. MRI data processing
All MRI data were processed in MATLAB (MathWorks, Natick, MA, USA). The relaxation maps of the water pool were obtained by least square fitting of the measured intensity against the inversion time (T 1 map) and echo time (T 2 map). Six metrics were used to analyse the Z spectra: conventional asymmetry analysis (MTRasym),1 multiple‐offset analysis (APT*),24 inverse Z‐spectrum multiple‐offset analysis (MTRRex),12 AREX,12 and two variants of a Bayesian model‐based analysis (CESTR*),13 as defined in Equations (1)–5, respectively. B 0 inhomogeneity was corrected prior to MTRasym, APT* and MTRRex analysis by shifting the minimum point of the Z spectrum to 0 ppm on a voxel‐wise basis; CESTR* corrects for B 0 inhomogeneity during the analysis. All analyses were performed on a voxel‐wise basis, and the data presented for each phantom are the mean ± standard deviation for a fixed‐area region of interest (ROI) over each phantom.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
In Equations (1)–5, ω is the offset frequency of interest, Z(ω) is the signal measured following saturation at the frequency ω, Z0 is the signal measured following saturation at ±100 ppm, , and Sn − pool is the signal from a simulated Z spectrum with n pools, and labile pool properties defined by those measured by a Bayesian model‐based algorithm,13 implemented in BayCEST as part of the FMRIB Software Library (www.fmrib.ox.ac.uk/fsl/baycest). CEST effects were measured for all metrics at ω = 2.8 ppm with δω = 1.4 ppm.
Three pools were fitted using BayCEST: the water pool at 0 ppm (W), the labile amine proton pool at 2.8 ppm (CEST) and an exchange pool centred at −3.5 ppm. BayCEST fits the Bloch–McConnell equations to the measured Z spectra with the exchange rate and relaxation times for each pool defined by Bayesian prior distributions. BayCEST measures fitted values of the exchange rate and relative concentration of the protons in each pool, and T 1 and T 2 relaxation times for all proton pools (Supplementary Figure S1). BayCEST was run for each phantom with ‘default’ values for the mean of the prior distributions for water T 1 (1.8 s) and T 2 (100 ms). Subsequently, the water T 1 and T 2 times measured from each phantom in the T 1 and T 2 maps were included as the means of the associated prior distributions in the model fitting (Supplementary Table S1). In both cases the T 1 and T 2 values remained as parameters within the fitting procedure to be estimated from the data.
CESTR* was calculated from the 2.8 ppm pool by simulating one‐pool (W only) and two‐pool (W + CEST) systems using only the fitted estimates of exchange rate and relative concentration, and measuring the difference in signal at 2.8 ppm (Supplementary Figure S2). This produced two values for CESTR*—one calculated with ‘default’ priors for water T 1 (1.8 s) and T 2 (100 ms), and a second with phantom specific measured T 1 and T 2 prior means—hereafter called ‘CESTR* with measured T 1/T 2 priors’. The fitted exchange rate was not used directly, as a degree of correlation exists between the fitted exchange rate and concentration.13 Further details of the fitting and analysis procedure for CESTR* can be found in the Supplementary Methods.
2.6. Determination of optimal metric
The relationship between the calculated CEST effect using each metric and the serially varied parameters was determined by linear regression, and its absolute value (in |% M 0|/parameter unit change) compared between phantom models using a t test corrected for multiple comparisons using the Holm–Sidak method.25 Statistical significance was defined as P < 0.05, which after correction gave an effective significance level of P < 0.003. These comparisons were used to determine whether pooling the data from the two phantom models was appropriate.
Subsequently, a further multi‐parameter linear regression model was used to determine the optimal analysis metric in terms of specificity. Data from both phantom models (tumour and naïve brain) were combined and fitted to a model of the form of Equation (6), which describes the response of an ideal CEST quantification metric (i.e. only dependent on pH and [BSA]).
| (6) |
The coefficients α , β , ε of Equation (6) are constants that describe the level of sensitivity of the experimentally measured data to the varied parameters in the phantoms. Using these coefficient values and the known pH and [BSA] for each phantom, theoretical CEST effects were calculated and correlated to the experimentally measured CEST effects for each metric. The R 2 values for these correlations were used as indications of the specificity of the metric to changes in only pH and [BSA]. The optimal metric was defined as that with the highest R 2 value for the correlation between calculated and experimentally measured CEST effects, which represents a metric with minimal contamination by T 1 and T 2 time.
2.7. Measurement of pH differences using optimal metric
For the optimal metric, differences in experimentally measured CEST effects were calculated between each pair of phantoms (ΔCEST = CEST1 − CEST2). These differences were tested for statistical significance, defined as a difference larger than the standard deviations on each CEST effect measurement added in quadrature .
For statistically significant differences in CEST effect, pH differences as measured by pH probe (‘Experimental ΔpH’) and back calculated from the linear regression coefficients from Equation (6) (‘Calculated ΔpH’) were correlated to verify the suitability of the metric for measuring pH differences.
3. RESULTS
3.1. Phantom validation
NMR spectra of the tissue and cellular models were compared. The metabolite peaks in spectra obtained from PCA‐extracted in vitro cultured 4T1‐GFP cells and the same cells grown in vivo as a subcutaneous tumour were very similar in magnitude (Figure 1A). Thus, in vitro cultured 4T1‐GFP cells are metabolically similar to an in vivo tumour. However, clear differences were seen in the distribution and magnitude of metabolite peaks from PCA‐extracted naïve mouse brain and in vivo tumour, revealing their distinctly different metabolite compositions (Figure 1B). Upon comparing the spectra from the lysate of in vitro cultured 4T1‐GFP cells and the representative phantom model (Figure 1C), the marked similarities in the magnitude of the broad protein lineshapes indicate that the phantom (extract) model is a reasonable approximation of the intracellular environment of 4T1‐GFP cells.
Figure 1.
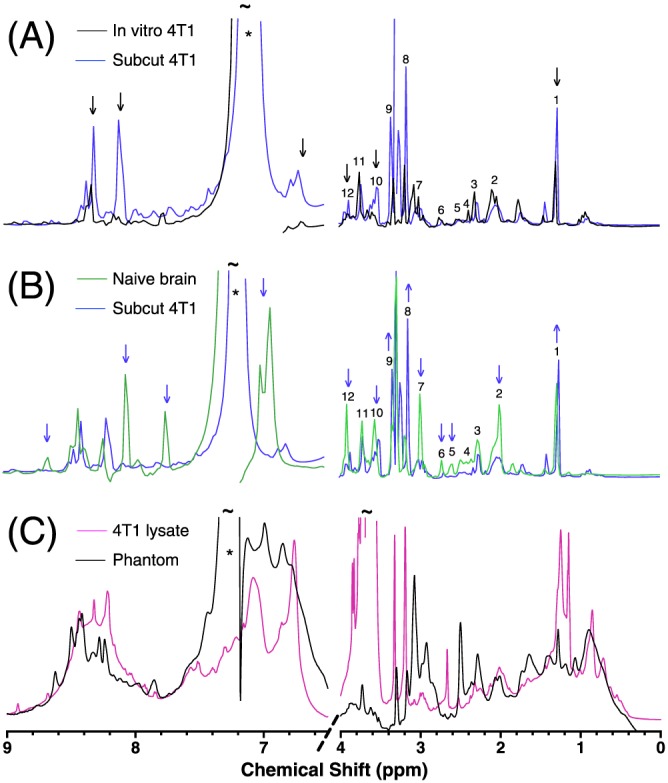
One‐dimensional 1H NMR spectra, showing (A), the metabolic similarity of 4T1‐GFP cells grown in vivo as a subcutaneous tumour ( ) or in vitro (
) or in vitro ( ) in culture flasks, (B), the metabolic distinctness of 4T1‐GFP mouse mammary carcinoma cells (
) in culture flasks, (B), the metabolic distinctness of 4T1‐GFP mouse mammary carcinoma cells ( ) from naïve mouse brain (
) from naïve mouse brain ( ) and (C), the similarity of the broad line shape component of the spectrum from cell lysate of 4T1‐GFP cells (
) and (C), the similarity of the broad line shape component of the spectrum from cell lysate of 4T1‐GFP cells ( ) to the PCA extract of the same cell line supplemented with 8% w/v BSA (
) to the PCA extract of the same cell line supplemented with 8% w/v BSA ( ). Coloured arrows signify relative differences between spectra, and * signifies signal from a contaminant from the PCA extraction procedure. ~ signifies points where the peaks exceed the axis limits. Numbers are metabolite identification: 1, Lac; 2, NAA; 3, Glu; 4, Gln; 5, NAA; 6, Asp; 7, Cr/PCr; 8, PC/GPC; 9, Tau; 10, Myo‐ins; 11, Asc/Gln/Glu/GSH; 12, Cr/PCr
). Coloured arrows signify relative differences between spectra, and * signifies signal from a contaminant from the PCA extraction procedure. ~ signifies points where the peaks exceed the axis limits. Numbers are metabolite identification: 1, Lac; 2, NAA; 3, Glu; 4, Gln; 5, NAA; 6, Asp; 7, Cr/PCr; 8, PC/GPC; 9, Tau; 10, Myo‐ins; 11, Asc/Gln/Glu/GSH; 12, Cr/PCr
Clear differences between the Z spectra from phantoms of BSA only and those containing 4T1‐GFP cell PCA extracts were evident in the −1.0 to −5.0 ppm region, and indicates nuclear Overhauser enhancement (NOE)‐mediated saturation of the water signal owing to the presence of the intracellular metabolites (Figure 2). The CEST effect centred at 2.8 ppm is also altered with increasing concentration of PCA‐extracted tissue.
Figure 2.
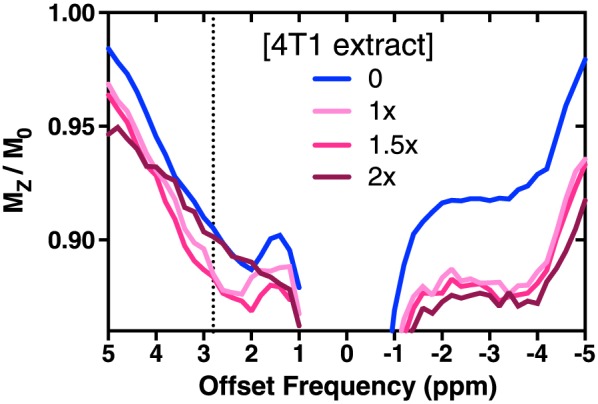
Z spectra of 8% w/v BSA phantoms at pH 7.2 supplemented with PCA extract from 4T1‐GFP cells, replicating metabolite concentrations of 1×, 1.5× or 2× intracellular levels. The 4T1‐GFP intracellular metabolites clearly alter the measured Z spectrum from the BSA‐only Z spectrum (0×). The CEST effect at 2.8 ppm broadens with increasing metabolite content, consistent with an increasing average chemical exchange rate
3.2. Quantification of CEST effects by multiple metrics
The relationships between the measured CEST effect at 2.8 ppm and the pH, BSA concentration, T 1 time and T 2 time were determined using multiple analysis metrics for phantoms containing BSA supplemented with extracts from either 4T1‐GFP cells or naïve mouse brain (Figure 3). The T 2 time was considered constant for increasing concentrations of gadolinium‐DTPA, and the T 1 time constant for increasing concentrations of iron nanoparticles, as these varied minimally compared with the objective relaxation time (Supplementary Figure S3).
Figure 3.
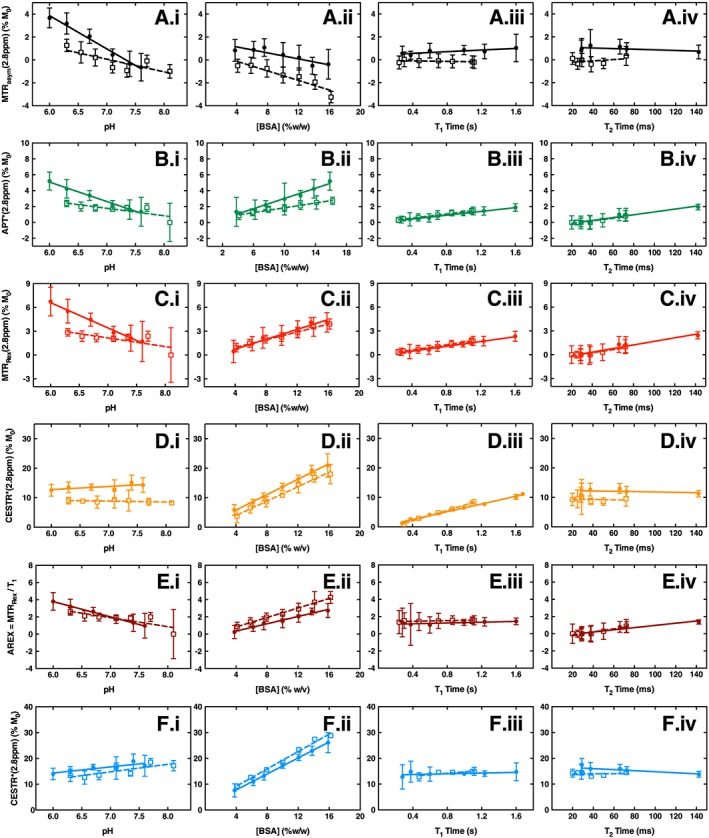
Linear regression relationships of MTRasym A, APT* B, MTRRex C, CESTR* calculated with default T 1/T 2 priors D, AREX E, and CESTR* calculated with measured T 1/T 2 priors F, as a function of pH (i), BSA content (ii), T 1 time (iii) and T 2 time (iv) for the CEST effect at 2.8 ppm in phantoms containing 8% w/v BSA and PCA extract from 4T1‐GFP cells (solid circles) and naïve mouse brains (open squares). Solid and dashed lines are the fitted linear regression relationships to tumour and naïve brain phantoms, respectively
Significance levels for all linear regression relationships are shown in Table 1. Significant decreases in MTRasym, APT* and MTRRex were observed with increasing pH, which is expected for the fast‐exchanging amine protons at this frequency21 (Figure 3A.i–C.i). Conversely, however, since CESTR* estimates the exchange rate and concentration directly from the Z spectrum, an increase in CESTR* (calculated with default T 1/T 2 priors) was seen as pH increased (Figure 3D.i). The AREX metric also showed a significant decrease as pH increased (Figure 3E.i), and the increase in CESTR* became significant when measured T 1/T 2 priors were included (Figure 3F.i).
Table 1.
P values for the linear regression fits of CEST effect as measured by the four analysis metrics compared, for each of the varied parameters (pH, [BSA], T 1 and T 2), in both phantom models. P values marked * are statistically significant results, defined as P < 0.05
| pH | [BSA] | T 1 Time | T 2 Time | ||
|---|---|---|---|---|---|
| 4T1‐GFP cell phantoms | MTRasym | <0.0001* | 0.006* | 0.04* | 0.25 |
| MTRRex | <0.0001* | <0.0001* | <0.0001* | 0.001* | |
| APT* | <0.0001* | 0.0004* | <0.0001* | 0.001* | |
| CESTR* (default T 1/T 2 priors) | 0.12 | <0.0001* | <0.0001* | 0.56 | |
| AREX | <0.0001* | <0.0001* | 0.12 | 0.003* | |
| CESTR* (measured T 1/T 2 priors) | 0.02* | <0.0001* | 0.32 | 0.11 | |
| Naïve brain phantoms | MTRasym | 0.02* | 0.002* | 0.33 | 0.46 |
| MTRRex | 0.05 | <0.0001* | <0.0001* | 0.006* | |
| APT* | 0.04* | <0.0001* | <0.0001* | 0.006* | |
| CESTR* (default T 1/T 2 priors) | 0.243 | <0.0001* | <0.0001* | 0.72 | |
| AREX | 0.03* | <0.0001* | 0.06 | 0.006* | |
| CESTR* (measured T 1/T 2 priors) | 0.03* | <0.0001* | 0.06 | 0.96 |
Significant increases in all metrics apart from MTRasym were evident with increasing protein concentration (Figure 3B.ii–F.ii). In contrast, MTRasym decreased as protein concentration increased (Figure 3A.ii). APT*, MTRRex and CESTR* (default T 1/T 2 priors) were found to be sensitive to changes in both proton relaxation times in both phantom models (Figure 3B.iii,iv–D.iii,iv), whilst MTRasym was sensitive only to changes in T 1 in the 4T1‐GFP phantom model (Figure 3A.iii,iv). Some measurements of MTRRex and APT* were negative because in these instances the relaxation time change resulted in no discernible CEST peak at 2.8 ppm (see Supplementary Figure S4). Since a negative CEST effect measurement is unphysical, these measurements were set to zero. As expected, AREX was insensitive to T 1 relaxation time variations in both phantom models, but sensitive to T 2 time changes (Figure 3E.iii,iv). CESTR* (measured T 1/T 2 priors) was the only metric insensitive to both relaxation times in both models (Figure 3F.iii,iv).
Significance levels for the comparisons of linear regression gradients between the two phantom models are shown in Table 2. Significant differences were found between phantom models for MTRasym, APT* and MTRRex as pH was varied, and for CESTR* with default T 1/T 2 priors as T 1 time was varied (Figure 3A.i–C.i,D.iii, P values in Table 2).
Table 2.
P values for the results of t tests comparing the linear regression gradient values for CEST effect measurements from 4T1‐GFP and naïve brain phantom. P < 0.05 was defined as statistically significant, with correction for multiple t tests using the Holm–Sidak method. P values marked * are statistically significant differences
| MTRasym | MTRRex | APT* | CESTR* (default T 1/T 2 priors) | AREX | CESTR* (measured T 1/T 2 priors) | |
|---|---|---|---|---|---|---|
| pH | 0.001* | 0.001* | 0.002* | 0.02 | 0.02 | 0.45 |
| [BSA] | 0.04 | 0.01 | 0.02 | 0.10 | 0.003 | 0.04 |
| T 1 time | 0.05 | 0.10 | 0.06 | 0.001* | 0.54 | 0.03 |
| T 2 time | 0.49 | 0.36 | 0.36 | 0.99 | 0.09 | 0.16 |
3.3. Determination of optimal metric
MTRasym, APT*, MTRRex and CESTR* with default T 1/T 2 priors all showed a significant sensitivity to serial variation in T 1 and T 2 time, indicating the contaminant effect that the water relaxation times have on these metrics when quantifying CEST effects. Of the two methods that incorporate compensation for relaxation times (AREX and CESTR* with measured T 1/T 2 priors), the CESTR* measurements showed minimal sensitivity to serial variation in either T 1 or T 2 time (Figure 3F.iii,iv). As expected, AREX was not significantly sensitive to variations in T 1 time, but did vary with T 2 time. Notably, CESTR* with measured T 1/T 2 priors was the only metric to show no significant dependence on T 1 or T 2 time in either phantom model, indicating the specificity of CESTR* to measuring changes in only the CEST pool properties (Table 1).
Correlation analysis between the experimentally measured CEST effects and the theoretically calculated CEST effects from Equation (6) yielded the highest R 2 value (0.88) for CESTR* with measured T 1/T 2 priors (Figure 4A–F). This high R 2 value means that CESTR* with measured T 1/T 2 priors is dependent only on pH and protein concentration. MTRasym, APT*, MTRRex and CESTR* with default T 1/T 2 priors (Figure 4A–D) display constant calculated CEST effect in many cases, because these metrics do not directly account for the effects of T 1 or T 2 variations, making it difficult to use these metrics for pH estimation. One contributing factor to the low R 2 values observed for MTRasym (0.53), MTRRex (0.14) and APT* (0.45) may be the significant difference in linear regression gradients between tumour and naïve brain phantom models as pH is varied. However, it is unlikely that this is the only factor, since AREX and CESTR* with default T 1/T 2 priors both display similarly low R 2 values (0.48 and 0.07 respectively) with non‐significant differences between phantom models. On this basis, the optimal metric was found to be CESTR* with measured T 1/T 2 priors.
Figure 4.
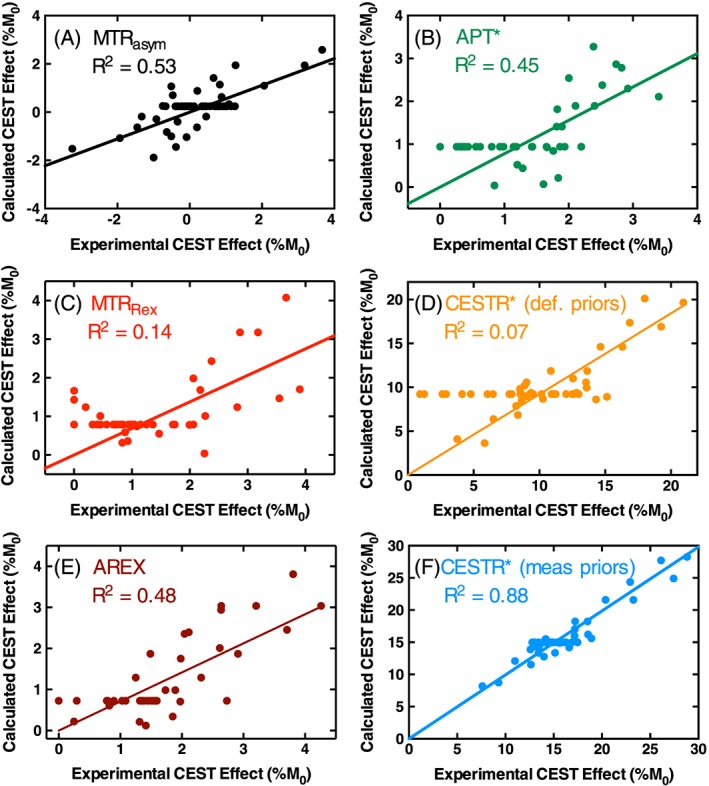
Correlations between calculated CEST effects from Equation (6) and the experimentally measured CEST effects in each phantom as measured by each analysis metric: MTRasym A, APT* B, MTRRex C, CESTR* calculated with default T 1/T 2 priors D, AREX E, and CESTR* calculated with measured T 1/T 2 priors F. R 2 values are MTRasym = 0.53, MTRRex = 0.14, APT* = 0.45, CESTR* with default priors =0.07, AREX =0.48 and CESTR* with measured priors =0.88
3.4. Measuring pH differences using CESTR*
Differences in the experimentally measured CESTR* values (with measured T 1/T 2 priors) from each phantom were measured and tested for statistical significance. A total of 28 ΔCESTR* values were found to be significant. For these differences, the experimentally measured ΔpH and the calculated ΔpH using a rearrangement of Equation (6) were correlated (Figure 5). These findings validate CESTR* as a reliable measure of ΔpH by CEST MRI, with a root mean square deviation for the correlation in Figure 5—and expected quantitative pH accuracy—of 0.6 pH units for the case of no variation in protein concentration.
Figure 5.
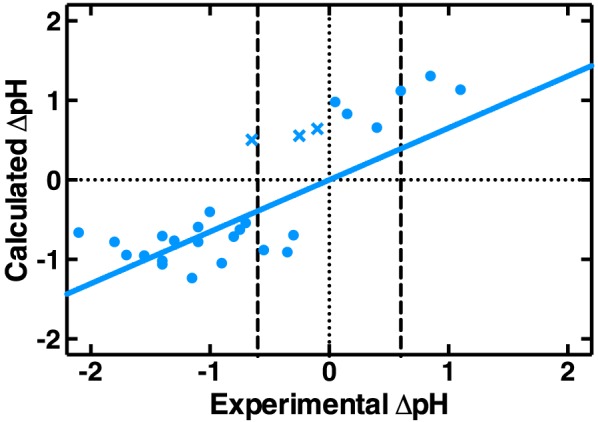
Correlation between ΔpH calculated using a rearrangement of Equation (6) for statistically significant ΔCESTR* measurements between phantoms, and the ΔpH experimentally measured by pH probe. The R 2 value is 0.61. Cross markers (X) indicate the data points where CESTR* incorrectly predicted the sign of the pH change
Further, considering the data points in distinct groups based on the magnitude of the experimental ΔpH value, CESTR* correctly predicted the sign of ΔpH in 94% of cases (16/17) where experimental ΔpH < −0.6 pH units and 100% of cases where experimental ΔpH > 0.6 pH units (3/3). For the group where experimental ΔpH was within ±0.6 pH units of zero, CESTR* was successful in 75% of cases (6/8).
4. DISCUSSION
The current study examines the sensitivity and specificity of various CEST MRI quantification methods, in novel phantom models that closely reflect the intracellular environment of brain metastases and naïve mouse brain. In contrast to all other metrics, CESTR* with measured T 1/T 2 priors was found to be sensitive only to variations in pH and [BSA] in both tumour and naïve brain phantom models. CESTR* can remove the effects of T 1 and T 2, which are known to vary with pathological changes in vivo,26 from the CEST measurement, allowing a more accurate quantification of the CEST effect. We propose, therefore, that CESTR* with measured T 1 and T 2 priors is the most specific metric for quantification of CEST MRI data. CESTR* with measured T 1/T 2 priors can be applied robustly both between samples, and between voxels within a single experiment, to measure pH differences with an accuracy of 0.6 pH units in these phantoms.
Other studies have suggested that the T 1 contamination of the CEST signal is counteracted by changes in water content in vivo, and that the CEST contrast in tumours originates from a higher mobile protein concentration.27 If this is the case, it may be difficult to quantify pH in tumours as both the pH and protein concentration may be changing simultaneously. However, as shown by this study and others,12, 28 T 1 correction is absolutely necessary for reliable, specific quantification of the CEST signal, regardless of the counteracting effect of water content. Assuming that the effects of T 1 and water content perfectly cancel may lead to inaccurate quantification of CEST effects in vivo in pathologies where only one of these parameters changes.
MTRasym measured from our phantoms decreased as the protein concentration increased, in contrast to previous studies.5, 10, 21 This discrepancy can be explained by the difference in saturation parameters used in the studies. In this study, a 7.8 s pulse train with CW equivalent power 0.8 μT was employed, which is preferentially sensitive to slowly exchanging protons. The effect of these saturation parameters is to enhance the NOE effects seen from the BSA and extracted metabolites in the phantoms. As the protein concentration increases, these NOE effects increase more than the CEST effects at 2.8 ppm, leading to a decreasing MTRasym. Other studies employing BSA phantoms21 or in vivo 5, 10 all used much shorter (4 s) and higher powers (1.3–1.5 μT), which are less sensitive to the slowly exchanging NOE effects.
Other methods not examined in this study can also be used to quantify the various contributions to a measured CEST effect, such as qCEST.14 However, qCEST separates the contributions of labile proton exchange rate and concentration to the Z spectrum by measuring the CEST effect as a function of the saturation power. When applied to a clinical setting this approach is impractical owing to acquisition duration and specific absorption rate (SAR) concerns. In addition, the phantom model used in this study does not include a contribution from macromolecular magnetization transfer, which may remain as a confounding issue in interpreting changes in CEST metrics in vivo. However, macromolecular magnetization transfer effects can be accounted for by CESTR* with measured T 1/T 2 priors by including another pool in the BayCEST fitting algorithm.
4.1. Sensitivity of CESTR* to pH changes in tumours
One major result of this phantom study is that CESTR* measurement is dependent on a good choice of prior values of T 1 and T 2 time used by the BayCEST fitting algorithm. This implies that there is insufficient information in a single Z spectrum for the BayCEST algorithm to accurately estimate water T 1 and T 2 times when provided with generic, rather than individually measured, values for the prior distributions. The CESTR* metric with default T 1/T 2 priors has been used to identify the ischemic penumbra in acute stroke patients,7 and to generate quantitative pH maps in healthy volunteers and acute stroke patients.3 The apparent success of these pH maps (i.e. that the anticipated drop in pH was observed in known stroke regions) may be due to the lack of variation in T 1 across the healthy brain and in the acute stage of stroke. In addition, the simulated CESTR*–pH calibration in that study was generated using a constant amide concentration of 100 mM.
However, assumptions of constant T 1 and amide concentration may not be valid when assessing tumours. Consequently, accurate estimations of both T 1 and labile proton concentration are necessary for reliable pH quantification in tumours using CESTR*. While T 1 is easy to measure in vivo, the labile proton concentration is much harder to quantify reliably. We have shown in this phantom study that CESTR*, with knowledge of the T 1 time and labile proton concentration, provides a means for immediate, quantitative and non‐invasive pH measurement, with an accuracy of 0.6 pH units based on the root mean square deviation of Figure 5. However, as the ΔpH measurements in Figure 5 were made on phantoms with known BSA concentration, application of this method in vivo is limited. Importantly, the non‐significant difference in sensitivities of CESTR* to pH in both tumour and normal brain phantoms implies that no manual tumour segmentation should be necessary when evaluating the pH of tumours using CESTR* in vivo.
Extracellular pH acidifications of the order of 0.6 pH units are not uncommon in tumours in vivo.9 Though intracellular pH changes of this order are rare, there are numerous cellular environments (mitochondria and other organelles) where the pH is very alkaline, and which may contribute to the CEST signal by virtue of the majority of their protein content being largely mobile.29, 30 The exact contribution of each of these compartments to the CEST signal measured in vivo remains to be elucidated.
5. CONCLUSION
Novel, realistic phantom models of the in vivo intracellular environment of brain metastases and naïve mouse brain have been developed to determine an analysis metric for quantification of CEST MRI data that is sensitive to only labile proton exchange rate and concentration. We demonstrate that the CESTR* metric with T 1 and T 2 time compensation overcomes many challenges facing interpretation of CEST MRI data. When combined with prior knowledge of protein concentration, CESTR* with T 1/T 2 compensation allows quantification of pH differences with a mean accuracy of 0.6 pH units. These results suggest that CEST MRI may enable pH differences between tumour and normal tissue to be quantified in vivo without the need for exogenous contrast agents.
Supporting information
Supplementary Figure S1: Demonstration of the applicability of the Bayesian Bloch‐McConnell fitting algorithm BayCEST to measured Z spectra. The measured data are from an 8% w/v BSA supplemented with 4 T1‐GFP PCA extract phantom at pH 6.0 (left) and pH 7.6 (right). The red line shows the result of the Bloch‐McConnell equation fitting with three pools. The residual between the measured data and fitted Z‐spectrum is also shown, demonstrating a good fit for both phantoms, with the largest residuals appearing around the water frequency.
The insets in each panel show a zoomed version of the data and Bayesian Bloch‐McConnell fit for offset frequencies 1–5 ppm. Looking at the raw Z spectra, it is apparent that two peaks appear at higher pH. However, in this study, a 3 pool model fits the low and high pH phantoms equally well (pH = 6.0 data are fitted with R2 = 0.9849, pH = 7.6 data fitted with R2 = 0.9892). Visually, however, it appears that the fits could be improved by moving to a 4 pool model at high pH. We have chosen to maintain the 3 pool model because we would be in danger of over‐fitting the measured Z spectra, and the results of this phantom study would have limited applicability to the in vivo environment.
Supplementary Figure S2: Graphical representation of the CESTR* calculation procedure. The W and W + CEST Z spectra are simulated using the Bloch‐McConnell equations. The exchange rate and concentration parameters used in the simulation of W + CEST are those fitted from the Bayesian Bloch‐McConnell fitting (see Supplem[Link]), and the T1 and T2 times of each pool are kept constant. CESTR* is calculated as the difference in Z‐spectrum signal at the frequency of interest between the 1‐pool and 2‐pool simulations.
Supplementary Figure S3: The measured variation in T2 time for varying concentration of gadolinium‐DTPA to adjust T1 time (A) and T1 time for varying concentration of iron nanoparticles to adjust T2 time (B), for tumour (solid circles) and naïve brain (open squares) phantoms. Solid and dashed lines show the linear regression of both relationships for tumour and naïve brain phantoms, respectively. In all cases a significant variation in both relaxation times is measured, highlighting the difficulty in altering relaxation times independently with contrast agents. However, the variation in T1 with varying iron nanoparticle concentration to change T2 was four times less (76% change in T2 vs. 18% change in T1). Similarly, the variation in T2 as gadolinium‐DTPA was added to adjust T1 time was much less (78% change in T1 vs. 34% change in T2). Hence, the T1 and T2 times were treated as remaining constant for increasing concentration of iron nanoparticles and gadolinium‐DTPA, respectively, since the change in the target relaxation time was at least twice that of the other relaxation time.
Supplementary Figure S4: Raw Z‐spectrum for a tumour phantom with T2 relaxation time of 29 ms, showing that at such short T2 relaxation times the broadening of the water lineshape in the Z‐spectrum prevents the delineation of any discernible CEST peak at 2.8 ppm. This gives Zref(2.8 ppm) < Z(2.8 ppm), and hence negative APT* and MTRRex values.
Supplementary Figure S5: Z‐spectrum (left) and MTRasym spectrum (right) acquired from a phantom containing only 3 M perchloric acid (PCA) used to extract the metabolites from 4 T1 cells and naïve brain tissue in this study. No CEST effect is discernible in the Z‐spectrum, indicating that no contaminant effect from the PCA is expected in our phantoms.
Supplementary Figure S6: Goodness‐of‐fit (R2) for a 3‐pool Bayesian Bloch‐McConnell fitting algorithm as shown in Supplem[Link] varies as the pH of the phantom changes. Goodness‐of‐fit is consistently high (> 0.976) for the full range of pH values.
Supplementary Table 1: Model parameter prior values used for Bayesian fitting of Bloch‐McConnell equations to measured Z‐spectra. Values are expressed as the mean ± standard deviation of a normal distribution.
Supporting info item
ACKNOWLEDGEMENTS
This work was funded by Cancer Research UK (grant number C5255/A15935), the CRUK & EPSRC Cancer Imaging Centre in Oxford (grant number C5255/A16466). K.J.R. was funded by a Medical Research Council studentship (MC_ST_U13080) and supplementary award (MR/K501256/1). Y.K.T. is funded by the UTAR Research Fund (project number IPSR/RMC/UTARRF/2015‐C1/T03) and the Wellcome Trust (grant number WT088877/Z/09/Z). A.J.B. is a BBSRC David Phillip's Research Fellow.
Ray, K. J. , Larkin, J. R. , Tee, Y. K. , Khrapitchev, A. A. , Karunanithy, G. , Barber, M. , Baldwin, A. J. , Chappell, M. A. , and Sibson, N. R. (2016) Determination of an optimally sensitive and specific chemical exchange saturation transfer MRI quantification metric in relevant biological phantoms. NMR Biomed., 29: 1624–1633. doi: 10.1002/nbm.3614.
REFERENCES
- 1. Zhou J, Payen JF, Wilson DA, Traystman RJ, van Zijl PC. Using the amide proton signals of intracellular proteins and peptides to detect pH effects in MRI. Nat Med. 2003a;9:1085–1090. [DOI] [PubMed] [Google Scholar]
- 2. van Zijl PC, Yadav NN. Chemical exchange saturation transfer (CEST): what is in a name and what isn't? Magn Reson Med. 2011;65:927–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Tee YK, Harston GWJ, Blockley N, et al. Comparing different analysis methods for quantifying the MRI amide proton transfer (APT) effect in hyperacute stroke patients. NMR Biomed. 2014;27:1019–1029. doi: 10.1002/nbm.3147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Zaiss M, Windschuh J, Paech D, et al. Relaxation‐compensated CEST‐MRI of the human brain at 7 T: unbiased insight into NOE and amide signal changes in human glioblastoma. Neuroimage. 2015;112:180–188. doi: 10.1016/j.neuroimage.2015.02.040 [DOI] [PubMed] [Google Scholar]
- 5. Zhou J, Tryggestad E, Wen Z, et al. Differentiation between glioma and radiation necrosis using molecular magnetic resonance imaging of endogenous proteins and peptides. Nat Med. 2011;17:130–134. doi: 10.1038/nm.2268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Goerke S, Zaiss M, Kunz P, et al. Signature of protein unfolding in chemical exchange saturation transfer imaging. NMR Biomed. 2015;28:906–913. doi: 10.1002/nbm.3317 [DOI] [PubMed] [Google Scholar]
- 7. Harston GWJ, Tee YK, Blockley N, et al. Identifying the ischaemic penumbra using pH‐weighted magnetic resonance imaging. Brain. 2015;138:36–42. doi: 10.1093/brain/awu374 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Hanahan D, Weinberg RA. Hallmarks of cancer: the next generation. Cell. 2011;144:646–674. doi: 10.1016/j.cell.2011.02.013 [DOI] [PubMed] [Google Scholar]
- 9. Gillies RJ, Raghunand N, Garcia‐Martin ML, Gatenby RA. pH imaging. A review of pH measurement methods and applications in cancers. IEEE Eng Med Biol Mag. 2004;23:57–64. [DOI] [PubMed] [Google Scholar]
- 10. Zhou J, Lal B, Wilson DA, Laterra J, van Zijl PC. Amide proton transfer (APT) contrast for imaging of brain tumors. Magn Reson Med. 2003b;50:1120–1126. [DOI] [PubMed] [Google Scholar]
- 11. Salhotra A, Lal B, Laterra J, Sun PZ, van Zijl PCM, Zhou J. Amide proton transfer imaging of 9 L gliosarcoma and human glioblastoma xenografts. NMR Biomed. 2008;21:489–497. doi: 10.1002/nbm.1216 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Xu J, Zaiss M, Zu Z, et al. On the origins of chemical exchange saturation transfer (CEST) contrast in tumors at 9.4 T. NMR Biomed. 2014;27:406–416. doi: 10.1002/nbm.3075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Chappell MA, Donahue MJ, Tee YK, et al. Quantitative Bayesian model‐based analysis of amide proton transfer MRI. Magn Reson Med. 2013;70:556–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Sun PZ, Wang Y, Dai Z, Xiao G, Wu R. Quantitative chemical exchange saturation transfer (qCEST) MRI—RF spillover effect corrected omega plot for simultaneous determination of labile proton fraction ratio and exchange rate. Contrast Media Mol Imaging. 2014;9:268–275. doi: 10.1002/cmmi.1569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Dixon WT, Ren J, Lubag AJM, et al. A concentration‐independent method to measure exchange rates in PARACEST agents. Magn Reson Med. 2010;63:625–632. doi: 10.1002/mrm.22242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Zaiss M, Xu J, Goerke S, et al. Inverse Z‐spectrum analysis for spillover‐, MT‐, and T1 ‐corrected steady‐state pulsed CEST MRI—application to pH‐weighted MRI of acute stroke. NMR Biomed. 2014;27:240–252. doi: 10.1002/nbm.3054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Desmond KL, Moosvi F, Stanisz GJ. Mapping of amide, amine, and aliphatic peaks in the CEST spectra of murine xenografts at 7 T. Magn Reson Med. 2013. doi: 10.1002/mrm.24822 [DOI] [PubMed] [Google Scholar]
- 18. Jones CK, Huang A, Xu J, et al. Nuclear Overhauser enhancement (NOE) imaging in the human brain at 7 T. Neuroimage. 2013;77:114–124. doi: 10.1016/j.neuroimage.2013.03.047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Serres S, Martin CJ, Sarmiento Soto M, et al. Structural and functional effects of metastases in rat brain determined by multimodal MRI. Integr Cancer Ther. 2014;134:885–896. doi: 10.1002/ijc.28406 [DOI] [PubMed] [Google Scholar]
- 20. Bhujwalla ZM, Aboagye EO, Gillies RJ, Chacko VP, Mendola CE, Backer JM. Nm23‐transfected MDA‐MB‐435 human breast carcinoma cells form tumors with altered phospholipid metabolism and pH: a 31P nuclear magnetic resonance study in vivo and in vitro. Magn Reson Med. 1999;41:897–903. [DOI] [PubMed] [Google Scholar]
- 21. McVicar N, Li AX, Gonçalves DF, et al. Quantitative tissue pH measurement during cerebral ischemia using amine and amide concentration‐independent detection (AACID) with MRI. J Cereb Blood Flow Metab. 2014. doi: 10.1038/jcbfm.2014.12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Banay‐Schwartz M, Kenessey A, DeGuzman T, Lajtha A, Palkovits M. Protein content of various regions of rat brain and adult and aging human brain. Age. 1992;15:51–54. doi: 10.1007/BF02435024 [DOI] [PubMed] [Google Scholar]
- 23. Delaglio F, Grzesiek S, Vuister GW, Zhu G, Pfeifer J, Bax A. NMRPipe: a multidimensional spectral processing system based on UNIX pipes. J Biomol NMR. 1995;6:277–293. [DOI] [PubMed] [Google Scholar]
- 24. Jin T, Wang P, Zong X, Kim S‐G. MR imaging of the amide‐proton transfer effect and the pH‐insensitive nuclear Overhauser effect at 9.4 T. Magn Reson Med. 2013;69:760–770. doi: 10.1002/mrm.24315 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Holm S. A simple sequentially rejective multiple test procedure. Scand J Stat. 1979;6:65–70. [Google Scholar]
- 26. Damadian R, Zaner K, Hor D, DiMaio T. Human tumors detected by nuclear magnetic resonance. Proc Natl Acad Sci U S A. 1974;71:1471–1473. doi: 10.1073/pnas.71.4.1471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Yan K, Fu Z, Yang C, et al. Assessing amide proton transfer (APT) MRI contrast origins in 9 l gliosarcoma in the rat brain using proteomic analysis. Mol Imaging Biol. 2015;17:479–487. doi: 10.1007/s11307-015-0828-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Zong X, Wang P, Kim S‐G, Jin T. Sensitivity and source of amine‐proton exchange and amide‐proton transfer magnetic resonance imaging in cerebral ischemia. Magn Reson Med. 2014;71:118–132. doi: 10.1002/mrm.24639 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Porcelli AM, Ghelli A, Zanna C, Pinton P, Rizzuto R, Rugolo M. pH difference across the outer mitochondrial membrane measured with a green fluorescent protein mutant. Biochem Biophys Res Commun. 2005;326:799–804. doi: 10.1016/j.bbrc.2004.11.105 [DOI] [PubMed] [Google Scholar]
- 30. Overly CC, Lee KD, Berthiaume E, Hollenbeck PJ. Quantitative measurement of intraorganelle pH in the endosomal–lysosomal pathway in neurons by using ratiometric imaging with pyranine. Proc Natl Acad Sci U S A. 1995;92:3156–3160. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figure S1: Demonstration of the applicability of the Bayesian Bloch‐McConnell fitting algorithm BayCEST to measured Z spectra. The measured data are from an 8% w/v BSA supplemented with 4 T1‐GFP PCA extract phantom at pH 6.0 (left) and pH 7.6 (right). The red line shows the result of the Bloch‐McConnell equation fitting with three pools. The residual between the measured data and fitted Z‐spectrum is also shown, demonstrating a good fit for both phantoms, with the largest residuals appearing around the water frequency.
The insets in each panel show a zoomed version of the data and Bayesian Bloch‐McConnell fit for offset frequencies 1–5 ppm. Looking at the raw Z spectra, it is apparent that two peaks appear at higher pH. However, in this study, a 3 pool model fits the low and high pH phantoms equally well (pH = 6.0 data are fitted with R2 = 0.9849, pH = 7.6 data fitted with R2 = 0.9892). Visually, however, it appears that the fits could be improved by moving to a 4 pool model at high pH. We have chosen to maintain the 3 pool model because we would be in danger of over‐fitting the measured Z spectra, and the results of this phantom study would have limited applicability to the in vivo environment.
Supplementary Figure S2: Graphical representation of the CESTR* calculation procedure. The W and W + CEST Z spectra are simulated using the Bloch‐McConnell equations. The exchange rate and concentration parameters used in the simulation of W + CEST are those fitted from the Bayesian Bloch‐McConnell fitting (see Supplem[Link]), and the T1 and T2 times of each pool are kept constant. CESTR* is calculated as the difference in Z‐spectrum signal at the frequency of interest between the 1‐pool and 2‐pool simulations.
Supplementary Figure S3: The measured variation in T2 time for varying concentration of gadolinium‐DTPA to adjust T1 time (A) and T1 time for varying concentration of iron nanoparticles to adjust T2 time (B), for tumour (solid circles) and naïve brain (open squares) phantoms. Solid and dashed lines show the linear regression of both relationships for tumour and naïve brain phantoms, respectively. In all cases a significant variation in both relaxation times is measured, highlighting the difficulty in altering relaxation times independently with contrast agents. However, the variation in T1 with varying iron nanoparticle concentration to change T2 was four times less (76% change in T2 vs. 18% change in T1). Similarly, the variation in T2 as gadolinium‐DTPA was added to adjust T1 time was much less (78% change in T1 vs. 34% change in T2). Hence, the T1 and T2 times were treated as remaining constant for increasing concentration of iron nanoparticles and gadolinium‐DTPA, respectively, since the change in the target relaxation time was at least twice that of the other relaxation time.
Supplementary Figure S4: Raw Z‐spectrum for a tumour phantom with T2 relaxation time of 29 ms, showing that at such short T2 relaxation times the broadening of the water lineshape in the Z‐spectrum prevents the delineation of any discernible CEST peak at 2.8 ppm. This gives Zref(2.8 ppm) < Z(2.8 ppm), and hence negative APT* and MTRRex values.
Supplementary Figure S5: Z‐spectrum (left) and MTRasym spectrum (right) acquired from a phantom containing only 3 M perchloric acid (PCA) used to extract the metabolites from 4 T1 cells and naïve brain tissue in this study. No CEST effect is discernible in the Z‐spectrum, indicating that no contaminant effect from the PCA is expected in our phantoms.
Supplementary Figure S6: Goodness‐of‐fit (R2) for a 3‐pool Bayesian Bloch‐McConnell fitting algorithm as shown in Supplem[Link] varies as the pH of the phantom changes. Goodness‐of‐fit is consistently high (> 0.976) for the full range of pH values.
Supplementary Table 1: Model parameter prior values used for Bayesian fitting of Bloch‐McConnell equations to measured Z‐spectra. Values are expressed as the mean ± standard deviation of a normal distribution.
Supporting info item


