Enhanced NMR Discrimination of Pharmaceutically Relevant Molecular Crystal Forms through Fragment-Based Ab Initio Chemical Shift Predictions

Abstract

Chemical shift prediction plays an important role in the determination or validation of crystal structures with solid-state nuclear magnetic resonance (NMR) spectroscopy. One of the fundamental theoretical challenges lies in discriminating variations in chemical shifts resulting from different crystallographic environments. Fragment-based electronic structure methods provide an alternative to the widely used plane wave gauge-including projector augmented wave (GIPAW) density functional technique for chemical shift prediction. Fragment methods allow hybrid density functionals to be employed routinely in chemical shift prediction, and we have recently demonstrated appreciable improvements in the accuracy of the predicted shifts when using the hybrid PBE0 functional instead of generalized gradient approximation (GGA) functionals like PBE. Here, we investigate the solid-state ¹³C and ¹⁵N NMR spectra for multiple crystal forms of acetaminophen, phenobarbital, and testosterone. We demonstrate that the use of the hybrid density functional instead of a GGA provides both higher accuracy in the chemical shifts and increased discrimination among the different crystallographic environments. Finally, these results also provide compelling evidence for the transferability of the linear regression parameters mapping predicted chemical shieldings to chemical shifts that were derived in an earlier study.

Short abstract

Fragment-based electronic structure methods allow nuclear magnetic resonance chemical shifts to be predicted with higher accuracy and lower computational cost. Higher-accuracy chemical shifts lead to increased discrimination between correct and incorrect structural assignments in the NMR crystallography of polymorphic molecular crystals.

Introduction

Molecular crystal structure is governed by a delicate balance among intra- and intermolecular interactions, and even small changes in the crystallization process may lead to different crystal packing motifs, or polymorphs. Despite having identical chemical compositions, different polymorphs often manifest significantly altered physical properties. In pharmaceutical applications, changes in crystal packing can significantly impact bioavailability, shelf life, and even intellectual property protection.¹⁻³ Modern pharmaceutical development involves extensive polymorph screening, and it is often important to identify the structures of the resulting crystals.

While single-crystal and powder X-ray diffraction remain the primary methods for crystal structure determination and fingerprinting solid forms, solid-state nuclear magnetic resonance (NMR) is an increasingly used alternative. The combination of solid-state NMR and powder X-ray diffraction has proven particularly potent for solving crystal structures.^4,5 NMR chemical shielding is a function of the local electronic structure, making it sensitive to both the molecular geometry and local crystallographic environment, and is therefore an excellent tool for investigating polymorphism. In addition to solving or confirming crystal structures, pharmaceutical companies increasingly rely upon NMR to monitor crystallization, test samples, and investigate new formulations, especially when crystal structures cannot be obtained easily.

However, translating an NMR spectrum into a 3-D crystal structure is challenging and often requires computational chemical shift predictions to facilitate spectral assignment. Chemical shift prediction is frequently used to confirm structures solved from powder X-ray diffraction,^4,6 to identify structures consistent with the experimental NMR spectrum,⁷⁻¹⁶ to assign NMR spectra,¹⁷⁻²¹ or even to help refine crystal structures.²¹⁻³⁰ Despite its sensitivity to local crystal packing, the changes in chemical shift across different polymorphs or crystallographic environments can be subtle. In sulfanilamide, for example, key ¹³C chemical shifts vary by only 1–3 ppm across three polymorphs that differ primarily in their hydrogen bonding networks.³¹ In α-testosterone, which has two testosterone molecules in the asymmetric unit (Z′ = 2), most of the differences between pairs of ¹³C shifts corresponding to the two crystallographically inequivalent molecules are less than 2 ppm.¹⁷

The ability to discriminate among distinct crystallographic environments is one of the fundamental theoretical challenges in NMR crystallography. This is especially true when trying to identify the relevant structure(s) from a large set of candidate structures generated via crystal structure prediction techniques.^9−14,32,33 Various strategies to address this discrimination challenge have been advanced in recent years. For example, chemical shifts for ¹H, ¹⁵N, and ¹⁷O nuclei can be more sensitive to changes in hydrogen bonding patterns than those for ¹³C, making those preferable to study in some cases.^11,34−39 Individual chemical shielding tensor components can also provide additional information about the crystallographic environment that is lost in the isotropic shifts.^13,14,28 Careful treatment of finite-temperature nuclear dynamics can also be important, even in the solid state.^15,40−48 Here we focus on a different strategy: can we increase discrimination among distinct crystallographic environments by improving the accuracy of the chemical shift prediction?

Since the advent of the gauge-including projector augmented wave (GIPAW) plane wave density functional theory (DFT) method in 2001,^49,50 it has become the de facto standard for chemical shift prediction in the solid state. GIPAW provides high-quality chemical shifts and has been successfully employed in many NMR studies, as discussed in recent reviews.^48,51,52 Despite its successes, the statistical errors obtained with GIPAW and the commonly used PBE density functional are comparable to the variations in chemical shifts that are often seen across different crystallographic environments or polymorphs. Benchmark tests on GIPAW PBE ¹³C chemical shifts in molecular crystals typically obtain errors around ∼2 ppm,^10,53−55 for instance, which is on par with the magnitude of the chemical shift resolution needed to distinguish known crystal forms of molecules such as testosterone or sulfanilamide. Reducing the errors in the predicted chemical shifts would improve discrimination in challenging NMR crystallography applications.

Before the widespread use of GIPAW DFT, molecular crystal chemical shift calculations often mimicked the crystalline environment using an individual molecule surrounded by a field of point charges^56,57 or by a few key neighboring molecules. Recently, there has been renewed interest in modernized versions of these sorts of methods. Thanks to increased computer power and efficient algorithms for chemical shift calculations⁵⁸⁻⁶² within the gauge-including atomic orbital (GIAO) formalism,⁶³ chemical shift prediction on larger clusters of molecules can now be performed routinely. Clusters consisting of ∼10–15 molecules within a few angstroms of a molecule in the asymmetric unit mimic the effect of the extended molecular crystal lattice on the chemical shielding of the central molecule very effectively. Various cluster-type models have also been employed in biological systems.⁶⁴⁻⁷⁷ When using the same density functional, the accuracy of these cluster models is competitive with GIPAW for several different nuclei.^53−55,78 However, the rapidly increasing computational cost with system size becomes a concern when computing shifts on a cluster of large molecules.

Fragment methods are similar to cluster models in that they treat one or more central molecules interacting with other nearby molecules in the crystal. However, they decompose those interactions into sums of contributions from small groups of molecules, or fragments. We have demonstrated that when coupled with electrostatic embedding, fragment methods allow one to predict isotropic ¹H, ¹³C, and ¹⁵N chemical shieldings with accuracy similar to both cluster methods and GIPAW, albeit with lower computational cost.^78,79

The key advantage of these cluster and fragment methods is that they enable the practical use of a wider range of electronic structure methods for chemical shift prediction. In particular, extensive molecular crystal benchmark testing indicates that hybrid density functionals predict appreciably higher-accuracy isotropic chemical shifts for several different nuclei.^55,78 In a plane wave method like GIPAW, hybrid density functionals require at least an order of magnitude more computational effort than generalized gradient approximation (GGA) functionals, which makes them impractical. In contrast, the computational cost premium for switching from a GGA to a hybrid functional when using Gaussian basis sets, as in fragment and cluster models, is only ∼50%. In other words, hybrid density functionals can be used routinely with these cluster and fragment methods.

High-accuracy chemical shielding calculations are of particular interest in examining NMR shift differences between polymorphs or solvates and between crystallographically unique molecules in a given crystal, i.e., in crystals for which Z′ is greater than one. Accordingly, we examine two polymorphic crystals—acetaminophen (a.k.a. paracetamol) and phenobarbital—as well as the monohydrate and neat forms of testosterone. The differences in intramolecular conformation among the different crystal forms of each molecule are small, so much of the variation in the chemical shifts stems from differences in the (intermolecular) crystallographic environments. Thus, these represent challenging cases for NMR discrimination.

We find that fragment and cluster models generally predict the same ¹³C and ¹⁵N spectral assignments as GIPAW. More significantly, we demonstrate that switching from a GGA functional to a hybrid one both provides higher-accuracy chemical shifts and increases discrimination among the different crystallographic environments found in these crystal forms. Finally, chemical shift referencing is always important in both experimental and theoretical studies. We demonstrate that the referencing models fitted in our previous benchmark studies⁷⁸ are highly transferable to the crystals studied here, underscoring their suitability for broader use.

Theory

Fragment-based chemical shift prediction techniques have been described previously.^{53−55,78,79} In brief, they rely on a many-body expansion for the shielding tensor

1

which can be derived by differentiating the many-body expansion for the energy with respect to the nuclear magnetic moment and the external magnetic field. This expansion decomposes the shielding tensor of atom A on molecule i in the unit cell into the shielding tensor on the isolated molecule (σ̃_i^A) plus corrections due to the interactions of that molecule with other molecules in the crystal. The leading corrections involve pairwise interactions of molecule i with nearby molecules (Δ²σ̃_ij), followed by nonadditive three-body (trimer) corrections (Δ³σ̃_ijk^A). The pairwise correction Δ²σ̃_ij is defined as the difference between the chemical shift of atom A in the dimer ij and the same atom in isolated monomer i

2

Note that monomer j does not contain atom A, so σ̃_j^A = 0. The nonadditive three-body correction Δ³σ̃_ijk is defined as

3

where all terms on the right-hand side of eq 3 which do not contain monomer i are zero. See ref (78) for more details.

Four different chemical shielding prediction models will be compared here. First, the two-body fragment model truncates this many-body expansion by neglecting long-range pairwise interactions and all three-body and higher terms. The two-body interactions are computed between the central molecule and any other molecule lying within a user-defined cutoff distance of the central one (typically R_2bd = 6 Å). Because the neglected long-range and many-body terms involve substantial contributions from polarization, their effects can be approximately captured via electrostatic embedding. Specifically, the one-body and two-body terms are calculated in a field of point charges that mimic the extended lattice.^55,78

Second, the cluster model performs a single supermolecular calculation on a central molecule surrounded by nearby molecules (typically those with any atom lying within 4 Å). This cluster calculation captures local pairwise and many-body effects explicitly. However, due to computational constraints that limit the overall size of the cluster, the cluster approach can miss potentially important longer-range interactions. Electrostatic embedding is employed here to capture some of the polarization arising from the extended lattice.

Third, the combined cluster/fragment approach seeks to achieve the best of both models. It describes the local interactions (out to 4 Å) with a cluster calculation, and longer-range interactions in a pairwise fashion (out to 6 Å). Again, electrostatic embedding is employed to approximate longer-range and missing many-body effects. Figure 1 summarizes these first three models. Fourth, fully periodic GIPAW calculations make no such truncation, so should be equivalent to the many-body expansion carried out to all orders.

Figure 1.

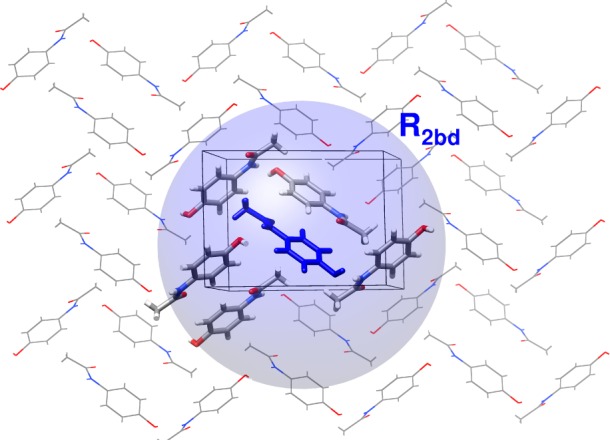
Illustration of the fragment, cluster and combined cluster/fragment models for computing NMR chemical shieldings. Depicted is a cross section from the optimized acetaminophen form I molecular crystal with the crystallographically unique molecule shown in blue. The fragment model includes pairwise interactions between the central molecule and any other molecule whose atoms lie within the distance R_2bd (blue sphere). The cluster model uses a cluster of molecules surrounding the central molecule, as represented by a licorice model. The cluster/fragment model combines the cluster with pairwise interactions involving other molecules in the blue sphere that are not present in the cluster. In all cases, electrostatic embedding is employed and extends well beyond the two-body cutoff region.

Benchmark studies on many different molecular crystals have demonstrated that, for a given density functional, the inexpensive two-body fragment model predicts ¹H, ¹³C, and ¹⁵N chemical shifts on par with the cluster, cluster/fragment, and GIPAW approaches.^55,78,79 For ¹⁷O, many-body effects are more important, and cluster-type and GIPAW models perform moderately better than the fragment approach. As noted in the Introduction, fragment methods also enable the routine use of hybrid density functionals like PBE0 instead of the GGA PBE, and this provides appreciable improvements in the chemical shifts. Table 1 summarizes the root-mean-square (rms) errors from these benchmark studies for ¹³C and ¹⁵N, which are the two nuclei considered here.

Table 1. Root-Mean-Square Errors (in ppm) between Predicted and Experimental Isotropic Chemical Shifts from Benchmarks Involving 25 Crystals/169 Shifts for ¹³C and 24 Crystals/51 Shifts for ¹⁵N⁷⁸.

	13C		15N
	PBE	PBE0	PBE	PBE0
two-body fragment	2.1	1.5	5.5	4.2
cluster	2.1	1.5	5.7	3.9
cluster/fragment	2.1	1.5	5.8	4.0
GIPAW	2.2	–	5.4	–

Computationally, the two-body fragment approach is the least expensive of the four models considered here, especially for large unit cells. The computational effort scales linearly with the number of molecules in the asymmetric unit, so calculating the chemical shifts for a polymorph with two independent molecules (Z′ = 2) requires roughly double the effort of one with Z′ = 1. On the other hand, the computational cost is independent of the total number of molecules Z in the unit cell. Fragment approaches are also inherently parallel, since each fragment calculation can be performed on a separate group of processors. This allows the calculation to scale efficiently to hundreds of processors, so that chemical shifts can be obtained very quickly when sufficient processors are available (e.g., often within a few hours of wall time for the sorts of crystals described in this work).

Computational Methods

Crystal Structures

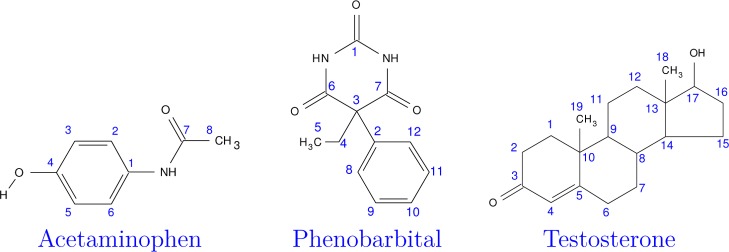
The three molecules studied here are depicted in Figure 2, along with their atom numbering. Room-temperature X-ray or neutron diffraction crystal structures for each polymorph were obtained from the Cambridge Structure Database (CSD). Experimental solid-state NMR data under magic angle spinning (MAS) conditions were taken from the literature. CSD reference codes and citations to the experimental data for each crystal are given as follows: Acetaminophen:^27,80 form I (HXACAN26⁸¹), form II (HXACAN23⁸²), and form III (HXACAN29⁸³); Phenobarbital:¹⁹ form II (PHBARB06⁸⁴) and form III (PHBARB09⁸⁵); Testosterone:¹⁷ α form (TESTON10⁸⁶) and β (monohydrate) form (TESTOM01⁸⁷).

Figure 2.

Molecular structures and atom numbering for the three species studied here.

All ¹³C and ¹⁵N chemical shifts reported here are referenced relative to neat TMS and external solid NH₄Cl, respectively.⁸⁸ The chemical shifts were measured experimentally at room temperature for acetaminophen and phenobarbital, and at 273 K for testosterone. Accordingly, testosterone might exhibit small discrepancies between the room temperature crystal structure used to predict the chemical shifts and the actual crystal structure at 273 K.

The study here focuses on isotropic chemical shifts. To the best of our knowledge, chemical shielding anisotropy (CSA) parameters have not been reported for most of the crystal forms studied here. They are available for form I acetaminophen,²⁷ and we previously compared GIPAW and fragment model predictions for those CSA parameters as part of a larger benchmark study on predicting ¹³C chemical shifts.⁵⁵

Computational Techniques

Experimental crystal structures were refined using all-atom geometry optimizations with fixed room temperature unit cell parameters. Using room-temperature lattice parameters mimics the effects of thermal expansion of the unit cell at finite temperatures, though it does not compensate for other finite-temperature dynamical effects. All geometry optimizations were carried out using the freely available, open-source Quantum Espresso software package.⁸⁹ The PBE⁹⁰ density functional and the D2 dispersion correction,⁹¹ ultrasoft pseudopotentials with a plane wave cut off of 80 Ry, and a 3 × 3 × 3 Monkhorst–Pack k-point grid were used for all geometry optimizations. We used the pseudopotentials H.pbe-rrkjus.UPF, C.pbe-rrkjus.UPF, N.pbe-rrkjus.UPF, O.pbe-rrkjus.UPF, S.pbe-n-rrkjus_psl.0.1.UPF from http://www.quantum-espresso.org. Structure overlays and root-mean-square deviations (RMSD) between the optimized and experimental structures are provided in Supporting Information. RMSD values in 15-molecule clusters are typically 0.05–0.15 Å (excluding hydrogen atoms).

Isotropic chemical shieldings were computed on the relaxed structures using the fragment, cluster, cluster/fragment, and GIPAW techniques. For the fragment-based techniques, crystal structure fragmentation out to a 6 Å two-body radius from the asymmetric unit was carried out using our hybrid many-body interaction (HMBI) code.⁹²⁻⁹⁴ All cluster-based calculations used a 4 Å cluster to include many-body effects involving nearest-neighbor molecules. Individual fragment shielding tensor calculations were performed using Gaussian09⁹⁵ with the PBE0⁹⁶ and PBE⁹⁰ density functionals and numerical integration grid involving 150 radial points and 974 angular Lebedev points.

Atomic point-charges were computed for each crystal using distributed multipole analysis,^97,98 and point charge embedding out to 30 Å was employed in all fragment and/or cluster calculations. Locally dense basis sets^99,100 were used for increased computational efficiency. A 6-311++G(2d,p) basis was used on the molecule(s) of interest, 6-311G(d,p) on all atoms within 4 Å of the central molecule, and 6-31G on more distant atoms. See our previous work for more detailed discussion of these protocols.^78,101

Gauge-including projector augmented wave (GIPAW) chemical shielding calculations were performed using CASTEP¹⁰² with the PBE functional, ultrasoft pseudopotentials generated on-the-fly and an 850 eV (62.5 Ry) plane wave basis set cut off. Electronic k-points were sampled on a Monkhorst–Pack grid to give a maximum separation between k-points of 0.05 Å^–1. The basis set cut off and k-point density were chosen based on previous testing⁷⁸ to converge relative chemical shifts to better than 0.01 ppm. Full space-group symmetry was used in all GIPAW calculations. For consistency with the other calculations reported here, the same Quantum Espresso-optimized crystal structures were used in the CASTEP calculations without further relaxation. We previously found that GIPAW chemical shifts obtained from crystal geometries optimized with either Quantum Espresso or CASTEP differ by less than 0.1 ppm in root-mean-square error relative to experiment for a set of 169 ¹³C isotropic chemical shifts.^55,78

Data Analysis

Experimentally observed isotropic chemical shifts δ^A are reported relative to a reference compound. Therefore, the computed absolute isotropic shieldings σ^A must be appropriately referenced to compare with the experimental values. Although numerous techniques exist for referencing the predicted shifts,¹⁰³ one particularly useful method uses a linear regression model of the form

4

where a and b are obtained via a linear least-squares fit between calculated shieldings and experimental shifts. In the absence of systematic error, slope a would take a value of −1, and slope b would represent the absolute shielding of the reference compound. Allowing a to deviate from −1 helps compensate for systematic errors in the predicted shieldings. Systematic errors can arise from, for example, basis set incompleteness, limitations of the approximate density functionals used, and from the neglect of nuclear dynamics, zero-point vibrational energy, and other nuclear quantum effects.

The linear regression parameters used for ¹³C and ¹⁵N here were obtained from our recent benchmark study of 25 crystals/169 ¹³C isotropic shifts and 24 crystals/51 ¹⁵N isotropic shifts.⁷⁸ Note that form I acetaminophen was included in the ¹³C benchmark data set, but none of the other polymorphs studied in the current work were present in the training set upon which the linear regressions were fitted. The specific regression parameters used for each nucleus type and each of the four theoretical models are listed in Table 2.

Table 2. Linear Regression Parameters Used for ¹³C and ¹⁵N Nuclei, Which Were Obtained by Fitting to Benchmark Test Sets Consisting of 169 ¹³C and 51 ¹⁵N Isotropic Chemical Shifts⁷⁸.

	13C		15N
	slope	intercept	slope	intercept
PBE0
two-body fragment	–0.9676	179.58	–1.0201	197.84
cluster	–0.9657	179.42	–0.9978	196.87
cluster/fragment	–0.9661	179.49	–0.9997	197.15
PBE
two-body fragment	–1.0808	180.43	–1.0808	197.53
GIPAW	–0.9902	169.19	–1.0165	184.98

Two statistical metrics are used here to assess the quality of the predicted shifts. The first is the RMS error between the predicted and experimental shifts. The second is a reduced χ-squared analysis, χ̃², which provides a measure of how consistent the errors observed for a given set of predicted shifts are with the expected distribution of errors. The χ̃² is computed as

5

where N is the number of isotropic shifts, δ_i^pred is the predicted chemical shift, δ_i is the experimentally observed chemical shift, and σ_rms is the width of the expected error distribution. Here, the σ_rms for each model/nucleus type is given by the RMS errors for the benchmark test sets summarized in Table 1.

Smaller χ̃² values indicate that the errors for a given system are more consistent with the errors one expects based on the benchmark sets. Those benchmark error distributions are roughly Gaussian, albeit with longer tails (i.e., large errors occur more frequently than one would expect for an ideal normal distribution).⁷⁸ This means that larger χ̃² values are moderately more probable than one would typically expect, but they still provide a useful metric for comparing different potential assignments.

In many ways, the differences in χ̃² values for different potential assignments are more important than the values themselves. In several cases discussed later in this work, the χ̃² values computed with PBE are smaller than those from PBE0, even though the PBE RMS errors are larger than the PBE0 ones. This simply reflects the larger uncertainty (σ_rms) expected for PBE than for PBE0 based on the benchmark sets. Accordingly, larger errors are more likely to occur when using PBE on the systems here, and they therefore do not skew the PBE χ̃² values as much. On the other hand, the differences among χ̃² values computed with a given method for different shift assignments indicate the ability of that method to discriminate between correct and incorrect assignments. This is an important consideration when using NMR for validation of proposed crystal structures. To investigate this, we evaluate χ̃² summed over all crystal forms of each molecule for the correct assignment of measured chemical shifts to the monomers in each structure, as well as for all possible permutations where the observed chemical shifts are assigned to the incorrect monomers. These differences in χ̃² will be the primary focus of the discussion of the results.

Results and Discussion

For each of the three chemical systems examined here, we compare the performance of GIPAW and the two-body fragment model with the PBE density functional to check for the similarity between GIPAW and fragment predictions. Then we investigate how the quality of the predictions changes upon switching to the PBE0 functional using the two-body fragment, cluster, and cluster/fragment models. The ability of each method to discriminate between correct and incorrect assignments of the measured chemical shifts to the known crystal structures is then examined using the χ̃² calculations.

Acetaminophen

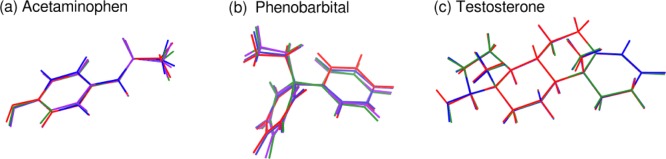
Acetaminophen (a.k.a. paracetamol) is a widely used, over-the-counter pain reliever and fever reducing agent which adopts three known crystal polymorphs (forms I, II, and III). The solid state versatility of acetaminophen serves as an excellent example of how crystal packing impacts the drug manufacturing process. Form I is easily isolated and is characterized by puckered hydrogen-bonded sheets (see Figure 3a). This packing configuration inhibits shearing, which in turn impacts the compressibility of the solid and the tableting process. On the other hand, form II is more difficult to isolate and consists of flat hydrogen-bonded sheets which are more amenable to direct compression (Figure 3b).^80,104−109 Form III, with two molecules in the asymmetric unit, consists of alternating layers of symmetrically independent, flat two-dimensional sheets (Figure 3c). Historically, form III has been much more difficult to obtain,^109,110 and its structure was solved only in 2009.⁸³ The intramolecular acetaminophen geometries are very similar across all four crystallographically unique molecules which occur in the three polymorphs, with only subtle variations in the hydroxyl and methyl groups. Structure overlays among the four monomers (Figure 4a) find root-mean-square deviations (rmsd) of only 0.07–0.19 Å for the non-hydrogen atoms. The two monomers in form III are the most similar (rmsd 0.07 Å), followed by form I and form II (rmsd 0.09 Å). Accordingly, much of the variation in the observed NMR chemical shifts across the different polymorphs stems from differences in the crystallographic environment, rather than changes in the intramolecular geometry. See Supporting Information for a more detailed discussion of intra- versus intermolecular contributions to the chemical shielding in these systems.

Figure 3.

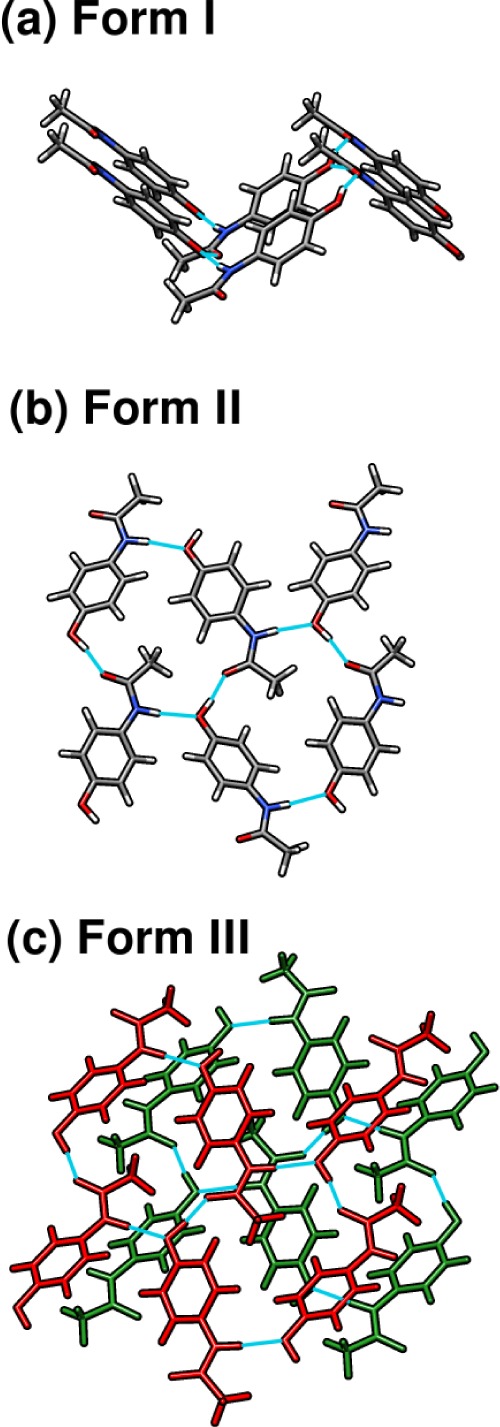
Optimized acetaminophen crystal structures for (a) form I showing puckered hydrogen-bonded sheets, (b) form II showing flat hydrogen-bonded sheets, and (c) form III with two independent flat hydrogen-bonded sheets (colored red and green) which are similar to the sheets found in form II.

Figure 4.

Monomer overlays for the crystallographically unique monomers in each set of crystals. (a) Acetaminophen: forms I (red), II (blue), IIIa (green), and IIIb (purple). (b) Phenobarbital: forms IIa (red), IIb (blue), IIc (green), and III (purple). (c) Testosterone: αu (red), αv (blue), and β (green).

The literature contains multiple sets of ¹³C shifts for form I.^27,80,111 Data from ref (80) is used here because it includes ¹³C and ¹⁵N chemical shifts for all three forms. With revised referencing, the form I ¹³C shifts from ref (80) are consistently 0.3–0.4 ppm lower in frequency than the more recent ones reported by Harper et al.²⁷ Similarly, the re-referenced values for the form I ¹⁵N isotropic shift from ref (80) agree with a more recent study to within ∼0.1 ppm.²⁸ See Supporting Information for referencing details.

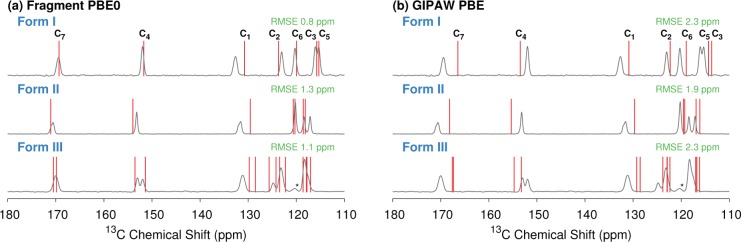
Figure 5 compares the experimental and predicted ¹³C isotropic chemical shifts using (a) fragment PBE0 or (b) GIPAW PBE for the three acetaminophen polymorphs. Both models predict chemical shifts in good agreement with the experimental spectra. To our knowledge, the experimental structure of form III solved via crystal structure prediction and powder X-ray diffraction⁸³ has not been validated against the NMR spectrum. The consistency between the predicted and experimental spectra here provides additional support for this structure.

Figure 5.

Overlay of experimental acetaminophen spectra⁸⁰ and predicted shifts (in red) for (a) the two-body fragment PBE0 calculations and (b) GIPAW PBE calculations. The C8 methyl peak at 23 ppm is not shown.

Because they arise largely from differences in intermolecular packing, the variations in experimental ¹³C shifts among the three polymorphs are often subtle. For instance, the minor differences in the hydrogen bonding to oxygen or nitrogen atoms between polymorphs lead to differences in ¹³C chemical shifts (C1, C4, and C7) of only ∼1 ppm. Nevertheless, the individual peak assignments suggested by both two-body PBE0 and GIPAW PBE are very similar. Both reproduce the general trends in peak positions across the three polymorphs. The main difference between the two models occurs for the C3/C5 peaks near ∼115–118 ppm in all three structures. The differences in chemical shift among these peaks is ∼1 ppm or less in each polymorph. Interestingly, both two-body PBE and two-body PBE0 predict C5 at lower frequency than C3, while the cluster, cluster/fragment, and GIPAW results predict the opposite ordering (see Table S1). In other words, the ordering of these two resonances appears to be sensitive to many-body effects.

A recent ¹H/¹³C heteronuclear correlation and ¹³C shielding tensor study on form I suggests the GIPAW and cluster-based model assignment is correct for form I,²⁷ and it is used throughout this work. For the sake of computing RMS errors below, we assume the GIPAW and cluster-based model assignment of C3/C5 is correct for form II as well, though this is uncertain. In form III, C3 and C5 are unresolved experimentally.

The ordering of C2 and C6 in form II shows similar disagreement between the two-body models versus the cluster and GIPAW results. In this case, the predicted difference in shifts between the two atoms is even smaller, at ∼0.5 ppm or less, while the two experimental shifts are unresolved. In all of these cases where the models disagree on the shift ordering, the differences in chemical shift between the resonances are small compared to the benchmark ¹³C RMS errors (Table 1). In other words, such differences probably cannot be resolved with confidence with either GIPAW or fragment methods. Overall, the RMS error across all 24 ¹³C chemical shifts is 2.0 ppm for GIPAW/PBE and 1.9 ppm for two-body PBE. Fragment, cluster, and cluster/fragment methods using the PBE0 hybrid functional nearly halve the overall RMS error to 1.1–1.2 ppm (Figure 6).

Figure 6.

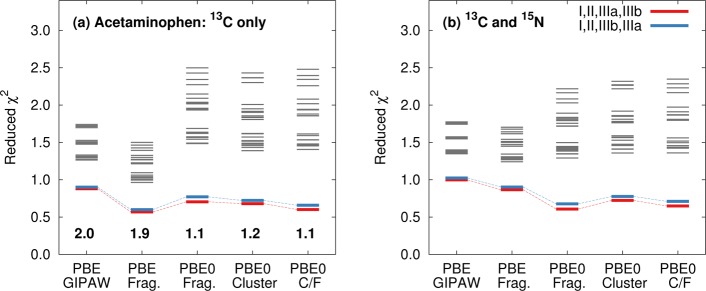
Reduced χ² analysis using (a) ¹³C or (b) ¹³C and ¹⁵N isotropic shifts for the 24 possible acetaminophen polymorph assignments using fragment, cluster, and cluster/fragment methods. The best assignment (I, II, IIIa, IIIb) is shown in red, while the blue line indicates the assignment that swaps the two monomers in form III. Gray lines correspond to other possible assignments. The ¹³C RMS errors (in ppm) for the best assignment with each model are reported near the bottom of (a).

The three polymorphs contain four unique ¹⁵N chemical shifts. Figure 7 compares the experimental and predicted shifts. All the theoretical methods predict the shifts to occur at too high of chemical shifts compared to experiment. The largest errors versus experiment occur with GIPAW PBE (RMSE 7.5 ppm), while the two-body fragment PBE0 model gives the best agreement (RMSE 3.6 ppm). Interestingly, all the models tested here predict that the form I nitrogen shift should lie at lower chemical shift than the form IIIa one, contrary to the experimental results. Of course, all four experimental shifts span only 3.3 ppm, which is small relative to the ∼4–6 ppm RMS errors found in the nitrogen benchmarks (Table 1).⁷⁸

Figure 7.

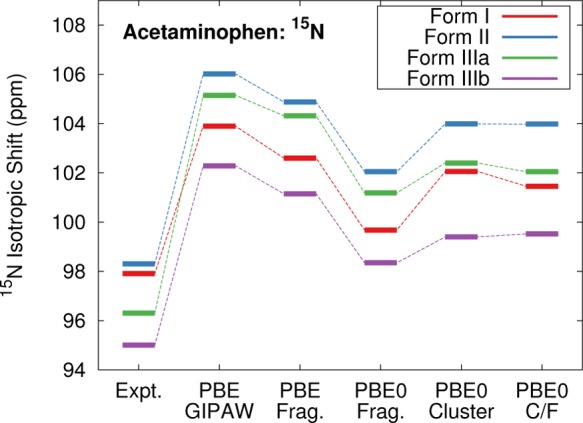
Comparison of the predicted and experimental ¹⁵N isotropic chemical shifts for the three polymorphs of acetaminophen.

While the good agreement between predicted and experimentally observed chemical shifts is valuable, a more challenging question is to what extent can the chemical shift predictions discriminate among the different crystallographic environments of the acetaminophen molecules found in the various polymorphs? The three polymorphs provide a total of four crystallographically unique molecules: forms I and II each contribute one and form III contributes two. There are 24 possible ways one can assign the predicted shifts from these four crystallographically unique molecules to the experimental shifts (assuming the carbon atom assignments within the monomer are fixed according to the discussion above). Figure 6 illustrates the reduced χ² values for each of the 24 possible assignments using either the ¹³C isotropic shifts or both the ¹³C and ¹⁵N isotropic shifts as computed with the various different models.

Several features stand out in Figure 6. First, the experimental assignment of the two inequivalent monomers in form III is unknown, but all five models considered predict the same assignment to have the smallest χ̃² values (I, II, IIIa, IIIb in Figure 6). However, the methods cannot clearly distinguish this monomer assignment from the one that swaps the two monomers in form III. The difficulty distinguishing these crystallographically unique monomers in form III is unsurprising, since the two molecules adopt nearly identical intramolecular geometries (rmsd 0.07 Å) and are in very similar crystallographic environments, which results in overlap of most of the ¹³C shifts. Only the pair of peaks corresponding to C4 are clearly resolved in the experimental spectrum, and those two resonances are separated by only ∼1 ppm. We also note that, despite the geometric similarity of the hydrogen bonded layers in polymorphs II and III, the methods all effectively discriminate between the molecular environments in those two polymorphs: χ̃² increases significantly if the set of shifts for either monomer in form III is swapped with those of form II. Although the molecules in forms I and II adopt very similar intramolecular conformations, their ¹³C spectra are comparatively easy to distinguish (particularly near 120 ppm) due to the appreciable differences in the crystallographic environments.

Second, although the RMS errors with PBE are almost twice as large as those from PBE0, the PBE χ̃² values tend to be smaller than those from PBE0. This reflects the fact PBE exhibits broader error distributions than PBE0 in the benchmark sets,⁷⁸ which leads to a larger denominator in eq 5. A more useful interpretation of these χ̃² plots focuses on the resolution between different crystallographic environments. The hybrid PBE0 functional provides increased separation among the χ̃² values for different potential assignments, which corresponds to increased discrimination among the different crystallographic environments. Interestingly, the more expensive combined cluster/fragment PBE0 mode exhibits marginally smaller RMS errors than the fragment PBE0 model, but it provides no additional discrimination among the monomer assignments.

Third, combining both ¹³C and ¹⁵N shift predictions (Figure 6b) does not appreciably alter the discrimination among the different potential assignments relative to the ¹³C-only data (Figure 6a). As noted above, the ∼3 ppm variations among the four unique ¹⁵N shifts are smaller than the ∼4–6 ppm errors expected from the ¹⁵N benchmark set, so the χ̃² analysis does not readily discriminate among the different potential ¹⁵N shift assignments in acetaminophen. The low discriminatory power of ¹⁵N compared to ¹³C shifts is unsurprising given the nature of the structural differences between the three polymorphs: the hydrogen bonding environment around the nitrogen atom in each polymorph is nearly the same in each structure, while the differences in the geometry of the layers and the way that these layers are packed has a much stronger influence on the crystalline environments of the carbon atoms (and hence the ¹³C shifts).

Phenobarbital

Phenobarbital (5-ethyl-5-phenyl-2,4,6(1H,3H,5H)-pyrimidine-trione) is a widely administered barbiturate and has been in clinical use for close to a century. With 12 polymorphs reported in the literature to date,¹¹² only a few of which have been structurally characterized,^112,113 phenobarbital makes a particularly interesting test-case for assessing the accuracy of NMR chemical shielding calculations.¹⁹ In the present work, we examine polymorph II (Z′ = 3) and III (Z′ = 1), for which experimental X-ray crystal structures, ¹³C, and ¹⁵N NMR isotropic chemical shifts have been reported. The experimental shifts have previously been assigned with the help of GIPAW.¹⁹

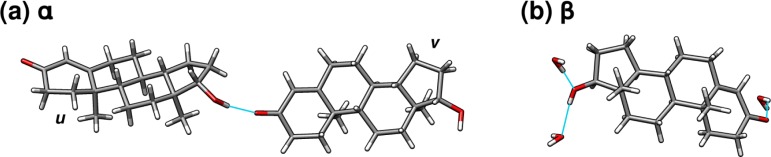
Phenobarbital is more flexible than acetaminophen, which leads to two slightly different intramolecular conformations among the four crystallographically unique monomers found in these two polymorphs. Figure 4b overlays the four monomer structures. The conformation of molecules IIa and IIb is very similar (rmsd 0.12 Å), as is the conformation for molecules IIc and III (rmsd 0.08 Å). However, these two pairs differ from each other by 0.28–0.36 Å in rmsd, due primarily to differences in the dihedral angles among the moieties surrounding the quaternary carbon.

Despite these modest differences in intramolecular conformation, much of the chemical shielding variation stems from intermolecular interactions (see Supporting Information), particularly the hydrogen bonding patterns (Figure 8). The molecules in polymorph III form linear chains consisting of pairs of N–H···O hydrogen bonds (Figure 8b). The same chains are formed by monomers a and c in polymorph II (blue and red molecules in Figure 8a). The third crystallographically unique molecule b in form II hydrogen bonds to monomer a, connecting the chains into a two-dimensional motif.

Figure 8.

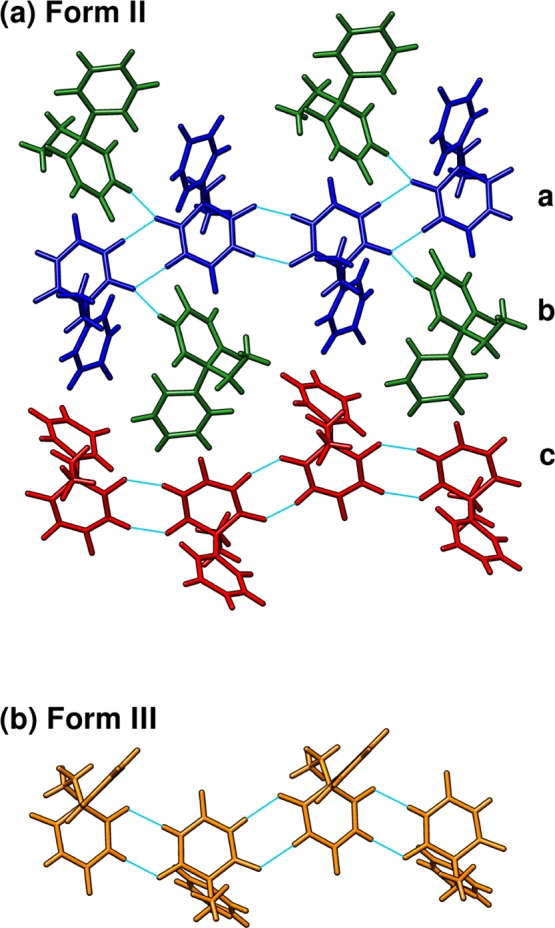
(a) Two hydrogen bonding motifs in phenobarbital form II colored according to symmetry equivalency. (b) Depiction of the linear chain hydrogen-bonding motif in form III.

The similarities between the linear hydrogen-bonded chains and intramolecular conformation manifests in similar experimental isotropic ¹³C chemical shieldings, provided in Table 3. The experimental chemical shifts for the carbonyl carbons (C6 and C7) which are involved in hydrogen bonding in form II monomer c and form III differ by 1 ppm or less, while the same shifts on form II monomers a and b differ from the c ones by ∼3 ppm. Furthermore, the observed chemical shifts correlate nicely with the hydrogen bonding patterns. The C4/C6 signal for form II molecule a exhibits the highest frequency chemical shift and displays the greatest degree of hydrogen bonding, having both strong hydrogen bonds (blue linear chain in Figure 8) and weaker hydrogen bonds to molecule b. Molecule b, on the other hand, which has no hydrogen bonds at C4 or C6, exhibits the lowest-frequency chemical shifts.

Table 3. Experimental and Calculated ¹³C Isotropic Chemical Shifts (in ppm) for Phenobarbital Forms II and III^a.

	form IIa		form IIb		form IIc		form III
carbon	expt.	calc.	expt.	calc.	expt.	calc.	expt.	calc.
C1 – Carbonyl	147.15	147.53	148.91	149.43	147.15	147.80	149.01	149.00
C2 – Ispo	136.00	133.02	137.17	137.54	137.17	137.17	137.56	136.94
C3 – Quaternary	61.68	63.50	61.00	62.15	62.37	63.46	62.27	63.27
C4 – Methylene	30.35	33.78	32.21	36.10	27.22	28.74	27.12	28.63
C5 – Methyl	6.86	8.67	7.93	9.53	8.91	10.47	11.36	12.98
C6 – CO (edge)	177.41	179.70	169.87	171.61	173.20	175.19	174.20	176.89
C7 – CO	177.41	178.30	173.20	174.44	174.96	175.79	174.20	175.89
C8 – Ortho (edge)	125.76	125.02	127.02	127.10	125.40	124.93	127.57	128.12
C9 – Meta (edge)	131.39	131.12	130.18	130.72	133.74	134.39	130.70	130.29
C10 – Para	132.41	133.08	129.30	129.32	130.18	131.60	129.53	129.18
C11 – Meta	132.81	130.19	127.02	126.90	130.18	130.57	129.92	130.93
C12 – Ortho	129.70	131.72	127.02	128.20	125.76	126.52	127.57	128.26
RMSE		1.95		1.46		1.09		1.24

^aPredicted shieldings are reported for two-body fragment calculations using PBE0.

Table 3 provides the predicted isotropic ¹³C chemical shifts using a two-body fragment model with PBE0 for each crystallographically unique molecule in phenobarbital forms II and III, and the results from GIPAW PBE and two-body fragment PBE0 are plotted in Figure 9. Complete predicted shieldings for the other computational methods used in this study are provided in Table S2 of the Supporting Information. The carbon atoms in Table 3 are labeled using the same convention used by Abraham et al.¹⁹ designating ring carbons which are in closer proximity to the adjacent ring as “edge”. This data clearly shows that both trends regarding the impact of hydrogen bonding on the chemical shifts mentioned above are faithfully reproduced at the fragment level. The overall RMS errors for fragment PBE0 are a couple tenths of a ppm smaller than those from either fragment PBE or GIPAW PBE (1.5 vs 1.7 ppm).

Figure 9.

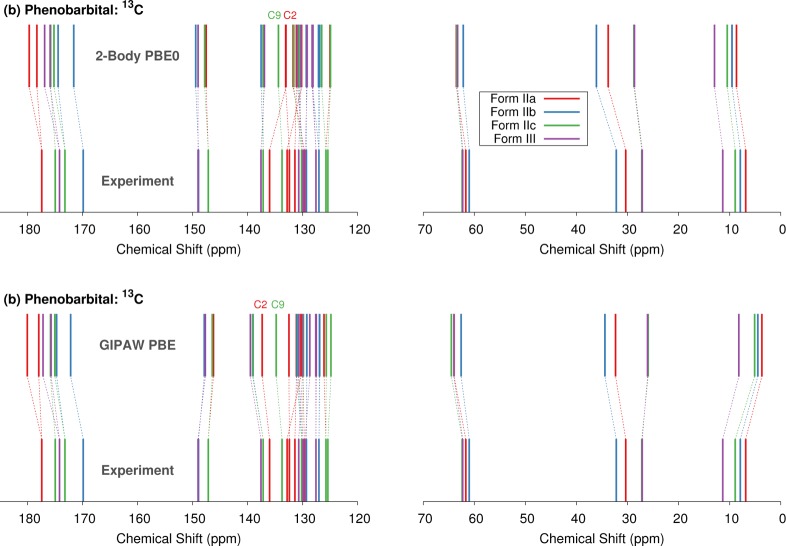
Comparison between experimental and predicted ¹³C chemical shifts for forms II and III phenobarbital using either the (a) two-body fragment PBE0 or (b) GIPAW PBE models. For convenience, shift assignments are based on those inferred from GIPAW in ref (19), though those have not been confirmed experimentally.

The GIPAW/PBE calculations performed in this study, the fragment PBE0 calculations, and the cluster/fragment PBE0 calculations largely support the previously reported GIPAW PBE assignments.¹⁹ There are some exceptions in the 129.7–133.7 ppm range of the form II spectrum, where peaks for eight distinct carbons appear. However, the ordering discrepancies typically involve closely spaced peaks where one would not necessarily expect the theoretical predictions to discriminate reliably. More notable, however, is one significant discrepancy at the fragment PBE0 level. Fragment PBE0 reverses the GIPAW PBE assignment of the resonances for C2 from monomer IIa and C9 from monomer IIc. While the true assignment here is uncertain, the cluster/fragment PBE0 model agrees with GIPAW PBE assignment. Therefore, it seems likely that the two-body fragment PBE0 model is in error in this case. This result hints that further refinements to the electrostatic embedding model might be useful for improving the approximate treatment of many-body effects in the two-body model.

Isotropic ¹⁵N chemical shifts are also available for the two polymorphs. Assignment of the ¹⁵N spectra is unambiguous with all of the different models (see Table S2). However, Table 4 illustrates a significant improvement in the agreement between the predicted and experimental shifts when using the hybrid PBE0 functional instead of PBE. The RMS errors associated with both GIPAW and fragment-based calculations using PBE are ∼9–9.5 ppm, compared to ∼5.5–6 ppm with the PBE0 models. Comparison of individual ¹⁵N shifts computed with GIPAW PBE and fragment PBE0 is plotted in Figure 10. The fragment PBE0 model provides better agreement with the specific shift values and the relative shift differences.

Table 4. RMS Errors in the Predicted ¹⁵N Isotropic Shieldings for Phenobarbital.

method	RMSE (ppm)
GIPAW PBE	9.5
Fragment PBE	8.8
Fragment PBE0	5.5
Cluster PBE0	5.8
Cluster/Fragment PBE0	5.9

Figure 10.

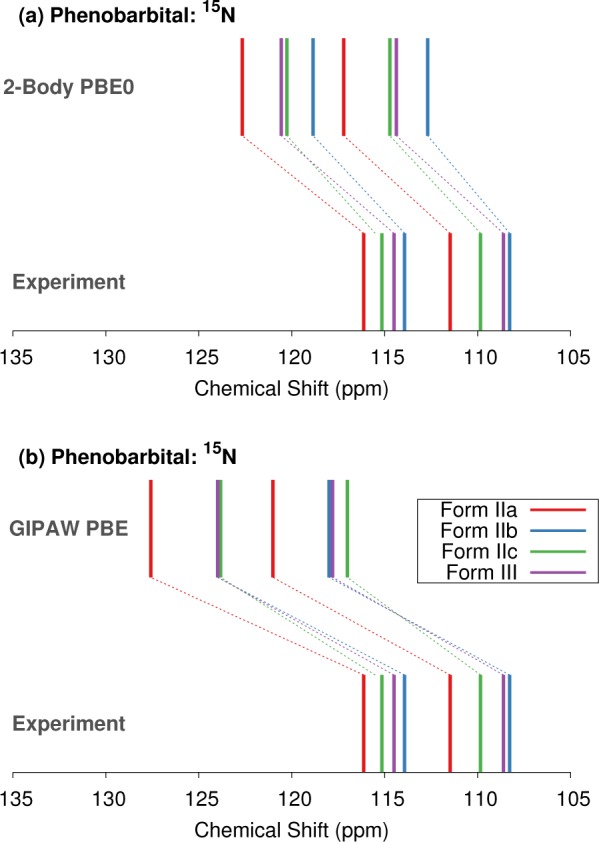
Comparison between experimental and predicted ¹⁵N chemical shifts for forms II and III phenobarbital using either the (a) two-body fragment PBE0 or (b) GIPAW PBE models.

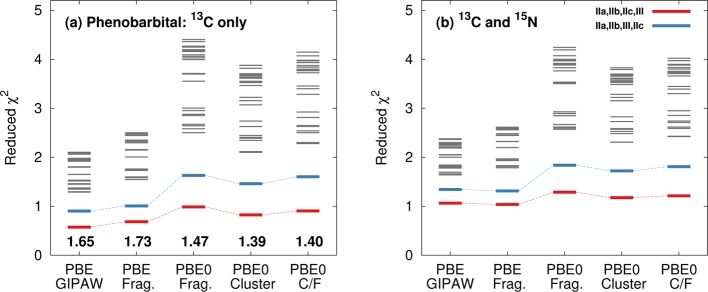
Finally, Figure 11 illustrates the χ̃² for each of the possible permutations for assigning the four phenobarbital monomers in these two polymorphs to the four sets of chemical shifts. The correct assignment (shown in red) has the lowest χ̃² for every model. The most difficult discrimination (shown in blue) involves interchanging the molecules IIc and III, which have very similar intramolecular conformations and the same intermolecular hydrogen bonding motif. Each model identifies this incorrect assignment as having a larger χ̃², but the magnitude of the resolution is greater using the PBE0 fragment approach (see separation between red and blue lines in Figure 11a). In addition, the overall ¹³C RMS error (bottom of Figure 11a) is close to ∼0.2 ppm smaller using the hybrid density functional. All other incorrect assignments interchange molecules with different hydrogen bonding and lead to a larger increase in χ̃². For example, molecule IIa forms the same hydrogen bonded chains, but it also hydrogen bonds to IIb and has a slightly different intramolecular conformation, making it easier to distinguish.

Figure 11.

Reduced χ² analysis for phenobarbital using either (a) ¹³C isotropic shifts or (b) both ¹³C and ¹⁵N isotropic chemical shifts. The red lines correspond to the correct assignment, while the blue lines swap the assignment of monomer c in form II with the form III monomer. Gray lines correspond to other possible assignments.

Like the acetaminophen case, including ¹⁵N isotropic shielding data in the χ̃² analysis (Figure 11b) here does not significantly improve the resolution between the different possible assignments. Assignment of the two nitrogens within a given phenobarbital monomer is unambiguous from the calculations (see Figure 10). Incorrect assignments between the polymorphs introduce errors of only ∼2–3 ppm, which is small relative to the errors expected for ¹⁵N. Accordingly, the nitrogen shifts contribute little to the overall χ̃² values. Nevertheless, with or without inclusion of the ¹⁵N shift data, the fragment PBE0 shows roughly a 2-fold improvement in the χ̃² resolution between the correct and incorrect structures over GIPAW PBE.

Testosterone

The results for acetaminophen and phenobarbital demonstrate that the chemical shift calculations are able to distinguish correct and incorrect assignments of ¹³C spectra, despite strong similarities in hydrogen bonding arrangements between polymorphs. Another important situation is the distinction between neat and hydrate crystal forms, which we illustrate with the crystal forms of testosterone.

Two crystal forms of testosterone have been investigated using both cross-polarization MAS and two-dimensional carbon–carbon NMR experiments.¹⁷ The α form contains two crystallographically distinct molecules in the asymmetric unit (denoted u and v), while the β monohydrate contains one testosterone molecule and one water in the asymmetric unit (Figure 12). The intramolecular conformation is very similar in all three crystallographically unique molecules, with molecular structure overlay root-mean-square deviations of 0.05–0.06 Å for the non-hydrogen atoms (Figure 4c). The only major conformational difference is seen in the hydroxyl orientation between αu and the conformation in αv and β, which affects the environment of C17. Accordingly, variations in the chemical shifts stem primarily from differences in the crystallographic environments of the three monomers (see Supporting Information for more details). The presence of 19 unique carbon atoms in each testosterone molecule in the α form gives rise to a congested solid-state ¹³C NMR spectrum with numerous closely spaced peaks, especially in the ∼30–40 ppm region (see Figure 13). The assignment of each doublet of peaks to molecules u and v is particularly challenging.

Figure 12.

Structures showing the hydrogen bonding patters in the (a) α and (b) β forms of testosterone.

Figure 13.

Comparison of experimental¹⁷ and predicted ¹³C chemical shifts in the low-frequency region for α-testosterone using either (a) two-body fragment PBE0 or (b) GIPAW PBE. Shifts from molecule u and v are indicated in red or blue, respectively.

Harris et al. were able to assign most of the ¹³C resonances through the use of two-dimensional INADEQUATE carbon–carbon correlation experiments.¹⁷ However, the experiments alone did not allow unambiguous assignment of the shifts for C3 and C4 to molecules u and v. Instead, they used GIPAW PBE calculations on the experimentally determined crystal structures (with only hydrogen atom positions relaxed) to predict the chemical shifts for this system and make tentative assignments for each of these two sets of carbon shifts. In addition, the u/v assignments of C7, C13, and C16 are suggested by the experiments, although not definitive. Finally, the experimental difference in chemical shift for C15 in molecules u and v is extremely small and might be interchanged. Table S3 in the Supporting Information lists the carbon assignments from ref (17).

The large number of chemical shifts in a small region of the spectrum make testosterone an excellent system for assessing the performance of cluster and fragment-based NMR chemical shielding calculations. Figure 13 compares the predicted and experimental ¹³C chemical shifts for α-testosterone in the low-frequency region for two-body fragment PBE0 and GIPAW PBE. Qualitatively, the GIPAW PBE calculations underestimate many of the chemical shifts in this region, while the fragment PBE0 shifts show improved agreement with experiment.

Overall, the PBE0 fragment-based models reduce the RMS error for the α and β forms to around 1.9–2.1 ppm, compared to 3.3 ppm with PBE (Figure 15). Most individual ¹³C chemical shifts are reproduced to within a few ppm (Table S3), with the notable exception of C5. In the earlier GIPAW PBE work by Harris et al.,¹⁷ this shift was overestimated by ∼11–14 ppm, which they attributed to a possible artifact of having relaxed only the hydrogen atoms in the crystal structure. However, even with our structures in which all atomic coordinates were relaxed with PBE-D2, C5 still exhibits errors of 11 ppm in the α form and 7.4 ppm in the β form at the GIPAW PBE level (Table 5). Similarly large errors occur for fragment PBE. Switching to the PBE0 functional improves the results moderately, but the errors remain ∼5–8.5 ppm. The reasons for these unusually large errors are unclear, but they may indicate the importance of dynamics, temperature (the crystal structure was determined at room temperature, while the NMR was measured at 273 K), or some other issue with the crystal structure.

Figure 15.

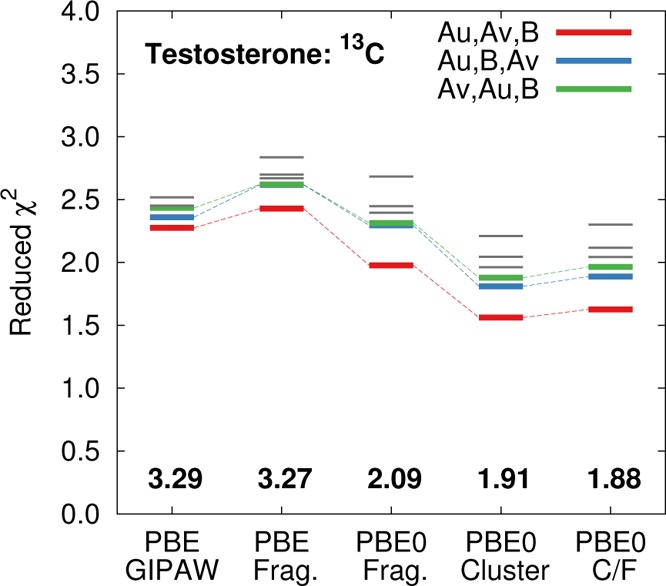
Reduced χ² analysis for the monomer assignments in the α and β forms of testosterone. The correct assignment is shown in red. The blue line swaps molecules αu and β, while the green line swaps molecules αu and αv. Gray lines correspond to other possible assignments.

Table 5. Predicted ¹³C Isotropic Shieldings for the C5 Carbon in Each of the Testosterone Polymorphs.

	α form				β form
	molecule u		molecule v
	shift	error	shift	error	shift	error
experiment	170.64		172.09		173.75
PBE0
two-body Fragment	177.87	7.23	178.32	6.23	182.29	8.54
cluster	175.98	5.34	176.90	4.81	182.33	8.58
cluster/fragment	176.24	5.60	176.95	4.86	182.08	8.33
PBE
two-body fragment	180.62	9.98	180.93	8.84	185.20	11.45
GIPAW	181.69	11.05	183.09	11.00	181.11	7.36

Consider next the assignments in α-testosterone that were experimentally ambiguous. Figure 14 plots the chemical shift differences between the shifts for molecules u and v. GIPAW PBE, fragment PBE0, and cluster/fragment PBE0 are generally in qualitative agreement with experiment. All three models predict the same assignments for the doublets ascribed to C3, C4, and C16. For C7 and C13, fragment PBE0 predicts the opposite sign for the chemical shift difference than either GIPAW PBE or cluster/fragment PBE0. However, in both cases, the magnitude of the experimental shift differences are only ∼0.1–0.2 ppm, and the discrepancies among the predictions are less than 1 ppm. For C15, all the theoretical predictions suggest the opposite sign of chemical shift difference from the one inferred experimentally, which suggests that perhaps the experimental assignment should be reversed. Of course, the small chemical shift differences associated with all of these discrepancies between the models are probably below the threshold of significance, based on the 1.5–2.2 ppm errors expected for these models from earlier benchmark tests.

Figure 14.

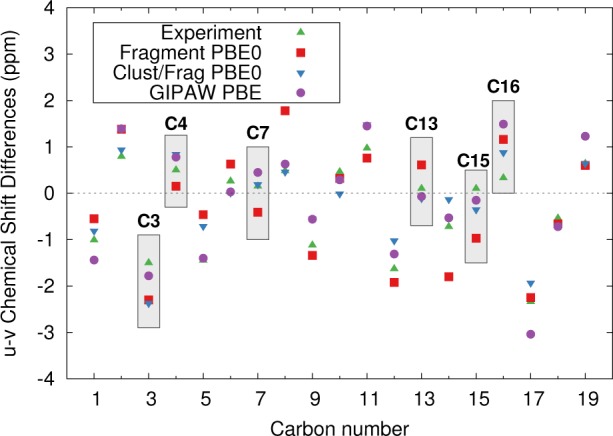
Comparison of the differences between the chemical shifts for atoms in molecules u and v in α-testosterone, according to prediction and experiment. Atoms discussed in the text are highlighted.

Finally, we investigate the ability of the models to discriminate among the different crystallographic environments for the three unique monomers in the two crystal structures (using the atom assignments from ref (17)). Six different ways of assigning the three structures to the three sets of isotropic shifts exist. Figure 15 demonstrates that all four computational methods produce the smallest RMS errors and reduced χ² for the assignment that is consistent with the earlier work by Harris et al.,¹⁷ despite the strong similarities in the intramolecular testosterone geometries (see Figure 12c). Due to the anomalously large errors for C5, the smallest χ̃² values for testosterone are roughly double the corresponding values for acetaminophen and phenobarbital. Nevertheless, using the hybrid PBE0 functional instead of PBE both lowers the RMS error from 3.3 ppm to 1.9–2.1 ppm and modestly increases the resolution between the correct and incorrect monomer environment assignments (e.g., compare fragment PBE0 vs fragment PBE or GIPAW PBE).

Accuracy of the Chemical Shielding Regression Models

The work here is predicated on the transferability of previously determined⁷⁸ linear regression models for scaling the chemical shieldings computed in the systems here. As mentioned above, the earlier ¹³C regression model was fitted to data from 25 crystals and 169 isotropic shifts, while the nitrogen line was fitted to 24 crystals and 51 isotropic shifts. The resulting linear regression parameters were previously shown to be highly robust with respect to the specific composition of the test set through statistical cross-validation.⁷⁸

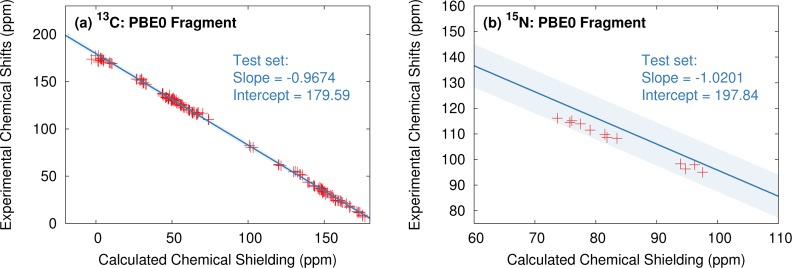
To test this robustness further, we investigate the consistency between the chemical shieldings computed for the systems here and those from our previous work. As an example, Figure 16 illustrates the previously published fragment PBE0 regression lines (in blue) along with the predicted ¹³C and ¹⁵N isotropic shieldings for the crystals in the present study (shown in red). Note that acetaminophen form I was included in the original ¹³C regression (8 out of the 169 shifts), but none of the other crystal forms considered here were used in fitting the regression models. Figure 16 demonstrates that the predicted ¹³C shieldings for each of the polymorphs in this study are in excellent agreement with the earlier regression model. The ¹⁵N regression line overestimates the 12 experimental ¹⁵N chemical shifts considered here, particularly for the 8 phenobarbital ones (calculated shieldings in the 70–85 ppm range). These 8 shifts all involve functionally similar nitrogen atoms (NH groups bonded to a carbonyl and hydrogen-bonded to oxygen atoms), so the similar behavior observed for all of them is perhaps not too surprising. The regression line was fitted to a fairly diverse set of nitrogen atoms, but certain classes of nitrogen atoms do exhibit systematic errors. We previously noted the systematic overestimation of the shifts for sp2-hybridized nitrogen atoms hydrogen bonded to carboyxl groups, for instance.⁷⁸ The neglect of dynamics and/or nuclear quantum effects association with the hydrogen-bonding could be a factor contributing to these systematic errors. Nevertheless, the predictions still fall within 2 standard deviations (shaded region in Figure 16) of the data from the original benchmark set.

Figure 16.

Comparison between the shielding regression line from ref (78) (in blue) and the chemical shifts predicted here (in red) for (a) the ¹³C isotropic shieldings and (b) the ¹⁵N isotropic shieldings. The blue-shaded region indicates plus or minus two standard deviations in the errors from the ref (78) benchmarks.

Next, Table 6 compares both the linear regression parameters and the RMS errors for three different choices in fitting set: (1) regression parameters from the previously reported ¹³C test set with the acetaminophen form I shifts removed (24 crystals/161 shifts); (2) regression parameters fitted to only the ¹³C isotropic shift data from the polymorphic crystals studied in the present work (7 crystals/137 shifts); and (3) regression parameters for the union of both data sets (31 crystals/298 shifts). For the fragment-based PBE0 model, the overall RMS errors on the polymorphic crystals considered here vary by less than ∼0.2 ppm across the three different sets, and the linear regression parameters vary only slightly (Table 6). The GIPAW RMS errors and regression parameters exhibit slightly larger variability across the three different training sets (e.g., RMS error variations of ∼0.4 ppm), but such deviations are well within the larger ∼2–2.5 ppm errors inherent in the model. These results provide strong support for the transferability of the regression parameters developed in ref (78) previously and used here.

Table 6. Impact of Training Set on Linear Regression Parameters for the ¹³C and ¹⁵N Isotropic Shieldings^a.

training set	slope	intercept	RMSE	slope	intercept	RMSE
	13C: Fragment PBE0			15N: Fragment PBE0
1. Benchmark Set	–0.9661	179.45	1.74	–1.0201	197.84	4.93
2. Polymorph Set	–0.9633	178.50	1.59	–0.8987	182.86	0.73
3. Combined Set	–0.9648	179.01	1.63	–1.0209	197.00	4.05
	13C: GIPAW PBE			15N: GIPAW PBE
1. Benchmark Set	–0.9893	169.05	2.46	–1.0165	184.98	9.19
2. Polymorph Set	–0.9663	167.62	2.02	–0.8496	164.87	2.38
3. Combined Set	–0.9746	168.13	2.08	–1.0126	183.30	7.84

^aReported slopes and intercepts were fitted using (1) only the previously published benchmark test set shifts (excluding form I acetaminophen from the ¹³C test set), (2) only the polymorph shifts from this work, or (3) the combination of both the benchmark and polymorph shifts. The RMS errors are reported for the polymorphic crystal ¹³C and ¹⁵N isotropic shifts in the polymorphic crystals studied in this work.

The same three fitting scenarios were considered for ¹⁵N. Fitting directly to the 12 ¹⁵N shifts here reduces the errors dramatically, down to 0.7 ppm with fragment PBE0. However, this fitting produces a slope that deviates substantially from unity. This could suggest problems in describing the nitrogen environments present in these molecules that are corrected in the direct fit, or perhaps some issues in the experimental shift referencing (particularly for phenobarbital). Of course, dynamics can also play an important role, and deviations from a unit slope might also result from neglecting those effects.^45,46 Because the ¹⁵N benchmark set contains only 51 shifts, adding the dozen more shifts with a systematic error from this study does modestly alter the regression line and improves the errors for these 12 shifts by about 1 ppm at the fragment PBE0 level. Nevertheless, because including so many nitrogen shifts from only two systems might overly bias the overall test set, we continue to advocate use of the original regression line from ref (78). Qualitatively similar behavior is observed for ¹⁵N with GIPAW PBE, but the regression lines and rms errors exhibit even higher sensitivity to the composition of the fitting set.

Conclusion

In conclusion, the relative performance of GIPAW, fragment, cluster, and combined cluster/fragment models for predicted ¹³C and ¹⁵N isotropic chemical shieldings has been assessed in several different polymorphic crystal systems. Consistent with our recent benchmark studies,^55,78 the hybrid PBE0 density functional provides higher-accuracy chemical shifts than the GGA functional PBE. More importantly, this improved accuracy stemming from the use of a hybrid density functional provides increased discrimination among different crystallographic environments, which is an essential ingredient in NMR crystallography studies. The chemical shift prediction methods are able to reliably distinguish between the monomers in different crystal structures, even when the strong intermolecular interactions are nearly identical in the various structures.

The two-body and GIPAW methods generally agree on the assignments for individual isotropic ¹³C chemical shift assignments. In the handful of cases where the two models disagreed, the differences in chemical shifts were usually (but not always) ∼1 ppm or less, which is below the resolving power of the models. In those cases, switching to a cluster or cluster/fragment model produced assignments that are fully consistent with the GIPAW ones, suggesting that these minor discrepancies result from the simplified description of many-body effects in the two-body fragment model. So, despite the successes of the two-body fragment model demonstrated here, there may be room for refining the electrostatic embedding treatment further to improve the approximate treatment of many-body effects.

Finally, we demonstrated that the linear regression parameters for scaling chemical shieldings to chemical shifts which were developed in our previous benchmark study⁷⁸ are transferable to the systems studied here, which bodes well for their widespread application. In the examples studied here, ¹³C isotropic chemical shifts were sufficient to discriminate among the different crystal structures, but this is not always the case. In the future, it will be interesting to apply these fragment chemical shift prediction techniques to structure determination problems through their combination with crystal structure prediction techniques, where PBE GIPAW ¹³C shifts alone have previously proved insufficient for identifying the correct structures.¹¹

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.cgd.6b01157.

• Complete lists of experimental and predicted isotropic chemical shifts, comparison between experimental and optimized crystal structures, and analysis of the intra- and intermolecular contributions to the chemical shieldings (PDF)

• Optimized crystal structure coordinates (ZIP)

The authors declare no competing financial interest.