Across language families: Genome diversity mirrors linguistic variation within Europe

ABSTRACT

Objectives: The notion that patterns of linguistic and biological variation may cast light on each other and on population histories dates back to Darwin's times; yet, turning this intuition into a proper research program has met with serious methodological difficulties, especially affecting language comparisons. This article takes advantage of two new tools of comparative linguistics: a refined list of Indo‐European cognate words, and a novel method of language comparison estimating linguistic diversity from a universal inventory of grammatical polymorphisms, and hence enabling comparison even across different families. We corroborated the method and used it to compare patterns of linguistic and genomic variation in Europe. Materials and Methods: Two sets of linguistic distances, lexical and syntactic, were inferred from these data and compared with measures of geographic and genomic distance through a series of matrix correlation tests. Linguistic and genomic trees were also estimated and compared. A method (Treemix) was used to infer migration episodes after the main population splits. Results: We observed significant correlations between genomic and linguistic diversity, the latter inferred from data on both Indo‐European and non‐Indo‐European languages. Contrary to previous observations, on the European scale, language proved a better predictor of genomic differences than geography. Inferred episodes of genetic admixture following the main population splits found convincing correlates also in the linguistic realm. Discussion: These results pave the ground for previously unfeasible cross‐disciplinary analyses at the worldwide scale, encompassing populations of distant language families. Am J Phys Anthropol 157:630–640, 2015. © 2015 Wiley Periodicals, Inc.

Why are humans biologically different, and how did they come to speak different languages? Taken separately, these questions have certainly been faced for millennia now, but it was Charles Darwin (1859) who explicitly put forth the idea of a parallelism between biological evolution and language diversification; Darwin foresaw that a perfect pedigree of human populations would also represent the best possible phylogenetic tree of the world's languages. Indeed, factors isolating populations from each other (such as barriers to migration, or just distance) are expected to promote both biological and cultural divergence, while factors facilitating contacts should have the opposite effect; but gene/language parallelisms might in fact be deeper than that, in many respects (and recently some scholars went as far as claiming a role even for adaptation, not only in biological evolution, but in certain linguistic changes as well (Levinson and Gray, 2012).

Darwin's evolutionary framework was immediately accepted by linguists such as Schleicher (1863); however, it took more than a century for his parallelism intuition to be tried against actual data (Sokal, 1988; Cavalli‐Sforza et al., 1988), and to become part of a broader research program (Renfrew, 1987; Cavalli Sforza et al., 1994). The idea is that linguistic diversification caused by demographic processes, mainly population dispersal, would generate parallel patterns of genetic and linguistic variation. That would often be the rule, but where a small group imposes its language upon a larger population (élite dominance: Renfrew, 1992), there might arise a local mismatch between genetic and linguistic diversity, so that already from this exception to the general rule one could detect the occurrence of an important event of language replacement.

The results of the line of studies above were illuminating on the one hand, but controversial on the other. The case for analogies between linguistic and genetic variation in empirical fact (Barbujani and Sokal, 1990; Barbujani and Pilastro, 1993; Cavalli‐Sforza et al., 1994; Sajantila et al., 1995; Poloni et al., 1997; Belle and Barbujani, 2007) and in methods (Ringe et al., 2002; Gray and Atkinson, 2003; McMahon and McMahon, 2003; Heggarty, 2006; Gray et al., 2009; Bouckaert et al., 2012; Berwick et al., 2013), clearly emerged at a regional level; instead, at the larger geographical scale, many such conclusions were received with skepticism, especially by linguists.

One weakness of early approaches was in fact the unavailability of numerical taxonomies of languages to be matched with the biological ones: classical methods have produced chance‐proof demonstrations of absolute relatedness for words/languages, but hardly provided quantitative cognacy measures even for subarticulation of acknowledged families. The second reason for skepticism was that solid linguistic relationships have so far been inferred from comparing vocabulary items (words/morphemes) and their sound structures; now, formally identifiable correspondences of such items in sound/meaning (chance‐safe etymologies) are known to dissolve with time, while accidental similarities emerge, due to the arbitrariness of lexical variation combined with general constraints on possible phonological systems. Therefore, although the time depth at which these processes disrupt the potential for long‐range linguistic classification is far from established (Nichols, 1996; Greenhill et al., 2010), it has been anyway impossible to convincingly infer distant relationships (across evident families) from lexical comparisons. As a consequence, large‐scale gene/language comparisons were undermined by scientifically unsupported linguistic classifications and taxonomic procedures (Ringe, 1996; Bolnick et al., 2004; Greenhill, 2011; Ringe and Eska, 2013).

In this article, we try to overcome such problems through two tools recently developed for language comparison: Bouckaert et al.'s (2012) expanded list of Indo‐European (henceforth IE) lexical cognates and Longobardi and Guardiano's (2009) Parametric Comparison Method (PCM). We used these new resources to interpret patterns of genome‐wide variation in 15 European populations (from three different linguistic families), inferred from autosomal single nucleotide polymorphisms (SNPs) data; the final dataset included 805 individuals, and after data cleaning and integration we had >177,000 SNPs autosomal SNPs for the analysis.

MATERIALS AND METHODS

The linguistic approaches

Computational approaches to phylogenetic linguistics have led to refinements of lists of taxonomic characters available for classifying Indo‐European (IE) languages. The latest breakthrough in this domain is Bouckaert et al.'s (2012) IE cognate list, IELex, which summarizes the etymological expert judgments assigned by Dyen et al. (1992), Ringe et al. (2002), along with other sources, for a 207 Swadesh‐list (Swadesh, 1952) in several IE languages. This makes available a richer device for quantitative experiments on IE lexical diversification. To take into proper account language‐internal polymorphism (synonymy), in Bouckaert et al. (2012) several lexical roots are often listed for the same meaning.

The second tool, the PCM, is a more radical departure from traditional procedures and databases. Languages are increasingly studied by theoretical linguists not merely as lists of words, but also as sets of recursive rules (technically, generative grammars: Chomsky, 1955) combining words into an infinite number of sentences (Chomsky, 1965). Therefore, an alternative to comparison of vocabularies is precisely exploring the phylogenetic potential of grammatical diversity (different rules of (co‐)occurrence, order, and interpretation of various classes of words, morphemes, and features: Nichols, 1992; Longobardi, 2003; Guardiano and Longobardi, 2005).

Longobardi and Guardiano's (2009) central hypothesis is that syntactic change, though insightfully shown to be “catastrophic” in specific “local” instances (Lightfoot, 1991), when considered as an overall phenomenon might arise slowly enough to produce retrievable evolution (Longobardi, 2003). If so, generative grammars could encode a historical signal, useful for deeper classifications of languages and populations.

In the PCM, the core grammar of any language is represented as a string of binary symbols, each encoding the value of a syntactic parameter (Chomsky, 1981; Clark and Roberts, 1993; Baker, 2001; Roberts, 2007; Biberauer, 2008). Parameters are drawn from a supposedly universal list, defining a structured variation space within the human capacity often labeled “universal grammar” (UG) or “faculty of language.” Therefore, through the PCM, in principle, all languages, no matter how lexically distant, could now be compared, bypassing many problems arising with word collation. Case studies suggested that the chance probability of parametric resemblance can be computed and controlled for (Bortolussi et al., 2011), as well as certain amounts of homoplasy (Longobardi, 2012) and admixture (Longobardi et al., 2013); finally, there is less a priori reason to expect external (e.g. cultural) factors to exert selective pressure on syntax than on lexical items (Guardiano and Longobardi, 2005; Longobardi and Guardiano, 2009; Ringe and Eska, 2013). A proof‐of‐concept study of gene/language congruence in a small sample of Old‐World populations has already shown how correlations can be found between a preliminary set of parametric distances and genetic ones (Colonna et al., 2010).

However, the more sophisticated linguistic samples become, the more pervasive appear internal implications (nonindependence of characters, leading to redundant information). They saliently arise in grammar (Greenberg, 1963; Hawkins, 1983; Baker, 2001; Biberauer, 2008), but also affect vocabularies, once synonymy is encoded, and may have a disruptive potential for calculating taxonomic distances, if ignored. Hence, in this study, to compute plausible distances from Bouckaert et al.'s (2012) list, we propose a specific weighted measurement (see below). Since the PCM has been already originally designed for spelling out hypotheses on, and controlling for, crossparametric implications (Longobardi and Guardiano, 2009; Bortolussi et al., 2011), here, the non‐independence of characters is controlled by making explicit hypotheses about implications of syntactic properties and adopting a distance calculation appropriate for them (see below).

Languages and populations

Recently, the PCM has been empirically validated on a set of 26 IE languages (Longobardi et al., 2013), syntactically defined through 56 binary parameters described in the corresponding online support material (https://benjamins.com/#catalog/journals/jhl.3.1.07lon/additional). The method produced near‐perfect taxonomies within IE, and also suggested that diachronic resetting of syntactic parameters is slower than lexical replacement. Thus, to investigate gene‐language congruence in Europe, we took the intersection between the languages of this syntactic dataset and those of the much wider sample of Bouckaert et al. (2012), and selected from it a further subset of 12 varieties, for whose speakers genome‐wide data are publicly available.

Then, we expanded the analysis to include three non‐IE‐speaking populations, for which we also found available genomic information and whose languages had been previously analyzed in terms of PCM (Longobardi and Guardiano, 2009). For such languages (Finnish, Hungarian, and Basque), we set the same 56 parameters of Longobardi et al. (2013) (Supporting Information Table 1).

Genetic analyses

Genomic data on 13 populations were found in POPRES (dbGap accession phs000145.v1.p1; Nelson et al., 2008), a public resource for genetic research including 5,886 subjects genotyped at 500,568 loci using the Affymetrix 500K SNP chip. To determine the geographic location that best represents each individual's ancestry, we used a strict criterion of sample selection excluding individuals who reported mixed grandparental ancestry. A Basque (Henn et al., 2012) and a Finnish (1000 Genomes Project Consortium, 2012) sample were then added (Fig. 1). Outliers and individuals showing high levels of genetic similarity, which may point to biological relatedness, were excluded, and all data were merged using PLINK (Purcell et al. 2007). To avoid any ambiguity in strand alignment, we removed from the merged genotype datafile the alleles carrying ambiguities in strand‐flipping, namely A/T and C/G polymorphisms. The final dataset comprises 177,949 markers that passed quality filters in all datasets for 805 individuals (minor allele frequency = 0.01, genotyping rate = 98%). Genetic distances (d _GEN), i.e., F _ST values between pairs of populations (Weir and Cockerham, 1984) were calculated by the 4P software (Benazzo et al., 2015). As a preliminary test, we summarized the genetic structure of the studied populations by ADMIXTURE (Alexander et al., 2009).

Figure 1.

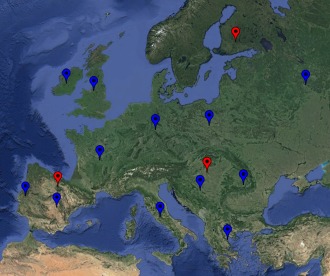
Geographic distribution of the samples considered in this study. Indo‐European‐speaking populations in blue, populations speaking Finno‐Ugric languages (Hungarian, Finnish) and the linguistic isolate (Basque) in red.

Distance matrices

We started by inferring four matrices of pairwise distances between the 12 IE‐speaking populations and for the whole set of 15 European populations: geographic (d _GEO), genomic (d _GEN), and two types of linguistic distances, syntactic (d _SYN, from Longobardi and Guardiano, 2009) and lexical (d _LEX, from Bouckaert et al., 2012 new word list).

Syntactic distances have been calculated according to the formula already proposed in previous works (Longobardi and Guardiano, 2009, Bortolussi et al., 2011) to account for the existence of parameter values neutralized by system‐internal implications: normalized Hamming distance or Jaccard distance (Jaccard, 1901), i.e. the number of differences between two languages divided by the sum of their identities and differences (cf. also Lewandowsky and Winter, 1971). As a consequence, all the pairwise syntactic distances (d _SYN) end up falling between 0 and 1.

In calculating d _SYN, all differences and identities in each parameter value are computed as having the same taxonomic value and the two values of every parameter are considered equiprobable. We are aware that different parameters may have different phylogenetic weights, as for instance argued in Rigon (2009, 2012). However, since syntactic arguments for parameter hierarchies, diachronic stability, and markedness hypotheses seem to be still under development (Roberts, 2012), we do not have an appropriate theory of parametric weights to rely on. Hence, we decided to consider all parameters and values, as a scientific idealization, of equal import, waiting for stronger evidence on markedness, stability, and related issues: for, if correct phylogenetic results are already attained through less fine‐grained characters, it would be curious if they were substantially worsened once theoretically more refined (hence less idealized, in principle more realistic) characters and analyses were employed. The opposite strategy instead would introduce a further source of arbitrariness, casting doubts on the robustness and noncircularity of the taxonomic achievements.

The second type of pairwise linguistic distances, d _LEX, is based on lexical comparisons. Such distances were initially estimated as the number of character differences out of the number of all lexical roots expressed at least in one of the two languages compared; again, this way all distances fall between a minimum of 0 and a maximum of 1. However, in our particular dataset, it turned out that almost all values of the resulting matrix were scattered around 0.9, hence scarcely informative and historically not plausible. This is likely to be a natural consequence of the criteria adopted to compute differences: indeed, Swadesh‐lists require each meaning to be expressed by at least one lexical root in each of the languages; since polymorphism within the same language is expected to be a marked phenomenon, every lexical root displayed in a language but not in another is likely to predict a different lexical root to express the same meaning in the second language, thus doubling differences. It was necessary to take this into account and to assign differences a weight of 0.5 (rather than 1), so obtaining a more informative distance matrix (d _LEX), whose values pattern better on average with those previously obtained (Longobardi et al., 2013) from Dyen et al. (1992). Given that, by definition, only within the same family is it possible to compute some safe rate of common lexical etymologies, for comparison between languages from different families, which accordingly share no etymology, distance 1 was assigned by default. An approximation to the distance between Hungarian and Finnish was tentatively computed from some literature references (Laasko, 2000; Peust, 2013).

Matrix comparisons

Correlations between pairs of these distance matrices were calculated according to the Mantel (1967) procedure, using the mantel function of the R Vegan package. The significance was empirically estimated over 10,000 permutations. To exclude the potentially confounding effect of some variable, we also ran partial Mantel tests, thus calculating the correlation between two matrices while controlling for (i.e. keeping constant) a third distance matrix. To this end, we used the mantel.partial function of the R Vegan package. Finally, to compare tree topologies (Steel and Penny, 1993), we calculated the path difference distance between trees using the treedist function of the R phangorn package, and we generated the 100,000 pairs of random trees for 12 and 15 taxa with the rtree function of the R ape package.

An improved method to describe population splits and later gene flow

Population structure depends on a number of evolutionary and demographic processes which may be difficult or impossible to summarize in the form of a simple bifurcating tree. Therefore, we also represented genomic variation by a network in which populations may exchange migrants after they have split from their common ancestors, thus violating the simplistic assumptions of most tree‐building models (Pickrell and Pritchard, 2012). The first step in this exercise is the estimation of a maximum‐likelihood tree. Populations poorly fitting the tree model are then identified, and migration events involving them are superimposed, so that the tree with the added migration episodes will account for a greater proportion of the overall genetic variance than the simple tree itself. This way, each population may have multiple origins, and the migrational contacts in the descendant populations are highlighted.

RESULTS

First of all, we made sure that the smaller subset of 12 IE languages displays a significant syntax‐lexicon correlation, and retains as a plausible phylogenetic structure as that generated from the wider sample of 26 in Longobardi et al. (2013). Thus, for such 12 IE languages/populations, we compared d _SYN and d _LEX with one another. The two linguistic matrices appeared highly correlated (r = 0.82).

To better understand to what extent lexical and syntactic differences mirror each other, we represented the matrices in tree form (Fig. 2A,B), calculated the path difference distance between trees (Steel and Penny, 1993), and compared this value with those obtained in 100,000 pairs of random topologies drawn, with replacement, from the total set of the possible topologies for 12 taxa. No closer match between topologies was observed (hence P < 10⁻⁵). Notice that the deep branches in the lexical tree in Figure 2A are short: this seems to reflect a phenomenon observed and preliminarily discussed in Longobardi and Guardiano (2009) and Longobardi et al. (2013): while syntactic distances do not show any sign of saturation at least within the domain of IE and European languages, lexical distances capture well the more recent separations within IE subfamilies, but already lose resolution when different subfamilies of IE are compared.

Figure 2.

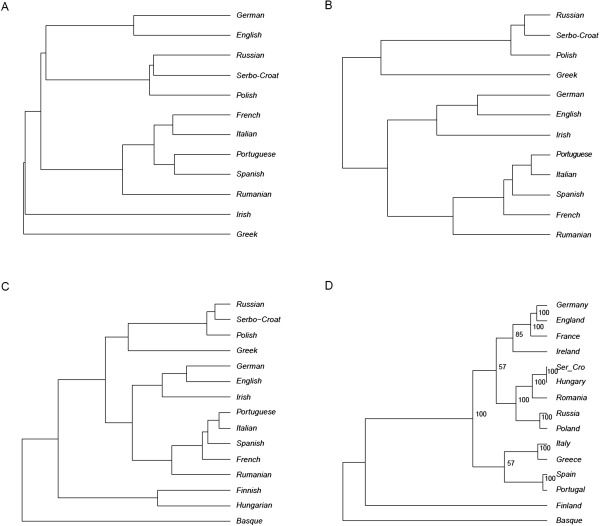
UPGMA trees summarizing population relationships. Distances inferred from: (A) lexical and (B) syntactic comparisons among 12 Indo‐European‐speaking European populations; (C) syntactic comparisons among 15 European languages, and (D) F _ST distances among 15 populations sharing 177,949 SNPs. Lexical distances were estimated from lists of cognate words, amounting to over 6,000 roots (http://ielex.mpi.nl/); syntactic distances were measured over 56 parameters of nominal phrases (http://dx.doi.org/10.1075/jhl.3.1.07lon.additional). In (D), numbers indicate the support of the branching after 100 bootstrap replicates. The matrix perturbation techniques usable to test the robustness of trees (bootstrapping and jackknifing) provide stable topologies, but owing to the small number of characters involved they are only relatively reliable (cf. Longobardi et al., 2013 for more details). Therefore, bootstrapping scores have been only reported here for the genetic tree D.

The syntactic and lexical matrices are highly correlated with each other, and showed very similar levels of correlation with genetic distances (r = 0.49 and 0.51, respectively), both with high statistical significance, which stands Bonferroni correction for multiple tests (Table 1). Syntactic distances also show a tighter association with geography than their lexical counterparts. Most importantly, the correlations of both lexicon and syntax with genetic distances are higher than between genes and geography (r = 0.38). I.e. once precise measurements of linguistic differences are used, language turns out a better predictor of genetic differences than geography in Europe.

Table 1.

Mantel correlations between genetic, geographic, and two kinds of linguistic distances in Indo‐European‐speaking populations of Europe

Distance matrices	r	P
d LEX d GEO Linguistic (lexical)‐geographic	0.206	0.077
d LEX d GEN Linguistic (lexical)‐genetic	0.514	0.0001
d SYN d GEO Linguistic (syntactic)‐geographic	0.385	0.008
d SYN d GEN Linguistic (syntactic)‐genetic	0.491	0.0004
d LEX d SYN Linguistic (lexical)‐linguistic (syntactic)	0.822	0.0001
d GEN d GEO Genetic‐geographic	0.390	0.011

After Bonferroni correction for multiple tests, these results are significant at the P = 0.0006 level.

Such results arose from already available IE databases. In order to strengthen them, we extended the analysis to the three non‐IE languages of Europe mentioned above (i.e. Finnish, Hungarian, and Basque). To do so, we crucially relied on PCM's ability to compare languages even from different families. Recall, indeed, that calculating lexical distances from cognates for languages from different families is an essentially vacuous procedure, since by definition such languages share no common etymologies: hence the theoretically maximal distance must a priori be assigned, so that the result is largely uninformative. A way to overcome this shortcoming was the development of the PCM, precisely because it relies on polymorphic characters which are in principle universal.

The same four matrices and six correlations as above were recalculated for the whole set of 15 populations (Table 2). The correlations between genes and languages, both for syntax (0.60) and lexicon (0.54), remain much higher than between genes and geography (0.30). Actually, the latter correlation further decreases, while the one most significantly rising is that between genes and syntax (from 0.49 to 0.60), confirming that syntax, in Europe, is a better predictor of genomic variation than geography. Indeed, the correlation remains significant even after removing the effects of geography through a partial Mantel test (d _SYN vs. d _GEN r = 0.57), and after Bonferroni correction for multiple tests.

Table 2.

Mantel correlations and partial Mantel correlations between matrices of syntactic, lexical, geographic, and genetic distance in 15 populations in Europe

Distance matrices	r	P
d GEN d GEO Genetic‐geographic	0.299	0.030
dSYNdLEX Syntactic‐lexical	0.850	0.001
d SYN d GEO Syntactic‐geographic	0.240	0.039
dLEX d GEO Lexical‐geographic	0.084	0.264
d SYN d GEN Syntactic‐genetic	0.599	0.001
dLEX d GEN Lexical‐genetic	0.537	0.001
d GEN d GEO (d SYN) Genetic‐geographic (syntax held constant)	0.200	0.114
d GEN d GEO (dLEX) Genetic‐geographic (lexicon held constant)	0.302	0.035
d SYN d GEO (d GEN) Syntactic‐Geographic (genetics held constant)	0.079	0.264
dLEX d GEO (d GEN) Lexical‐geographic (genetics held constant)	−0.095	0.736
d SYN d GEN (d GEO) Syntactic‐genetic (geography held constant)	0.570	0.002
dLEX d GEN (d GEO) Lexical‐genetic (geography held constant)	0.538	0.001

After Bonferroni correction for multiple tests, these results are significant at the P = 0.012 level.

Instead, all the correlations with geography become lower in the 15‐unit sample, probably because not all the three linguistic outliers added are also geographical outliers. Also, the correlation of genes and lexicon appears to increase, though hardly significantly, presumably beginning to suffer from the mentioned saturation of cross‐family lexical distances. Thus, the more languages from different families will be added for comparison, the more we expect reliance on the PCM to become crucial. To better understand gene‐language congruence at the cross‐family European level, we focused in more detail on syntactic distances.

We drew a UPGMA tree and carried out a Principal Component Analysis (PCA) from d _SYN. The tree (Fig. 2C) singles out IE and meets all further basic expectations: the deepest nodes first separate Basque, and then the pair of Finno‐Ugric languages, from the cluster comprising all the IE varieties. Within this cluster, Romance, Germanic and Slavic form three subclusters; then Greek and Irish, as the only representatives of their subfamilies in this study, occur on separate branches, although close to their geographic neighbors.

In the PCA, the combination of the first two axes, jointly accounting for 34.5% of the variance, separates IE languages (but Greek) from the others: Greek, an IE language without very close relatives, falls anyway opposite to Finnish, Hungarian, and Basque (Fig. 3A). This pattern is largely expected, and the position of Greek as the outlier of IE in our sample agrees with previous computational experiments on lexical datasets (Bouckaert et al., 2012, Gray and Atkinson, 2003).

Figure 3.

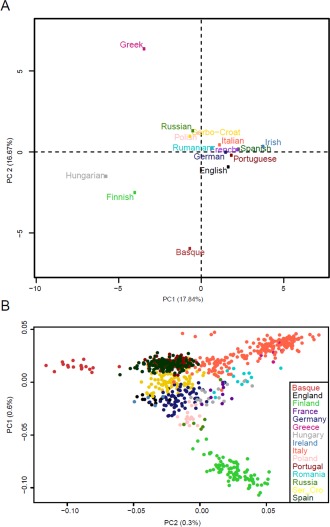
Projection on two dimensions of the main components (PCA) of linguistic (A) and individual genomic (B) variation. The linguistic PCA was performed using the R FactoMineR program, with neutralized parameter values coded as “NA,” whereas the genomic PCA was calculated with the R SNPRelate package (Lê et al., 2008). Note that the linguistic scatter diagram accounts for a fraction of the total variance that is >25‐fold as large as that accounted for by the genomic scatter diagram.

In short, through syntax, precise comparison and measuring is finally possible even across established linguistic families: the main families and subfamilies of Europe were discriminated by means of just 56 abstract characters, suggested by formal grammatical theory, through standard methods of evolutionary biology, without resorting to methodologically disputable cross‐family lexical comparisons.

Then, to synthetically visualize genomic diversity in a parallel way, we drew the corresponding UPGMA tree and carried out a PCA analysis from d _GEN. The tree (Fig. 2D) shows that two out of the three linguistic outliers, Finns and Basques, are clearly differentiated also genomically, and connected to the other populations by long independent branches. The rest of the tree mainly reflects geographical distances, and contains all IE‐speaking populations, as well as Hungarians, who appear genetically related with their geographical neighbors, Serbs and Rumanians. Again, the path difference distance (Steel and Penny, 1993) was calculated between the syntactic and the genetic tree, and the probability to obtain a closer match between random trees with 15 populations turned out P <0.004. This implies a tight relationship between the tree topologies inferred from syntax and genes, one highly unlikely to have arisen just by chance. The only salient divergence is represented by the position of Hungarians, mostly falling within a large group of Central Europeans. Note that a sharp genomic differentiation of Basques from most other Europeans has not been confirmed in all previous genomic studies (see Laayouni et al., 2010).

Then, we carried out a parallel PCA of the >177,000 SNPs in 805 individuals from the 15 populations representative of the previously considered languages. As expected, given the well‐known low levels of cross‐population diversity in humans in general (Barbujani and Colonna, 2010) and in Europe in particular (Novembre et al., 2008), the proportion of the overall variance accounted for by the two main axes is much lower (less than 1%) than in the analysis of linguistic data (Fig. 3B), as previously observed. However, the two PCAs are qualitatively similar in several respects, with a main central cluster containing all IE speakers along with Hungarians, and with Finns and Basques appearing as outliers though both relatively close to their nearest geographical neighbors (Poles and Spaniards, respectively).

An unsupervised analysis of population structure through ADMIXTURE basically led to the same conclusions as the PCA, and confirmed the peculiar genetic position of Hungarians. Postulating three ancestral genomic clusters for Europe, i.e. as many as the language families in the database (k = 3 plot, Fig. 4), such clusters largely correspond to: (i) Basques, (ii) Finns, and (iii) all other Europeans including Hungarians; the Basque sample shows connections with the Spanish and French ones (blue component), and Finns seem to share some ancestry with Northern Europeans (Germans and Poles, orange component). Other analyses, assuming different numbers of clusters in the genomic data, are also given for completeness of information.

Figure 4.

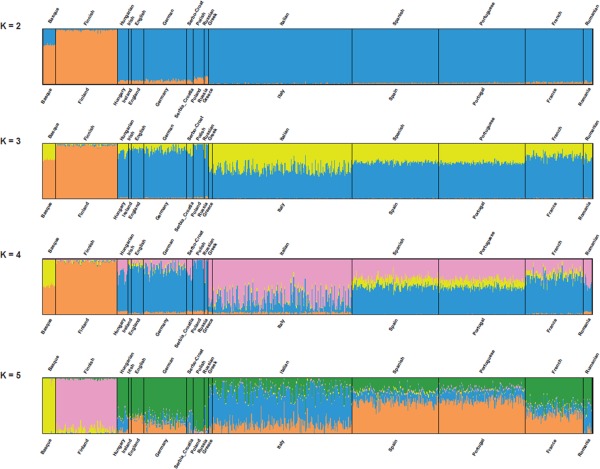
Unsupervised ancestry‐inference analysis based on the software ADMIXTURE. Each individual genotype is represented by a column in the area representing the appropriate population, and colors correspond to the fraction of the genotype that can be attributed to each of the K groups (2 ≤ K ≤ 5) assumed to have contributed to the populations' ancestry.

We further investigated the evolutionary relationships between populations by a method designed to identify gene flow episodes after the main population splits (Fig. 5). Indeed, a tree‐like representation of genomic (or linguistic, for that matter) relationships disregards the possibility of exchanges occurring after populations separated from their common ancestor. The contribution of migrants to Rumania from Russia (0.43) as well as from Greece is in agreement with the populations' geographical proximity, and their traditionally well‐assessed horizontal linguistic connection: the received concept of a Balkan common linguistic area, or Sprachbund, has found at least some suggestive correspondence even in the parametric linguistic analysis, for in three parameters Rumanian, the outlier of the Romance branch of the language tree (Fig. 3A), shares a state with Greek in contrast to the rest of Romance, in one also with Bulgarian (Longobardi et al., 2013). The Southern European origin of a fraction of the Hungarians (0.31), instead, is not apparently matched either in the linguistic PCA (Fig. 4A) or tree (Fig. 3A), only finding a loose potential correspondence in one of the 56 syntactic characters, Parameter 7 (DGP), whose Hungarian state might in theory have been borrowed from either German or Rumanian. Relatively recent gene flows, occurring after the main population splits, seem therefore to nicely match at least a fraction of the linguistic variation not immediately representable by classifying languages into families. It is an intriguing conjecture that biological relationships unpredictable by vertical linguistic history might reflect secondary gene flow independently detected by TreeMix.

Figure 5.

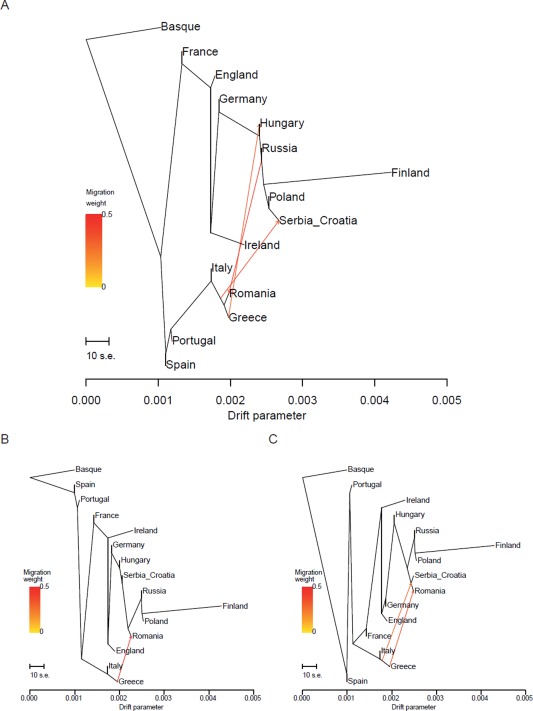
Maximum‐likelihood population trees. The algorithm chosen, TreeMix (28), estimates phylogenetic relationships with (A) three, (B) one, and (C) two superimposed migration events after the main population splits.

The peculiar gene‐language mismatch of Hungarians was already noticed by Cavalli Sforza et al. (1994), though without the possibility of quantifying cross‐family linguistic distances. Now this has become possible thanks to the PCM, and indeed, the genes‐syntax correlation recalculated after removing Hungary further rises very significantly (r = 0.74; Table 3), while the genes‐geography one remains low (r = 0.28), confirming Hungary as an exception, in this respect. The skew becomes even sharper in partial Mantel tests (respectively r = 0.72 for gene/syntax, with geography held constant, and r = 0.09 for gene/geography, with syntax held constant), the sharpest demonstration to date of a language/biology correlation for the core of Europe.

Table 3.

Mantel correlations and partial Mantel correlations between matrices of syntactic, lexical, geographic, and genetic distance for 14 populations in Europe (after removing Hungary)

Distance matrices	r	P
d GEN d GEO Genetic‐geographic	0.275	0.048
dSYNdLEX Syntactic‐lexical	0.850	0.001
d SYN d GEO Syntactic‐geographic	0.291	0.026
dLEX d GEO Lexical‐geographic	0.152	0.144
d SYN d GEN Syntactic‐genetic	0.740	0.001
dLEX d GEN Lexical‐genetic	0.687	0.001
d GEN d GEO (d SYN) Genetic‐geographic (syntax held constant)	0.093	0.254
d GEN d GEO (dLEX) Genetic‐geographic (lexicon held constant)	0.238	0.083
d SYN d GEO (d GEN) Syntactic‐geographic (genetics held constant)	0.135	0.178
dLEX d GEO (d GEN) Lexical‐geographic (genetics held constant)	−0.053	0.615
d SYN d GEN (d GEO) Syntactic‐genetic (geography held constant)	0.717	0.001
dLEX d GEN (d GEO) Lexical‐genetic (geography held constant)	0.679	0.001

After Bonferroni correction for multiple tests, these results are significant at the P = 0.012 level.

DISCUSSION

Reliable evidence for parallelism of genetic and linguistic change had previously been provided, although only on a regional scale (Sokal, 1988) and without formal quantification of language distances. Here, first through a quantitative approach to cognate words (Bouckaert et al., 2012), and then through a syntactic method (the PCM, Longobardi and Guardiano, 2009) designed for comparing languages across separate families, we overcome both limits of previous studies. In particular, through syntax, precise comparison and measuring is finally possible even across established linguistic families: the main families/subfamilies of Europe are discriminated by means of just 56 abstract characters suggested by formal grammatical theory, using standard methods of evolutionary biology and without resorting to unsafe long‐range etymologies.

This allowed a series of cross‐family correlation tests which reach precise conclusions on a broader continental scale: populations speaking similar languages in Europe tend to resemble each other at the genomic level, thus suggesting that cultural change and biological divergence have proceeded in parallel in Europe, at least as a rule (for exceptions, also see Bolnick et al., 2004). The partial correlation tests show that populations speaking similar languages also tend to be genetically closer than expected on the sheer basis of their geographic location, so that in Europe language, i.e. basic vocabulary and now, at an even wider scale, syntax, appear to offer a better prediction of genomic distances than geography.

These correlations with independent historical variables provide a new type of evidence for the PCM and in turn for the general biolinguistic approach it is inspired by (Lightfoot, 1999; Di Sciullo and Boeckx, 2011; Berwick et al., 2013), and strengthens the controversial hypothesis that parameters do encode a phylogenetic signal (Lightfoot, 2006). Working out parameter theory against such historical evidence is also a new way of evaluating it with respect to its major critical points, e.g., the learnability issues (Boeckx and Leivada, 2013). Note that the trees in this study were inferred from the distance matrices, since character‐based programs seem less suitable for heavily implicational systems (Longobardi et al., 2013). It has also been argued (Heggarty, 2006) that, despite the admitted loss of information, distances may even remedy some shortcomings of parsimony‐based character programs in dealing with occasional homoplasies or backmutations. Finally, and most crucially, for the purpose of calculating Mantel correlations between qualitatively and quantitatively very different entities (56 parameters, 178.000 SNPs), distances seem a necessary mediation/conversion.

We could thus move on to a more detailed analysis of population diversity in Europe and of the possible exceptions to the conclusions above. When population relationships were summarized by trees, the main elements of disagreement were represented by the positions of Hungarians and Rumanians, which cluster genetically with speakers of Serbo‐Croatian despite being highly differentiated syntactically. These populations all dwelling in Central Europe, it is reasonable to suspect an effect of geographical proximity, enhancing gene flow between neighboring countries.

Using a method that highlights the most significant episodes of genetic exchange after population splits, a likely situation among humans (Barbujani and Colonna, 2010), especially in Europe, we could precisely find evidence of the possibly relevant biological contacts among speakers of IE‐subfamilies (from Slavic‐speaking areas into Rumania and from Southern Europe into the Balkans) and between Ugric and IE speakers (from the Balkans into Hungary). Pending further investigation, it appears that where biological relationships are not those expected from vertical linguistic history, they are plausibly accounted for by relatively recent gene flow processes independently detected by Treemix.

In particular, concerning the real exception to our congruence pattern, notice that the presence in modern Hungarians of DNA markers currently common in Northern and Central Asia has been interpreted as a consequence of westward gene flow in Medieval times (Csányi et al., 2008; Bíró et al., 2009; Hellenthal et al., 2014); this is obviously connected with historical migrations in the 9th century and with the fact that the current language is closely related to the Ugric‐speaking communities along the Ob river. However, the current low frequency of those markers is not what one would expect to observe, had a substantial demographic replacement occurred (Nadasi et al., 2007; Hellenthal et al., 2014). Careful analyses of 10th century ancient DNA in Hungary showed a predominance of European mitochondrial haplotypes in burials attributed to the lower classes, and a high incidence of Asian haplotypes in high‐status individuals of that period (Tömöry et al., 2007), which points to the Asian immigrants as representing a social élite, rather than the bulk of the population. The exception to the results of the present study is thus nicely justified in this scenario, suggesting that when a Finno‐Ugric language was introduced in Hungary, the genetic buildup of the population changed only in part, thus retaining similarities with its geographic neighbors, an example of the process called élite dominance by Renfrew (1992). On the contrary, the same case cannot be easily made for Basques (Alonso et al., 2005; Rodríguez‐Ezpeleta et al., 2010; Young et al., 2011; Martinez‐Cruz et al., 2012) or Finns, for whom, to the best of our knowledge, no available evidence suggests a similar model of partial demographic replacement associated with language replacement (Nelis et al., 2009). Thus, the comparative linguistic/genomic analysis, attempted in the present study, seems able to single out and precisely assess these differences in the population histories of the three non‐IE members of our sample.

Our results confirm the fruitfulness of importing numerical and biostatistical methods into language phylogenetics (McMahon and McMahon, 2005), but even more of resorting to radically new (Heggarty et al., 2005) and deeper (Longobardi, 2012) levels of taxonomic characters for a thorough reconstruction of both demographic and linguistic history.

In particular, we see good chances to obtain trustworthy taxonomic insights when the PCM is applied to longer‐range computations that could not be safely attempted through traditional lexical methods, and we expect to find interesting and illuminating correlations between genetic and linguistic diversity across other continents, contributing to the “New Synthesis” research line (Renfrew, 1987). Sokal (1988) and Cavalli‐Sforza et al. (1988) could venture into addressing Darwin's gene‐language congruence issue thanks to the theoretical progress of 20th century genetics; along with the availability of broad genomic datasets, the corresponding progress of formal grammatical theory over the past 50 years may now enable us to accurately test the hypothesis on ever larger and more solid grounds.

Supporting information

Supporting Information