Mitigation of eddy current heating during magnetic nanoparticle hyperthermia therapy

Abstract

Magnetic nanoparticle hyperthermia therapy is a promising technology for cancer treatment. The technique involves delivering magnetic nanoparticles (MNPs) into tumors, then activating the MNPs using an alternating magnetic field (AMF). The AMF generating system produces not only a magnetic field, but also an electric field. The electric field penetrates normal tissue and induces eddy currents, which result in unwanted heating of normal tissues. The magnitude of the eddy current depends, in part, on the AMF source and the size of the tissue exposed to the field. The majority of in vivo MNP hyperthermia therapy studies have been performed in small animals, which, due to the spatial distribution of the AMF relative to the size of the animals, do not reveal the potential toxicity of eddy current heating in larger tissues. This limitation has posed a nontrivial challenge for researchers who have attempted to scale up from a small animal model to clinically relevant volumes of tissue. For example, the efficacy limiting nature of eddy current heating has been observed in a recent clinical trial, where patient discomfort was reported. Until now, much of the literature regarding increasing the efficacy of MNP hyperthermia therapy has focused on increasing MNP specific absorption rate or increasing the concentration of MNPs in the tumor; i.e. - improving efficacy at what is thought to be the maximum safe field strength and frequency. There has been a relative dearth of studies focused on decreasing the maximum temperature resulting from eddy current heating, to increase therapeutic ratio. This paper presents two simple and clinically applicable techniques for decreasing maximum temperature induced by eddy currents. Computational and experimental results are presented to understand the underlying physics of eddy currents induced in conducting, biological tissues and to leverage these insights for the mitigation of eddy current heating during MNP hyperthermia therapy. Phantom studies show that these techniques, termed the displacement and motion techniques, reduce maximum temperature due to eddy currents by 74% and 19% in simulation, and by 77% and 33% experimentally. Further study is required to optimize these methods for particular scenarios; however, these results suggest larger volumes of tissue could be treated, and/or higher field strengths and frequencies could be used to attain increased MNP heating, when these eddy current mitigation techniques are employed.

I. INTRODUCTION

Over the past several decades magnetic nanoparticle (MNP) hyperthermia therapy has been a rapidly developing area of research. Clinical hyperthermia has been shown to work well in an adjuvant setting [1–12], and is advantageous in its capacity to treat repeatedly, in a minimally invasive or entirely non-invasive manner. Since hyperthermia techniques must exhibit high specificity to be effective and safe, magnetic nanoparticles have an advantage in that they provide an amorphously distributed heat source which can conform to the shape of the tumor and be targeted to cancer cells on an individual basis using antibody targeting [13–18]. MNP hyperthermia therapy is undergoing clinical trials in Europe [19–24] and focus in the US has been steadily moving toward clinical translation. However, when considering clinically relevant volumes of tissue, one of the factors which most significantly limits treatment efficacy is the adverse effect of the non-specific heating due to eddy currents (EC) in normal tissue. These eddy currents are a direct consequence of the applied external alternating magnetic field (AMF) used to excite the nanoparticles in the tumor, and have been shown to limit treatment efficacy in clinical trials [21–23]. To overcome these challenges, this paper presents simple, clinically applicable techniques which decrease the thermal dose due to eddy currents in normal tissue by decreasing the maximum heat deposition in non-tumor regions.

A. Eddy Current Limitations

Defined by Faraday’s law, within an idealized, long solenoid, the absorbed power density in tissue due to eddy currents is σ(πμ₀Hfr)² = σE², where f is the frequency, σ is the tissue conductivity, μ₀ is the permeability of free space, r is the radial position within the solenoid in which the tissue exists, E is the electric field and H is the magnetic field [25]. The tissue can be placed at any point inside the solenoid along the radial direction from 0 to R, where R is the radius of the solenoid. As the location of the tissue is moved close to R, the absorbed power density (i.e. – power at each point within the target) changes as a function of r². For a single-turn surface coil, there is no known, simple, closed form expression; however, the electric field can be generally characterized as decaying between 1/d and 1/d² with distance d from the coil surface [26]. In either case it is generally accepted that, to prevent unwanted heating in normal tissue, the field strength frequency product should be limited. Various independent clinical studies have evaluated the Hf limitations that test subjects could withstand for more than one hour without major complications [20–23], and have shown limits varying from $450\frac{\mathrm{M}\mathrm{A}}{\mathrm{m}·\mathrm{s}}$ to $850\frac{\mathrm{M}\mathrm{A}}{\mathrm{m}·\mathrm{s}}$. It was also found that the Hf limitations depended on anatomical region. In [22] it was observed that the higher field strengths were tolerated in the thoracic region, neck and head, as opposed to the pelvic region, and that the observed treatment-limiting heating occurred in skin folds. A summary of these studies is found in [27]. This undesirable heating is exacerbated in the case of deep seated tumors, such as pancreatic and rectal cancers, where large volumes of tissue must be exposed to a strong AMF.

B. Improving Efficacy

In order to expand the applicable cases where MNP hyperthermia therapy is effective, much work has focused on increasing thermal dose to the tumor, while maintaining what is thought to be the maximum safe Hf product. One approach is to increase the MNP specific absorption rate (SAR) by modifying MNP core size, core shape, core material type, coating thickness, magnetic interaction effects, etc. [28–34], with recent work focusing on developing MNPs with high SAR at low field strength [35]. Another method focuses on increasing the MNP concentration at the target, thereby increasing the SAR per unit volume of the tumor, using various methods such as surface modification of MNPs, ionizing radiation or chemotherapy to modify the tumor, and antibody-targeting [36–41].

Most of the aforementioned work has been focused on increasing tumor cytotoxicity without attempting to decrease normal tissue toxicity due to eddy current heating (ECH). This type of development has been the focus of most of the research community interested in increased therapeutic ratio for MNP hyperthermia therapy. A few groups have worked on increasing therapeutic ratio by decreasing ECH cytotoxicity in some way. Nieskoski et al. considered the choice of coil type (optimized single-turn coil vs. Helmholtz coil) to optimize MNP heating constrained by ECH, in a simplified geometry [27]. Other groups have developed improved AMF coil designs [42–46]. Kumar et al. have tested the efficacy of applying surface cooling to the skin to reduce temperature rise due to eddy currents [47]. To our knowledge, the work presented here marks the first attempt to decrease thermal dose due to ECH by considering the placement of tissue in time and space, relative to the field, or vice versa.

C. Eddy Current Modeling

By their nature eddy currents and eddy current heating are difficult to monitor in vivo. For this reason, it is important to model eddy currents in complex tissue, to inform the design of eddy current heating mitigation techniques. Substantial effort has been made to model eddy current heating over the past several decades. Most of these efforts have focused on the medium frequency (0.3–3MHz) and high frequency (3–30MHz) ranges [48–54]; however, some work has focused on low frequency (30–300kHz) [55–58]. These models can be used to determine safe exposure levels on either a patient specific basis, or at least a site specific basis, as the diverse tissue regions in which tumors may be present can vary greatly in physical dimension and tissue thermal and electrical properties, resulting in different safe levels of AMF [22].

D. Objective

In this paper, instead of limiting the field strength and frequency we consider two ways of manipulating the tissue exposed to the field. In the first technique, normal tissue is displaced away from the region nearest the coil conductor, which corresponds to regions of high electric field. This method leverages the fact that EC heating is related to the square of the E-field, and that the E-field falls off with distance from the coil. As a result, the amount of EC heating is reduced substantially by small displacements of the conductive tissue away from the coil. The second technique involves keeping the coil in constant motion relative to the tissue, dispersing the cumulative EC SAR to a larger volume of tissue, thereby preventing overheating at any one point. Note that this paper presents results for a single-turn surface coil, however, application of these techniques to other surface and tissue-encompassing type coils is discussed in Section VI. Also, note that the work presented here is intended as a proof of concept study. Although some examples of applicable clinical scenarios are presented in the discussion, the application of these techniques to specific clinical scenarios is beyond the scope of this work. For the purpose of highlighting the possibilities of the techniques, the application toward improving MNPH treatment of breast cancer is chosen. Breast cancer provides an excellent clinical situation for the tissue displacement technique, as the tissue is often highly compressible, a property leveraged in mammography to decrease radiation dose and improve image quality [59, 60]. This allows for the normal tissue to be displaced while keeping the cancerous tissue in the treatment region (the region in which magnetic field strength is sufficient to cause therapeutically relevant MNP heating). The motion technique does not require compressible tissue, and could feasibly be applied in any case where the coil is not physically impeded from being repositioned without significant loss of magnetic field strength at the tumor site. The depth of tumors which could be adequately treated clinically using this method is dependent upon the type of coil chosen. Ultimately, for either of these techniques to be effective, the ratio of minimum MNP SAR to maximum EC SAR must increase.

II. THEORY

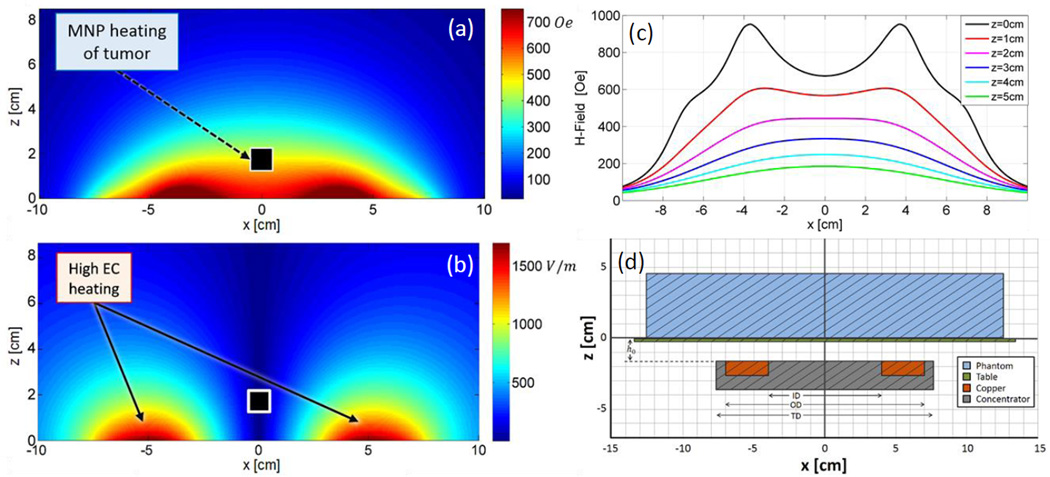
In this section we present techniques for mitigating eddy current heating which are particle agnostic and, when implemented well, do not affect MNP heating. These methods seek to take advantage of the inherent differences between the electric and magnetic field distributions in the near-field region of an AMF induction coil. Figure 1a shows the simulated magnetic field data (H-field) for a single-turn coil (ID = 8cm, OD = 14cm) with a magnetic core and a fixed amplitude alternating primary current. The coil is located in the xy-plane at z=−1.55cm (Fig. 1d). Note the features of the field shape along the x-axis at various heights, which correspond to tissue depths (Fig. 1c). The H-field map can be classified into three distinct regions. For z < ~2cm the H-field is highest near the coil conductor. At z ≈ 2cm, the field strength is nearly constant within an ~8cm diameter circular area in the xy-plane. At z > ~2cm the field strength exhibits a single peak along the center axis of the coil (i.e. – where x = y = 0). Now compare these features to the electric field map (E-field) in Figure 1b. The E-field can be generally characterized by one feature, strength decreases with distance from the conductor, with zero field along the center axis. The importance of this comparison lies in the fact that magnetic nanoparticle heating depends on H-field strength, whereas eddy current induction depends upon E-field strength. Note that the following theoretical discussion pertains to an idealized thin loop system whose field distribution varies only slightly from that of the experimental system described in Seciton III-A; therefore, for the sake of brevity, only the field distributions for the experimental system are shown in Figure 1.

Figure 1.

Modeled (a) magnetic and (b) electric field distributions of the single-turn coil with a magnetic core located in the xy-plane at z = −1.55cm. (c) Magnetic field strength along x, at y=0, for various z values. The transition between bimodal and unimodal behavior occurs at z ≈ 2. (d) Cross-sectional diagram of the experimental setup at y = 0 (i.e. – vertically bisecting the phantom), drawn to scale and further described in Section III-A.

A. Tissue Displacement

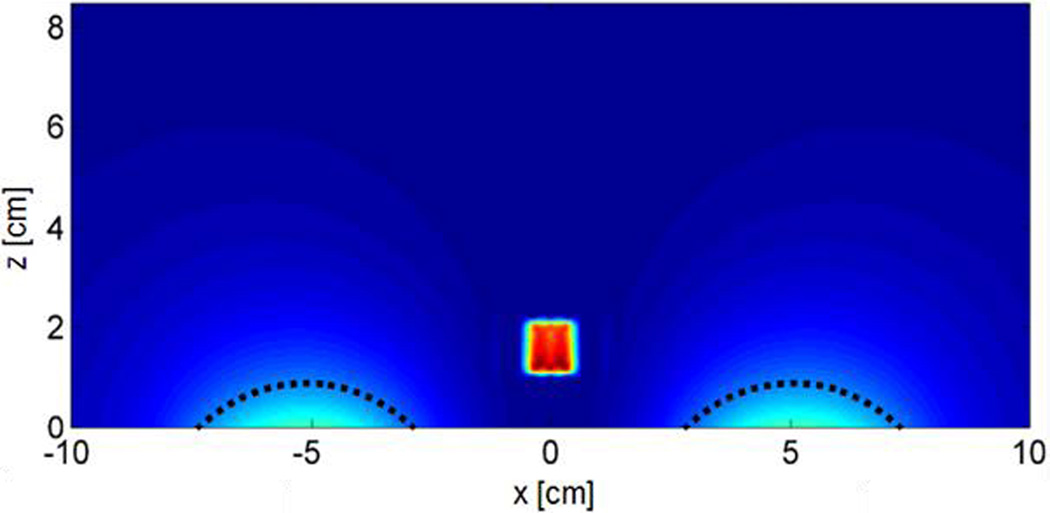
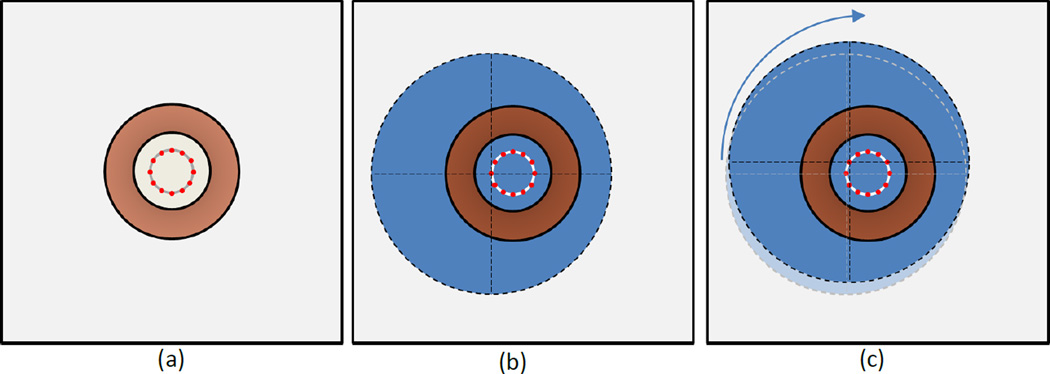
When a conductive object is placed over the coil, an eddy current is induced which equals the product of the E-field in the object and its conductivity. Since electric field from a current source is inversely proportional to the distance from the source, we can reduce the maximum induced eddy current in the conductive target by displacing parts of the conducting volume away from regions of high electric field near the source. For a large rigid conductive body, this EC SAR reduction approach cannot be exploited. However, many tumor bearing tissues are somewhat pliable and/or compressible, an exemplary case being breast tissue. By physically pushing the normal breast tissue away from the regions of highest E-field (indicated by the dashed lines in Figure 2) using a non-conductive spacer apparatus, the volume of space capable of producing the greatest eddy currents no longer contributes to the total current induced in tissue. We have termed this method of eddy current heating mitigation the tissue displacement technique.

Figure 2.

Modeled cross sectional SAR distribution (xz-plane at y = 0) for a 0.6 S/m phantom with 1cm³ uniformly distributed MNP inclusion. Regions of high EC SAR to be blocked by a tissue displacer are marked with dashed lines.

For idealized tissue where this perturbation would result in no translation of the tumor in z, there is a clear benefit. In the case of tissue with realistic mechanical properties, the tumor will move into a region of lower H-field, resulting in lower MNP SAR. If the MNP SAR were to decrease more than the maximum EC SAR, the technique would be invalid. To address this concern, assume two extreme cases of a conducting half-space embedded with an MNP inclusion to simulate a tumor. First, a best case scenario where the tumor does not shift in z, and second, a worst case scenario where the tissue is completely rigid, resulting in a tumor shift in z equal to the tissue displacer height. Assume an optimal spacer shape on which E is equal on the entire surface, and that SAR_MNP varies linearly with H. If the primary coil current is increased to compensate for any decrease in H experienced by the tumor, the reduction in maximum SAR_EC can be calculated as:

$${\mathit{\text{SAR}}}_{\mathit{\text{EC Reduction}}}=1-\frac{{[E_{\mathit{\text{max}}}(x,y,z_1)]}^2}{{[E_{\mathit{\text{max}}}(x,y,z_0)·\frac{H(0,0,z_2)}{H(0,0,z_3)}]}^2}$$ (1)

Where z₀ is the height of the treatment table (i.e. – the initial position of the phantom), z₁ is the maximum height of the spacer, z₂ is the initial height of the tumor, z₃ is the final height of the tumor.

In the best case scenario, z₂ = z₃, reducing Equation 1 to:

$${\mathit{\text{SAR}}}_{\mathit{\text{EC Reduction}}}=1-\frac{{[E_{\mathit{\text{max}}}(x,y,z_1)]}^2}{{[E_{\mathit{\text{max}}}(x,y,z_0)]}^2}$$ (2)

Alternatively, when the coil current is increased such that max SAR_EC is equal in the control and displaced cases, the MNP_SAR increases by:

$${\mathit{\text{SAR}}}_{\mathit{\text{MNP Increase}}}=\sqrt{\frac{1}{1-{\mathit{\text{SAR}}}_{\mathit{\text{EC Reduction}}}}}-1$$ (3)

For a conducting half-space z > 0, with a 7cm thin loop coil at z = −1.55cm, using a displacer with a maximum height of 2cm, and an initial tumor depth of 2cm, the reduction in maximum SAR_EC is 71% in the best case scenario, and 37% in the worst case scenario (Eq. 1, 2). Alternatively, SAR_MNP can be increased by 85% in the best case scenario, and 26% in the worst case scenario, when SAR_EC is kept constant between cases (Eq. 3).

B. Motion

The second proposed method of eddy current heating mitigation is based on the lateral distribution of the magnetic field. This method is also a form of tissue displacement, but in contrast to the displacement method the total energy absorbed by the normal tissue is not reduced. Instead, the heat deposition per unit volume is spread out to a greater volume of tissue, thus decreasing the maximum energy absorption at any one point. This can be achieved in one of two ways; either the patient can be moved about with respect to the field, or the field can be moved about with respect to the patient. In practice, patient comfort and clinician ease of use will determine which method will be implemented. To illustrate the applicability of this technique, let us consider the case where the coil is moving slowly beneath a fixed treatment surface in a circular path with a radius of several centimeters. As the coil moves beneath the patient, the region of tissue exposed to the highest E-field is shifted gradually. As a result, in this case of constant relative motion, instead of the eddy currents following the same path for what might be an hour long treatment session (building up heat in the same regions throughout the therapy), the current is forced into different regions thereby resulting in distributed heating. We have termed this method of eddy current mitigation the motion technique.

The tumor depth and motion path radius both have an effect on the ratio of MNP SAR in the tumor to maximum EC SAR. Any decrease in H experience by the tumor due to the lateral shift away from the maximum will reduce MNP SAR. To address this concern, consider the simplified case of a homogeneous conducting half-space embedded with an MNP inclusion to simulate a tumor and assume SAR_MNP varies linearly with H. When the primary coil current is increased to compensate for any decrease in H experienced by the tumor, the reduction in maximum SAR_EC can be calculated as:

$${\mathit{\text{SAR}}}_{\mathit{\text{EC Reduction}}}=1-C·\frac{\text{max}\_\mathrm{s}\left\{{\sum }_{i=1}^N\right[{[E_m(I_0,t_i)]}^2·\frac{t_i}{T}\left]\right\}}{\text{max}\_\mathrm{s}\{{[E_c(I_0)]}^2\}}$$ (4)

where max_s determines the spatial maximum within the conducting half-space, E_c is the electric field experienced by the conducting half-space in the static control case, and E_m is the electric field experienced by the conducting half-space while the coil is in motion at position i, where the coil is moved to N positions throughout the total exposure time T, occupying each position for a period t_i. The ratio of EC SARs is scaled by a factor C, which is determined as

$$C={\left[\frac{H_{{\mathit{\text{MNP}}}_{\mathit{\text{control}}}}}{H_{{\mathit{\text{MNP}}}_{\mathit{\text{motion}}}}}\right]}^2={\left[\frac{H(I_0,0,\theta ,z_0)}{H(I_0,r_m,\theta ,z_0)}\right]}^2$$ (5)

where H is the rotationally symmetric magnetic field in cylindrical coordinates, r_m is the radius of the motion path, and z₀ is the height of the tumor.

In this scenario, there is no effect on the secondary E field due to discontinuities in electrical conductivity. Note that for a sufficiently small value of σ, as is the case with human tissue conductivities (generally σ < 1 S/m), the total electric field within the conducting half-space is not significantly perturbed. For a conducting half-space which exists for z ≥ 0, with the transmitting coil lying parallel to the boundary at z = −1.55cm (within the non-conducting half-space), a simulated tumor depth, z₀ = 1cm (bimodal H field zone), using a motion path radius, r_m = 4.0cm, the reduction in max SAR_EC is 44.8%. If instead z₀ = 2cm (transitional H field zone), and r_m = 3.8cm, the reduction in maximum SAR_EC is 35.5%. When z₀ = 3cm (unimodal H field zone) and r_m = 3.8cm the reduction in max SAR_EC is 28.9%. Alternatively, if the primary coil current is instead increased such that max SAR_EC is equal in the control and motion cases (Eq. 3), the resulting increase in SAR_MNP for these three cases are 34.6%, 24.5%, and 18.6%, respectively. In all cases the control tumor position was chosen to maximize SAR_MNP at the specified tumor height. Note that the path radii have been chosen to maximize SAR_MNP/SAR_EC (to within 2mm of the optimal radii), ignoring thermal effects which may affect path optimization.

III. METHODS

A. AMF System

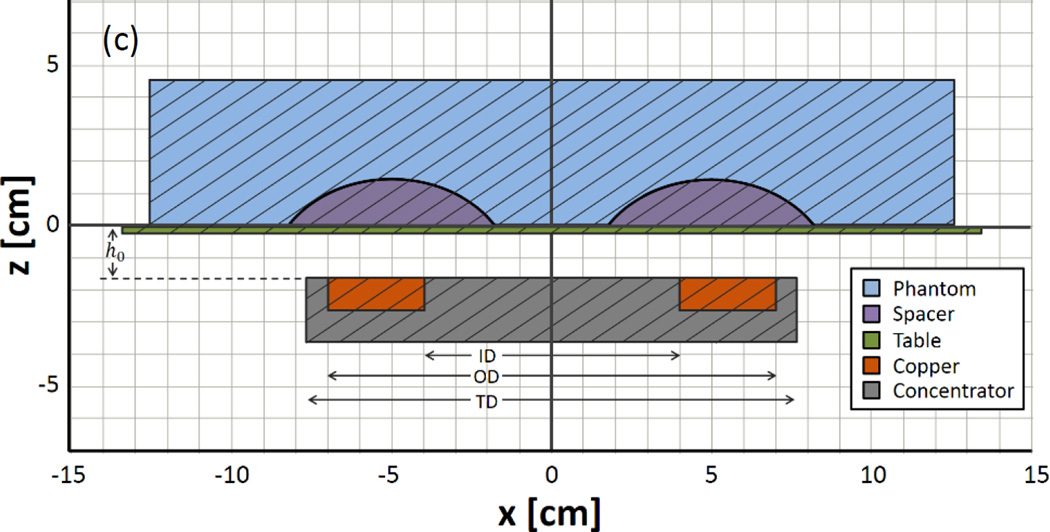
The AMF induction coil used in these experiments is a single-turn surface coil with a magnetic core (Fluxtrol Inc., Aubrun Hills, MI, USA). It is powered by a 25kW generator (Radyne Corp., Milwaukee, WI, USA), which drives 135–400kHz AC current through the coil, thus generating a 135–400kHz AMF [56]. The frequency used in the following experiments was 162kHz. The coil (Fig. 3b) consists of a single-turn of rectangular copper tubing with ID = 8cm, OD = 14cm, H = 1cm, with a magnetic core (Fluxtrol 75) which surrounds three sides of the tubing resulting in a total diameter, TD = 15.2cm (Fig. 1d). The upper surface of the copper tubing faces the target tissue and is flush with the face of the magnetic material. A treatment table with airflow between the coil and table ensures the phantom or tissue is electrically and thermally isolated from the coil. The coordinate system has been chosen such that the table surface exists in the xy-plane at z = 0, with the origin located along the centerline of the coil (Fig. 1d). The distance between the coil surface and the table surface, h₀, is 1.55cm. Surface temperature distributions are measured using a thermal camera (Model SC325, FLIR Systems Inc., Wilsonville, OR, USA).

Figure 3.

(a) AMF system with a phantom experiment in progress. The generator, treatment table, thermal camera, and thermal camera software interface are shown. The induction coil (b) is obscured from view in (a) by the treatment table.

B. Computational Methods

The computational results presented in this paper were generated using a custom electromagnetics model, which implements the Method of Auxiliary Sources (MAS), coupled with the Pennes bioheat equation.

MAS is a robust and accurate numerical technique for evaluating electromagnetic wave propagation and scattering problems [61, 62]. In this method, boundaries between materials of differing electrical parameters are defined and discretized into pairs of points along a surface. Each pair consist of an inner and outer point, which define fictitious surfaces both inside and outside of the true surface, and are designated as a dipole source with unknown magnitude and direction. These are the auxiliary sources, and they are evaluated directly using the boundary equations for the tangential components of the electric and magnetic fields. The result is a linear system of equations.

After the magnitude of the auxiliary sources are determined, the fields in each region are evaluated as a sum of fields from the auxiliary sources of the fictitious surfaces [63]. The accuracy of the MAS method was studied for the single-turn surface coil in [56]. The coil was modeled using the manufacturer’s schematics and magnetic core material properties (Fluxtrol Inc. Aubrun Hills, MI, USA), and has been shown to be in good agreement with measured data [56]. Once the electric field is computed, the SAR (W/kg) due to eddy currents is simply calculated as,

$${\mathit{\text{SAR}}}_{\mathit{\text{EC}}}=\frac{\mathit{J}·\mathit{E}}{2\rho }=\frac{\sigma {\mathit{E}}^2}{2\rho }$$ (6)

where σ is the electrical conductivity (S/m), J is the current density (A/m²), and ρ is the density of tissue (kg/m³). For the case of a non-uniform E field, and an axially oriented non-permeable cylindrical target,

$${\mathit{\text{SAR}}}_{\mathit{\text{EC}}}=\frac{\sigma {\mathit{E}}^2}{2\rho }=\frac{2\sigma {(\pi f{\mu }_0)}^2}{\rho r^2}{[{\int }_0^r{H}_z(r\prime )r\prime dr\prime ]}^2$$ (7)

where f is the frequency of the field (Hz), μ₀ is the permeability of free space [64]. Furthermore, in the case a constant H field [25, 64],

$${\mathit{\text{SAR}}}_{\mathit{\text{EC}}}=\sigma {\pi }^2{\mu }_0^2{(H_{z}rf)}^2/2\rho$$ (8)

However, even for an idealized solenoid, there is a non-zero axial E field due to the angle of the turns relative to z, and significant coupling between turns; thus, one must use the general case (Eq. 6) to describe real world systems. Additionally, the SAR due to MNP is estimated by using the computed magnetic fields and MNP distributions. The total SAR is calculated as,

$$\mathit{\text{SAR}}={\mathit{\text{SAR}}}_{\mathit{\text{EC}}}+{\mathit{\text{SAR}}}_{\mathit{\text{MNP}}}$$ (9)

where, SAR_MNP is determined using the MNP heating model discussed in [35, 65]. Finally, the total SAR distribution and thermal boundary conditions are fed into the Pennes Bioheat Equation [66, 67] which is solved using a standard finite difference time domain method [68–70].

In the computational studies, cylindrical phantoms (D = 25.0 cm, H = 4.5 cm) were modeled with electrical conductivity 0.6 S/m, thermal conductivity 0.58 W/[m · °C], specific heat 4182 J/[kg · °C], density 998 kg/m³, and exposed to the simulated AMF of a single-turn coil. This simplified geometry was chosen to minimize confounding factors affecting eddy current heating such as inhomogeneities and boundary effects in a system that could be accurately recreated experimentally. The electrical conductivity was set to the value of human muscle which fell at the high end of values reported at 100 kHz [71]. Final thermal distributions were determined using boundary conditions simulating natural convection (heat transfer coefficient, h_T = 10 W/[m² · °C]) at all surfaces except the bottom surface, for which an insulating boundary condition was implemented (h_T = 0).

1. Displacement Specific Computational Methods

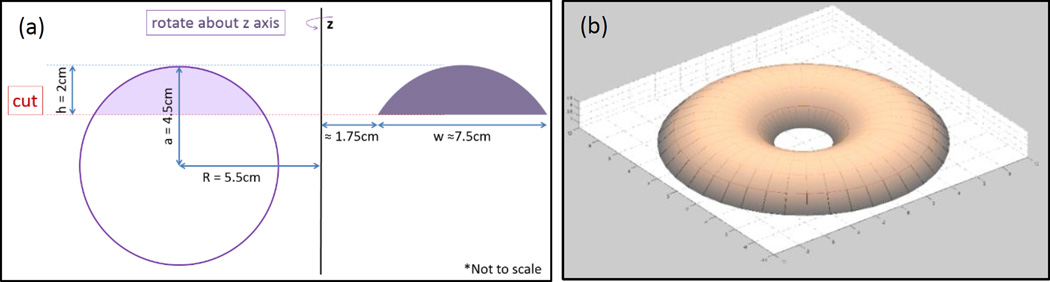
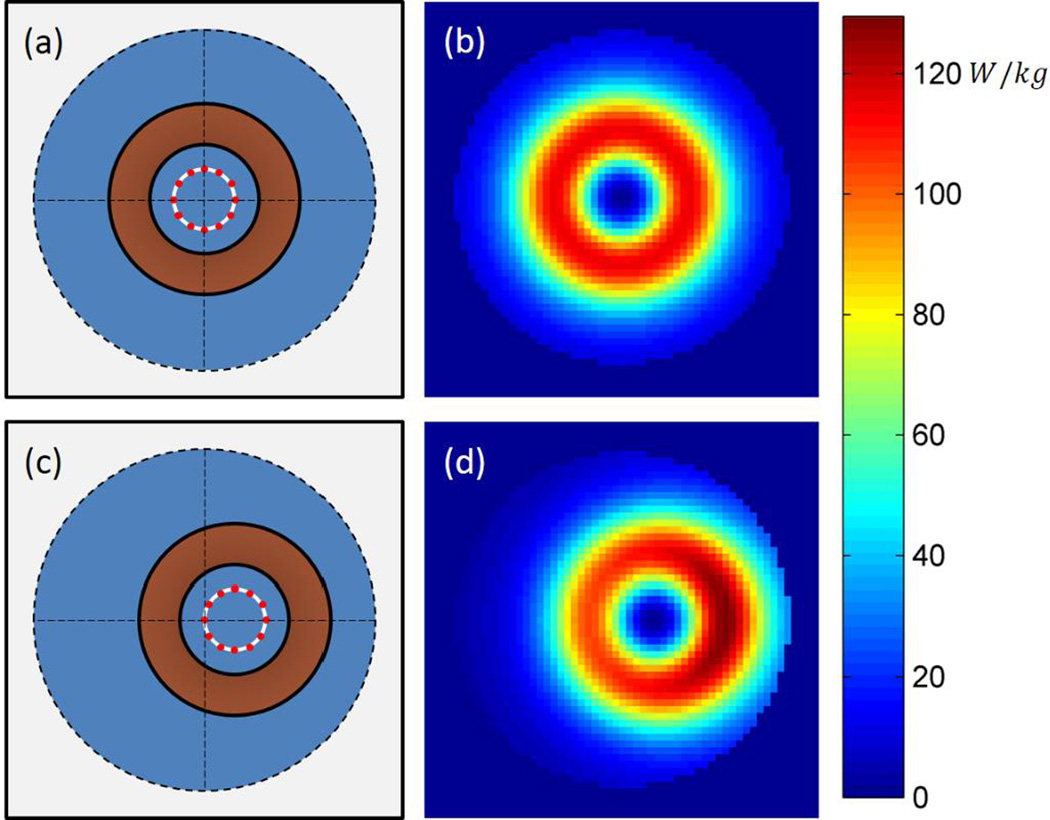
A simulated phantom was modeled with an embedded torus section (ID = 3.5 cm, OD = 18.5 cm, H = 2.0 cm) electrical insulator (Figure 4), to model the effect of displacing tissue away from the highest electric field region. A second simulation of an identical phantom with no insulating displacer was modeled for comparison.

Figure 4.

(a) A 2D cross-sectional diagram showing the geometry and relevant dimensions of the displacer. (b) 3D model of toroid section shaped tissue displacer. (c) Cross-sectional diagram of the experimental setup at y = 0 (drawn to scale).

2. Motion Specific Computational Methods

The simulated phantom was initially positioned 2.5cm off center from the coil. It was translated at 30 second intervals to one of 12 different positions, with a total exposure time of 30 minutes. Each position was radially 2.5cm distant from the centerline of the coil with a 30 degree angle between them (Figure 5). Note that, due to the asymmetry of the modeled system at a single position, the magnetic core of the coil was not modeled (air core). Due to the rotational symmetry inherent to the motion, the remaining 11 SAR distributions can be inferred from the first by simply rotating the resulting SAR distribution in the xy-plane, about the center of the phantom, in increments of 30 degrees (Fig. 5).

Figure 5.

Top-down diagram of phantom positions during ECM-motion technique, note the phantom is positioned above the coil. (a) Coil position (copper colored ring) shown with 12 positions for placement of the center of the phantom. (b) Phantom (blue) in position 1, and (c) in position 2. Note that the phantom is simply translated to the next position and undergoes no rotation.

C. Experimental Methods

For experimental verification of the computational results, cylindrical phantoms (D = 25.0 cm, H = 4.5 cm) were constructed using 20g agarose, 2.6g NaCl, and 2L deionized water. All phantoms were created with the highest reported values for electrical conductivity of human muscle (0.6 Ω⁻¹ · m⁻¹ at 100kHz) [71]. The temperature distribution of the surface of the phantoms was measured using a thermal camera. Each phantom was exposed to AMF at 16.25 kW nominal generator power setting for 30 minutes. The phantoms were cut immediately after heating and half on the phantom was flipped up onto the other half to expose the cut faces to the thermal camera, resulting in a mirror image with a horizontal axis of symmetry.

1. Displacement Specific Experimental Methods

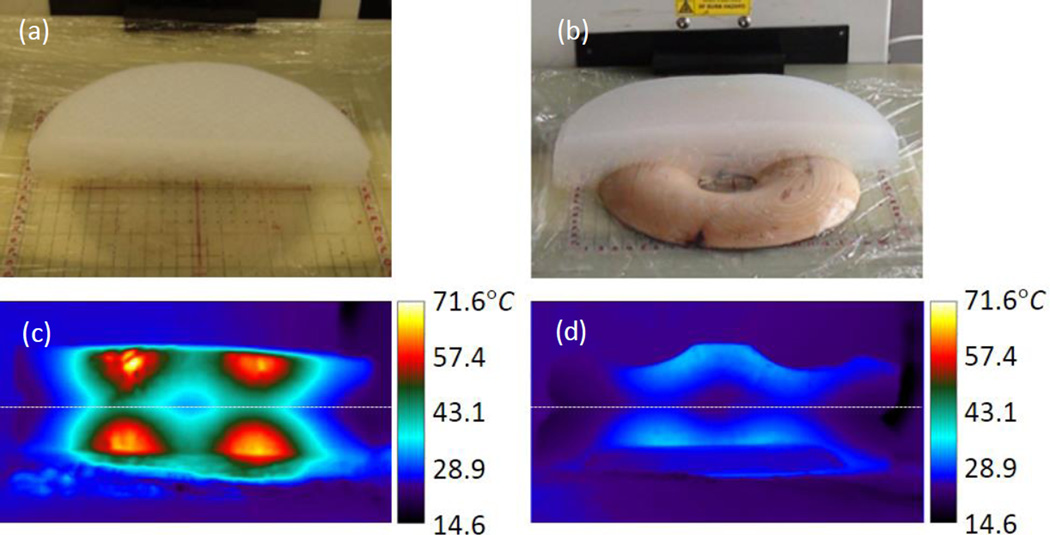
A laminated wooden spacer was fabricated to the specifications shown in Figure 4. Due to the phantom material’s lack of compressibility and elasticity, the wooden spacer was embedded in the phantom to mimic the displacement of compressible tissue (Fig 4c). The resulting phantom retained the diameter and volume of the control (non-displaced) phantom; however, the height increased slightly.

2. Motion Specific Experimental Methods

The control phantom was positioned centrally on the table, over the induction coil on a plastic sheet of transparency paper <0.2mm thickness to facilitate moving the phantom without compromising it mechanically. The motion phantom was initially placed 2.5cm off center from the coil. It was then moved at 30 second intervals, during AMF exposure, by sliding (translating) the phantom along the table to one of 12 different positions, each position was radially 2.5cm distant from the centerline of the coil with 30 degree angle between them.

IV. TISSUE DISPLACEMENT RESULTS

A. Computational Study

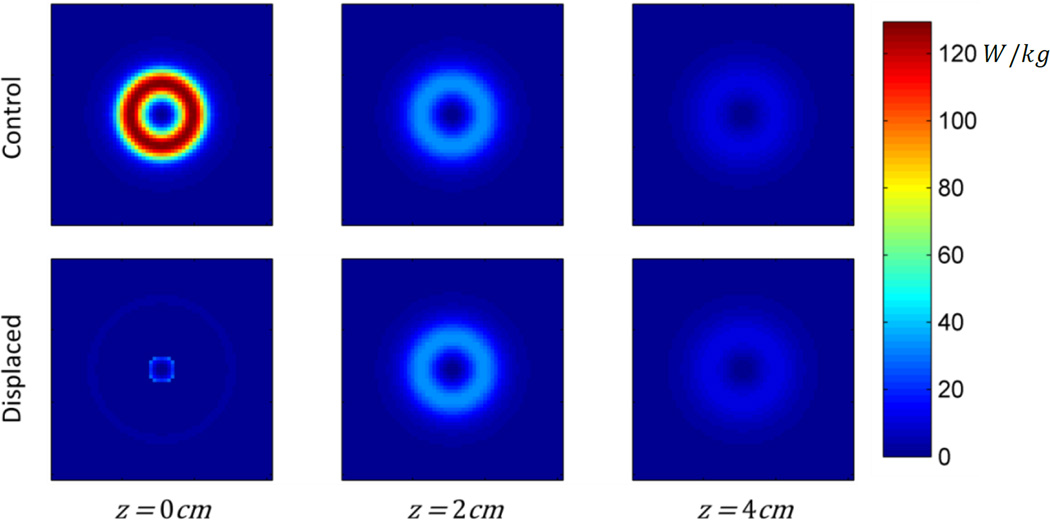
The resulting SAR distributions are shown in Figures 6 and 7. Note that at the base of the phantom (z = 0), the total SAR in the plane is strongly reduced due to the presence of the displacer. At z > 2 cm the SAR distributions are identical, with and without the spacer, because current distribution is unaffected in this region. In this simulation, total power absorption in the phantom is decreased by 55%.

Figure 6.

Modeled cross sectional SAR distributions of control and displaced phantoms at z = 0, 2, and 4cm (i.e. – the base of the phantom, the height of the displacer, and 2cm above the displacer).

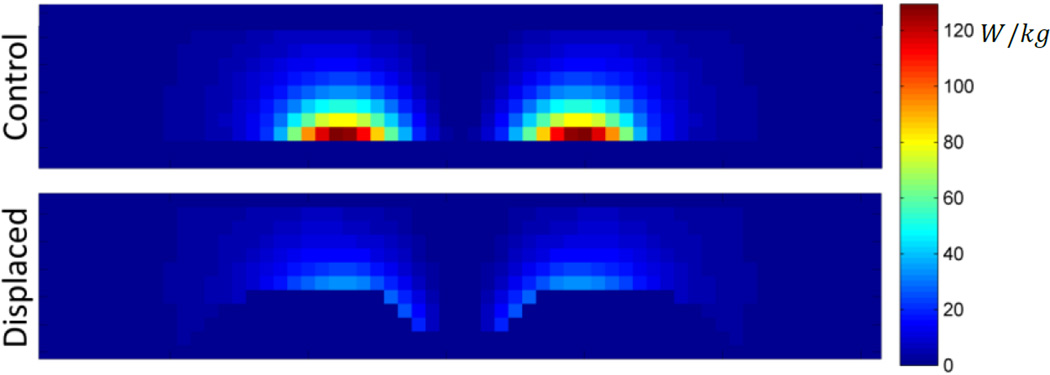
Figure 7.

SAR distribution for control and displaced phantoms. Cross-sections shown at y = 0cm.

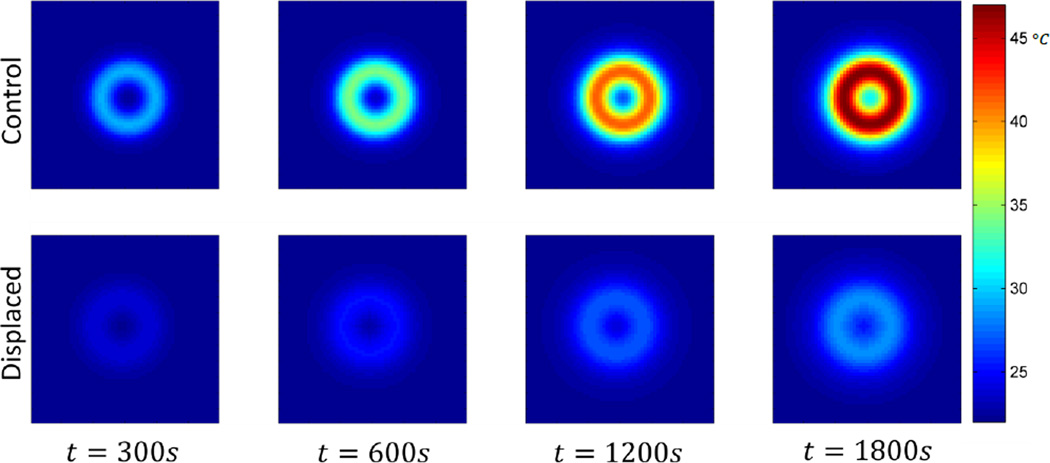
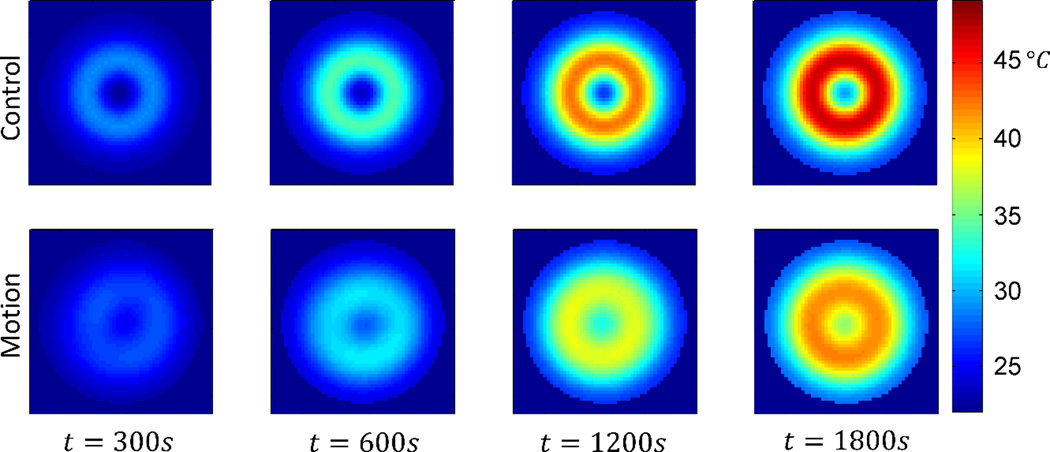
Including the effects of thermal diffusion throughout the phantom, and heat transfer with the environment, results in a 74% decreased maximum temperature change in the displaced phantom as compared to the non-displaced control (Fig. 8, 9). The plane in which the maximum temperature point exists (control – z=0, displaced – z=2cm) exhibits lower temperatures throughout the 30 minute exposure (Fig. 8). From the cross-sectional view in Figure 9, it can be seen that the spacer has greatly reduced the temperature of the material closest to the coil, and that the shape has not been optimized to reduce the maximum temperature point while displacing the least possible volume of tissue.

Figure 8.

Resulting temperature distribution at various time points for the control phantom at z = 0cm, and the displaced phantom at z = 2cm. The cross-sections shown each contain the maximum temperature.

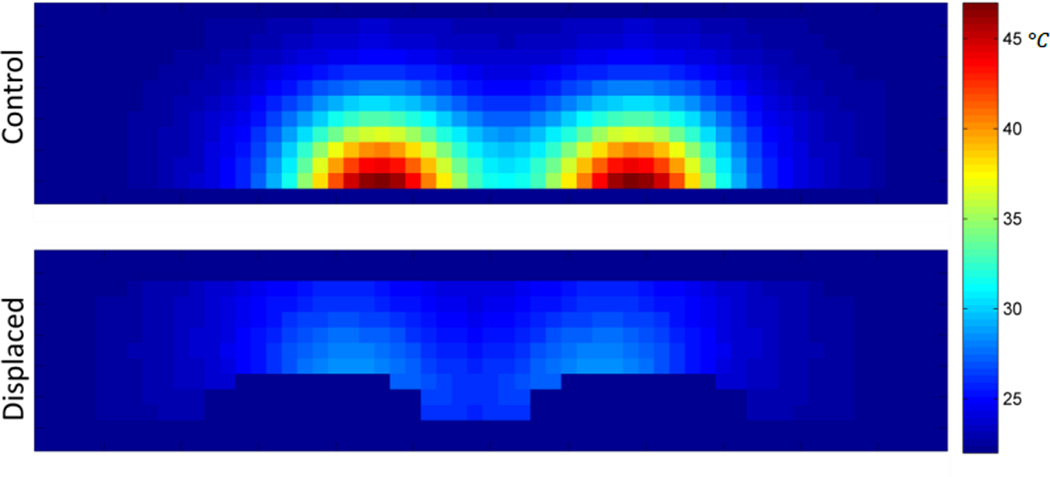
Figure 9.

Resulting temperature distribution at t = 1800s, y = 0cm, for the control and displaced phantoms.

Following the analysis in Section II-A, for an initial tumor depth of 2cm the reduction in maximum SAR_EC is 76% in the best case scenario, and 23% in the worst case scenario (Eq. 1, 2). Alternatively, SAR_MNP can be increased by 104% in the best case scenario, and 14% in the worst case scenario, when SAR_EC is kept constant between cases (Eq. 3).

B. Experimental Study

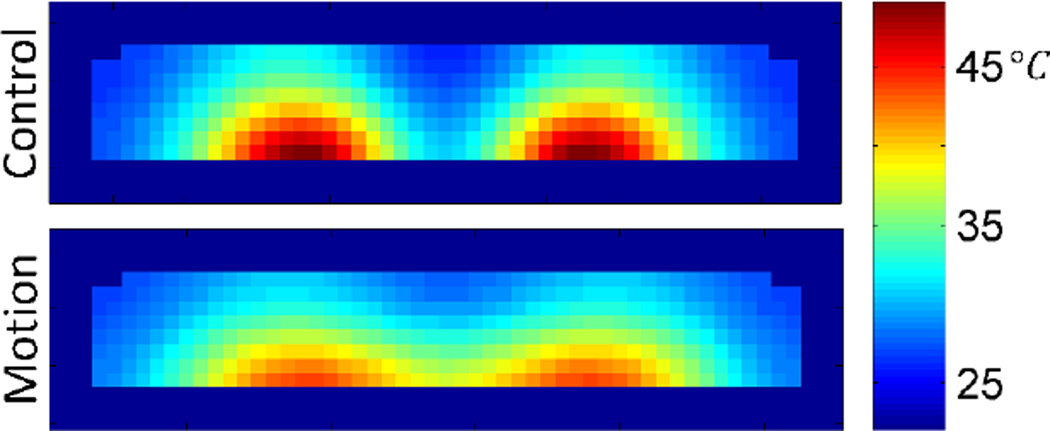
The phantoms each began at 23°C. The control phantom reached a maximum cross sectional temperature of 71°C at 100s post-exposure (t = 1900s), the displaced phantom reached 34°C (Fig. 10). This represents a 77% reduction in maximum temperature change.

Figure 10.

Position of bottom half of (a) control phantom and (b) displaced phantom, after sectioning. Resulting cross-sectional temperature distributions at t = 1900s for (c) control and (d) displaced phantoms.

V. FIELD-TISSUE MOTION RESULTS

A. Computational Study

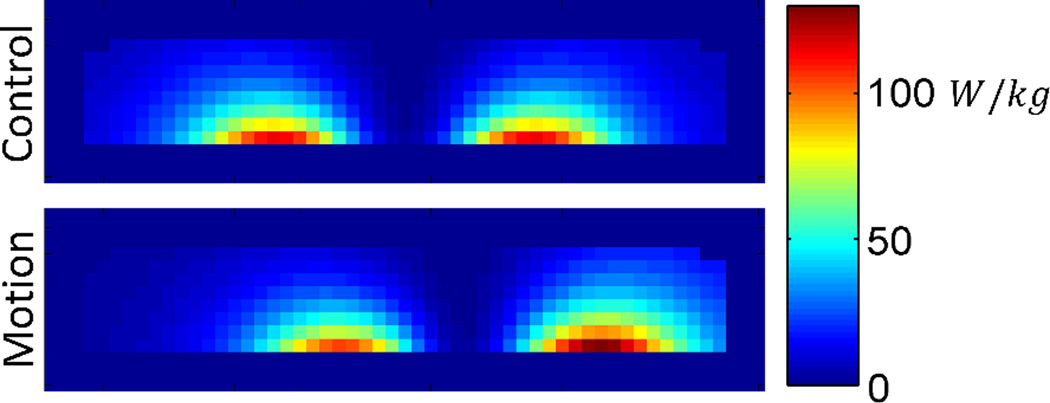
The resulting SAR distribution for the phantom shifted to x= −2.5cm, y = 0cm is shown in Figures 11 and 12. As compared to the control case (i.e. – phantom centered over coil), placing the phantom in the offset position causes not only a shift in the SAR distribution relative to the phantom, but also an asymmetry in the SAR distribution within the phantom, which is weighted toward the origin (i.e. - coil center). Note also that at a single offset position, asymmetries are experienced not only laterally (Fig. 11), but also vertically (Fig. 12), due to the discontinuity at the boundary. As a consequence of this effect, in the case of realistic (non-homogeneous) tissue, deeper regions may experience greater EC heating due to the effect of electrical discontinuities, especially at air- tissue interfaces (discussed further in Section VI-B).

Figure 11.

Diagram of phantom in (a) control position, i.e. - centered over coil, (b) resulting SAR distribution of phantom in control position, at z = 0cm, (c) diagram of phantom in position 1 (x = −2.5cm, y = 0cm), (d) resulting SAR distribution of phantom at position 1, (cross-section shown at z = 0cm).

Figure 12.

SAR distribution of the centered control phantom, and of the motion phantom at position 1. Cross-sections shown at y = 0cm.

If the phantom were left in a single offset position throughout the entirety of the 30 minute exposure, the maximum temperature achieved would increase; however, by moving the phantom between the 12 offset positions, the region of phantom which experiences the highest SAR at any one position is only heated at the maximum rate for 1/12 of the time. With the effects of thermal diffusion throughout the phantom, and heat transfer with the environment, the result is a broader temperature distribution (Figures 13 and 14). In this simulation, the difference in total power absorption between the control and motion phantom is minimal (<4% decrease) and the maximum SAR at a single offset position is actually 13% higher; however, the time averaged SAR distribution shows a 28% decrease in maximum SAR. This resulted in a 19% decreased maximum temperature change in the motion phantom as compared to the static control.

Figure 13.

Resulting temperature distribution at the base of the phantom (z = 0cm), for various time points, with the phantom in the control position (centered) throughout the exposure, and having moved between the 12 offset positions at 30 second intervals throughout the exposure.

Figure 14.

Resulting temperature distribution at t = 1800s, with the phantom in the control position throughout the exposure, and having moved between the 12 offset positions at 30 second intervals throughout the exposure. Cross-sections shown in the xz-plane at y = 0cm, i.e. – bisecting the phantoms.

Considering a tumor located at z = 1.7cm, i.e. at the transition height between bimodal and unimodal behavior of the H field, the reduction in maximum SAR_EC is 28% (Eq. 4, 5). At this height there is no change in SAR_MNP between the control and motion cases since the tumor experiences the same magnetic field strength in the control and the offset position. If the primary coil current is instead increased to keep max SAR_EC equal between the control and displaced cases, the resulting increase in SAR_MNP is 18% (Eq. 3).

B. Experimental Study

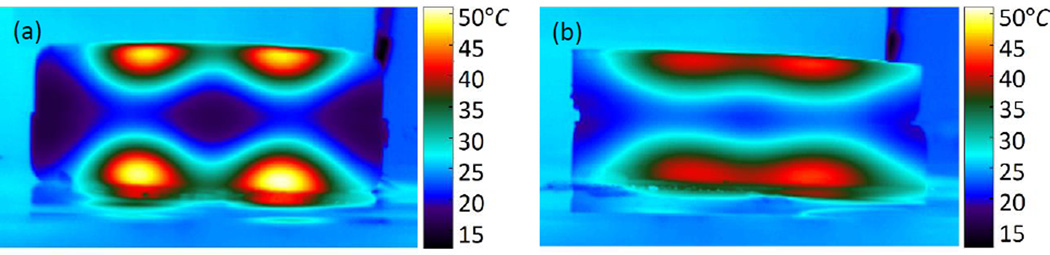
The control phantom began at 6°C and rose to a maximum cross sectional temperature of 51°C at 90s post-exposure (Fig. 15a). The motion phantom began at 11°C and rose to a maximum cross sectional temperature of 42°C (Fig. 15b). This represents a 33% reduction in maximum temperature change.

Figure 15.

Resulting cross sectional temperature distributions at t = 1890s (90s post-exposure) for (a) control and (b) motion phantoms.

VI. DISCUSSION

A. Tissue Displacement

In the tissue displacement study, it was shown both computationally and experimentally that physically displacing the phantom away from the areas of high E field decreased the maximum temperature induced by 74% and 77% percent respectively. As shown in Eq. 6 the current induced per unit volume is dictated by the electric field strength and the conductivity. Therefore, by essentially changing the conductivity in regions of space coinciding with high E field from 0.6S/m to 0 S/m, any current which would have been induced in this volume is no longer generated. This resulted in decreased total energy absorbed by the phantom and thus decreased maximum temperature.

Ultimately, the greatest limitation of this technique will likely be the anatomical position of the treatment site, such as tumors near tissue with low compressibility. Breast cancer tumors are likely to be the most favorable target since breast tissue is highly compressible. This technique will yield the best results when the clinically practical tissue displacement is greatest, however, any amount of displacement away from the regions of high E-field will yield a decrease in eddy current heating.

In this study the displacer used in the phantom experiment was not optimized to block the maximum E field with the minimum tissue displacement necessary. Also, anatomical restrictions, the mechanical properties of the tissue affecting tumor displacement, and the coil design will dictate the shape of the optimal displacer on a case by case basis. Ultimately, these results warrant further study of displacer design and the efficacy of this technique when applied to specific disease sites with complex tissue geometry, as well as electrical, thermal and mechanical properties.

B. Field-Tissue Motion

In the motion study it was shown that relatively small movements of the phantom with respect to the coil can significantly reduce the maximum temperature induced. In phantom, this reduction in maximum temperature change was shown to be 19% computationally and 33% experimentally. The concept behind this effect is fundamentally different from the tissue displacement technique. Instead of relying primarily on decreasing the total energy absorbed by the tissue, this technique causes energy to be distributed more evenly throughout the tissue. In the control case the same region of tissue is exposed to the maximum current density throughout the entire AMF exposure. By moving the tissue within the field during the exposure, different volumes of tissue are exposed to the highest current density at different times, and the maximum temperature induced is determined by a combination of time averaged current densities, electrical conductivity, and thermal diffusion.

It should be noted that, under certain circumstances, this technique has the potential to cause greater eddy current heating in non-homogeneous tissue. This could happen due to inhomogeneities in electrical conductivity affecting the current distribution. At any instant in time, there is a distinct current density distribution throughout the tissue. Consider the simplified case of inhomogeneous electrical properties, and homogenous thermal properties. In the static case, the volume which develops the highest temperature will be that which has the highest net volumetric heat. It is theoretically possible that maximum volumetric current density can be increased from the homogenous tissue case, due to low conductivity inclusions within the high E-field region, causing the current to divert its course to a smaller cross section of tissue. Considering this effect in the motion technique case, higher maximum current density could occur, compared to an optimal static position. This type of effect is observed in Figure 11d, where increased SAR occurs near the edge of the phantom; this is a result of the change in the current distribution caused by the material discontinuity at the edge and its position relative to the coil. With this potential drawback noted, it should be stated that the impact of these positions with higher local SAR is marginalized by the use of continual motion, ensuring no one position is held for an extended time, averaging the effect. In addition to the potential to decrease maximum temperature, this technique also has the advantage of minimizing the patient-to-patient, and treatment-to-treatment, eddy current heating variability which is inherent in patients due to complex tissue.

Determining the optimal path radius in the case of a simplified homogenous half-space such as that presented in Section II-B simply consists of determining the motion radius which results in maximum SAR_MNP/SAR_EC for the given field distribution, tumor depth, and MNP_SAR dependence on H. However, for inhomogeneous tissue the optimal motion path will likely be more complex than a simple circular path, and may not be limited to two dimensional translation depending on the specific treatment site in question. The optimal path will likely be patient/treatment specific, and would be best implemented using a robust treatment planning model. For instance, in the case of breast cancer a treatment planning model would need to take into account tumor location, depth, and size, as well as the thermal and electrical properties of the tissue exposed to the field. It would also need to take into consideration the geometry of the surface of the patient’s body to determine feasible coil positions, then iterate through simulated motion paths to maximize the minimum thermal dose in the tumor while maintaining the maximum allowable thermal dose to normal tissue by modulating the coil current. Ideally the patient would be treated on a fixed surface with the field source mounted on an electromechanical mechanism similar to the gantry of a clinical linear accelerator (used in external beam radiation treatments). These results for homogenous tissue warrant further study, including the development of the motion optimization component, and evaluation in complex tissue.

C. Applicability to Other Coil Types

Though a single-turn surface coil was chosen as the model system in this work, these methods can be generalized to both classes of MNP coils, namely surface coils and tissue-encompassing coils. The results presented apply directly to any coil used as a surface coil, including single-turn, pancake, solenoid, and by extension, to simultaneous application of multiple coils as is the case with a Helmholtz coil. What has not been directly shown is the application of these techniques to tissue-encompassing coils, i.e. when the treatment area is placed within the coil. Any of the aforementioned coil configurations, with the exception of a full-spiral pancake coil, can be used in this manner. Consider the case of a tissue-encompassing solenoid of finite length L and radius R, with z as the axis of symmetry. In this case, for any z, the electric field is strongest at the conductor and falls off radially toward the center. Additionally, the electric field is strongest at L/2 and falls off toward both ends of the coil. Thus, displacement of tissue away from the conductor is still beneficial when the tissue can be displaced throughout a significant length of the coil (i.e. the displaced tissue is pushed toward the ends of the coil bore). The motion technique also has potential with the solenoid case, in which the electric field is spread throughout a larger volume of tissue by continuously moving the coil, either by translation along the axis of symmetry, by radial gyration, by precession, or some combination of these motions. The potential of EC heating mitigation techniques illustrated for the case of a single-turn surface coil warrant further study regarding various coil configurations and specific clinical applications.

VII. CONCLUSIONS

Undesirable eddy current heating presents a major challenge in MNP hyperthermia therapy. Existing works have focused on methods of increasing MNP heating in tumors without attempting to modify EC heating. In this paper, two novel methods for decreasing the maximum temperature induced by eddy currents are presented. The motion technique involves moving the tissue relative to the coil during the exposure. In phantom studies, this resulted in a decrease in the maximum temperature change in normal tissue of 19% in simulation, and a 33% experimentally. The displacement technique involves selectively shifting normal tissue away from regions of high E field. In phantom studies, this resulted in simulated and experimental reductions of 74% and 77%, respectively. These results suggest that larger volumes of tissue with deeper tumors could be treated, and that higher field strengths and frequencies could be used for MNP hyperthermia, thereby attaining improved treatment efficacy. Further study is required to optimize these methods.