Crystallographic and Dynamic Aspects of Solid‐State NMR Calibration Compounds: Towards ab Initio NMR Crystallography

Abstract

The excellent results of dispersion‐corrected density functional theory (DFT‐D) calculations for static systems have been well established over the past decade. The introduction of dynamics into DFT‐D calculations is a target, especially for the field of molecular NMR crystallography. Four ¹³C ss‐NMR calibration compounds are investigated by single‐crystal X‐ray diffraction, molecular dynamics and DFT‐D calculations. The crystal structure of 3‐methylglutaric acid is reported. The rotator phases of adamantane and hexamethylbenzene at room temperature are successfully reproduced in the molecular dynamics simulations. The calculated ¹³C chemical shifts of these compounds are in excellent agreement with experiment, with a root‐mean‐square deviation of 2.0 ppm. It is confirmed that a combination of classical molecular dynamics and DFT‐D chemical shift calculation improves the accuracy of calculated chemical shifts.

1.  Introduction

Solid‐state nuclear magnetic resonance (ss‐NMR) spectroscopy is a powerful technique for studying the structural information and dynamics of organic solid phases, which has already been utilized in many fields1 including protein science,2 nanoporous materials3 and pharmaceuticals.4 For crystallography of small organic molecules, ¹³C is one of the most commonly used isotopes, because carbon, along with hydrogen, is the most abundant element in organic compounds; the ¹³C chemical shifts of a bulk substance are sensitive to its surroundings, which enables us to distinguish, for example, different polymorphs.4, 5, 6 Moreover, ¹³C ss‐NMR spectra are usually recorded with complete proton decoupling, which allows us to obtain single lines that are distinguishable from other spectra.7

In challenging cases in which the three‐dimensional structural information cannot be obtained by single‐crystal X‐ray diffraction, a combination of powder X‐ray diffraction (PXRD), crystal structure prediction (CSP) and ss‐NMR can provide complementary insight into the structure of the molecule.8, 9 One CSP method, based on dispersion‐corrected density functional theory (DFT‐D), has thus far systematically achieved significantly higher success rates than other methods, as evidenced by a series of CSP blind tests;10, 11 the computational ss‐NMR methodology described in the current paper is based on the same DFT‐D method, which allows seamless integration. On the basis of the advancement of these techniques, it is possible to investigate structural information of molecular crystals in silico even if the experimental data is limited to a single ¹³C spectrum. The application of the ss‐NMR technique to the study of crystal structures has been developed into the field of “NMR crystallography”.12

The acquisition of high‐quality experimental ¹³C ss‐NMR data requires external compounds for the optimization of the spectrometer settings: for example, setting up the magic angle and calibrating the chemical shift.13, 14 On the other hand, ab initio ss‐NMR calculations compute magnetic shielding constants that must be converted to chemical shifts to compare the calculations with experimental data. The magnetic shielding and the chemical shift are related by Equation (1):

$${\displaystyle {\delta }_{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}={\sigma }_{\mathrm{r}\mathrm{e}\mathrm{f}}-{\sigma }_{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}}}$$ (1)

where σ _ref, the reference shielding, is the unknown offset between the calculated and the experimental chemical shifts, σ _calc is the calculated shielding and δ _calc is the calculated chemical shift. A widely‐used technique to obtain σ _ref is to fit the theoretical shieldings against the experimental chemical shifts in a linear function [Eq. (2)]:5, 15

$${\displaystyle f\left(x\right)=ax+b}$$ (2)

Ideally, a is equal to −1 and b is equal to σ _ref. However, due to an intrinsic error of current DFT approximations,15, 16, 17 which under‐ and overestimates chemical shifts at low‐ and high‐field resonance, respectively,5, 18 the slope a in Equation (2) generally deviates from −1, especially for calculations on static crystal structures.

Apart from the fact that the reference shielding (σ _ref) depends on the exchange‐correlation functional,19 different reference shielding constants were obtained from different studies. Because of the abovementioned conversion, the calculated chemical shifts are biased towards the experimental chemical shifts. For ab initio NMR crystallography, the significance of this statement is that the number of independent peaks in the ss‐NMR spectrum is reduced by one, that is, in the absence of a standard value for σ _ref, some of the information in a ss‐NMR spectrum must be sacrificed in order to estimate a value for σ _ref. Experimentally, ss‐NMR chemical shifts are referenced to a calibration compound, and it therefore makes sense to establish a value for σ _ref based on calibration compounds.

In reality, all molecular crystals undergo motion and lattice expansion due to the effect of temperature, and averaging over thermally occupied states is of significance to reduce the discrepancy between ss‐NMR theoretical calculations and experiments, even for non‐plastic phases. These phenomena have been studied in combination with, for example, vibrational averaging on a series of generated configurations at zero and finite temperatures,15, 20 classical molecular dynamics (MD) simulations21 and ab initio MD simulations (including Born–Oppenheimer MD and path integral MD).15, 16, 21, 22, 23, 24, 25, 26

On the one hand, the size of the MD simulation boxes should be as large as possible (for example, 30×30×30 ų) to capture the physics of an infinite crystal as realistically as possible. Ab initio MD simulations are inadequate for MD simulations with large supercells due to the computational cost; in most cases, ab initio MD simulations with the constant number–volume–temperature (NVT) ensemble for 1×1×1 unit cells were used—this is not always physically realistic and can give problems for certain systems. Classical mechanics is the most likely option for simulating the behavior of a large supercell with the unit cell parameters allowed to vary, however, the accuracy of classical MD simulations relies on the quality of the force field used for the MD; force fields are unsuitable for certain crystal structures.27 MD simulations must be used for adamantane and hexamethylbenzene because these two crystals have dynamic phases at room temperature. MD was also utilized for the study of 3‐methylglutaric acid. On the other hand, ss‐NMR calculations on such box sizes would be prohibitively expensive due to the quantum‐mechanical calculations involved (of the order of months, even on a university cluster). Satisfying these two contradicting conditions simultaneously was solved by clever switching between box sizes.

Herein, we report a protocol to calculate a computational reference shielding by investigating five commonly used ss‐NMR standard reference systems, adamantane, hexamethylbenzene, glycine (α and γ forms) and 3‐methylglutaric acid (Scheme 1), by single‐crystal X‐ray diffraction and in silico methods, including MD and DFT‐D. The determination of ¹H, ¹³C and ¹⁵N chemical shieldings for a wide range of reference compounds has been investigated by gas‐phase quantum mechanical methods, also in combination with solvent effects;28, 29, 30 however, ab initio studies of solid‐phase chemical shieldings, especially for benchmarking compounds, are much fewer. The aim of the study was to reproduce the ss‐NMR spectra of the five reference solid phases computationally, which proved to be surprisingly difficult. At room temperature, adamantane is a rotator phase, whereas hexamethylbenzene molecules hop in their crystal structure; no chemically meaningful average atomic coordinates can be assigned. The ss‐NMR spectra of these compounds consist of only two peaks each: for adamantane, one peak arises from the secondary carbon and the other from the tertiary carbon; for hexamethylbenzene, one arises from the aliphatic carbon and the other from the aromatic carbon.31 Glycine has two polymorphs that are stable at room temperature: α and γ forms;32, 33 commercial glycine samples usually contain both polymorphs.34 In 2006, Barich et al. suggested 3‐methlyglutaric acid as a candidate for the calibration of an ss‐NMR spectrometer.13 However, its crystal structure has not been reported. The lack of structural information limits our ability to perform computational studies of these standard compounds.

Scheme 1.

The chemical structures of a) adamantane, b) glycine, c) hexamethylbenzene and d) 3‐methylglutaric acid.

Methods

Polymorph Screening and Single‐Crystal X‐ray Diffraction of 3‐Methylglutaric Acid

3‐Methylglutaric acid was purchased from Sigma–Aldrich and used without further purification. For the polymorph screen, samples (mass depending on solubility) were dissolved in different solvents at room temperature or at their respective boiling points and crystallized by (slow) solvent evaporation at room temperature. The solvents used were acetone (with a concentration of 100 mg 3‐methylglutaric acid in 1 mL), acetonitrile (100 mg mL⁻¹), butanone (100 mg mL⁻¹), chloroform (100 mg mL⁻¹), diisopropyl ether (20 mg mL⁻¹), dimethylsulfoxide (100 mg mL⁻¹), acetic acid (100 mg mL⁻¹), ethanol (100 mg mL⁻¹), ethyl acetate (100 mg mL⁻¹), tetrahydrofuran (100 mg mL⁻¹), and water (150 mg mL⁻¹). After solvent evaporation, the resulting powders were examined by powder diffraction on a STOE STADI‐P diffractometer with a linear position‐sensitive detector and germanium monochromator in the transmission mode, using CuKα1 radiation. All powders were identified as the same phase.

The obtained powder samples were also analyzed by differential thermal analysis (DTA) and thermogravimetric analysis (TGA) for phase transitions or solvate decomposition on a SETARAM TGA92 thermal analyzer at a heating rate of 5 K min⁻¹ over the range 293–773 K under a nitrogen atmosphere.

The crystallization experiments from chloroform, acetonitrile and butanone yielded single crystals suitable for structural analyses. The crystals grown from chloroform were measured on a STOE‐IPDS‐II diffractometer equipped with a Genix microfocus source and mirror optics. The data were scaled by the frame‐scaling routine in the X‐area package (STOE & Cie., Darmstadt, Germany, 2002). The structure was solved by direct methods using SHELXS and refined by the full‐matrix least‐square method using SHELXL.35 All non‐H atoms were refined anisotropically. All H atoms were found in difference Fourier maps. The coordinates of the H atoms bonded to O atoms were refined, whereas their displacement parameters were set to 1.5 U _eq(O). The crystal was a non‐merohedral twin with a fractional contribution of 0.078(3) for the minor domain.

Modeling of the Experimental Crystal Structures

Adamantane

The single‐crystal X‐ray diffraction data of the rotator phase of adamantane at room temperature were reported by Amoureux et al.36 It has a space group Fm−3m, a=9.445 Å, Z=4. The coordinates of the room‐temperature structure were not available. The coordinates of an adamantane molecule were obtained from the Cambridge Structural Database (CSD)37 with reference code ADAMAN08. A room‐temperature crystal structure of adamantane was then built up by using a combination of the molecular coordinates from a low‐temperature single‐crystal structure and the cell parameters provided by the room‐temperature structure.

Hexamethylbenzene

There are no known solved coordinates of hexamethylbenzene at room temperature. The unit‐cell parameters38 and the coordinates of a low‐temperature structure at 123 K39 of hexamethylbenzene were available. A modeling protocol similar to that used for adamantane, combining the coordinates from a low‐temperature structure with the cell parameters reported at room temperature, was adopted for hexamethylbenzene. The cell parameters of the room‐temperature structure (CSD reference code: HMBENZ) were then transformed according to [0 0 −1, 0 1 −1, 1 0 1] to make them compatible with those of the low‐temperature structure.

Glycine

There are two stable polymorphs at room temperature, namely the α and the γ forms.34, 40 The crystal structures of both the α‐polymorph (CSD reference code: GLYCIN20)41 and the γ‐polymorph (CSD reference code: GLYCIN33)42 were used in this study.

DFT‐D Energy Minimizations and ss‐NMR Calculations

DFT‐D energy minimizations for the two polymorphs of glycine and 3‐methylglutaric acid, and ss‐NMR calculations for all five phases were performed using CASTEP (Academic Release 6.1).43 The DFT‐based gauge‐induced project augmented wave (GIPAW) method,44 applied with Vanderbilt‐type ultrasoft pseudopotentials45 enables an effective way to calculate chemical shieldings for crystals. The Perdew–Burke–Ernzerhof exchange‐correlation functional46 with the Grimme 2006 dispersion correction (PBE‐D2)47 were applied. The contribution of dispersion interactions to intermolecular forces is essential to calculate the energy minimizations and for the accuracy of ab initio ss‐NMR calculations of molecular crystals, which has been validated by several studies.48, 49, 50, 51, 52 Integrals taken over the first Brillouin zone were measured on a Monkhorst–Pack grid53 with a sample spacing of approximately 0.07 Å⁻¹ for energy minimizations, and 0.05 Å⁻¹ with at least two k‐points along each direction for ss‐NMR calculations. The energy minimization was split into three steps and the first two were applied with an energy cut‐off of 520 eV and ultrasoft pseudopotentials: first, atomic positions were allowed to vary with the unit‐cell parameters fixed; second, both the atomic positions and the unit cell were allowed to vary. Afterwards, the structure was energy‐minimized with norm‐conserving pseudopotentials and a higher energy cut‐off of 1200 eV and then subjected to the ss‐NMR calculation at an energy cut‐off of 1200 eV with ultrasoft pseudopotentials generated on‐the‐fly.45

Molecular Dynamics Simulations

MD simulations were performed using Forcite Plus in Materials Studio 6.0 (Accelrys Inc., 2011) with the COMPASS force field.54 The time step of all the MD simulations was 1 fs. The space groups of all the supercells in the MD simulations were P1. Large supercells were used in classical MD simulations for two reasons. First, self‐interactions of the molecules due to the periodic boundary conditions must be avoided. Second, a relatively large cut‐off distance of 15.5 Å should be used for the accurate description of non‐bonded interactions (i.e., electrostatic and van der Waals). For a large supercell MD simulation in this study, the shortest distance between any two faces was at least twice the cut‐off distance, that is, each supercell was at least 30×30×30=27 000 ų. By contrast, these supercells are too large for the electronic structure methods. Hence, in order to calculate ss‐NMR chemical shieldings for the snapshots from an MD simulation, a small cell was built on the basis of its corresponding MD simulation of the large supercell, and the small cell was subjected to an MD simulation with the NVT ensemble.

Adamantane and 3‐Methylglutaric Acid

The MD simulation was split into three steps: first, a 4×4×4 supercell was built for adamantane; for 3‐methylglutaric acid, a 3×6×4 supercell was built; second, the supercell was used to perform an MD simulation with the NPT ensemble, the Nosé–Hoover–Langevin thermostat55 and the Parrinello barostat56 at 300 K for 1 ns; third, average lattice parameters were calculated based on the last 500 ps of the simulation. A 1×1×1 small cell was built using their averaged cell lengths and underwent a 10 ns MD simulation using the NVT ensemble and the Nosé–Hoover–Langevin thermostat at 300 K. Twenty‐six frames were selected with the same interval (0.4 ns) from the 10 ns MD trajectory and the ss‐NMR calculations were performed upon these frames.

Hexamethylbenzene

For the case of hexamethylbenzene, a 7×6×5 supercell was constructed and underwent two consecutive temperature series. The first was from 50 to 275 K with increments of 25 K, and the second was from 275 to 285 K with increments of 5 K. The same ensemble, thermostat and barostat were adopted from the treatment of adamantane and 3‐methylglutaric acid. An equilibrium time of 250 ps and a production time of 500 ps were performed at each temperature; the averaged lattice parameters were calculated from the production part of the previous 285 K MD simulation and applied to the 7×6×5 supercell, which was then subjected to a 10 ns MD simulation with the NVT ensemble at 285 K; the Nosé‐Hoover‐Langevin thermostat was used to control the temperature; 13 frames were selected with the same interval (0.8 ns) from the MD simulation. For each of these, a cubic cluster of eight molecules was extracted to construct a 2×2×2 small cell. Fewer frames were selected here to keep the total number of molecules similar in each ss‐NMR calculation. For example, there are eight hexamethylbenzene molecules in the 2×2×2 small cell, but only four adamantane molecules (Z=4) in the 1×1×1 small cell for its ss‐NMR calculations. Finally, each 2×2×2 small cell was subjected to a short 2 ps MD simulation with the NVT ensemble and the Nosé–Hoover–Langevin thermostat. The last frame of each short 2 ps MD simulation was then used to calculate the ss‐NMR chemical shieldings.

Glycine

The DFT‐D energy‐minimized crystal structures of the two polymorphs of glycine were subjected to energy minimizations with the COMPASS force field. The force‐field energy‐minimized structure of α‐glycine was then replicated 8×2×8 in the x, y and z directions, respectively; for γ‐glycine, it was replicated 4×4×8. A temperature series was used for the two polymorphs of glycine from 50 to 300 K with an interval of 50 K. At each temperature, first 100 ps was allowed for the equilibrium and 500 ps for the production, except at 300 K, at which the production time was 1 ns. The 100 ps equilibrium was divided into three steps: first, 20 ps with the NVT ensemble and the Berendsen thermostat;57 second, 30 ps with the NPT ensemble, the Berendsen thermostat and Berendsen barostat; and third, 50 ps with the NPT ensemble, the Nosé–Hoover–Langevin thermostat and the Parrinello barostat. A 1×1×1 small cell was built using their averaged cell lengths and subjected to a 10 ns MD simulation using the NVT ensemble and the Nosé–Hoover–Langevin thermostat. Twenty‐six frames were selected with an interval of 0.4 ns and subjected to ss‐NMR calculations.

2.  Results and Discussion

The crystal structure of 3‐methylglutaric acid was determined by single crystal X‐ray diffraction at 173 K58 and at room temperature.59 The structures at both temperatures were the same within thermal expansion. A polymorph screen was performed, which resulted in no further phases. The compound was analyzed by DTA and TGA. No phase transition was observed between room temperature and 358 K (the melting point). The DTA–TGA diagram and the X‐ray powder diffraction pattern of 3‐methylglutaric acid at room temperature can be found in the Supporting Information, SI.

The crystallographic information from the experimental and the statically energy‐minimized structures of the two polymorphs of glycine and 3‐methylglutaric acid are shown in Table 1. Differences between the energy‐minimized and the experimental structures are small and agree with previous validations.60, 61 Overlays of the energy‐minimized and experimental structures are shown in Figure 1.

Table 1.

The cell parameters of the DFT‐D energy minimized molecular crystals.

Compound	Lattice parameters
	a [Å]	b [Å]	c [Å]	α [°]	β [°]	γ [°]	RMSCD[a] [Å]
α‐Gly,[b] exp.41	5.10	11.95	5.46	90	111.78	90	–
α‐Gly, DFT‐D	5.06	11.78	5.47	90	112.67	90	0.089
γ‐Gly, exp.42	7.04	7.04	5.48	90	90	120	–
γ‐Gly, DFT‐D	6.93	6.93	5.51	90	90	120	0.065
3‐MGA,[c] exp. (173 K)	13.85	5.32	10.13	90	110.28	90	–
3‐MGA, DFT‐D	13.60	5.30	9.66	90	108.29	90	0.077

[a] RMSCD: Root‐mean‐square Cartesian displacement (hydrogen atoms excluded). [b] Gly: glycine. [c] 3‐MGA: 3‐methylglutaric acid.

Figure 1.

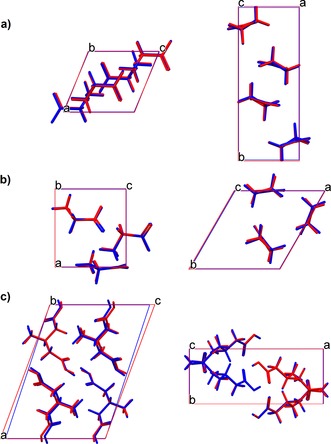
Overlays of the DFT‐D energy‐minimized (blue) and the experimental (red) structures. Each overlay was viewed along two different axes. a) α‐Glycine, b) γ‐glycine, c) 3‐methylglutaric acid.

The spinning of adamantane was successfully reproduced in the MD simulation. The hopping of hexamethylbenzene from one minimum to another in the crystal was also captured in the MD simulation. Moreover, the timescale of the MD simulations for both adamantane and hexamethylbenzene was 10 ns, whereas the acquisition time for an ss‐NMR measurement is 30 to 60 ms,14 which is about 10⁶ times longer than that of the MD simulations. As the rotator phases were observed in short‐duration MD simulations, the ¹³C chemical shifts of these two compounds could thus be averaged.

The MD simulation was not applied for the α and γ forms of glycine because all of our attempts at energy minimization with the COMPASS force field were unsuccessful; the structures underwent large distortions during the energy minimizations (see the SI).

The results of the ¹³C ss‐NMR calculations are listed in Table 2. The σ _ref value for ¹³C chemical shifts of the standard compounds in this study was found to be 168.9 ppm, which yields a root‐mean‐square deviation (RMSD) between the calculated and the experimental chemical shifts of 2.0 ppm: this value is within the expected range.8

Table 2.

Calculated and room temperature experimental ¹³C chemical shifts for standard compounds.

Site	Method	Calcd CS [ppm]	Exp. CS [ppm]	Deviation [ppm]
α‐Gly,[d] CO	DFT‐D	179.3	176.562	+2.8
α‐Gly, CH2	DFT‐D	41.8	43.762	−1.9
γ‐Gly, CO	DFT‐D	176.4	173.462	+3.0
γ‐Gly, CH2	DFT‐D	40.1	41.462	−1.3
ADA,[e] CH	MD	30.9	29.563	+1.4
ADA, CH2	MD	39.4	38.563	+0.9
HMB,[f] CH (aromatic)	MD	129.4	132.063	−2.6
HMB, CH3 (aliphatic)	MD	16.1	17.263	−1.1
3‐MGA,[g] COOH (1)	MD	179.0	180.7[h]	−1.7
3‐MGA, COOH (2)	MD	179.7	181.6[h]	−1.9
3‐MGA, CH2 (1)	MD	40.0	38.3[h]	+1.7
3‐MGA, CH2 (2)	MD	42.9	39.5[h]	+3.4
3‐MGA, CH	MD	24.1	25.2[h]	−1.1
3‐MGA, CH3	MD	17.3	18.8[h]	−1.5
Reference shielding [ppm]	168.9
MAD [ppm]	1.9
RMSD [ppm]	2.0

[a] Calcd CS: calculated chemical shift. [b] Exp. CS: experimental chemical shift. [c] Deviation=Calcd CS−Exp. CS. [d] Gly: glycine. [e] ADA: adamantane. [f] HMB: hexamethylbenzene. [g] 3‐MGA: 3‐methylglutaric acid. [h] Unpublished data, provided by Dr. Sean Delaney and Prof. Dr. Eric Munson. [i] MAD: mean absolute deviation. [j] RMSD: root‐mean‐square deviation.

As discussed, it is extensively reported that the DFT method under‐ and overestimates chemical shifts at low and high field resonances, respectively. This can be clearly identified in data presented in the SI, which show that two chemical shifts of carboxyl carbon atoms of 3‐methylglutaric acid in the low‐field region are overestimated by 5.6 and 4.8 ppm, whereas the chemical shifts of all alkyl carbons are underestimated. The chemical shifts of the carboxyl carbons of α‐ and γ‐glycine are also overestimated (Table 2). The results in Table 2 demonstrate that the MD simulation is able to eliminate the systematic overestimation in the low‐field region: when it was applied to 3‐methylglutaric acid, chemical shifts of two carboxyl carbons were underestimated by 1.7 and 1.9 ppm (Table 2). We note that with the inclusion of the thermal motion by means of MD simulations for 3‐methylglutaric acid, together with the static calculations for the two phases of glycine and MD simulations for adamantane and hexamethylbenzene, the slope in Equation (2) becomes −1.00 for five different phases, as it should be, whereas using the static ss‐NMR calculations for 3‐methylglutaric acid, along with the other four phases, it evaluates to −1.03 as usual. Further research would be required to establish if this is a general trend or a mere coincidence. To further illustrate the influence of thermal motion on the accuracy of ab initio ss‐NMR calculations, the ¹³C chemical shifts of 3‐methylglutaric acid calculated from its static DFT‐D energy‐minimized structure were compared to the results from the MD‐averaged data, the calculated shieldings for the other four phases being the same in both cases. The RMSD value between the experimental values and the calculated chemical shifts increased from 2.0 to 2.9 ppm (see the SI), confirming earlier reports that the inclusion of thermal motion improves the accuracy of ss‐NMR calculations.

To confirm that the better fit was due to an improved description of the instantaneous positions of the atoms and not merely due to averaging over multiple positions, the α and γ forms of glycine were subjected to MD simulations with the COMPASS force field, which gave the aforementioned large distortions, to calculate their average ¹³C chemical shifts based on the MD trajectories, and to compare those with their corresponding static DFT‐D energy minimized structures. The RMSD value for the two distorted glycine crystal structures combined with the other three phases is 4.8 ppm, which is larger than the benchmark value 2.0 ppm (see the SI).

These two examples reveal that a correct static DFT‐D calculation gives better results than an MD simulation with the wrong structure, and an MD simulation with correct structures gives even better results, even though the COMPASS energy potential used for the MD simulation is less accurate than the DFT‐D potential. The accuracy of the predicted ss‐NMR chemical shifts depends crucially on the accuracy of the structures from the MD simulations, and hence on the accuracy of the energy potential used for the MD simulations. Whereas the DFT‐D method, used for the static calculations, has shown excellent transferability to a large spectrum of chemical compounds, the same is not necessarily true for traditional molecular mechanics force fields. This limitation can be overcome by switching to so‐called “tailor‐made force fields”, which are force fields parameterized for individual molecules against DFT‐D reference data.64 We currently have a working implementation of such DFT‐D‐based tailor‐made force fields in an MD software package, providing a seamless integration of the MD simulations and the ss‐NMR calculations that does not depend on the accuracy of transferable force fields.

3.  Conclusions

In summary, we devised a protocol with the combination of MD, DFT‐D and ab initio ss‐NMR calculations to compute the chemical shifts of five ¹³C ss‐NMR standard reference phases, which are accurate within 2.0 ppm with a single computational reference shielding constant, σ _ref, of 168.9 ppm. This was achieved by relating the calculated ss‐NMR spectra of five ss‐NMR calibration phases to their crystal structures at the atomic level, which required the determination of the single‐crystal structure of 3‐methylglutaric acid and MD simulations for the rotator phases of adamantane and hexamethylbenzene. The accuracy of the force field used for the MD simulations was shown to be crucial for the results. By publishing more and more fitted reference shieldings, research groups in the field of NMR crystallography can collectively build up increasingly more accurate and independent estimates of a universal reference shielding, σ _ref.9, 16, 21 This ab initio NMR crystallography approach, together with state‐of‐the‐art experimental NMR spectroscopy,65, 66 will be valuable for the elucidation of the structural and dynamic properties of challenging solid‐state phases, even if no single crystals are available.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

X. Li, L. Tapmeyer, M. Bolte, J. van de Streek, ChemPhysChem 2016, 17, 2496.