SUMMARY
When multiple drugs are administered simultaneously, investigators are often interested in assessing whether the drug combinations are synergistic, additive, or antagonistic. Existing response surface models are not adequate to capture the complex patterns of drug interactions. We propose a two-component semiparametric response surface model with a parametric function to describe the additive effect of a combination dose and a nonparametric function to capture the departure from the additive effect. The nonparametric function is estimated using the technique developed in thin plate splines, and the pointwise bootstrap confidence interval for this function is constructed. The proposed semiparametric model offers an effective way of formulating the additive effect while allowing the flexibility of modeling a departure from additivity. Example and simulations are given to illustrate that the proposed model provides an excellent estimation for different patterns of interactions between two drugs.
Keywords: Additivity, Antagonism, Loewe additivity model, Thin plate splines, Synergy, Wild bootstrap
1. Introduction
Studies of interactions among biologically active agents, such as drugs, carcinogens, or environmental pollutants, have become increasingly important in many branches of biomedical research. For example, in cancer chemotherapy the therapeutic effect of many anticancer drugs is limited when they are used as a single drug (Kanzawa, Nishio, Fukuoka, Sunami, and Saijo, 1999). Finding the combination therapies with increasing treatment efficacy and reduced toxicity is an active and promising research area. In this paper, we focus on assessing drug interactions for experiments performed in in vitro and/or in vivo studies to help to determine whether a combination therapy should be further investigated in a clinical trial.
The literature supports the notion that the Loewe additivity model (Berenbaum, 1989; Greco, Bravo, and Parsons, 1995 and references therein; Lee, Kong, Ayers, and Lotan, 2007) can be considered as the “gold standard” to define drug interactions. Based on the Loewe additivity model, the following two approaches are often used: (1) the marginal dose-effect curve model method (MDECM), or (2) the response surface method (RSM). The MDECM (Kelly and Rice, 1990) fits a dose-effect curve for each single drug, uses the fitted dose-effect curves to calculate the expected additive effect to a particular combination, and then compares the expected additive effect to the observed effect. The MDECM methods can only assess drug interactions at observed combinations, and do not give a complete picture of drug interactions over all possible combination doses. The RSM (Greco et. al., 1995), which involves an estimation of the k + 1 dimensional response surface in k drug combinations, can take all of the information present in the full dose-effect data set for k drugs to assess drug interactions at all levels of combination doses. However, most of the RSMs either use a single parameter (e.g., Carter, Gennings, Staniswalis, Cambell, and White, 1988) or use a 50% maximal effect isobole (White, Faessel, Slocum, Khinkis, and Greco, 2004) to capture synergy, additivity, or antagonism. These approaches are not adequate to capture different patterns of drug interactions.
To overcome this limitation, we recently developed a parametric response surface model with a complete quadratic function of combination doses to capture synergy, additivity, and antagonism (Kong and Lee, 2006). Similar to many other settings, these parametric models are efficient when the model assumptions hold but not necessarily robust when the assumptions fail. Therefore, our goal in the paper is to develop a semiparametric model to capture complex patterns of drug interactions and provide statistical inference. Although fully nonparametric models have been explored in the literature, the accomplishment is quite limited. Suhnel (1990) used bivariate splines to fit dose effect data. The determination of drug interactions was based on the visualization of whether the contours of the response surface were concave up or concave down. Prichard and Shipman (1990) proposed using the differences of the theoretical additive surface and the experimental data surface to reveal regions of synergy and antagonism. However, the theoretical additive surface was not constructed accurately, and the assessment of drug interaction was not derived from a statistical point of view. Kelly and Rice (1990) and Kong and Eubank (2006) proposed using B-spline to estimate a marginal dose-effect curve. However, the fitted smoothing curve can not be extrapolated beyond the observed range of effects for each single drug. Thus, the additive effects for those combination doses beyond the range of the effects produced by each single drug cannot be modeled. To predict the additive effects for all combination doses, our idea in this paper is to use parametric model to estimate dose-effect curve for single drug. Based on the reasonably chosen parametric dose-effect curve model and the Loewe additivity model, we can estimate the theoretical additive surface. Subsequently, we use a nonparametric function to describe the effect beyond the additive model. The confidence surfaces for the nonparametric function are constructed so that the local synergy or local antagonism can be estimated from the statistical point of view. This approach combines the idea used in the MDECM but also incorporates the advantages of the RSM. We describe our model and its estimation in Sections 2 and 3, and give a case study in Section 4 and simulations in Section 5. The last section is devoted to discussion.
2. The proposed model
Recall the Loewe additivity model (Berenbaum, 1989; Greco et al., 1995 and references therein)
| (1) |
where d1, d2 are doses of drug 1 and drug 2 in the mixture, y is the theoretic additive effect at (d1, d2), and Dy,1 and Dy,2 are the respective single-agent doses of drug 1 and drug 2 that elicit the effect y. The theoretic additive effect y at (d1, d2) can be predicted as long as the dose-effect curves for each of the two drugs are known. Denote the dose-effect curves for drug 1 and drug 2 used alone as F1(D1) and F2(D2), respectively. Then, the predicted additive effect, say y, can be obtained by solving equation (1) after replacing Dy,1 by and Dy,2 by , where is the inverse function of Fi (i = 1, 2). If the effect measured at (d1, d2) is more than or less than the predicted effect, the combination dose (d1, d2) corresponds to synergy or antagonism. We denote the predicted effect at the combination dose (d1, d2) by Fp(d1, d2).
To capture different patterns of drug interaction, we propose a two-component model to describe the effect of combination treatment:
| (2) |
Please note that in equation (2) and equations (3), (4), and (6) below, a mean zero random error term is suppressed from the right hand side of the model. Here f(d1, d2) is a function that is estimated nonparametrically to capture local synergy and local antagonism, i.e., drug effect beyond the additive effect. To see this point, suppose the marginal dose-effect curves are decreasing, then f(d1, d2) < 0 implies that the effect at (d1, d2) is more than the predicted effect Fp(d1, d2), thus the combination dose (d1, d2) is synergistic. On the other hand, f(d1, d2) > 0 implies that the effect at (d1, d2) is less than the predicted effect, thus the combination dose (d1, d2) is antagonistic. Contrarily, in the case of increasing marginal dose-effect curves, f(d1, d2) > 0 or f(d1, d2) < 0 implies that the combination dose (d1, d2) is synergistic or antagonistic, respectively.
3. Estimation for the proposed model
From this point on we assume that the observed data are (d1i, d2i, Ei) for i = 1, …, n. Here (d1i, d2i) (i = 1, …, n) is the observed combination dose, and Ei (i = 1, …, n) is the corresponding observed effect. If the data contain enough observations for each drug when used alone, then, the marginal dose-effect curves, and subsequently, predicted additive effects, may be estimated with small error. The choices of the dose-effect curves may be based on the biology-driven mechanistic models, such as the median effect model by Chou and Talalay (1984), if the model provides adequate fit. Once we obtain an appropriate dose-effect curve for each drug, the predicted effects based on the Loewe additivity model can be obtained. In the literature, two commonly used classes of marginal dose-effect curves are reported. We illustrate how to obtain the predicted effect F̂p(d1, d2) under each class in Subsection 3.1. Next, we can obtain the difference of the observed effect and the predicted effect at each observed combination dose (d1i, d2i) (i = 1, …, n). Based on this information, we can then estimate the function f(d1, d2) using the technique described in Subsection 3.2. To account for the variability in estimation, the bootstrap confidence interval for f(d1, d2) is given in Subsection 3.3.
3.1. Estimation of the marginal dose-effect curves and the predicted effects
One class of commonly used dose-effect curves is based upon a linear relationship between the effect or transformed effect and the dose or concentration. The dose-effect curves for drug 1 and drug 2 have the following form:
| (3) |
where g(E) is a monotonic function of E, for example, we may take (Carter et. al., 1988). The intercepts in (3) are assumed to be the same since the baseline effects without drugs (i.e., Dy,1 = Dy,2 = 0) should be the same. We refer to Y as the transformed effect. Based on the Loewe additivity model, the predicted effect in Y scale can be obtained from . The resulting predicted additive response function of the combination dose is, then,
| (4) |
In application, we may first regress g(E) on dose with the observations of each drug when used alone to see whether the fit is adequate and the intercepts of the two regression lines for the two drugs are close. If so, we may force the intercepts to be the same by regressing g(E) on d1 and d2 using only the marginal data (i.e., the data with d1 = 0 or d2 = 0). Thus, we obtain the estimates of β0, β1, and β2. Plugging these estimates in equation (4), we obtain the theoretic additive effect F̂p(d1, d2) in the transformed scale for each combination dose (d1, d2). The predicted additive effect in the original scale at (d1, d2) is obtained by the inverse transformation
| (5) |
Another class of dose-effect curves is based upon a linear relationship between the effect or transformed effect and the log(dose) or log(concentration). This class is very general and includes many families (Kong and Lee, 2006). We assume that the effect or transformed effect follows a linear function of log(dose) for each of the two drugs when acting alone:
| (6) |
Again g(E) is a monotonic function of E, and Y is the transformed effect. Kong and Lee (2006) showed that, based on the Loewe additivity model, the predicted effect at combination dose (d1, d2) is Y = Fp(d1, d2) = β0 + β1 log(d1 + ρd2), where ρ can be obtained by solving .
3.2 Estimation of f(d1, d2)
In the previous subsection, we illustrated how to estimate the additive effect for each combination dose. Particularly, we can estimate the additive effect, F̂p(d1i, d2i), for each observed combination dose (d1i, d2i) (i = 1, …, n). Then we can easily compute the difference of the observed effect and the predicted additive effect, Yi − F̂p(d1i, d2i), at each observed combination dose (d1i, d2i) (i = 1, …, n), where Yi = g(Ei). Note that f(d1, d2) in (2) is used to capture the departure from the additive effect, which only exists for non-marginal combination dose, i.e., (d1, d2) with d1 ≠ 0 and d2 ≠ 0 because by definition, there is no interaction when a drug is used alone. Theoretically, f(d1, d2) should be set as zero whenever d1 = 0 or d2 = 0. However, as far as we know, in the framework of bivariate splines, there are no basis functions such that their linear combination is zero at (d1, d2) whenever d1 = 0 or d2 = 0. In order to estimate f(d1, d2) as close to zero as possible whenever d1 = 0 or d2 = 0, we force the differences between the observed and predicted effects at the marginal observations to be zero. Thus, we define an indicator function
Then, we can proceed to estimate the function f(d1, d2) based on the observed doses (d1i, d2i) and the estimated differences (Yi − F̂p(d1i, d2i)) 1{d1i≠0 & d2i≠0} for i = 1, …, n.
We use thin plate splines (Green and Silverman, 1994) to represent f(d1, d2). The thin plate splines can incorporate observations from any kind of design, such as a factorial design, ray design (Chou and Talalay, 1984), and a uniform design (Tan, Fang, Tian, and Houghton, 2003). We adopted the techniques developed in a mixed effect model (Ruppert, Wand, and Carroll, 2003) to select the smoothing parameter and to estimate the function f(d1, d2).
The estimated function f(d1, d2) can be obtained by minimizing the following penalized residual sum of squares (Green and Silverman, 1994):
| (7) |
where the first term measures the goodness of fit, the second term, J(f), measures the smoothness of the function f(d1, d2), and the smoothing parameter, λ, measures the trade-off between the goodness of fit and the smoothness of the function f. The minimizer of PRSS is necessarily a natural thin plate spline, which can be expressed as a linear combination of the radial basis functions:
| (8) |
where the radial basis function
| (9) |
The knots, say, (κ1k, κ2k)T (k = 1, …, K), are all the distinct values among (d1i, d2i)T (i = 1, …, n), and the distance between two combination doses is defined as the Euclidean distance:
If we define a K × K matrix Ω = [η(‖(κ1k, κ2k)T − (κ1k′, κ2k′)T‖)1≤k,k′≤K], a K × 3 matrix TT = [1, κ1k, κ2k]1≤k≤K and a vector υ = (υ1, …, υK)T, then the minimizer of (7) satisfies J(f) = υTΩυ and Tυ = 0. Let us denote
Consider a QR decomposition of TT, say, TT = FG, where F is an K × K orthogonal matrix and G is K × 3 upper triangular. Let F1 be the first 3 columns and F2 be the remaining K − 3 columns of F respectively. Following the argument in Green and Silverman (1994, p.166), we can show that Tυ = 0 if and only if υ can be expressed as F2ξ, where ξ is a K − 3 vector. Thus the minimizer of (7) is essentially equivalent to minimizing
| (10) |
Set , where is the matrix square root of (Ruppert et al. 2003, p.329). Thus minimizing (10) is equivalent to minimizing
| (11) |
where . Expression (11) is proportional to the negative exponential part of the joint distribution of YR and u under the following model assumption:
| (12) |
where λ is replaced by . The solution of minimizing (11) is the same as the best linear unbiased predictor (BLUP) for γ and u in the mixed model (12). This solution can be written as
| (13) |
with C = [X Z] and D = diag(0, 0, 0, 1, …, 1), where the number of zeros in the matrix D corresponds to the number of γi's (i = 0, 1, 2) and the number of ones corresponds to the number of ui's (i = 1, …, K − 3).
For any combination dose (d1, d2), if we denote f(d1, d2) = γ0 + γ1d1 + γ2d2 + Z0u with , then f̃(d1, d2) = γ̃0 + γ̃1d1 + γ̃2d2 + Z0ũ is the best linear unbiased prediction (BLUP) for f(d1, d2). Usually and are unknown, and consequently, is unknown, therefore, γ̃ and ũ are unknown. Let and be the restricted maximum likelihood estimators (REML) of and in the mixed model (12). Replacing λ by in (13), we can obtain the estimated BLUP for γ and u, say γ̂ and û. Thus the estimated BLUP for f(d1, d2) is f̂(d1, d2) = γ̂0 + γ̂1d1 + γ̂2d2 + Z0û. Especially, the fitted value f̂(d1i, d2i) (i = 1, …, n) is the ith component of C(CTC + λ̂D)−1CTYR.
To assess drug interactions from the statistical point of view, we need to examine the variability of f̂(d1, d2). To our knowledge, it is rather difficult to derive a theoretic formula for the variance of the estimated function f(d1, d2) in the framework of two-stage estimation. Therefore, we use the bootstrap method (Davison and Hinkley, 1997; Liang, Hardle, and Sommerfeld, 2000) to estimate the variance of f(d1, d2), and then construct the corresponding confidence interval for f(d1, d2) accordingly.
3.3 Estimate the variance of f(d1, d2) using bootstrap method
Under the semiparametric framework, Liang et al. (2000) presented a bootstrap approximation for a partially linear regression model. However, in our setting, the standard errors of the residuals from estimating dose-effect curves and from estimating the function f(d1, d2) may be quite different. Hence, a wild bootstrap method (Davison and Hinkley, 1997), which can account for the different error structures, would be more appropriate. Instead of simply resampling the residuals, the wild bootstrap uses the product of each residual and a random number which has mean zero and standard deviation 1, thus the different error structures can be maintained (Hardle and Marron, 1991, and references therein). In addition, we adopted the recommendation by Davison and Hinkley (1997, Section 7.6) to reduce the biases in estimating the standard error for f̂(d1, d2). We summarize the procedure as following:
Step 1. Fit the model based on the original observations, obtain f̂(d1i, d2i) and λ̂, where f̂(d1i, d2i) is the ith components of C(CTC + λ̂D)−1CTYR.
Step 2. Obtain the residuals from the undersmoothed estimation of f(d1, d2), i.e., ε̂i = Yi − F̂p(d1i, d2i) − f̂0.5λ̂ (d1i, d2i). Here f̂0.5λ̂ (d1i, d2i) is the ith component of C(CTC + 0.5λ̂D)−1CTYR.
Step 3. Generate n i.i.d. random variables with mean 0 and variance 1, for example, with probability and with probability (Hardle and Marron, 1991).
Step 4. Obtain the fitted value from the oversmoothed estimation of f(d1, d2), say, for i = 1, …, n. Here f̂2λ̂(d1i, d2i) is the ith component of C(CTC + 2λ̂D)−1CTYR
Step 5. Fit the model using the generated data (d1i, d2i, ) (i = 1, …, n), and then obtain the estimated function f*(d1, d2).
Step 6. Repeat Step 2 to Step 5 B (say, 50) times.
If we denote the estimated f(d1, d2) in the bth (b = 1, …, B) iteration as f*b(d1, d2), the standard deviation for f(d1, d2) will be estimated by
thus a 100(1 − α)% pointwise confidence interval for f(d1, d2) can be constructed as
| (14) |
where is the upper percentile of the standard normal distribution, and f̂(d1, d2) is the estimated BLUP for f(d1, d2) in Section 3.2. Our case study in Section 4 showed that the estimated variance for f(d1, d2) can account for the carry-over errors from estimating the marginal dose-effect curves. Our simulations given in Section 5 showed that the proposed bootstrap confidence intervals have good coverage properties.
4. Case Study
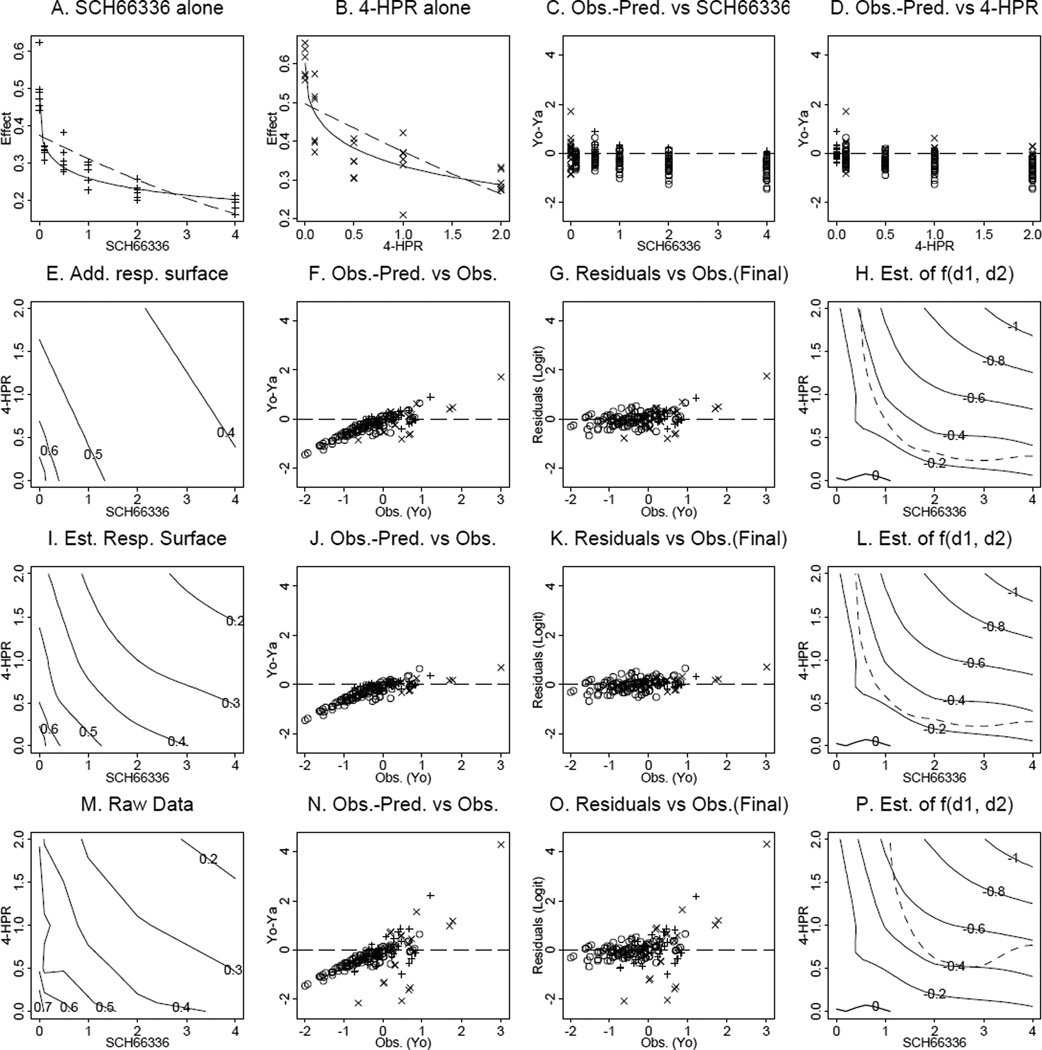
Table 1 shows the fractions of surviving cells after cancer cells from cell line UMSCC22B were treated with SCH66336, a farnesyl transferase inhibitor, and 4-HPR, a retinoid, alone and in combinations (data were provided by Dr. Reuben Lotan at M.D. Anderson Cancer Center). Both agents have a role in producing apoptosis. The objective was to study the efficacy and quantify the drug interaction when the two agents were used in combination. The experiment was conducted in six trays as shown in Table 1. The cells were untreated (control group), or were treated with single drug doses or combination doses. The fraction of surviving cells was recorded. We fitted the marginal data to model (6) by taking with Emax as the mean of the control group (solid curves in Figure 1, Panels A and B), and the model (3) with (dashed curves in Figure 1, Panels A and B). In these two panels, the observed data are shown as “+” for SCH66336 and “×” for 4-HPR, respectively. From the two panels, it is clear that model (6) fits the data better. Therefore, we choose model (6) as the marginal dose-effect curve. Taking Emax as the mean of the control group, fitting model (6) with is equivalent to fitting this model with and effect as the surviving cell fraction divided by the mean of the control. In the following data analysis, the effects will be taken as the observed fractions of surviving cells divided by the mean of the corresponding control group in each tray (c.f., Kanzawa et al. (1999) for a similar procedure). Based on the processed data, we obtained the two marginal dose-effect curves: for SCH66336 with a residual error of 0.2684 (i.e., σ̂ = 0.2684), and for 4-HPR with a residual error of 0.5618. Then, we can obtain the predicted effect in the E scale using the inverse transformation (5) (Panel E). The differences between the observed effects and predicted effects in logit scale versus SCH66336 doses, 4-HPR doses, and the observed effects (in logit scale) are plotted in Panels C, D, and F, respectively. Here the circles correspond to the non-marginal data. Panels C and D show that the differences for the lower combination doses are roughly centered around zero, indicating additivity of the associated combination doses, and the differences for the median to large combination doses are less than zero, indicating synergy of the associated combination doses. The results indicate that the additive model is not adequate to explain the observed data.
Table 1.
Observed fractions of surviving cells from cell line UMSCC22B after treatment with SCH66336 and 4-HPR.
| Tray | (0, 0) | (0.1, 0) | (0.5, 0) | (1.0, 0) | (2.0, 0) | (4.0, 0) | ||||||
| 1 | 0.422 | 0.498 | 0.328 | 0.345 | 0.383 | 0.306 | 0.255 | 0.303 | 0.202 | 0.235 | 0.163 | 0.205 |
| 0.473 | 0.453 | 0.335 | 0.336 | 0.282 | 0.329 | 0.297 | 0.228 | 0.258 | 0.229 | 0.213 | 0.196 | |
| 0.491 | 0.623 | 0.307 | 0.346 | 0.297 | 0.277 | 0.296 | 0.283 | 0.223 | 0.209 | 0.180 | 0.162 | |
|
| ||||||||||||
| Tray | (0, 0) | (0.1, 0.1) | (0.5, 0.1) | (1.0, 0.1) | (2.0, 0.1) | (4.0, 0.1) | ||||||
| 2 | 0.456 | 0.513 | 0.317 | 0.312 | 0.303 | 0.236 | 0.256 | 0.212 | 0.163 | 0.233 | 0.133 | 0.168 |
| 0.479 | 0.458 | 0.322 | 0.310 | 0.234 | 0.307 | 0.255 | 0.213 | 0.226 | 0.178 | 0.121 | 0.166 | |
| 0.456 | 0.429 | 0.255 | 0.309 | 0.262 | 0.334 | 0.252 | 0.236 | 0.202 | 0.171 | 0.149 | 0.155 | |
|
| ||||||||||||
| Tray | (0, 0) | (0.1, 0.5) | (0.5, 0.5) | (1.0, 0.5) | (2.0, 0.5) | (4.0, 0.5) | ||||||
| 3 | 0.33 | 0.335 | 0.187 | 0.176 | 0.185 | 0.175 | 0.163 | 0.158 | 0.133 | 0.116 | 0.083 | 0.108 |
| 0.392 | 0.36 | 0.176 | 0.216 | 0.182 | 0.221 | 0.143 | 0.205 | 0.151 | 0.145 | 0.123 | 0.108 | |
| 0.439 | 0.448 | 0.168 | 0.185 | 0.186 | 0.194 | 0.174 | 0.212 | 0.134 | 0.121 | 0.152 | 0.118 | |
|
| ||||||||||||
| Tray | (0, 0) | (0.1, 1.0) | (0.5, 1.0) | (1.0, 1.0) | (2.0, 1.0) | (4.0, 1.0) | ||||||
| 4 | 0.358 | 0.382 | 0.215 | 0.215 | 0.176 | 0.186 | 0.145 | 0.176 | 0.148 | 0.108 | 0.130 | 0.093 |
| 0.361 | 0.447 | 0.162 | 0.222 | 0.159 | 0.181 | 0.107 | 0.125 | 0.165 | 0.07 | 0.089 | 0.100 | |
| 0.431 | 0.367 | 0.187 | 0.212 | 0.187 | 0.196 | 0.134 | 0.146 | 0.112 | 0.120 | 0.068 | 0.107 | |
|
| ||||||||||||
| Tray | (0, 0) | (0.1, 2.0) | (0.5, 2.0) | (1.0, 2.0) | (2.0, 2.0) | (4.0, 2.0) | ||||||
| 5 | 0.380 | 0.386 | 0.173 | 0.165 | 0.165 | 0.135 | 0.157 | 0.113 | 0.073 | 0.115 | 0.066 | 0.067 |
| 0.417 | 0.409 | 0.157 | 0.153 | 0.140 | 0.133 | 0.116 | 0.114 | 0.087 | 0.103 | 0.051 | 0.071 | |
| 0.393 | 0.411 | 0.136 | 0.156 | 0.127 | 0.115 | 0.097 | 0.086 | 0.098 | 0.085 | 0.075 | 0.048 | |
|
| ||||||||||||
| Tray | (0, 0) | (0, 0.1) | (0, 0.5) | (0, 1.0) | (0, 2.0) | |||||||
| 6 | 0.558 | 0.573 | 0.515 | 0.509 | 0.347 | 0.396 | 0.371 | 0.422 | 0.332 | 0.292 | ||
| 0.638 | 0.619 | 0.397 | 0.372 | 0.407 | 0.348 | 0.368 | 0.209 | 0.281 | 0.328 | |||
| 0.569 | 0.655 | 0.402 | 0.574 | 0.306 | 0.303 | 0.338 | 0.353 | 0.276 | 0.273 | |||
Figure 1.
The results from analyzing the data set derived from cell line UMSCC22B treated with SCH66336 and 4-HPR. Panels A and B show the fitted dose-effect curves for SCH66336 and 4-HPR, respectively. The solid lines are based on model (6) while the dashed lines are based on model (3). Panels C, D, and F are the plots of the differences between the observed and the predicted effects in logit scale versus the SCH66336 doses, the 4-HPR doses, and the observed effects, respectively. Panel E is the contour plot of the predicted additive surface. Panel G is the plot of the final residuals versus the observed effects. Panel H is the contour plot of the estimated f(d1, d2) along with the intersection line of its upper 95% bootstrap confidence surface based on (14) with the dose plane shown in the dashed line. Panel I is the contour plot of the estimated response surface based on the semiparametric model. Panel M is the contour plot of the raw data. Panels J, K, and L are results parallel to Panels F, G, and H but in the case of the decreased marginal residuals (0.4 times of the original residuals), while panels N, O, and P are the parallel results in the case of the increased marginal residuals (2.5 times of the original residuals).
Now, we proceed to estimate f(d1, d2). The estimated residual error σ̂ε = 0.217 and the estimated smoothing parameter λ̂ = 0.1326. The final residuals (i.e., Yi − F̂p(d1i, d2i) − f̂(d1i, d2i) for i = 1, …, n) versus the observed effects (i.e., Yi for i = 1, …, n) are plotted in Panel G, which indicates that the fit has improved compared to Panel F under the additive model. The contour plot of the estimated f(d1, d2) is shown in Panel H. The 95% pointwise confidence surfaces for f(d1, d2) are constructed based on the bootstrap method (14). The 95% confidence bound for f(d1, d2) = 0 can be formed by taking the intersection lines of the upper and lower confidence surfaces with the dose plane. The dashed line in Panel H is the intersection line of the upper confidence surface based on the bootstrap confidence interval (14) with the dose plane. From Panel H, we conclude that the combination doses above the dashed line are synergistic (i.e., f(d1, d2) < 0), and the combination doses below the dashed line are additive (i.e., f(d1, d2) is not significantly different from zero). To show the contour plot of the fitted response surface in the original effect scale, we add f(d1, d2) to the predicted effect surface, and then use the inverse transformation (5) to obtain the fitted response surface on the original scale (Panel I). The contour plot in Panel I based on the model is similar to the contour plot of the raw data in Panel M, which indicates that the fit is reasonable.
Further, in order to examine whether the proposed bootstrap procedure can account for the errors from estimating the marginal dose-effect curves, we performed additional analysis for our case study by keeping the fitted marginal dose-effect curves the same as above, while perturbing the residuals of the marginal observations. In the first case, we changed the marginal observations (fractions of cell survival using one agent alone) to yield the same estimated marginal dose-effect curves but with smaller residuals (0.4 times of the original residuals). The data for the combination doses remained unchanged. Under this new setting, we estimated the predicted effects, plotted the differences of observed effects and predicted effects versus observed effect, in logit scale (Panel J). Then we estimated the function f(d1, d2), Panel K shows the final residual plot, and Panel L shows the contour plot of the estimated f(d1, d2) along with its 95% confidence bound for f(d1, d2) = 0 based on the bootstrap method (14) in dashed line. To compare, in the second case, we increased the residuals by 2.5-fold from estimating marginal dose-effect curves. Panels N, O, and P are the parallel results as Panels J, K, and L, respectively. Comparing the dashed lines in Panels H, L, and P, it is clear that, even when the estimated marginal dose-effect curves are all the same, the larger the estimated errors from estimating the marginal dose-effect curves, the wider the confidence bound is. Notice that because the marginal dose-effect curves and the effects of combination doses in the two new settings are the same as the original case study, the predicted additive effect surfaces as well as the estimated f(d1, d2) would remain the same. However, the bootstrap confidence bounds would account for the errors from estimating the marginal dose-effect curves. In the next section, we illustrate that the confidence interval based on the bootstrap method has a coverage rate which is close to the nominal coverage rate 95%.
5. Simulation studies
We use simulations to examine whether the estimation of the function f in our semiparametric model is accurate, and whether the semiparametric model can detect different patterns of drug interactions successfully.
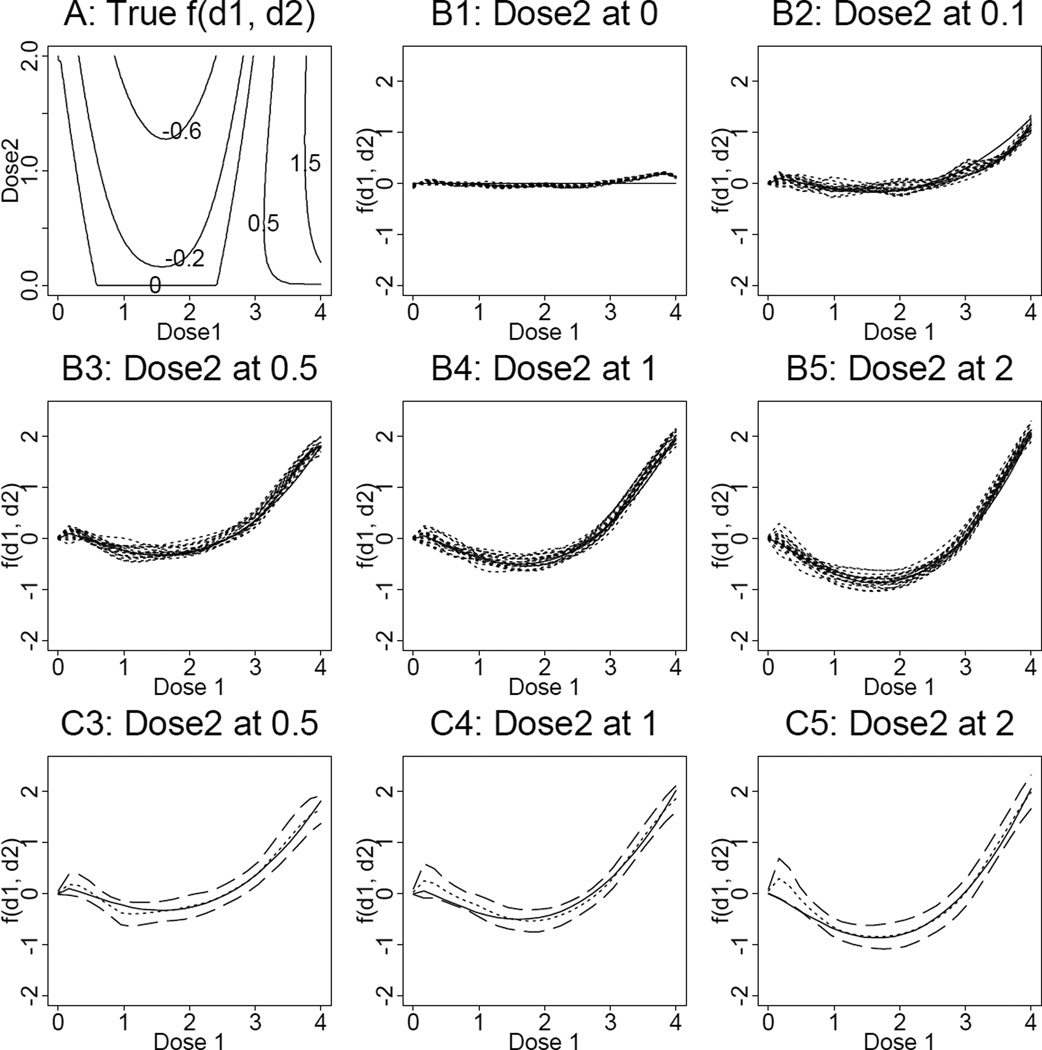
To examine whether or not the function f(d1, d2) can be estimated accurately, we generated data based on the marginal dose-effect curves estimated in the previous studied case, but take
| (15) |
shown in Figure 2, Panel A. The construction of f(d1, d2) mimics the scenario that there are different patterns of drug interactions within the same data. Note that the shape of f(d1, d2) chosen in the simulation studies here is quite different from the case study presented in Section 4. We generated the marginal data by adding the white noise from to the “true” effect on the logit scale. Similarly, we generated the non-marginal data by adding the white noise from to the sum of the additive effect and f(d1, d2), where the additive response surface is constructed based on the underlying marginal dose-effect curves. We took the same settings as those in the studied case in Section 4 except that we added one more dose level for drug 1 at d1 = 3. Including dose 0, there were 7 levels for drug 1 and 5 levels for drug 2. The sample size for each sample is 7 × 5 = 35 which includes 6 × 4 = 24 combination doses. For each dose or combination dose, we generated 6 replicates as were done in the experiment except for d1 = d2 = 0, the fraction of cell survival is set to 1. We took σ1 = 0.3, which lies between the estimated residual errors for SCH66336 and 4-HPR, and σ2 = 0.217, which is the estimated residual error for f. We generated 20 samples, estimated f(d1, d2), and plotted the f̂(d1, d2) at each unique d2 level (Figure 2, Panel B1 through Panel B5). In each panel, the solid line is the underlying f(d1, d2) by varying d1, and the dotted lines are the estimated curves for each of the 20 samples. In addition, for a particular sample, we estimated f(d1, d2) and constructed its bootstrap confidence interval based on (14). Figure 2, Panel C3 through Panel C5 show the underlying f(d1, d2) (solid line), the estimated f(d1, d2) (dotted line), and their 95% pointwise bootstrap confidence bound based on (14) with B = 50 (dashed lines) for this particular sample. It is evident that the fitted curves are close to the underlying curves, and the bootstrap confidence interval (14) performs well.
Figure 2.
The results from simulation studies presented in Section 5. Panel A shows the contour plot of the underlying true function f(d1, d2). Each panel of Panels B1–B5 shows the underlying curve (solid lines) and the fitted curves (dotted lines) based on a sample of 35 doses with 6 replicates for each dose level and 20 simulation runs under the setting σ1 = 0.3 and σ2 = 0.217. Each panel of Panels C3–C5 shows the underlying curve (solid lines), the fitted curve (dotted line), and the 95% point-wise bootstrap confidence bound (dashed lines) for a particular sample.
To further examine the performance of the bootstrap confidence interval (14), and also to examine whether the semiparametric method can detect different patterns of drug interactions, we generated data from the same scenario as above with f(d1, d2) shown in (15) and ran 150 simulated samples. For each sample, we estimated the marginal dose-effect curves, estimated the predicted additive effects and the function f(d1, d2) at (d1i, d2i) for i = 1, …, n, and constructed the 95% bootstrap confidence interval based on (14) with B = 50. For each sample, we recorded (a) the estimated function f̂(d1i, d2i) and the squared difference f̂(d1i, d2i) − f(d1i, d2i) (i = 1, …, n), (b) whether f(d1i, d2i) lies inside its associated confidence interval (14), (c) whether the associated bootstrap confidence interval (CI) contained zero (additivity), the lower limit of the associated bootstrap CI was greater than zero (antagonism), or the upper limit of the bootstrap CI was less than zero (synergy). Table 2 shows the combination dose (d1, d2), the underlying function f(d1, d2), and the averages of the above quantities over the simulated samples, which include: (a) the average of the 150 estimated f(d1, d2) (denoted as f.ave), the mean squared error (denoted as f.mse), and the estimated variance based on the simulated samples (denoted as f.var), (b) the percentage of counts of the underlying value lying inside the bootstrap confidence interval (14) (denoted as cr.bci), (c) the percentage of counts of the lower limit being greater than zero (denoted as p.ant), the confidence interval containing zero (denoted as p.add), and the upper limit being less than zero (denoted as p.syn), indicating predicted antagonism, additivity, and synergy, respectively. From Table 2, we conclude that: (i) overall, the averages of the estimated function f(d1, d2) are close to the underlying function values, and the mean square errors are similar to the variance estimates except that at the combination dose (4.0, 0.1) the mean square error is much bigger, indicating bias of the estimation; (ii) the coverage rates based on the bootstrap method (cr.bci) are close to the nominal coverage rate of 95%; (iii) when f(d1, d2) > 0, the larger the f(d1, d2) is, the higher the percentage (p.ant) of the lower limit of the bootstrap confidence interval (14) being greater than 0, indicating the correct assessment of drug interaction as antagonism at (d1, d2); (iv) when f(d1, d2) < 0, the larger the absolute value of f(d1, d2) is, the higher percentage (p.syn) of the upper limit being less than 0, indicating the correct assessment of drug interaction as synergy at (d1, d2); (v) when f(d1, d2) is close to zero, the percentage of the confidence intervals containing zero (p.add) is close to 95%, indicating the correct assessment of drug interaction as additivity at (d1, d2). These facts illustrated that both the estimation for the model and the constructed bootstrap confidence intervals perform well.
Table 2.
Simulation results for evaluating mixed pattern of drug interaction with 24 combination doses and 150 runs under the setting σ1 = 0.3 and σ2 = 0.217.
| (d1, d2) | f(d1, d2) | f.ave | f.mse | f.var | cr.bci | p.ant | p.add | p.syn |
|---|---|---|---|---|---|---|---|---|
| (0.1, 0.1) | 0.101 | 0.080 | 0.0074 | 0.0070 | 0.97 | 5 | 95 | 0 |
| (0.1, 0.5) | 0.113 | 0.092 | 0.0076 | 0.0072 | 0.91 | 17 | 82 | 1 |
| (0.1, 1.0) | 0.078 | 0.053 | 0.0088 | 0.0082 | 0.90 | 2 | 97 | 1 |
| (0.1, 2.0) | −0.041 | −0.052 | 0.0098 | 0.0097 | 0.95 | 1 | 93 | 6 |
| (0.5, 0.1) | 0.014 | 0.015 | 0.0070 | 0.0070 | 0.97 | 1 | 97 | 2 |
| (0.5, 0.5) | −0.035 | −0.039 | 0.0083 | 0.0083 | 0.92 | 0 | 89 | 11 |
| (0.5, 1.0) | −0.126 | −0.136 | 0.0107 | 0.0107 | 0.90 | 0 | 66 | 34 |
| (0.5, 2.0) | −0.350 | −0.380 | 0.0131 | 0.0123 | 0.92 | 0 | 15 | 85 |
| (1.0, 0.1) | −0.110 | −0.093 | 0.0073 | 0.0071 | 0.96 | 0 | 77 | 23 |
| (1.0, 0.5) | −0.231 | −0.241 | 0.0090 | 0.0089 | 0.95 | 0 | 33 | 67 |
| (1.0, 1.0) | −0.375 | −0.384 | 0.0101 | 0.0100 | 0.95 | 0 | 3 | 97 |
| (1.0, 2.0) | −0.684 | −0.690 | 0.0120 | 0.0120 | 0.94 | 0 | 0 | 100 |
| (2.0, 0.1) | −0.130 | −0.109 | 0.0082 | 0.0072 | 0.96 | 0 | 68 | 32 |
| (2.0, 0.5) | −0.275 | −0.277 | 0.0076 | 0.0081 | 0.97 | 0 | 28 | 72 |
| (2.0, 1.0) | −0.446 | −0.452 | 0.0081 | 0.0129 | 0.91 | 0 | 5 | 95 |
| (2.0, 2.0) | −0.813 | −0.816 | 0.0129 | 0.0129 | 0.92 | 0 | 0 | 100 |
| (3.0, 0.1) | 0.300 | 0.271 | 0.0094 | 0.0086 | 0.97 | 47 | 53 | 0 |
| (3.0, 0.5) | 0.360 | 0.365 | 0.0094 | 0.0094 | 0.95 | 91 | 9 | 0 |
| (3.0, 1.0) | 0.296 | 0.287 | 0.0116 | 0.0115 | 0.95 | 71 | 29 | 0 |
| (3.0, 2.0) | 0.039 | 0.028 | 0.0115 | 0.0115 | 0.97 | 2 | 95 | 3 |
| (4.0, 0.1) | 1.276 | 1.115 | 0.0406 | 0.0146 | 0.99 | 100 | 0 | 0 |
| (4.0, 0.5) | 1.814 | 1.826 | 0.0113 | 0.0113 | 0.97 | 100 | 0 | 0 |
| (4.0, 1.0) | 2.015 | 2.007 | 0.0124 | 0.0125 | 0.94 | 100 | 0 | 0 |
| (4.0, 2.0) | 2.060 | 2.042 | 0.0114 | 0.0111 | 0.97 | 100 | 0 | 0 |
6. Discussion
The case study in Section 4 and the simulations in Section 5 indicate that our proposed method can be used to successfully assess drug interaction even when different patterns of drug interactions exist within the same data. In addition, the fitted dose response surface F̂p(d1, d2) + f̂(d1, d2) gives an overall picture of the dose-effect relationship, which can help us to identify the optimal combination therapy.
In our two stage procedure, since both the errors from estimating the dose-effect curves and the errors for measuring the effects at combination doses impact the precision of the estimated f(d1, d2), in the case that the errors are large, further efforts such as better control of experimental conditions and increasing the number of replicates will be required to improve the assessment of drug interaction. As in any data analysis, model fitting needs to be examined carefully, for example, by plotting residuals and predicted values versus observed values, etc. Sensitivity analysis can be done by removing or down weighing suspected outliers. Statistical inference should be made in conjunction with meaningful biological evidence and knowledge.
In the semiparametric model, we use a function f to capture the patterns of drug interactions. The estimated function f and its 95% confidence surfaces can guide us to explore whether some parametric models are sufficient to describe the data. If the fitted function f and its confidence surfaces indicate that the modes of drug interactions for all combination doses are similar, a parametric model with a single parameter capturing drug interaction may suffice. If the fitted function f and its confidence surfaces indicate that the modes of drug interactions for the combination doses at each fixed ratio are unique, the parametric models based on a 50% maximal effect isobole may be appropriate. We advocate the use of our proposed semiparametric method for model building since we typically do not know the true patterns of drug interactions. Blindly using any parametric model can be dangerous and may lead to the wrong conclusions of drug interactions. In our proposed model, we do not assume any parametric patterns for f(d1, d2). The conclusions of drug interactions are based on the estimated f and its confidence surfaces, which are determined by the underlying data.
Our current model can be extended in several ways. One extension is that we may use nonparametric dose-effect curves to describe the marginal dose-effect relationship. Then, we can use the same procedure to estimate the function f(d1, d2) and construct its confidence surfaces, and assess drug interactions accordingly. However, since the curves estimated nonparametrically can not be extrapolated, larger range of dose levels for each single drug is needed so that the range of effects from each single drug covers the range of the effect for the combination doses so that the additive effect can be estimated for each combination dose (Kelly and Rice, 1990).
Another extension of our current model is that our two-stage model can be extended to assess multiple drug interactions (say, k > 2 drugs). The predicted additive effect can be obtained from , and f(d1, …, dk) can be estimated by using high-dimensional thin plate spline (Green and Silverman, 1994).
In the current setting, we first estimate the parameters β's, and then estimate f(d1, d2). Here f(d1, d2) is used to characterize drug interaction, which should be zero whenever d1 = 0 or d2 = 0. Currently, we forced the difference between observed effect and predicted additive effect as zero for each marginal dose so that the estimated f(d1, d2) could be as close to zero as possible. However, it will be beneficial to research on how this constraint could be transferred to the constraint on γ's and υ's. In addition, whether and how to estimate β's and f(d1, d2) simultaneously may be further investigated. We may also consider to formulate the response surface model in different manner, such as (Kong and Lee, 2006). In that setting, β's and f(d1, d2) may be estimated simultaneously. But how to estimate them remains a very challenging and interesting problem. Last but not the least, further research is needed to develop the theoretical properties of the bootstrap method for constructing the confidence interval for f(d1, d2) in the current setting.
Acknowledgments
This research was supported in part by grants from the National Cancer Institute CA106451, CA97007, CA91844, and the Department of Defense W81XWH-04-1-0142 and W81XWH-05-2-0027. The authors are thankful to Dr. Reuben Lotan for providing data, to Dr. Raymond Carroll and Dr. Somnath Datta for their discussion, to Lee Ann Chastain for editorial assistance, and to the two reviewers, the Associate Editor, and the Editor for their constructive comments.
Footnotes
Supplementary Materials: The data and S-PLUS code can be accessed at the Biometrics website http://www.tibs.org/biometrics.
References
- 1.Berenbaum MC. What is synergy? Pharmacological Reviews. 1989;41:93–141. [PubMed] [Google Scholar]
- 2.Carter WH, Jr, Gennings C, Staniswalis JG, Cambell ED, White KL., Jr A statistical approach to the construction and analysis of isobolograms. Journal of American College Toxicology. 1988;7:963–973. [Google Scholar]
- 3.Chou TC, Talalay P. Quantitative analysis of dose-effect relationships: the combined effects of multiple drugs or enzyme inhibitors. Advances in Enzyme Regulation. 1984;22:27–55. doi: 10.1016/0065-2571(84)90007-4. [DOI] [PubMed] [Google Scholar]
- 4.Davison AC, Hinkley DV. Bootstrap Methods and their Application. Cambridge University Press; 1997. [Google Scholar]
- 5.Greco WR, Bravo G, Parsons JC. The search of synergy: A critical review from a response surface perspective. Pharmacological Reviews. 1995;47(2):331–385. [PubMed] [Google Scholar]
- 6.Green PJ, Silverman BW. Nonparametric Regression and Generalized Linear Models. London: Chapman & Hall; 1994. [Google Scholar]
- 7.Hardle W, Marron JS. Bootstrap simultaneous error bars for nonparametric regression. Annuls of Statistics. 1991;19:778–796. [Google Scholar]
- 8.Kanzawa F, Nishio K, Fukuoka K, Sunami T, Saijo N. In vitro inter- actions of a new derivative of spicamycin, KRN5500, and other anticancer drugs using a three-dimensional model. Cancer Chemother. Pharmacol. 1999;43:353–363. doi: 10.1007/s002800050907. [DOI] [PubMed] [Google Scholar]
- 9.Kelly C, Rice J. Monotone smoothing with application to dose-response curves and the assessment of synergism. Biometrics. 1990;46:1071–1085. [PubMed] [Google Scholar]
- 10.Kong M, Eubank RL. Monotone smoothing with application to dose-response curve. Communications in Statistics - Simulation and Computation. 2006;35:991–1004. [Google Scholar]
- 11.Kong M, Lee JJ. A generalized response surface model with varying relative potency for assessing drug interactions. Biometrics. 2006;62(4):986–995. doi: 10.1111/j.1541-0420.2006.00579.x. [DOI] [PubMed] [Google Scholar]
- 12.Lee JJ, Kong M, Ayers GD, Lotan R. Interaction index and different methods for determining drug interaction in combination therapy. To appear in Journal of Biopharmaceutical Statistics. 2007 doi: 10.1080/10543400701199593. [DOI] [PubMed] [Google Scholar]
- 13.Liang H, Hardle W, Sommerfeld V. Bootstrap approximation in partially linear regression model. Journal of Statistical Planning and Inference. 2000;91:413–426. [Google Scholar]
- 14.Prichard MN, Shipman C., Jr A three-dimensional model to analyze drug-drug interactions. Antiviral Research. 1990;14:181–206. doi: 10.1016/0166-3542(90)90001-n. [DOI] [PubMed] [Google Scholar]
- 15.Ruppert D, Wand MP, Carroll RJ. Semiparametric Regression. Cambridge University Press; 2003. [Google Scholar]
- 16.Suhnel J. Evaluation of synergism or antagonism for the combined action of antiviral agents. Antiviral Research. 1990;13:23–40. doi: 10.1016/0166-3542(90)90042-6. [DOI] [PubMed] [Google Scholar]
- 17.Tan M, Fang H, Tian G, Houghton PJ. Experimental design and sample size determination for testing synergism in drug combination studies based on uniform measures. Statistics in Medicine. 2003;22:2091–2100. doi: 10.1002/sim.1467. [DOI] [PubMed] [Google Scholar]
- 18.White DB, Faessel HM, Slocum HK, Khinkis L, Greco WR. Nonlinear response surface and mixture experiment methodologies applied to the study of synergy. Biometrical Journal. 2004;46:56–71. [Google Scholar]