Asymptotic properties of the number of matching coalescent histories for caterpillar-like families of species trees

Abstract

Coalescent histories provide lists of species tree branches on which gene tree coalescences can take place, and their enumerative properties assist in understanding the computational complexity of calculations central in the study of gene trees and species trees. Here, we solve an enumerative problem left open by Rosenberg concerning the number of coalescent histories for gene trees and species trees with a matching labeled topology that belongs to a generic caterpillar-like family. By bringing a generating function approach to the study of coalescent histories, we prove that for any caterpillar-like family with seed tree t, the sequence (h_n)_n≥0 describing the number of matching coalescent histories of the nth tree of the family grows asymptotically as a constant multiple of the Catalan numbers. Thus, h_n ~ β_tc_n, where the asymptotic constant β_t > 0 depends on the shape of the seed tree t. The result extends a claim demonstrated only for seed trees with at most 8 taxa to arbitrary seed trees, expanding the set of cases for which detailed enumerative properties of coalescent histories can be determined. We introduce a procedure that computes from t the constant β_t as well as the algebraic expression for the generating function of the sequence (h_n)_n≥0.

1 Introduction

Coalescent histories, mathematical structures representing combinatorially distinct ways in which a given gene tree can coalesce along the branches of a given species tree, are important in a variety of phylogenetic problems [6], [14], [15]. They arise, for example, in proofs concerning theoretical properties of species tree inference algorithms [1], [18], in empirical analyses of gene tree probability distributions [16], and in studies of gene trees under hybridization [21]. Many of these applications trace to the appearance of coalescent histories in a sum performed in a fundamental calculation for inference of species trees from information on multiple genetic loci, the evaluation of gene tree probabilities conditional on species trees [5].

Owing to uses of coalescent histories in sets over which sums are computed, as well as in state spaces of certain phylogenetic Markov chains [7], [10], [11], solutions to enumerative problems involving coalescent histories contribute to an understanding of the computational complexity of phylogenetic calculations. A recursion for the number of coalescent histories for a given gene tree and species tree has been established [13], and several studies have reported exact numerical results and closed-form expressions for the number of coalescent histories for small trees and for specific types of trees of arbitrarily large size [4]–[6], [13]–[15], [19]. The latter computations have proceeded both by solving or deploying the recursion in specific cases [13]–[15], [19], as well as by identifying correspondences between coalescent histories and other combinatorial structures for which enumerative results have already been established [4]–[6].

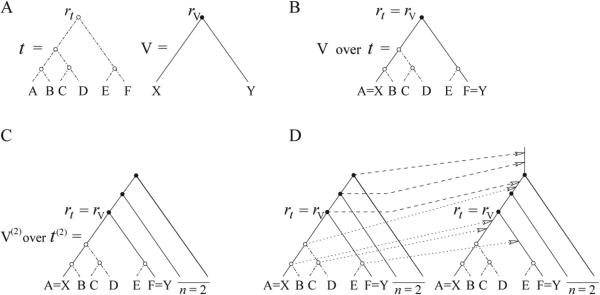
One class of gene trees and species trees of particular interest for enumeration of coalescent histories is the caterpillar-like families, trees that have a caterpillar shape, except that the caterpillar subtree with r taxa is replaced by a subtree of size r that is not necessarily a caterpillar subtree (Fig. 1). For the simplest caterpillar-like family, the caterpillar trees themselves, if the gene tree and species tree have the same caterpillar labeled topology with n taxa, then, as reported in [5], the number of coalescent histories is a Catalan number,

$$c_{n-1}=\frac{1}{n}\left(\begin{array}{c}\hfill 2n-2\hfill \\ \hfill n-1\hfill \end{array}\right).$$ (1)

Fig. 1.

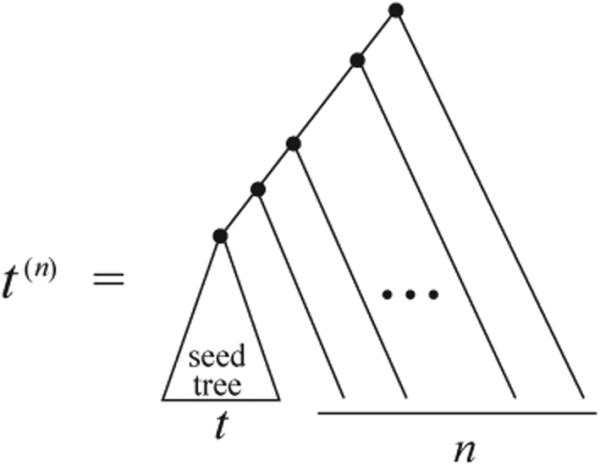
A caterpillar-like family of species trees (t⁽ⁿ⁾)_n≥0. For a seed tree t, by adding n ≥ 0 branches each with 1 leaf, we obtain the nth tree of the family, t⁽ⁿ⁾. If t has 2 taxa, then (t⁽ⁿ⁾)_n≥0 is simply the caterpillar family.

For T_r-caterpillar-like families, in which the r-taxon subtree of an n-taxon caterpillar species tree is replaced by an r-taxon subtree T_r (Fig. 1), by employing the recursion, Rosenberg [14] obtained the exact number of coalescent histories for all n, for each T_r with r ≤ 8, in the case that the gene tree and species tree have the same labeled topology. Rosenberg [14] argued that in each of these cases, as n → ∞, the number of coalescent histories is asymptotic to a constant multiple of the Catalan numbers. A proof of this result has been presented in full for each case with r ≤ 5 [4], [13], [14], and by computer algebra for cases with r = 6, 7, and 8 [14].

Each case considered by [14] involved cumbersome computations specific to the choice of T_r, limiting the generality of the approach. While no reason exists to suspect that the method of [14] would not extend to larger r, it is desirable to find another method that is practical for a general T_r. Here, using a substantially different strategy that brings to studies of coalescent histories the methods of analytic combinatorics, we produce an enumeration result that covers caterpillar-like families in general. We show that the result of [14] applies to all caterpillar-like families, not only those for which T_r has r ≤ 8. That is, we demonstrate that for any T_r, as n → ∞, the number of coalescent histories in the T_r-caterpillar-like family is asymptotic to a constant multiple of the Catalan numbers—thus extending a result known only for r ≤ 8 to arbitrarily large r. We describe a method and symbolic tool for computing the constant. Finally, we discuss the impact of the results in mathematical phylogenetics.

2 Preliminaries

2.1 Species trees and coalescent histories

We consider binary rooted leaf-labeled species trees, taking a single arbitrary labeling (without loss of generality) to represent a given unlabeled species tree topology. We consider an arbitrarily labeled species tree and its unlabeled tree interchangeably, treating the labeling as implicit.

We examine coalescent histories for the case in which gene trees and species trees have the same labeled topology t, terming a coalescent history in this case a matching coalescent history. To be a matching coalescent history, a mapping h from the internal nodes of t (viewed as the gene tree) to the branches of t (viewed as the species tree) must satisfy two conditions (Fig. 2): (a) for each leaf x in t, if x descends from node k in t, then x descends from branch h(k) in t; (b) for each pair of internal nodes k₁ and k₂ in t, if k₂ descends from k₁ in t, then branch h(k₂) descends from or coincides with branch h(k₁) in t. We henceforth consider only matching coalescent histories, treating “matching” as implicit; we also refer simply to histories for short.

Fig. 2.

Matching coalescent histories. (A) A matching coalescent history. (B) A mapping from the internal nodes of a tree to its branches that does not satisfy condition (a). Leaf B is descended from node k but does not descend from branch h(k). (C) A mapping from the internal nodes of a tree to its internal branches that does not satisfy condition (b). Node k₂ is descended from node k₁, but branch h(k₂) is strictly ancestral to branch h(k₁).

2.2 Caterpillar-like families of species trees

For a binary species tree t with at least 2 taxa, we denote by (t⁽ⁿ⁾)_n≥0 the caterpillar-like family generated by seed tree t. This family is recursively defined by taking t⁽⁰⁾ = t and letting t⁽ⁿ⁺¹⁾ be the tree obtained by appending t⁽ⁿ⁾ and a single leaf to a shared root (Fig. 1).

Our interest is in the number of matching coalescent histories of t⁽ⁿ⁾ for n ≥ 0, a quantity we denote by h_n(t) or simply h_n. We note that whereas [14] indexed trees by their numbers of taxa, here n represents the number of taxa appended above the root of the seed tree, so that if seed tree t has |t| taxa, then |t| + n gives the number of taxa in t⁽ⁿ⁾.

2.3 Principles of analytic combinatorics

We rely on techniques of analytic combinatorics [8] to obtain our enumerative results, and recall several key points. In general, an integer sequence (a_n)_n≥0 can be associated with a formal power series $A\left(z\right)={\sum }_{n=0}^{\infty }{a}_n{z}^n$, also termed the generating function of the integers a_n. Considering z as a complex variable, typically in a neighborhood of 0, features of the function A(z) are related to the growth of the coefficients a_n.

More precisely, generating functions, considered as complex functions, enable analyses of the asymptotic growth of the associated integer sequences through the analysis of their singularities in the complex plane. In particular, under suitable conditions, there exists a general correspondence between the singular expansion of a generating function A(z) near its dominant singularities—those nearest the origin—and the asymptotic behavior of the associated coefficients a_n (Chapter VI of [8]). We make use of theorems that describe this correspondence.

2.4 Catalan numbers

The Catalan sequence appears often in combinatorics [8], [9], [17] and features prominently in our analysis. Rewriting eq. (1) with index n rather than n − 1,

$$c_n=\frac{1}{n+1}\left(\begin{array}{c}\hfill 2n\hfill \\ \hfill n\hfill \end{array}\right).$$ (2)

The associated generating function is well known [17]:

$$C\left(z\right)=\sum _{n=0}^{\infty }{c}_n{z}^n=\frac{1-\sqrt{1-4z}}{2z}.$$ (3)

By definition, if [zⁿ]f(z) denotes the nth term in the power series expansion of f(z) at z = 0, we have

$$\begin{array}{cc}\hfill c_n& =\left[z^n\right]C\left(z\right)=\frac{1}{2}\left[z^{n+1}\right](1-\sqrt{1-4z})\hfill \\ \hfill & =\frac{1}{2}\left[z^{n+1}\right](-\sqrt{1-4z}).\hfill \end{array}$$ (4)

Here, $1-\sqrt{1-4z}$ is replaced by $-\sqrt{1-4z}$, as the constant 1 does not contribute to the power series expansion for terms of order n+1, with n ≥ 0. Asymptotically, applying Stirling's formula $n!\sim \sqrt{2\pi n}{(n∕e)}^n$ to eq. (2), the Catalan sequence satisfies

$$c_n\sim \frac{4^n}{n^{3∕2}\sqrt{\pi }}.$$ (5)

3 The number of matching coalescent histories for caterpillar-like families

We aim to find a procedure that evaluates the number of coalescent histories h_n(t) for matching gene trees and species trees in the caterpillar-like family that begins with seed tree t, and moreover, to show that

$$h_n\left(t\right)\sim {\beta }_t{c}_n,$$ (6)

where the multiplier β_t > 0 for the Catalan sequence is a constant depending on t. In other words, we wish to demonstrate that as n → ∞, h_n/c_n converges to a constant β_t > 0 that depends on the seed tree t.

First, in Section 3.1, we determine a lower bound for the number of matching coalescent histories of the nth tree t⁽ⁿ⁾ of the caterpillar-like family with seed tree t. Next, in Section 3.2, we introduce a concept of m-rooted histories of a species tree t⁽ⁿ⁾. The section provides an iterative construction of the rooted histories of t⁽ⁿ⁺¹⁾ from those of t⁽ⁿ⁾, describing the construction by means of a convenient labeling scheme. We follow a commonly used combinatorial enumeration strategy [2], [3] that determines a recursive succession rule for successive collections of objects in a sequence and then uses this rule to compute a generating function. In Section 3.3, we use the iterative construction to produce a bivariate generating function whose coefficients h_n,m are the numbers of m-rooted histories for trees t⁽ⁿ⁾. We next obtain the generating function for the integer sequence (h_n)_n≥0 describing the number of matching coalescent histories for the t⁽ⁿ⁾. Finally, using the lower bound from Section 3.1, in Section 3.4, we apply methods of analytic combinatorics to study the asymptotic behavior of h_n.

3.1 Lower bound for h_n

For our asymptotic analysis, we will need an initial lower bound for h_n. To produce this bound, we first define V as the tree with 2 taxa. Recalling that we index trees so that the number of taxa in a tree exceeds by n the number of taxa in the seed tree, we have [4], [13], [14]

$$h_n\left(\mathrm{V}\right)=c_{n+1}.$$

We can then use a constructive procedure, illustrated in detail in Figure 3, to show that for any seed tree t with |t| ≥ 2,

$$h_n\left(t\right)\ge h_n\left(\mathrm{V}\right)=c_{n+1}.$$ (7)

For a seed tree t, we can superimpose V on t so that the root r_V of V matches the root r_t of t (Fig. 3B). The two leaves of V are identified with two of the leaves of t, one on each side of the root of t. Generating caterpillar-like families by adding n single branches separately to V and to t, the superposition of V on t extends, so that V⁽ⁿ⁾ is superimposed on t⁽ⁿ⁾ (Fig. 3C). The n caterpillar branches of t⁽ⁿ⁾ and V⁽ⁿ⁾ then correspond.

Fig. 3.

Superposition of the caterpillar tree family on a caterpillar-like tree family with arbitrary seed tree of size |t| ≥ 2. (A) A seed tree t and the seed tree V for the caterpillar family. (B) Superposition of V on t, so that the roots r_V and r_t overlap. (C) Superposition of V⁽²⁾ (shaded internal nodes) on t⁽²⁾ (shaded and unshaded nodes). The n = 2 caterpillar branches in V⁽²⁾ and t⁽²⁾ overlap, and r_V still matches r_t. (D) A matching coalescent history of t⁽²⁾ (dashed and dotted arrows) determines a matching coalescent history of V⁽²⁾ (dashed arrows) by ignoring arrows from the unshaded nodes.

Each matching coalescent history h of t⁽ⁿ⁾ determines a corresponding matching coalescent history h′ of V⁽ⁿ⁾ by considering the restriction of h to the set of internal nodes of t⁽ⁿ⁾ that correspond to internal nodes of V⁽ⁿ⁾ (Fig. 3D). Thus, for any seed tree t, the number of matching coalescent histories of t⁽ⁿ⁾ is greater than or equal to that of V⁽ⁿ⁾. In symbols, we have eq. (7). We will use this result in Section 3.4.

3.2 Iterative generation of rooted histories

This section describes the iterative procedure that for a seed tree t eventually enables us to determine a formula for h_n. First, in Section 3.2.1, we discuss m-rooted histories, which extend the concept of matching coalescent histories, introducing an additional parameter m. Next, in Section 3.2.2, we examine the relationship between rooted histories and the extended coalescent histories of [13], importing results on extended coalescent histories into the more convenient framework of rooted histories. We expand our goal of enumerating matching coalescent histories for t⁽ⁿ⁾, considering a more general problem of enumerating for m ≥ 1 the m-rooted histories of t⁽ⁿ⁾.

In Section 3.2.3, we define an operator Ω for constructing the rooted histories of t⁽ⁿ⁺¹⁾ from the rooted histories of t⁽ⁿ⁾. Next, in Section 3.2.4, we introduce a labeling scheme that in Section 3.2.5 enables us to switch from counting rooted histories to counting multisets of labels. At the end of Section 3.2, we will have converted our enumeration problem into an enumeration that is more convenient for constructing a generating function.

3.2.1 m-rooted histories

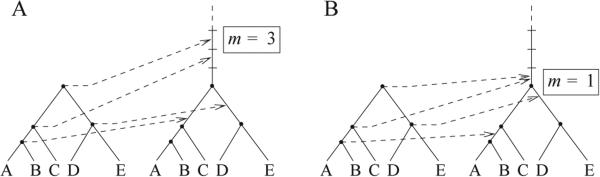
Consider a tree t with |t| ≥ 2, and suppose that the branch above the root of t (the root-branch) is divided into infinitely many components. A matching coalescent history mapping the internal nodes of t onto the branches of t is said to be m-rooted for m ≥ 1 if the root of t is mapped exactly onto the mth component of the root (Fig. 4). It is said to be rooted if it is m-rooted for some m. Branches are numbered so that branch m = 1 is immediately above the root node, and m is greater for components that are farther from the root.

Fig. 4.

Rooted histories of a tree. (A) A 3-rooted history. The root-branch is divided into infinitely many components, the third of which receives the image of the root. (B) A 1-rooted history. The number of 1-rooted histories corresponds to the number of matching coalescent histories of the tree.

For a rooted history h of a tree t, m = m(h) denotes the component of the root-branch of t that receives the image of the root of t. H_n,m(t) denotes the set of m-rooted histories of t⁽ⁿ⁾, and $H_n\left(t\right)={\bigcup }_{m=1}^{\infty }{H}_{n,m}\left(t\right)$ the set of its rooted histories. The number of m-rooted histories of t⁽ⁿ⁾ is h_n,m = |H_n,m|, and the number of 1-rooted histories h_n = h_n,1 is also the number of matching coalescent histories. Enumerating the matching coalescent histories of t⁽ⁿ⁾ is equivalent to enumerating its 1-rooted histories.

3.2.2 Rooted histories and extended histories

Rooted histories are closely related to extended coalescent histories, as defined by [13]. We use this relationship to study properties of rooted histories. Rosenberg [13] defined the set of k-extended coalescent histories of a tree t with |t| ≥ 1 for integers k ≥ 1; we also consider k = 0 by setting the number of 0-extended histories to 0.

A k-extended history is defined as a coalescent history for a species tree whose root-branch is divided into exactly k ≥ 0 parts. In other words, the root-branch has exactly k ≥ 0 possible components onto which a k-extended history can map the gene tree root. Here we consider matching k-extended histories, so that the internal nodes of a tree t are mapped to the branches of t and its k components above the root. For convenience, we refer to extended histories by the index k, reserving the index m for rooted histories.

By the definitions of k-extended and m-rooted histories, for each k ≥ 0, the set of k-extended histories of a tree is exactly the set of all m-rooted histories with 1 ≤ m ≤ k. Therefore, for a tree t with at least 2 leaves, if we label by e_t,k its number of k-extended histories, then for each m ≥ 1 the number of m-rooted histories of t is

$$h_{0,m}=e_{t,m}-e_{t,m-1}.$$ (8)

Note that for m = 1, we explicitly use in eq. (8) the fact that e_t,0 is defined and equal to 0. In addition to setting e_t,0 = 0 for any tree t, as in [13] we set e_t,k = 1 for all k ≥ 1 in the case that t has exactly 1 leaf.

Suppose |t| ≥ 1 and k ≥ 0. Denote by t_L and t_R the left and right subtrees of the root of t. We can compute e_t,k recursively as in Theorem 3.1 of [13]:

$$e_{t,k}=\{\begin{array}{cc}0\hfill & \text{if}\mid t\mid \ge 1\text{and}k=0\hfill \\ 1\hfill & \text{if}\mid t\mid =1\text{and}k\ge 1\hfill \\ {\sum }_{i=1}^k{e}_{t_L,i+1}{e}_{t_R,i+1}\hfill & \text{if}\mid t\mid \ge 2\text{and}k\ge 1.\hfill \end{array}\phantom{\}}$$ (9)

As was already observed in the remarks following Corollary 3.2 of [13], by eq. (9), for any tree t with |t| ≥ 1, for positive integers k ≥ 1, the function f(k) = e_t,k is a polynomial in k. With our extension to permit k = 0, we can extend this fact to k ≥ 0 for |t| ≥ 2: for any tree t with |t| ≥ 2, and for k ≥ 0, we claim that the function f(k) = e_t,k is a polynomial in k. Note that in allowing k = 0, we claim e_t,k is a polynomial in k only for |t| ≥ 2; for |t| = 1, e_t,k is not a polynomial in k because e_t,0 = 0 and e_t,k = 1 for k ≥ 1.

To prove the claim, fix t with |t| ≥2 and consider the variable k over domain [1, ∞). We demonstrate that f(k) is a polynomial in k for domain [0, ∞) by showing that the closed-form for f(k) has a factor of k, so that our choice e_t,0 = 0 in eq. (9) is compatible with the polynomial expression valid for k ≥ 1.

Observe that for i ≥ 1, e_tL,i and e_tR,i are polynomials in i, say P_tL(i) and P_tR(i). Replacing terms e_tL,i+1 and e_tR,i+1 in the recursion in eq. (9) by polynomials P_tL(i + 1) and P_tR(i + 1), we obtain

$$\sum _{i=1}^k{e}_{t_L,i+1}{e}_{t_R,i+1}=\sum _{i=1}^k{P}_{t_L}(i+1)P_{t_R}(i+1)=\sum _{i=1}^k{P}^{\prime }\left(i\right),$$ (10)

where P′(i) denotes a polynomial in i that results from the product of P_tL(i + 1) and P_tR(i + 1). By Faulhaber's formula for sums of powers of integers, symbolic sums of the form ${\sum }_{i=1}^k{i}^p$ for a fixed integer p ≥ 0 are polynomials containing a factor of k in their closed forms (Section 6.5 of [9])—for example, ${\sum }_{i=1}^k{i}^3=k^2{(k+1)}^2∕4$. Thus, because the polynomial P′(i) is a linear combination of terms of the form i^p, the closed-form expression for the sum ${\sum }_{i=1}^k{P}^{\prime }\left(i\right)$ appearing in eq. (10) also has a factor of k. It therefore has a value of 0 at k = 0.

Functions e_t,k for trees t with 1 ≤ |t| ≤ 9 and k ≥ 1 appear in Tables 1-4 of [13]. For |t| ≥ 2, as we have shown, these example polynomials are divisible by the variable representing the number of components of the root-branch. By eq. (8), we immediately obtain the following result.

Proposition 1

For any tree t with |t| ≥ 2 and for m ≥ 1, the number h_0,m of m-rooted histories of t is a polynomial in m that can be computed by the difference in eq. (8) using e_t,k as in eq. (9).

As an example of Proposition 1, consider the tree t = ((A, B), (C, D)), identifying this arbitrary labeling with the unlabeled tree (()()). By applying the recursive procedure in eq. (9), we find that for k ≥ 0, the number of k-extended coalescent histories for t is $e_{t,k}=\frac{1}{6}k(2k^2+9k+13)$ [13]. The difference eq. (8) yields that for m ≥ 1, the number of m-rooted histories of t is h_0,m = e_t,m − e_t,m−1 = m² + 2m + 1.

3.2.3 Rooted histories of t⁽ⁿ⁺¹⁾ from those of t⁽ⁿ⁾

This section introduces an operator Ω that generates the rooted histories of t⁽ⁿ⁺¹⁾ from those of t⁽ⁿ⁾. For each rooted history h′ of t⁽ⁿ⁺¹⁾, there exists exactly one rooted history h of t⁽ⁿ⁾ with h′ ∈ Ω(h). Recalling the definitions of the sets H_n,m(t) and H_n(t) of m-rooted and rooted histories of t⁽ⁿ⁾, we define Ω as follows.

Definition

Let $\mathcal{P}\left(X\right)=\{x:x\subseteq X\}$ denote the power set of set X, and fix tree t. The operator Ω is a function

$$\Omega :H_n\left(t\right)\to \mathcal{P}\left(H_{n+1}\left(t\right)\right),$$

where for a rooted history h ∈ H_n(t), Ω(h) is the set of rooted histories h′ ∈ H_n+1(t) for which the restriction of h′ to t⁽ⁿ⁺¹⁾ excluding its most basal caterpillar branch coincides with the rooted history h of t⁽ⁿ⁾.

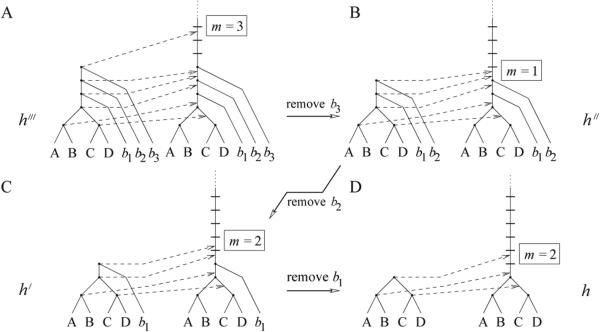
Denote by b₁, b₂, . . . , b_n+1 the caterpillar branches in t⁽ⁿ⁺¹⁾, from the least basal b₁ to the most basal b_n+1 (Fig. 5). Upon removal of the most basal caterpillar branch b_n+1 from t⁽ⁿ⁺¹⁾, the root of t⁽ⁿ⁺¹⁾—to which branch b_n+1 is attached—is replaced by a demarcation between the first and second components of the root-branch of t⁽ⁿ⁾. For instance, in Fig. 5A, starting from tree t = ((A, B), (C, D)), we consider h‴, a 3-rooted history of t⁽³⁾. By removing the most basal caterpillar branch b₃ of t⁽³⁾, we reduce to the 1-rooted history h″ of t⁽²⁾ (Fig. 5B). Next, by removing the caterpillar branch b₂ of t⁽²⁾, we reduce to the 2-rooted history h′ of t⁽¹⁾ (Fig. 5C). By removing the remaining caterpillar branch b₁ from t⁽¹⁾, we reduce to the 2-rooted history h of t = t⁽⁰⁾ (Fig. 5D). Therefore, by the definition of Ω, we have h′ ∈ Ω(h), h″ ∈ Ω(h′), and h‴ ∈ Ω(h″).

Fig. 5.

The relationships among rooted histories for sequential members of caterpillar-like families. For a rooted history h‴ of t⁽³⁾, with t = ((A, B), (C, D)), the figure sequentially removes caterpillar branches. By definition, a rooted history h′ of t⁽ⁿ⁺¹⁾ belongs to the set Ω(h) if, by removing the most basal caterpillar branch b_n+1 in t⁽ⁿ⁺¹⁾, we recover the rooted history h of t⁽ⁿ⁾. Note that when we remove the basal caterpillar branch b_n+1 from t⁽ⁿ⁺¹⁾, the root of t⁽ⁿ⁺¹⁾—to which the branch b_n+1 is attached—becomes the boundary between the first and second components of the root-branch of t⁽ⁿ⁾, and is depicted as a horizontal segment. (A) h‴ ∈ Ω(h″). (B) h″ ∈ Ω(h′). (C) h′ ∈ Ω(h). (D) h. For each rooted history, the value of the parameter m, representing the component of the root-branch that receives the image of the root, is shown.

By definition, Ω has the property that for each rooted history h′ ∈ H_n+1(t), with n ≥ 0, there exists exactly one rooted history h ∈ H_n(t) such that h′ ∈ Ω(h). In other words, for each n ≥ 0, the set of rooted histories H_n+1(t) can be partitioned as a disjoint union,

$$H_{n+1}\left(t\right)=\underset{h\in H_n\left(t\right)}{⨆}\Omega \left(h\right).$$ (11)

The set H_n+1(t) is therefore generated without double occurrences of any rooted history by applying Ω to the rooted histories in H_n(t). It follows immediately that in performing n iterations of Ω to obtain Ω[. . . [Ω[Ω(H₀)]] . . .] from the set H₀ of rooted histories of t⁽⁰⁾, all the rooted histories of t⁽ⁿ⁾ are generated exactly once.

3.2.4 Labels for rooted histories

The operator Ω, starting from the rooted histories of t⁽ⁿ⁾, generates the rooted histories of t⁽ⁿ⁺¹⁾. In this section, we introduce a labeling scheme, giving each m-rooted history h of t⁽ⁿ⁾ a label L(h) = (n, m). We then describe how Ω acts on the labels of the rooted histories, characterizing the set of labels L[Ω(h)] = {L(h′) : h′ ∈ Ω(h)}. Our goal is to represent each set H_n of rooted histories of t⁽ⁿ⁾ by the multiset of its labels, reducing the enumeration of |H_n,m| to the problem of counting certain ordered pairs (n, m) iteratively generated by simple rules that reflect how the rooted histories in H_n+1 are generated according to rule Ω from the rooted histories in H_n by eq. (11).

In our labeling, each rooted history h ∈ H_n(t) that maps the root of t⁽ⁿ⁾ onto the mth component of the root-branch of t⁽ⁿ⁾ receives label L(h) = (n, m). Enumeration of h_n = |H_n,1| then reduces to enumeration of those rooted histories labeled by (n, 1).

Note that a label (n, m) does not uniquely specify an m-rooted history of t⁽ⁿ⁾: a tree t⁽ⁿ⁾ has in general many m-rooted histories, each receiving the label (n, m). In other words, if h, h̄ ∈ H_n(t) and L(h) = L(h̄), then h and h̄ are not necessarily the same rooted history of t⁽ⁿ⁾. We will, however, consider for n ≥ 0 multisets of labels in which we find a copy of the label (n, m) for each m-rooted history of t⁽ⁿ⁾.

To characterize how the operator Ω acts on the labels for rooted histories, consider an m-rooted history h ∈ H_n(t), so that h maps the root of t⁽ⁿ⁾ onto the mth component of the root-branch of t⁽ⁿ⁾. This history is labeled L(h) = (n, m). For instance, taking the seed tree t = ((A, B), (C, D)), the history h of t = t⁽⁰⁾ depicted in Figure 6A is labeled L(h) = (0, 3), whereas the history h of t⁽¹⁾ in Figure 6C has L(h) = (1, 1).

Fig. 6.

Generation of rooted histories of t⁽ⁿ⁺¹⁾ from rooted histories of t⁽ⁿ⁾, as given by rule Ω applied to seed tree t = ((A, B), (C, D)). To obtain rooted histories of t⁽ⁿ⁺¹⁾ (right) from rooted histories of t⁽ⁿ⁾ (left), we choose the component m′ of the root-branch of t⁽ⁿ⁺¹⁾ onto which the root of t⁽ⁿ⁺¹⁾ is mapped (solid arrows). The smallest among infinitely many possible choices are depicted. For all nodes of t⁽ⁿ⁺¹⁾ except the root, the rooted history generated for t⁽ⁿ⁺¹⁾ coincides with the generating rooted history of t⁽ⁿ⁾ (dashed arrows). (A) A case with m ≥ 2. A 2-rooted history h of t⁽⁰⁾, labeled (0, 3), is shown. (B) Ω(h) for h in (A). 2-, 3-, and 4-rooted histories of t⁽¹⁾ belonging to Ω(h) are shown and are labeled (1, 2), (1, 3), and (1, 4), respectively. Because m ≥ 2, m′ ≥ m − 1 as in eq. (12). (C) A case with m = 1. A 1-rooted history h of t⁽¹⁾, labeled (1, 1), is shown. (D) Ω(h) for h in (C). 1- and 2-rooted histories of t⁽²⁾ belonging to Ω(h) are shown and are labeled (2, 1) and (2, 2), respectively. Because m = 1, m′ ≥ m.

By applying Ω to a history h of t⁽ⁿ⁾ with L(h) = (n, m), we produce a set of rooted histories Ω(h) ⊆ H_n+1(t). The set of labels for Ω(h),

$$L\left[\Omega \left(h\right)\right]=\{L\left(h^{\prime }\right):h^{\prime }\in \Omega \left(h\right)\},$$

is determined according to the rule:

$$L\left[\Omega \left(h\right)\right]=\{\begin{array}{cc}\{(n+1,m^{\prime }):m^{\prime }\ge m\}\hfill & \text{if}m=1\hfill \\ \{(n+1,m^{\prime }):m^{\prime }\ge m-1\}\hfill & \text{if}m\ge 2,\hfill \end{array}\phantom{\}}$$ (12)

where m′ denotes the value of the parameter m—the component of the root-branch of t⁽ⁿ⁺¹⁾ to which the root is mapped—for the rooted histories h′ ∈ Ω(h) of t⁽ⁿ⁺¹⁾.

The rule in eq. (12) distinguishes between two cases depending on whether the value of the parameter m = m(h) of the generating rooted history h is equal to or exceeds 1. In both cases, the set L[Ω(h)] contains infinitely many labels, each with its first component equal to n+1, as the labels refer to rooted histories of t⁽ⁿ⁺¹⁾. The value of the second component m′ ranges in [m − 1, ∞) if m ≥ 2, and in [1, ∞) if m = 1.

Recall that according to the definition of Ω, from an m-rooted history h of t⁽ⁿ⁾ (Fig. 6A and 6C), we generate an m′-rooted history h′ ∈ Ω(h) of t⁽ⁿ⁺¹⁾ (Fig. 6B and 6D) by (i) choosing the component m′ of the root-branch of t⁽ⁿ⁺¹⁾ onto which h′ maps the root of t⁽ⁿ⁺¹⁾, and (ii) letting h′ coincide with h on all nodes of t⁽ⁿ⁺¹⁾ except the root. The rooted history h′ coincides with h once we remove the most basal caterpillar branch of t⁽ⁿ⁺¹⁾.

Figure 6 illustrates both cases of eq. (12). In step (i), infinitely many choices of m′ are possible, because the root-branch of t⁽ⁿ⁺¹⁾ is divided into infinitely many parts. The most basal caterpillar branch in t⁽ⁿ⁺¹⁾ is attached at the border between the first and second components of the root-branch of t⁽ⁿ⁾. Thus, the addition of the (n + 1)st caterpillar branch eliminates a component of the root-branch, so that if the starting rooted history h has m ≥ 2 (Fig. 6A), then the root of t⁽ⁿ⁾ maps to component m − 1 of the root-branch of t⁽ⁿ⁺¹⁾. The root of t⁽ⁿ⁺¹⁾ can map to this same branch, or to any branch m′ with m′ ≥ m − 1. For instance, in Figure 6B, one of the rooted histories h′ generated by a rooted history h with m = 3 has m′ = m − 1 = 2.

If h has m = 1, however, then production of h′ is slightly different (Fig. 6C). By definition, the parameter m for a rooted history cannot be smaller than 1. The value m′ = m − 1 is not permitted, and m′ remains greater than or equal to m = 1 (Fig. 6D).

3.2.5 Counting the labels of rooted histories

The labeling scheme in Section 3.2.4 encodes the application of the operator Ω to the rooted histories of t⁽ⁿ⁾. Now that we have described the set of labels L[Ω(h)] arising from the label L(h) according to the rule in eq. (12), the problem of counting a set of rooted histories becomes a problem of counting the set of the associated labels along with their multiplicities—or the multiset of the labels.

For n ≥ 0 and m ≥ 1, we use Ω((n, m)) to denote, with an abuse of notation, the set of labels L[Ω(h)] when L(h) = (n, m). Recalling that iterative application of Ω to the rooted histories H₀ of tree t⁰⁾ generates the rooted histories H_n of t⁽ⁿ⁾, the enumeration of |H_n,m| for tree t = t⁽⁰⁾ becomes a problem of counting those labels of the form (n, m) that are generated when we iteratively apply the operator Ω as Ω[. . . [Ω[Ω(L₀)]] . . .] starting from the multiset of labels L₀ = {L(h) : h ∈ H₀(t)} (Fig. 7).

Fig. 7.

Iterative application of a rule for generating the multiset of the labels of the rooted histories of a tree t⁽ⁿ⁾. The iterative procedure starts with the multiset L₀ that contains those labels of the form {(0, m) : m ≥ 1} associated with the rooted histories of a seed tree t = t⁽⁰⁾. In the first step of the iteration, we apply Ω (eq. (13)) to each label of L₀. In the second step, we apply Ω to each label resulting from the first step, and so on. The number of m-rooted histories of t⁽ⁿ⁾ corresponds to the number of labels (n, m), considered with their multiplicity, generated after the nth step of the iteration.

Eq. (12) characterizes the set of labels L[Ω(h)] of the rooted histories in Ω(h) in terms of the label L(h) of rooted history h. If L(h) = (n, m), then Ω((n, m)) denotes the set of labels L[Ω(h)]. Thus, converting the notation from histories to labels, eq. (12) becomes

$$\Omega \left((n,m)\right)=\{\begin{array}{cc}\{(n+1,m^{\prime }):m^{\prime }\ge m\}\hfill & \text{if}m=1\hfill \\ \{(n+1,m^{\prime }):m^{\prime }\ge m-1\}\hfill & \text{if}m\ge 2.\hfill \end{array}\phantom{\}}$$ (13)

For the seed tree t, we count h_n,m = |H_n,m| by evaluating number of occurrences of the ordered pair (n, m) in the multiset L_n defined as

$$L_n=L\left[H_n\left(t\right)\right]=\{L\left(h\right):h\in H_n\left(t\right)\}.$$ (14)

In symbols, we have

$$h_{n,m}=\mid \{\ell \in L_n:\ell =(n,m)\}\mid .$$ (15)

By eq. (11), each multiset L_n is generated iteratively (Fig. 7). We start with the multiset of labels

$$L_0=\{L\left(h\right):h\in H_0\left(t\right)\}.$$ (16)

For each n ≥ 0, the multiset L_n+1 is obtained as

$$L_{n+1}=\underset{(n,m)\in L_n}{⨄}\Omega \left((n,m)\right),$$ (17)

where the symbol ⨄ denotes the union operator for multisets. Thus, in M = M₁ ⨄ M₂, if an element x appears n₁ times in M₁ and n₂ times in M₂, then it appears n₁ + n₂ times in M. Eq. (17) provides an iterative generation of the labels for the rooted histories of H_n+1(t) from the labels of the rooted histories of H_n(t), retaining information about the multiplicity of occurrences of each label.

3.3 Rooted histories and generating functions

We have now obtained eq. (15), which gives an equivalence between the number of m-rooted histories of t⁽ⁿ⁾ and the number of labels (n, m) in the multiset L_n, and eqs. (16) and (17), which give through Ω (eq. (13)) an iterative procedure that generates the family of multisets (L_n)_n≥0. In this section, we translate the iterative procedure into algebraic terms, determining the generating function associated with the integer sequence (h_n)_n≥0.

First, in Section 3.3.1, we characterize a generating function g(y) for the sequence (h_0,m)_m≥1. Next, in Section 3.3.2, we deduce an equation satisfied by the bivariate generating function F(y, z) for (h_n,m)_n≥0,m≥1. In Section 3.3.3, we solve the equation, obtaining the desired generating function f(z) for the sequence (h_n,1)_n≥0. This generating function can be written in turn as a function of g(y).

3.3.1 Generating function for (h_0,m)_m≥1

In this section, we characterize the generating function g(y) that counts for a given seed tree t the labels in the multiset L₀ describing the labels of the rooted histories of t.

Fix the seed tree t. Recalling the equivalence in eq. (15), define the generating function

$$g\left(y\right)=\sum _{(0,m)\in L_0}{y}^m=\sum _{m=1}^{\infty }{h}_{0,m}{y}^m,$$ (18)

the mth coefficient of whose power series expansion provides the number h_0,m of labels (0, m) appearing in L₀. By Proposition 1, h_0,m can be expressed as a polynomial in the variable m and can thus be decomposed as a finite linear combination of terms of the form m^k, where k is a non-negative integer. That is, for a certain finite set of non-negative integers with largest element K,

$$h_{0,m}=\sum _{k=0}^K{w}_k{m}^k,$$ (19)

where the w_k are constants.

We introduce generating functions g_m^k, one for each k from 0 to K, in which the mth coefficient is m^k:

$$g_{m^k}\left(y\right)=\sum _{m=1}^{\infty }{m}^k{y}^m.$$ (20)

Because K is finite, the desired generating function g(y) can be written as a finite linear combination of this new collection of generating functions g_m⁰ (y), g_m¹ (y), . . . , g_m^K (y). More precisely, by substituting in eq. (18) the polynomial in eq. (19) and switching the order of summation, we obtain

$$g\left(y\right)=\sum _{k=0}^K{w}_k{g}_{m^k}\left(y\right).$$ (21)

We now state a lemma that characterizes the generating functions g_m^k (y)

Lemma 1

For each non-negative integer k from 0 to K, the generating function g_m^k (y) in eq. (20) is rational with denominator (1 − y)^k+1. That is, g_m^k (y) has the form

$$g_{m^k}\left(y\right)=\frac{P\left(y\right)}{{(1-y)}^{k+1}},$$

where P(y) is a polynomial in y.

Proof

We proceed by induction on k. If k = 0, then by eq. (20), g_m⁰ (y) = 1/(1 − y)−1 = y/(1 − y). Assume the inductive hypothesis for g_m^k (y). Applying eq. (20) to g_m^k+1 (y), we can recover g_m^k+1 (y) as

$$g_{m^{k+1}}\left(y\right)=y\frac{\partial g_{m^k}\left(y\right)}{\partial y},$$ (22)

which by the quotient rule for derivatives is a rational function with denominator (1 − y)^k+2.

The proof of the lemma gives a recursive procedure in eq. (22) to compute the functions g_m^k (y). By eq. (21), we immediately obtain from the lemma a result about the generating function g(y).

Proposition 2

The generating function g(y) whose mth coefficient [y^m]g(y) is the number of m-rooted histories h_0,m of a seed tree t can be written as a finite linear combination

$$g\left(y\right)=\sum _{j=1}^J{q}_j\frac{y^{a_j}}{{(1-y)}^b},$$ (23)

where b ≥ 1 and J ≥ 1 are positive integers, each a_j is a non-negative integer, and the q_j are constants.

As an example, we show how the procedure in Proposition 2 can determine the generating function g(y) for t = ((A, B), (C, D)), the same example seed tree for which we computed the polynomial h_0,m via Proposition 1. Recall from Section 3.2.2 that h_0,m = m² + 2m + 1. To obtain the generating function g(y) that has coefficients [y^m]g(y) = m² + 2m + 1, we sum generating functions for monomials m², 2m, and 1. We already know g_m⁰ (y), and by applying eq. (22), we have

$$\begin{array}{cc}\hfill g_{m^0}\left(y\right)& =\frac{y}{1-y}\hfill \\ \hfill g_{m^1}\left(y\right)& =y\frac{\partial g_{m^0}\left(y\right)}{\partial y}=\frac{y}{{(1-y)}^2}\hfill \\ \hfill g_{m^2}\left(y\right)& =y\frac{\partial g_{m^1}\left(y\right)}{\partial y}=\frac{y(y+1)}{{(1-y)}^3}.\hfill \end{array}$$

Thus,

$$g\left(y\right)=g_{m^0}\left(y\right)+2g_{m^1}\left(y\right)+g_{m^2}\left(y\right)=\frac{y^3-3y^2+4y}{{(1-y)}^3}.$$ (24)

In eq. (24), g(y) is written as in eq. (23), taking b = 3, J = 3, (a₁, a₂, a₃) = (1, 2, 3), and (q₁, q₂, q₃) = (4, −3, 1).

3.3.2 Bivariate generating function for (h_n,m)_n≥0,m≥1

Given t, the polynomial nature of h_0,m in m enabled us to obtain a generating function for h_0,m. We now use the iterative procedure in eq. (17) to determine an equation that characterizes the bivariate generating function with coefficients h_n,m. We represent each label of the form (n, m) by a symbolic algebraic expression in the variables y and z, so that (n, m) is replaced by zⁿy^m. Let $L={\cup }_{n=0}^{\infty }{L}_n$ be the multiset of all m-rooted histories for all trees t⁽ⁿ⁾. Considering y and z as complex variables in two sufficiently small neighborhoods of 0, we aim to characterize the bivariate function F(y, z) that admits the expansion

$$F(y,z)=\sum _{(n,m)\in L}{z}^n{y}^m,$$

where the sum is over all labels in the multiset L and thus has a term for each m-rooted history of each t⁽ⁿ⁾. In particular, the function F(y, z) is the bivariate generating function of the integers h_n,m, and its Taylor expansion can be written as

$$F(y,z)=\sum _{m=1}^{\infty }\sum _{n=0}^{\infty }{h}_{n,m}{z}^n{y}^m,$$ (25)

where the coefficients h_n,m appear explicitly.

By differentiating F(y, z) with respect to y and then taking y = 0, we obtain

$$\frac{\partial F}{\partial y}(0,z)=\sum _{n=0}^{\infty }{h}_{n,1}{z}^n.$$ (26)

Thus, for each n ≥ 0, we have

$$h_n=h_{n,1}=\left[z^n\right]\left(\frac{\partial F}{\partial y}(0,z)\right).$$

By representing each label of the form (n, m) by the symbolic expression zⁿy^m and assuming the complex variables y and z are sufficiently close to 0, the recursive generation in eq. (17) of the multisets of labels L₀, L₁, L₂, . . . determines an equation for F(y, z), demonstrated in Appendix 1:

$$F(y,z)\left[1-\frac{z}{y(1-y)}\right]=g\left(y\right)-z\frac{\partial F}{\partial y}(0,z).$$ (27)

Eq. (27) holds if the complex variables y and z are in two sufficiently small neighborhoods of 0, and it characterizes the generating function F(y, z).

3.3.3 Generating function for (h_n,1)_n≥0

We now have an equation satisfied by the bivariate generating function F(y, z). Further, we have eq. (26), which demonstrates that the desired generating function for the sequence (h_n)_n≥0 is obtained from $\frac{\partial F}{\partial y}(0,z)$. By applying the kernel method [2], [12], we can determine the power series $\frac{\partial F}{\partial y}(0,z)$ from eq. (27).

The idea of the method consists of coupling the two variables (z, y) as (z, y(z)) in such a way that two conditions hold. First, (i) substituting y = y(z) cancels the kernel of the equation, that is, the factor 1−z/[y(1−y)] on the left-hand side of eq. (27). Second, (ii) for z near 0, the value of y(z) remains in a sufficiently small neighborhood of y = 0, so that eq. (27) still holds near z = 0 after substituting y = y(z). This condition is required, as the power series expansion in eq. (25) for F(y, z) has been assumed to be valid in a neighborhood of (y, z) = (0, 0), and the derivation of eq. (27) relies on the fact that y and z are sufficiently close to 0. If the two conditions hold, then

$$z\frac{\partial F}{\partial y}(0,z)=g\left(y\left(z\right)\right),$$

so that g(y(z)) must be a power series for z = 0, because so must be $z\frac{\partial F}{\partial y}(0,z)$.

The required substitution couples y and z in such a way that 1 − z/[y(1 − y)] = 0, so that $y\left(z\right)=(1\pm \sqrt{1-4z})∕2$. To determine whether to take the negative root y₁(z) or the positive root y₂(z), we note that if z is near 0, then y₁(z) approaches 0, so that y₁(z) lies in a neighborhood of y = 0 and g(y₁(z)) admits a power series expansion for z near 0. For y₂(z), however, if z is near 0, then y₂(z) approaches 1, and thus, g(y₂(z)) is not a power series for z near 0 due to the pole of the function g(y) at y = 1 (Proposition 2). The only solution satisfying both (i) and (ii) is consequently

$$Y\left(z\right)=y_1\left(z\right)=\frac{1-\sqrt{1-4z}}{2},$$ (28)

which, with the generating function C(z) of the Catalan numbers as in eq. (3), satisfies Y(z) = zC(z). Substituting y = Y(z) in eq. (27), we have $\frac{\partial F}{\partial y}(0,z)=g\left(Y\left(z\right)\right)∕z$, yielding the following result.

Proposition 3

Fix tree t. Let g(y) be the generating function associated with the polynomial h_0,m (eq. (18)). Let Y(z) be as in eq. (28). Then the generating function $f\left(z\right)={\sum }_{n=0}^{\infty }{h}_n{z}^n$ is given by

$$f\left(z\right)=\frac{\partial F}{\partial y}(0,z)=\frac{g\left(Y\left(z\right)\right)}{z}=\frac{g\left(\frac{1-\sqrt{1-4z}}{2}\right)}{z}.$$ (29)

The proposition thus determines the generating function f(z) = g(Y(z))/z for the integer sequence describing the number of matching coalescent histories of species trees in the caterpillar-like family (t⁽ⁿ⁾)_n≥0. The function g depends on the seed tree t, whereas Y(z) is fixed in eq. (28) and does not depend on t.

As an example, recall that for t = ((A, B), (C, D)), in eq. (24), we have computed the generating function g for the number h_0,m of m-rooted histories of t = t⁽⁰⁾. By Proposition 3, the generating function for the number h_n of matching coalescent histories of t⁽ⁿ⁾ is

$$\begin{array}{cc}\hfill f\left(z\right)& =\sum _{n=0}^{\infty }{h}_n{z}^n=\frac{g\left(\frac{1-\sqrt{1-4z}}{2}\right)}{z}\hfill \\ \hfill & =\frac{4(1-\sqrt{1-4z})(3-z+\sqrt{1-4z})}{z{(1+\sqrt{1-4z})}^3}.\hfill \end{array}$$

Taking the Taylor expansion of f, we obtain

$$f\left(z\right)=4+13z+42z^2+138z^3+462z^4+1573z^5+5434z^6+19006z^7+67184z^8+\dots$$ (30)

The coefficients h_n accord with the enumeration of matching coalescent histories reported in Corollary 3.9 of [13] and Table 3 of [14] for caterpillar-like families with seed tree t = ((A, B), (C, D)), except that those results tabulated numbers of coalescent histories by the number of taxa, whereas here, we use the index of the caterpillar-like family. Thus, in this example, the coefficient of zⁿ gives the number of matching coalescent histories for a tree with n+4 taxa, as |t| = 4. Shifting the index in the formula from [13], [14] to agree with our indexing scheme, we obtain [(5(n+4) − 12)/(4(n + 4) − 6)]c_(n+4)−1 = [(5n + 8)/(4n + 10)]c_n+3 for the number of matching coalescent histories of t⁽ⁿ⁾. This formula gives precisely the coefficients in the Taylor expansion in eq. (30).

3.4 Asymptotic behavior of h_n

From Proposition 3, we have the generating function f that counts matching histories of t⁽ⁿ⁾ for a given fixed seed tree t. Applying techniques of analytic combinatorics as introduced in Section 2.3, we can determine the asymptotic behavior of the coefficients of the generating function

$$\tilde{f}\left(z\right)=\sum _{n=1}^{\infty }{h}_{n-1}{z}^n=zf\left(z\right)=g\left(Y\left(z\right)\right),$$ (31)

with Y(z) as in eq. (28). To simplify notation, we work with f̃ instead of f.

First, in Section 3.4.1, we obtain an asymptotic equivalence between h_n and β_tc_n, where β_t is a constant depending on the seed tree t, and the c_n are the Catalan numbers (eq. (1)). Next, in Section 3.4.2, we produce a general procedure to determine the constants β_t, employing this procedure to obtain values of β_t for all seed trees t with |t| ≤ 9. We demonstrate that our values of β_t accord with constant multiples of the Catalan numbers previously obtained according to a different method [14] for seed trees with |t| ≤ 8.

3.4.1 A general asymptotic result

Recall that given t, Proposition 2 provides a procedure to determine the rational function g in eq. (31). Writing g as the finite linear combination in eq. (23), the values of b, J, and the (a_j)_1≤j≤J and (q_j)_1≤j≤J can all be computed.

As noted in Section 2.3, the expansion of f̃ at its dominant singularity characterizes the asymptotic behavior of the coefficients h_n−1. Appendix 2 obtains this expansion at the dominant singularity $z=\frac{1}{4}$,

$$\tilde{f}\left(z\right)={\alpha }_t+{\beta }_t\left(-\frac{\sqrt{1-4z}}{2}\right)\pm \mathcal{O}(1-4z)$$ (32)

$$\sim {\alpha }_t+{\beta }_t\left(-\frac{\sqrt{1-4z}}{2}\right),$$ (33)

with

$${\alpha }_t=\sum _{j=1}^J{2}^{b-a_j}{q}_j$$ (34)

$${\beta }_t=\sum _{j=1}^J{2}^{b+1-a_j}(a_j+b)q_j.$$ (35)

Note that in eq. (32), the seed tree affects only the constants α_t and β_t computed in eqs. (34) and (35) from g, as written in the linear combination in eq. (23). Excluding the constant α_t that does not influence the asymptotic behavior of the coefficients, the main term of the expansion of f̃(z) (eq. (33)) is the product of β_t and the generating function $-\sqrt{1-4z}∕2$, whose nth is Catalan number c_n−1 (eq. (4)).

Theorem VI.4 of [8] indicates that under conditions satisfied by f̃, the asymptotic coefficients of a generating function as n → ∞ are obtained from the expansion of the function at the dominant singularity; moreover, the error term in the asymptotic coefficients can be computed from the error term in the singular expansion. Applying the theorem to the expansion in eq. (32), we obtain the asymptotic behavior of the coefficients [zⁿ]f̃(z) = h_n−1.

Proposition 4

For any seed tree t, when n → ∞, the number h_n of matching coalescent histories for t⁽ⁿ⁾ satisfies

$$\begin{array}{cc}\hfill h_{n-1}& =\left[z^n\right]\tilde{f}\left(z\right)\sim {\beta }_t\left[z^n\right]\left(-\frac{\sqrt{1-4z}}{2}\right)\pm \mathcal{O}\left(\frac{4^n}{n^2}\right)\hfill \\ \hfill & ={\beta }_t{c}_{n-1}\pm \mathcal{O}\left(\frac{4^n}{n^2}\right),\hfill \end{array}$$ (36)

where β_t is a constant that depends on t. The constant β_t is computed in eq. (35) once the function g, defined in eq. (18), is written as the linear combination in eq. (23).

We immediately obtain the following corollary, corresponding to our initial claim in eq. (6).

Corollary 1

For any seed tree t, there exists a constant β_t > 0 (eq. (35)) such that when n → ∞,

$$h_n\sim {\beta }_t{c}_n.$$ (37)

Proof

The result follows from Proposition 4 by noting that if β_t > 0, then

$$\underset{n\to \infty }{\lim }\frac{h_{n-1}}{{\beta }_t{c}_{n-1}}=1\pm \underset{n\to \infty }{\lim }\frac{\mathcal{O}(4^n∕n^2)}{{\beta }_t{c}_{n-1}}=1.$$

Note that we are claiming β_t > 0. From the definition of β_t in eq. (35), because the q_j are permitted to be negative, it is not immediately clear that β_t > 0. Proposition 4 eliminates the possibility that β_t is negative, as h_n−1 is necessarily positive. To show that β_t ≠ 0, note that by eq. (36), β_t = 0 would give

$$h_{n-1}=\mathcal{O}\left(\frac{4^n}{n^2}\right),$$ (38)

so that h_n−1/(4ⁿ/n²) would remain bounded by a constant as n → ∞.

We now apply the lower bound h_n ≥ c_n+1 from eq. (7). By eq. (7), we have

$$\frac{h_{n-1}}{4^n∕n^2}\ge \frac{c_n}{4^n∕n^2}=\frac{\sqrt{n}}{\sqrt{\pi }}\frac{c_n}{4^n∕\left(n^{3∕2}\sqrt{\pi }\right)}.$$

As n → ∞, $\sqrt{n}∕\sqrt{\pi }$ diverges to ∞, while $c_n∕[4^n∕\left(n^{3∕2}\sqrt{\pi }\right)]$ converges to 1 by eq. (5). Therefore, the sequence h_n−1/(4ⁿ/n²) must diverge and eq. (38) cannot hold. Thus, β_t ≠ 0.

As an example of Corollary 1, consider t = ((A, B), (C, D)). By decomposing the function g of eq. (24) as in eq. (23), we have already obtained the parameters b, J, (a_j)_1≤j≤J, and (q_j)_1≤j≤J in Section 3.3.1. Therefore, computing β_t as in eq. (35), we obtain

$${\beta }_t=2^{1+3-1}(1+3)\left(4\right)+2^{1+3-2}(2+3)(-3)+2^{1+3-3}(3+3)\left(1\right)=80.$$

Eq. (37) then produces h_n ~ 80c_n. Note that the limit $h_n\sim \frac{5}{4}{c}_{n+3}$ produced for this tree from h_n = [(5n + 8)/(4n + 10)]c_n+3 in Section 3.3.3 agrees with the limiting result h_n ~ 80c_n. Recalling eq. (2),

$$\frac{h_n}{c_n}=\frac{5n+8}{4n+10}\frac{c_{n+3}}{c_n}\sim \frac{5}{4}\frac{\left(\begin{array}{c}\hfill 2n+6\hfill \\ \hfill n+3\hfill \end{array}\right)∕(n+3)}{\left(\begin{array}{c}\hfill 2n\hfill \\ \hfill n\hfill \end{array}\right)∕(n+1)}\sim \frac{5}{4}{4}^3=80.$$

3.4.2 Determining β_t from the seed tree t

We have shown in Corollary 1 that the number of matching coalescent histories h_n for the caterpillar-like family t⁽ⁿ⁾ is, for a constant β_t, asymptotic to β_tc_n. We can now assemble our results to describe a procedure that given a seed tree t with |t| ≥ 2 determines both the generating function with coefficients h_n and the constant β_t.

• (i)Determine by eq. (9) the polynomial e_t,k in k ≥ 0 that counts k-extended histories of t.
• (ii)Compute from eq. (8) the polynomial in m that counts for m ≥ 1 the number of m-rooted histories of t.
• (iii)Obtain the generating function $g\left(y\right)={\sum }_{m=1}^{\infty }{h}_{0,m}{y}^m$ with coefficients h_0,m by using Proposition 2.
• (iv)Determine the generating function $f\left(z\right)={\sum }_{n=0}^{\infty }{h}_n{z}^n$ with coefficients h_n by applying Proposition 3.
• (v)Write g(y) as a linear combination according to eq. (23), determining the values of b, J, and the a_j and q_j.
• (vi)Compute the asymptotic constant β_t from eq. (35).

We have programmed this procedure in Mathematica; starting from a given seed tree t, our program CatFamily.nb can automatically compute for the caterpillar-like family t⁽ⁿ⁾ the generating function with coefficients h_n and the asymptotic constant β_t. Using this program, we have evaluated β_t for each seed tree with 9 taxa, collecting the results in Table 1.

TABLE 1.

Asymptotic constants β_t with h_n ~ β_tc_n, for seed trees t with 9 taxa.

Seed tree t	β t	${\beta }_t^{\ast }$	Seed tree t	β t	${\beta }_t^{\ast }$
	65,536	1		128,864	$\frac{4,027}{2,048}$
	81,920	$\frac{5}{4}$		166,624	$\frac{5,207}{2,048}$
	94,208	$\frac{23}{16}$		197,296	$\frac{12,331}{4,096}$
	104,448	$\frac{51}{32}$		224,704	$\frac{3,511}{1,024}$
	138,240	$\frac{135}{64}$		308,576	$\frac{9,643}{2,048}$
	118,784	$\frac{29}{16}$		262,000	$\frac{16,375}{4,096}$
	113,408	$\frac{443}{256}$		250,272	$\frac{7,821}{2,048}$
	148,480	$\frac{145}{64}$		339,504	$\frac{21,219}{4,096}$
	177,664	$\frac{347}{128}$		417,632	$\frac{13,051}{2,048}$
	141,312	$\frac{69}{32}$		326,240	$\frac{10,195}{2,048}$
	193,536	$\frac{189}{64}$		464,128	$\frac{1,813}{256}$
	121,472	$\frac{949}{512}$		182,912	$\frac{1,429}{512}$
	157,888	$\frac{2,467}{1,024}$		243,904	$\frac{3,811}{1,024}$
	187,776	$\frac{1,467}{512}$		296,064	$\frac{2,313}{512}$
	214,720	$\frac{3,355}{1,024}$		344,512	$\frac{5,383}{1,024}$
	296,192	$\frac{1,157}{256}$		487,808	$\frac{3,811}{512}$
	251,136	$\frac{981}{256}$		410,112	$\frac{801}{128}$
	162,560	$\frac{635}{256}$		214,016	$\frac{209}{64}$
	219,136	$\frac{107}{32}$		306,112	$\frac{4,783}{1,024}$
	268,288	$\frac{131}{32}$		294,784	$\frac{2,303}{512}$
	177,664	$\frac{347}{128}$		425,216	$\frac{1,661}{256}$
	249,344	$\frac{487}{128}$		366,720	$\frac{2,865}{512}$
	353,536	$\frac{1,381}{256}$		532,224	$\frac{2,079}{256}$

Values of β_t appear for each of the 46 unlabeled species trees with 9 taxa. For each species tree t, we also provide the constant ${\beta }_t^{\ast }={\beta }_t∕4^8$ (eq. (40)). Trees are listed in increasing order by rank as defined in Section 2 of [14]. In the left column, each seed tree t belongs to a caterpillar-like family (t̃⁽ⁿ⁾)n, with |t̃| < 9. In these cases, we recover the values of ${\beta }_t^{\ast }$ as determined in Table 3 of [14].

Recall that Rosenberg [14] reported the asymptotic constant multiples of the Catalan numbers, ${\beta }_t^{\ast }$, which represent asymptotic numbers of coalescent histories for seed trees with up to 8 taxa, indexing the results by the number of taxa m rather than by the index n of the caterpillar-like family. Also recall that for seed tree t, tree t⁽ⁿ⁾ has m = |t| + n taxa (Fig. 1). In the notation of [14], writing A_tm,1 as the number of matching coalescent histories in the caterpillar-like tree with seed tree t and m ≥ |t| taxa, we have h_n = A_tm,1.

By eq. (5), we have the asymptotic equivalence c_n ~ c_n+k/4^k for each positive integer k. Therefore,

$$A_{t_m,1}=h_n\sim {\beta }_t{c}_n\sim \frac{{\beta }_t}{4^{\mid t\mid -1}}{c}_{n+\mid t\mid -1}={\beta }_t^{\ast }{c}_{m-1},$$ (39)

where the asymptotic constant β_t of Corollary 1 is normalized to obtain

$${\beta }_t^{\ast }=\frac{{\beta }_t}{4^{\mid t\mid -1}}.$$ (40)

This computation converts the asymptotic constant multiple β_t of c_n into a corresponding multiple ${\beta }_t^{\ast }$ of c_m−1, as reported in [14] for small trees. Comparing Table 1 with Table 3 of [14], we see that for the cases examined by [14], the values of ${\beta }_t^{\ast }$ we compute from the associated β_t agree with the values that were previously reported. This agreement is unsurprising; our method for calculating the constants β_t and ${\beta }_t^{\ast }$ is simply a computational implementation based on our theorems, and the agreement confirms the validity of the implementation. Although [14] considered only |t| ≤ 8, our method applies for arbitrary |t|.

Evaluation of β_t proceeds quadratically in |t|. The recursive step (i) requires at most |t| − 1 recursive calls, one for each internal node of t. Step (ii) is a polynomial subtraction at most linear in |t|, producing the polynomial h_0,m with order at most equal to the order of e_t,m minus 1—that is, at most |t| − 2. Step (iii) determines the generating function g(y) (eq. (18)) from h_0,m and the generating functions g_m^k (y) (eq. (20)). For each k with 0 ≤ k ≤ |t| − 2, g_m^k (y) is computed in k recursive calls of eq. (22). As the order of h_0,m is at most |t| − 2, the total cost for calculating g(y) is thus quadratic in |t|. Steps (iv), (v), and (vi) do not involve recursion and are at most linear in |t|. Thus, because step (iii) is the most expensive step, we see that the cost of the procedure that determines the asymptotic constant β_t increases as $\mathcal{O}\left({\mid t\mid }^2\right)$.

4 Conclusions

In this paper, we have solved a problem left open by [14] on determining the number of coalescent histories for gene trees and species trees that have a matching labeled topology and that belong to a generic caterpillar-like family. We have proven that for any seed tree t, the integer sequence (h_n)_n≥0, whose nth element represents the number of matching coalescent histories of the caterpillar-like tree t⁽ⁿ⁾, grows asymptotically as a constant multiple of the Catalan numbers, that is, h_n ~ β_tc_n, where the constant β_t > 0 depends on the shape of the seed tree t. Rosenberg [14] had previously obtained this result for seed trees with at most 8 taxa; here, by using a succession rule for recursive enumeration and then applying techniques of analytic combinatorics, we have not only proven the existence of the constant β_t for seed trees of any size, we have also produced a procedure that computes β_t as well as the expression for the generating function of the integers (h_n)_n≥0.

The numerical results on the constants β_t extend the empirical observation of [14] that the caterpillar-like families that produce the largest numbers of matching coalescent histories are those whose seed tree has a high level of balance. By extending from seed trees with |t| ≤ 8 taxa to those with |t| = 9, we observe that the constants β_t for the caterpillar-like families with the largest and smallest numbers of matching coalescent histories become further separated, so that for n large, many more coalescent histories exist by which a gene tree can match the species tree for some species trees than for others. For the 9-taxon seed tree with the largest ${\beta }_t^{\ast }$, ${\beta }_t^{\ast }\approx 8.12$ compared to ${\beta }_t^{\ast }=1$ for the seed tree with the smallest ${\beta }_t^{\ast }$. Our procedure for evaluating β_t and ${\beta }_t^{\ast }$ as a function of the seed tree can now enable further systematic analyses of the correlates of the constants β_t and ${\beta }_t^{\ast }$, to facilitate additional explorations of determinants of the numbers of matching coalescent histories.

Nevertheless, although the constants β_t and ${\beta }_t^{\ast }$ do depend on the seed tree, we have shown that otherwise, all caterpillar-like families are asymptotically equivalent in their numbers of matching coalescent histories. Computation time is often a challenge in phylogenetic problems, as the discrete structures of phylogenetics can grow rapidly in number with the number of taxa. Our results contribute to the study of computational complexity in phylogenetics, as the complexity of the evaluation of probabilities important in characterizing gene tree distributions [5] is proportional to the number of coalescent histories. That all caterpillar-like families have the same growth pattern up to a constant suggests that as the number of taxa increases, such evaluations will be comparably complex for all caterpillar-like trees. In large trees, the caterpillar branches contribute to the asymptotic growth of the number of matching coalescent histories—which follows a multiple of the Catalan numbers—and the seed tree only to the constant by which the Catalan numbers are multiplied.

The extent to which other tree families follow the Catalan sequence in their numbers of matching coalescent histories remains unknown, though we have recently found a family, the lodgepole family—defined iteratively by setting λ₀ to a tree with one taxon and sequentially forming λ_n+1 by appending λ_n and a cherry to a shared root—for which the number of matching coalescent histories grows faster than with a constant multiple of the Catalan numbers [6]. Further analysis of this heterogeneous behavior of the increase in the number of coalescent histories will be useful in performing comparisons of coalescent history algorithms with algorithms that obtain similar phylogenetic probabilities but that do not rely on coalescent histories [20]. The use of our substantially different approach employing analytic combinatorics opens new methods for theoretical analysis of coalescent histories and can potentially assist in understanding when Catalan-like growth, the rapid growth of the lodgepole family, and intermediate or perhaps still faster growth patterns will apply.

We note, however, that our strategy for evaluating the asymptotic properties of the number of coalescent histories in caterpillar-like families has, like the work of [14], relied on the fact that the difficulty of the general problem of enumerating coalescent histories is partly evaded by restricting attention to caterpillar-like trees. In the recursion for the number of coalescent histories given a matching gene tree and species tree [13, eq. 1], a term arising from the subtree with fewer branches collapses to 1 for the caterpillar case, greatly simplifying the recursion. This reduction enabled the work of [14] for caterpillar-like families, and it also enables our approach of iteratively adding single-taxon branches to define the operator Ω and the generating function h_n,m. Thus, in enumerating coalescent histories for matching lodgepole gene trees and species trees, we proceeded by a different method, establishing a bijection between coalescent histories and established combinatorial structures [6]. We do expect, however, that a generating function approach will be fruitful in other scenarios, perhaps including cases with gene trees and species trees that are caterpillar-like, but non-matching.

Biographies

Filippo Disanto received the PhD degree in theoretical computer science from both the University of Siena and the University of Paris VII in 2010. After receiving the PhD degree, he was a postdoc at CNRS in Montpellier and at the Institut für Genetik, University of Cologne. Since November 2013, he has been a postdoc in the Rosenberg Laboratory, Stanford University. His main research interests include combinatorics and its applications.

Noah A. Rosenberg received the PhD degree in biological sciences from Stanford University in 2001 and completed postdoctoral training at the University of Southern California. He was on the faculty of the University of Michigan from 2005 to 2011, and he is currently a professor in the Department of Biology at Stanford University. His research interests include human evolutionary genetics, population-genetic theory, and mathematical phylogenetics.

Appendix 1. The equation for F(y, z)

In this appendix, we complete the derivation of eq. (27) satisfied by F(y, z). In the generating function F(y, z) (eq. (25)), each monomial zⁿy^m corresponds to a label (n, m) ∈ L_n that in turn represents an m-rooted history of t⁽ⁿ⁾. Recall that the multisets of labels L₀, L₁, L₂, . . . (eq. (14)) can be iteratively generated according to eq. (17) through the operator Ω defined in eq. (13), starting from the multiset L₀. Also recall that by considering the multiset of labels $L={\cup }_{n=0}^{\infty }{L}_n$, we can write $F(y,z)={\sum }_{(n,m)\in L}{z}^n{y}^m$. We use the iterative generation of the family of multisets (L_n)_n≥0 to obtain an equation for F.

By eq. (13), for n ≥ 0 and m ≥ 2, for each occurrence in L_n of a label (n, m), a copy of each label in set

$$\Omega \left((n,m)\right)=\{(n+1,m+j):j\ge -1\}$$

belongs to the multiset L_n+1. Thus, in algebraic terms, each time that an expression zⁿy^m with n ≥ 0 and m ≥ 2 is counted in the generating function F—written zⁿy^m ∈ F in what follows—the terms $z^{n+1}{\sum }_{j=m-1}^{\infty }{y}^j$ appear in F as well. Summing over all zⁿy^m ∈ F with n ≥ 0 and m ≥ 2, we obtain

$$\sum _{z^n{y}^m\in F:n\ge 0,m\ge 2}\left(z^{n+1}\sum _{j=m-1}^{\infty }{y}^j\right)=\frac{z}{y}\sum _{z^n{y}^m\in F:n\ge 0,m\ge 2}\left(z^n{y}^m\sum _{j=0}^{\infty }{y}^j\right).$$ (41)

Similarly, for n ≥ 0 and m = 1, for each occurrence in L_n of a label (n, 1), a copy of each label in set Ω((n, 1)) = {(n + 1, j) : j ≥ 1} appears in multiset L_n+1. Thus, for each term zⁿy ∈ F, with n ≥ 0, the terms $z^{n+1}{\sum }_{j=1}^{\infty }{y}^j$ are counted in F as well. Summing these terms for all zⁿy ∈ F with n ≥ 0,

$$\sum _{z^{n}y\in F:n\ge 0}\left(z^{n+1}\sum _{j=1}^{\infty }{y}^j\right)=zy\sum _{z^{n}y\in F:n\ge 0}\left(z^n\sum _{j=0}^{\infty }{y}^j\right).$$ (42)

Notice that the sum of the expressions in eqs. (41) and (42) is the algebraic representation of the multiset of labels L \ L₀. More precisely, each term zⁿy^m ∈ F associated with a label (n, m) ∈ L_n, with n ≥ 1, is counted—and counted exactly once—in the sum of eqs. (41) and (42). Therefore, to complete the description of F, we require only those terms z⁰y^m associated with labels (0, m) ∈ L₀. These terms are represented

$$\sum _{(0,m)\in L_0}{z}^0{y}^m=\sum _{m=1}^{\infty }{h}_{0,m}{y}^m=g\left(y\right),$$ (43)

considering that $h_{0,m}=\mid \{\ell \in L_0:\ell =(0,m)\}$ (eq. (15)) and that by definition, $g\left(y\right)={\sum }_{m=1}^{\infty }{h}_{0,m}{y}^m$ (eq. (18)).

We can now equate the full generating function F(y, z) to the sum of eqs. (43), (41), and (42), obtaining

$$F(y,z)=g\left(y\right)+\frac{z}{y}\sum _{z^n{y}^m\in F:n\ge 0,m\ge 2}\left(z^n{y}^m\sum _{j=0}^{\infty }{y}^j\right)+zy\sum _{z^{n}y\in F:n\ge 0}\left(z^n\sum _{j=0}^{\infty }{y}^j\right).$$

Applying the fact that ${\sum }_{j=0}^{\infty }{y}^j=1∕(1-y)$ for y near 0 in the complex plane, we then have

$$F(y,z)=g\left(y\right)+\frac{z}{y(1-y)}\left(\sum _{z^n{y}^m\in F:n\ge 0,m\ge 2}{z}^n{y}^m\right)+\frac{zy}{1-y}\left(\sum _{z^{n}y\in F:n\ge 0}{z}^n\right).$$ (44)

By eq. (25) and the fact that the multisets L_n of labels (n, m) for m-rooted histories of t⁽ⁿ⁾ have h_n,m elements,

$$\begin{array}{cc}\hfill \sum _{z^{n}y\in F:n\ge 0}{z}^n& =\frac{\partial F}{\partial y}(0,z)\hfill \\ \hfill \sum _{z^n{y}^m\in F:n\ge 0,m\ge 2}{z}^n{y}^m& =\left(\sum _{z^n{y}^m\in F:n\ge 0,m\ge 1}{z}^n{y}^m\right)-\left(\sum _{z^{n}y\in F:n\ge 0}{z}^{n}y\right)\hfill \\ \hfill & =F(y,z)-y\frac{\partial F}{\partial y}(0,z).\hfill \end{array}$$

Substituting in eq. (44), the last two expressions yield

$$F(y,z)=g\left(y\right)+\frac{z}{y(1-y)}\left(F(y,z)-y\frac{\partial F}{\partial y}(0,z)\right)+\frac{zy}{1-y}\frac{\partial F}{\partial y}(0,z),$$ (45)

which can be rewritten as in eq. (27).

Appendix 2. The dominant singularity and singular expansion of f̃(z)

This appendix obtains the singular expansion of f̃(z) described in eq. (32). In eq. (31), we have defined f̃(z) as a composition f̃(z) = g(Y(z)), with the internal function Y(z) as in eq. (28) and the external function g(y) as in eq. (23). Owing to the presence of the square root in the expression for Y(z), the dominant singularity of the internal function Y(z)—the singularity nearest the origin of the complex plane—is at $z=\frac{1}{4}$. Computing the value of Y(z) at its dominant singularity, we obtain $Y\left(\frac{1}{4}\right)=\frac{1}{2}$. In particular, we have $Y\left(\frac{1}{4}\right)<1$, where 1 is the radius of convergence of the finite series corresponding to the external function g in f̃. Indeed, it immediately follows from Proposition 2 that y = 1 is the dominant singularity of g(y).

As detailed in Section VI.9 of [8], on dominant singularities of compositions, we are in the setting of the subcritical case, in which the inequality $Y\left(\frac{1}{4}\right)<1$ implies that the dominant singularity of g(Y(z)) coincides with the dominant singularity $z=\frac{1}{4}$ of the internal function Y(z) rather than the dominant singularity y = 1 of the external function g(y). The desired singular expansion of f̃(z) = g(Y(z)) at the dominant singularity $z=\frac{1}{4}$ can be obtained by inserting y = Y(z) in the regular (non-singular) expansion of g(y) at $y=Y\left(\frac{1}{4}\right)=\frac{1}{2}$.

To recover the expansion of g(y) at $y=\frac{1}{2}$, we expand and then sum each term q_j[y^a_j/(1 − y)^b] of the finite linear combination in eq. (23). At $y=\frac{1}{2}$, each of these terms is an analytic function, and we can thus use Taylor's formula to produce the desired expansion. We obtain at $y=\frac{1}{2}$

$$q_j\frac{y^{a_j}}{{(1-y)}^b}=2^{b-a_j}{q}_j+2^{b+1-a_j}(a_j+b)q_j\left(y-\frac{1}{2}\right)\pm \mathcal{O}\left({(y-\frac{1}{2})}^2\right).$$

By summing over the indices 1 ≤ j ≤ J of eq. (23), the expansion of g(y) at $y=\frac{1}{2}$ is

$$g\left(y\right)={\alpha }_t+{\beta }_t\left(y-\frac{1}{2}\right)\pm \mathcal{O}\left({(y-\frac{1}{2})}^2\right),$$ (46)

with the constants α_t and β_t defined as in eqs. (34) and (35). Plugging y = Y(z) from eq. (28) into eq. (46), we finally obtain the singular expansion of f̃(z) at $z=\frac{1}{4}$ as in eq. (32).