The effect of resolution on viscous dissipation measured with 4D flow MRI in patients with Fontan circulation: Evaluation using computational fluid dynamics

Abstract

Viscous dissipation inside Fontan circulation, a parameter associated with the exercise intolerance of Fontan patients, can be derived from computational fluid dynamics (CFD) or 4D flow MRI velocities. However, the impact of spatial resolution and measurement noise on the estimation of viscous dissipation is unclear. Our aim was to evaluate the influence of these parameters on viscous dissipation calculation. Six Fontan patients underwent whole heart 4D flow MRI. Subject-specific CFD simulations were performed. The CFD velocities were down-sampled to isotropic spatial resolutions of 0.5 mm, 1 mm, 2 mm and to MRI resolution. Viscous dissipation was compared between (1) high resolution CFD velocities, (2) CFD velocities down-sampled to MRI resolution, (3) down-sampled CFD velocities with MRI mimicked noise levels, and (4) in-vivo 4D flow MRI velocities. Relative viscous dissipation between subjects was also calculated. 4D flow MRI velocities (15.6±3.8 cm/s) were higher, although not significantly different than CFD velocities (13.8±4.7 cm/s, p=0.16), down-sampled CFD velocities (12.3±4.4 cm/s, p=0.06) and the down-sampled CFD velocities with noise (13.2±4.2 cm/s, p=0.06). CFD-based viscous dissipation (0.81±0.55 mW) was significantly higher than those based on down-sampled CFD (0.25±0.19 mW, p=0.03), down-sampled CFD with noise (0.49±0.26 mW, p=0.03) and 4D flow MRI (0.56±0.28 mW, p=0.06). Nevertheless, relative viscous dissipation between different subjects was maintained irrespective of resolution and noise, suggesting that comparison of viscous dissipation between patients is still possible.

1. Introduction

Hypoplastic left or right heart syndrome is among the most severe congenital heart diseases, typically requiring multiple successive surgical interventions to reconstruct the cardiovascular system into a single ventricle physiology (Gewillig, 2005). The final surgical procedure creates the total cavo-pulmonary connection (TCPC), also known as Fontan circulation, which results in systemic venous return being supplied directly to the lungs through the pulmonary arteries without passing through the right ventricle (Khairy et al., 2007). Although advances in surgical procedures and treatment have significantly improved life expectancy of these patients, long term drawbacks such as exercise intolerance exist. Recent studies have suggested that limited exercise tolerance of Fontan patients might be associated with complex flow patterns and specifically elevated viscous dissipation inside the Fontan connection (Whitehad et al., 2007). Khiabani et al. (2014) reported an inverse relationship between viscous dissipation and oxygen consumption during exercise in a cohort study of 32 Fontan patients. Haggerty et al. (2014) showed an inverse relationship between viscous dissipation and systemic venous flow and cardiac index in a cohort study of 100 Fontan patients. These results suggest that the ability to directly measure viscous dissipation in-vivo might shed extra light on Fontan function and risk for impaired outcome in these patients.

Typically, viscous dissipation is calculated by solving the mechanical energy balance equation (Bossers et al., 2014; Itatani et al., 2011). This approach requires pressure, which is determined either by invasive measurements or computational fluid dynamics (CFD) simulations. Patient specific CFD simulations have been used in a number of studies to derive viscous dissipation and have provided a better understanding of the impact of the individual Fontan geometry on Fontan hemodynamics (Baretta et al., 2011; Bove et al., 2007; de Leval et al., 1996; Dubini et al., 1996; Itatani et al., 2009; Sundareswaran et al., 2012). However, CFD relies on the accurate definition of geometric and in-flow boundary conditions and requires non-clinical expertize, engineering tools, powerful computer systems and extensive computational time. Due to these requirements and limitations, it is challenging to include CFD in routine clinical practices. Alternatively, viscous dissipation can be calculated using the viscous term of the Navier–Stokes equation (Barker et al., 2014; Venkatchari et al., 2007). This approach bypasses the need for the pressure and requires only the blood flow velocities inside the TCPC, which can be non-invasively obtained in-vivo by 4D flow MRI (time-resolved 3D phase contrast MRI with 3-directional velocity encoding) (Markl et al., 2011; Sundareswaran et al., 2008). However, the 4D flow MRI based velocities are expected to result in lower viscous dissipation since the dissipation term involves spatial derivatives of the velocity field and the low spatial resolution of MR images causes under-estimation of the spatial derivatives. Nevertheless, we hypothesize that MRI based viscous dissipation might still be sufficient to detect the cases with relatively high viscous dissipation which is clinically important.

In this study, we firstly aim to analyze the effect of resolution and noise of the velocity field on the estimated viscous dissipation of Fontan patients. In order to study the effect of spatial resolution, we performed subject specific CFD simulations and we generated MRI-like data by down-sampling the CFD velocities to different resolutions. Secondly, we aim to compare patient-specific 4D flow MRI and CFD based viscous dissipation. We compared four results obtained with: (1) CFD velocities at high resolution, (2) CFD velocities down-sampled to MRI resolution, (3) down-sampled CFD velocities with subject-specific noise added posteriori, (4) in-vivo 4D flow MRI velocities.

1.1. Theory

The viscous dissipation per unit volume can be calculated by the associated term of the Navier Stokes equation in laminar flow regimes

$${\Phi }_{VD}=\frac{1}{2}\mu \sum _i\sum _j{\left[\left(\frac{\partial v}{\partial x_i}+\frac{\partial v}{\partial x_j}\right)-\frac{2}{3}(\Delta \cdot v){\delta }_{ij}\right]}^2$$ (1)

where Φ_VD is viscous dissipation per unit volume based on viscous dissipation term and μ is the dynamic viscosity. δ_ij = 1 for i=j and δ_ij = 0 for i≠j, i and j are the principal directions x, y, z (Bird et al., 1960). Eq. (1) consists of dynamic viscosity and the spatial derivatives of velocity field. Viscous dissipation per unit volume can therefore be calculated by Eq. (1) if velocity field is known, e.g. by 4D flow MRI measurements. Total viscous dissipation is calculated by the integral of unit viscous dissipation (Eq. (1))

$$\int {\Phi }_{VD}dV=\sum _{i=1}^{\text{num voxels}}{\Phi }_{VD}{V}_i$$ (2)

2. Methods

2.1. Study cohort and MR imaging

Six Fontan patients underwent MRI scans (ages: 9–21 years, gender: 5 male, operation type: 4 extra cardiac conduit and 2 lateral tunnel) with coverage of the heart and great arteries using a 1.5 T system (Avanto or Aera, Siemens, Germany). ECG synchronized and diaphragm navigator gated 4D flow MRI was performed during free breathing. All data were acquired with three directional velocity encoding (3D spatial resolution: 1.9–2.5 × 1.9–2.5 × 2.2–3.3 mm³, temporal resolution: 38.4–41.6 ms, venc: 100–150 cm/s, TE: 2.4–2.7 ms, TR: 4.8–5.2 ms, flip angle: 15°). The scan time was in the range of 6 to 12 min including the navigator gating efficiency. All scans were performed using navigator respiration gating with scan efficiencies ranging from 60–80% and with accelerated imaging. Four scans were performed using regular GRAPPA with acceleration factor of R=2 and k–t GRAPPA (R=5) was available for the last two scans. Post-processing of 4D flow MRI data included corrections for Maxwell terms, eddy current induced phase off-sets, and velocity aliasing (Bernstein et al., 1998; Bock et al., 2007; WalkerPG et al., 1993). The study was approved by our local Institutional Review Board and informed consent was obtained from all participants or their parents.

2.2. Segmentation and meshing

3D segmentation of the Fontan geomety was performed manually on the time-averaged magnitude images using an open source segmentation tool, ITK-SNAP (Yushkvich et al., 2006). The segmentations included inferior vena cava (IVC), superior vena cava (SVC) and left and right pulmonary arteries (LPA and RPA) with the segmental branches excluded. The segmentations were then converted into volumetric meshes of tetrahedral elements using GAMBIT. The mesh size of 0.6 mm was chosen after performing a mesh independency study using a generic t-shape model.

2.3. CFD simulations

All CFD simulations were performed using the commercial finite element software FIDAP V.8.7.4 (ANSYS) on a standard desktop computer (Intel Xeon six core processor, 2.40 GHz CPU and 12 GB RAM). Time resolved IVC, SVC, LPA and RPA flows were calculated at the inlets and outlets of the geometry using 4D flow MRI measurements. The LPA and RPA flows were corrected to match inflow (sum of IVC and SVC flows) while maintaining their split ratio. IVC, SVC and RPA velocity profiles were preserved and used as boundary conditions in CFD simulations. LPA boundary was left as stress free. The walls were assumed as rigid and no-slip condition was prescribed. Blood density was assumed to be 1.06 g/cm³ and viscosity was assumed to obey the Carreau–Yasuda model (Seo et al., 2005). For the simulations, we chose a pressure-based segregated algorithm and the backward Euler method for time integration. The convergence criterion was set to 0.1%. Time resolved CFD simulations were performed for 2 cardiac cycles with time intervals of 3 ms. The results of the 2nd cardiac cycle were analyzed. The Reynolds number at the inlets and outlets was 165±77.

2.4. Down-sampling velocities

Firstly, the velocities obtained from CFD were mapped into equally sized voxels of 0.1 mm, followed by 3D convolution integration with a 3D Gaussian operator (Casas et al., 2015; Morbiducci et al., 2012). Finally, down-sampled velocities were obtained by averaging the high resolution velocities within the voxels of the down-sampled grid (Cibis et al., 2014).

2.5. Viscous dissipation calculations

We calculated viscous dissipation by using Eqs. (1) and (2) at the time point with highest inflow (sum of IVC and SVC flows). The down-sampled viscous dissipation was calculated at isotropic resolutions of 0.5 mm, 1.0 mm, 2.0 mm and at patient-specific MRI resolution. The subject specific noise, which was defined as the standard deviation of measured velocities in static regions, was added to the velocities down-sampled to MRI resolution and down-sampled viscous dissipation was calculated also after adding noise.

2.6. Analysis

The down-sampled viscous dissipations obtained with down-sampled CFD velocities were quantified. The velocity and the viscous dissipation fields were only qualitatively compared with the maximum intensity projection (MIP) visualization. We compared the mean velocity and the viscous dissipation obtained from (1) CFD velocities at resolution of 0.1 mm, (2) the CFD velocities down-sampled to MRI resolution, (3) the down-sampled CFD velocities with added noise and (4) the patient-specific 4D flow MRI velocities. Relative viscous dissipation of each subject was also calculated by dividing viscous dissipation by the mean viscous dissipation of all subjects.

All numbers were reported as mean±standard deviation. Differences between CFD and 4D flow MRI derived findings were analyzed using the Wilcoxon signed rank test, p < 0.05 was considered statistically significant.

3. Results

The CFD based viscous dissipation at resolution of 0.1 mm and the down-sampled viscous dissipation obtained with the CFD velocities down-sampled to the resolutions of 0.5 mm, 1.0 mm and 2.0 mm are shown in Fig. 1. CFD based viscous dissipation was 0.81±0.55 mW and down-sampled viscous dissipation was 0.60±0.41 mW at resolution of 0.5 mm, 0.45±0.30 mW at resolution of 1.0 mm and 0.27±0.19 mW at resolution of 2.0 mm.

Fig. 1.

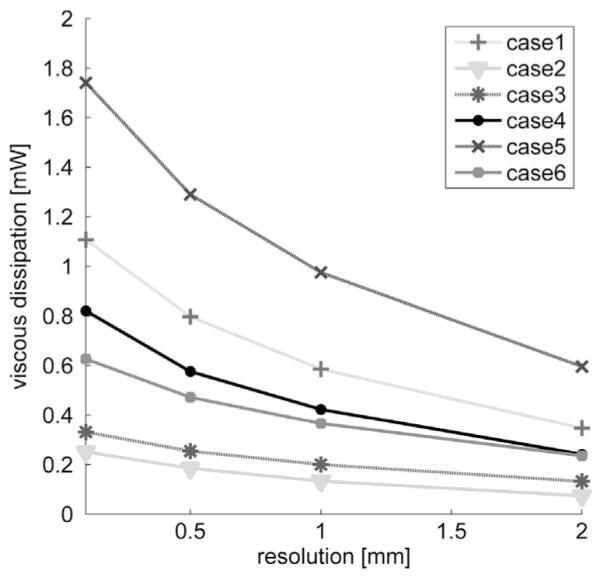
Viscous dissipation calculated with the CFD velocities at resolution of 0.1 mm and with the CFD velocities down-sampled to isotropic resolutions of 0.5 mm, 1.0 mm and 2.0 mm.

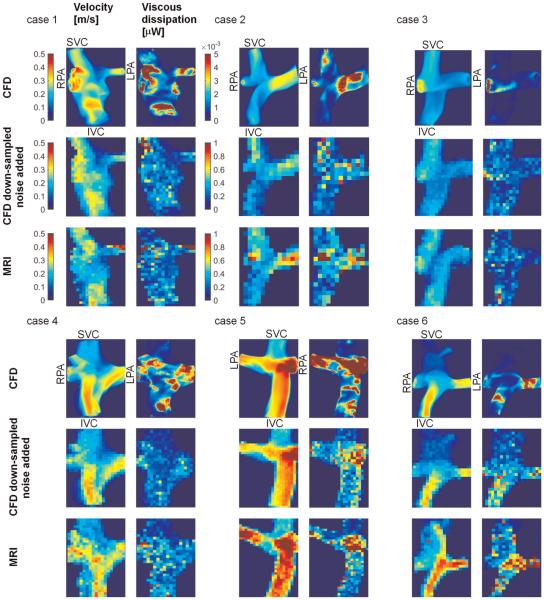
MIPs of the 3D velocity and viscous dissipation fields of all six Fontan cases are shown in Fig. 2. Blood flow velocities were generally lower and more uniform in the SVC, while higher velocities were found in the IVC and pulmonary arteries. In addition, high velocities and velocity gradients were observed in the Fontan junctions. Viscous dissipation was found to be larger in the junction and the pulmonary arteries due to colliding IVC and SVC flows and thus complex flow patterns. The velocity and viscous dissipation patterns were generally in good agreement between CFD and 4D flow MRI based results although discrepancies were observed in some cases.

Fig. 2.

MIP of velocity (Left) and viscous dissipation (Right) fields obtained by CFD, down-sampled CFD with added noise and 4D flow MRI are shown for each subject. The color-maps given for case 1 are valid for all subjects. Note that the color-map scale of CFD-based viscous dissipation was 200 times smaller than others since the volume of the voxels in CFD was ~1000 times smaller than those in MRI. Hence viscous dissipation per voxel was also smaller.

Velocity and viscous dissipation averaged over the Fontan connection for all subjects are shown in Fig. 3. The 4D flow MRI measured velocities (15.6±3.8 cm/s) were higher although not significantly different than the CFD based velocities (13.8±4.7 cm/s, p=0.16), down-sampled CFD based velocities (12.3±4.4 cm/s, p=0.06) and the down-sampled CFD velocities with noise (13.2±4.2 cm/s, p=0.06). Viscous dissipation based on CFD velocities (0.81±0.55 mW) was significantly higher than others. Down-sampling CFD velocities resulted in significant underestimation of viscous dissipation (0.25±0.19 mW, p=0.03). Adding noise increased viscous dissipation in down-sampled CFD (0.49±0.26 mW, p=0.03), but the values remained lower than 4D flow MRI derived findings (0.56±0.28 mW, p=0.06). Despite differences in magnitude of viscous dissipation, no significant difference was found between relative viscous dissipations calculated with CFD, down sampled CFD with and without noise and MRI velocities (p=0.56). Relative viscous dissipation changed by 0±29% between high resolution CFD and MRI based calculations. Relative viscous dissipation of all subjects calculated by 4 velocity types is shown in Fig. 4.

Fig. 3.

Mean velocity [cm/s] (left) and viscous dissipation [mW] (right) by using velocities of CFD, down-sampled CFD velocities without noise (CFDd), down-sampled CFD velocities with noise added (CFDd + noise) and MRI measurements.

Fig. 4.

Relative viscous dissipation [%] per subject calculated using CFD velocities, down-sampled CFD velocities without noise (CFDd), down-sampled CFD velocities with noise added (CFDd + noise) and MRI measurements.

4. Discussion

The aim of our study was to investigate the influence of resolution and noise of 4D flow MRI velocities on in vivo viscous dissipation. The effect of spatial resolution of 4D flow MRI was studied by down-sampling patient-specific CFD simulations and creating MRI-like data instead of performing MRI measurements at several resolutions. This was necessary since in vivo MRI scans at different resolutions were not feasible due to long scan times required for 4D flow MRI.

Down-sampling the velocities resulted in lower viscous dissipation and we found a nonlinear inverse relationship between spatial resolution and the estimated viscous dissipation. The viscous dissipation calculated with CFD velocities at resolution of 0.1 mm was 66±4% larger than that based on CFD velocities down-sampled to the isotropic resolution of 2 mm. This large underestimation of viscous dissipation was due to the complex flow and larger velocity gradients which were missing after down-sampling. The effect of down-sampling on viscous dissipation was however very consistent for all patients. Adding noise to the down-sampled velocities caused an increase in the estimated viscous dissipation due to increase in spatial gradients around noisy data. While lowering the resolution decreased the magnitude of estimated viscous dissipation, we set out to understand if relative relationships between subjects were retained. Regardless of measurement noise and spatial resolution, the relative viscous dissipation between subjects was obtained similarly by the CFD and MRI based calculations. This was due to the fact that CFD and MRI based velocity patterns and the regions of high and low velocity gradients were mostly in good agreement.

At peak flow, the mean of the Reynolds numbers at inlet and outlets was 165±77 which is much lower than Reynolds numbers that would cause transition to turbulence. Therefore, use of viscous dissipation term of the Navier–Stokes equations was possible.

Although not significant, the MRI-based mean velocity was higher than that based on CFD in five out of six cases. We imposed MRI measured velocities as boundary conditions for CFD and we preserved the velocity profile as measured by 4D flow MRI. After imposing velocities, we forced the velocities at near wall elements to zero to satisfy no-slip boundary condition which reduced the mean of the velocities within the volume resulted in deviations between MRI and CFD based mean velocities.

The accuracy of the velocities measured by 4D flow MRI and consequently the accuracy of the estimated viscous dissipation were influenced by the magnitude of velocities and the venc defined. Since there is a linear relationship between magnitude of velocity and the velocity to noise ratio (VNR), the higher velocities were expected to be more accurate. One can therefore expect that the estimated unit viscous dissipation is more accurate at regions of higher velocities.

The study of Venkatachari et al. (Sutera and Skalak, 1993) was the first to calculate viscous dissipation in experimental phantoms using the viscous dissipation term of the Navier Stokes equation with velocities measured by MRI. Barker et al. (2014) conducted a study to obtain in vivo viscous dissipation by viscous dissipation term of the Navier Stokes equation in patients with aortic diseases but the results were not validated. To our knowledge our study is the first that investigates in-vivo viscous dissipation based on MRI and CFD and verifies the potential of MRI-based viscous dissipation calculation in detecting the cases with high viscous dissipation.

The viscous dissipation inside Fontan circuit varies within a wide range of values depending on many parameters such as the age of the subject, amount of blood flow, the operation type, and size of the conduit (Bossers et al., 2014). Most of the viscous dissipation values calculated in our study were within the range of the values reported in the literature. In the study of Bossers et al., they calculated losses under simulated exercise which increases blood flow and causes higher viscous dissipation in the range of 0.6–7.7 mW in their recent study which they also excluded segmental branches. Other studies reported 5–10 times larger viscous dissipation (Marsden et al., 2007; WalkerPG et al., 1993) since they included segmental branches.

In this study, our intention was not to perform PC-MRI simulations by solving the Bloch equations (Casas et al., 2015). Instead we generated PC-MRI like data to study the effect of resolution and noise by mimicking MRI velocities by down-sampling the velocities to lower resolutions and adding subject-specific noise.

This study is clearly limited by the small size but the primary purpose was to understand the impact of imaging parameters and methodological approach played in the computation of viscous dissipation. Secondly, the patient data was collected at different spatial resolutions but ideally the data should have been collected with the same resolution. Also of note, is that the segmentations were performed using time-averaged images and wall motion was neglected. Furthermore, Venc was sub-optimally chosen being two times higher than the maximum velocity inside the Fontan circulation to measure velocities inside heart and aorta and thereby resulting in a lower signal to noise ratio.

4.1. Clinical implications

Viscous dissipation inside TCPC has been of interest since it is related to TCPC resistance and contributes to the limited outcome of these patients. Gathering information on viscous dissipation might therefore be useful for clinical assessment of Fontan patients. Calculation of viscous dissipation by using 4D flow MRI velocities is straightforward hence easily applicable to the clinical routine. The main drawback of using 4D flow MRI is that it causes underestimation of the magnitude of viscous dissipation. One remedy might be increasing the spatial resolution of MRI measurements which would increase the scan time. Despite under-estimation of viscous dissipation due to resolution, when CFD and MRI based results were compared, relative viscous dissipation between subjects remained the same. These results suggest that although the magnitude of viscous dissipation might be difficult to ascertain accurately, Fontan circuits with comparable or elevated viscous dissipation can still be captured by using an approach which employs MRI velocities. Therefore, use of viscous dissipation term and MRI velocities at low resolution can still lead to valid conclusions in comparative studies which make use of similar image resolution.

The MRI based viscous dissipation can be used in the clinics only after a large number of reference datasets are obtained by using a consistent protocol and a clear connection with exercise capacity of Fontan patients is shown as was observed by Khiabani et al. (2014). Therefore, more clinically oriented studies have to be performed which involve the assessment of exercise capacity of Fontan patients and the down-sampled viscous dissipation within a larger patient population to set a threshold value for clinical decision making.

5. Conclusion

In this study, viscous dissipation was calculated using the viscous dissipation term of the Navier–Stokes equation. This approach has the advantage of bypassing the need for pressure, since it requires information only on the velocity field. However, the trade-off is that the estimated viscous dissipation is low if the spatial resolution of the velocity field is low, such as in 4D flow MRI measurements. Nevertheless, we found that the ranking of patient-specific viscous dissipation was retained within the patient group at different spatial resolution of the velocities and also after noise added. We therefore suggest that the subjects with elevated viscous dissipation can be detected by 4D flow MRI based viscous dissipation calculations despite underestimation of the magnitude of viscous dissipation.

Abbreviations

TCPC

Total cavo-pulmonary connection

CFD

Computational fluid dynamics

IVC

Inferior vena cava

SVC

Superior vena cava

LPA

Left pulmonary artery

RPA

Right pulmonary artery

TR

Repetition time

TE

Echo time

Venc

Velocity encoding

MEB

Mechanical energy balance

VNR

Velocity to noise ratio