The Cation–π Interaction in Small-Molecule Catalysis

Abstract

Catalysis by small molecules (≤ 1000 Da, 10⁻⁹ m) capable of binding and activating substrates via attractive, noncovalent interactions has emerged as an important approach in organic and organometallic chemistry. While the canonical noncovalent interactions—including hydrogen-bonding, ion-pairing, and π-stacking—have become mainstays of catalyst design, the cation–π interaction has been comparatively underutilized in this context since its discovery in the 1980s. However, like a hydrogen bond, the cation–π interaction exhibits a typical binding affinity of several kcal/mol with substantial directionality. These properties render it attractive as a design element for the development of small-molecule catalysts, and in recent years, the catalysis community has begun to take advantage of these features, drawing inspiration from pioneering research in molecular recognition and structural biology. This review surveys the burgeoning application of the cation–π interaction in catalysis.

Graphical Abstract

This minireview discusses the burgeoning role of the cation–π interaction in small-molecule catalysis of organic and organometallic reactions. Here, an extensive survey of the state-of-the-art research emphasizes how unexpected discoveries and systematic mechanistic studies have begun to enable rational application of the cation–π interaction in catalyst design.

1. Introduction

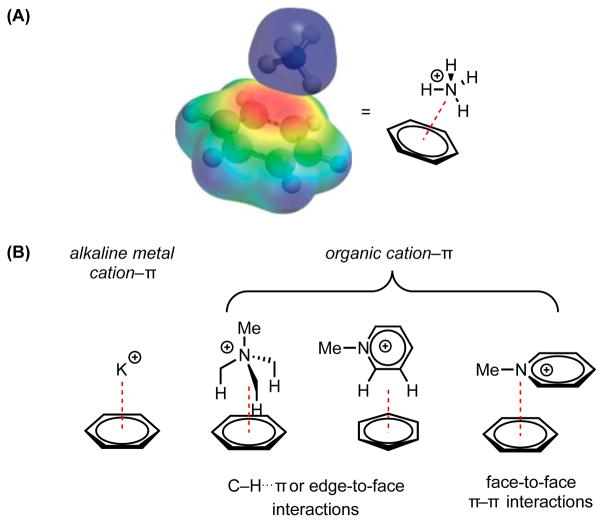
The cation–π interaction is a noncovalent attractive force between an electron-rich π-system (e.g. benzene, ethylene, acetylene) and a proximal cation (e.g. Na⁺, NBu₄⁺) (Figure 1).^[1] Since its discovery in the 1980s,^[2] experimental and computational methods have been applied to quantify and further understand the basis for and magnitude of this interaction in both gas and condensed phases.^[3] In this vein, the early discovery that a molecule of benzene could out-compete water to bind K⁺ in the gas phase—the association enthalpy of K⁺ and benzene being 19 kcal/mol while that of K⁺ and water is 18 kcal/mol—was particularly noteworthy.^[2a],[4]

Figure 1.

The cation–π interaction. (A) Molecular electrostatic potential surface (negative potential in red, positive in blue) illustrating the electrostatic basis for a cation–π interaction between benzene and an ammonium cation. Adapted with permission from ref. 1c. Copyright 2013 American Chemical Society. (B) Examples of different interaction modes available to small-molecule systems engaging in cation–π interactions (red dotted lines).

The thermodynamic features of this attractive interaction have also been studied in solution.^[5] While the strengths of cation–π interactions are attenuated in solution relative to the gas phase, they are of comparable magnitude to other critically important, strong, noncovalent interactions—including hydrogen bonds and ion pairs.^[6] The significant binding energy is primarily attributed to the electrostatic attraction of a cation to an electron-rich π-face,^[7] while dispersion and charge-transfer terms are proposed to play contributing roles.^[8] Furthermore, the cation–π interaction exhibits a high degree of directionality, wherein the cation has a pronounced energetic preference for resting directly over the centroid of the π-system, thereby maximizing charge and orbital interaction.^[5f],[9]

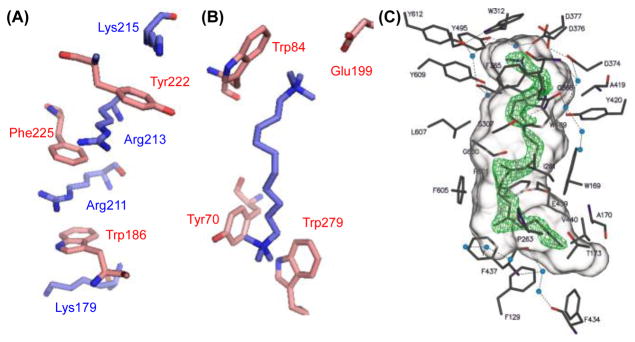
The impact of these seminal studies on the field of structural biology was rapid and significant. A host of examples of the cation–π interaction in biological macromolecules, such as protein-based receptors and enzymes, have been documented.^[10] This ongoing work provides much of the framework for understanding how cation–π interactions can serve structural and functional roles, as these interactions are typically found to be responsible for either: a) controlling protein conformation to generate a ligand- or substrate-binding site (as in Figure 2A),^[11] or, b) aiding recognition and binding of a ligand or substrate molecule in such an active site (as in Figure 2B).^[12] In the latter case, the cation–π interactions exerted by an enzyme can also stabilize a transition state relative to its precursor resting ground state, imparting rate acceleration and kinetic control of selectivity in a chemical transformation (as in Figure 2C).^[13]

Figure 2.

Examples of cation–π interactions in biological systems. (A) Extended cation–π interactions in the human growth hormone receptor extracellular domain (ref. 11e). (B) Crystal structure of acetylcholine esterase bound to a bis “quat” salt (ref. 12a). (C) Crystal structure of squalene-hopene cyclase bound to a transition state analog for the cationic polycyclization of squalene. Adapted with permission from ref. 13e. Copyright 2004 Elsevier.

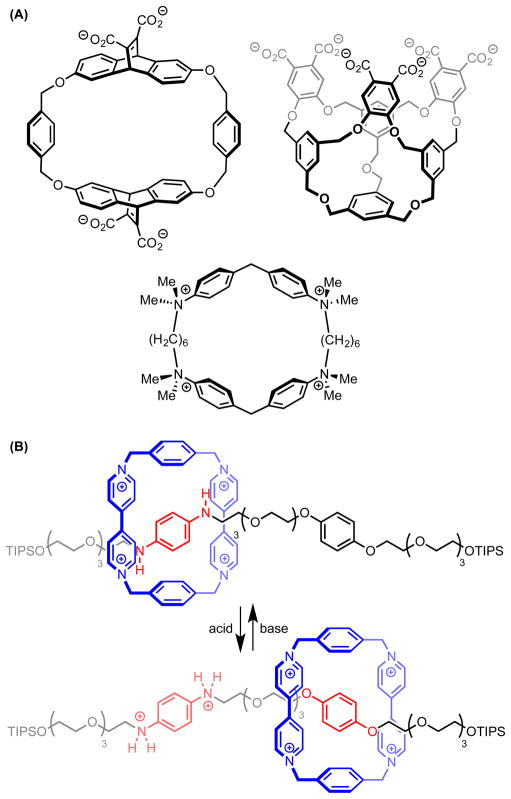
Both the fundamental studies on the thermodynamics of the cation–π interaction and the growing documentation of its importance in biological systems helped frame the potential for its application as a design element in synthetic chemistry.^[14] Recognizing that the complementary strength and directionality of the cation–π interaction could drive association of small molecules into organized assemblies, researchers sought to utilize this attractive interaction for molecular recognition,^[15] crystal engineering,^[16] and materials design.^[17] As a result, many of the early insights into the nuances of the cation–π interaction arose from work in these fields (Scheme 1).^[18]

Scheme 1.

Cation–π interactions in molecular recognition. (A) Select small-molecule cation acceptors (ref. 15a–c). (B) A switchable molecular shuttle based on cation–π interactions (ref. 15d). TIPS = triisopropylsilyl.

The thorough characterization of the cation–π interaction in enzymatic function and molecular recognition served to lay the foundation for its incorporation into the mechanistic understanding and design of small-molecule catalysts for organic synthesis.^[1],[13] In this review, we analyze the burgeoning role of the cation–π interaction in small-molecule catalysis, placing particular emphasis on elucidation of the mechanisms by which such interactions govern the reactivity and/or selectivity of reactions. The well-established area of cationic transition metal π-complexes will not be included,^[19] since the transition metal–π interaction possesses significant covalent character that renders it distinct from the noncovalent cation–π interaction. The systems described here are organized into three categories based on the role of the cation–π interaction(s):

1. Substrate–substrate cation–π interactions enable organization of the reacting components. These interactions may occur intermolecularly to arrange multiple reacting partners relative to each other or intramolecularly to dictate substrate conformation. In this scenario, the catalyst does not engage directly in the cation–π interaction.

2. Catalyst–catalyst cation–π interactions control catalyst conformation. The intramolecular cation–π interaction between different motifs within a catalyst can help define the specific three-dimensional structure responsible for catalyst function. The cationic component in such an interaction may be native to the catalyst structure or may result from formation of a covalent adduct with the substrate. In general, these intra-catalyst cation–π interactions are analogous to those that influence biological macromolecule tertiary structures, as noted above.

3. Catalyst–substrate cation–π interactions enhance the association of a catalyst with its substrate. These intermolecular interactions may exist in the ground state of a reactant–catalyst complex, or may serve to stabilize the transition structure of a reaction preferentially. These interactions may be further categorized as those in which the catalyst serves as: a) the π-acceptor (i.e. the cation) or, b) the π-donor. Cation–π interactions of this type are again analogous to enzyme active site interactions identified in biological systems.

2. Substrate–Substrate Cation–π Interactions

Organic small molecules bearing both a cationic component and a neutral aromatic residue tend to pack in the solid state with the two motifs in close spatial proximity.^[20] The cation–π interactions governing such packing can occur either between neighboring molecules or in an intramolecular fashion. This type of preorganization has been exploited to enable regioselective bond-formation in solid-phase reactions.^[21] While similar principles can be engineered into solution-phase reactions, the cation–π interactions driving selective substrate preorganization must compete effectively with solvation effects. This section reviews the application this approach in solution-phase small-molecule catalyzed or promoted reactions.

2.1 Intramolecular Cation–π Interactions

Lewis Acid-Promoted, Regioselective Schmidt Annulation Reactions

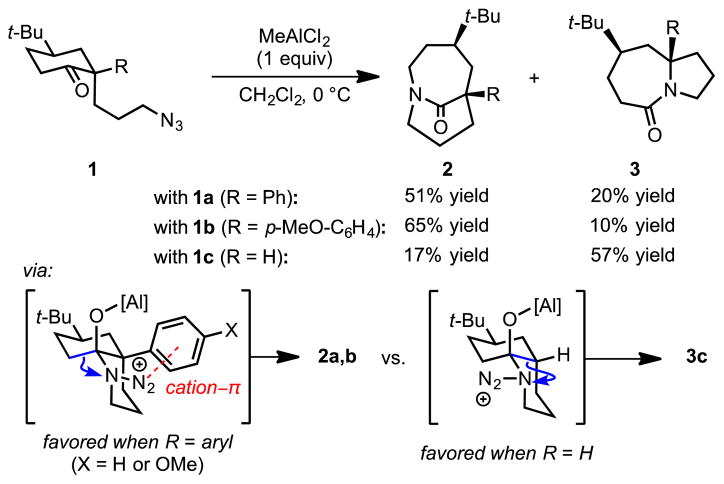
Bridged bicyclic lactams bearing bridgehead nitrogen atoms are of considerable synthetic and structural interest due to the exceptional reactivity of the distorted amide functionality.^[22] In an elegant approach to accessing these motifs, Aubé and coworkers developed a Lewis acid-promoted method for the intramolecular Schmidt reaction of alkyl azide-substituted cyclohexanones (1).^[23] As depicted in Scheme 2, alkyl azide addition to the activated carbonyl is followed by C–C bond migration to afford either of two constitutional isomers: bridged bicyclic lactam 2, or fused bicyclic lactam 3.

Scheme 2.

Lewis acid-promoted regioselective Schmidt annulation reactions. Blue arrows indicate C–C bond migration. The red dotted line indicates a cation–π interaction.

For 4-tert-butyl-substituted cyclohexanones, which react through a locked trans-decalin-like conformation, the regioselectivity of bond-migration was shown to be controllable through careful substrate design. A π-system installed at the α-position (as in 1a and 1b) is appropriately situated to stabilize the intermediate placing the diazonium cation in the axial position via a cation–π interaction. Vicinal C–C bond-migration from this conformation yields the desired bridged product (2). However, an unsubstituted substrate (1c), which lacks the potential to engage in this cation–π interaction, reacts to form predominantly the fused byproduct (3). Computational investigation of this system using Density Functional Theory (DFT) corroborated the importance of such cation–π interactions in controlling the regioselectivity of the bond-migration step.^[24]

Lewis Acid-Promoted, Diastereoselective Schmidt Ring-Expansion Reactions

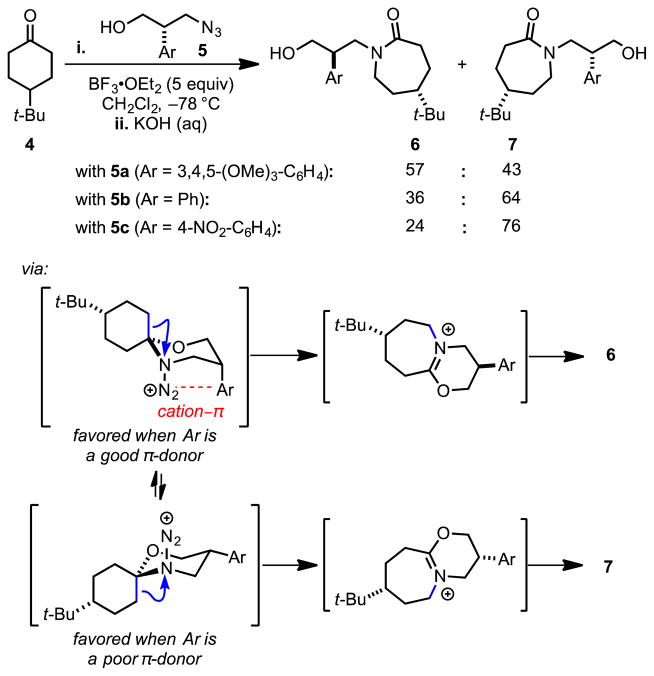
Aubé and coworkers extended this strategy with a detailed study of the Lewis acid-promoted diastereoselective Schmidt-type ring expansion of 4-tert-butyl-cyclohexanone (4) to form seven-membered lactams (6 and 7, Scheme 3).^[25] In this transformation, the oxocarbenium ion intermediate formed from the condensation of 4 and chiral hydroxyalkyl azide 5 undergoes nucleophilic attack by the pendant azide to form either of two diastereomeric diazonium ion intermediates. Only one of the two situates the diazonium ion in a position to engage in a cation–π interaction with the aryl group. This interaction stabilizes the diazonium ion in an otherwise unfavorable axial conformation, from which C–C bond-migration affords diastereomer 6. Ring expansion from the equatorial conformation affords diastereomer 7. The proposed role of this attractive interaction in stereodifferentiation is corroborated by the observation that the product diastereomeric ratio depends on arene substitution, with the most electron-rich arenes affording the highest 6:7 ratios.

Scheme 3.

Lewis acid-promoted, diastereoselective, Schmidt ring-expansion reactions. Blue arrows indicate C–C bond migration. The red dotted line indicates a cation–π interaction.

2.2 Intermolecular Cation–π Interactions

Lewis Acid-Catalyzed, Diastereoselective [4+3] Cycloaddition Reactions

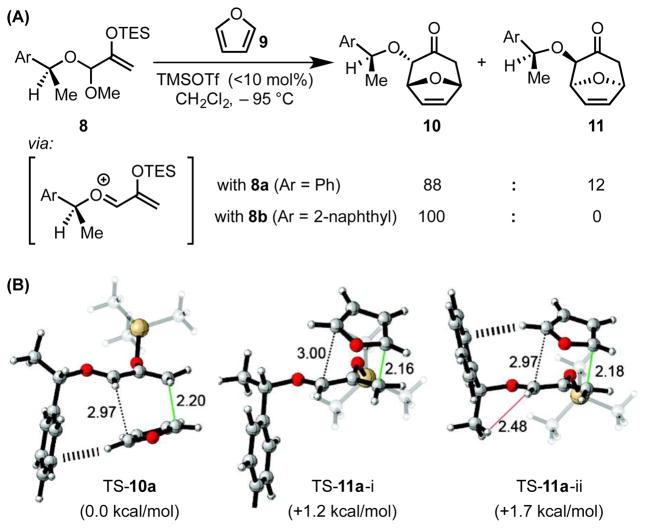
Lewis acid-catalyzed [4+3] cycloaddition reactions of alkoxy-substituted siloxyallyl cations with electron-rich 1,3-dienes, such as furan, have long been successfully applied to the efficient generation of substituted [3.2.1]-tricyclic scaffolds with good regio- and diastereoselectivity.^[26] More recently, Hoffmann and coworkers demonstrated that 2-arylethyl chiral auxiliaries can induce high levels of stereocontrol in cycloadditions to afford enantiomerically pure 2-alkoxy-8-oxabicyclo[3.2.1]oct-6-en-3-ones (Scheme 4A).^[27] For example, Lewis acid-promoted cycloaddition of furan (9) with acetal 8a, which bears a 1-phenylethanol-derived auxiliary, affords a mixture of endo-cycloadducts 10a and 11a in 88:12 d.r. Use of a 1-(2-naphthyl)ethanol-derived auxiliary bearing a more extended aryl group (as in 8b) affords 10b as a single diastereomer.

Scheme 4.

(A) Lewis acid-catalyzed, [4+3] cycloaddition, and (B) a stereochemical model for the observed diastereoselectivity. Black hashes indicate cation–π interactions, while the red line represents a steric repulsion. Black and green dotted lines show the forming C–C bonds, with bond distances indicated in Å. The differential enthalpies of activation are shown in kcal/mol (B3LYP/6-31G(d)). Adapted with permission from ref. 28a. Copyright 2010 American Chemical Society. TMS = trimethylsilyl, TES = triethylsilyl, OTf = trifluoromethanesulfonate

Computational analysis shed light on the origin of the observed diastereoselectivity (Scheme 4B).^[28] In the lowest-energy computed transition structure (TS-10a), the chiral auxiliary is oriented to allow an edge-to-face contact between the phenyl ring and the incoming furan (≈ 3 Å). This contact reflects an attractive cation–π interaction between the π-face of the auxiliary and the partial positive charge developing at the 2-position of furan nucleophile in the first transition state of the stepwise addition. In the two lowest-energy transition structures en route to minor diastereomer 11a, this cation–π stabilization is either absent (TS-11a-i) or accompanied by repulsive steric interactions (TS-11a-ii). Furthermore, this computational model reproduces the improved diastereoselectivity observed experimentally with the 1-(2-naphthyl)ethanol-derived auxiliary, reflecting the strengthened cation–π interaction resulting from the increased expanse of the π-donor.

Lewis Acid-Catalyzed, Diastereoselective Additions of Silyl Enol Ethers to a Chiral Oxazolinium Ion

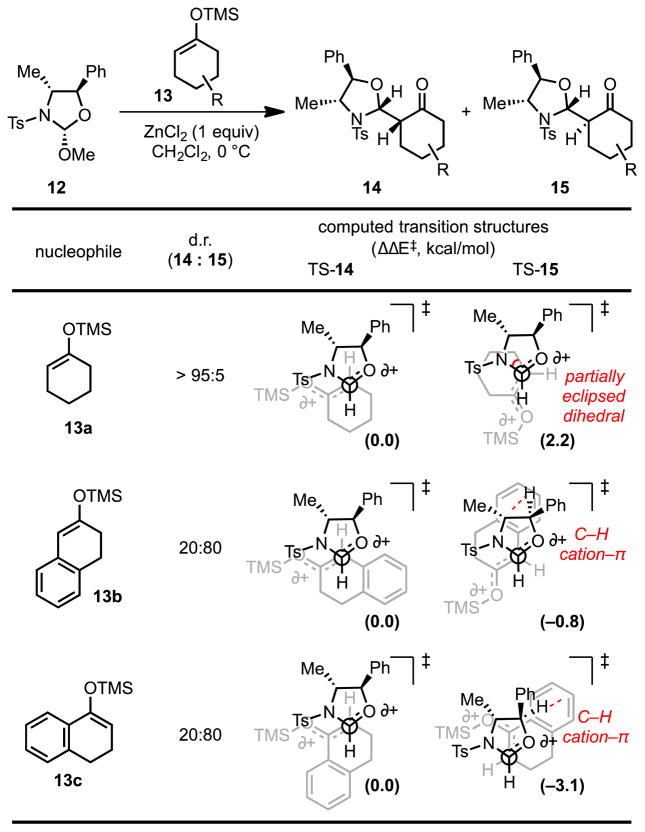
Lewis acid-catalyzed, nucleophilic additions to enantioenriched oxazolinium ions offer an efficient method for formal, stereoselective formylations of silyl enol ethers and allyl silanes.^[29] Over the course of developing conditions for this transformation, Hoppe and coworkers found that a pseudoephedrine-derived oxazolidine (12) undergoes reaction with silyl enol ethers to afford α-substituted ketones. Remarkably, silyl enol ethers bearing aromatic substituents are alkylated with the opposite sense of diastereoselectivity relative to simpler aliphatic analogs (14 vs. 15, Scheme 5).^[29e]

Scheme 5.

Lewis acid-promoted diastereoselective additions of silyl enol ethers to a chiral oxazolinium ion and computational stereochemical models for the observed diastereoselectivity. Red dotted lines indicate attractive cation–π interactions, while the solid red curve represents the dihedral angle leading to repulsive steric interactions. Black and grey dotted lines show the breaking and forming bonds. The differential energies of activation are shown in kcal/mol (M06–2X/6-311+G(d,p)//B3LYP/6-31G(d)). TMS = trimethylsilyl,

While diastereoselective formation of 14a may be rationalized simply on the basis of steric repulsion between the nucleophile and the electrophile in the minor transition state, computational analysis provided insights regarding the basis for selectivity with aromatic substrates.^[30] Computational models utilizing density functionals corrected to account for dispersion interactions predict the correct sense of diastereoselectivity for both classes of silyl enol ethers (e.g., 13a–c). The lowest-energy computed transition structures en route to aromatic products 15b and 15c exhibit van der Waals contacts (2.71–2.92 Å) between the substrate arenes and the oxazolinium ion’s α-C–H bond, which bears partial positive charge. These cation–π interactions override the energetic cost of distortion to avoid steric interactions in the stacked transition structure. Consequently, the reversal of diastereoselectivity observed in reactions with silyl enol ethers 13b,c is attributed to stabilizing cation–π interactions in the transition structure.

3. Catalyst–Catalyst Cation–π Interactions

As noted in Section 1, structural biologists have found that evidence for cation–π interactions is ubiquitous among the structures in the Protein Data Bank. For example, when a cationic amino acid side chain (e.g. Lys, Arg) is positioned near an aromatic side chain (e.g. Phe, Tyr, Trp), the global protein structure is often biased to enable effective cation–π interaction between the residues.^[1],[11] Along with hydrogen-bonding, salt bridge formation, hydrophobic packing, and disulfide formation, such cation–π interactions between amino acid residues play a major role in determining the tertiary and quaternary structures of proteins, which in turn, govern their functions. The spatial organization of small-molecule catalysts can be guided in a similar manner by cation–π interactions between discreet functional groups within the catalyst framework.^[31] The cationic component in such an interaction may be native to the catalyst structure or may result from formation of a covalent adduct with a substrate in situ. This section reviews several cases in which one or more intramolecular cation–π interactions alter the conformation of the catalyst active site to influence reactivity and/or selectivity.

3.1. Native Cationic Catalysts

3.1.1 Peptidic Thiazolium Ion Catalysts for Stetter Reactions

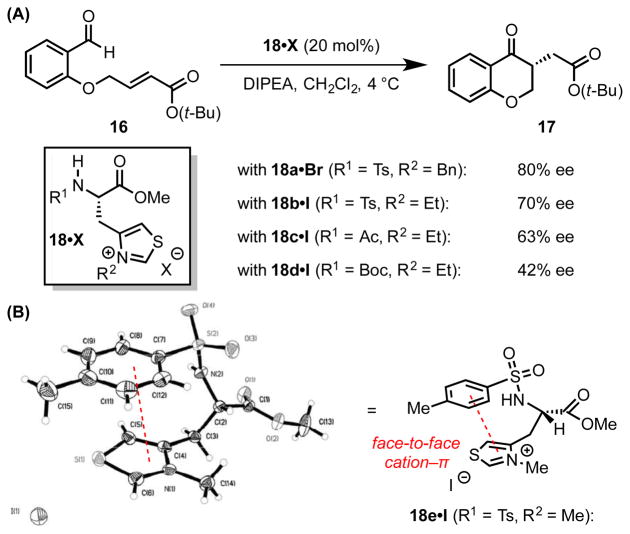
Miller and coworkers evaluated a family of short peptidic thiazolium catalysts for the asymmetric Stetter cyclization of salicylaldehyde-derived enoates (16, Scheme 6A).^[32] Simple β-thiazolyl alanine derivatives were found to be among the most effective catalysts, with catalyst 18a affording cyclization product 17 in up to 80% ee. Extensive studies on the effect of catalyst structure demonstrated that enantioselectivity is highly dependent on the identity of the catalyst N-substituent. When the p-toluenesulfonyl group (Ts) of catalyst 18b is replaced with an acetyl (Ac, catalyst 18c) or tert-butyloxycarbonyl (Boc, catalyst 18d) group, cyclization proceeds with markedly diminished enantioselectivity.

Scheme 6.

(A) Asymmetric Stetter reaction catalyzed by β-thiazolyl alanine derivatives. (B) X-ray crystal structure and line representation of one such catalyst. Red dotted lines indicate cation–π interactions. Adapted from ref. 32 with permission of the Royal Society of Chemistry. DIPEA = N.N-diisopropylethylamine.

X-ray crystallographic analysis of 18e revealed that an intramolecular cation–π interaction between the aromatic ring of the Ts-substituent and the thiazolium ion favors a folded conformation (Scheme 6B), which is proposed to be maintained in the cationic Breslow intermediate involved in the key C–C bond-forming step of the catalytic cycle. Accordingly, the effective enantioinduction is attributed to the stereochemically well-defined environment shaped by this cation–π interaction.

3.1.2 Guanidinium Ion Catalysts for Claisen Rearrangement s

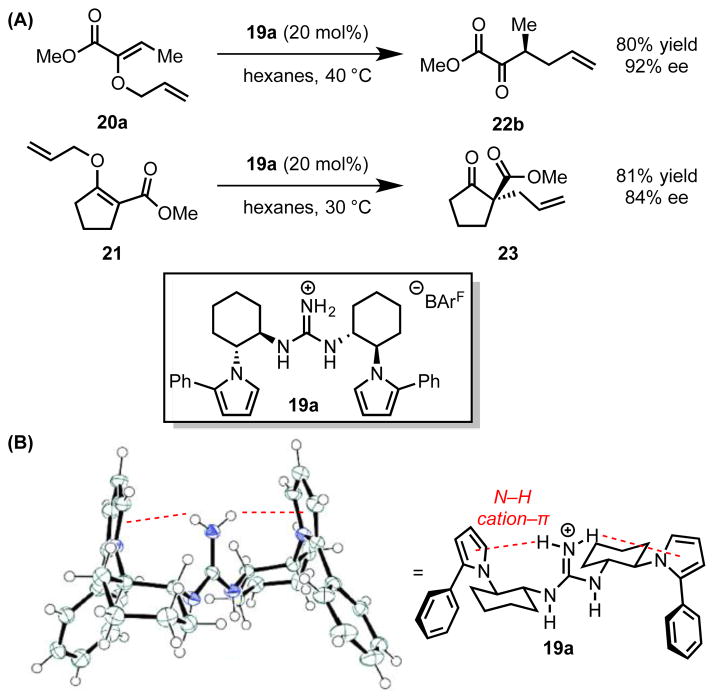
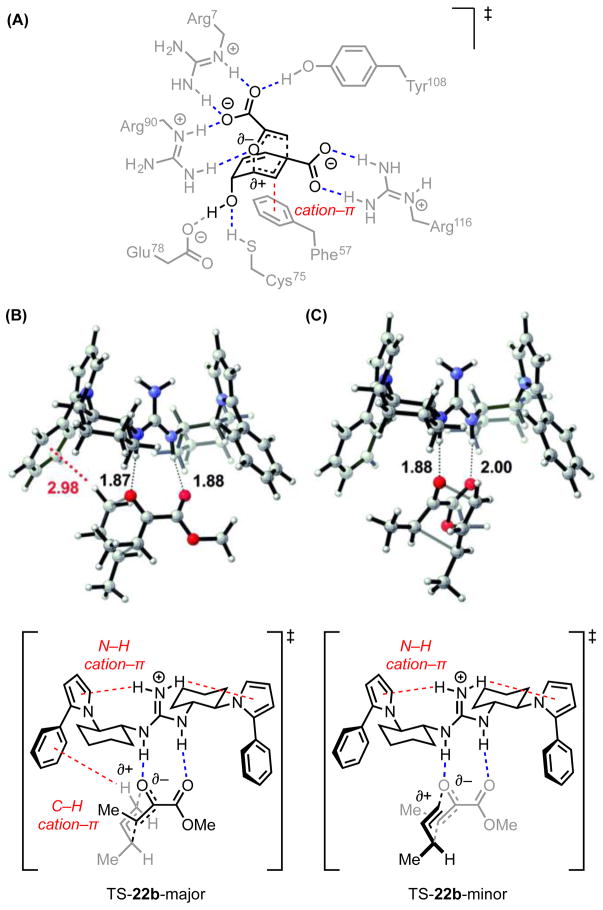
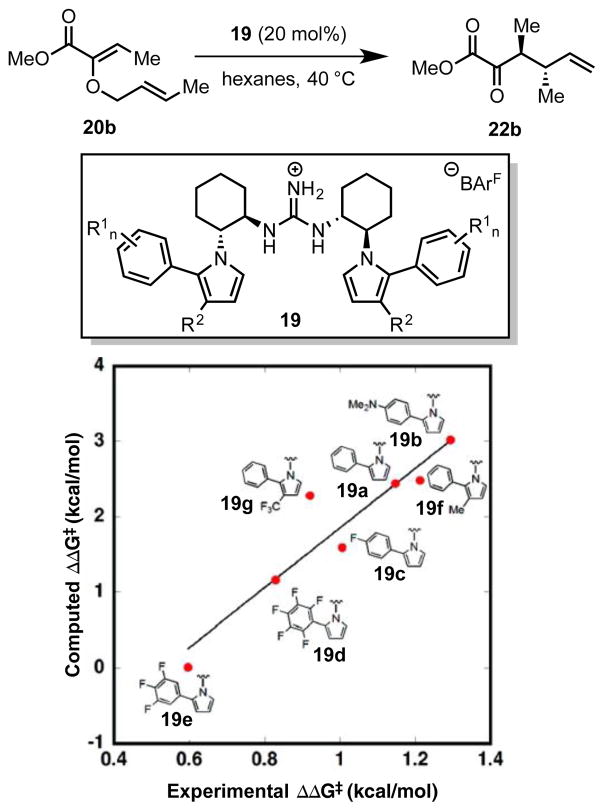
Jacobsen and coworkers disclosed a series of C₂-symmetric guanidinium ion catalysts (19) for enantioselective, Claisen rearrangements of α- and β-ketoesters (20 and 21, Scheme 7A).^[33] X-Ray structural analysis, solution-phase ROESY studies, and gas-phase computations all indicated that the ground-state catalyst conformation positions the guanidinium NH₂ hydrogen atoms in close contact with the π-faces of the proximal pyrrole rings (3.23 Å in the calculated structure, 3.22 and 3.19 Å in the crystal structure, Scheme 7B). These cation–π interactions serve to rigidify the catalyst conformation and position the aryl substituents of the pyrroles appropriately to participate in stereodifferentiating interactions in the rearrangement transition state. The nature of these secondary interactions will be discussed in Section 4.2.6.

Scheme 7.

(A) Guanidinium ion-catalyzed asymmetric Claisen rearrangements. (B) X-ray crystal structure and line representation of the guanidinium ion catalyst. Red dotted lines indicate cation–π interactions. Solvent molecules omitted for clarity. Adapted with permission from ref. 33c. Copyright 2011 American Chemical Society.

3.1.3 Oxoammonium Ion Catalysts for Alcohol Oxidations

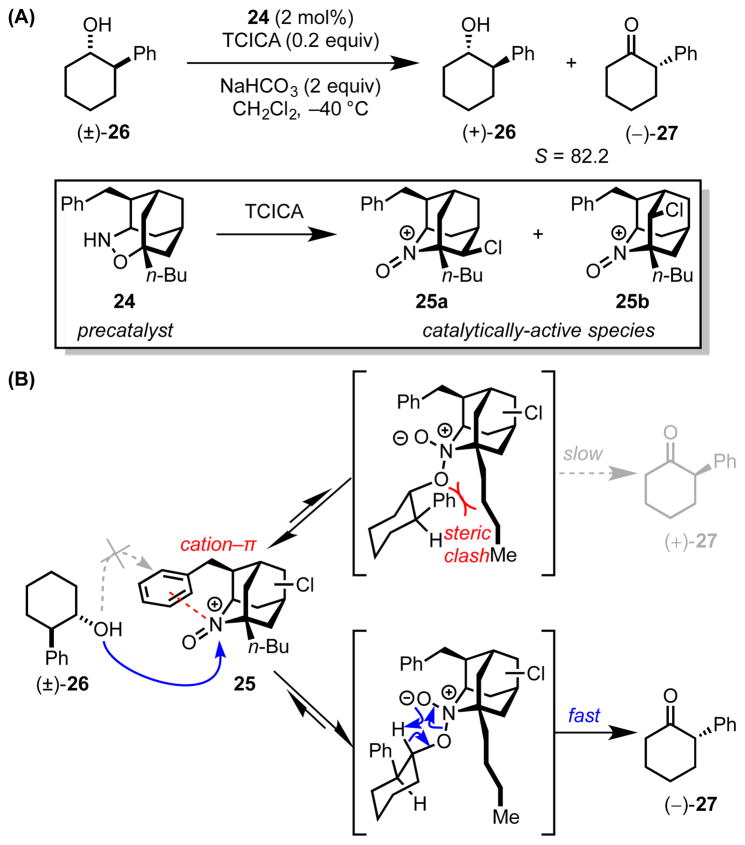
Iwabuchi and coworkers recently advanced a method employing adamantine-derived alkoxyamine precatalyst 24 for highly stereoselective oxidative kinetic resolution (OKR) of unactivated secondary alcohols (Scheme 8A).^[34] This method was based on prior work utilizing the same family of precatalysts for simple oxidations and the kinetic resolution of activated alcohols.^[35] On the basis of careful spectroscopic analysis and independent isolation experiments, the active catalytic species was identified as a pair of chlorinated oxoammonium ions (25a and 25b) generated from the reaction of 24 with trichloroisocyanuric acid (TCICA).

Scheme 8.

(A) Alkoxyamine-catalyzed kinetic resolution of secondary alcohol 26, and (B) a stereochemical model for the observed enantiodiscrimination. The red dotted line indicates an attractive cation–π interaction, while the red curves indicate a repulsive steric interaction. TCICA = trichloroisocyanuric acid.

In the proposed mechanism, the benzyl substituent in either active catalyst (25a or 25b) forms an intramolecular cation–π interaction with the oxoammonium ion, thereby shielding one face as the alcohol substrate (26) adds reversibly to the exposed face to form a covalent adduct (Scheme 8B). Stereodifferentiation with a selectivity factor as high as S = 296 is achieved in the subsequent, oxy-Cope-type elimination through differential steric interactions with the α-alkyl group. In this example, the cation–π interaction is deemed to play a critical role in the overall kinetic resolution process by enforcing diastereoselective formation of the initial covalent intermediate.

3.2. Cationic Catalyst States formed On-Cycle

3.2.1 Nucleophilic Catalysts for Acyl-Transfer Reactions

Nucleophilic heterocycles, and pyridine derivatives in particular, have been studied extensively as efficient catalysts for a range of acyl-transfer reactions.^[36] In the generally accepted mechanism, these nucleophilic catalysts undergo N-acylation to form highly electrophilic, cationic, covalent adducts prior to acyl transfer to a substrate nucleophile. In principle, π-donating groups could be integrated into the scaffolds of these catalysts to enable cation–π stabilization of specific conformations of the acylated intermediate, potentially leading to improved reactivity or selectivity. The viability of this strategy has been demonstrated in several systems, as described below.

Peptidic N-Alkylimidazole Catalysts

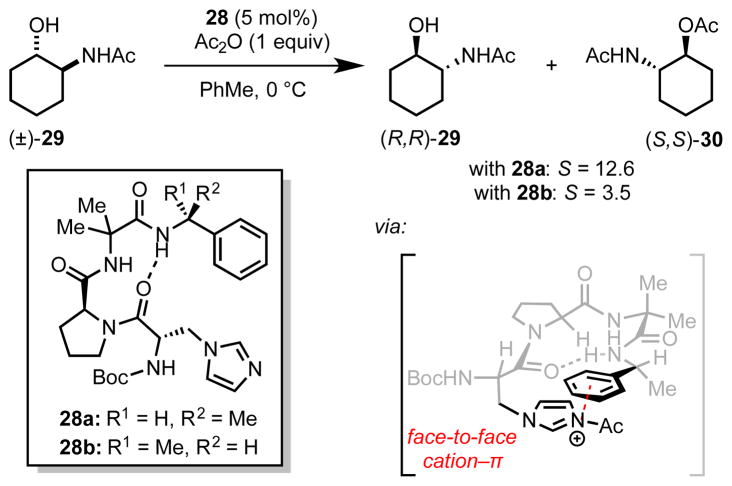
Inspired by the catalytic efficiency of N-methylimidazole (NMI) in alcohol acylations, Miller and coworkers sought to develop structurally analogous, chiral, peptidic catalysts for asymmetric acylation reactions. Toward this aim, they identified β-imidazolyl alanine-containing tripeptide catalyst 28a for the kinetic resolution of acetamide-substituted, secondary alcohols (29, Scheme 9).^[37] The C-terminal α-methylbenzylamide moiety was incorporated to allow for an intramolecular cation–π-interaction with the charged acylimidazolium ion intermediate. In line with the hypothesized role, the selectivity factor in the kinetic resolution of model secondary alcohol 29 was found to be highly sensitive to the configuration of the α-methylbenzylamide moiety; diastereomeric catalyst 28b affords acylated product 30 with significantly reduced stereoselectivity (S = 3.5 with 28b compared to S = 12.6 with 28a). While the precise mechanistic role of the α-methylbenzylamide group has not been ascertained, its presumed participation in a cation–π-interaction has served as the basis for further catalyst development.^[37b]

Scheme 9.

Tripeptide-catalyzed acylative kinetic resolution of acetamide- substituted secondary alcohols. The red dotted line indicates a putative cation–π interaction.

Chiral Aminopyridine Catalysts

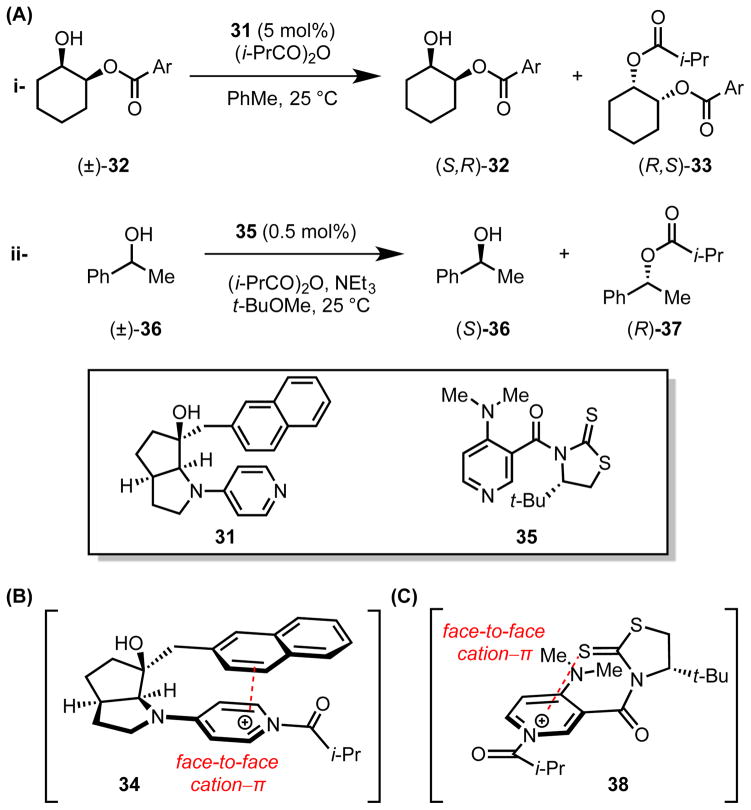
Fuji and coworkers disclosed a naphthyl-substituted pyrrolidinopyridine catalyst for the acylative kinetic resolution of secondary alcohols (Scheme 10A).^[38] Nuclear Overhauser effect (nOe) experiments with the parent (31) and acylated (34) catalysts revealed that acylation induces a conformational change driven by an intramolecular cation–π interaction between the pendent naphthyl group and the pyridinium ion (Scheme 10B).

Scheme 10.

(A) Chiral pyridine-catalyzed acylative kinetic resolution of secondary alcohols. (B and C) Line representation of the stacked conformations adopted by the N-acylpyridinium catalyst adducts. Red dotted lines indicate cation–π interactions.

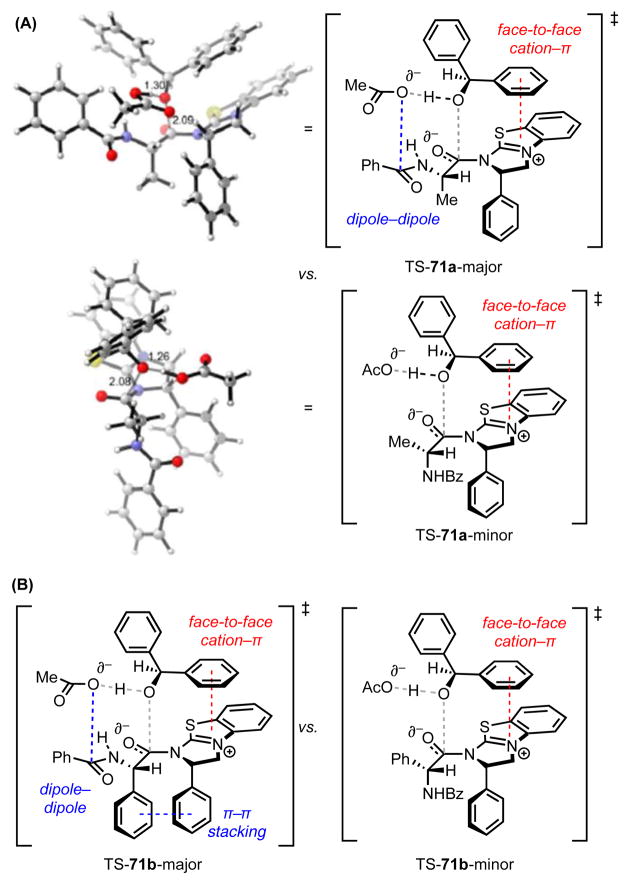
Yamada et al. explored a related conformation-switching strategy in the application of a chiral thiazolidinethione-functionalized N,N-dimethyl-4-aminopyridine (DMAP) catalyst (35) to the acylative kinetic resolution of secondary, benzylic alcohols (36, Scheme 10A).^[39] X-Ray structural analysis, NMR characterization, and UV-Vis spectroscopic studies all indicated that 35 also undergoes a conformational change upon acylation, driven by an intramolecular cation–π interaction between the thiocarbonyl group and the pyridinium ion (Scheme 10C).^[40] Computational (MP2) studies corroborate the role of the cation–π interaction in the conformation-switching properties of catalysts 31 and 35.^[41]

In both cases, the chiral environment defined by the cation–π interaction controls the π-facial reactivity of the N-acylpyridinium intermediate in enantioselective acyl transfer to alcohol substrates. Differential recognition of enantiomeric substrates is purportedly assisted by additional intermolecular cation–π interactions between the aromatic group on the substrate and the pyridinium ion, as described further in Section 4.1.3. Similar catalytic conditions enable acylative dynamic kinetic resolution of hemiaminals,^[42] and an analogous chiral pyridine auxiliary has been applied successfully to two-step, enantioselective cyclopropanation reactions.^[43]

3.2.2 Secondary-Amine Catalysts for Activation of Enals

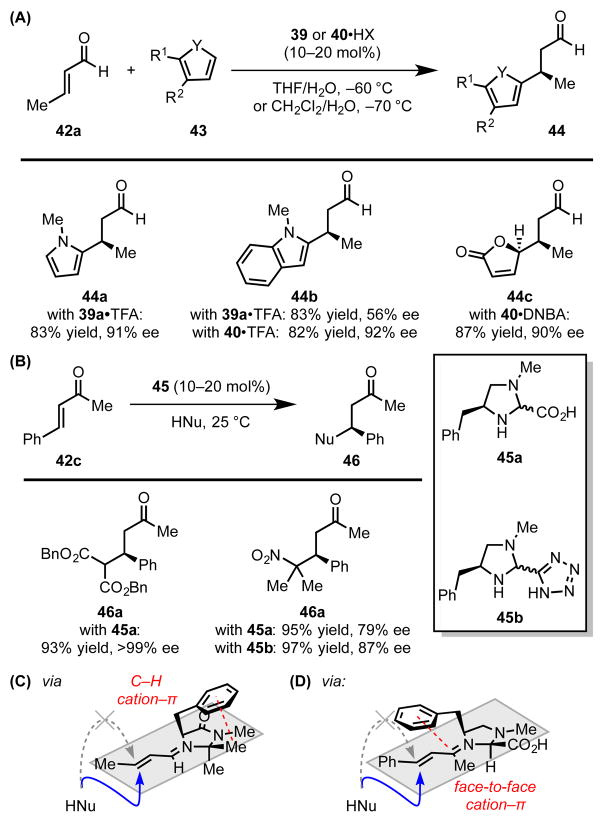
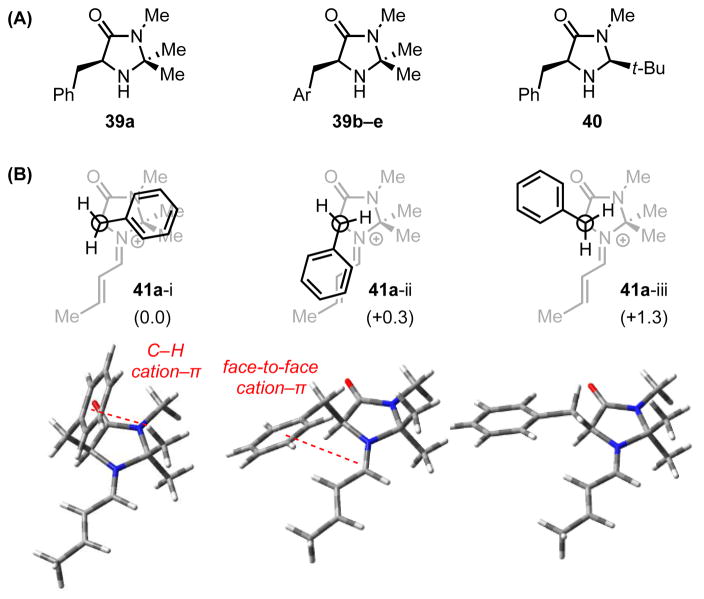
Following their introduction by MacMillan and coworkers, chiral imidazolidinone derivatives, such as 39 and 40, have been utilized widely to promote catalytic, enantioselective transformations of α,β-unsaturated aldehydes and ketones via iminium ion intermediates (Scheme 11A).^[44] MacMillan,^[45] Houk,^[46] and Yamada^[47] independently undertook computational studies of these catalytic systems in an effort to elucidate the seemingly general basis for enantioinduction across a broad range of reactions. Using molecular mechanics and DFT to evaluate the accessible ground-state structures of the preferred (E)-iminium adduct (41a), three low-energy conformations differing in their Ph–C–C–N dihedral angle have been identified (Figure 3).

Scheme 11.

(A) Select imidazolidinone- and (B) imidazoline-catalyzed Michael reactions, and (C and D) stereochemical models for stereoselective nucleophile addition to the activated iminium ion intermediates. Red dotted lines indicate cation–π interactions. Blue arrows indicate favorable trajectories for nucleophile approach, while grey dotted arrows indicate sterically blocked trajectories. TFA = trifluoroacetic acid. DNBA = 3,5-dinitrobenzoic acid.

Figure 3.

(A) Selected chiral imidazolidinone catalysts. (B) Lowest energy conformations of the iminium ion intermediate formed from 39a and crotonaldehyde. Relative energies (kcal/mol) predicted by DFT calculation (B3LYP/6-31g(d)) are shown in parenthesis. Red dotted lines indicate cation–π interactions.

Taken together, conformations 41a-i and 41a-ii, both of which position the phenyl ring over regions of the iminium ion that bear positive charge, are predicted to account for 85% of all possible species at 25 °C.^[46a] Further ab initio (MP2) energy decomposition analysis predicts that the electrostatic and polarization terms dominate the attractive interactions between the phenyl ring and the iminium cation.^[47] Conformation 41a-iii, in which the phenyl ring is splayed away from the face of the iminium ion, cannot partake in any such stabilizing interactions and is, accordingly, markedly higher in energy. Iminium ions derived from tert-butyl-substituted catalyst 40 exhibit similar conformational preferences. With either catalyst, the cation–π interaction enables the phenyl ring to effectively shield the si face of the iminium ion intermediate, thereby favoring nucleophilic addition to the re face of the electrophile (Scheme 11C). This facial preference and the preservation of the cation–π interaction in the C–C bond-forming step are further reflected in computed transition state energies.

Jørgensen and coworkers introduced related imidazoline catalysts (45a and b) for conjugate additions to α,β-unsaturated ketones (Scheme 11B).^[48] Based on computational modeling (PM3), the authors suggested that these catalysts achieve enantiocontrol due to cation–π interactions analogous to those described above. The benzyl substituent of the imidazoline catalyst shields the re face of the iminium ion intermediate, thereby favoring nitronate or enolate addition from the si face of the electrophile (Scheme 11D).

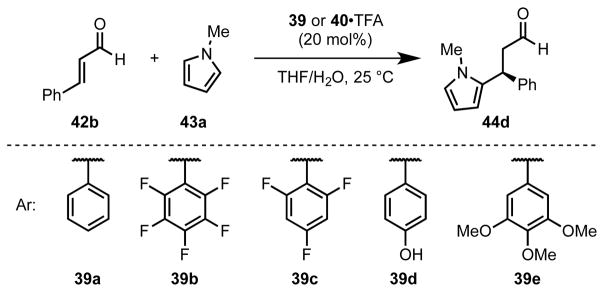
To evaluate this stereochemical model rigorously, Gilmour and coworkers examined a series of imidazolidinone catalysts (39a–f) differing only in their aryl substituents.^[49] In a model reaction involving conjugate addition of N-methylpyrrole to cinnamaldehyde (42b), the observed enantioselectivity was shown to display a strong dependence on the arene quadrupole moment (Q_ZZ) (Scheme 12, Table 1). X-ray structural analysis, supported by DFT calculations, further revealed that the ground-state distribution of iminium ion conformations (41x-i–iii where x = a–e) is affected by the electronic properties of the aryl group. Catalysts bearing electron-rich arenes favor conformers 41x-i and 41x-ii, while catalysts bearing electron-deficient arenes display a preference for splayed conformer 41x-iii. Taken together, these results offer compelling evidence that attractive cation–π interactions play an important role in the stereochemical organization of the reactive iminium ion intermediate, thereby enabling highly selective nucleophilic addition.

Scheme 12.

Asymmetric conjugate addition catalyzed by chiral imidazolidinones bearing electronically varied aryl substituents. TFA = trifluoroacetic acid.

Table 1.

The table shows the reaction enantioselectivity as a function of the electronic properties of the aromatic group on the catalyst.

Entry	Catalyst [a]	QZZ	Iminium Ion Mole Fraction:			ee[b] (%)
			41x-i	41x-ii	41x-iii
1	39b	+3.01	0.37	0.16	0.47	65
2	39c	+0.28	0.39	0.21	0.40	70
3	39a	−3.46	0.75	0.03	0.23	84
4	39d	−3.71	0.76	0.04	0.20	90
5	39e	−5.68	0.65	0.17	0.18	94
6	40	−3.46	--	--	--	85

^[a]See the catalyst substitution pattern in Scheme 12.

^[b]Enantiomeric excess of 44d, formed by the reaction shown in Scheme 12.

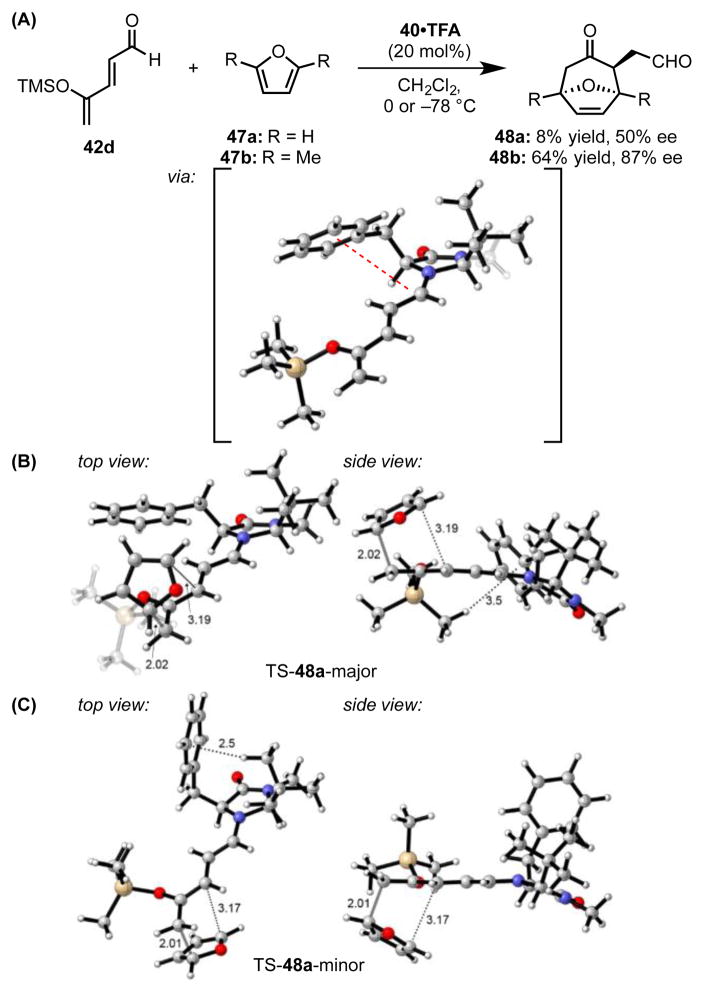
In an independent effort, Harmata and coworkers developed methodology for the formal [4+3] cycloaddition reaction of 4-trialkylsilyloxypentadienal 42d with furan nucleophiles (47) (Scheme 13).^[50] Remarkably, the sense of enantioinduction observed with catalyst 40 is opposite that anticipated from analyses of MacMillan’s [4+2] and conjugate addition systems.^[51] Further computational studies were, therefore, undertaken to rationalize this deviation from known models^.[52]

Scheme 13.

(A) Imidazolidinone-catalyzed [4+3] cycloaddition and the lowest-energy computed iminium ion conformation. The lowest-energy computed transition structures (M06-2X/6-311+G(d,p)//B3LYP/6-31G(d)) en route to the (B) major and (C) minor enantiomers of 48. The red dotted line indicates a cation–π interaction, and black dotted lines indicate other noncovalent interactions. Faded grey lines indicate forming bonds. Key distances shown in Å. Adapted from ref. 52. TFA = trifluoroacetic acid.

DFT calculations identified low-energy iminium ion conformations analogous to 41x-i–iii, wherein intramolecular cation–π interactions favor positioning the phenyl ring over the iminium ion. However, because enantioselectivity-determining C–C bond formation occurs at the most-distal δ-position of the conjugated iminium ion, it was hypothesized that the furan nucleophile could approach either the si or re face without steric penalty. However, furan approach requires rotation of the trimethylsilyl group out of the plane of the iminium ion. While rotation toward the re face (opposite si-face furan approach) requires minimal reorganization of the benzyl and tert-butyl groups in the transition state (Scheme 13B), rotation toward the si face induces significant distortion (Scheme 13C). The energetic cost for this transition state distortion from the cation–π-stabilized ground state geometry was proposed to account for chirality transfer in this unusual system. This example provides yet another illustration of how cation–π interactions can exert long-ranging and subtle effects on catalyst conformation.

4. Catalyst–Substrate Cation–π Interactions

The importance of cation–π interactions for substrate recognition and transition state stabilization in enzymatic catalysis has been established in numerous studies.^[10] In a quintessential example, the dense array of cation–π interactions in the active site of a squalene–hopene cyclase stabilizes charge redistribution in the transition state of the cationic polycyclization central to steroid biosynthesis.^[13] Squalene–hopene cyclase and a host of other enzymes achieve remarkable rate acceleration and precise stereocontrol through the cooperative action of multiple amino acid residues, many of which contain charged or aromatic moieties, lining the active site. Elucidation of substrate–active site interactions in enzymatic systems has paved the way for application of the cation–π interaction as a design element for small-molecule catalysis. This section reviews key examples in which cation–π interactions have been invoked or demonstrated to play a key role in influencing reaction outcomes in synthetic catalyst systems.

4.1. Substrate π-Donors

4.1.1 Alkali Metal Ion-Controlled Diastereoselective Photoisomerization of Diphenylcyclopropane

Trans- and cis-diphenylcyclopropane (49a and 50a) can undergo photoisomerization in the presence of an acetanisole sensitizer to form a thermodynamic mixture of the two diastereomers (55:45 trans:cis).^[53] Ramamurthy and coworkers hypothesized that introduction of alkali metal ions to the reaction mixture could perturb the equilibrium distribution to favor the cis isomer (50a), which would presumably bind the cation more tightly within the concave arrangement of its phenyl rings. They subsequently demonstrated that free alkali metal ions introduced into the reaction medium via a dry, metal-exchanged zeolite exert significant influence over the diastereomeric composition of the photostationary state (Scheme 14, Table 2).^[54] While all of the alkali metal ions (Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺) favor the formation of cis isomer 50a, the smaller ions (Li⁺ and Na⁺), which generally engage in stronger cation–π interactions, afford the highest diastereomeric ratios.

Scheme 14.

(A) Alkali metal ion-promoted diastereoselective photoisomerization of diphenylcyclopropanes, and (B) a schematic representation of the cation–π interactions favoring formation of the cis isomer. Red dotted lines indicate cation–π interactions.

Table 2.

Perturbation of the photostationary state of diphenylcyclopropanes with alkali metal cations.

Entry	Substrate[a]	X =	M+	Eint [b] (kcal/mol)	49: 50[c]
1	49/50a	H	none	n/a	44:55
2			Li+	−75.8	91:9
3			Na+	−53.9	92:8
4			K+	−32.6	88:12
5			Rb+	−28.2	85:15
6			Cs+	−22.7	65:35
7	49/50b	OMe	Na+	−53.7	n.d.
8	49/50c	CN	none	n/a	45:55
9			Na+	−43	44:46

^[a]See the substrate structure and substitution pattern in Scheme 14.

^[b]E_int is the computed interaction energy between 50 and M⁺, calculated with MP2/6-31g*/Hay–Wadt ECP (K, Rb, Cs).

^[c]Isomer ratio at the photostationary state.

The critical role of the cation–π interaction in the stereocontrol of the photoisomerization was further substantiated by control experiments with monosubstitued diphenylcyclopropane derivatives (49/50b,c). Consistent with prior studies,^[7] the computed cation-binding energies for p-methoxy substituted 50b are similar to those for the parent diphenylcyclopropane 50a. However, p-cyano substituted 50c is calculated to be a much weaker π-donor, thereby compromising its ability to participate in a templating cation–π interaction with the metal ions. Accordingly, the photostationary diastereomeric ratio obtained with 50c in the presence of Na⁺ (44:56 trans:cis) exhibits little deviation from that obtained in the absence of a template (45:55 trans:cis), highlighting the importance of electronic effects on the π-system in such interactions.

4.1.2 Cation-Templated Cyclization Reactions

Large and medium-sized rings are pervasive among natural products and pharmaceuticals; however, cyclization reactions to form these structural motifs are generally quite challenging due to the significant entropic and enthalpic costs of bringing remote termini into close proximity.^[55] Some small rings can be equally challenging to form due to the precise stereoelectronic alignment required for bond formation. In any of these cases, the use of attractive interactions to preorganize the reactive functional groups prior to cyclization may, in theory, reduce the entropic barrier to cyclization and control the stereoelectronic alignment necessary for selective bond formation. Toward this aim, the cation–π interaction has been applied as a design element to enable several challenging cyclization reactions.

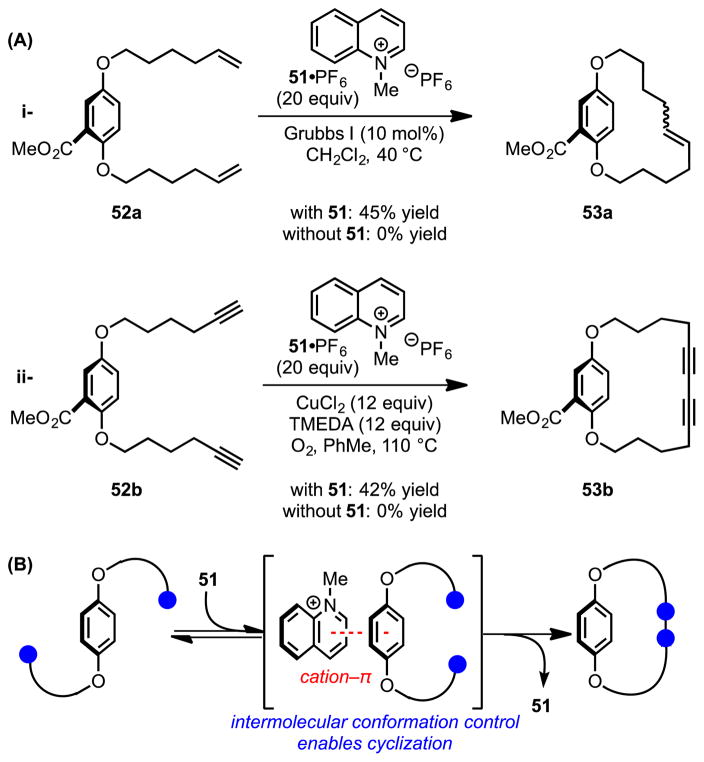
Quinolinium Ion-Promoted Macrocyclization Reactions

In an elegant demonstration of the application of cation–π interactions to facilitate cyclization reactions, Collins and coworkers explored the use of pyridinium salts as intermolecular conformational control elements for macrocyclization of hydroquinone derivatives (52).^[56] While no detectable cyclization occurs in the absence of a template, upon introduction of quinolinium salt 51 to the reaction medium, cation–π interactions enforce a substrate conformation that enables ring-closing metathesis or intramolecular Glaser–Hay coupling (Scheme 15). This intermolecular conformational control strategy enables preparation of cyclophanes (53) in 40–60% yield, even under relatively concentrated conditions. Similarly, pyridinium and tetraalkylammonium salts have been employed as templates to amplify production of high-affinity macrocyclic hosts in the synthesis of dynamic combinatorial libraries.^[57]

Scheme 15.

(A) Pyridinium-promoted macrocyclization reactions through (B) conformational control enabled by the cation–π interaction. The red dotted line indicates a cation–π interaction. Blue circles indicate reactive functional groups. TMEDA = N,N,N′,N′-tetramethylethylenediamine.

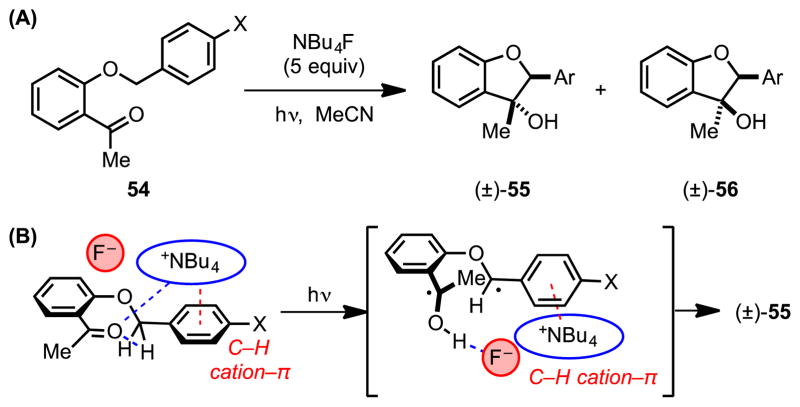
Tetrabutylammonium-Templated Norrish–Yang Cyclizations

In a related vein, Yamada et al. reported methodology for the diastereoselective, tetraalkylammonium-templated Norrish–Yang cyclization of 2-benzyloxy-acylbenzenes (54) to afford trans-dihydrobenzofuranols (55).^[58] In the absence of any additive, the photochemical cyclization of 54a yields exclusively cis-dihydrobenzofuranol 56a in trifluorotoluene. However, in the presence of excess tetraalkylammonium salt, this diastereoselectivity is overturned to favor trans-dihydrobenzofuranol with a diastereomeric ratio as high as 93:7 55a:56a. Furthermore, the degree of stereoselectivity depends on the π-donating ability of the substrate benzyl group (as in substrates 54a–d), with the most electron-rich substrates affording the highest trans:cis ratios (Scheme 16A, Table 3). The high degree of diastereomeric control was attributed to the cooperative effect of multiple attractive interactions between the substrate and ammonium ion, including a cation–π interaction with the benzyl substituent and a Lewis acid–base interaction with the carbonyl oxygen (Scheme 16B). The importance of these attractive interactions was further corroborated by ground-state computational analysis, which indicated that tetrabutylammonium-complexation favors the reactive substrate conformation leading to H-atom abstraction en route to formation of trans-dihydrobenzofuranol 55a.

Scheme 16.

(A) Tetrabutylammonium-templated Norrish-Yang cyclization, and (B) a model for the observed diastereoselectivity. Red dotted lines represent cation–π interactions; blue dotted lines represent other noncovalent interactions.

Table 3.

Tetrabutylammonium-Templated Norrish-Yang Cyclization.

Entry	Substrate[a]	X =	Solvent	NBu4F (equiv)	Conv.[b] (%)	d.r. (55: 56)
1	54a	H	PhCF3	0	17 [c]	0:100 [c]
2				5	93 [c]	93:7 [c]
3			MeCN	0	35 [c]	17:83 [c]
4				5	96 [c]	84:16 [c]
5	54b	Me	MeCN	0	35	20:80
6				5	84	93:7
7	54c	OMe	MeCN	0	70	11:89
8				5	99	94:6
9	54d	CF3	MeCN	0	33	23:77
10				5	6	59:41

^[a]See the substrate structure and substitution pattern in Scheme 16.

^[b]Conversion of 54 after 24 hours.

^[c]After 10 hours.

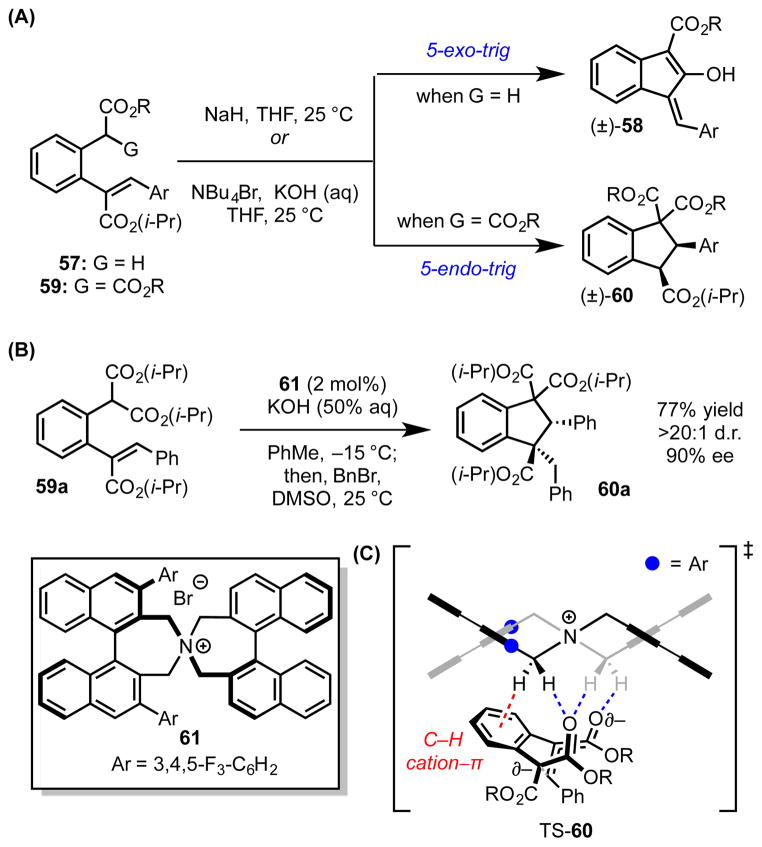
Chiral Ammonium Ion-Catalyzed 5-Endo-Trig Cyclizations

Baldwin’s rules for ring-closing reactions delineate the kinetic ease with which different cyclization modes occur due to the stereoelectronic constraints of bond formation between the reacting termini.^[59] On the basis of these guidelines, the 5-endo-trig cyclization is generally considered to be highly unfavorable.^[60] Paton, Smith, and coworkers recently reported unusual tetraalkylammonium-enabled 5-endo-trig intramolecular Michael reactions in the synthesis of substituted indanes (60).^[61] When simple α-benzyl esters (57) are treated with base in the presence of achiral tetraalkylammonium ions, Dieckmann-type cyclization affords the traditional 5-exo-trig product (58). However, α-benzyl malonates (59) subjected to the same conditions undergo exclusively 5-endo-trig cyclization (Scheme 17A). The polysubsituted indane derivatives (60) generated through the action of chiral tetraalkylammonium catalyst (58) are, correspondingly, formed with high enantio- and diastereoselectivity (Scheme 17B).

Scheme 17.

(A) 5-Exo-trig vs. 5-endo-trig cyclizations reactions. (B) Chiral ammonium ion-catalyzed 5-endo-trig intramolecular Michael reaction. (C) The lowest-energy, computed transition structure en route to 60 (B97D/6-31G(d)). The red dotted line represents a cation–π interaction; blue dotted lines represent hydrogen bonds. Grey and black dotted lines indicate breaking or forming bonds.

Computational studies into the origins of stereoinduction revealed that the lowest-energy transition structure en route to the major product is characterized by three key interactions defining the arrangement of the catalyst–substrate tight ion pair (Scheme 17C). The partially positive α-C–H bonds of the ammonium ion form a cation–π interaction with the substrate’s aromatic linker and two non-classical hydrogen bonds to the carbonyl oxygen atoms of the malonate and Michael acceptor. These cooperative, attractive interactions, which are largely absent in the minor transition structures, are proposed to underlie the transition state stabilization responsible for stereoinduction. Consistent with this model, substrates with electron-withdrawing substituents on the aromatic linker undergo cyclization with diminished enantioselectivity.

4.1.3 Heterocycle-Catalyzed Acyl Transfer Reactions

Chiral Pyridine-Catalyzed Kinetic Resolutions

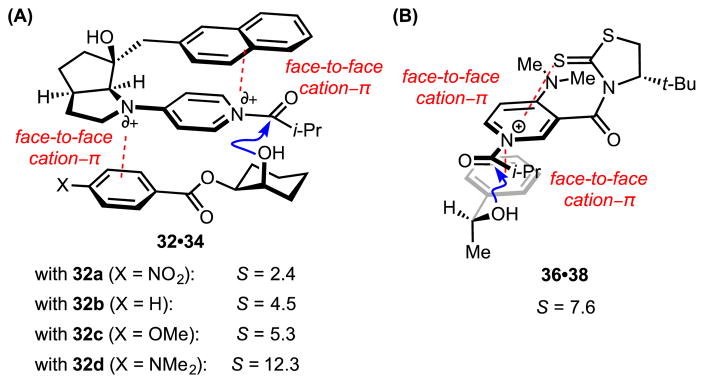
As discussed in Section 3.2.1, Fuji and coworkers disclosed a naphthyl-substituted pyrrolidinopyridine catalyst (31) for the acylative kinetic resolution of benzoate-substituted, secondary alcohols.^[38] With substrates 32a–d, enantioselectivity tracks with the electron-donating ability of the benzoate substituent, such that alcohols bearing the most electron-rich group (32d) undergo acylation with a selectivity factor as high as S = 12.3 (Figure 4A). Discrimination between the enantiomers of the substrate was therefore attributed to an intermolecular cation–π interaction between the benzoate directing group and the cationic acyl-catalyst intermediate (34) on the face opposite the intramolecular cation–π interaction controlling catalyst conformation. Yamada et al. proposed that a similar cation–π interaction between the secondary, benzylic alcohol substrate (36) and the acylated derivative of the DMAP catalyst (38) organizes the reactive complex to enable discrimination between the substrate enantiomers with selectivity factors up to S = 30 (Figure 4B).^[39]

Figure 4.

Chiral 4-aminopyridine catalyst–substrate complexes en route to alcohol acylation. Red dotted lines indicate cation–π interactions. Blue arrows indicate favorable trajectories for nucleophile approach.

Chiral Amidine- and Isothiourea-Catalyzed Kinetic Resolutions

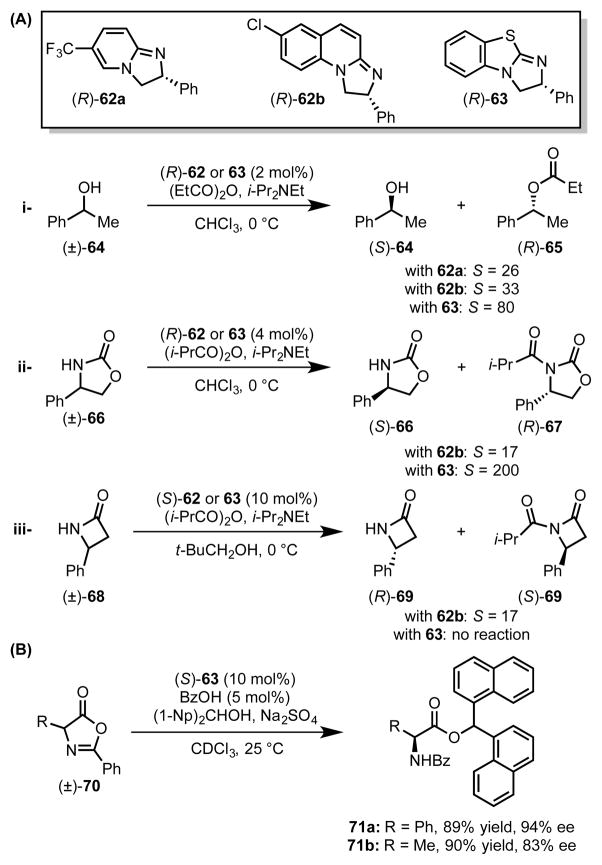
Inspired by the modularity and reactivity profile of imidazopyridine derivatives, Birman et al. crafted a family of structurally analogous chiral amidine (62) and isothiourea (63) catalysts for stereoselective acyl transfer reactions. The efficacy of these catalysts has been demonstrated in the acylative kinetic resolution of secondary alcohols,^[62] oxazolidinones,^[63] and lactams (Scheme 18A).^[64] These catalysts have also been employed for dynamic kinetic resolution (DKR) of azlactones en route to natural and unnatural α-amino esters (Scheme 18B).^[65]

Scheme 18.

Amidine- and isothiourea-catalyzed acylative kinetic resolutions.

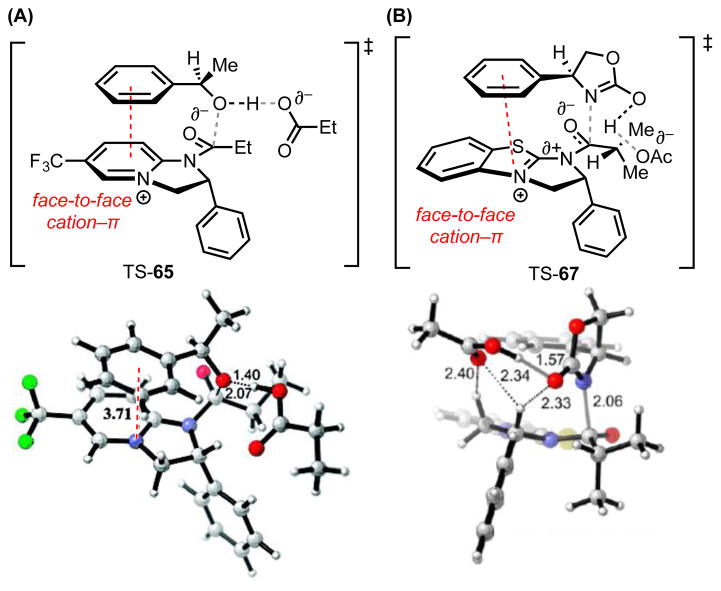
In each of these transformations, π-donating functionality on the acyl acceptor plays a critical role in controlling reactivity and stereoselectivity, suggesting that cation–π interactions with the acylated intermediate are important in the catalytic mechanism. To evaluate this hypothesis, computational (DFT) studies were directed toward assessing the basis for stereoselectivity in the kinetic resolution of alcohols and lactams (Figure 5).^[64],[66] In the lowest-energy transition structure located for the fast-reacting enantiomer of oxazolidinone 66, the phenyl ring of the substrate is predicted to engage in a cation–π interaction with the thiazolium moiety of isothiourea catalyst 63, favoring reaction through a stacked conformation. This general arrangement was also found to be operative for reactions with amidine catalyst 62 across representative substrates including 1-phenylethanol (64), 4-phenyloxazolidinone (66), and 4-phenylazetidinone (68).

Figure 5.

(A) Lowest energy, computed transition structures for acylation of the fast-reacting (R)-enantiomers of alcohol 64 (B3LYP/6-31G(d)/CPCM(CHCl₃)) and (B) oxazolidinone 66 (M06-2X/6-31G(d)/SMD(CHCl₃)). Red dotted lines represent cation–π interactions. Black dotted lines represent other noncovalent interactions. Grey lines indicate breaking or forming bonds. Key distances shown in Å. Adapted with permission from references 64 and 66. Copyright 2008 and 2012 American Chemical Society.

However, the basis for the absolute sense of stereoselectivity observed in the DKR of azalactones required further investigation.^[67] In the lowest-energy major and minor diastereomeric transition structures, strong cation–π interactions between the benzhydryl group of the acyl acceptor and the acylated catalyst (≈ 3.3 Å) were found to organize the catalyst–substrate complexes (Scheme 19B). This organization enables C–C bond formation to be directed by additional stereodifferentiating interactions, including H-bonding, π–π stacking, and dipole–dipole interactions with a bridging carboxylate.

Scheme 19.

Acylative kinetic resolution of secondary benzylic alcohols by amidinium catalysts bearing matched planar and central chirality elements.

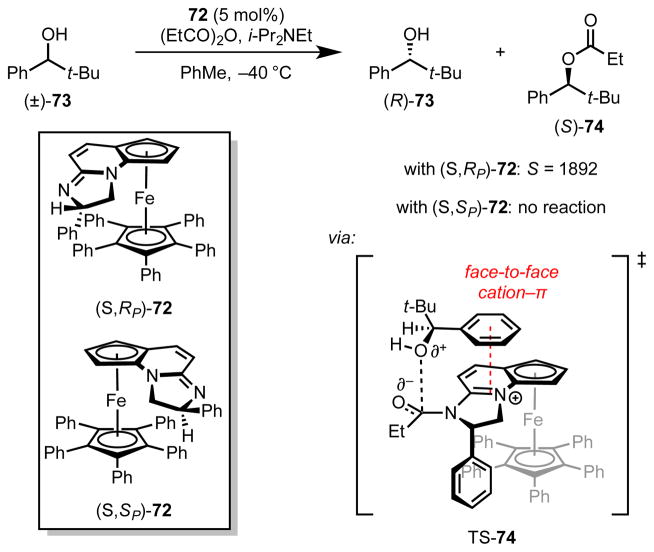
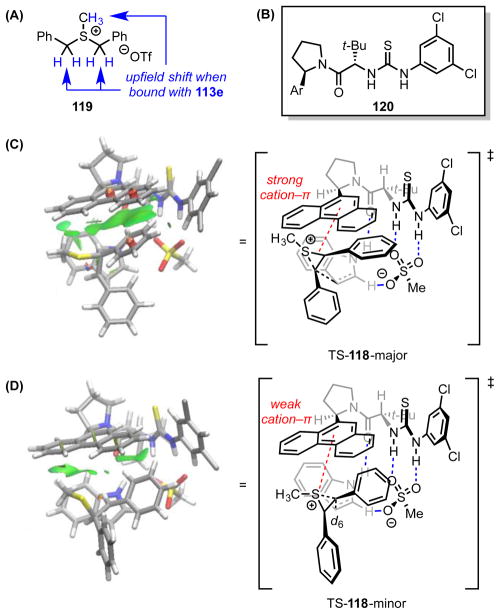
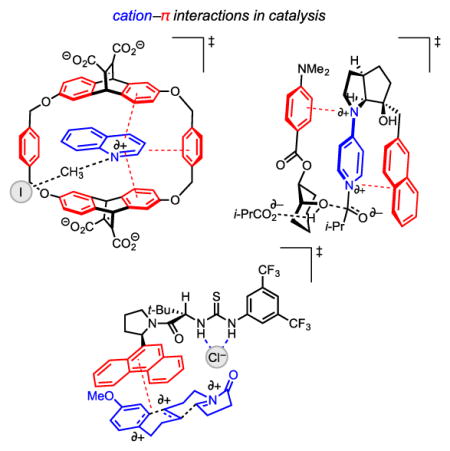
Fossey and coworkers subsequently combined insights from work by Fu^[36] and Birman^[62],[66] to develop a ferrocene-based amidine catalyst (72) containing elements of planar and central chirality for the acylative kinetic resolution of secondary benzylic alcohols (Scheme 19).^[68] The stereoselectivity observed with this catalyst system is dependent on the matched arrangement of the pentaphenyl ferrocene floor and a second α-aryl appendage to shield the bottom face of the catalyst. The authors proposed that this arrangement forces acylation to proceed through an entirely stacked conformation. When the mismatched catalyst diastereomer is employed, the α-aryl catalyst substituent precludes reaction through this stacked arrangement, and no reaction occurs. These effects underscore the importance of the purported cation–π interaction in substrate recognition responsible for the impressive selectivity factors as high as S = 1892.

4.1.4 Pyridinium Ion-Catalyzed Decarboxylation

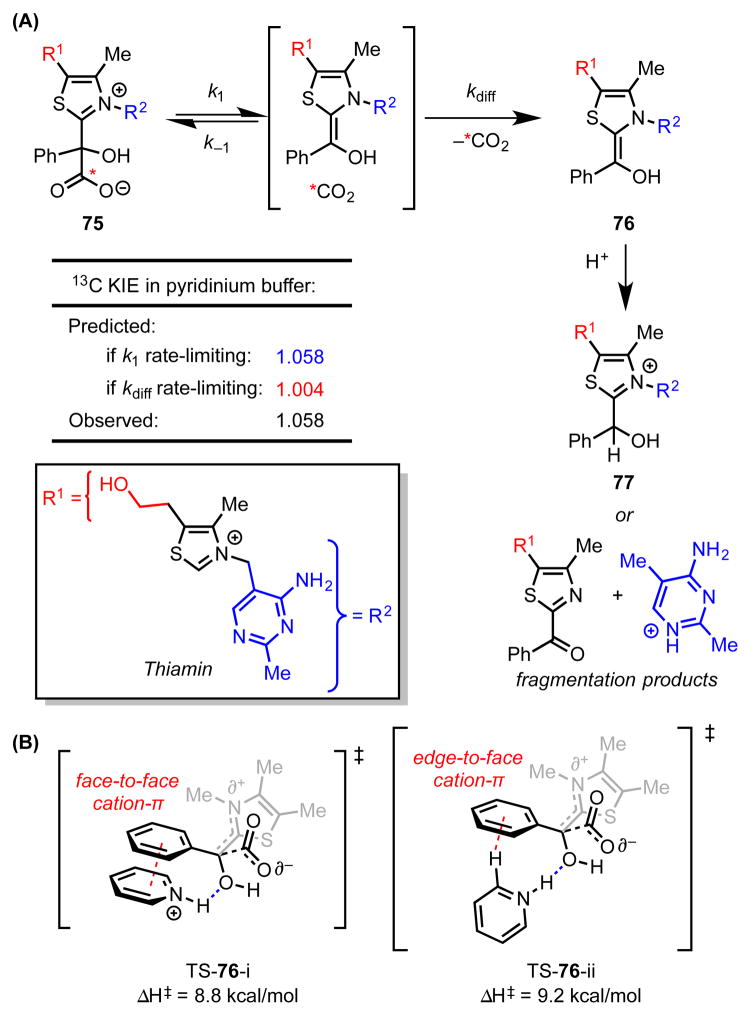
Mandelylthiamin (75) is a simple analogue of the first covalent intermediate formed by the thiamin diphosphate (TDP)-dependent enzyme benzoylformate decarboxylase en route to the formation of benzaldehyde and CO₂. While 75 undergoes decarboxylation in water at pH 5 to 7, the rate constant (k_cat) is six orders of magnitude smaller than that of the enzyme-catalyzed process. Furthermore, the immediate product of decarboxylation fragments readily with loss of the pyrimidine side-chain. While a number of Brønsted acid additives reduce the degree fragmentation, the conjugate acid of pyridine is uniquely effective at both accelerating decarboxylation and efficiently suppressing fragmentation (Scheme 20A).^[69]

Scheme 20.

(A) Agreement between predicted and experimental ¹³C kinetic isotope effects indicates that C–C bond-cleavage is the rate-limiting step of the decarboxylation mechanism. (B) The two lowest-energy computed transition structures for the decarboxylation of mendelylthiamin in the presence of a pyridinium catalyst involve cation–π interactions between the phenyl group and the pyridinium. Red dotted lines represent cation–π interactions. Blue dotted lines represent hydrogen bonds. Predicted KIEs and enthalpies of activation calculated with M06-2X/6-31G**/PCM(water).

In an effort to understand the pronounced impact of the simple pyridinium catalyst on the reaction profile, Singleton and coworkers sought to elucidate the mechanistic features of the transformation.^[70] Analysis of ¹³C isotope effects revealed that, contrary to initial proposals, irreversible decarboxylation of 75 is rate-determining in both the catalyzed and uncatalyzed reaction mechanisms. Rapid CO₂ diffusion and subsequent protonation afford intermediates 76 and 77 en route to benzaldehyde and free thiamin.

Computational (DFT and MP2) analysis indicated that both face-to-face and edge-to-face complexation of the pyridinium catalyst and mandelylthiamin are highly favorable.^[8] Furthermore, in cooperation with H-bond donation to the nascent enolate, this cation–π interaction stabilizes the decarboxylation transition state, affording calculated rate accelerations in good agreement with experimental measurements (Scheme 20B). Computations also predict that this cooperative interaction is critical for effective transition state stabilization, consistent with the experimental observation that no rate acceleration is observed with N-alkylpyridinium ions or neutral Brønsted acids.

4.2. Catalyst π-Donors

4.2.1 Cyclophane-Catalyzed Alkyl Transfer Reactions

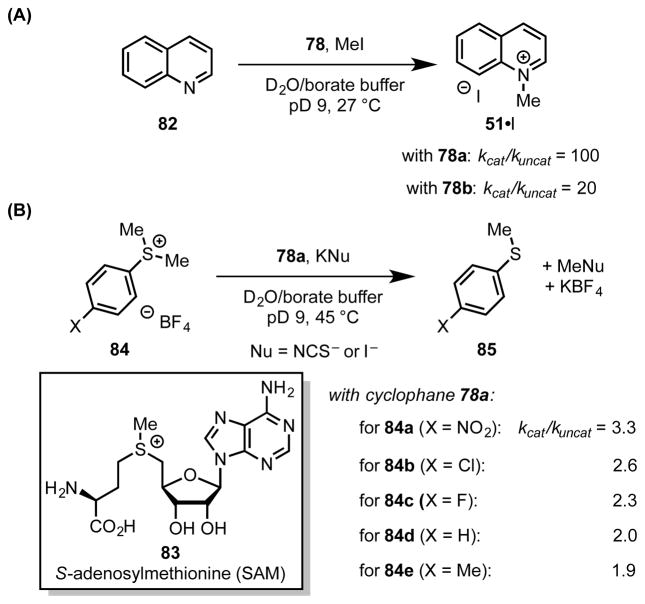
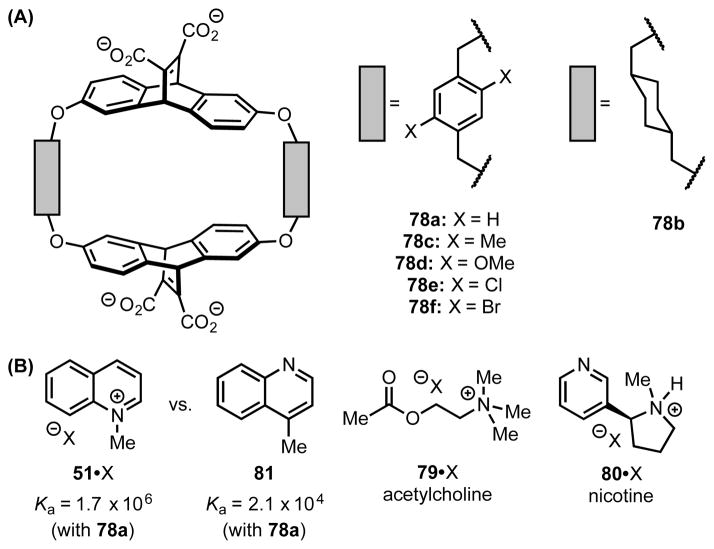
As part of their pioneering work investigating the thermodynamics of solution-phase cation–π interactions, Dougherty and coworkers developed a set of water-soluble, cyclophane-derived host molecules (78).^[1],[71] These hosts, which are characterized by their hydrophobic, arene-lined cavities, recognize and desolvate cationic species such as quinolinium (51) and ammonium ions (79 and 80), even in aqueous media.^[5a],[15a] Furthermore, the hosts exhibit a pronounced energetic preference for binding positively-charged guests over their isostructural, neutral analogs (i.e. 51 vs. 81), indicating that the cation–π interaction plays a central role in the recognition event.

Following evaluation of the thermodynamics of guest complexation with cyclophane hosts (78), Dougherty and coworkers sought to translate ground-state binding into transition-state stabilization, thereby utilizing cation–π interactions to influence the reaction rate and/or selectivity. Toward this aim, they found that cyclophane 78a imparts notable rate acceleration (k_cat/k_uncat = 100) in the N-alkylation of quinoline (82) with methyl iodide in aqueous buffer (Scheme 21A).^[8a],[72] The rate-acceleration provided by the host could, in principle, be explained simply on the basis of desolvation due to the hydrophobic effect. However, cyclophane 78b, which possesses cyclohexyldimethylene linkers rather than p-xylyl linkers, was found to exhibit a 5-fold reduction in catalytic activity (k_cat/k_uncat = 20). Given the importance of the host’s π-donating ability to catalysis, stabilizing cation–π interactions between the π-faces lining the cyclophane and the positive charge developing in the highly alkylation transition state were also proposed to contribute to the rate acceleration. The transition state-binding energy was calculated from the rate acceleration (k_cat/k_uncat) to enable comparison with the binding affinity for N-methyl quinolinium ions (51•X). Remarkably, the authors observed that the cyclophane hosts exhibit a greater binding affinity for the transition state, which bears only a partial positive charge, than for the product, which bears a full positive charge.

Scheme 21.

Cyclophane 78-catalyzed methyl transfer reactions.

Dougherty and coworkers extended the application of these cyclophane catalysts to biomimetic methyl-transfer reactions with sulfonium ion electrophiles resembling the ubiquitous cofactor S-adenosylmethionine (SAM, 83), which commonly engages in cation–π interactions in biological systems (Scheme 21B).^{[8],[13],[73]} Demethylation of sulfonium 84 by an anionic nucleophile to afford sulfide 85 involves a net decrease in formal charge. Therefore, it might be expected that a catalyst designed to stabilize positive charge would be ineffective in this reaction, as it might bind the ground-state starting material more tightly than the rate-limiting transition structure. However, cyclophane 78a was found to accelerate the reaction by a factor of 3. To rationalize this observation, the authors proposed that an interplay of electrostatic ^[7] and polarizability effects governs the overall strength of cation–π interactions.^[8] Since transition structures generally have longer bonds and more diffuse charge distribution than their substrate and product ground states, they are effectively more polarizable. This increased transition state polarizability was proposed to compensate for the decreased cationic character in the sulfonium ion demethylation, thereby enabling the cyclophane host to promote the reaction by binding the transition state more tightly than the precursor ground state, effectively lowering the energy of activation.

The validity of this hypothesis was evaluated by Hammett analysis of the rate of demethylation of substituted sulfonium ions (84a–e), both in the presence and absence of cylclophane host 78a. While both k_cat and k_uncat increase with incorporation of electron-withdrawing substituents (increasing σ) on the sulfonium ion, the slope (ρ) is greater in the presence of the cyclophane host. As such, the host enhances the substituent effect on reaction rate; the greatest acceleration is observed with electron-deficient substrates, which react through early, highly cationic transition states.^[8a] Furthermore, substituted cyclophanes (78a,c–f) spanning a range of polarizabilites show marked substituent effects in the dealkylation of 84a (Table 4).^[8b] While hosts 78a,c–f show little difference in ground state binding affinity (ΔG_a), the substituent-dependent rate acceleration (k_cat/k_uncat) correlates well with the polarizability of the substituted linker (Table 4). Taken together, these results provide compelling evidence that cation–π interactions contribute substantially to catalysis, wherein differential stabilization of the transition state over the ground state depends both on electrostatic attraction and on the polarizability of the π-donor and acceptor.

Table 4.

Correlation between polarizability, binding and catalysis of sulfonium ion demethylation.

Entry	Host	Polarizability [a]	−ΔGa[b] (kcal/mol)	kcat/kuncat	−ΔΔG‡ [c] (kcal/mol)
1	78a	10.3 (PhH)	5.7	4.9	1.0
2	78c	12.3 (PhMe)	5.2	6.4	1.2
3	78d	13.1 (PhOMe)	4.6	9.7	1.4
4	78e	14.1 (PhCl)	5.8	9.8	1.4
5	78f	14.7 (PhBr)	5.6	12.0	1.6

^[a]Polarizability of the corresponding arene with the same substituent (indicated in the parenthesis).

^[b]ΔG_a: free energy of association at 298 K.

^[c]ΔΔG^‡ differential free energy of activation between catalyzed and uncatalyzed pathways at 319 K. See Scheme 21B.

4.2.2 Supramolecular Assembly-Mediated Reactions

The design and development of hosts that behave as molecular vessels for reacting guest partners is a longstanding goal in the field of supramolecular chemistry. Utilizing the hydrophobic effect to bind small-molecule guests, these supramolecular hosts can create unique chemical microenvironments, distinct from that of the bulk solution, that enable reactions to take place with accelerated rates or altered selectivity. The rate and selectivity enhancements in such systems are inherently linked to the nature of the constrained the binding cavity, which imparts strict size-discrimination while potentially increasing the effective molarity of reactants, thereby significantly reducing the entropic price of reaction. Additionally, cation–π interactions involving the aromatic groups lining the binding cavities of many hosts play a crucial role in determining the strength, orientation, and selectivity of guest-binding events. Elegant demonstrations of the catalytic potential of such supramolecular assemblies abound.^[74]

Cation–π Interactions in Guest-Encapsulation

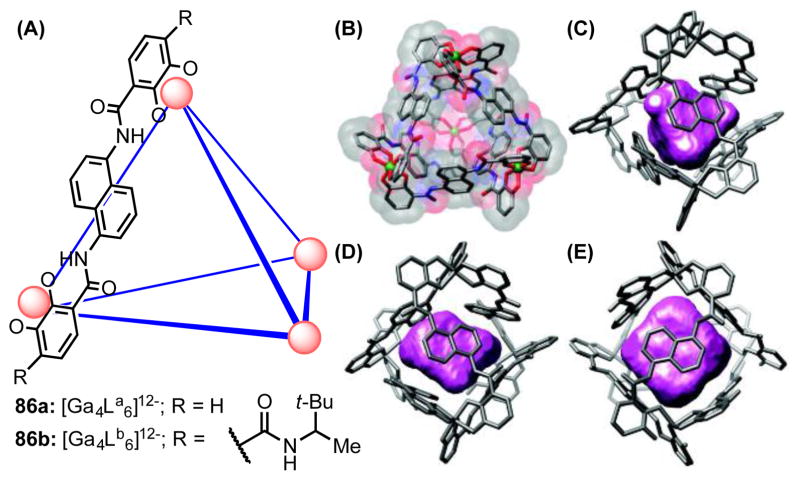
As part of a broader program in developing supramolecular assemblies for exploring host–guest chemistry, Raymond and coworkers designed a series of tetrahedral molecular vessels (M₄L₆, 86) that self-assemble upon combination of trivalent metal ions (M = Ga³⁺, Al³⁺, In³⁺ or Fe³⁺) and naphthalene-bridged bis-bidentate catchol ligands (Figure 8A).^[75] These dodecaanionic supramolecular scaffolds are soluble in water, yet they contain a central, arene-lined, hydrophobic cavity spanning 0.35–0.5 nm³ (Figure 8B). As such, these supramolecular clusters bind a range of positively charged organic and organometallic compounds with high affinity (Figure 8C–E). For example, appropriately sized phosphonium ions, ammonium ions and iminium ions are encapsulated with association constants as high as 10⁵ M⁻¹ in aqueous media.^[76] Furthermore, crystallographic analysis of cluster-encapsulated benzyltrimethylammonium ion (BnNMe₃⁺ ⊂ 86a) revealed a close contact (3.63 Å) between the cation and the cluster’s naphthalene walls, suggesting that cation–π interactions likely contribute to the overall binding strength (Figure 8D).^[77]

Figure 8.

(A) Schematic representation of the [M₄L₆]¹²⁻ assembly, with one molecule of ligand L^a shown explicitly. (B) A space-filling model of 86a. Crystal structures showing (C) NEt₄⁺, (D) BnNMe₃⁺, and (E) [Cp*₂Co]+ ions encapsulated in Ga₄L^a₆ (86a). Adapted with permission from ref 77. Copyright 2009 American Chemical Society.

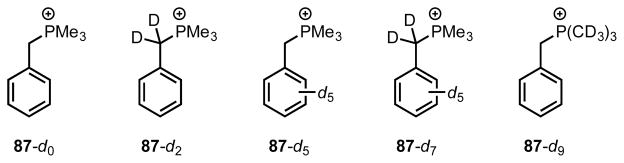
The role of the cation–π interaction in guest-binding was probed quantitatively through equilibrium isotope effect (EIE) studies using a series of benzyltrimethylphosphonium isotopologues (87-d_n, Figure 9).^[78] Host 86a exhibits a greater affinity for protiated isotopologue 87-d₀ than for its deuterated isotopologues (i.e. K_d0/K_dn ≥ 1, Table 5), and Van’t Hoff analysis indicates that the differential binding affinity is enthalpically determined. These EIE values arise from changes in the guest vibrational force constants and zero-point energies, which result from attractive interactions weakening these C–H/D bonds, upon binding to the host. Furthermore, larger EIEs per deuterium are observed at the methyl and benzylic C–H/D positions compared to the aromatic positions. Given that the methyl and benzylic C–H/D bonds bear a significant portion of the phosphonium ion’s net charge, while the aromatic C–H/D bonds do not, these EIEs are consistent with specific, enthalpically stabilizing cation-π interactions between these bonds and the arenes lining the host cavity. Theoretical EIE values calculated using DFT are in good agreement with the experimental values and further validate this interpretation.

Figure 9.

Isotopologues of benzyltrimethylphosphonium ion.

Table 5.

EIE values for interior binding of guest 87-d_n to host 86a.

Entry	Isotopologue[a]	EIE (Kd0/Kdn)[b]	EIE per D[c]
1	87-d2	1.07(1)	1.034(6)
2	87-d5	1.00(2)	1.000(3)
3	87-d7	1.103(7)	1.014(1)
4	87-d9	1.14(1)	1.015(1)

^[a]See Figure 9.

^[b]Measured in D₂O at 298 K.

^[c]EIE per D = (K_d0/K_dn)^1/n.

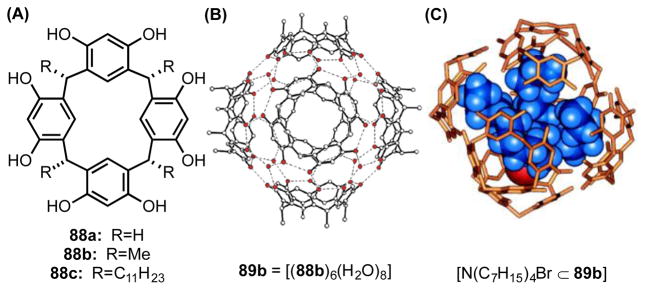
In an independent effort, MacGillivray and Atwood introduced a spherical molecular vessel (89a) comprised of six calix[4]resorcinarene subunits (88) that self-assemble through hydrogen-bonding interactions in water-saturated, nonpolar media (Figure 10A).^[79] This neutral supramolecular scaffold and its alkyl-substituted derivatives (89b,c) form hydrophobic, arene-lined cavities with volumes of approximately 1.4 nm³ (Figure 10B), and persist both in the solid state and in water-saturated chloroform.^[80] Rebek and coworkers subsequently demonstrated that 89b,c bind cationic guests, such as tetraalkylammonium ions, with high affinity (Figure 10C). They attributed this favorable cation encapsulation to the combined effect of enthalpically-stabilizing cation–π interactions between the guests and the aromatic walls of the capsule and entropically-stabilizing release of encapsulated solvent molecules.^[80b,c]

Figure 10.

(A) One calix[4]resorcinarene subunit. (B) A crystal structure of 89b, comprised of six calix[4]resorcinarene subunits and eight water molecules. Adapted with permission from ref 80c. Copyright 2004 American Chemical Society. (C) Energy-minimized structure of tetraheptylammonium bromide encapsulated within 88b. Methyl substituents omitted for clarity. Image adapted from ref. 80a.

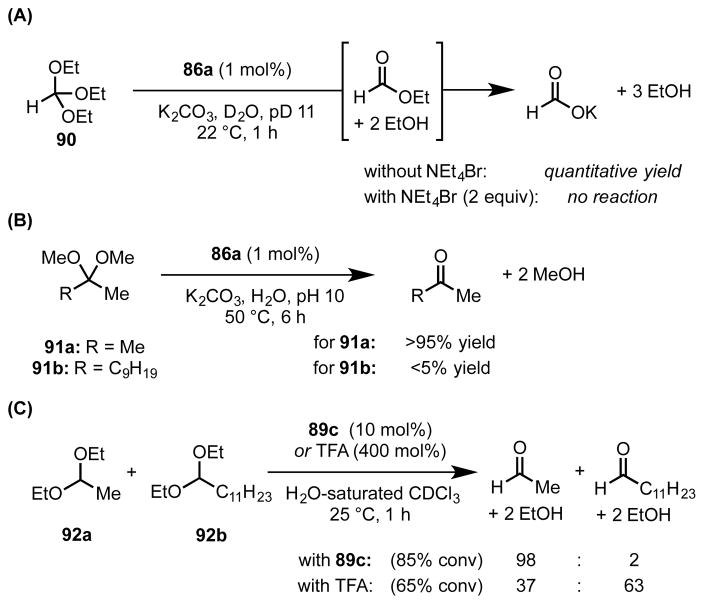
Subsequent studies revealed that phenolic residues of 89c act as Brønsted acids (pKa 5.5–6) in order to bind neutral, basic guests as their cationic conjugate acids.^[81] For example, triethylamine is encapsulated within the conjugate base of 89c as the dimeric ammonium ion (i.e. [Et₃N•HNEt₃]⁺). Tiefenbacher and coworkers attributed this increase in acidity relative to free resorcinol (pKa ~ 9) to the energetic preference for encapsulation of cationic guests due to formation of stabilizing cation–π interactions with the arenes lining the central cavity. Given their demonstrated ability to stabilize cationic species, assemblies 86 and 89 have been the focus of growing interest for the catalysis of reactions involving cationic substrates and/or intermediates.

Supramolecular Vessel-Mediated Acid Catalysis

While both orthoformates and acetals are generally stable in neutral and basic media, they undergo rapid hydrolysis in acidic solution. Inspired by the observation that 86a can increase the basicity of encapsulated guests by up to 4.5 pKa units, Pluth et al. employed the complex as a catalyst for the hydrolysis of orthoformates and acetals (Scheme 22A,B).^[82] In the presence of 86a, triethyl orthoformate and dimethoxypropane rapidly undergo hydrolysis, even under basic conditions, to afford the corresponding formate ester, which is readily hydrolyzed outside the vessel to afford formate, and acetone respectively. These reactions are inhibited by tetrabutylammonium bromide, which is known to block the cavity of vessel 86a, and the substrate scope displays a pronounced size-dependence wherein only sufficiently compact substrates undergo hydrolysis. These observations are consistent with the proposal that the reaction occurs exclusively within the host’s inner cavity.

Scheme 22.

Supramolecular vessel-mediated hydrolysis of acid-labile functional groups.

In order to elucidate the mechanism of catalysis, these reactions were monitored by ¹H NMR spectroscopy. This analysis revealed that the resonances of the naphthalene protons on the bridging ligand of 86a undergo a downfield shift in the presence of reactive substrates; however, no change occurs in the presence of unreactive orthoformates.^[82b] This downfield shift provides evidence for a specific substrate–vessel interaction, which was determined to be the complex with neutral substrate (89 or 90 ⊂ 86a). While the corresponding cationic, protonated intermediates were not observed spectroscopically, the authors proposed that the stabilizing interaction would be strengthened upon development of positive charge, thereby contributing to acceleration of rate-limiting protonation (as in orthoformate hydrolysis) or nucleophile addition (as in acetal hydrolysis).

The resorcinarene-derived capsule 89c was also demonstrated to be a competent catalyst for the hydrolysis of acetals^[81] and the hydration of isonitriles^[83] in water-saturated chloroform (Scheme 22C). As observed with 86a, the reactions catalyzed by 89c were inhibited by exogenous tetrabutylammonium bromide and exhibited pronounced size-selectivity. The differential rates of substrate ingress and egress were demonstrated to enable selective hydrolysis of one acetal in the presence of another. The selective yet efficient reactivity observed under mild conditions was attributed to Brønsted acid catalysis by the phenol residues of the capsule and by stabilizing cation–π interactions with the resultant cationic intermediates and transition structures.

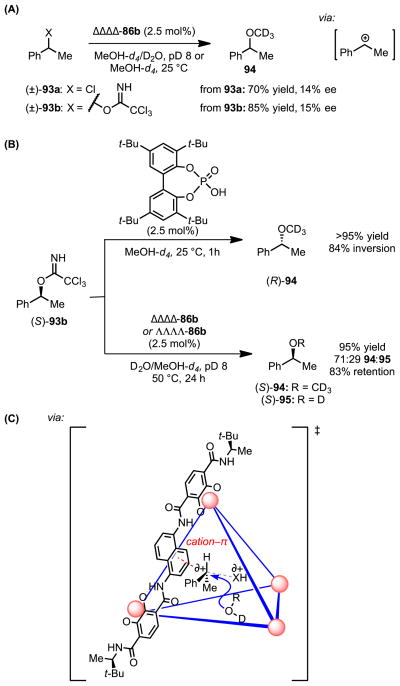
In an extension of the Brønsted acid catalysis enabled by these supramolecular assemblies, Zhao et al. demonstrated that tetrahedral assembly 86b catalyzes the solvolysis of secondary, benzylic trichloroacetimidates (93a) and chlorides (93b).^[84] The formation of enantioenriched product was achieved from racemic 93, albeit with very low levels of stereoinduction, in the presence of a single enantiomer of the capsule (either ΔΔΔΔ-86b or ΛΛΛΛ-86b) (Scheme 23A). As the identity of the leaving group (trichloroacetimidate vs. chloride) was observed to be inconsequential to the degree of enantioenrichment, the authors proposed that both substrates react through a shared intermediate, presumed to be the secondary, benzylic carbocation. However, they also noted that the reaction of a single enantiomer of substrate 93a or b in the presence of either enantiomer of 86b yields solvolysis products (94 and 95) with predominantly retention of stereochemistry (Scheme 23B). While secondary, benzylic electrophiles typically undergo stereoinvertive S_N2 solvolyses, the authors advanced that an S_N1 mechanism could account for the unusual stereochemical outcome. They proposed that a transition structure cation–π interaction between the naphthalene walls of the cavity and the positive charge developing at the benzylic carbon reduces the barrier to ionization (Scheme 23C). Preservation of this interaction with the resultant carbocationic intermediate would shield one of its faces, forcing subsequent, rapid nucleophile addition to occur from the same face as leaving group departure to afford the product with net stereoretention. This work provides a compelling example of the impact stabilizing cation–π interactions can exert on reaction outcomes.

Scheme 23.

Supramolecular vessel-catalyzed stereoretentive solvolysis of secondary, benzylic trichloroacetimidates and chlorides. The red dotted line represents a cation–π interaction; the grey dotted line represents the breaking bond. The blue arrow represents the trajectory accessible to the nucleophile in the subsequent bond-forming step.

Supramolecular Vessel-Catalyzed Cyclization Reactions

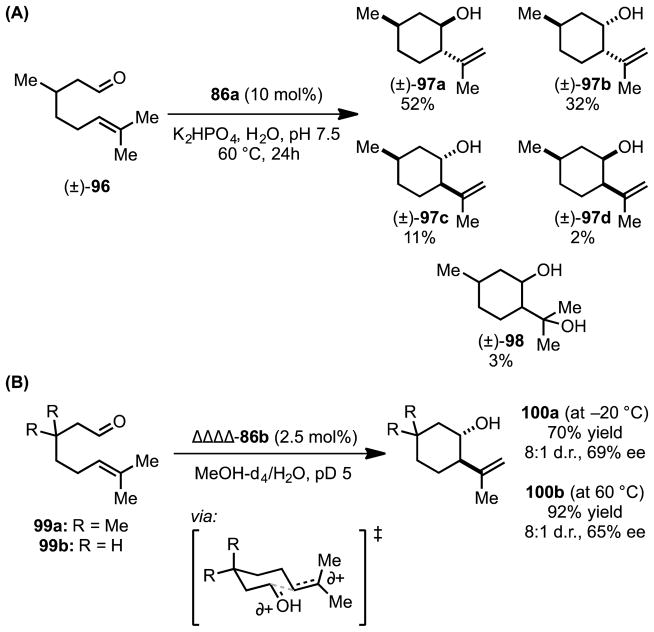
Inspired by the head-to-tail terpene cyclase enzymes, which exercise exquisite control over C–C bond-formation from cationic intermediates via networks of cation–π and other noncovalent interactions, Hart-Cooper et al. sought to apply Brønsted acid catalysis enabled by 86 to the Prins cyclization of citronellal and related substrates.^[85] Assembly 86a was observed to catalyze the Prins cyclization of citronellal (96) to afford isopulegol (97a) and its stereoisomers (97b–d) (Scheme 24A). Unlike the acid-catalyzed reaction in the absence of 86, the reaction proceeding within the catalyst’s hydrophobic cavity affords cyclic elimination products (97) rather than their hydrated analogs (98). Furthermore, use of enantiopure assembly 86b enables enantioselective Prins cyclization of achiral citronellal analogs (99a,b) in up to 65% ee (Scheme 24B).^[85b,c] Enantioinduction is proposed to be due to interactions between the cationic C–C bond-forming transition structure and the naphthelene spacer of the chiral assembly.

Scheme 24.

Supramolecular vessel-catalyzed Prins cyclization reactions.

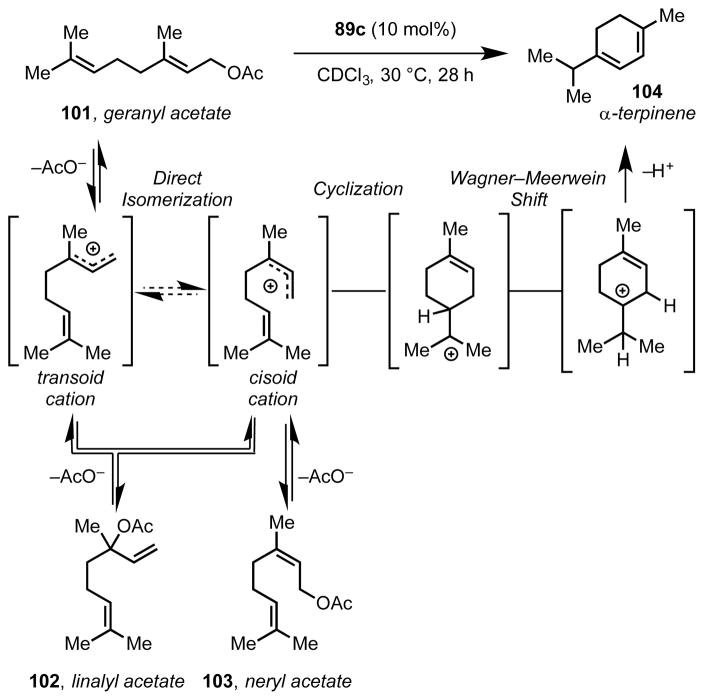
Tiefenbacher and coworkers were similarly inspired by the tail-to-head terpene cyclase enzymes to apply hexameric resorcinarene capsule 89c to the cyclization of monoterpenes, including geraniol, nerol, and linalool, and their corresponding acetates (101–103).^[86] While tail-to-head terpene cyclization is common for enzyme-catalyzed reactions, this mode of reactivity has been challenging to reproduce with synthetic systems. Remarkably, the authors were able to demonstrate that assembly 89c effectively catalyzes the “non-stop” cyclization of geranyl acetate (101) to afford α-terpinene (104) selectively (Scheme 25). To account for the intermediate α-terpinyl cation’s long lifetime, which is sufficient to allow for a 1,2-Wagner–Meerwein shift, the authors invoked stabilizing cation–π interactions between the intermediate and the aromatic walls of the capsule. They also proposed that analogous, stabilizing, transition structure cation–π interactions are responsible for reducing the activation barrier for direct isomerization of the transoid allylic cation intermediate into the cisoid form, allowing for cyclization directly from geranyl acetate and bypassing the linalyl acetate intermediate previously considered necessary. The disparate product distributions and reaction rates observed with geranyl, neryl, and linalyl acetate substrates under identical reaction conditions is consistent with this proposal. This mechanism of catalysis is loosely analogous to that employed by terpene cyclase enzymes, which control reaction outcomes by selectively stabilizing cationic intermediates and transition structures through multiple interactions with aromatic residues lining the active site.^[87]

Scheme 25.

Supramolecular vessel-catalyzed tail-to-head terpene cyclization.

Encapsulated Transition Metal-Catalyzed Transformations

In a collaborative effort, the Raymond, Bergman, and Toste groups have also explored the use of supramolecular assemblies 86a and 86b to bind cationic organometallic complexes capable of catalyzing a range of transformations.^[74g],[88] Although the precise nature of the interactions between these cationic organometallic complexes and the cavity of the supramolecular host requires further elucidation, the potential for these encapsulated catalyst systems to enable both enthalpic and entropic transition-state stabilization offers tantalizing opportunities for future development.

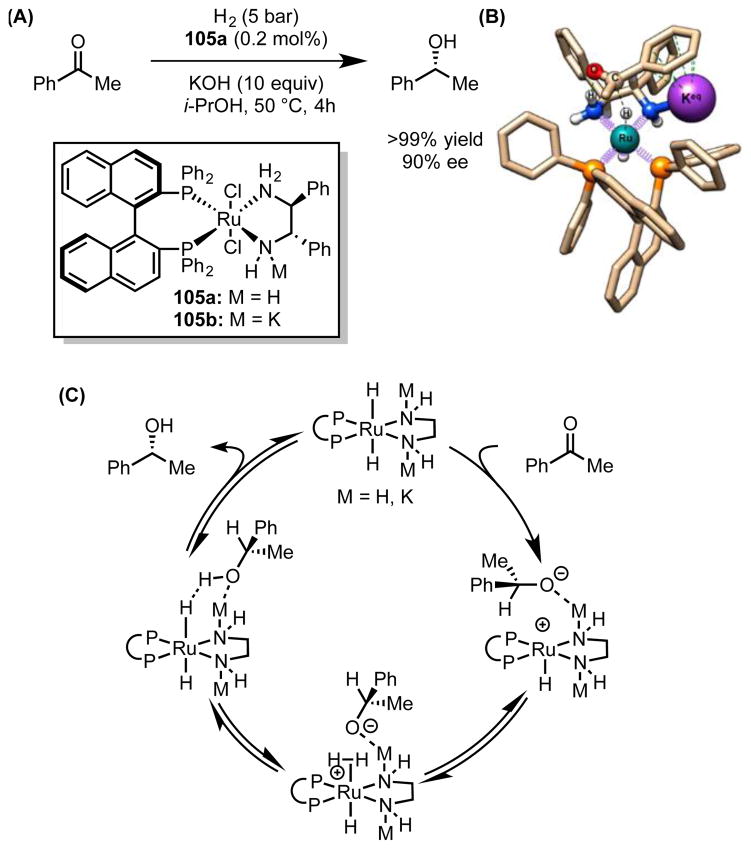
4.2.3 Alkali Metal Cation-Assisted, Ru-Catalyzed, Asymmetric Hydrogenation Reactions

Since Noyori’s seminal report,^[89] asymmetric, Ru-catalyzed, ketone hydrogenation has become a powerful and practical method for preparation of highly enantioenriched, chiral, secondary alcohols (Scheme 26A). These reactions typically require superstoichiometric quantities of an alkali metal hydroxide or alkoxide additive to attain optimal rates. Initial proposals suggested that the alkoxide may serve to neutralize HCl formed from the activation of the ruthenium precatalyst or to accelerate deprotonation of a purported η²-H₂ Ru complex. However, Hartmann and Chen demonstrated that the Lewis acidic alkali metal cation is also essential for rapid turnover.^[90] Nevertheless, its precise role in the catalytic cycle remained ambiguous.

Scheme 26.

(A) Ru-catalyzed hydrogenation of acetophenone. (B) Lowest energy computed transition structure (ωB97X-D/SDD(Ru)/6-31G*(C,H,N,O,P,K)/SMD(propan-2-ol)) for rate- and selectivity-determining C–H bond formation catalyzed by amidato complex 105b. The proposed cation–π interaction is depicted by green dotted lines. Adapted with permission from ref. 91. Copyright 2014 American Chemical Society. (C) Revised catalytic cycle.

In recent work to elucidate the role of the metal alkoxide, Dub et al. proposed a modification to the conventionally accepted mechanism, thereby reconciling it with several prior experimental studies and their own computational results.^[91] According to a reaction coordinate analysis for enantioselective reduction of acetophenone with trans-[RuH₂ (S)-binap (S,S)-dpen] (105a, where BINAP = 2,2′-Bis(diphenylphosphino)-1,1′-binaphthalene and DPEN = 1,2-Diphenyl-1,2-diaminoethane), outer-sphere hydride transfer is calculated to be the rate- and enantiodetermining step. The rate acceleration induced by a large excess of potassium tert-butoxide was attributed to the equilibrium formation of potassium amidato Ru complex 105b, which is stabilized by cation–π interactions between the alkali metal countercation and the aryl groups on both the DPEN and BINAP ligands (Scheme 26B). Reaction through this potassium amidato complex reduces the barriers to rate-determining hydride transfer by 1–2 kcal/mol and to subsequent H–H bond cleavage by 10 kcal/mol (Scheme 26C). Consistent with the importance of the cation–π interaction, the experimentally determined catalytic activity was found to depend on the identity of the cation (K⁺ > Na⁺ ≈ Rb⁺ > Li⁺),^[90] in striking agreement with the relative strengths of metal cation–π interactions in aqueous solution (K⁺ > Rb⁺ > Na⁺ > Li⁺).^[1a]

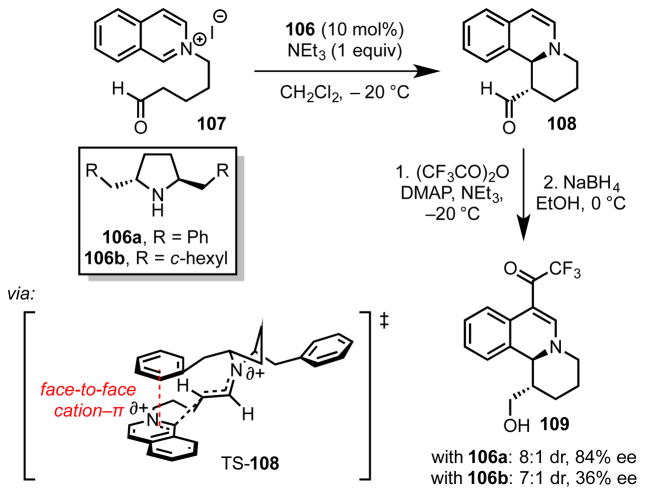
4.2.4 Pyrrolidine-Catalyzed Mannich Annulation Reactions

Jørgensen and coworkers developed a Mannich-type annulation strategy for the enantio- and diastereoselective construction of 1,2-dihydroisoquinolines (108, Scheme 27).^[92] The C₂-symmetric secondary amine catalyst (106a) activates 2-(5-oxopentyl)isoquinolinium derivatives (107) via enamine formation, thereby triggering cyclization onto the N-alkylisoquinolinium core. In this process, the pendent benzyl groups on the amine catalyst are essential for good stereoinduction. Catalyst 106b, which bears cyclohexylmethylene rather than benzyl motifs, affords 109 with similar diastereoselectivity but markedly reduced enantioselectivity. To explain this observation, Jørgensen and coworkers proposed a stereochemical model in which an attractive cation–π interaction between the benzyl group of the catalyst and the isoquinolinium cation favors reaction through a stacked conformation. This conformation exposes the si face of the isoquinolinium ion selectively, and poises the enamine to undergo addition to form (S,S)-108 in accordance with the experimentally determined absolute configuration.

Scheme 27.

Chiral pyrrolidine-catalyzed asymmetric Mannich reaction with a stereochemical model for the transition structure leading to the major product. The red dotted line represents a cation–π interaction. Black dotted lines represent breaking or forming bonds.

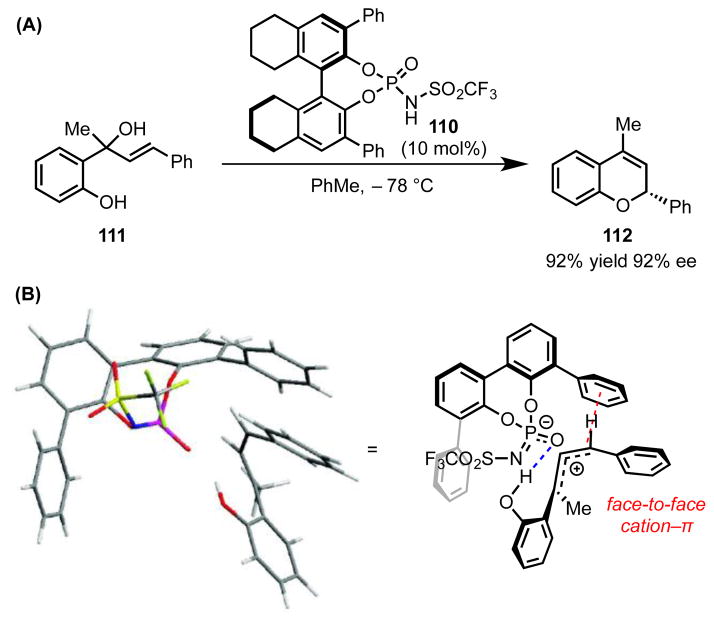
4.2.5 Phosphoramide-Catalyzed Allylic Etherifications

Achieving high enantioinduction in reactions proceeding through unstabilized carbocationic intermediates presents a major challenge in selective catalysis. Kinetic differentiation of diastereomeric reaction manifolds involving these highly reactive electrophiles is difficult due to the very early nature of transition states en route to stable products. In a step toward harnessing the reactivity of such carbocations, Rueping and coworkers employed a chiral phosphoramide Brønsted acid catalyst (110) for S_N1′ substitution of tertiary, benzylic, cinnamyl alcohols (e.g., 111) to form enantioenriched 2-arylchromenes (112, Scheme 28).^[93]

Scheme 28.

(A) Phosphoramide-catalyzed etherification of allylic alcohols, with (B) a stereochemical model of the carbocationic intermediate en route to major product 112. The red dotted line represents a cation–π interaction. The blue dotted line represents a hydrogen bond. The cyclohexyl rings of catalyst 110 are omitted for clarity. Adapted with permission from ref 93. Copyright 2011 American Chemical Society.

In this example of asymmetric ion-pair catalysis, the chiral acid is proposed to protonate 111, triggering dehydration and formation of an allylic cation. This electrophile is stabilized through electrostatic interactions with the chiral phosphoramide counteranion, which then directs cyclization to afford 112 with good enantiomeric excess. Notably, asymmetric induction is highly dependent on the substituents at the 3,3′-positions of the BINOL (1,1′-binaphthalene-2,2′-diol) framework. Only catalysts with phenyl groups at these sites catalyze the cyclization with good enantiocontrol. The authors postulated that this effect is due to an enantiodetermining cation–π interaction between this phenyl substituent and the allylic cation, orienting the substrate appropriately for highly enantiocontrolled addition of the phenol nucleophile.

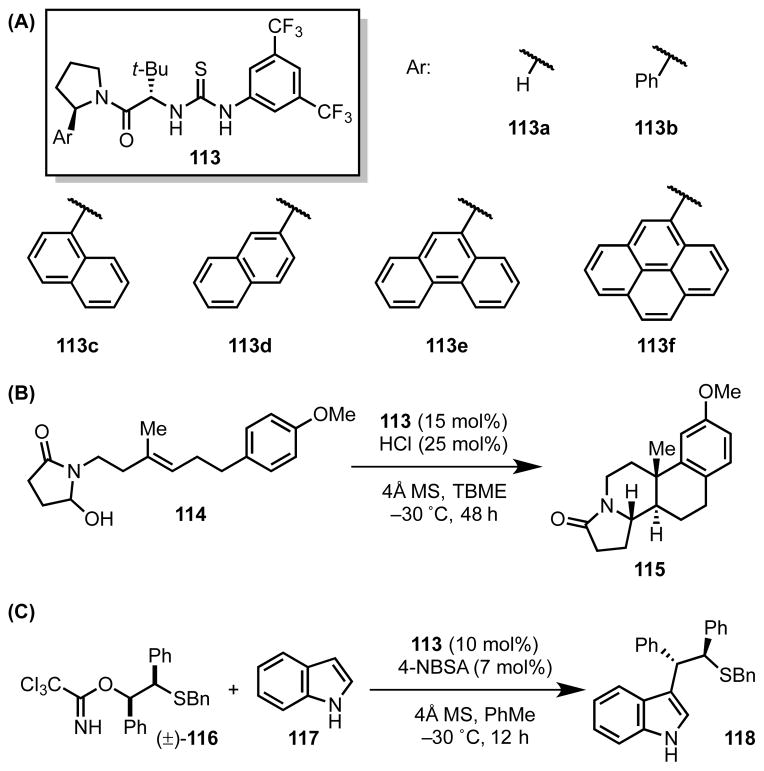
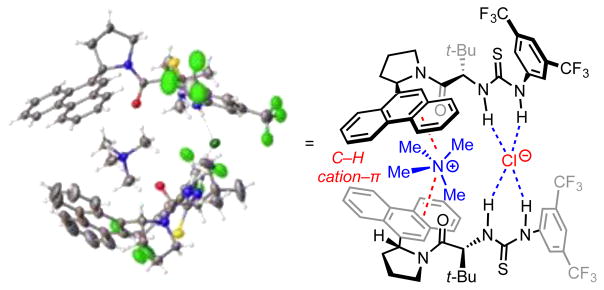
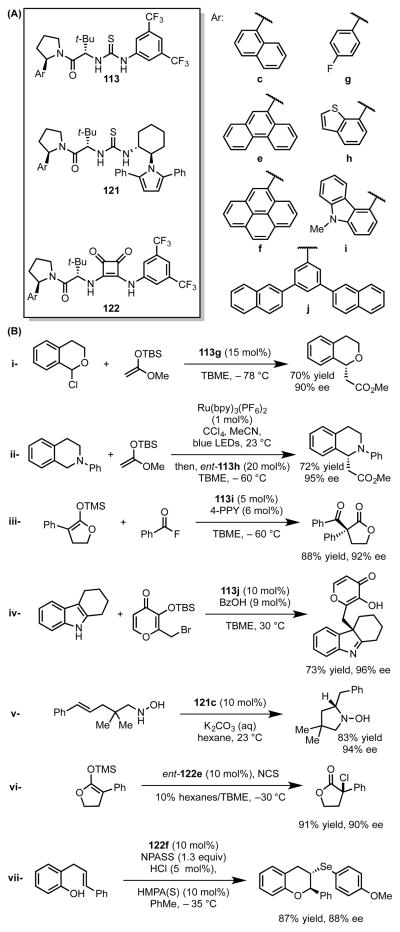
4.2.6 Guanidinium Ion-Catalyzed Claisen Rearrangements

In the first committed step of the shikimic acid pathway for biosynthesis of aromatic amino acids, chorismate mutase catalyzes the Claisen rearrangement of chorismate to prephenate with exquisite enantioselectivity and remarkable rate accelerations (up to k_cat/k_uncat = 10⁶).^[94] Crystal structures of multiple organismic variants of this enzyme bound to transition state analogs provide strong evidence that the amino acid side chains lining the active site engage chorismate with a network of attractive noncovalent interactions that cooperatively stabilize the transition state of the sigmatropic rearrangement (Figure 11A).^[94a,b] While H-bonding interactions are dominant, evidence for an additional, active site cation–π interaction has been advanced in the case of Bacillus subtilis chorismate mutase (BsCM).^[95] Inspired by this enzymatic mechanism, the Jacobsen group developed a series of C₂-symmetric guanidinium ion catalysts (19) for the Claisen rearrangements of α- and β-ketoesters (20 and 21), as discussed in Section 3.1.2.^[33a,b] Crystallographic and computational analysis indicated that cation–π interactions between the guanidinium NH₂ hydrogens and pendent pyrrole rings control the ground-state catalyst conformation, framing the space around the H-bond donor with aromatic groups.^[33c]

Figure 11.

(A) Depiction of the BsCM active site binding to the Claisen rearrangement transition state inferred from the crystal structure of the enzyme bound to a transition state mimic. Calculated major (B) and minor (C) transition structures of guanidinium 22a-catalyzed Claisen rearrangement. Calculated with B3LYP/6-31G(d). Red dotted lines represent cation–π interactions. Blue dotted lines represent hydrogen bonds. Black or grey dotted lines indicate forming or breaking bonds. Key distances are shown in Å. Adapted with permission from ref. 33c. Copyright 2011 American Chemical Society.

NMR titration experiments and computational studies further revealed that catalyst 19a binds α-ketoester 20 through dual hydrogen-bonding interactions to the ether and ester oxygen atoms. These stabilizing interactions are strengthened in the polarized transition state as the partial negative charge on the enol fragment increases. Correspondingly, the allyl fragment accumulates significant partial positive charge, which can engage in a cation–π interaction with the catalyst’s phenyl rings. DFT calculations indicated that this attractive cation–π interaction exists in only one of the two, diastereomeric transition states and is, therefore, responsible for enantiodifferentiation (Figure 11B,C).

This finding subsequently informed the design of a more enantioselective catalyst (19b) bearing electron-rich aryl groups capable of providing greater cation–π stabilization in the enantiodetermining transition state. The experimentally observed relationship between catalyst substitution (catalysts 19a–g) and enantioselectivity was reproduced by DFT calculations, lending credence to the mechanistic model (Scheme 29). The cooperative action of the cationic hydrogen-bond donor and electron-rich π-donor is thus directly analogous to the mechanism by which BsCM is proposed to catalyze the Claisen rearrangment in Nature.

Scheme 29.

Guanidinium-catalyzed asymmetric Claisen rearrangements. Relative free energies of activation were estimated according to classical transition-state theory (ΔΔG^‡ = −RT ln([(S,S)-22b]/[(R,R)-22b]), T = 313.15 K) Computed energies determined with M05-2X/6-31g(d). The black line represents a least-squares fit to a linear function (intercept, −2.10; slope, 3.95; R² = 0.88). Adapted with permission from ref. 33c. Copyright 2011 American Chemical Society.

4.2.7 Chiral Aryl-Pyrrolidino Thiourea-Catalyzed Reactions

The guanidinium-catalyzed Claisen rearrangement described above operates by selective stabilization of a polarized transition structure bearing only partial charge separation. In principle, the energetic benefits of catalysis utilizing cooperative cation–π and H-bonding interactions can be amplified in reactions involving fully charged ion-pair intermediates. Motivated by this postulate, Jacobsen and coworkers developed a family of thiourea H-bond donor catalysts (113) bearing precisely positioned aromatic substituents (Scheme 30A).^[96] Crystal structures of these catalysts bound to tetramethylammonium chloride provide compelling evidence of specific, attractive interactions with both components of the ion pair (Figure 12).^[96b] The thiourea binds the chloride anion through H-bonding interactions, while the ammonium cation associates with the π-face of the aryl-pyrrolidine. As outlined below, this type of ion pair recognition has also been extended successfully to selective stabilization of transition states, thereby enabling enantioselective reactions.

Scheme 30.

(A) Chiral aryl-pyrrolidine-thiourea catalysts for enantioselective (B) polycyclization and (C) episulfonium ring-opening reactions. TBME = tert-butyl methyl ether. 4-NBSA = 4-nitrobenzenesulfonic acid.

Figure 12.

Crystal structure of thiourea 113e binding to tetramethylammonium chloride with a 2:1 stoichiometry. Red dotted lines represent cation–π interactions. Blue dotted lines represent hydrogen bonds.

Chiral Thiourea-Catalyzed Cationic Polycyclization Reactions

This utility of these aryl-pyrrolidine thiourea catalysts was first demonstrated in the alkylation of oxocarbenium ions^[97] and was, soon after, reinforced with catalysis of the cationic polycyclization of hydroxylactam derivatives.^[98] Catalyst structure–enantioselectivity relationship studies, revealed a linear free energy relationship (LFER) between the polarizability of the catalyst aryl substituent and enantioselectivity in the cyclization of 114 (Scheme 30B, Table 5). Furthermore, analysis of temperature effects on enantioselectivity revealed that the improved stereoinduction afforded by catalysts bearing expanded aromatics is due to increased differential enthalpic stabilization of the major transition structure. Taken together, these results provide compelling evidence that attractive cation–π interactions between the cyclization transition structure and the catalyst serve to dictate the stereochemical outcome of the cyclization cascade. This mechanism of catalysis is loosely analogous to that employed by oxidosqualene cyclase, which stabilizes the highly delocalized cationic transition structure for oxidosqualene polycyclization through multiple interactions with aromatic residues lining the active site.^[13]

Table 5.

Dependence of reactivity and enantioselectivity on arene expanse in the aryl-pyrrolidine-thiourea-catalyzed polycyclization and episulfonium ring-opening reactions ^[a]

Entry	Prod	Yield (ee) with:
		113a	113b	113c	113d	113e	113f
1	115	n.d.	12% (25%)	46% (60%)	33% (61%)	52% (87%)	78% (95%)
2	118	15% (12%)	72% (73%)	84% (84%)	80% (85%)	93% (93%)	91% (91%)

^[a]See Scheme 30 for catalyst and product structures.

Chiral Thiourea-Catalyzed Episulfonium Ring-Opening Reactions

Lin and Jacobsen subsequently extended this strategy for cooperative noncovalent catalysis to a method for desymmetrization of meso-episulfonium ions (formed in situ from 116) with indole derivatives (117, Scheme 30C).^[99] As for the cationic polycylizations, enantioselectivity is highly dependent on the expanse of the π-system of the catalyst, with the 9-phenanthryl-substitued catalyst (113e) affording product 118 with the highest level of enantioinduction (Table 5). Furthermore, comparison of the absolute rates of reaction with different catalysts revealed that enantioselectivity correlates directly with rate acceleration. Because C–C bond-formation is both rate- and enantiodetermining across the catalyst series (113a–f), this observation unambiguously demonstrates that the arene-dependent increase in enantioselectivity is due to selective stabilization of the major transition state rather than to destabilization of the minor transition state.

NMR spectroscopic analysis of thiourea catalysts 113e and 113a in the presence of episulfonium model 119 provided insight into the nature of the stabilizing interactions. The resonances of the benzylic and methyl protons of model 119 undergo a significant upfield shift upon complexation with 113e, while these protons are not measurably perturbed upon complexation with 113a, which lacks an aryl substituent. The relevance of these ground-state interactions in the enantiodetermining transition state was supported by computational (DFT) studies of simplified catalysts (120b,c,e,f).^[100]

The lowest-energy, diastereomeric transition structures calculated for the ring-opening in the presence of catalyst 120e differ primarily on the basis of the distance from the catalyst aromatic group to the cationic reactants. Noncovalent interaction analysis^[101] of these structures indicates that an attractive interaction exists between the π-face of the phenanthryl group and the reacting episulfonium in the major transition structure but is almost completely absent in the minor transition structure. Taken together, these experimental and computational studies are fully consistent with the conclusion that the differential strength of the cation–π interaction between the catalyst and episulfonium ion in the major and minor transition states is responsible for enantioinduction. The mechanism of thiourea-catalyzed alkylation of indoles with episulfonium electrophiles is highly reminiscent of alkylation mediated by SAM-dependent methyltransferases as well as Dougherty’s cyclophanes (Section 4.2.1), which rely on similar cation–π interactions to engage the cofactor in the ground and transition state.

Since the initial disclosure of catalysts with the general structure depicted in Scheme 30 (113b–f) this family of aryl-pyrrodine-derived dual H-bond-donor catalysts has been applied by Jacobsen and coworkers to a range of highly enantioselective transformations in addition to those outlined above. In these studies, the H-bond donor is generally hypothesized to activate a neutral substrate by binding and/or abstracting an achiral, anionic leaving group (typically a halide, carboxylate, or sulfonate) to generate a reactive, cationic electrophile. The rest of the catalyst structure, and the aryl group of the pyrrolidino amide in particular, is proposed to provide stabilizing, secondary interactions in selectivity-determining events leading to enantioselective nucleophilic addition. Examples include the alkylation of isoquinolines,^[102] C-acylation of silyl ketene acetals,^[103] alkylation of pyrone derivatives,^[104] Cope-type hydroamination of olefins,^[105] electrophilic chlorination of silyl ketene acetals,^[106] and selenoetherification of olefins (Scheme 31).^[107] In each of these cases, the identity of the aryl-pyrrolidine substituent is seen to exert a strong, if not defining, influence on enantioselectivity. On a broader level, these examples illustrate how lessons from enzymology and molecular recognition can inform and inspire applications of noncovalent interactions, like the cation–π interaction, for the development of productive strategies in small-molecule catalysis.

Scheme 31.

Representative reactions catalyzed by arylpyrrolidine-derived H-bond donor catalysts. TBME = tert-butyl methyl ether. 4-PPY = 4-pyrrolidinopyridine. NPASS = N-p-anisylselenyl succinimide. HMPA(S) = tris(dimethylamino)phosphorus sulfide.

5. Summary and Outlook

Since its discovery in the 1980s, the importance of the cation–π interaction has become increasingly recognized in many fields of chemical science. Recent efforts, grounded in the extensive characterization of the energetics of cation–π interactions, have sought to incorporate these attractive, non-covalent interactions into functional catalyst systems in order to influence the rate and selectivity of chemical reactions through binding of reaction intermediates and differential stabilization of transition structures. This review has highlighted examples of small-molecule catalyst systems in which cation–π interactions have been invoked in the mechanism of catalysis, granting emphasis to cases in which the nature and role of the cation–π interaction have been evaluated in detail. Experimental techniques for elucidation of these effects—including kinetic analysis, modern spectroscopic methods, and crystallographic structural analysis—in combination with state-of-the-art computational methods have been critical in this endeavor. Indeed, the interplay of theory and experiment is likely to continue to play a crucial role in the exploration of applications of the cation–π interaction in small-molecule catalysis. Research in this field is just beginning to flourish, and its scope will undoubtedly continue to expand with identification of new modes of reactivity, design of novel catalyst structures, and refinement of the current understanding of these noncovalent interactions.

Figure 6.

(A) Lowest energy computed transition structures for acylation of the fast-reacting (S)-enantiomer (top) and slow-reacting (R)-enantiomer (bottom) of substrate 70a and (B) substrate 70b (M06-2X/6-311+G(d,p)/SMD(CHCl₃)//M06-2X/6-31G(d)/SMD(CHCl₃)). Red dotted lines represent cation–π interactions; blue dotted lines represent other noncovalent interactions. Grey and black dotted lines indicate breaking or forming bonds. Key distances shown in Å. Adapted with permission from ref. 67. Copyright 2012 American Chemical Society.

Figure 7.

Representative (A) cyclophane hosts and (B) small-molecule guests.

Figure 13.

(A) The benzylic proton ¹H NMR resonances of episulfonium model 119 undergo a significant upfield shift upon complexation with 113e. (B) Simplified catalysts used to approximate 113 in computational analyses. The lowest-energy computed transition structures (M05-2X/6-31G(d)) with catalyst 120e en route to the (C) major and (D) minor enantiomers of product 118. Noncovalent interactions (green surfaces) were visualized with NCIPLOT. Red dotted lines represent cation–π interactions. Blue dotted lines represent hydrogen bonds. Black or grey dotted lines indicate forming or breaking bonds. Adapted from ref. 100.

Biographies

C. Rose Kennedy was raised in Tucson, Arizona. She earned her B.S. degree from the University of Rochester, where she conducted research with Professor Alison Frontier. She is currently working on her Ph.D. at Harvard University under the direction of Professor Eric Jacobsen. Her research is focused on the development and mechanistic evaluation of enantioselective methods relying on the cooperative action of organic small-molecule catalysts and alkali metal salts.

Song Lin was born and raised in Tianjin, China. He earned his B.S. degree from Peking University in 2008, where he conducted research with Professor Zhang-Jie Shi. In 2013, he earned his Ph.D. at Harvard University, working under the direction of Professor Eric Jacobsen. His doctoral research was focused on the development and mechanistic understanding of enantioselective reactions catalyzed by multifunctional, organic small molecules. He is currently a postdoctoral fellow with Professor Christopher Chang at UC Berkeley.

Eric N. Jacobsen was born and raised in New York City. He earned his B.S. from New York University in 1982, working with Professor Yorke Rhodes, and his Ph.D. from UC Berkeley in 1986, working under the direction of Professor Robert Bergman. He then carried out postdoctoral studies with Professor Barry Sharpless at MIT. He began his independent career at the University of Illinois at Urbana-Champaign in 1988, and he moved to Harvard University in 1993, where he is currently the Sheldon Emory Professor of Organic Chemistry. His research interests lie in the discovery, mechanistic elucidation, and application of new catalytic processes.