Optimally combining propensity score subclasses

Abstract

Propensity score methods, such as subclassification, are a common approach to control for confounding when estimating causal effects in non-randomized studies. Propensity score subclassification groups individuals into subclasses based on their propensity score values. Effect estimates are obtained within each subclass and then combined by weighting by the proportion of observations in each subclass. Combining subclass-specific estimates by weighting by the inverse variance is a promising alternative approach; a similar strategy is used in meta-analysis for its efficiency. We use simulation to compare performance of each of the two methods while varying: a) the number of subclasses, b) extent of propensity score overlap between the treatment and control groups (i.e., positivity), c) incorporation of survey weighting, and d) presence of heterogeneous treatment effects across subclasses. Both methods perform well in the absence of positivity violations and with a constant treatment effect with weighting by the inverse variance performing slightly better. Weighting by the proportion in subclass performs better in the presence of heterogeneous treatment effects across subclasses. We apply these methods to an illustrative example estimating the effect of living in a disadvantaged neighborhood on risk of past-year anxiety and depressive disorders among U.S. urban adolescents. This example entails practical positivity violations but no evidence of treatment effect heterogeneity. In this case, weighting by the inverse variance when combining across propensity score subclasses results in more efficient estimates that ultimately change inference.

1. Introduction

Propensity score methods are one approach to control for confounding when estimating causal effects in non-randomized studies [1, 2]. These methods have several advantages. First, confounding is controlled for in the design stage instead of the analysis stage of the research, similar to a randomized control trial. Second, such approaches facilitate examination of the extent to which there is common support between those in the treatment and control groups (e.g., the extent of propensity score overlap between the two groups). Low-or no-support scenarios indicate violations of the positivity assumption [3]. Identification of such scenarios allow the researcher to employ approaches to reduce reliance on model extrapolation. Third, when propensity score approaches are coupled with an outcome analysis, like regression adjustment, the approach can be thought of as double robust [4]. Propensity score methods typically include matching, weighting, and subclassification. We focus on subclassification in this paper.

Propensity score subclassification has been described previously [5] and has been used in a variety of disciplines, including economics [6], health economics [7], psychology [8], and epidemiology [9]. It is a recommended approach for using propensity scores with complex survey data [10]. Briefly, it involves the following steps. First, a propensity score is estimated for each individual, i, that is the predicted probability of being treated given observed potential confounding variables. Next, the vector of propensity scores is divided into subclasses, typically based on quantiles. Once the subclasses have been identified, the average treatment effect (ATE) or another desired estimand is estimated within each of the j subclasses. Finally, the subclass-specific effect estimates are combined to estimate the overall effect.

How many propensity score subclasses to create remains a matter of debate. In theory, if each propensity score subclass contains a set of identical propensity scores (and treatment assignment is strongly ignorable and the sample size is large), then propensity score subclassification will control for all confounding [1]. However, in practice, each subclass will not be composed of individuals with equal propensity scores. The number of subclasses necessary to control for the majority of confounding will depend on the sample size and data generating mechanism, but traditional guidance is that 5 subclasses should remove 90% of the bias contributed by each covariate [5]. Another consideration in determining the number of subclasses and their quantile cutpoints is ensuring adequate numbers of treated and untreated observations within each subclass. If the sample size allows, increasing the number of subclasses beyond 5 should provide further confounding control [11, 12].

In this paper, we estimate the ATE. The overall ATE estimated from propensity score subclassification is the weighted mean of the subclass-specific effect estimates where each subclass-specific weight is equal to the proportion of observations in the jth subclass [13, 5]. This approach is sometimes called weighting by the sample size. Combining subclass-specific effects has a number of analogies with other methods. One well-known approach that underlies the Mantel-Haenszel method [14, 15] and is commonly used in combining studies for meta-analysis [16] is weighting by the inverse variance [17]. In this approach, each weight is equal to the inverse estimated variance of the study/subclass-specific ATE estimate. An advantage of this approach is that it will result in optimal efficiency if 1) the subclass-specific ATEs are normally distributed, 2) the subclasses are independent, and 3) the subclass-specific ATEs are estimating a common estimand [17]. Although these assumptions may be violated to varying degrees when combining estimates across propensity score subclasses, it is possible that inverse variance weighting may nonetheless outperform weighting by the proportion in subclass in some scenarios. The inverse variance weighting method is expected to result in more efficient ATE estimates than weighting by the proportion in the subclass because inverse variance weighting gives more weight to subclasses with more information (the inverse variance is the same as the information matrix). For example, there is little information in subclasses dominated by one treatment group, which is reflected in large variance estimates for the subclass-specific ATE estimate. The inverse variance weighting approach would down-weight such unreliable subclass-specific estimates whereas the proportion in subclass weighting approach would not.

To our knowledge, these two approaches have not been compared for estimating a difference or risk difference using propensity score subclassification. Austin conducted a simulation comparing the two methods in estimating an odds ratio [18]. However, his method of estimating the odds ratio was biased [8]. Thus, it is of interest to compare the two approaches in the scenario where the outcome is linearly related to the propensity score and the estimand is collapsible, since Cochran’s theory underlying subclassification is based on such a relationship [19]. Sanchez-Meca et al. conducted a simulation comparing weighting by the sample size to weighting by the inverse variance for combining studies in meta-analysis [20]. The authors found that in terms of bias, weighting by the sample size nearly always performed better, especially in the presence of treatment effect heterogeneity and with small sample sizes. However, in terms of efficiency, weighting by the inverse variance nearly always performed better. It is unclear whether or not the results of this simulation, which was designed to mimic meta-analysis, would translate to propensity score subclassification. In addition, Hullsiek and Louis and Myers and Louis used weighting by the inverse variance to combine propensity score subclasses in simulations comparing different methods for forming and choosing the number of subclasses [21, 22], but they did not compare weighting by the inverse variance to other methods of combining subclasses.

Our objective is to compare the well-established practice of combining propensity score subclasses by weighting by the proportion in each subclass to weighting by the inverse variance. We consider various data-generating scenarios commonly encountered in observational studies such as practical positivity violations, treatment effect heterogeneity in which the effect modifier is also related to treatment, and a complex survey design with survey weights. Propensity score subclassification with complex survey data has been discussed previously [10], but the extent to which practical violations of the positivity assumption and heterogeneity of effects across propensity score subclasses affect performance of propensity score subclassification have not been examined. The paper is organized as follows. In Section 2, we introduce notation. In Section 3, we detail the two methods we compare for combining subclass-specific estimates. The simulation studies are described in Section 4. In Section 5, we apply the two approaches to an illustrative example estimating the association between living in a disadvantaged neighborhood and past-year anxiety or depression among U.S. urban adolescents. Section 6 concludes.

2. Notation

We consider two overarching scenarios: one where the data come from a complex survey and one where the data do not. For the non-survey scenario, we observe the following data: O₁ = (W, A, Y) for each of N i.i.d. observations i = 1, …, N. For the survey scenario, we observe O₂ = (W, Δ, ΔA, ΔY) for each observation i. W is a vector of four covariates, Δ is a binary (0/1) variable indicating membership in a survey sample, A is a binary (0/1) variable indicating treatment status, and Y is continuous outcome variable.

We assume the following causal relationships. In defining them, we use Pearl’s notation where f denotes a deterministic function and U denotes exogenous random errors [23]. Three of the covariates, W₁, W₃, and W₄ are exogenous: (W₁, W₃, W₄) = f_W(U_W). W₂ is a function of W₁: W₂ = f_W2(W₁, U_W2). Survey membership is a function of the three exogenous covariates: Δ = f_Δ(W₁, W₃, W₄, U_Δ). Treatment status is a function of W₁ and W₂: A = f_A(W₁, W₂, U_A). The outcome is a function of treatment, W₁, and W₂: Y = f_Y (W₁, W₂, A, U_Y).

We are interested in estimating the ATE, defined as E(Y (1) − Y (0)) with the expectation taken over all i, where for each a ∈ {0, 1}, Y (a) is the potential outcome had treatment A = a been assigned. This estimand is identifiable under several assumptions. First, we assume strongly ignorable treatment assignment: (Y (0), Y (1)) ⫫ A|W and 0 < P(A = 1) < 1 (i.e., positivity) [1]. Second, we assume consistency, which means that the potential outcome of individual i under his/her observed treatment equals his/her observed outcome: $Y_i^{\mathit{\text{obs}}}=A_i{Y}_i(1)+(1-A_i)Y_i(0)$. Third, we assume that the stableunit treatment value assumption (SUTVA) holds, which means that there is one version of treatment and the potential outcome of individual i does not depend on the treatment assignment of another individual [1].

3. Propensity score subclassification approach

We estimate the propensity score using a correctly specified parametric logistic regression model of treatment, A, as a function of covariates, W. For the survey scenario, we estimate the model among those observations with Δ = 1, as those would be the individuals with observed data in a typical survey application. As previously recommended, we fit the propensity score model without incorporating the survey weights for the survey scenario [24].

Next, observations are categorized into subclasses by dividing the distribution of propensity scores into J quantiles of equal total size (treated and control subjects combined), where J is the number of subclasses desired. All observations are retained. In practice, other approaches may be used: quantiles of unequal size, quantile divisions based on the size of either the treated and control groups, and discarding observations outside the area of common support.

Within each propensity score subclass, the subclass-specific ATE and its variance are estimated. For the non-survey scenario, the ATE for subclass j is estimated as follows: ${\widehat{ATE}}_j=\frac{1}{N_j}{\sum }_i^{N}I({ê}_i\in {\hat{Q}}_j)((Y_i|A_i=1)-(Y_i|A_i=0))$, where N is the total number of observations, N_j is the number of observations in subclass j, ê_i is the estimated propensity score, Q̂_j = (q̂_j−1, q̂_j], and q̂_j is the j sample quantile. [11] For the survey scenario, we assume that the survey weights, defined as svywt_i = 1/P(Δ_i = 1|W_i), are known and correctly specified, which is a common assumption in survey analyses [25]. In this case, the ATE for subclass j is estimated as follows: ${\widehat{ATE}}_j=\frac{{\sum }_i^{N}I({ê}_i\in {\hat{Q}}_j){\mathit{\text{ svywt}}}_i((Y_i|A_i=1)-(Y_i-A_i=0))}{{\sum }_i^{N}I({ê}_i\in {\hat{Q}}_j){\mathit{\text{ svywt}}}_i}$. We estimate the variance of each subclass-specific, survey-weighted ATE estimate using Taylor linearization in the the survey package in R [25, 26].

The next step, which is primary concern of the study, entails combining the subclass-specific ATE estimates to estimate the overall ATE.

3.1. Weighting by the proportion in subclass

In the non-survey scenario, when combining across propensity score subclasses by weighting by the proportion in each subclass, each subclass weight is defined as w_j = N_j/N. The overall ATE is estimated as $\widehat{ATE}={\sum }_{j=1}^J{w}_j{\widehat{ATE}}_j$. The variance of $\widehat{ATE}$ is estimated as ${\hat{\sigma }}^2={\sum }_{j=1}^J{w}_j^2{\hat{\sigma }}_j^2$, where ${\hat{\sigma }}_j^2$ is the estimated variance of $\widehat{AT{E}_j}$.

In the survey scenario, ${\widehat{ATE}}_j$ is now the survey-weighted ATE estimate in subclass j. Each subclass weight is now defined as $w_j=\frac{{\sum }_i^{N}I({ê}_i\in {\hat{Q}}_j){\mathit{\text{ svywt}}}_i}{{\sum }_{j=1}^J{\sum }_i^{N}I({ê}_i\in {\hat{Q}}_j){\mathit{\text{ svywt}}}_i}$ [10] (i.e., the proportion of the population in that subclass). The overall ATE and its variance are estimated as above with these modified weights.

3.2. Weighting by the inverse variance

In the non-survey scenario, when combining across propensity score subclasses by weighting by the inverse variance, the weights now equal the proportion of inverse estimated variance in the jth subclass, $w_j=\frac{1/{\hat{\sigma }}_j^2}{{\sum }_{j=1}^{J}1/{\hat{\sigma }}_j^2}$, and the overall ATE is estimated as $\widehat{ATE}={\sum }_{j=1}^J{w}_j{\widehat{ATE}}_j$. The variance of the overall ATE estimate is estimated as ${\hat{\sigma }}^2={\sum }_{j=1}^J{w}_j^2{\hat{\sigma }}_j^2=\frac{1}{{\sum }_{j=1}^{J}1/{\hat{\sigma }}_j^2}$.

In the survey scenario, ${\widehat{ATE}}_j$ is the survey-weighted ATE estimate in subclass j, and ${\hat{\sigma }}_j^2$ is the variance of the survey-weighted, subclass-specific ATE. The overall ATE and its variance can be estimated as above.

4. Simulations

4.1. Overview and setup

We conducted a simulation study to compare performance of inverse variance weighting versus proportion in subclass weighting for combining propensity score subclasses to estimate the ATE under several scenarios.

In the base simulation, we consider a simple data-generating mechanism with a constant treatment effect in which the positivity assumption is met. We call this data-generating mechanism DGM 1 and provide its details in Table 1. In this base simulation, we consider both the survey and non-survey scenarios described in Section 2. We vary the number of subclasses, considering 5, 10, and 30 subclasses. We use N = 2, 000 for 5 and 10 subclasses, and use N = 5, 000 for 30 subclasses to ensure adequate numbers of treated and untreated observations in each subclass.

Table 1.

Simulation data generating mechanisms (DGMs). bface denotes instances where DGMs 2 and 3 differ from DGM 1. DGM 1 is the base simulation scenario with a constant treatment effect and where the positivity assumption is met. DGM 2 incorporates practical violations of the positivity assumption. DGM 3 incorporates heterogeneity of treatment effects across propensity score subclasses, but the positivity assumption is met as in DGM 1. W is a vector of four covariates, {W₁, W₂, W₃, W₄}. A represents treatment, Δ represents membership in the survey sample, and Y represents the outcome. We also provide descriptive statistics for the estimated propensity score, ê, average treatment effect (ATE) in the survey sample, and ATE in the population for each DGM.

DGM 1	DGM 2	DGM 3
W1 ~ Unif(0.02, 0.7)	W1 ~ Unif(0.02, 0.7)	W1 ~ Unif(0.02, 0.7)
W2 ~ N(0.2 + 0.125W1, 1)	W2 ~ N(0.2 + 0.125W1, 1)	W2 ~ N(0.2 + 0.125W1, 1)
W3 ~ N(−2, 0.7)	W3 ~ N(−2, 0.7)	W3 ~ N(−2, 0.7)
W4 ~ Ber(0.4)	W4 ~ Ber(0.4)	W4 ~ Ber(0.4)
A ~ Ber (Logit−1 (−0.5 + W1 + 0.1 $W_1^2$ − 0.5W2 + 0.5W1W2))	A ~ Ber (Logit−1 (−0.3 + W1 − 1.5 ${\mathit{W}}_{\mathbf{1}}^{\mathbf{2}}$ − 1.5W2 + 1.5W1W2))	A ~ Ber (Logit−1 (−0.5 + W1 + 0.1 $W_1^2$ − 0.5W2 + 0.5W1W2))
Y ~ N (−0.5 + 3W1 + 3$W_1^2$ − 2W2 + 2A, 1)	Y ~ N (−0.5 + 3W1 + 3$W_1^2$ − 2W2 + 2A, 1)	Y ~ N (−0.5 + 3W1 + 3${\mathit{W}}_{\mathbf{1}}^{\mathbf{2}}$ −2W2 + 1.5A + 2 AW1 + 2 A${\mathit{W}}_{\mathbf{1}}^{\mathbf{2}}$ −AW2, 1)
Δ ~ Ber(Logit−1(W1 − W3 + W4))	Δ ~ Ber(Logit−1(W1 − W3 + W4))	Δ ~ Ber(Logit−1(W1 − W3 + W4))
ê, mean (SD), (min, max)
0.45 (0.10) (0.10, 0.80)	0.41 (0.20) (0.003, 0.99)	0.45 (0.10) (0.10, 0.80)
ATE in survey sample: 2	ATE in survey sample: 2	$\widehat{ATE}$ in survey sample, median (IQR): 2.59 (1.38, 3.82)
ATE in population: 2	ATE in population: 2	$\widehat{ATE}$ in population, median (IQR): 2.15 (0.93, 3.38)

We perform two additional simulations in which we slightly change the data-generating mechanism from the base simulation. For the first variation, we incorporate practical violations of the positivity assumption, which occur when some observations in the treated group have a low predicted probability of being in the untreated group and some observations in the untreated group have a low predicted probability of being in the treated group. Such violations of the positivity assumption are not unusual when using observational data [27] and may compromise performance of estimators (e.g., in terms of bias, decreased efficiency) [28]. The data-generating mechanism reflecting practical violations of the positivity assumption (DGM 2) is given in Table 1 and its effect on the estimated propensity scores is also given in Table 1. For the second variation, we incorporate treatment effect heterogeneity where the effect modifier is also associated with the treatment. Such a scenario results in heterogeneity of treatment effects by the propensity score or propensity score subclasses. This final data-generating mechanism (DGM 3) is also given in Table 1 and its effect on the estimated ATE is also given in Table 1.

We evaluate performance of each method in terms of average percent bias, variance, 95% confidence interval (CI) coverage and mean squared error (MSE) across 1,000 simulation iterations. This number of iterations was sufficient for convergence of the MSE for all results. In addition, we present the percent difference comparing the MSE from the inverse variance weighting method to the MSE from the proportion in subclass weighting method and identify the best performing method for each simulation scenario, taking into account all of the performance metrics. We use R version 3.1.2 for all analyses.

4.2. Results

Table 2 summarizes the results from the base simulation (DGM 1), Table 3 summarizes results from the simulation incorporating violations of the positivity assumption (DGM 2), and Table 4 summarizes results from the simulation incorporating heterogeneous effects across propensity score subclasses (DGM 3).

Table 2.

Simulation results comparing combining subclasses by weighting by the inverse variance to weighting by the proportion in subclass in the base simulation without positivity violations and with a constant treatment effect (DGM 1). Results given by number of subclasses for the non-survey and survey scenarios for 1,000 simulations. The results assume correct specification of the propensity score model. N = 2, 000 for 5 and 10 subclasses. N = 5, 000 for 30 subclasses to ensure adequate numbers of treated and control units in each subclass.

		Proportion in Subclass Weighting (PSW)				Inverse Variance Weighting (IVW)				Comparison
N subclass	Survey scenario	| Bias |	%Bias	95%CI Cov	MSE	| Bias |	%Bias	95%CI Cov	MSE	MSE % diff	Rec
5	No	0.069	3.19	76.90	0.007	0.062	2.69	82.50	0.005	−17.77	IVW
10	No	0.044	1.35	91.70	0.003	0.042	1.07	93.30	0.003	−9.16	IVW
30	No	0.024	0.37	93.70	0.001	0.024	0.28	94.00	0.001	−1.31	IVW
5	Yes	0.097	3.89	86.70	0.014	0.085	3.14	88.20	0.011	−22.98	IVW
10	Yes	0.073	1.55	93.80	0.008	0.064	1.24	94.40	0.006	−21.67	IVW
30	Yes	0.042	0.33	94.60	0.003	0.038	0.25	94.90	0.002	−20.70	IVW

(Note: MSE % diff = (MSE_IVW − MSE_PSW)/MSE_PSW; Rec=Recommendation.)

Table 3.

Simulation results comparing combining subclasses by weighting by the inverse variance to weighting by the proportion in subclass in the alternative simulation using DGM 2 that incorporates practical violations of the positivity assumption. Results given by number of subclasses for the non-survey and survey scenarios for 1,000 simulations. The results assume correct specification of the propensity score model. N = 2, 000 for 5 and 10 subclasses. N = 5, 000 for 30 subclasses to ensure adequate numbers of treated and control units in each subclass.

		Proportion in Subclass Weighting (PSW)				Inverse Variance Weighting (IVW)				Comparison
N subclass	Survey scenario	| Bias |	%Bias	95%CI Cov	MSE	| Bias |	%Bias	95%CI Cov	MSE	MSE % diff	Rec
5	No	0.132	6.60	28.80	0.020	0.100	4.96	52.70	0.013	−38.15	IVW
10	No	0.062	2.74	81.50	0.006	0.048	1.76	88.90	0.004	−34.85	IVW
30	No	0.028	0.72	92.70	0.001	0.026	0.38	94.70	0.001	−11.69	IVW
5	Yes	0.161	7.53	75.40	0.036	0.154	7.30	71.50	0.032	−10.86	IVW
10	Yes	0.098	3.03	91.00	0.015	0.094	3.32	88.90	0.013	−12.61	IVW
30	Yes	0.053	0.66	95.20	0.004	0.051	1.17	93.40	0.004	−7.84	IVW

(Note: MSE % diff = (MSE_IVW − MSE_PSW)/MSE_PSW; Rec=Recommendation.)

Table 4.

Simulation results comparing combining subclasses by weighting by the inverse variance to weighting by the proportion in subclass in the alternative simulation using DGM 3 that incorporates heterogeneous treatment effects across propensity score subclasses. Results given by number of subclasses for the non-survey and survey scenarios for 1,000 simulations. The results assume correct specification of the propensity score model. N = 2, 000 for 5 and 10 subclasses. N = 5, 000 for 30 subclasses to ensure adequate numbers of treated and control units in each subclass.

		Proportion in Subclass Weighting (PSW)				Inverse Variance Weighting (IVW)				Comparison
N subclass	Survey scenario	| Bias |	%Bias	95%CI Cov	MSE	| Bias |	%Bias	95%CI Cov	MSE	MSE % diff	Rec
5	No	0.092	3.43	69.80	0.011	0.112	3.78	79.60	0.018	54.71	PSW
10	No	0.056	1.59	87.50	0.005	0.133	4.02	85.30	0.025	420.87	PSW
30	No	0.030	0.59	92.80	0.001	0.184	6.99	48.40	0.041	2792.12	PSW
5	Yes	0.656	30.39	0.60	0.450	0.657	30.32	30.10	0.502	11.50	IVW
10	Yes	0.627	29.05	1.10	0.412	0.613	28.28	38.60	0.448	8.75	IVW
30	Yes	0.627	29.03	0.00	0.401	0.628	29.06	20.50	0.443	10.36	IVW

(Note: MSE % diff = (MSE_IVW − MSE_PSW)/MSE_PSW; Rec=Recommendation.)

In Table 2, we see that both methods of combining estimates across propensity score subclasses perform well. This is expected as the assumptions underlying propensity score subclassification are met. The inverse variance weighting method performs slightly better than the proportion in subclass weighting method for all scenarios.

In Table 3, which reflects practical positivity violations in DGM 2, the performance of each method worsens slightly, as expected. The two combining methods continue to perform similarly, and the inverse variance weighting method performs slightly better than the proportion in subclass weighting method for all scenarios.

In Table 4, performances of the two methods differ across the survey and non-survey scenarios. In the non-survey scenario, weighting by the proportion in subclass performs better than weighting by the inverse variance in terms of bias, coverage, and MSE. In the survey scenario, both methods perform poorly. Weighting by the proportion in subclass performs slightly better in terms of MSE, but weighting by the inverse variance performs better in terms of confidence interval coverage.

We also examined performances of the two weighting methods when the propensity score model was misspecified, which was operationalized as including only the main terms of the regression of the covariates on treatment status. Relative performance was similar as seen for Tables 2–4 and is summarized in Table A1 of the online appendix.

5. Illustrative Example

5.1. Overview and setup

We now apply both the inverse variance and proportion in subclass weighting methods to estimate the association between living in a disadvantaged neighborhood and past-year DSM-IV anxiety or depressive disorder among urban-dwelling U.S. adolescents. This association has been estimated previously using propensity score subclassification [9]. The data are from the National Comorbidity Survey Replication Adolescent Supplement (NCS-A), which has been described previously and uses survey sampling weights to generalize results to the population of U.S. adolescents [29, 30, 31]. We use the same exposure, outcome, and covariates as in the original paper [9]. Covariates include adolescent age, race/ethnicity, immigrant generation, family income, maternal age at birth of the adolescent, maternal level of education, whether or not the adolescent lived his/her whole life with his/her mother and/or father, and residence in the Northeast, Midwest, South, or West. We restrict to the subsample of urban-dwelling adolescents, because the effect of living in a disadvantaged neighborhood on adolescent anxiety and depression has been shown to differ by urbanicity [9]. For illustrative purposes, we use only one imputed dataset for missing variables. Each adolescent and her/his parent or guardian provided informed assent and consent. The Human Subjects Committees of Harvard Medical School and the University of Michigan approved recruitment and consent procedures.

In this example, the propensity score is the predicted probability of living in a disadvantaged neighborhood as a function of covariates. As was done previously, we classify participants into one of eight subclasses with divisions at the 30th, 40th, 50th, 60th, 70th, 80th, and 90th propensity score percentiles. We group all participants below the 30th propensity score percentile together to ensure adequate sample size in the treated and control groups in this first subclass. We discard individuals with propensity scores outside the convex hull to limit practical positivity violations. Excluding these individuals improves internal validity but compromises external validity. Including individuals without comparable counterparts in the other treatment group would rely on extrapolation in estimation, thereby compromising internal validity. By excluding these individuals, we improve internal validity but lose the ability to interpret our results as strictly applying to the population of urban, U.S. adolescents. The lack of an interpretable population may be of concern in cases where there is demonstrated treatment effect heterogeneity. We run survey design-based, weighted linear regression models in each of the eight propensity score subclasses to estimate the difference in risk of having a prevalent anxiety or depressive disorder comparing those living in disadvantaged versus non-disadvantaged neighborhoods. Variances are calculated as for the simulation. We compare results when we ignore the survey design and weights, which estimates the effect of living in a disadvantaged neighborhood on risk of having a prevalent anxiety or depressive disorder in the NCS-A sample of urban-dwelling adolescents with comparable counterparts in disadvantaged and non-disadvantaged neighborhoods, and when we incorporate the survey design and weights, which estimates the risk in the U.S. population of urban-dwelling adolescents with comparable counterparts in disadvantaged and non-disadvantaged neighborhoods.

Table 5 summarizes the treatment probabilities and survey weights for this illustrative example and compares them to those used in the simulation scenarios. The survey weights are stabilized for ease of comparison; stabilization is achieved by dividing an individual i’s weight by the mean of all weights $\left(\frac{{\mathit{\text{svywt}}}_i}{(1/N)\sum {\mathit{\text{ svywt}}}_i}\right)$. The distribution of treatment probabilities in the illustrative example falls in between the distributions for DGMs 1 and 2, but is closer to the practical positivity violations scenario in DGM 2, suggesting that practical violations of the positivity assumption may be a slight concern even after dropping individuals outside the area of common support. Although our decision to drop individuals whose propensity scores fall outside the area of common support and to combine the first two quantiles differ from our simulation, they follow the the approach used in the original paper [9]. Moreover, data-generating mechanisms from the simulation align with key characteristics from the illustrative data after restriction to the area of common support, like degree of propensity score overlap between the treatment and control groups and distribution of survey weights (Table 5).

Table 5.

Predicted treatment probabilities (propensity scores) and stabilized survey weights for the illustrative example and data-generating mechanisms with and without practical positivity violations from the scenario with a constant treatment effect. The minimum, maximum, mean and standard deviation (SD) are given.

	Propensity Scores			Survey Weights (stabilized)
Analysis	Mean (SD)	Minimum	Maximum	Mean (SD)	Minimum	Maximum
No positivity violations, simulation	0.45 (0.10)	0.10	0.80	1.00 (1.58)	0.14	19.94
Positivity violations, simulation	0.41 (0.20)	0.003	0.99	1.00 (1.58)	0.14	19.94
Illustrative Example	0.30 (0.24)	0.03	0.92	1.00 (1.22)	0.04	13.23

5.2. Results

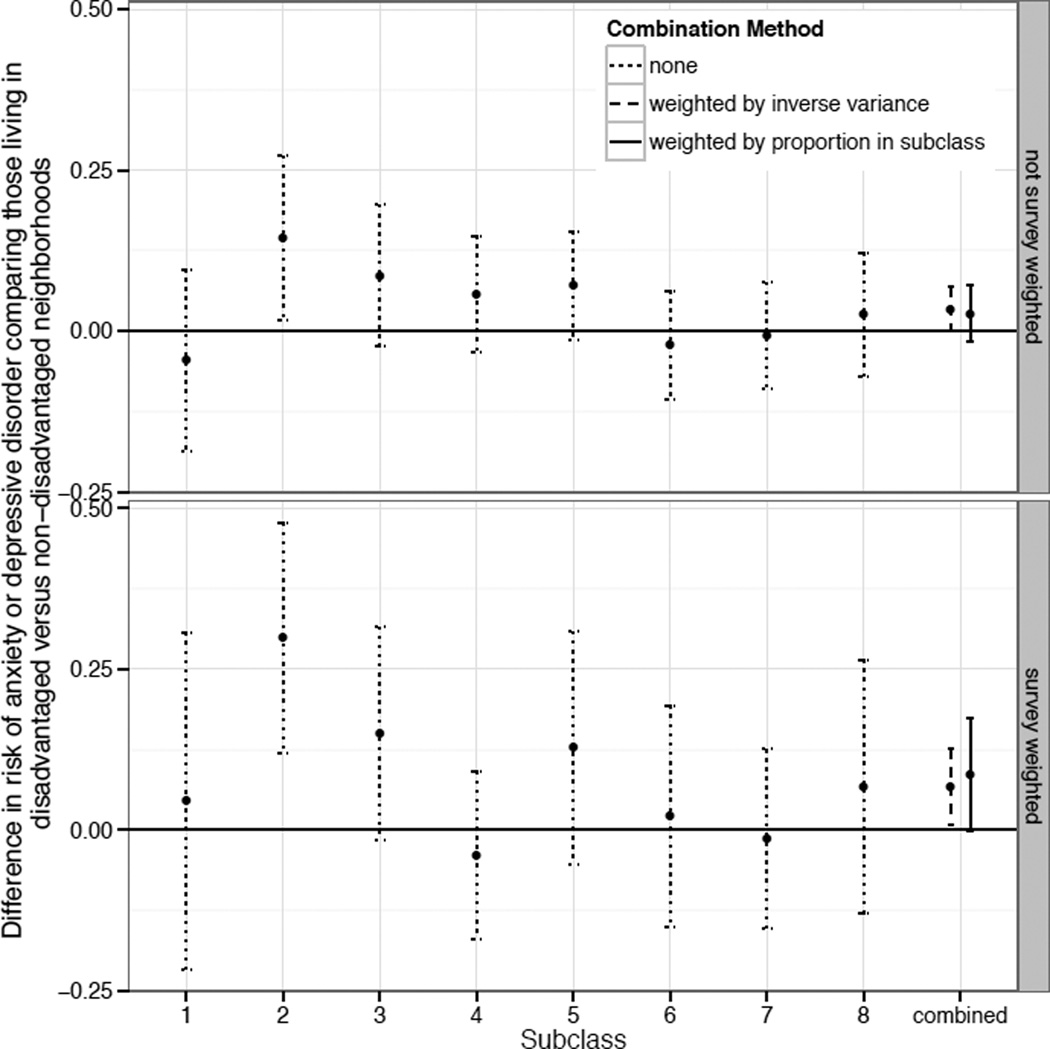
Figure 1 shows the estimated associations and 95% CIs for living in a disadvantaged neighborhood and past-year depression or anxiety disorder (interpreted as the difference in risk of current anxiety or depressive disorder comparing a scenario where all adolescents live in a disadvantaged neighborhood to one where none of them do). First, we show the association ignoring survey weights (top panel, labeled “not survey weighted” in Figure 1), which is the association among urban-dwelling adolescents in the survey sample. Second, we show the association incorporating survey weights (bottom panel, labeled “survey weighted”), which is the association among urban-dwelling adolescents in the U.S. For each of the two associations—among those in the survey sample and those in the U.S.—we compare weighting by the proportion in subclass to weighting by the inverse variance.

Figure 1.

Illustrative example: subclass-specific and overall ATEs estimated without (top panel) and without (bottom panel) survey weights. Overall ATEs compares combining subclasses by weighting by the proportion in each subclass versus weighting by the inverse variance. Each ATE is the estimated difference in risk of anxiety or depressive disorder comparing those living in disadvantaged versus non-disadvantaged neighborhoods.

For both the survey-weighted and non-survey-weighted associations, the confidence intervals are narrower when weighting by the inverse variance. This narrowing is enough to result in a change in inference between the two methods. If we were to weight by the proportion in subclass, we would conclude that there is no statistically significant association between neighborhood disadvantage and adolescent depression and anxiety in either the survey sample or in the U.S. population. However, if we were to weight by the inverse variance, we would conclude that there is a statistically significant association between living in a disadvantaged neighborhood and increased prevalence of current anxiety or depressive disorder for both the survey sample and U.S. population of urban adolescents.

Because this is not a simulation, we do not know the true effect, so we cannot know the optimal method in this particular case. However, we can align this illustrative example with the simulation scenario it most closely resembles. Based on model fit statistics, there is no evidence of treatment effect heterogeneity in the outcome model (i.e., models that incorporated treatment effect heterogeneity did not fit as well), and based on a partial F test, there is no evidence of treatment effect heterogeneity across propensity score subclasses. However, we acknowledge that this does not rule out the presence of heterogenous treatment effects. There is evidence of practical positivity violations, and we use 8 subclasses with a sample size of 4,172. Therefore, this illustrative example may be best represented by the simulation using DGM 2 (reflecting positivity violations) and 10 subclasses (Table 3, rows 2 and 5). In this simulation scenario, weighting by the inverse variance was found to perform best. Therefore, we conclude that, for urban-dwelling U.S. adolescents, living in a disadvantaged neighborhood is associated with a 6.7 percentage point increased risk of having an anxiety or depressive disorder in the past year (RD: 0.067, 95% CI: 0.007, 0.126).

6. Conclusion

In this paper, we compare two methods for combining propensity score subclasses to estimate an ATE. The first, which is the main propensity score subclass effect estimate combining method referenced in the literature, is a weighted combination of subclass-specific ATE estimates where the weights equal the proportion of individuals in each subclass. The second, a popular method for combining studies for meta-analysis, uses weights that are the inverse variances of the subclass-specific ATE estimates. We find that both methods perform well under standard assumptions of positivity and constant treatment effects, with weighting by the inverse variance slightly outperforming weighting by the proportion in subclass. However, weighting by the proportion in subclass outperforms inverse variance weighting in the presence of heterogeneous effects across propensity score subclasses in the non-survey scenario. Our results suggest that, in some cases, combining propensity score subclasses by weighting by the inverse variance can improve upon the usual approach.

Within a subclass, the ATE estimate equals the average treatment effect on the treated (ATT) estimate. Although we focus on estimating the ATE in this paper, the ATT can be easily estimated by combining subclass-specific estimates weighting by the proportion of treated individuals in each subclass. Although it is possible to estimate the ATT by combining subclass-specific estimates using the inverse variance weighting method, estimating the variance of a subclass-specific ATT estimate is not straightforward. This is a limitation of the inverse variance method for combining subclasses.

Another limitation of the inverse variance weighting method is that it is only recommended for constant effects [32]. This is because when there are heterogeneous effect estimates across propensity score subclasses, the weights should reflect the estimand of interest—in this case, the ATE [19]. Weights representing the proportion of individuals in each subclass weight the subclass-specific ATE estimates to reflect the ATE in the full sample. In contrast, while inverse variance weights are related to the sample size, they are not designed to weight the subclass-specific estimates to reflect the ATE in the total sample. It is also important to point out that depending on the causal question of interest, in the presence of treatment effect heterogeneity, the ATE may no longer be an appropriate estimand. In addition, weighting by the inverse variance can reduce the number of effective subclasses [21].

In addition, we identify an area for caution in using propensity score subclassification: in a complex survey scenario in the presence of heterogeneous effects across subclasses, 95% CI coverage of both methods is poor and other methods to address confounding should be examined.

For simplicity, we do not combine propensity score subclassification with outcome model-based adjustment like regression or g-computation. However in practice, such combination is recommended and can fully (as opposed to mostly) control for confounding if the outcome model is correct [11]. Future work should examine whether this study’s findings hold when there is additional adjustment in each subclass.

The 95% CI coverage in our simulation results is slightly less than 95% in the baseline scenario where the positivity assumption is met and the treatment effect is constant (Table 2). For lower numbers of subclasses, this is likely due to bias due to incomplete confounding control [11]. Indeed, we see that as the number of subclasses increases, coverage increases and approaches 95%. It is possible that even at 30 subclasses, coverage does not reach 95% due to remaining confounding as well as slightly underestimating the variance by not accounting for estimation of the propensity score or estimation of the subclass-specific weights [32, 11]. However, previous guidance suggests that this is typically of little practical importance [32].

In conclusion, our simulation study provides evidence that combining propensity score subclasses by weighting by the inverse variances of the subclass-specific ATE estimates may outperform the standard method of weighting by the proportion in the subclass in the case of a constant treatment effect. Both methods of combining propensity score subclasses are simple to implement in any standard statistical software, making them accessible and practical options for applied researchers.