A Note on Posterior Predictive Checks to Assess Model Fit for Incomplete Data

Abstract

We examine two posterior predictive distribution based approaches to assess model fit for incomplete longitudinal data. The first approach assesses fit based on replicated complete data as advocated in Gelman et al. (2005). The second approach assesses fit based on replicated observed data. Differences between the two approaches are discussed and an analytic example is presented for illustration and understanding. Both checks are applied to data from a longitudinal clinical trial. The proposed checks can easily be implemented in standard software like (Win)BUGS/JAGS/Stan.

1 Introduction

The posterior predictive distribution for replicated data y_rep under a data model, p(y|θ) with prior p(θ) is given by

$$p({\mathit{y}}_{\text{rep}}\mid \mathit{y})=\int p({\mathit{y}}_{\text{rep}}\mid \theta )p(\theta \mid \mathit{y})d\theta ,$$

where p(θ|y) ∝ p(y|θ)p(θ) is the posterior distribution of θ. Samples from the posterior predictive distribution are replicates of the data generated by the model. In this paper we will discuss approaches for Bayesian model checking for models for incomplete data (so y is not completely observed) based on the posterior predictive distribution. We first review the relevant literature on posterior predictive checks.

1.1 Model Fit for Complete Data

Rubin et al. [1] first used the posterior predictive distribution of a statistic to calculate the tail-area probability corresponding to the observed value of a test statistic. Meng [2] called this probability a posterior predictive p-value. In following, we will refer to it as posterior predictive probability due to its problematic interpretation as a p-value [3]. This probability is a measure of discrepancy between the observed data and the posited modeling assumptions as measured by a summary quantity T (·). The posterior predictive distribution of T (y_rep) can identify problems when the wrong model is fitted on the data and compared with (the distribution of) T (y). For the assumed model, the posterior predictive approach provides a reference distribution. The fit of the model to the data is assessed by comparing the posterior predictive distribution of T (y_rep) with T (y). Meng [2] formally defined this probability as,

$$P(T\left({\mathit{y}}_{\text{rep}}\right)>T\left(\mathit{y}\right)\mid \mathit{y})=\int \int I\left\{[T\left({\mathit{y}}_{\text{rep}}\right)>T\left(\mathit{y}\right)]\right\}p({\mathit{y}}_{\text{rep}}\mid \theta )p(\theta \mid \mathit{y})d{\mathit{y}}_{\text{rep}}d\theta .$$ (1)

In the Bayesian formulation this approach also allows the use of a parameter dependent test statistic, called a discrepancy statistic [2, 4]. For a discrepancy, D(y; θ), the reference distribution can be computed from the joint distribution of (y_rep, θ),

$$p({\mathit{y}}_{\text{rep}},\theta \mid \mathit{y})=p({\mathit{y}}_{\text{rep}}\mid \theta )p(\theta \mid \mathit{y}).$$

However locating the realized value of D(y; θ) within the reference distribution is not feasible since D(y; θ) depends on the unknown θ. This complication has led authors to use the tail area probability of D under its posterior reference distribution. Gelman et al. [5] constructed a probability as in (1) but eliminated the dependence on unknown θ, by integrating out θ with respect to its posterior distribution. The tail area probability of the discrepancy statistic is then given by

$$P(D({\mathit{y}}_{\text{rep}};\theta )\ge D(\mathit{y};\theta )\mid \mathit{y})$$

This is analogous to the posterior predictive probability in (1). The choice of test or discrepancy statistic is clearly very important and often reflects the inferential interests. In general, these checks are called posterior predictive checks.

1.2 Incomplete Data Model Fit

1.2.1 Notation and Review

To introduce posterior predictive checks for incomplete longitudinal data, we need to first introduce some notation and concepts. Let Y_i : i = 1, … , n denote the J -dimensional longitudinal response vector (with components Y_ij : j = 1, … , J ) for individual i and Y = (Y ₁, … , Y_n). Let R be the vector, ordered as Y, of observed data indicators; i.e., R_ij = I{Y_ij is observed} and let Y _obs be {Y_ij : r_ij = 1}. The full data is given as (y, r); the observed data as (y_obs, r). The extrapolation factorization of the full data model is,

$$p(\mathit{y},\mathit{r}\mid \omega )=p({\mathit{y}}_{\text{mis}},{\mathit{y}}_{\text{obs}},\mathit{r}\mid \omega )=p(\mathit{y}{y}_{\text{mis}}\mid {\mathit{y}}_{\text{obs}},\mathit{r},{\omega }_E)p({\mathit{y}}_{\text{obs}},\mathit{r}\mid {\omega }_O),$$ (2)

where ω_E indexes the conditional distribution of missing responses given observed data (the extrapolation distribution) and ω_O indexes the distribution of the observed data. The parameters ω_E and ω_O are both functions of ω and can be overlapping, often with ω_E containing a subset of ω_O (see Section 3 for an example). Inference about the full data distribution, p(y, r|ω), and the full data response model, p(y|θ(ω)), clearly requires unverifiable assumptions about the extrapolation distribution p(y_mis|y_obs, r, ω_E ) for which the observed data provide no information. Sensitivity parameters are functions of ω_E [6] and are used to introduce (external) information about the missing data mechanism.

As an example, consider a bivariate normal model (similar to the data example in Section 4). With only missingness in the second measurement, the extrapolation distribution is p(y₂|y₁, r = 0) and its parameters are ω_E ; the observed data distribution consists of the following four components: p(y₁|r = 0), p(y₁|r = 1), p(r), and p(y₂|y₁, r = 1) and ω_O are the parameters of these four distributions.

1.2.2 Current status quo

Gelman et al. [7] proposed an extension of the posterior predictive approach to the setting of missing and latent data. To assess the fit of the model they defined a test statistic T (·), which is a function of the complete data. The ’missing’ data, either truly missing or latent, were filled in at each iteration using data augmentation. The test statistic was compared to the test statistic computed based on replicated complete data. Graphical approaches were implemented for model checking along with the calculation of posterior predictive probabilities.

1.2.3 Problems with status quo

In our setting of missing data, in particular non-ignorable missingness, the current checks based on replicated complete data are problematic in that the checks will provide different evidence about the fit of the model to the observed data by varying sensitivity parameters (which are not identified by the observed data). This is an issue since sensitivity parameters a necessary component for the analysis of missing data [8]. We provide more details in Section 2.

1.3 Layout of the paper

In Section 2, we provide further details on posterior predictive checks for incomplete longitudinal data, point out the problems with replicated complete data checks of Gelman et al. [7], and propose an alternative. In Section 3, we provide an analytic example of the two approaches. We demonstrate the checks on a data example in Section 4. Finally, we provide conclusions, recommendations, and extensions in Section 5.

2 Posterior Predictive Checks for Incomplete Data

In this section we explore posterior predictive checks for incomplete longitudinal data. To implement these checks, we will sample from the posterior predictive distribution, p(y^rep, r^rep|y_obs, r), though the complete data checks will ignore r^rep. When we model the missing data mechanism, as in nonignorable missingness, we can compute data summaries based on replicates of observed data and replicates of complete data. Gelman et al. [7] proposed doing checks using complete data. However Gelman considered more general settings that include latent variables (as missing data), ignorable missingness and nonignorable missingness. We focus on the nonignorable case for which we will argue complete data checks are not appropriate (at least for assessing model fit to the observed data).

2.1 Complete Data Replications

We now review replicated complete data and the corresponding posterior predictive checks. The ’data’ for these checks are sampled from p(y^rep, r^rep, y_mis|ω, y_obs, r) (and r^rep is ignored). For each sample from the above distribution, the complete data is defined as (y_obs, y_mis) and the replicated complete data are y^rep; the dimension of y^rep is the same as (y_obs, y_mis).

To assess the fit, we choose a test statistic of interest, T_c(·), which we evaluate at each sample of complete data, (y_obs, y_mis) and replicated complete data, y^rep. We then compute the following posterior predictive probability

$$\begin{array}{cc}\hfill P(T_c\left({\mathit{Y}}^{\text{rep}}\right)>T_c({\mathit{Y}}_{\text{obs}},{\mathit{Y}}_{\text{mis}})\mid {\mathit{y}}_{\text{obs}},\text{r})& =\int \int I\left\{[T_c\left({\mathit{y}}^{\text{rep}}\right)>T_c({\mathit{y}}_{\text{obs}},{\mathit{y}}_{\text{mis}})]\right\}p({\mathit{y}}^{\text{rep}}\mid \omega )\hfill \\ \hfill & p({\mathit{y}}_{\text{mis}}\mid \omega ,{\mathit{y}}_{\text{obs}},\mathit{r})p(\omega \mid {\mathit{y}}_{\text{obs}},\mathit{r})d{\mathit{y}}^{\text{rep}}d{\mathit{y}}_{\text{mis}}d\omega .\hfill \end{array}$$

In the above, we have implicitly integrated over r^rep.

2.2 Observed Data Replications

We now introduce replicated observed data. These are sampled from p(y^rep, r^rep|ω, y_obs, r and defined as

$${\mathit{y}}_{\text{obs}}^{\text{rep}}=\{y_j^{\text{rep}}:r_j^{\text{rep}}=1\},$$

i.e., the components of y^rep (the replicated complete datasets) for which the corresponding replicated missing data indicators, r^rep are equal to one. Note that samples of r^rep will not exactly match r. As such, it is good to use a statistic that is ’normalized’ based on the dimension of the (replicated) observed data (e.g., a mean).

To assess the fit, we choose a test statistic of interest, T_o(·), which we evaluate at y_obs and each sample from the posterior predictive distribution of ${\mathit{y}}_{\text{obs}}^{\text{rep}}$. We then compute the following posterior predictive probability

$$\begin{array}{cc}\hfill P(T_o\left({\mathit{Y}}_{\text{obs}}^{\text{rep}}\right)>T_o\left({\mathit{Y}}_{\text{obs}}\right)\mid {\mathit{y}}_{\text{obs}},\mathit{r})& =\int \int I\left\{[T_o\left({\mathit{y}}_{\text{obs}}^{\text{rep}}\right)>T_o\left({\mathit{y}}_{\text{obs}}\right)]\right\}p({\mathit{y}}^{\text{rep}}\mid {\mathit{r}}^{\text{rep}},\omega ,{\mathit{y}}_{\text{obs}},\mathit{r})\hfill \\ \hfill & p(\omega \mid {\mathit{y}}_{\text{obs}},\mathit{r})d{\mathit{y}}^{\text{rep}}dF({\mathit{r}}^{\text{rep}}\mid \omega ,{\mathit{y}}_{\text{obs}},\mathit{r})d\omega ,\hfill \end{array}$$ (3)

where ${\mathit{y}}_{\text{obs}}^{\text{rep}}$ is a function of (y^rep, r^rep), F is the conditional cdf for r^rep, and typically p(y^rep|r^rep, ω, y_obs, r) = p(y^rep|r^rep, ω). Computational details for complete and observed data replications and checks are given in the next subsection.

2.3 Posterior computations

Here, we provide details on the steps for generating both complete and observed data replications.

At iteration k,

1. Sample ω^(k) from the observed data posterior, p(ω^(k)|y_obs,r) or from the data augmented posterior, $p({\omega }^{\left(k\right)}\mid {\mathit{y}}_{\text{obs}},{\mathit{y}}_{\text{mis}}^{(k-1)},\mathit{r})$ whichever is simpler (the later uses data augmentation explicitly)

2. Sample ${\mathit{y}}_{\text{mis}}^{\left(k\right)}$ from $p({\mathit{y}}_{\text{mis}}^{\left(k\right)}\mid {\mathit{y}}_{\text{obs}},\mathit{r},{\omega }^{\left(k\right)})$; this step is only needed for the complete data replications, but can simplify step 1 for the observed data replications via data augmentation.

3. Sample replicated data from $p({\mathit{y}}^{{\text{rep}}^{\left(k\right)}},{\mathit{r}}^{{\text{rep}}^{\left(k\right)}}\mid {\omega }^{\left(k\right)})$

   • (a) Complete data replication: Keep ${\mathit{y}}^{{\text{rep}}^{\left(k\right)}}$
   • (b) Observed data replication: Keep $({\mathit{y}}^{{\text{rep}}^{\left(k\right)}},{\mathit{r}}^{{\text{rep}}^{\left(k\right)}})$
4. Compute summary quantities

   • (a) Complete data replication: Compute the summary quantities T_c(·) and I{T_c(y^rep(k)) > T_c(y^(k))}, where ${\mathit{y}}^{\left(k\right)}=({\mathit{y}}_{\text{obs}},{\mathit{y}}_{\text{mis}}^{\left(k\right)})$
   • (b) Observed data replication: Compute the summary quantities T_o(·) and $I\left\{T_o\left({\mathit{y}}_{\text{obs}}^{{\text{rep}}^{\left(k\right)}}\right)>T_o\left({\mathit{y}}_{\text{obs}}\right)\right\}$ where ${\mathit{y}}_{\text{obs}}^{{\text{rep}}^{\left(k\right)}}=\{y_j^{{\text{rep}}^{\left(k\right)}}:r_j^{{\text{rep}}^{\left(k\right)}}=1\}$

For the complete data replications, estimate the desired probability using the empirical average of $I\{T_c\left({\mathit{y}}^{{\text{rep}}^{\left(k\right)}}\right)>T_c\left({\mathit{y}}^{\left(k\right)}\right\}$ across all iterations. For the observed data replications, estimate the desired probability using the empirical average of $I\left\{T_o\left({\mathit{y}}_{\text{obs}}^{{\text{rep}}^{\left(k\right)}}\right)>T_o\left({\mathit{y}}_{\text{obs}}\right)\right\}$ across all iterations.

2.4 Issues

Posterior predictive checks based on replications of complete data have some advantages. For example, under ignorable missingness, which does not require explicit specification of the missing data mechanism, it is not a problem to create replications of the complete data. But of course, in that situation, it is not possible to assess the joint fit of the observed responses and the missingness indicators and checks condition on the observed missingness indicators. Obviously, this approach loses some power versus a setting with no missing data since the missing data are filled in (via data augmentation) under the assumed model; thus, slightly biasing the checks in favor of the model. However, in the setting of nonignorable missingness, the checks have a fatal flaw as they are not invariant to the extrapolation distribution [9] and are not in the spirit of sensitivity analysis (an essential part of the analysis of missing data as documented in a recent NRC report [8]). To be more explicit, two models with the same fit to the observed data, i.e., the same p(y_obs, r|ω_O) but different (implicit) extrapolation distributions, p(y_mis|y_obs, r, ω_E ) can give different conclusions on model fit using posterior predictive checks based on replicated complete data, i.e., the values of posterior predictive probabilities change with different extrapolation distributions. This is not a desirable property for a check designed to assess model fit to the observed data.

Checks based on replicated observed data satisfy the property of invariance to the extrapolation distribution and provide the same conclusions as the extrapolation distribution (i.e., sensitivity parameters are) is varied (unlike checks based on replicated complete data), i.e., different nonignorable models with the same fit to the observed data. In addition, they can assess any features of the joint distribution of (y_obs, r) as desired. However, one would surmise that some power is lost relative to checks with no missing data (and possibly complete data replication checks) given a lack of one-to-one correspondence between the observed data responses and the replicated observed data responses; for example, Y_ij might be observed in the actual data, but is not necessarily ’observed’ in the replicated data.

We will explore these checks further in practice using a simple analytical example in the next section.

3 Analytical Example

In this section we examine analytically the behavior of the posterior predictive probability based on observed data and complete data replications under a simple, illustrative model: a mixture model for a bivariate response given by

$$\begin{array}{cc}\hfill Y_1\mid R_2=k& ~N(\mu +\xi I\{k=1\},{\sigma }_{k+1}^2):k=0,1\hfill \\ \hfill Y_2\mid Y_1,R_2=0& ~N(\alpha +\Delta +\varphi Y_1,{\tau }^2)\hfill \\ \hfill Y_2\mid Y_1,R_2=1& ~N(\alpha +\varphi Y_1,{\tau }^2)\hfill \\ \hfill R_2& ~Ber\left(\eta \right),\hfill \end{array}$$ (4)

where there is only missingness in Y₂ and [Y₂|Y₁, R₂ = 0 ] is the extrapolation distribution. Here, ${\omega }_O=(\mu ,\xi ,{\sigma }_1^2,{\sigma }_2^2,\alpha ,\varphi ,{\tau }^2,\eta )$ and ${\omega }_E=(\alpha ,\varphi ,{\tau }^2,\Delta )$; note that we have set some of the parameters in the extrapolation distribution equal to corresponding observed data parameters. Δ is the only parameter that only appears in the extrapolation distribution. Δ is a sensitivity parameter that measures departures from MAR; Δ = 0 corresponds to MAR. The purpose of this is to better understand and illustrate the behavior of both checks described in Section 2 in a simple setting.

3.1 Derivation of posterior predictive probabilities

Let n be the total number of subjects and n₁ the number of subjects with r₂ = 1. Assume the data are sorted so that all the units with missing Y₂ are at the end. Let ${\stackrel{‒}{y}}_{2,\text{obs}}=\frac{{\sum }_{i=1}^{n_1}{y}_{2i}}{n_1},{\stackrel{‒}{y}}_{1,\text{obs}}=\frac{{\sum }_{i=1}^{n_1}{y}_{1i}}{n_1}$ and ${\stackrel{‒}{y}}_{1,\text{mis}}=\frac{{\sum }_{i=n_1+1}^n{y}_{1i}}{n-n_1}$.

We specify a (diffuse) normal prior on the regression parameter, α, α ~ N (0, ν²), and to simplify the below derivation, we assume the remaining parameters are known. The test statistic for the complete data replication, T_c(·), and the observed data replication, T_o(·) are defined as the corresponding means of Y₂ (details in what follows). For the observed data replications approach, T_o(·) is evaluated at the observed data at time 2, $T_o\left({\mathit{y}}_{\text{obs}}\right)={\stackrel{‒}{Y}}_{2,\text{obs}}$, and the replicated observed data at time 2, $T_o\left({\mathit{y}}_{\text{obs}}^{\text{rep}}\right)={\overline{Y}}_{2,\text{obs}}^{\text{rep}}$. The corresponding (posterior predictive) tail area probability can be approximated as

$$\begin{array}{cc}\hfill P({\stackrel{‒}{y}}_{2,\text{obs}}^{\text{rep}}>{\stackrel{‒}{y}}_{2,\text{obs}}\mid {\mathit{y}}_{\text{obs}},{\mathit{r}}_2)& \approx \Phi \left(\frac{-\frac{{\tau }^2}{{\tau }^2+n_1{\nu }^2}\sqrt{n_1}({\stackrel{‒}{y}}_{2,\text{obs}}-\varphi (\mu +\xi ))-\frac{n_1{\nu }^2}{{\tau }^2+n_1{\nu }^2}\varphi \sqrt{n_1}({\stackrel{‒}{y}}_{1,\text{obs}}-(\mu +\xi ))}{\sqrt{\frac{n_1}{n\eta }({\tau }^2+{\varphi }^2{\sigma }_2^2)+\frac{n_1{\tau }^2{\nu }^2}{{\tau }^2+n_1{\nu }^2}}}\right)\hfill \\ \hfill & =\Phi \left(\frac{-o_p\left(1\right)A-O_p\left(1\right)\varphi B}{\sqrt{O_p\left(1\right)({\tau }^2+{\varphi }^2{\sigma }_2^2)+O_p\left(1\right){\tau }^2}}\right)\hfill \\ \hfill & =\Phi \left(\frac{m}{\sqrt{V}}\right),\hfill \end{array}$$ (5)

where $A=\sqrt{n_1}({\stackrel{‒}{y}}_{2,\text{obs}}-\varphi (\mu +\xi )),B=\sqrt{n_1}({\stackrel{‒}{y}}_{1,\text{obs}}-(\mu +\xi )),m=-o_p\left(1\right)A-O_p\left(1\right)B$ and $V=\sqrt{O_p\left(1\right)({\tau }^2+{\varphi }^2{\sigma }_2^2)+O_p\left(1\right){\tau }^2}$.

For the complete data replication approach, T_c(·) is evaluated at the completed data at time 2, $T_c\left(\mathit{y}\right)={\overline{Y}}_{2,\text{com}}$ and the replicated complete data at time 2, $T_c\left({\mathit{y}}^{\text{rep}}\right)={\overline{Y}}_{2,\text{com}}^{\text{rep}}$. The corresponding tail area probability can be approximated as

$$\begin{array}{cc}\hfill & P({\stackrel{‒}{y}}_{2,\text{com}}^{\text{rep}}>{\stackrel{‒}{y}}_{2,\text{com}}\mid {\mathit{y}}_{\text{obs}},{\mathit{r}}_2)\hfill \\ \hfill & \approx \Phi \left(\frac{m+\sqrt{\frac{n}{n_1}}\frac{n_1-n\eta }{\sqrt{n}}(\Delta -\varphi \xi )+\sqrt{\frac{n-n_1}{n_1}}\varphi \sqrt{n-n_1}(\mu -{\stackrel{‒}{y}}_{1,\text{mis}})}{\sqrt{V+\frac{n\eta }{n_1}(1-\eta ){(\Delta -\varphi \xi )}^2+{\tau }^2(\frac{2n-n_1}{n_1}-\frac{n_1}{n\eta })+{\varphi }^2{\sigma }_2^2(\frac{n\eta }{n_1}-\frac{n_1}{n\eta })+{\varphi }^2{\sigma }_1^2\frac{n-n\eta }{n_1}}}\right)\hfill \\ \hfill & =\Phi \left(\frac{m+O_p\left(1\right)\frac{1}{\sqrt{\eta }}(\Delta -\varphi \xi )C-O_p\left(1\right)\sqrt{\frac{1-\eta }{\eta }}\varphi D}{\sqrt{V+O_p\left(1\right)(1-\eta ){(\Delta -\varphi \xi )}^2+O_p\left(1\right)\frac{2(1-\eta )}{\eta }{\tau }^2+o_p\left(1\right){\varphi }^2{\sigma }_2^2+O_p\left(1\right)\frac{1-\eta }{\eta }\varphi {\sigma }_1^2}}\right),\hfill \end{array}$$ (6)

where $C=\frac{n_1-n\eta }{\sqrt{n}}$ and $D=\sqrt{n-n_1}({\overline{y}}_{1,\text{mis}}-\mu )$. Details on the derivation of both these probabilities can be found in the supplementary materials.

3.2 Comparison and implications

We will examine two main properties of the posterior predictive checks: ’power’ and ’Type I error’. In what follows, we will define ’power’ as the ability of the posterior predictive check to detect model departures or inadequacies. Good ’power’ results when the posterior predictive probabilities approach either zero or one when there are model departures/inadequacies. On the other hand, ’Type I error’ refers to the situation of having probabilities approaching zero or one when a correct model is specified.

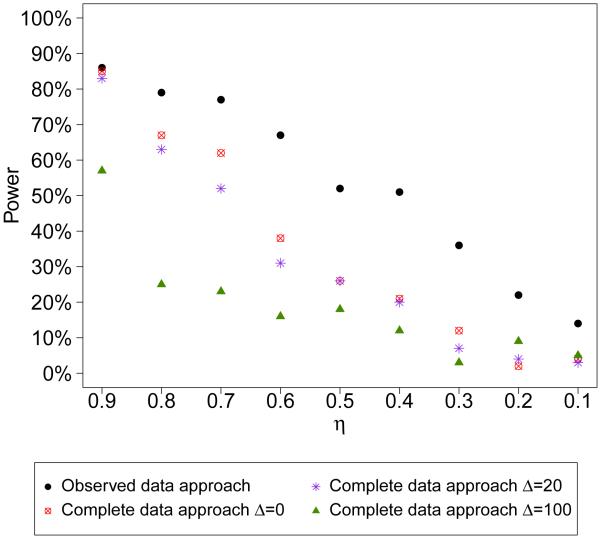
Note that given a fixed sample size, n, as η → 0 (more and more missing data), the term $\sqrt{n_1}\xi$ will be smaller so that both approaches will have less “power” to detect model departures. As an illustration, Figure 1 shows the number of times that the checks detect model departures (based on the posterior predictive probability being less than 0.05 or greater than 0.95) at various values of η when the model is misspecified with parameter values based on the data example in Section 4. Both approaches detect less model departures (less power) as η increases.

Figure 1.

’Power’ of detecting model departures using the observed data replication approach and complete data replication approach (percent of times the posterior predictive probability < 0.05 or < 0.95 in 100 replicated datasets) at various values of η. The true data model has parameters n = 100, µ = 62, ξ = 9, σ₁ = 28, σ₂ = 24, α = 16, φ = 0.9, τ = 16. The model is misspecified by assuming ξ = 0 when performing model checks. Δ = 0, 20, 100 are used for complete data approach.

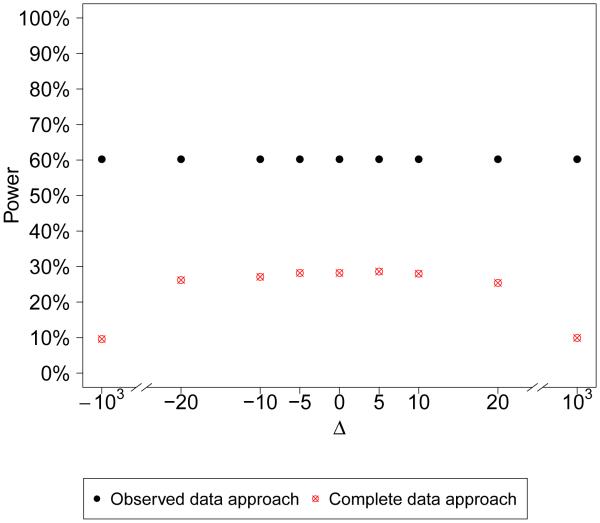
We first examine the posterior probability for the complete data replication approach. Since C is O_p(1), (6) can be written as $\Phi \left(\frac{m+c(\Delta )}{\sqrt{V+v(\Delta )}}\right)$, where c(Δ) and v(Δ) are functions of Δ. So the probability using complete data depends on the sensitivity parameter, Δ, which indicates the check is not invariant to the extrapolation distribution. In addition, as |Δ| → ∞, the denominator and numerator in (6) are both O_p(Δ), so the probability can be approximated by $\Phi \left(\frac{\frac{1}{\sqrt{n}}C}{\sqrt{1-\eta }}\right)\text{or}\Phi (-\frac{\frac{1}{\sqrt{n}}C}{\sqrt{1-\eta }})$, which only depends on n₁ but no other data. Figure 2 plots the posterior predictive probabilities using both the observed data replication approach and complete data replication approach at various values of Δ when one model is correctly specified and the other misspecified. The probabilities using the observed data stay the same across different Δ, but the probabilities using the complete data approach change with Δ and eventually converge to $\Phi \left(\frac{\frac{1}{\sqrt{n}}C}{\sqrt{1-\eta }}\right)$ as Δ → +∞ and $-\Phi \left(\frac{\frac{1}{\sqrt{n}}C}{\sqrt{1-\eta }}\right)$ as Δ → −∞

Figure 2.

Posterior predictive probabilities using the observed data replication approach and complete data replication approach at various values of Δ. The true data model has parameters n = 1000, µ = 62, ξ = 9, σ₁ = 28, σ₂ = 24, α = 16, φ = 0.9, τ = 16, η = 0.5. The data example has n₁ = 495, so $\frac{\frac{1}{\sqrt{n}}C}{\sqrt{1-\eta }}={-10}^{-0.5}$. When performing model checks, one model is correctly specified and the other misspecified by assuming ξ = 0.

One specific departure from the model fit is if we assume ξ = 0, but in truth, ξ ≠ 0. The term B in the posterior probability for the observed data replications is now $\sqrt{n_1}({\stackrel{‒}{y}}_{1,\text{obs}}-\mu )=\sqrt{n_1}({\stackrel{‒}{y}}_{1,\text{obs}}-(\mu +\xi ))+\sqrt{n_1}\xi$. In (5), the dominating term in the numerator, $\sqrt{n_1}\xi =O_p\left(\sqrt{n_1}\right)$ will drive the probabilities to zero or one. In (6), although for a given Δ, the probability will go to zero or one when n₁ → ∞, the complete replicate approach will have less power than the observed replicate approach because (6) has a larger denominator than (5). Furthermore, its power is inversely correlated with |Δ|, i.e. the larger |Δ| is, the less power the complete data replication approach has. In the extreme case, when |Δ| is of higher order than $\sqrt{n_1}$, the probability will only depend on n₁ as shown earlier, which results in no power at all. Figure 3 shows the number of times that the checks detect model departures (the posterior predictive probability is less than 0.05 or greater than 0.95) at various values of Δ when the model is misspecified using parameter values based on the data example. The observed data replication approach identifies more model departures than the complete data replication approach. Also, the complete data replication approach identifies less as |Δ| increases.

Figure 3.

’Power’ of detecting model departures using the observed data replication approach and complete data replication approach (percent of times the posterior predictive probability < 0.05 or > 0.95 in 1000 replicated datasets) at various values of Δ. The true data model has parameters n = 100, µ = 62, ξ = 9, σ₁ = 28, σ₂ = 24, α = 16, φ = 0.9, τ = 16, η = 0.5. The model is misspecified by assuming ξ = 0 when performing model checks.

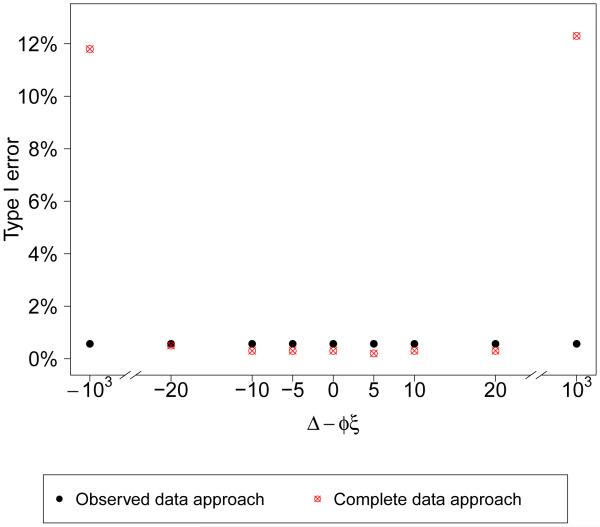
In the simple case when σ₁ = σ₂ and Δ is set to φξ, the probability in (5) is approximately $\Phi \left(\frac{-\varphi B}{\sqrt{2{\tau }^2+{\varphi }^2{\sigma }_2^2}}\right)$ (6) is approximately $\Phi \left(\frac{-\varphi B-\sqrt{\frac{1-\eta }{\eta }}\varphi D}{\sqrt{\frac{1}{\eta }(2{\tau }^2+{\varphi }^2{\sigma }_2^2)}}\right)$. When the correct model is specified, both (5) and (6) are Φ(H) where $H~N(0,\frac{{\varphi }^2{\sigma }_2^2}{2{\tau }^2+{\varphi }^2{\sigma }_2^2})$ since both B and D are $N(0,{\sigma }_2^2)$ and they are independent (though given the data the two probabilities are not necessarily the same). So the two approaches will have the same Type I error. When σ₁ = σ₂ but Δ ≠ φξ, the complete replicate approach will have larger Type I error, since it has larger variance than H. Figure 4 shows the number of times that the checks falsely detect model departures (based on the posterior predictive probability being less than 0.05 or greater than 0.95) at various values of Δ when the model is correctly specified in an example where σ₁ = σ₂. The observed data replication approach identifies the same number of model departures as the complete data replication approach when Δ = φξ. The complete data replication approach identifies more (larger Type I error) as |Δ| increases. In general, the complete data replication approach has larger Type I error especially when |Δ| is large. There are exceptions, for example, when Δ = φξ and σ₁ < σ₂, the observed approach has larger Type I error.

Figure 4.

Type I error using the observed data replication approach and complete data replication approach (percent of times the posterior predictive probability < 0.05 or > 0.95 in 1000 replicated datasets) at various values of Δ when model is correctly specified and σ₁ = σ₂. The true data model has parameters n = 500, µ = 62, ξ = 9, σ₁ = σ₂ = 28, α = 16, φ = 0.9, τ = 25, η = 0.7.

4 Data example

We illustrate the checks using the model in Section 3 on data from a randomized clinical trial. The objective of the trial was to examine the effects of recombinant human growth hormone therapy for building and maintaining muscle strength in the elderly. The study, which we will refer to as GH, enrolled 161 participants and randomized them to one of four treatments arms. Various muscle strength measures were recorded at baseline, 6 months, 12 months. We focus on mean quadriceps strength, measured as the maximum foot-pounds of torque that can be exerted against resistance provided by mechanical device. We will focus on two of the treatment groups, Exercise + Growth Hormone (EG) and Exercise + Placebo (EP), denoted as Z = 1 and Z = 2. Of the 78 randomized to these two arms, only 53 had complete follow-up (and the missingness was monotone); see Table 1. For illustration, we focus on the month 0 (baseline) and month 12 measures. As such, Y = (Y₁, Y₂)^T is quad strength measured at months 0 and 12. The corresponding observed data indicators are R = (R₁, R₂)^T. In this data, the baseline quad strength is always observed, so P (R₁ = 1) = 1.

Table 1.

Growth hormone trial: sample means (standard deviations) stratified by treatment group

Treatment	R 2	n	Y 1	Y 2
EG	0	16	58 (23)
	1	22	78 (24)	88 (32)
	All	38	69 (25)	88 (32)
EP	0	9	70 (35)
	1	31	65 (24)	72 (21)
	All	40	66 (26)	72 (21)
All	0	25	62 (28)
	1	53	70 (24)	79 (27)
	All	78	68 (26)	79 (27)

Let (y_obs,i, r_i, z_i) be the observed data for subject i, i = 1, …, 78. We fit the data from both treatment groups to the model introduced in Section 3. The parameters of the observed data model, ω_O, are given diffuse priors. The test statistic for each treatment group is defined as the corresponding means of Y₂. For example, for the treatment group EG, the test statistics used in the observed data replication approach are $T_o^{EG}\left({\mathit{y}}_{\text{obs}}\right)=\frac{{\sum }_{i=1}^{78}{y}_{2i}I(r_{2i}=1)I(z_i=1)}{{\sum }_{i=1}^{78}I(r_{2i}=1)(z_i=1)}$ and $T_o^{EG}\left({\mathit{y}}_{\text{obs}}^{\text{rep}}\right)=\frac{{\sum }_{i=1}^{78}{y}_{2i}^{\text{rep}}I(r_{2i}^{\text{rep}}=1)I(z_i=1)}{{\sum }_{i=1}^{78}I(r_{2i}^{\text{rep}}=1)I(z_i=1)}$, and the test statistics used in the complete data replication approach are $T_c^{EG}\left({\mathit{y}}_{\text{obs}}\right)=\frac{{\sum }_{i=1}^{78}{y}_{2i}I(z_i=1)}{{\sum }_{i=1}^{78}I(z_i=1)}$ and $T_c^{EG}\left({\mathit{y}}_{\text{obs}}^{\text{rep}}\right)=\frac{{\sum }_{i=1}^{78}{y}_{2i}^{\text{rep}}I(z_i=1)}{{\sum }_{i=1}^{78}I(z_i=1)}$. We calculate and compare the posterior predictive probabilities using complete and observed replications at various values (0, 5, 10, 20, −5, −10 and −20) of the sensitivity parameter Δ. Note previous analyses (e.g., [6]) considered negative Δ’s up to a value of −20 as dropouts were thought to be doing worse than completers. However, for illustration here, we also consider positive values of Δ.

Table 2 shows the marginal means of the responses E(Y₁) and E(Y₂) estimated from the model for different Δ. E(Y₂) changes with the sensitivity parameter. The posterior predictive probabilities using observed and complete replicated datasets at various values of the Δ are shown in Table 3. As shown in Section 3, the posterior predictive probabilities using observed replicated datasets are invariant to the sensitivity parameter Δ; those using complete replicated datasets change dramatically with Δ. Also using observed replicated datasets seems to have more power (posterior predictive probability of 0.08 for EG) to detect model departure than using complete replicated datasets (posterior probability probability ≥ 0.2 for EG) given the observed differences in means at month 12 in Table 1.

Table 2.

Marginal means of responses estimated from the model for different Δ

				Δ =
Response	0	5	10	20	−5	−10	−20
Y 1	67.6	67.6	67.6	67.6	67.6	67.6	67.6
Y 2	76.6	78.2	79.9	83.1	75.0	73.4	70.1

Table 3.

Posterior predictive probabilities using observed data replications and complete data replications for both treatments

Treatment	Type	0	5	10	Δ = 20	−5	−10	−20
EG	observed	0.08	0.08	0.08	0.08	0.08	0.08	0.08
EG	complete	0.30	0.27	0.24	0.20	0.33	0.36	0.43
EP	observed	0.84	0.84	0.84	0.84	0.84	0.84	0.84
EP	complete	0.69	0.72	0.75	0.80	0.66	0.62	0.55

Given the relatively poor fit, we tried to improve the fit by not assuming the parameters were the same for EP and EG. In particular, we use the same model but with separate parameters for EP and EG. Table 4 has the marginal means for the responses for EP and EG and Table 5 has posterior predictive probabilities in the new model. Clearly model fit is improved with posterior probabilities very close to 1/2.

Table 4.

Marginal means of responses estimated from the model for different Δ

					Δ =
Treatment	Response	0	5	10	20	−5	−10	−20
EG	Y 1	69.3	69.3	69.3	69.3	69.3	69.3	69.3
EG	Y 2	79.3	81.4	83.5	87.7	77.1	75.0	70.8
EP	Y 1	65.9	65.9	65.9	65.9	65.9	65.9	65.9
EP	Y 2	73.3	74.5	75.6	78.0	72.1	70.9	68.5

Table 5.

Posterior predictive probabilities using observed data replications and complete data replications for both treatments

Treatment	Type	0	5	10	Δ = 20	−5	−10	−20
EG	observed	0.50	0.50	0.50	0.50	0.50	0.50	0.50
EG	complete	0.50	0.50	0.50	0.50	0.49	0.49	0.49
EP	observed	0.50	0.50	0.50	0.50	0.50	0.50	0.50
EP	complete	0.50	0.50	0.50	0.51	0.50	0.50	0.49

5 Conclusion

We have proposed a convenient way to assess the fit of the Bayesian models in the presence of incomplete data using posterior predictive checks; such checks can easily be implemented in WinBUGS/JAGS/Stan (see the supplementary materials for WinBUGS code for the model and checks from Sections 3 and 4). Both approaches (based on either complete or observed data replications) not surprisingly result in less power than if we actually had complete data. And the analytical example and data example showed how sensitivity parameters, Δ in our development in Sections 3 and 4, can have a large impact on the assessment of model fit for complete replication approaches. The fact that the observed replications satisfy the invariance to the extrapolation distribution un- like the complete replications which arguably, is a necessary property [9], leads us to recommend checks based on the replicated observed data as the preferred approach for nonignorable missingness even at the potential loss of power in some settings. Our approach, using the observed replications, separates the fit of the model to the observed data from the (subjective) reasonableness of the imputations. These two pieces correspond respectively to the two components in the extrapolation distribution.

Clearly, further work needs to be done to better understand the behavior and operating characteristics of these checks based on replicated observed data in various settings with nonignorable missingness and potentially causal inference settings for which checks should also share a property similar to the invariance to the extrapolation distribution. However, comparing the complete and observed data replications by simulation will not serve a useful purpose since only the latter have the desired invariance property.

We do note that the complete replications can be useful to assess the ’reasonableness’ of imputed missing response (as in one of the examples in [7]), but not to assess model fit based on observed data. The other important message is that methods used for latent data are often not valid for (nonignorably) missing data (other than similar computational algorithms). We see the same idea in the recommendations for DIC in [10] which do not coincide with those in [11] and the fact that different distributions for latent variables provide differential fits to the observed data unlike different values for sensitivity parameters (in the extrapolation distribution) for nonignorable missngness.