Abstract
We describe a mathematical decision model for identifying dynamic health policies for controlling epidemics. These dynamic policies aim to select the best current intervention based on accumulating epidemic data and the availability of resources at each decision point. We propose an algorithm to approximate dynamic policies that optimize the population’s net health benefit, a performance measure which accounts for both health and monetary outcomes. We further illustrate how dynamic policies can be defined and optimized for the control of a novel viral pathogen, where a policy maker must decide (i) when to employ or lift a transmission-reducing intervention (e.g. school closure) and (ii) how to prioritize population members for vaccination when a limited quantity of vaccines first become available. Within the context of this application, we demonstrate that dynamic policies can produce higher net health benefit than more commonly described static policies that specify a pre-determined sequence of interventions to employ throughout epidemics.
Keywords: epidemics, dynamic resource allocation, approximate dynamic programming, approximate policy iteration, influenza, H1N1
1. Introduction
Despite the advent of effective vaccines and antimicrobial drugs, infectious diseases remain a leading cause of morbidity and mortality [1]. Over the past several decades, the appearance of novel pathogens (e.g. HIV, SARS, new strains of influenza) and the persistence of others (e.g. malaria, tuberculosis) have generated public concern and triggered extensive efforts to develop strategic plans to confront new and existing infectious threats using scarce resources (e.g. vaccine doses and budget) available to policy makers [2–5].
Classical approaches for identifying optimal strategies for infectious disease control use mathematical or simulation models of disease spread to compare the performance of a limited number of static policies, and select the one with the best projected outcome. Static policies specify a pre-determined sequence of future actions, such as “Keep schools closed between weeks 10 and 12 after the start of an influenza epidemic,” and are straightforward to evaluate and optimize using epidemic models [2,3,6–10]. In practice, these static policies would require a policymaker to commit to a sequence of future interventions specified at the onset of an epidemic and hence, are not structured to facilitate a decision making process that is responsive to the latest epidemic data.
Policy makers will likely desire (and feel public pressure) to use accumulating epidemic data (e.g. notified influenza hospitalizations) to dynamically revise and update their decisions. Policies that make recommendations based on latest epidemic data, such as “Close schools when the total number of hospitalizations passes a certain threshold” [3,9,11,12], therefore have substantial appeal. These dynamic policies do not pre-specify the timing of the future interventions and instead use epidemic observations to guide the employment of control interventions [13,14].
Despite their intuitive appeal, dynamic policies have gained less attention in the literature because defining and optimizing these policies is challenging. The observations that can be made during epidemics are numerous (e.g. notified hospitalizations, disease-related mortality, and vaccine availability) and measures of these observations must be made repeatedly over time. A large number of dynamic policies can thus be defined, each of which differs in the manner that the accumulating set of observations is used to inform decisions. A fundamental question is how one can construct dynamic policies that use simple, easily obtained measures of epidemic state and resource availability which still can inform (approximately) optimal decisions throughout epidemics.
Our objective in this paper is to develop a decision model that can be used to define and optimize dynamic policies for controlling epidemics. The optimality of these policies will be determined by their ability to minimize disease-related morbidity and mortality under defined resource constraints (e.g. vaccine doses and budget). To demonstrate the use of our decision model, we consider the problem of resource allocation during an emerging epidemic in which a novel viral pathogen spreads in a completely susceptible population. Examples of such epidemics include H1N1 and H5N1 influenza [3, 5, 15] and SARS [4, 16]. Although we will focus on the problem of resource allocation during a novel pathogen pandemic, the decision model proposed here can be used to characterize dynamic policies for control of other patterns of infectious disease spread.
2. Motivating Example: Resource Allocation during a Novel Pathogen Pandemic
While vaccination remains the most effective intervention to mitigate the impact of epidemics [3], vaccines against novel pathogens usually become available only in limited supply and with significant delay [17,18]. Vaccines against the 2009 H1N1 pathogen became publicly available early in October 2009, almost six months after the first reported H1N1 case [18]. In these circumstances, early public health responses may rely on social distancing and other non-pharmaceutical approaches. Among non-pharmaceutical interventions, school closure is commonly considered as part of national and international pandemic mitigation protocols [19–21]. Closing schools aims to reduce contacts among school-age children, who often play an important role in transmission, and consequently, to interrupt or decrease the speed and extent of transmission in the population [22, 23]
Despite these potential health benefits, social and economic costs associated with school closure are often high due to missing schoolwork, workplace absenteeism, and wage loss [24]. This control measure, therefore, should be implemented only when the reduction in disease transmission is high enough to offset the cost [25, 26]. If school closure were implemented too late in the epidemic, it would fail to have any meaningful mitigating effect while triggering the intervention too soon would incur unnecessary social and economic costs. Of equal importance is the decision about when to reopen schools. Lifting the intervention prematurely may result in a second epidemic peak and erosion of the accumulated benefit [22]. The first policy-related challenge we consider here is how to decide when to close or reopen schools as the pathogen is spreading in the population.
Efforts to control emerging pandemics are further challenged by the current lack of strain-transcendent vaccines which means that the production of vaccines against newly appearing variants (e.g. H1N5) can begin only after an epidemic has begun. As a consequence, an effective vaccine may become available in limited quantity and with considerable delay. During an emerging epidemic, individuals with particular risk factors or health conditions (e.g. the elderly or the immunocompromised) are particularly at higher risk of morbidity and mortality [27–29]. Providing vaccine to these high-risk individuals has a significant direct benefit in preventing mortality. However, individuals with high contact rates with the rest of the population (e.g. school-aged children) may also be attractive vaccine candidates due to their key role in transmission. The second policy-related question we study in this paper is how to rationalize the limited supply of vaccines between population subgroups who are at different level of mortality risk (e.g. healthy individuals versus those with certain conditions), and who play a different role in disease transmission (e.g. children versus the elderly) [30].
Although static policies to guide school closure and vaccine prioritization decisions have been the subject of several previous studies [6–8, 10, 31, 32], dynamic policies to inform the cost-effective use of these interventions cannot be characterized using currently available modeling methods.
3. Methods
3.1. Problem Formulation
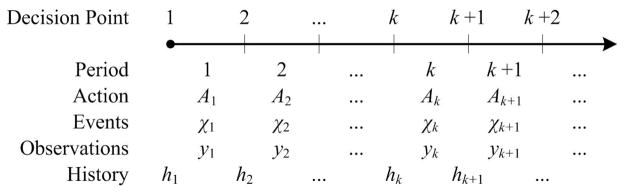
We assume that decisions to employ control measures are made at discrete points during the epidemic (e.g. every day or week). We use k ∈ {1, 2, 3, …} to index these decision epochs (see Figure 1). Spread of an infectious disease in a population triggers events that may be observed and which may incur costs and affect the population health status or resource availability. Examples of such events include new infections (changing population health status), hospitalizations (incurring costs, changing population health status and triggering observations) or deaths of infected individuals (changing population health status and triggering observations). We use the random variable Xk to denote events that may occur during the decision period [k, k + 1], k ∈ {1, 2, 3, …}. Various modeling frameworks can be used to characterize the stochastic process X = {Xk, k ≥ 1}, including Markov chain [33], agent-based [3, 34, 35], and contact network [36, 37] models. In §4.1 we describe a Markov model to characterize Xk for a novel viral epidemic.
Figure 1. Sequence of actions, events and observations during an epidemic.
“Actions” to control the epidemic are chosen at “Decision Points” (e.g. every week). The action in effect during a decision period impacts the epidemiological “Events” (e.g. new infections or hospitalizations) that may occur during this period. These events may generate “Observations” which can be used by the decision maker to form an epidemic “History” at the beginning of each decision point. A dynamic policy uses this history to inform which actions to implement during the next period.
Let 𝒜 be the set of available control interventions (e.g. 𝒜 = {School closure, Vaccinating children, Vaccinating adults}) and Ak ∈ 2𝒜 denote the set of control interventions in effect during the decision period [k, k + 1], where 2𝒜 is the power set of 𝒜 (the set of all subsets of 𝒜 including the empty set, representing the ‘no action’ choice, and 𝒜 itself, representing the employment of all available interventions). Clearly, the interventions in effect during period [k, k + 1] can influence the set of epidemic events that may occur over this period. An epidemic trajectory is defined as a realization of the stochastic process X = {Xk, k ≥ 1}, which we denote by 𝓧 = {χk, k ≥ 1} (see Figure 1). Neither the stochastic process X = {Xk, k ≥ 1} nor the epidemic trajectory 𝓧 = {χk, k ≥ 1} is fully observable. However, during decision periods, the policy maker may obtain observations on different epidemic measures, such as the number of disease-related hospitalizations or deaths (triggered by the realized events χk).
We use r(Ak, χk) to denote the loss over the decision period [k, k + 1] if action Ak ∈ 2𝒜 is in effect and the events χk occur during this period. The loss function r(Ak, χk) can be characterized in a variety of ways depending on the policy maker’s priorities. For example, if the policy maker wants to minimize the total number of influenza cases over the course of epidemic, then loss function r(Ak, χk) can be simply defined as the number of new influenza cases during the period [k, k + 1]. However, efforts to control epidemics may be bounded by the availability of resources, in particular budget. In these situations, where both health-related and financial outcomes are essential for determining the optimality of a health policy, a common approach is to assume that the policy maker’s objective is to minimize the loss in population’s net health benefit (NHB) [38]. If action Ak ∈ 2𝒜 is in effect and events χk occur during the decision period [k, k + 1], the loss in the population’s NHB is defined as r(Ak, χk) = q(χk) + (v(χk) + c(Ak))/λ where:
λ is the policy maker’s willingness-to-pay (WTP) for one additional unit of health (e.g. one life-year loss averted),
c(Ak) is the direct cost of implementing the interventions Ak ∈ 2𝒜 during the period [k, k + 1],
q(χk) is the loss in health during period [k, k + 1] if epidemic events χk occur, and
v(χk) is the cost incurred during period [k, k + 1] if epidemic events χk occur.
Accounting for both health and cost outcomes of alternatives, net health benefit is widely used as a measure of performance in economic evaluation of health care programs [39, 40]. The decision maker’s willingness to invest resources to improve the population’s health is represented by the WTP parameter λ; and therefore, the term (v(χk) + c(Ak))/λ represents the units of health that the decision maker is willing to forgo to save v(χk) + c(Ak) monetary units. A larger (smaller) value of λ indicates the abundance (scarcity) of resources.
For a realized trajectory 𝓧 = {χk, k ≥ 1}, we measure the overall outcome of the epidemic as the total discounted loss in population’s NHB:
| (1) |
where γ ∈ (0, 1] is the discount factor. In Eq. (1), the decision horizon K can be a constant predetermined by the decision maker (e.g. 2 years) or can be a random variable representing the time when the disease is eradicated.
Let yk denote the vector of observations made during the decision period [k, k + 1] (e.g. disease-related hospitalizations). We note that the observations yk may only partially represent the events occurring during the period [k, k + 1] and hence may not reveal the true epidemic state at the decision point k (see §4.1 for an illustration). As a result, policies for controlling epidemics will rely on use of accumulated but partially observed data [41]. We use hk to denote the observed history of the epidemic at decision point k defined as the sequence of past actions and observations up to the decision point k (see Figure 1). The history hk is updated recursively according to hk = {hk–1, Ak–1, yk–1}, k ≥ 1, where h1, the observed history at the first decision time, is an empty set. Let ℋ denote the set of all possible values that the history hk can take.
Our objective is to find a control policy π :ℋ→2𝒜 that specifies which interventions to implement based on the observed epidemic history up to a decision point k ∈ {1, 2, …} to minimize the expected total discounted loss in the population’s NHB:
| (2) |
The expectation in Eq. (2) is with respect to the stochastic process X = {Xk, k ≥ 1} which models the events that may occur throughout the epidemic given the actions Ak = π(hk), k ∈ {1, 2, …}. In §3.2, we propose an approximate policy iteration algorithm to approximate the optimal policy π* that minimizes the objective function (2).
3.2. Optimizing Dynamic Policies
The standard approach to identify a policy that minimizes the objective function (2) relies on dynamic programming techniques [42] where the aim is to select a long-term action plan (a policy) that optimizes the overall performance of the system (measured here by the objective function (2)). The optimality equations to maximize the objective function (2) can be written as [41]:
| (3) |
where v*(hk) is the optimal expected total discounted loss in the population’s NHB from the decision point k onward, given the history hk. If we solve Eq. (3) for v*(·), then the optimal choice at a given decision point k can be found by:
Finding the optimal value function v*(·) in Eq. (6) is computationally prohibitive because the history space ℋ can be a quite large and potentially unbounded set. A large body of dynamic programming literature is devoted to developing techniques to tackle the curse of dimensionality [43, 44]. A popular method to approximate the optimal policy π*, called approximate policy iteration, proceeds as follows [43,44]. We define the optimal Q-value Q*(hk, Ak) for the pair (hk, Ak) ∈ ℋ × 2𝒜 as:
| (4) |
The optimality equations (3) can now be written as
| (5) |
| (6) |
We note that finding the optimal Q-values Q*(hk, Ak) from Eq. (6) for each pair (hk, Ak) is still computationally prohibitive because, as mentioned before, the history space ℋ can be a quite large and potentially unbounded set. To overcome this problem, the approximate policy iteration method approximates the optimal Q-values, which can then be used guide decision making. To this end, we define a feature extraction function f :ℋ→ℝK as a mapping from the history space ℋ to a F-dimensional feature space: f = (f1, f2, …, fF ). The feature extraction function specifies which observable elements of the epidemic history (e.g. the notified incident during the last week or the total hospitalizations so far) should be included when defining a dynamic policy. As an example, suppose that schools have been open during the first three weeks of an epidemic, and 2, 5, and 9 hospitalized cases have been recorded during weeks 1, 2, and 3, respectively. For this scenario, the epidemic history at the beginning of week 4 can be denoted by h4 = {Open, 2, Open, 5, Open, 9}. Now, if the feature extraction function f(·) is defined to return the “total number of hospitalizations thus far” and “number of weeks schools have already been closed”, then f(h4) = (f1(h4), f2(h4)) = (16, 0).
We will approximate the optimal Q-values Q* (h, A) with a regression model Q̃(f(h), A; θA), where f(h) = (f1(h), f2(h), …, fF (h)) returns the values of features (f1, f2, …, fF ) given the history h, and θA is the vector of regression parameters. For example, Q̃(f(h), A; θA) can be a linear regression model:
| (7) |
where θA = (θA,0, θA,1, θA,2, …, θA,F ) is the vector of regression parameters.
Having characterized the regression models Q̃(·, A; θA), one can guide decision-making throughout an epidemic using the dynamic policy π̃ defined as:
| (8) |
The dynamic policy π̃ defined in Eq. (8) is referred to as greedy policy with respect to approximate models Q̃ (·, A; θA). In the following subsection, we describe an approximate policy iteration algorithm to tune parameters θA of regression models Q̃(·, A; θA) such that the greedy policy (8) approximate the policy that optimizing the objective function (2). We describe in §3.2.2 an approach for defining the feature extraction function f(·) for different epidemics.
3.2.1. An Approximate Policy Iteration Algorithm
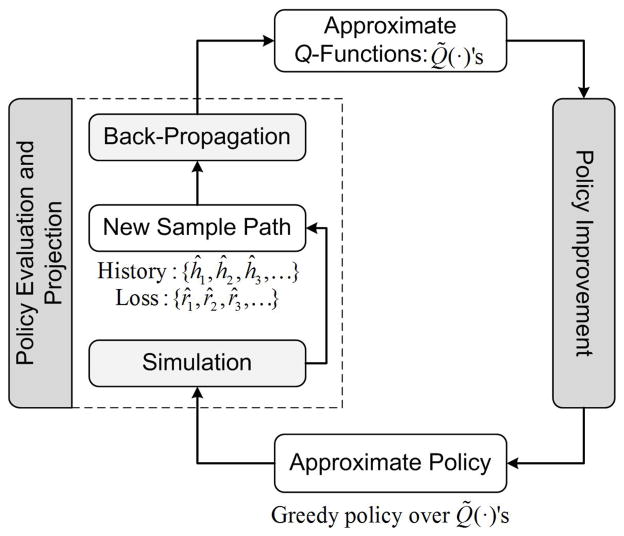
To find the approximation functions Q̃(·), we propose an approximate policy iteration algorithm which is motivated by Lagoudakis and Parr’s approach [45] and is modified for systems where states are only partially observable (see Figure 2). This proposed algorithm is an iterative procedure which searches for the optimal policy by generating a sequence of monotonically improving policies. Each iteration of the algorithm consists of two main steps: policy evaluation which samples (via simulation) the Q-values and updates (via back-propagation) the approximate Q-functions for the current policy, and policy improvement which updates the recommendation for each history h ∈ ℋ according to the greedy formula (8) using the new approximate Q-functions.
Figure 2.
Approximate policy iteration algorithm
To explain the steps of the algorithm, let Q̃n(·) be the approximate Q-functions at the beginning of iteration n ≥ 1. The policy improvement step (see Figure 2) involves characterizing a new policy π̃n using the greedy formula (8) with respect to approximate functions Q̃n(·). We note that the updated policy π̃n is not physically stored and is computed only on demand in the policy evaluation step.
In the policy evaluation step, we use the epidemic model to obtain a sample path which consists of a sequence of history stored at each decision point, {ĥ1, ĥ2, …, ĥK}, and a sequence of losses occurred during each decision interval, {r̂1, r̂2, …, r̂K–1}. Now, for this sample path, the loss-to-go for the observed history-action pair (ĥk, Âk) is calculated as: . In calculating q̂k, we note that if the disease is eradicated at the final decision point K, there is no reward after this time and hence the sampled loss-to-go at this point is q̂K = 0. Otherwise, we use as a sample for loss-to-go at the last decision point K.
The policy projection step in Figure 2 involves a back-propagation algorithm to update the tunable parameters of the approximate Q-functions Q̃n(·) using the sampled history-action pairs (ĥk, Âk) and the corresponding loss-to-go samples q̂k. For action A, the parameters of regression model Q̃(·, A; θA) can be updated using the sequence of history-action pairs (ĥk, Âk) and sampled loss-to-go q̂k, k ∈ {1, 2, …, K}:
| (9) |
where 1{S} = 1 if S is true and 1{S} = 0, otherwise. The L2 regularization term ωθ2 (with ω > 0) can be added to improve the stability of estimates θ̃A in case of collinearity among features.
To update the parameter estimate θ̃A, formula (9) uses only the current sample path and discards the sample paths gathered in the previous iterations of the algorithm, a process which can be inefficient. Alternatively, we prefer to use a recursive updating procedure that takes any new sample row (f(ĥ), Â, q̂) and returns an updated estimate θ̃ for the approximation function Q̃(·, Â;θ̃Â). If Q̃(·, A;θ̃A) is a linear regression (see Eq. (7)), the estimate θ̃A can be recursively updated using the following set of equations when the loss-to-go q̂ is incurred if action  is taken after observing history ĥ [43, Chapter 9]:
| (10) |
| (11) |
| (12) |
In this updating procedure:
i is an index incremented any time this updating procedure is executed;
θ̃A,i is the column vector of regression parameters;
f(ĥ) is the column vector of feature values evaluated for sampled history ĥ;
The series {λi} is referred to as learning rule which discounts older simulation observations in favor of more recently obtained observations when approximating the Q-functions. Learning rules should be selected such that λi → 1 as the algorithm converges. For example, according to the generalized harmonic rule, λi = i/(b + i − 1), where b ≥ 1. Greater values of b reduce the rate at which the forgetting factor declines and thus improve the responsiveness of the algorithm in the presence of initially transient simulation data.
To initialize the matrix BA, we can use BA,0 = I, where I is the identify matrix, but a better approach is to use , where matrix XA,0 contains enough f(ĥ)T rows such that the matrix is invertible.
We use θ̃ ← 𝒰(f(ĥ), Â, q̂; λ,θ̃Â) to denote the procedure that recursively updates the regression parameters θ̃A when the loss-to-go q̂ is incurred if action  is taken upon observing history ĥ.
Table 1 details the steps for finding approximation functions Q̃(·). The algorithm proceeds as follows. Step 0 initializes the algorithm. First, for each action A ∈ 2𝒜, we choose a suitable regression model Q̃(·, A; θA). There are multiple regression models that can be used including linear regression (see Eq. (7)), neural networks or kernel regression [43, 44]. Next, we choose a feature-extraction function f(·) which specifies the statistics to be extracted from history in order to make informed decisions. For example, f(·) may return the total number of hospitalized cases (see §3.2.2).
Table 1.
An approximate policy iteration algorithm for identifying dynamic policies
Step 0. Initialization
|
Step 1. While n ≤ N:
|
| Step 2. Return Q̃(·, A;θ̃A) for each action A ∈ 2𝒜. |
In Step 0c, we choose an exploration rule En, n ∈ {1, 2, …}, where n is the algorithm iteration number. At a given decision point, the exploration rule En specifies whether we should exploit our current knowledge of Q-functions and make a greedy decision using Eq. (8) or if we should choose a different action which is not optimal but may facilitate the exploration of new epidemic states. For the numerical analyses presented through this paper, we use a ε-greedy rule for exploration strategy. According to the ε-greedy rule, at each decision point, the optimal decision is chosen with probability 1 – εn, where εn = 1/nβ, β ∈ (0.5, 1], and n is the iteration number of the algorithm. Smaller values of β slow the rate at which the exploration probability declines. In Step 0d, we choose a learning rule {λi} as discussed before. Usually numerical experiments are necessary to select the value of optimization parameters (b, β) that results in a policy with the highest expected total discounted net health benefit. The remaining steps are consistent with the proceeding discussions.
3.2.2. Feature Selection
The core goal of feature selection is to identify statistics defined within the historical observations of disease spread that can be used to accurately differentiate the current trajectory from the infinite set of possible trajectories. Policy makers are usually able to observe some fraction of incident cases of disease. For example, the number of hospitalized cases is a potentially observable quantity. Several statistics can be defined based on these observations such as the number of new hospitalizations during the past week, the average or trend in the number of hospitalized cases during the past month, or the cumulative number of hospitalizations since the beginning of the epidemic [46, 47]. Some subset of these measures can be chosen as features.
While a large number of features can be defined, domain expert opinion coupled with proper numerical investigations can help to identify a limited number of strong features. Based on our experience applying the proposed algorithm to epidemics with different characteristics, we make the following recommendations.
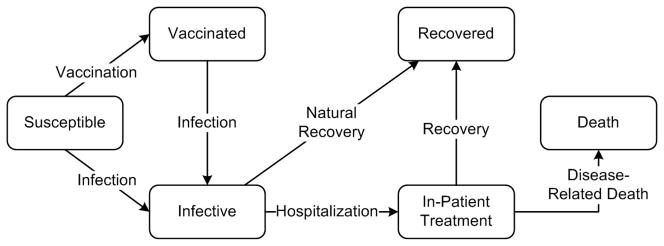
If the epidemic has an absorbing or partially absorbing compartment, such as the “Recovered” (absorbing) or “Vaccinated” (partially absorbing) compartments in the novel viral epidemic model in Figure 3, the total number of members who enter into these compartments (perhaps after vaccination) is often a strong feature. It is important to note that the process that generates observations during a given decision interval may be directly influenced by the interventions that are being used. For example, during an influenza epidemic, the case detection rate can be boosted through intensified case finding strategies, such as contact tracing. When these intensified interventions are lifted, the case detection rate may drop significantly. Hence, it will be important in this setting to use information about which interventions were employed during the period over which observations have been gathered as features as well. Additionally, levels of available resources can also be important features. For example, for influenza epidemics, the number of available vaccine doses at each decision time can be a strong feature.
Figure 3.
A model for the outbreak of a novel viral pathogen
When determining which features to include in the regression model for approximating the Q-values, one should also ensure that selected features have reasonably low multicollinearity. Correlation among features leads to unstable approximation and divergence of the proposed algorithm. In many situations, we would expect substantial correlation among the observations gathered during epidemics. For example, for most epidemics, hospitalized case notifications will be correlated with the number of the infection-associated deaths, and hence including both of these features leads to divergence of the proposed algorithm. This property may actually be advantageous in generating policies that are convenient to implement in practice since the policy maker needs only to gather data about features with the strongest predictive power and the least correlation with other potential features. Our experience shows that adding L2 regularization to the least squares problem (9) can significantly improve the stability and the convergence of the proposed algorithm for scenarios where features are partially correlated.
Using these recommendations to define features and their corresponding dynamic policies, we can then employ the algorithm described in Appendix, Table 2, to find the policy that leads to the lowest expected loss in the population’s NHB. We finally note that “time elapsed since the start of the epidemic” (which can be marked by the observation of the first confirmed case) can also be considered as a feature. Therefore, static policies (which only use time to guide decisions) are indeed a special case of dynamic policies and can therefore also be optimized using the algorithm proposed here.
Table 2.
Finding the optimal policy among M policies
|
3.2.3. Handling Large Action Space
The proposed approximate policy iteration algorithm (Table 1) requires tuning 2|𝒜| approximation models, one Q-function for each action A ∈ 2𝒜 (we hence refer to this approach as “Q-Approximation”). Controlling epidemics often involves the use of several control interventions and therefore, the number of regression models to tune by the algorithm can quickly become prohibitively large. For example, in the epidemic model described in §4.1, where four population groups (i.e. Children/Adult, Average Risk/High Risk) may be prioritized for vaccination and only children might be the target of social distancing interventions, the number of possible control measures is 2|𝒜| = 25 = 32. In reality, populations may be divided into even a larger number of subgroups [48] and additional measures for control, such as contact tracing [49, 50] and antiviral preventive therapy [51, 52], may be employed.
To reduce the number of required regression models, we investigate two approaches. The first method, which is proposed by [53], reduces the number of regression models from 2|𝒜| to 2|𝒜| but at the expense of performing additional regression updates at the back-propagation step. To characterize a policy, this approach utilizes two regression models, Ha0(·; θa0) and Ha1(·; θa1), for each available intervention a ∈ 𝒜. Table 3 in the Appendix describes the procedures for decision making and policy improvement using this approach. This approach, which we refer to as “H-Approximation”, uses the updating operator 𝒰 in Step 1b (see Table 1) |𝒜| times more than the Q-Approximation method.
Table 3.
Decision making and policy improvement in H-Approximation method
To make a decision when feature values
f(h) is observed:
|
To update regression models
H̃a1(·; θ̃a1) and
H̃a0(·; θ̃a0) when the loss-to-go
q̂
is incurred if action
Â
is taken upon observing history
ĥ:
|
In the second approach for handling a large action space, we assume that each intervention a ∈ 𝒜 has an additive effect on the future outcomes of the epidemic. Hence, for any action A ∈ 2𝒜, we approximate Q*(h, A) with an additive regression model defined as:
| (13) |
where ∅ denotes the decision to use no control intervention and Q̃a(·) is a regression model estimating the additive effect of intervention a ∈ 𝒜∪∅. Parameters of this regression model (i.e. θa’s) can be determined using the approximate policy iteration algorithm described in §3.2. Having characterized the regression model ℒ̃(·, A;θ̃), one can guide decision-making throughout an epidemic using:
| (14) |
Using the additive regression model (13), the approximate policy iteration algorithm now requires the tuning of only one regression model instead of 2|𝒜|. We refer to this approach as “A-Approximation”. The main disadvantage of this approach is that the regression model (13) can become unstable if every available intervention a ∈ 𝒜∪∅ is not adequately sampled as the algorithm iterates. This approach, however, may still be effective if the additivity assumption is satisfied and interventions are sampled adequately through the iterations of the algorithms. Therefore, we study the performance of this approach along with Q- and H- Approximation methods.
4. Numerical Analyses
4.1. A Model for Novel Viral Pathogen Outbreak
To evaluate the performance of control policies to inform resource allocation questions described in §2, we develop an epidemic model for the spread of a novel viral pathogen (see Figure 3). Our model is based on earlier epidemic models [54–57] with the following additions necessary to address the two policy-related questions described in §2. In this model, population members are grouped according to their age and their disease-associated mortality rates. Two age groups are considered in this model: “Children” and “Adults.” [27, 28]. Within each age group, members with particular risk factors (e.g. chronic pulmonary or cardiovascular conditions) are considered at higher risk of the disease-associated mortality [27–29]. While in reality individuals with multiple co-morbid conditions may be at highest risk of disease-associated mortality, for simplicity we assume that risk is characterized by a binary classification by “Average” (i.e. no co-morbid condition) and “High” (i.e. any comorbid condition). Since influenza epidemics typically last only a few months, we assume that the population structure does not fundamentally change during the epidemic; that is individuals do not move between age or risk subgroups and birth or deaths are negligible.
We calibrated our epidemic model to capture important characteristics of the U.S. 2009 H1N1 pandemic (see the SI document for details). In order to create a more severe pandemic scenario where closing schools is in fact worth the high societal and economic costs, we then adjusted parameter values of the model to produce pandemics with 60% average attack rates (a pandemic attack rate is defined as the proportion of the population that is expected to be infected during the outbreak if no control intervention is ever employed) [58, 59].
We choose decision periods to be of length one week and assume that the policy maker continues making weekly decisions until the disease is eradicated (in our model, simulated epidemics end within a year). At the beginning of each week the decision maker can observe the cumulative number of hospitalized cases, the cumulative number of vaccinated individuals, and the number of available vaccine doses [46, 47]. We will use these three streams of accumulating data to characterize dynamic policies to guide school-closure and vaccine-prioritization decisions.
4.1.1. Natural History and Transmission Dynamics
Infected individuals may infect susceptibles with whom they come into contact. Infected individuals may either recover from the disease or become hospitalized due to worsening symptoms (see Figure 3). Upon hospitalization, cases are assumed to immediately receive treatment and do not cause additional infections. Those who recover from the disease, either naturally or after receiving in-patient treatment, develop immunity against the pathogen. We assume that those who die due to disease-related complications have been first hospitalized.
To construct the model, we introduce the following notation:
i ∈ {1, 2} : index of age groups; i = 1 represents children and i = 2 represents adults;
j ∈ {1, 2} : index of risk groups; j = 1 represents average risk and j = 2 represents high risk;
(i, j): age-risk group representing age group i ∈ {1, 2} and risk group j ∈ {1, 2};
t: epidemic time (epidemic time t should not be confused with the decision point index k, defined in Figure 1. The discrete variable k ∈ {1, 2, 3, …} refers to the epidemic times {t1, t2, t3, …} when decisions are made);
Si,j(t): number of susceptibles in age-risk group (i, j) at time t;
Vi,j(t): number of vaccinated susceptible in age-risk group (i, j) at time t;
Ii,j(t): number of infectives in age-risk group (i, j) at time t;
Ti,j(t): number of in-patient cases in age-risk group (i, j) at time t;
Ri,j(t): number of recovered in age-risk group (i, j) at time t;
The state of the disease spread at any given time t can be identified by st = {(Si,j(t), Vi,j(t), Ii,j(t), Ti,j(t),Ri,j(t)), i ∈ {1, 2}, j ∈ {1, 2}}. Those who die from the disease no longer stay in the population to contribute to disease transmission and therefore, the epidemic state st does not include the total number of deaths at time t. We also note that the epidemic state st is only partially observed since only changes in the number of hospitalized patients, Ti,j(t), are often reported to the decision maker [46, 47].
Let τ denote the pathogen’s infectivity, which is defined as the probability that a fully susceptible individual becomes infected upon contact with an infectious person. We assume that a random susceptible person in age group i1 ∈ {1, 2} will contact with the members in age group i2 ∈ {1, 2} at the rate Λi1,i2 per day. Let φi,j(t) denote probability that a susceptible person in age-risk group (i, j) becomes infected during the interval [t, t+Δt]. When no intervention (such as school closure) is implemented, this probability can be calculated as (see Appendix):
| (15) |
where ζi,j is the relative susceptibility of age-risk group (i, j) with respect to average-risk children (we set ζ1,1 = 1) and Ni(t) is the population size of age group i at time t. Given the epidemic state st, the number of new infections among age-risk group (i, j) during the interval [t, t+Δt] will follow a binomial distribution with parameters (Si,j(t), φi(t)).
We assume that infected individuals (members of compartment “Infective” in Figure 3) in age-risk group (i, j) may naturally recover from the disease at a rate μi,j or may become hospitalized at a rate ςi,j. Therefore, for age-risk group (i, j), given the state of the epidemic at time t, st, the number of newly hospitalized patients and the number of patients who naturally recover from the infection during the interval [t, t+Δt] will have multinomial distributions with parameters (Ii,j(t), ), for i ∈ {1, 2} and j ∈ {1, 2}.
The recovery and mortality rates for cases receiving in-patient treatment is assumed to be ηi,j and ω̄i,j, respectively. Therefore, for age-risk group (i, j), the number of hospitalized patients who recover from the disease or die due to the infection during the interval [t, t+Δt] will have multinomial distributions with parameters (Ti,j(t), ), for i ∈ {1, 2} and j ∈ {1, 2}.
The random events (χk’s in Figure 1) that govern the evolution of the Markov chain {st : t = 0,Δt, 2Δt, 3Δt …} are (i) infection of a (unvaccinated) susceptible, (ii) infection of a vaccinated susceptible, (iii) natural recovery of an infective, (iv) hospitalization of an infective, (v) patient’s recovery after in-patient treatment, and (vi) patient’s death due to the infection while receiving in-patient treatment. The probability distributions of these events are described above.
To generate epidemic trajectories for this model, we use Monte Carlo simulation to sample from the Markov chain {st : t = 0,Δt, 2Δt, 3Δt, …}. To this end, given the epidemic state st, we first sample from the distribution of epidemic events over the interval [t, t+Δt], and then we use these realized events to calculate the new epidemic state st+Δt from the current state st.
4.1.2. Control Interventions: School Closure and Vaccination
We assume that school closure only reduces the daily number of contacts among children by factor σ ∈ (0, 1). Based on the findings reported by Cauchemez and colleaques (2008), we use σ = 0.25 to capture the effectiveness of school closure in reducing the number of contacts among school-age children. We note that this study did not detect any significant effect of school closures on the contact pattern of adults. Therefore, when schools are closed during the interval [t, t+Δt], the probability φ1,j(t), j ∈ {1, 2} in Eq. (15) will be reduced to:
| (16) |
When vaccines are available, susceptibles who are eligible for vaccination may present to health providers to receive vaccination. Vaccinated individuals are assumed to acquire partial immunity against the virus and will have a reduced probability of becoming infected upon contact with an infectious individual. Vaccination will also change the set of events that may occur in the compartment “Susceptibles” (Figure 3). We assume that if vaccine is made available to age-risk group (i, j), the susceptible members of this group will be vaccinated at a rate νi,j. Therefore, given the epidemic state st, the number of new infections and vaccinations among age-risk group (i, j) during the interval [t, t+Δt] will follow a multinomial distribution with parameters (Si,j(t), ).
We assume that vaccination will decrease the susceptibility of age group i ∈ {1, 2} by a factor αi ∈ [0, 1] (often referred to as vaccine efficacy). Therefore for vaccinated individuals, the susceptibility parameter ζi,j should be replaced with ζi,j(1 − αi) in Eqs. (15)–(16). Now, given the epidemic state st, the number of new infections among vaccinated age-risk group (i, j) during the interval [t, t+Δt] will follow a binomial distribution with parameters (Vi,j(t), φi(t)).
4.1.3. Observations, Health and Financial Outcomes of Outbreak
We use the objective function (2) to measure the performance of different control policies, π(·). To define the loss function r(·) = q(·) + (v(·) + c(·))/λ in this objective function, we use the number of life years lost due to the disease as a measure of health outcomes (i.e. q(χk) returns the number of life years lost during the period [k, k + 1]). Therefore, the WTP for health in this context is defined as the amount of money a policy maker is willing to spend to avert one life-year loss. To demonstrate the ability of the proposed framework to identify cost-effective policies, we assume that there are costs for school closure, vaccination and in-patient treatment (see SI document). School closure costs incurred during the period [k, k + 1] are captured in the function c(Ak) and vaccination and in-patient treatment costs are captured in v(χk).
In this model, the vector of observations obtained during the decision period [k, k + 1], yk, contains the number of disease-associated hospitalizations and deaths, and vaccinated individuals during this period [46, 47].
4.2. Optimization Settings
The optimality of a policy characterized by the proposed algorithm is affected by the chosen learning and exploration rules as well as the models approximating Q-values. Therefore, to optimize a particular dynamic policy, we employed the Q-, H-, and A-Approximation methods described in §3.2.3 with the following settings: the parameter of the generalized harmonic rule, b, selected from {100, 200, 300, 400, 500}, the parameter of ε-greedy rule, β, selected from {0.5, 0.6, 0.7}, and the model to approximate Q-values set to be quadratic, cubic, or quartic polynomial functions. To verify that our choice of the polynomial functions yields a proper approximation, we checked the prediction error at different decision points to ensure that errors were properly distributed around zero at convergence.
To identify the optimal dynamic policy among policies obtained using these settings, we employ the ranking algorithm described in Appendix (Table 2), and to optimize the static policies presented in the following subsections, we use the procedure described in Appendix §A.2.
4.3. Policies to Inform School-Closure Decisions in the Absence of Effective Vaccines
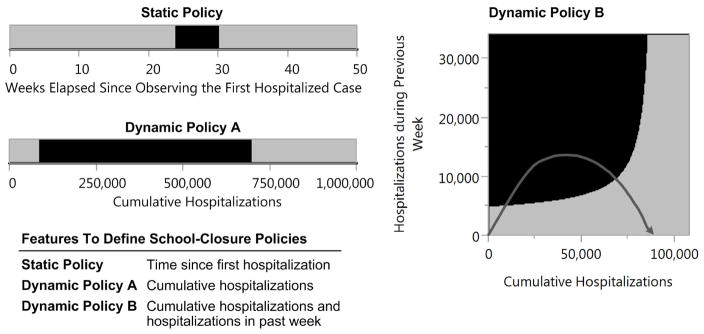
We first study a scenario where the probability that an effective vaccine becomes available during the epidemic is negligible, and hence, efforts to control the spread must rely on social distancing measures such as school closure. For this analysis, we consider a static policy that uses the time since the beginning of the epidemic to guide school-closure decisions, and two alternative forms of dynamic policies (see Figure 4). To inform decisions, dynamic policy A uses the ‘cumulative number of hospitalized cases, whereas dynamic policy B uses both the ‘cumulative number of hospitalized cases’ and the ‘number of hospitalized cases over the previous week’. Policies displayed in Figure 4 recommend keeping schools closed while the values of corresponding features are in the black regions. To illustrate how dynamic policy B guides decisions, we overlay a simulated epidemic trajectory onto this policy (represented by the dark grey curve). For the depicted trajectory, dynamic policy B recommends closing schools when the epidemic enters into the black region, and recommends reopening schools when the epidemic trajectory re-enters into the gray region.
Figure 4. School closure policies for a willingness-to-pay of $500,000 for averting one life-year loss.
These policies differ in the manner they utilize accumulating epidemic data to guide school closure decisions. While the Static Policy only utilizes the time since the first observed hospitalizations to guide decision making, Dynamic Policies A and B use continuously updated epidemic data to inform decisions. Black regions represents conditions where schools should remain closed. The dark grey curve overlaid on dynamic policy B corresponds to the values of features observed during one simulated epidemic trajectory.
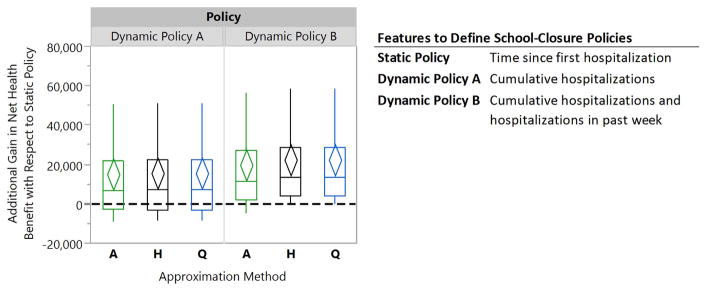
Figure 5 shows the relative performance of Dynamic Policies A–B with respect to the Static Policy displayed in Figure 4 for the WTP of $500, 000 per life-year saved. The diamonds represent 95% confidence intervals for the mean of paired performance differences which are constructed through the use of common random numbers as a variance reduction technique [60]. Compared to the scenario where schools are never closed, this Static Policy improved the population’s NHB by 33,257 life years (95% confidence interval (CI): [25,323, 41,191]). Dynamic Policy A and B, optimized using the A-, Q- or H-Approximation method, demonstrate greater performance compared to the Static Policy(see Figure 5).
Figure 5. Box plots comparing the relative performance of dynamic school-closure policies to a static policy for a willingness-to-pay of $500,000 for averting one life-year loss.
The diamonds represent 95% confidence intervals for the mean of paired performance differences using 50 simulation runs. The A-, H-, and Q-Approximation methods use, respectively, 1, 2n, and 2n regression models to characterize a dynamic policy when n interventions can be turned on or off (see §3.2.3 for details).
Wilcoxon signed-rank tests confirms that Dynamic Policy B, optimized using Q- or H-Approximation method, outperforms both the Static and Dynamic Policy A (p-values < 0.001). This observation is not surprising since the feature sets that define this policy provide information on both the current magnitude of epidemic and also for recent changes in growth or recession of the epidemic. This allows Dynamic Policy B to inform better decisions (see the SI for comparing the performance of these policies for different values of WTP). We also note in this figure that the three approximation methods perform similarly in this scenario.
In addition to the two forms of dynamic school-closure policies considered here, one may characterize other distinct policies that use alternative features. For example, the “recent trend in the number of hospitalizations,” defined for example as the slope of the line fitting the number of hospitalizations over the past 4 weeks, might be a viable choice to include in the feature set. Our experience, however, shows that the inclusion of this feature does not lead to a larger NHB gain compared to Dynamic Policies A and B.
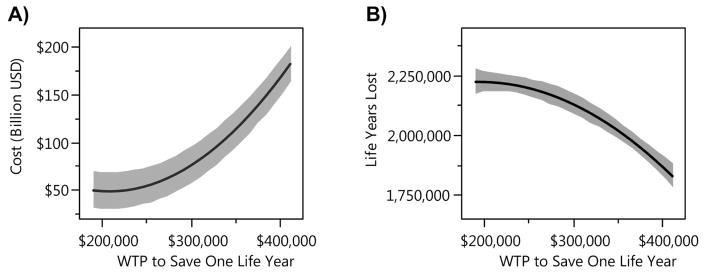
Figure 6 displays the effect of WTP value on the total cost incurred and the life years lost during an epidemic if Dynamic Policy B is used to guide school-closure decisions. The affordability curve (Figure 6(A)) returns the expected total costs, and the health outcome curve (Figure 6(B)) shows the expected life years lost as a function of the policy maker’s WTP for saving one life-year. This figure demonstrates that increasing the WTP value lead to higher costs to control the epidemic but also saves more life-years. In the absence of accurate estimate for the WTP for health, the policy maker can also use the affordability curve (Figure 6(A)) to select a level of WTP that satisfies existing budget constraints. Given the selected WTP, the policy maker can then use the corresponding Dynamic Policy B to guide decision making throughout the epidemic.
Figure 6. Total cost and life-year lost by using Dynamic Policy B with different values of WTP for health.
Higher level of WTP results in higher total cost incurred during the epidemic and fewer life years lost. Grey regions represent 95% prediction confidence intervals.
4.4. Policies to Inform Vaccine-Prioritization and School-Closure Decisions
For this second numerical analysis, we assume that a vaccine will become available, but only after a delay which is uniformly distributed over the range [5, 7] months. We note that vaccines against the 2009 H1N1 pathogen became publically available early in October 2009, almost six months after the first reported H1N1 case [18]. The National 2009 H1N1 Flu Survey shows that during the 2009 H1N1 pandemic, the quantity of vaccine that had been shipped to providers by December 2009 was sufficient for vaccinating about 21% of the U.S. population [61] and vaccination coverage grew approximately linearly in time [62]. Therefore, we assume that after vaccine production begins, 20 million doses of vaccines will be available for distribution each month. This quantity is sufficient to vaccinate approximately 21%/3 = 7% of the U.S. population per month which is similar to the scenario described above (see the SI for further details).
For this scenario, our goal is to characterize policies that utilize updated epidemic data reported at the beginning of each week to inform (1) whether schools should be closed during this week and (2) identify population subgroups that should be prioritized to receive vaccination (once the vaccine has become available). To this end, we consider three forms of dynamic policies that use the weekly hospitalization data as well as the current information about vaccine availability to guide decisions (see Figure 7 for definition of these dynamic policies).
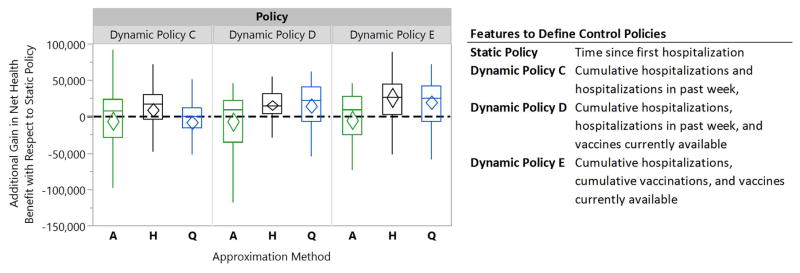
Figure 7. Box plots comparing the relative performance of dynamic school-closure and vaccine prioritization policies to a static policy for a willingness-to-pay of $300,000 for averting one life-year loss.
The diamonds represent 95% confidence intervals for the mean of paired performance differences using 50 simulation runs. The A-, H-, and Q-Approximation methods use, respectively, 1, 2n, and 2n regression models to characterize a dynamic policy when n interventions can be turned on or off (see §3.2.3 for details).
Figure 7 also displays the relative performance of dynamic policies C–E with respect to a static policy that only relies on the time since the start of the epidemic to specify when schools should be closed and which population subgroups should be prioritized for vaccine. Similar to Figure 5, the diamonds represent 95% confidence intervals for the mean of paired performance differences which are constructed through the use of common random numbers [60]. For this scenario, the static policy improved the population’s NHB by 186,871 life years (95% CI: [145,035, 228,708]) compared to the scenario where schools are never closed and vaccine never becomes available. Dynamic Policies C–E optimized using the H-Approximation method demonstrate greater performance compared to the static policy by 5% (95% CI: [0%, 10%]), 8% (95% CI: [5%, 11%]), and 14% (95% CI: [7%, 21%]) respectively (see Figure 7).
Wilcoxon signed-rank tests confirms that Dynamic Policy E, optimized using H-Approximation method, outperforms both Dynamic Policies C–D (p-values < 0.001). This can be explained by the fact that Dynamic policy E employs features to account for the magnitude of the spread, vaccination coverage and the vaccine availability; Dynamic policies C and D fail to account for the total vaccinations, and the dynamic policy C does not consider the level of vaccine availability when recommending decisions. We also observe that for the scenario considered here, A-Approximation method never leads to a policy with higher NHB gain than policies characterized by H- or Q-Approximation method. This suggests that the additivity condition assumed by the A-Approximation method (see §3.2.3) may not be valid in this scenario. See the SI for comparing the performance of these policies for different values of WTP.
To optimize dynamic policies C–E, we assume that once a population group is declared eligible for vaccination, revoking their eligibility status later during the epidemic results in a large penalty cost. While imposing this restriction may diminish the performance of dynamic vaccine prioritization policies, we instituted this assumption because we believe it would be quite difficult in practice to restrict the use of vaccines among subgroups in which vaccines were previously recommended.
Besides the three forms of dynamic policies considered here (Figure 7), other distinct policies can be characterized using alternative features. For example, features defined by hospitalization or vaccination data can be further stratified according to age or risk status. In a numerical experiment including these age or risk-stratified features, we found that the inclusion of these features did not result in superior policies compared to the policies studied in Figure 7. This may partially be explained by the fact that incorporating a larger number of features in regression models may increase the probability of collinearity among regressors which results in lower accuracy of predictions. This problem might be mitigated through the use of different regression models, such classification and regression trees [63]. Investigating the use of these alternative regression models to estimate Q-values is beyond the scope of this work and would be an important subject for future research.
5. Discussion
To date, the observations gathered during epidemics (e.g. weekly hospitalized cases) have been primarily used to estimate critical epidemic parameters such as the basic reproduction number (defined as the average number of secondary cases produced by an infectious individual in a fully susceptible population) or the disease mortality rate, which are often unknown during the early stages of epidemics [4, 64]. These analyses provide critical understanding about the characteristics of circulating pathogens which allow the development of mathematical and simulation models to project epidemic outcomes and investigate the performance of viable control strategies. This paper extends prior research on the control of epidemics by developing a decision model to define and optimize a novel class of control policies, referred to as dynamic policies. These policies utilize the cumulative epidemiological observations as well as the latest information about the availability of resources (e.g. vaccine) to guide decision making during epidemics.
Dynamic policies have two main advantages over static policies that are commonly considered in the literature. First, in contrast with static policies that require policy makers to commit to a pre-determined sequence of future actions [2, 3, 9, 11, 12], dynamic policies allow decision makers to revise their control approach as new data become available during epidemics. As novel sources of epidemic data, such as electronic medical and laboratory records [65,66], Internet queries [67,68] and Twitter feeds [69,70] become increasingly available, we expect that tools to inform dynamic policies will be in increasing demand, since these tools would provide a mechanism to translate epidemic observations into cost-effective decisions. Second, as demonstrated in this paper, dynamic policies can produce better health outcomes for similar investment than static policies.
The dynamic policies described here to control epidemics are closely related to dynamic treatment regimes that are more widely studies in the statistics literature [71–75]. Dynamic treatment regimes inform treatment recommendations that are responsive to an evolving illness in individual patients. This work extends the methodologies to guide decision making using accumulated data to address resource-allocation decisions in mitigating epidemics. The solution methodology proposed in this paper to characterize dynamic epidemic control policies does not restrict the type of epidemic model and hence various frameworks, including Markov chain [33], agent-based [3,34,35], or contact network [36,37] models may be used. This allows the decision maker to incorporate a broad range of pharmaceutical and non-pharmaceutical interventions and their attendant logistical constraints into the underlying epidemic model. A limitation of the proposed decision model is the fact that the specific choice of features, the approximation functions, and the learning and exploration rules affect the optimality and stability of the generated policies. If these optimization settings are not appropriately selected the algorithm may converge to a suboptimal and/or oscillating solution. This problem, however, can be mitigated through careful experimental design as discussed in §4.2.
We employed three approximation approaches, referred to as A-, H-, and Q-Approximation methods in this paper, to optimize dynamic policies. Our numerical results show that in the context of the resource allocation problems studied here, none of these methods uniformly outperforms the others. A-Approximation method, however, is often dominated by H- and Q-Approximation methods. Therefore, one should not rely on any single approximation approach to identify the most cost-effective policy but rather evaluate all three approaches to find the one which performs the best for each scenario.
The model for novel viral epidemics described in this paper is highly simplified. We have made simplifying assumptions about the natural history and transmission of the disease as well as the population structure so as to maintain focus on the presentation of the proposed decision model and the solution methodologies. Nonetheless, this epidemic model accommodates sufficient detail and is calibrated using data from the 2009 H1N1 pandemic in the U.S. to facilitate comparison of the relative performance of dynamic and static policies for the scenarios studied in this paper.
As a final note, the successful identification of dynamic health policies depends on proper specification of the underlying epidemic model, a concern that is also paramount for the model-based identification of static health policies. At this time, it is unclear whether the methods we have proposed for dynamic policy identification are more sensitive to model misspecification than those for determining static policies; this is an important area for future research as trade-offs between static and dynamic policies are further explored. In the meantime, we suggest that if the predictions made by the model do not match the new observations, within a desired degree of accuracy, the model should be re-calibrated. This goal can be achieved by a broad range of methods ranging from simple visual matching to more sophisticated statistical approaches, such as by maximizing a likelihood function [55,76–79]. If the model fails to make reasonably accurate short-term predictions, the underlying model structure and assumptions should be revisited. We note that inaccuracies in the surveillance and reporting system may result in suboptimal policies, emphasizing the tremendous importance of public health surveillance for the effective management of epidemics.
Supplementary Material
Acknowledgments
The project described was supported by Award U54GM088558 and DP2OD006663 from the U.S. National Institute of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
A. Appendix
A.1. Calculating the Probability of Disease Transmission
We first introduce the following notation:
τ : pathogen’s infectivity which is defined as the probability that a fully susceptible individual becomes infected upon contact with an infectious person.
ζi,j: relative susceptibility of age-risk group (i, j) with respect to average-risk children (we set ζ1,1 = 1).
pi(t): probability that the next interaction of a random susceptible person in age group i ∈ {1, 2} is with an infectious person during the interval [t, t+Δt].
φi,j(t): probability that a susceptible person in age-risk group (i, j) becomes infected during the interval [t, t+Δt].
Ni(t): population size of age group i at time t.
When mixing is homogenous, a random contact of a susceptible in age group i ∈ {1, 2} will be with a person in age group i′ ∈ {1, 2} with probability Λi,i′/Σi′ Λi,i′. Therefore, pi(t) is equal to:
| (17) |
To calculate the probability φi,j(t), first note that a random susceptible person will contact n individuals during the interval [t, t+Δt], where n has Poisson distribution with rate Λ̄iΔT = ΔT Σi′ Λi,i′. The number of infective persons, m, among these n individuals has binomial distribution (n, pi(t)); and finally, the susceptible person may become infected if the contact with at least one of these j individuals results in infection (so the probability that the susceptible person becomes infected is one minus the probability that none of the interactions with infectives results in infection). Hence,
| (18) |
The expression is the z-transform of the binomial distribution (n, pi(t)) for z = 1− τζi,j and is equal to [(1 − pi(t) + pi(t)(1 − τζi,j)]n. Therefore, Eq. (18) results in:
| (19) |
In Eq. (19), the expression is the z-transform of the Poisson distribution with rate Λ̄iΔt for z = 1− τζi,jpi(t) and hence, Eq. (19) results in:
| (20) |
Eq. (15) can be immediately obtained by using pi(t) from Eq. (17) in Eq. (20).
A.2. Optimizing Static Policies
The static policies considered in §4.3 specify a time interval [tS, tE] (tE > tS) during which schools should remain closed. According to this policy, schools should be closed at the beginning of day tS after observing the first hospitalized case and should be reopened at the beginning of day tE. To find the optimal school closure duration for a given value of WTP, we define a finite number of intervals {[tS,i, tE,i]|tS,i, tE,i ∈ {0, 7, 14, 28,…, 350}, tE,i > tS,i} and, for each static policy [tS,i, tE,i], use Monte Carlo simulation to estimate the expected total loss in the population’s NHB. For the H1N1 influenza epidemic model described in §4.1, simulated trajectories die out within a year and hence 350 days is selected as the upper bound for tE.
We then use the algorithm described in Table 2 to select the most desirable policy among a set of alternative policies. This algorithm searches for the policy with minimum expected loss in the population’s NHB. To choose between two policies with statistically indifferent performance, the algorithm selects the policy with less uncertainty around the estimated performance. It is straightforward to see that the policy selected as optimal by this algorithm is unique independent of how policies are initially ordered.
References
- 1.Lopez AD, Mathers CD, Ezzati M, Jamison DT, Murray CJL. Global burden of disease and risk factors. Oxford University Press; New York: 2006. [PubMed] [Google Scholar]
- 2.Ferguson NM, Cummings DAT, Cauchemez S, Fraser C, Riley S, Meeyai A, Iamsirithaworn S, Burke DS. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437(7056):209–214. doi: 10.1038/nature04017. [DOI] [PubMed] [Google Scholar]
- 3.Germann TC, Kadau K, Longini IM, Jr, Macken CA. Mitigation strategies for pandemic influenza in the United States. Proceedings of the National Academy of Sciences. 2006;103(15):5935–5940. doi: 10.1073/pnas.0601266103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lipsitch M, Cohen T, Cooper B, Robins JM, Ma S, James L, Gopalakrishna G, Chew SK, Tan CC, Samore MH, et al. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300(5627):1966–70. doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Yang Y, Sugimoto JD, Halloran ME, Basta NE, Chao DL, Matrajt L, Potter G, Kenah E, Longini IM., Jr The transmissibility and control of pandemic influenza A (H1N1) virus. Science. 2009;326(5953):729–733. doi: 10.1126/science.1177373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dushoff J, Plotkin JB, Viboud C, Simonsen L, Miller M, Loeb M, Earn DJD. Vaccinating to protect a vulnerable subpopulation. PLoS Medicine. 2007;4(5):e174. doi: 10.1371/journal.pmed.0040174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ferguson NM, Cummings DAT, Fraser C, Cajka JC, Cooley PC, Burke DS. Strategies for mitigating an influenza pandemic. Nature. 2006;442(7101):448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Flahault A, Vergu E, Coudeville L, Grais RF. Strategies for containing a global influenza pandemic. Vaccine. 2006;24(44–46):6751–6755. doi: 10.1016/j.vaccine.2006.05.079. [DOI] [PubMed] [Google Scholar]
- 9.Halloran ME, Ferguson NM, Eubank S, Longini IM, Cummings DAT, Lewis B, Xu S, Fraser C, Vullikanti A, Germann TC, et al. Modeling targeted layered containment of an influenza pandemic in the United States. Proceedings of the National Academy of Sciences. 2008;105(12):4639. doi: 10.1073/pnas.0706849105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Patel R, Longini IM, Halloran ME. Finding optimal vaccination strategies for pandemic influenza using genetic algorithms. Journal of Theoretical Biology. 2005;234(2):201–212. doi: 10.1016/j.jtbi.2004.11.032. [DOI] [PubMed] [Google Scholar]
- 11.Halder N, Kelso JK, Milne GJ. Developing guidelines for school closure interventions to be used during a future influenza pandemic. BMC Infectious Diseases. 2010 Jan;10(1):221. doi: 10.1186/1471-2334-10-221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lee BY, Brown ST, Cooley P, Potter MA, Wheaton WD, Voorhees RE, Stebbins S, Grefenstette JJ, Zimmer SM, Zimmerman RK, et al. Simulating school closure strategies to mitigate an influenza epidemic. Journal of Public Health Management and Practice. 2010;16(3):252–61. doi: 10.1097/PHH.0b013e3181ce594e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ludkovski M, Niemi J. Optimal dynamic policies for influenza management. Statistical Communications in Infectious Diseases. 2010;2(1):5. [Google Scholar]
- 14.Yaesoubi R, Cohen T. Dynamic Health Policies for Controlling the Spread of Emerging Infections: Influenza as an Example. PLoS ONE. 2011;6(9):11. doi: 10.1371/journal.pone.0024043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Longini IM, Jr, Nizam A, Xu S, Ungchusak K, Hanshaoworakul W, Cummings DAT, Halloran ME. Containing pandemic influenza at the source. Science. 2005;309(5737):1083–1087. doi: 10.1126/science.1115717. [DOI] [PubMed] [Google Scholar]
- 16.Dye C, Gay N. Modeling the SARS epidemic. Science. 2003;300(5627):1884–1885. doi: 10.1126/science.1086925. [DOI] [PubMed] [Google Scholar]
- 17.Knobler SL, Mack A, Mahmoud A, Lemon SM, et al. The threat of pandemic influenza. 2005 [PubMed] [Google Scholar]
- 18.Centers for Disease Control and Prevention. The 2009 H1N1 Pandemic: Summary Highlights, April 2009–April 2010. The United States Center for Disease Control and Prevention; 2009. http://www.cdc.gov/h1n1flu/cdcresponse.htm. [Google Scholar]
- 19.Centers for Disease Control and Prevention. Interim Pre-pandemic Planning Guidance : Community Strategy for Pandemic Influenza Mitigation in the United States. 2007 http://www.flu.gov/planning-preparedness/community/community\_mitigation.pdf.
- 20.Stern AM, Markel H. What Mexico taught the world about pandemic influenza preparedness and community mitigation strategies. Journal of American Medical Association. 2009 Sep;302(11):1221–2. doi: 10.1001/jama.2009.1367. [DOI] [PubMed] [Google Scholar]
- 21.World Health Organization. WHO global influenza preparedness plan The role of WHO and recommendations for national measures before and during pandemics. 2005 Report No. WHO/CDS/CSR/GIP/2005.5. http://www.who.int/csr/resources/publications/influenza/WHO\_CDS\_CSR\_GIP\_2005\_5.pdf.
- 22.Cauchemez S, Ferguson NM, Wachtel C, Tegnell A, Saour G, Duncan B, Nicoll A. Closure of schools during an influenza pandemic. The Lancet Infectious diseases. 2009 Aug;9(8):473–81. doi: 10.1016/S1473-3099(09)70176-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jackson C, Vynnycky E, Hawker J, Olowokure B, Mangtani P. School closures and influenza: systematic review of epidemiological studies. BMJ Open. 2013 Jan;3(2):e002, 149. doi: 10.1136/bmjopen-2012-002149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chen WC, Huang AS, Chuang JH, Chiu CC, Kuo HS. Social and economic impact of school closure resulting from pandemic influenza A/H1N1. The Journal of Infection. 2011 Mar;62(3):200–3. doi: 10.1016/j.jinf.2011.01.007. [DOI] [PubMed] [Google Scholar]
- 25.Brown ST, Tai JHY, Bailey RR, Cooley PC, Wheaton WD, Potter MA, Voorhees RE, LeJeune M, Grefenstette JJ, Burke DS, et al. Would school closure for the 2009 H1N1 influenza epidemic have been worth the cost?: a computational simulation of Pennsylvania. BMC Public Health. 2011 Jan;11(1):353. doi: 10.1186/1471-2458-11-353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sander B, Nizam A, Garrison LP, Postma MJ, Halloran ME, Longini IM. Economic evaluation of influenza pandemic mitigation strategies in the United States using a stochastic microsimulation transmission model. Value in Health. 2009;12(2):226–233. doi: 10.1111/j.1524-4733.2008.00437.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fowlkes AL, Arguin P, Biggerstaff MS, Gindler J, Blau D, Jain S, Dhara R, McLaughlin J, Turnipseed E, Meyer JJ, et al. Epidemiology of 2009 pandemic influenza A (H1N1) deaths in the United States, April–July 2009. Clinical Infectious Diseases. 2011;52(suppl 1):S60–S68. doi: 10.1093/cid/ciq022. [DOI] [PubMed] [Google Scholar]
- 28.Louie JK, Acosta M, Winter K, Jean C, Gavali S, Schechter R, Vugia D, Harriman K, Matyas B, Glaser CA, et al. Factors associated with death or hospitalization due to pandemic 2009 influenza A (H1N1) infection in California. Journal of American Medical Association. 2009;302(17):1896–1902. doi: 10.1001/jama.2009.1583. [DOI] [PubMed] [Google Scholar]
- 29.Jain S, Kamimoto L, Bramley AM, Schmitz AM, Benoit SR, Louie J, Sugerman DE, Druckenmiller JK, Ritger Ka, Chugh R, et al. Hospitalized patients with 2009 H1N1 influenza in the United States, April–June 2009. The New England Journal of Medicine. 2009 Nov;361(20):1935–44. doi: 10.1056/NEJMoa0906695. [DOI] [PubMed] [Google Scholar]
- 30.Goldstein E, Wallinga J, Lipsitch M. Vaccine allocation in a declining epidemic. Journal of the Royal Society Interface. 2012;9(76):2798–2803. doi: 10.1098/rsif.2012.0404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Larson RC, Teytelman A. Modeling the Effects of H1N1 Influenza Vaccine Distribution in the United States. Value in Health. 2011;15(1):158–166. doi: 10.1016/j.jval.2011.07.014. [DOI] [PubMed] [Google Scholar]
- 32.Scuffham PA, West PA. Economic evaluation of strategies for the control and management of influenza in Europe. Vaccine. 2002;20(19):2562–2578. doi: 10.1016/s0264-410x(02)00154-8. [DOI] [PubMed] [Google Scholar]
- 33.Daley CL, Small PM, Schecter GF, Schoolnik GK, McAdam RA, Jacobs WR, Jr, Hopewell PC. An outbreak of tuberculosis with accelerated progression among persons infected with the human immunodeficiency virus. New England Journal of Medicine. 1992;326(4):231–235. doi: 10.1056/NEJM199201233260404. [DOI] [PubMed] [Google Scholar]
- 34.Bonabeau E. Agent-based modeling: Methods and techniques for simulating human systems. Proceedings of the National Academy of Sciences. 2002;99(Suppl 3):7280–7287. doi: 10.1073/pnas.082080899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Epstein JM. Modelling to contain pandemics. Nature. 2009;460(7256):687. doi: 10.1038/460687a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Meyers LA. Contact network epidemiology: Bond percolation applied to infectious disease prediction and control. Bulletin-American Mathematical Society. 2007;44(1):63. [Google Scholar]
- 37.Reis BY, Kohane IS, Mandl KD. An epidemiological network model for disease outbreak detection. PLoS Medicine. 2007;4(6):e210. doi: 10.1371/journal.pmed.0040210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Stinnett AA, Mullahy J. Net Health Benefits: A New Framework for the Analysis of Uncertainty in Cost-Effectiveness Analysis. Medical Decision Making. 1998;18(2):S68. doi: 10.1177/0272989X98018002S09. [DOI] [PubMed] [Google Scholar]
- 39.Drummond MF, Sculpher MJ, Claxton K, Stoddart GL, Torrance GW. Methods for the Economic Evaluation of Health Care Programmes. 3. 2015. [Google Scholar]
- 40.Laska EM, Meisner M, Siegel C, Wanderling J. Statistical cost-effectiveness analysis of two treatments based on net health benefits. Statistics in Medicine. 2001;20(8):1279–1302. doi: 10.1002/sim.774. [DOI] [PubMed] [Google Scholar]
- 41.White CC. A survey of solution techniques for the partially observed Markov decision process. Annals of Operations Research. 1991;32(1):215–230. [Google Scholar]
- 42.Puterman ML. Markov Decision Processes: Discrete Stochastic Dynamic Programming. John Wiley & Sons, Inc; New York, NY: 1994. [Google Scholar]
- 43.Powell WB. Approximate Dynamic Programming: Solving the Curses of Dimensionality. 2. Wiley; 2011. [Google Scholar]
- 44.Bertsekas DP, Tsitsiklis JN. Neuro-Dynamic Programming. Athena Scientific; 1996. [Google Scholar]
- 45.Lagoudakis MG, Parr R. Least-squares policy iteration. The Journal of Machine Learning Research. 2003;4:1107–1149. [Google Scholar]
- 46.Centers for Disease Control and Prevention. CDC Estimates of 2009 H1N1 Influenza Cases, Hospitalizations and Deaths in the United States, April – October 17, 2009. The United States Center for Disease Control and Prevention; 2009. http://www.cdc.gov/h1n1flu/estimates/April\_October\_17.htm. [Google Scholar]
- 47.Reed C, Angulo FJ, Swerdlow DL, Lipsitch M, Meltzer MI, Jernigan D, Finelli L. Estimates of the prevalence of pandemic (H1N1) 2009, United States, April–July 2009. Emerging Infectious Diseases. 2009 Dec;15(12):2004–7. doi: 10.3201/eid1512.091413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Medlock J, Galvani AP. Optimizing influenza vaccine distribution. Science. 2009 Sep;325(5948):1705–8. doi: 10.1126/science.1175570. [DOI] [PubMed] [Google Scholar]
- 49.Armbruster B, Brandeau ML. Optimal mix of screening and contact tracing for endemic diseases. Mathematical Biosciences. 2007;209(2):386–402. doi: 10.1016/j.mbs.2007.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Eames KTD, Keeling MJ. Contact tracing and disease control. Proceedings of the Royal Society of London Series B: Biological Sciences. 2003 Dec;270(1533):2565–71. doi: 10.1098/rspb.2003.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dimitrov N, Goll S, Meyers LA, Pourbohloul B, Hupert N. Optimizing tactics for use of the US antiviral strategic national stockpile for pandemic (H1N1) Influenza, 2009. PLoS Curr Influenza. 2009:1. doi: 10.1371/currents.RRN1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Goldstein E, Apolloni A, Lewis B, Miller JC, Macauley M, Eubank S, Lipsitch M, Wallinga J. Distribution of vaccine/antivirals and the ‘least spread line’ in a stratified population. Journal of the Royal Society Interface. 2010;7(46):755–764. doi: 10.1098/rsif.2009.0393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Pazis Jason, Parr R. Generalized value functions for large action sets. Proceedings of the 28th International Conference on Machine Learning (ICML-11) 2011:1185–1192. [Google Scholar]
- 54.Arinaminpathy N, McLean AR. Antiviral treatment for the control of pandemic influenza: some logistical constraints. Journal of the Royal Society Interface. 2008;5(22):545–553. doi: 10.1098/rsif.2007.1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Birrell PJ, Ketsetzis G, Gay NJ, Cooper BS, Presanis AM, Harris RJ, Charlett A, Zhang XS, White PJ, Pebody RG, et al. Bayesian modeling to unmask and predict influenza A/H1N1pdm dynamics in London. Proceedings of the National Academy of Sciences. 2011;108(45):18 238–18 243. doi: 10.1073/pnas.1103002108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Grassly NC, Fraser C. Mathematical models of infectious disease transmission. Nature Reviews Microbiology. 2008;6(6):477–487. doi: 10.1038/nrmicro1845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.McCaw JM, McVernon J. Prophylaxis or treatment? Optimal use of an antiviral stockpile during an influenza pandemic. Mathematical Biosciences. 2007;209(2):336–360. doi: 10.1016/j.mbs.2007.02.003. [DOI] [PubMed] [Google Scholar]
- 58.Chowell G, Nishiura H, Bettencourt LMA. Comparative estimation of the reproduction number for pandemic influenza from daily case notification data. Journal of the Royal Society, Interface. 2007 Feb;4(12):155–66. doi: 10.1098/rsif.2006.0161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Vynnycky E, Trindall A, Mangtani P. Estimates of the reproduction numbers of Spanish influenza using morbidity data. International Journal of Epidemiology. 2007 Aug;36(4):881–9. doi: 10.1093/ije/dym071. [DOI] [PubMed] [Google Scholar]
- 60.Clark GM. Use of common random numbers in comparing alternatives. Proceedings of the 1990 Winter Simulation Conference. 1990:367–371. [Google Scholar]
- 61.Centers for Disease Control and Prevention. 2009 H1N1 Flu In The News. The United States Center for Disease Control and Prevention; 2009. http://www.cdc.gov/h1n1flu/in\_the\_news/influenza\_vaccination.htm. [Google Scholar]
- 62.Centers for Disease Control and Prevention. Interim Results: Influenza A (H1N1) 2009 Monovalent Vaccination Coverage-United States, October–December 2009. 2010 http://www.cdc.gov/mmwr/pdf/wk/mm59e0115.pdf. [PubMed]
- 63.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2. Springer; 2009. [Google Scholar]
- 64.Riley S, Fraser C, Donnelly CA, Ghani AC, Abu-Raddad LJ, Hedley AJ, Leung GM, Ho LM, Lam TH, Thach TQ, et al. Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Science. 2003 Jun;300(5627):1961–6. doi: 10.1126/science.1086478. [DOI] [PubMed] [Google Scholar]
- 65.Effler P, Ching-Lee M, Bogard A, Ieong MC, Nekomoto T, Jernigan D. Statewide system of electronic notifiable disease reporting from clinical laboratories. Journal of American Medical Association. 1999;282(19):1845–1850. doi: 10.1001/jama.282.19.1845. [DOI] [PubMed] [Google Scholar]
- 66.Evans RS, Pestotnik SL, Classen DC, Clemmer TP, Weaver LK, Orme JF, Jr, Lloyd JF, Burke JP. A computer-assisted management program for antibiotics and other antiinfective agents. New England Journal of Medicine. 1998;338(4):232–238. doi: 10.1056/NEJM199801223380406. [DOI] [PubMed] [Google Scholar]
- 67.Ginsberg J, Mohebbi MH, Patel RS, Brammer L, Smolinski MS, Brilliant L. Detecting influenza epidemics using search engine query data. Nature. 2008;457(7232):1012–1014. doi: 10.1038/nature07634. [DOI] [PubMed] [Google Scholar]
- 68.Wilson K, Brownstein JS. Early detection of disease outbreaks using the Internet. Canadian Medical Association Journal. 2009;180(8):829–831. doi: 10.1503/cmaj.090215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Lampos V, De Bie T, Cristianini N. Flu detector-tracking epidemics on twitter. Machine Learning and Knowledge Discovery in Databases. 2010:599–602. [Google Scholar]
- 70.Signorini A, Segre AM, Polgreen PM. The use of Twitter to track levels of disease activity and public concern in the US during the influenza A H1N1 pandemic. PLoS One. 2011;6(5):e19, 467. doi: 10.1371/journal.pone.0019467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Zhao YQ, Zeng D, Laber EB, Kosorok MR. New statistical learning methods for estimating optimal dynamic treatment regimes. Journal of the American Statistical Association. 2015;110(510):583–598. doi: 10.1080/01621459.2014.937488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Schulte PJ, Tsiatis AA, Laber EB, Davidian M. Q- and A-learning methods for estimating optimal dynamic treatment regimes. Statistical Science. 2014;29(4):640. doi: 10.1214/13-STS450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Huang X, Ning J, Wahed AS. Optimization of individualized dynamic treatment regimes for recurrent diseases. Statistics in Medicine. 2014;33(14):2363–2378. doi: 10.1002/sim.6104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Huang X, Choi S, Wang L, Thall PF. Optimization of multi-stage dynamic treatment regimes utilizing accumulated data. Statistics in Medicine. 2015;34(26):3424–3443. doi: 10.1002/sim.6558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Murphy SA. Optimal dynamic treatment regimes. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2003;65(2):331–355. [Google Scholar]
- 76.Higdon D, Gattiker J, Williams B, Rightley M. Computer model calibration using high-dimensional output. Journal of the American Statistical Association. 2008;103(482):570–583. [Google Scholar]
- 77.Brookhart MA, Hubbard AE, van der Laan MJ, Colford JM, Eisenberg JN. Statistical estimation of parameters in a disease transmission model: analysis of a cryptosporidium outbreak. Statistics in Medicine. 2002;21(23):3627–3638. doi: 10.1002/sim.1258. [DOI] [PubMed] [Google Scholar]
- 78.Weidemann F, Dehnert M, Koch J, Wichmann O, Höhle M. Bayesian parameter inference for dynamic infectious disease modelling: rotavirus in germany. Statistics in Medicine. 2014;33(9):1580–1599. doi: 10.1002/sim.6041. [DOI] [PubMed] [Google Scholar]
- 79.O’Neill PD. Introduction and snapshot review: relating infectious disease transmission models to data. Statistics in Medicine. 2010;29(20):2069–2077. doi: 10.1002/sim.3968. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.