The Role of Feedback Contingency in Perceptual Category Learning

Abstract

Feedback is highly contingent on behavior if it eventually becomes easy to predict, and weakly contingent on behavior if it remains difficult or impossible to predict even after learning is complete. Many studies have demonstrated that humans and nonhuman animals are highly sensitive to feedback contingency, but no known studies have examined how feedback contingency affects category learning, and current theories assign little or no importance to this variable. Two experiments examined the effects of contingency degradation on rule-based and information-integration category learning. In rule-based tasks, optimal accuracy is possible with a simple explicit rule, whereas optimal accuracy in information-integration tasks requires integrating information from two or more incommensurable perceptual dimensions. In both experiments, participants each learned rule-based or information-integration categories under either high or low levels of feedback contingency. The exact same stimuli were used in all four conditions and optimal accuracy was identical in every condition. Learning was good in both high-contingency conditions, but most participants showed little or no evidence of learning in either low-contingency condition. Possible causes of these effects are discussed, as well as their theoretical implications.

Introduction

Many studies have examined the role of feedback in category learning. This article describes the results of two experiments that examine one aspect of feedback that, to our knowledge, has never before been directly investigated – namely, the importance of the contingency of the feedback on the learner's behavior. Contingency is high if the valence of the feedback (i.e., whether it is positive or negative) eventually becomes predictable and low when it remains difficult or impossible to predict even after learning is complete. Although current theories assign little or no importance to this variable, our results suggest that a high level of feedback contingency is critical for category learning.

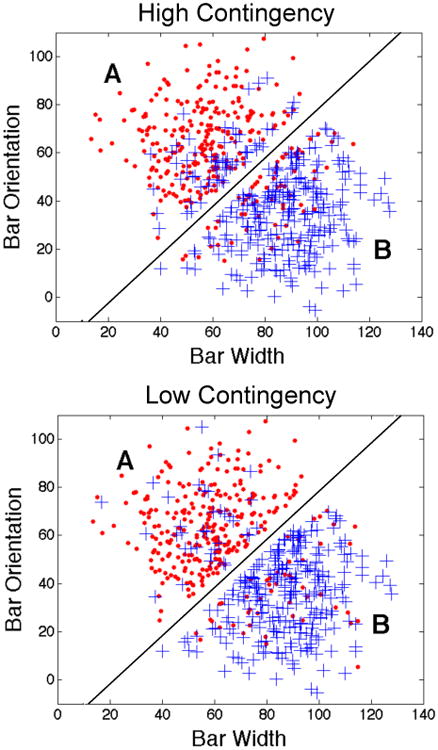
To make this discussion more concrete, consider Figure 1. The bottom two panels illustrate two different sets of overlapping categories. Each symbol denotes a different stimulus. The circles denote exemplars in category A and the plus signs denote exemplars in category B. Sample stimuli are shown in the top panel. Note that each stimulus is a circular, sine-wave grating and that the stimuli vary across trials on two stimulus dimensions – the width and orientation of the dark and light bars. The diagonal lines denote the optimal categorization strategy. In particular, in both of the lower two panels, accuracy is maximized at 80% if the participant responds A to any stimulus with coordinates above the diagonal line and B to any stimulus with coordinates below the line.

Figure 1.

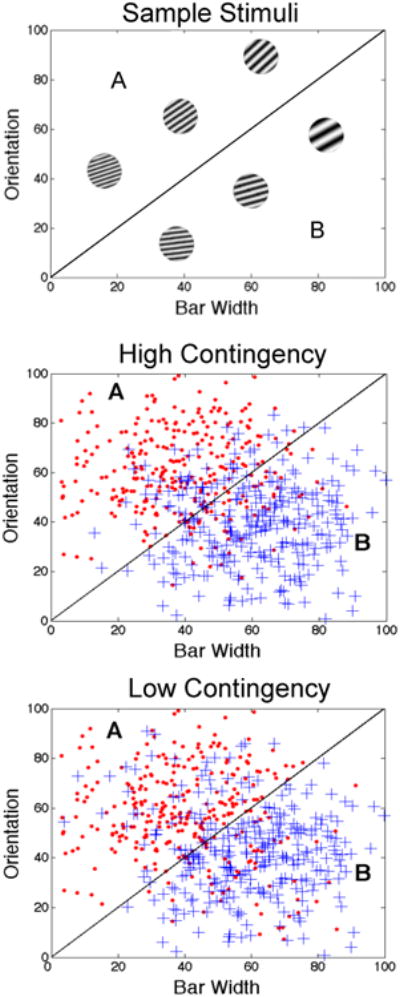
Stimuli and two sets of overlapping categories. The top panel shows six sample stimuli from the categories shown in the bottom two panels. The middle panel shows category structures in which feedback contingency is high and the bottom panel shows category structures in which feedback contingency is low. In both cases, optimal accuracy is 80% correct.

The stimuli in the middle panel of Figure 1 were selected by randomly sampling from two bivariate normal distributions – one that defines each category (Ashby & Gott, 1988). Note that the density of the 20% of B stimuli that fall above the diagonal bound decreases with distance from this bound. In other words, within the A response region, there are many B stimuli near the category bound and few far from the bound. Accuracy is typically higher for stimuli far from the bound, as is response confidence. Thus, a participant using the optimal strategy is much more likely to receive positive feedback on trials when accuracy and response confidence are high than on trials when accuracy and confidence are low. As a result, despite the overlap, feedback contingency is high – as the participant's accuracy improves, so does his or her ability to predict whether the feedback will be positive or negative. We call this the high-contingency condition.

The stimuli in the bottom panel of Figure 1 were selected in a three-step procedure. Step 1 was to generate the exact same stimuli as in the middle panel – that is, by using the same random sample from the same two bivariate normal distributions used in the middle panel. Step 2 was to assign all stimuli above and left of the diagonal bound to Category A and all stimuli below and right of the bound to Category B, regardless of their Step 1 category affiliation. Finally, in Step 3, 20% of the Category A stimuli were randomly selected and assigned to Category B, and 20% of the Category B stimuli were randomly selected and assigned to Category A. Thus, the critical point to note is that, in the bottom panel, the density of the 20% of B stimuli falling above the bound does not change with distance from the bound. As a result, in the bottom panel condition, a participant using the optimal strategy is just as likely to receive negative feedback when response confidence and accuracy are high as when response confidence and accuracy are low. In other words, even when accuracy is high, the valence of the feedback is difficult to predict. We call this the low-contingency condition.

In summary, the stimuli and optimal strategies in the low-and high-contingency conditions shown in Figure 1 are identical, and optimal accuracy is 80% correct in both conditions. One key difference however, is that response confidence (and accuracy) and the probability of receiving positive feedback are more highly correlated in the high-contingency condition than in the low-contingency condition. The critical question addressed in this article is whether (and how) this difference affects learning.

Feedback Contingency and Probabilistic Categorization

The study of feedback contingency has a long history – dating back at least to Skinner (1948) (for reviews see, e.g., Hammond, 1980; Beckers, De Houwer, & Matute, 2007). Many studies have conclusively demonstrated that humans and nonhuman animals are both extremely sensitive to feedback contingency (Alloy & Abramson, 1979; Chatlosh, Neunaber, & Wasserman, 1985; Rescorla, 1968). For example, in instrumental conditioning tasks, extinction can be induced simply by suddenly making the time of reward noncontingent on the behavior (Balleine & Dickinson, 1998; Boakes, 1973; Nakajima, Urushihara, & Masaki, 2002; Rescorla & Skucy, 1969; Woods & Bouton, 2007).

Almost all of this work used tasks with a single response option in which the participant had a choice to either respond or not respond at any time (e.g., by pressing a lever or a button; Alloy & Abramson, 1979; Dickinson & Mulatero, 1989; Corbit & Balleine, 2003; Dias-Ferreira et al., 2009; Shanks & Dickinson, 1991). Feedback (or reward) contingency was typically manipulated in one of three ways. One method was to vary the probability that reward was delivered following each response (e.g., Rescorla, 1968; Alloy & Abramson, 1979; Dickinson & Charnock, 1985). However, with a single response alternative, reducing this probability from one to a lower value is equivalent to changing from continuous reinforcement to partial reinforcement. Because of this equivalence, other methods for studying the effects of contingency degradation are also popular. A second method is to manipulate the temporal relationship between the behavior and reward (e.g., Elsner & Hommel, 2004; Wasserman, Chatlosh, & Neunaber, 1983). So for example, if the rewards are temporally noncontingent on the behavior, then rewards are still delivered, but the times when the rewards are given are uncorrelated with the times when the behaviors are emitted. In probabilistic categorization tasks like those shown in Figure 1, feedback contingency is degraded, relative to deterministic tasks, but the contingency is not temporal because feedback is delivered immediately after every response. The degraded contingency is between the state of the feedback and the participant's behavior. We refer to this as state-feedback contingency to emphasize the difference between this manipulation and temporal-feedback contingency. A third method is to degrade contingency by giving animals free access to the reward (e.g., Dickinson & Mulatero, 1989). Note though that free access to the reward reduces temporal feedback contingency, not state feedback contingency because the time of reward becomes dissociated from lever pressing, but the state of the reward stays the same.

The extensive literature on feedback contingency provides compelling justification for the present studies. Humans are highly sensitive to feedback contingency, so an obvious and important question to ask is how feedback contingency affects learning, not of the contingencies themselves, but of some other cognitive behavior in which performance improvements are feedback dependent. As mentioned, to our knowledge, this question has not been previously addressed. Furthermore, this research goal is sufficiently novel that it is difficult to make specific predictions about our experiments from the extensive literature on feedback contingency. This problem is exacerbated by the fact that the single-response-option tasks used in previous studies of feedback contingency differ fundamentally from the categorization task used here. For example, error feedback is delivered in both Figure 1 conditions, whereas negative feedback is never delivered in most single-response-option tasks (e.g., as when partial reinforcement is given in an operant-conditioning task).

Perhaps more relevant to the present research is the extensive literature on probabilistic categorization. During probabilistic category learning, some stimuli have probabilistic associations with the contrasting categories. A response that assigns a stimulus to category A might be rewarded with positive feedback on one trial and punished with negative feedback on another. Obviously, in such tasks, perfect performance is impossible. For example, in the probabilistic tasks illustrated in Figure 1, optimal accuracy is 80%. While studies of deterministic category learning are more common, research on probabilistic category learning also has a long history (Ashby & Gott, 1988; Ashby & Maddox, 1990, 1992; Estes, Campbell, Hatsopoulos, & Hurwitz, 1989; Gluck & Bower, 1988; Kubovy & Healy, 1977; Medin & Schaffer, 1978; Estes, 1986; Gluck & Bower, 1988).

Almost all probabilistic category-learning experiments are of one of two types. One approach uses stimuli that vary on binary-valued dimensions (Estes, 1986; Estes et al., 1989; Gluck & Bower, 1988; Medin & Schaffer, 1978). A common example uses the weather prediction task (Knowlton, Squire, & Gluck, 1994), in which one, two, or three of four possible tarot cards are shown to the participant, whose task is to indicate whether the presented constellation signals rain or sun. Each card is labeled with a unique, and highly discriminable, geometric pattern. Fourteen of the 16 possible card combinations are used (the zero- and four-card combinations are excluded) and each combination is probabilistically associated with the two outcomes. In the original version of the task, the highest possible accuracy was 76% (Knowlton et al., 1994). A second popular approach uses stimuli that vary on continuous dimensions and defines a category as a bivariate normal distribution. Probabilistic category assignments are created by using categories defined by overlapping distributions (Ashby & Gott, 1988; Ashby & Maddox, 1990, 1992; Ell & Ashby, 2006), exactly as in the high-contingency condition of Figure 1.

Besides the use of binary- versus continuous-valued stimulus dimensions, there is another fundamental difference between these two types of probabilistic category-learning tasks. With overlapping normal distributions feedback contingency is high because a participant using the optimal strategy will receive frequent error feedback for stimuli near the boundary and almost never receive error feedback for stimuli far from the boundary. In contrast, with binary-valued dimensions there are few stimuli that are each presented many times. The probability that a participant using the optimal strategy receives positive feedback on each stimulus is identical on every trial. Thus, if the participant's response confidence varies at all across repeated stimulus presentations, then the probability of receiving positive feedback will be relatively uncorrelated with response confidence. Thus, feedback contingency should be lower with binary-valued stimulus dimensions than with overlapping normal distributions. So to study the effects of feedback contingency on category learning one might compare performance in probabilistic categorization tasks that used binary-valued stimulus dimensions with performance in tasks that used continuous-valued stimulus dimensions and categories defined as overlapping normal distributions. No such comparisons have been attempted for good reason. There are simply too many differences between such tasks to make any comparison meaningful. Of course, the stimuli must necessarily be different, but in addition, there is no obvious way to equate such important variables as category separation. As a result, it would be impossible to attribute any performance difference to a difference in feedback contingency rather than to some other variable that could affect task difficulty.

A study of how state-feedback contingency affects learning is theoretically important because standard models of reinforcement learning seem to predict that degrading feedback contingency should either facilitate learning or at least have no detrimental effects – which sharply contradicts the results reported below. This is because standard reinforcement learning models assume that the amount of learning that occurs on each trial is proportional to the reward prediction error (RPE; Sutton & Barto, 1998), which is defined as the value of the obtained reward minus the value of the predicted reward. The idea is that when RPE = 0, the outcome was exactly as predicted, in which case there is nothing more to learn. However, an RPE that deviates from zero is a signal that an unexpected outcome occurred, and therefore that more learning is required.

When state-feedback contingency is high, positive and negative feedback are easy to predict, so extreme values of RPE will be rare. In contrast, when state-feedback contingency is low, positive and negative feedback become more difficult to predict, so the fluctuations in RPE will increase. There will be more unexpected errors, but also more unexpected correct feedbacks. For example, a B stimulus in the A response region will generate a larger RPE in the low-contingency condition of Figure 1 and therefore cause more unlearning of the correct A response on that trial. But these discrepant stimuli occur on only 20% of the trials. On the other 80% of trials, the stimuli are not discrepant. So for example, an A stimulus in the A response region will also generate a larger RPE in the low-contingency condition and therefore cause more (or better) learning of the correct A response on that trial¹. By definition, predicted reward is computed before stimulus presentation, so any RPE model that predicts larger RPEs to discrepant stimuli in our low-contingency condition must necessarily also predict larger RPEs to nondiscrepant stimuli. Since nondiscrepant stimuli outnumber discrepant stimuli in the Figure 1 tasks by 4-to-1, RPE models predict that for an ideal observer, on 4 out of 5 trials there will be more strengthening of the correct associations in the low-contingency condition, whereas on 1 out of 5 trials there will be more strengthening of the incorrect associations. All else being equal, this should cause better learning in the low-contingency condition. Even so, it might be possible to build an RPE model in which the detrimental effects of the 20% of discrepant stimuli outweighs the beneficial effects of the 80% of nondiscrepant stimuli². Unfortunately, investigating this possibility is well beyond the scope of the present article.

Rule-Based Versus Information-Integration Category-Learning Tasks

There is now abundant evidence that declarative and procedural memory both contribute to perceptual category learning (e.g., Ashby & Maddox, 2005, 2010; Eichenbaum & Cohen, 2001; Poldrack et al., 2001; Poldrack & Packard, 2003; Squire, 2004). Furthermore, many studies have reported evidence that the role of feedback is very different during declarative-memory mediated category learning than during procedural-memory mediated category learning (Ashby & O'Brien, 2007; Dunn, Newell, & Kalish, 2012; Filoteo, Lauritzen, & Maddox, 2010; Maddox, Ashby, & Bohil, 2003; Maddox, Ashby, Ing, & Pickering, 2004; Maddox & Ing, 2005; Maddox, Love, Glass, & Filoteo, 2008; Smith et al., 2014; Zeithamova & Maddox, 2007). These results call into question whether these differences might also extend to feedback contingency. As a result, the experiments described below examine the effects of degrading state-feedback contingency separately for tasks that recruit declarative versus procedural memory.

Much of the evidence that declarative and procedural memory both contribute to category learning comes from rule-based (RB) and information-integration (II) category-learning tasks. In RB tasks, the categories can be learned via some explicit reasoning process (Ashby, Alfonso-Reese, Turken, & Waldron, 1998). In the most common applications, only one stimulus dimension is relevant, and the participant's task is to discover this relevant dimension and then to map the different dimensional values to the relevant categories. A variety of evidence suggests that success in RB tasks depends on declarative memory and especially on working memory and executive attention (Ashby et al., 1998; Maddox et al., 2004; Waldron & Ashby, 2001; Zeithamova & Maddox, 2006). In II category-learning tasks, accuracy is maximized only if information from two or more incommensurable stimulus components is integrated at some predecisional stage (Ashby & Gott, 1988; Ashby et al., 1998). Evidence suggests that success in II tasks depends on procedural memory that depends on striatal-mediated reinforcement learning (Ashby & Ennis, 2006; Filoteo, Maddox, Salmon, & Song, 2005; Knowlton, Mangels, & Squire, 1996; Nomura et al., 2007).

Figure 1 shows examples of II category-learning tasks because bar width and orientation both carry useful but insufficient category information, and the optimal strategy requires integrating information from both dimensions in a way that is impossible to describe verbally. To create RB category-learning tasks, we simply rotated the II stimulus space in each condition 45° counterclockwise (and therefore all of the stimulus coordinates were also rotated). Note that this rotation converts the diagonal category bound to a vertical bound. Thus, following the rotation, the optimal categorization strategy is to use the explicit verbal rule “Respond A if the bars are narrow and B if the bars are wide.”

In summary, this article reports the results of what to our knowledge are the first experiments that examine the importance of feedback contingency on human category learning. As we will see, the results are striking. Degrading state-feedback contingency appears to abolish learning in most participants in two qualitatively different kinds of category-learning tasks.

Experiment 1

Experiment 1 directly examines the effects of feedback contingency on category learning. Four conditions are included: RB high contingency, RB low contingency, II high contingency, and II low contingency. The II conditions were exactly as shown in Figure 1. As mentioned, to create the RB conditions, we simply rotated the stimulus space from the two II conditions by 45° counterclockwise. Note that using this method, the RB and II categories are equivalent on all category separation statistics (e.g., optimal accuracy is 80% correct in all four conditions).

To our knowledge, no current theory makes a strong prediction about whether contingency degradation should have greater effects on RB or II learning. Even so, there are several reasons to expect a larger effect in our RB conditions. First, probabilistic category learning is thought to defeat the explicit learning strategies that succeed in deterministic RB tasks and instead to favor striatal-mediated procedural learning (Knowlton et al., 1996). This hypothesis seems to predict that the greater randomness of the feedback in the low-contingency conditions will disrupt RB learning more than II learning³. Second, II learning is thought to depend on a form of reinforcement learning (within the striatum), and since reducing feedback contingency increases RPEs, reinforcement learning models seem to predict better learning, or at least no disruption of learning in our II low-contingency condition than in our II high-contingency condition.

Methods

Participants and Design

Eighty participants were recruited from the University of California, Santa Barbara student community. There were a total of four experimental conditions: RB high contingency, RB low contingency, II high contingency and II low contingency. Twenty people each participated in only one of the four conditions, and they each received course credit for their participation. A priori power calculations using G*Power 3.1.9 (Faul, Erdfelder, Lang, & Buchner, 2007) suggest that with this sample size, power is greater than 0.8 for a moderate effect size (f = 0.25) with α = 0.05 and a between-measure correlation of 0.25. Each session was approximately 45 minutes in duration and included 6 blocks of 100 trials each.

Stimuli and Apparatus

The stimuli were circular sine-wave gratings presented on 21-inch monitors (1280 × 1024 resolution). All stimuli had the same size, shape and contrast, and differed only in bar width (as measured by cycles per degree of visual angle or cpd) and bar orientation (measured in degrees counterclockwise rotation from horizontal). The stimuli from the II high-contingency condition were generated first. The stimuli defining the A and B categories in this condition were generated as follows: 1) 300 random samples were drawn from the bivariate normal distribution that defined the category [means were (40, 60) and (60, 40) for categories A and B, respectively; all standard deviations were 17, and both covariances were 0]; 2) the samples were linearly transformed so that the sample statistics (means, variances, covariances) exactly matched the population parameters that defined the distributions; 3) each resulting sample value, denoted by the ordered pair (x₁, x₂), was used to generate a stimulus with bar width equal to $x_1^{\ast }=\frac{x_1}{30}+0.25$ cpd and bar orientation equal to $x_2^{\ast }=\frac{\pi }{200}{x}_2+\frac{\pi }{9}$ degrees counterclockwise rotation from horizontal.

The procedure for creating the II low-contingency stimuli was exactly as described in the Introduction. Specifically, the same stimuli were used as in the II high-contingency condition. Next, all stimuli in both categories above and to the left of the optimal decision bound (x₂ = x₁) were assigned to category A and all stimuli below and to the right of the optimal bound were assigned to category B. Finally, 20% of the stimuli in each category were selected randomly (all with the same probability) and re-assigned to the contrasting category.

The stimuli for the RB high-contingency condition were created by rotating the II high-contingency (x₁, x₂) stimulus space (and therefore all of the stimulus coordinates) 45° counterclockwise. The stimuli for the RB low-contingency condition were created by rotating the II low-contingency stimulus space 45° counterclockwise. Thus, the optimal strategy in both RB conditions was to respond A if the disk had thin bars and B if the disk had thick bars.

The stimuli were generated and presented using the Psychophysics Toolbox (Brainard, 1997) in the MATLAB software environment, and subtended an approximate visual angle of 5°. The order in which the stimuli were presented was randomized across participants and sessions.

Procedure

Participants were told that there were two equally likely categories, that on each trial they would see a single stimulus, and that they were to use the feedback to learn the correct category assignment for each of the presented stimuli. Within each condition, all participants saw the same 600 stimuli, but the presentation order was randomized across participants.

Stimulus presentation, feedback, response recording and RT measurement were acquired and controlled using MATLAB on a Macintosh computer. Responses were given on a standard QWERTY keyboard; the “d” and “k” keys had large “A” and “B” labels placed on them, respectively. Auditory feedback was given for correct and incorrect responses made within a 5-second time limit. Correct responses were followed by a brief (1-sec) high-pitched (500 Hz) tone, and incorrect responses were followed by a brief (1-sec) low-pitched (200 Hz) tone. If a key was pressed that was not one of the marked response keys, a distinct tone played and the screen displayed the words “wrong key.” If the response was made outside of the time limit, the words “too slow” appeared on the screen. In both the wrong key and the too slow cases, the trial was terminated with no category-related feedback, and these trials were excluded from analysis.

Results

Accuracy-based Analyses

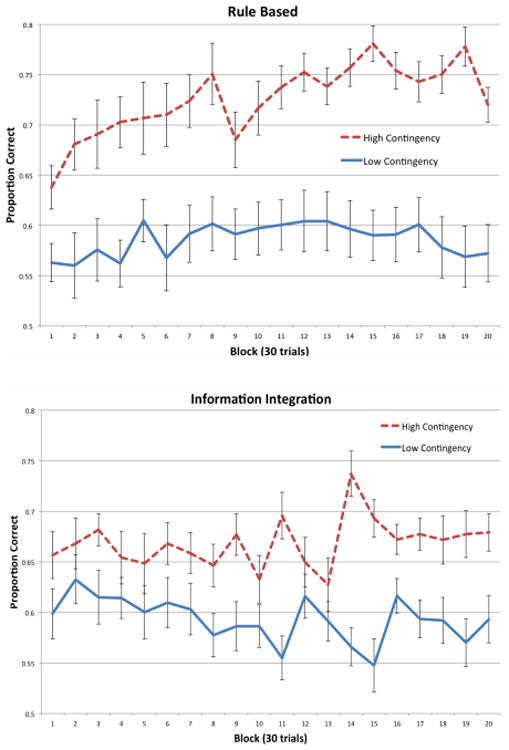
Figure 2 shows the proportion of correct responses in each 30-trial block for the RB conditions, and Figure 3 shows the same thing for the II conditions. Visual inspection suggests that average accuracy improved over the course of the experiment for both high-contingency conditions, but hovered slightly above chance (50%) with no improvement over the course of the experiment for both low-contingency conditions.

Figure 2.

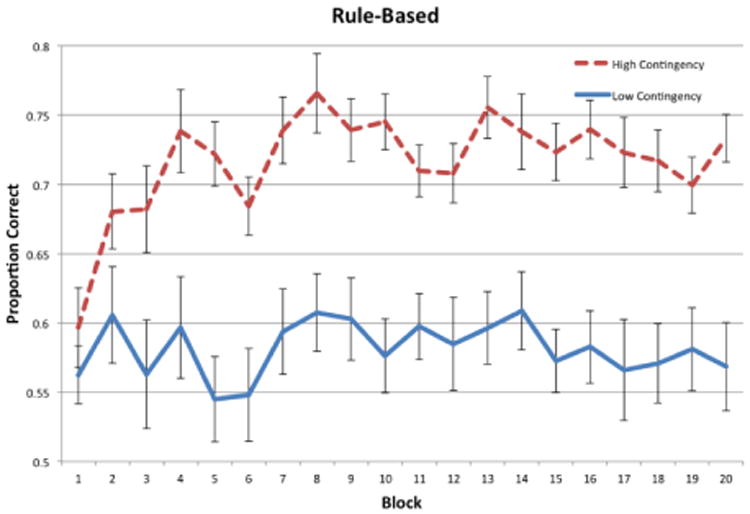
Accuracy for each block of trials in the RB conditions of Experiment 1.

Figure 3.

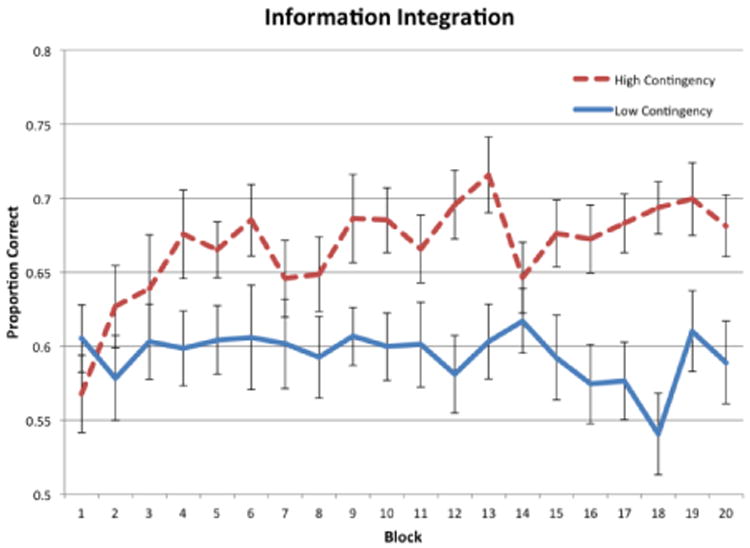
Accuracy for each block of trials in the II conditions of Experiment 1.

To test these conclusions more rigorously and to examine whether there were any differences in how well participants learned the category structures in each condition, a two-factors repeated measures ANOVA (high contingency versus low contingency × block) was performed separately for the RB and II conditions. For the RB conditions, there was a significant effect of condition, [F(1, 38) = 31.43, p < 0.001, η² = .326], a significant effect of block [F(19, 722) = 2.45, p < 0.001, η² = .040], but no significant interaction between condition and block [F(19, 722) = 1.17, p = 0.276, η² = .019]. This indicates that there was a significant difference in performance between RB high-contingency and RB low-contingency conditions. In the II conditions, there was a significant effect of condition, [F(1, 38) = 13.56, p < 0.001, η² = .126], no significant effect of block [F(19, 722) = 1.170, p = .277, η² = .025], and a small significant interaction between condition and block [F(19, 722) = 1.619, p = 0.046, η² = .035]. Similar to the RB results, this also indicates that there was a significant difference in performance between II high-contingency and II low-contingency conditions.

As another test of learning, post hoc repeated measures t-tests were performed to compare accuracy in the last block to accuracy in the first block. The results showed a significant increase in accuracy in both high-contingency conditions [RB: t(19) = 4.286, p < 0.001; II: t(19) = 3.823, p = .001], but not in either low-contingency condition [RB: t(19) = 0.1915, p = 0.85; t(19) = .434, p = 0.67]. This indicates that there was significant learning in both high-contingency conditions, but not in either of the low-contingency conditions.

Model-based Analyses

Statistical analyses of the accuracy data suggested that participants performed significantly better in both of the high-contingency conditions compared to the low-contingency conditions. However, before interpreting these results it is important to determine the decision strategies that participants adopted, and especially whether participants in the high-contingency conditions were using strategies of the optimal type.

To answer these questions, we fit decision bound models to the last 100 responses of each participant in the experiment. Decision bound models assume that participants partition the perceptual space into response regions (Maddox & Ashby, 1993). On every trial, the participant determines which region the percept is in and then gives the associated response. Three different types of models were fit to each participant's responses: models assuming an explicit rule-learning strategy, models assuming a procedural strategy, and models that assume random guessing. The rule-learning models assumed a one-dimensional rule and included two free parameters (a decision criterion on the single relevant dimension and perceptual noise variance). Although the optimal rule in the RB conditions was on bar width, we fit separate rule-learning models that assumed a rule on bar width or on bar orientation in every condition. The procedural-learning models, which assumed a decision bound of arbitrary slope and intercept, had three free parameters (slope and intercept of the decision bound and perceptual noise variance). Two different guessing models were fit – one that assumed the probability of responding A equaled $\frac{1}{2}$ on every trial (zero free parameters) and one that assumed the probability of responding A equaled p on every trial (where p was a free parameter). This latter model was included to detect participants who just responded A (or B) on almost every trial.

All parameters were estimated using the method of maximum likelihood and the statistic used for model selection was the Bayesian Information Criterion (BIC; Schwarz, 1978), which is defined as

$$\mathit{\text{BIC}}=rlnN-2lnL,$$ (1)

where r is the number of free parameters, N is the sample size, and L is the likelihood of the data given the model. The BIC statistic penalizes models for extra free parameters. To determine the best-fitting model within a group of competing models, the BIC statistic is computed for each model, and the model with the smallest BIC value is the winning model.

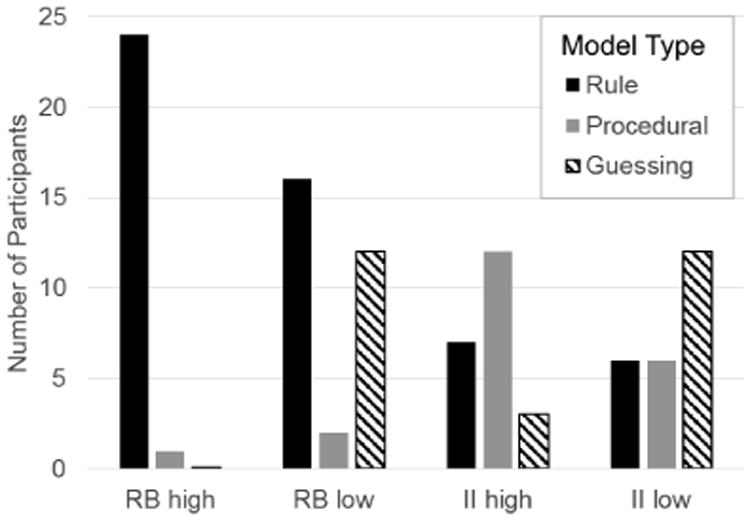
Each participant was classified according to whether his or her responses were best fit by a model that assumed a decision strategy of the optimal type – hereafter referred to as ‘optimal type’ participants – or whether those responses were best fit by a model that assumed a suboptimal decision strategy – hereafter referred to as ‘suboptimal type’ participants. Note that participants whose responses were best fit by a guessing model were classified as suboptimal types in all conditions. The results are shown in Figure 4. Note that in both high-contingency conditions, most participants were optimal types. These results are consistent with similar previous experiments (e.g., Ell & Ashby, 2006). In contrast, in both low-contingency conditions, fewer participants were optimal types and more participants resorted to guessing in both the RB and II conditions.

Figure 4.

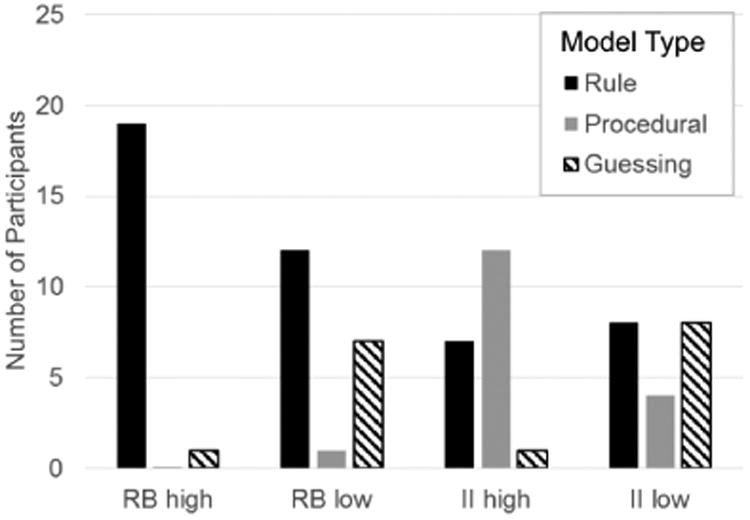
Number of participants whose responses were best fit by a model that assumed a rule-learning, procedural-learning, or guessing strategy in each of the four experimental conditions.

Figure 5 shows the best-fitting decision bounds for each participant in every condition, except for those participants whose responses were best accounted for by a guessing strategy (in these cases, there is no decision bound to plot). This figure clearly shows that degrading feedback contingency increased the number of participants who adopted suboptimal bounds that are associated with lower overall accuracy. In both the RB and II conditions, more participants had a best-fitting decision bound near the optimal bound when feedback contingency was high than when it was low. In fact, the figure underestimates this effect because it does not show participants who responded as if they were guessing. Whereas only one participant in each high-contingency condition was classified as a guesser, there were at least 7 guessers in each low-contingency condition.

Figure 5.

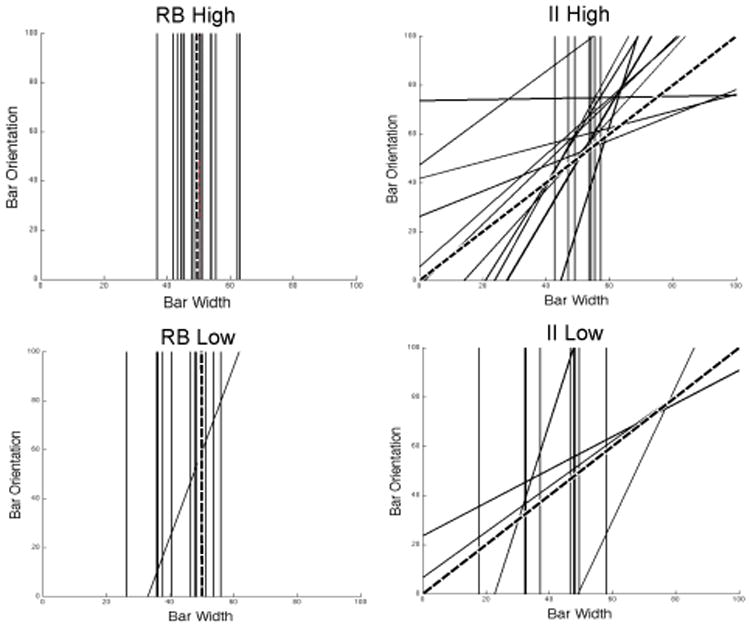
Best-fitting decision bounds for each participant in every condition. The broken lines denote the optimal boundaries. Note that participants whose responses were best accounted for by a guessing strategy are not represented in this figure.

So far our analyses indicate that a model assuming a decision strategy of the optimal type provides the best account of the responses of more participants in the high-contingency conditions than in the low-contingency conditions. But these analyses do not indicate how well or how consistently participants use that strategy. In other words, for each participant, we have goodness-of-fit values (i.e., BIC scores) for every candidate model. If the best fit (i.e., lowest BIC value) is by a model that assumes an optimal-type strategy then we know that that model provides a better account of the participant's responses than any other model, but from this fact alone we do not know whether the fit was good or bad. It is possible that all models provided poor fits and the optimal-type model just happened to provide the least poor fit. Unfortunately, the numerical value of the raw BIC score does not help with this problem because BIC scores increase with sample size, regardless of the quality of fit (see Eq. 1).

Any model that assumes either a rule or procedural decision strategy will provide a poor fit to randomly generated data. With random data, the guessing model will provide the best fit. So one way to assess how well a decision bound model (DBM; either rule or procedural) fits the data is to compare its fit to the fit of the guessing model. Bayesian statistics allows a method to make such comparisons (via the so-called Bayes factor). If the prior probability that the DBM model M_DBM is correct is equal to the prior probability that the guessing model M_G is correct, then under certain technical conditions (e.g., Raftery, 1995), it can be shown that

$$P(M_{\text{DBM}}|\text{Data})\doteq \frac{1}{1+exp[-\frac{1}{2}({\mathit{\text{BIC}}}_{\mathrm{G}}-{\mathit{\text{BIC}}}_{\text{DBM}})]},$$ (2)

where P(M_DBM|Data) is the probability that the DBM model is correct, assuming that either the DBM or guessing model is correct. Thus, for example, if the DBM model is favored over the guessing model by a BIC difference of 2, the probability that the DBM model is correct is approximately .73. In other words, even though the DBM fits better than the guessing model, the fit is not very good because there is better than 1 chance in 4 that the data were just generated by random coin tossing. In contrast, if the BIC difference is 10, then the probability that the DBM model is correct is approximately .99, which means that we can be very confident that this participant was consistently using a single decision strategy that is well described by our DBM. In this case, the DBM provides an excellent fit to the data.

Following this logic, we computed the Eq. 2 probabilities for every participant in Experiment 1, where BIC_DBM was the BIC score of the best-fitting DBM. In the RB conditions, the mean value of P(M_DBM|Data) (i.e., across participants) was .951 in the high-contingency condition and .632 in the low-contingency condition [t(38) = 2.73, p < .01]. So the DBMs are fitting the data well when contingency is high and poorly when contingency is low. In the II conditions, the means were .952 in the high-contingency condition and .700 in the low-contingency condition [t(38) = 2.51, p < .01]. Again, the DBMs fit much better when contingency is high than when it is low.

In summary, the modeling analysis reinforces the results of the more traditional statistical analyses. Degrading feedback contingency dramatically reduced the ability of participants to learn the category structures, and this reduction was approximately equally large with RB and II category structures. Furthermore, degrading feedback contingency not only significantly reduced accuracy, but it also impaired the ability of participants to discover a decision strategy of the optimal type.

Discussion

The results of this experiment were striking. Although exactly the same stimuli were used in the high- and low-contingency conditions, and the same optimal accuracy was possible, learning was good when feedback contingency was high and we saw little or no evidence for any learning when feedback contingency was low. This result was equally true for both RB and II categories. In fact, note that the effects of contingency degradation were so strong that they caused a violation of the ubiquitous result that human performance is far better in one-dimensional RB tasks than in II tasks (e.g., Ashby & Maddox, 2005) – specifically, Figures 2 and 3 show that performance in the high-contingency II condition was considerably better than in the low-contingency RB condition.

One somewhat puzzling aspect of Experiment 1, which occurred in both the RB and II conditions, is that although there was no evidence for any improvement in accuracy across blocks in the low-contingency conditions, accuracy was nevertheless above chance. Specifically, mean accuracy during the last 100 trials was .573 in the RB low-contingency condition and .580 in the II low-contingency condition, both of which are significantly above chance [RB: t(19) = 3.05, p < .05; II: t(19) = 3.81, p < .05]. A closer examination of the individual participant data somewhat clarifies this apparent paradox.

In the RB condition, 4 of the 20 low-contingency participants achieved an accuracy of better than 70% correct during their last 100 trials. This is in contrast to 13 of 20 who met this criterion in the high-contingency condition. If these 4 more accurate participants are removed from the analysis, then the mean accuracy of the remaining 16 low-contingency participants is not significantly above chance [mean proportion correct = .533, t(15) = 1.718, p > .05]. So the fact that accuracy in the RB low-contingency condition was significantly above chance was completely driven by these 4 participants. The modeling analysis suggested that 3 of these 4 participants used a one-dimensional rule and one used a procedural strategy. Figure 4 shows that 12 of the 20 RB low-contingency participants appeared to be using a one-dimensional rule of the optimal type (as opposed to 19 of 20 in the high-contingency condition). However, the rule users in the RB low-contingency condition were significantly less accurate than the rule-users in the RB high-contingency condition (high-contingency = 72.5% correct; low-contingency = 60.5% correct; t(29) = 3.99, p < .05) and the low-contingency participants used those rules significantly less reliably (mean Eq. 2 values: high-contingency = 1.0; low-contingency = .967; t(29) = 2.26, p < .05).

In the II low-contingency condition, only one participant achieved an accuracy of 70% correct or higher during the last 100 trials (in contrast to 10 of 20 participants in the high-contingency condition), but this participant's responses were best accounted for by a one-dimensional rule. In fact, 8 of the 20 II low-contingency participants appeared to be using a one-dimensional rule (see Figure 4), and these 8 participants averaged 63% correct during the last 100 trials, in contrast to an average of 54.6% for the other 12 participants. Of these 12 non-rule users, 8 appeared to be guessing (with a mean accuracy of 50.1% correct) and 4 appeared to be using a procedural strategy. The accuracy of these latter 4 participants over the last 100 trials averaged 63.8%, so 4 of our 20 participants showed evidence of weak procedural learning. Even so, these 4 procedural-strategy users were significantly less accurate than the 12 procedural-strategy users in the II high-contingency condition (high-contingency = 70.6% correct; low-contingency = 63.8% correct; t(14) = 2.136, p < .05).

In summary, in the RB and II high-contingency conditions, most participants successfully learned the categories, in the sense that their last-block accuracy was significantly above chance [RB: mean proportion correct = .733, t(19) = 13.511, p < .000; II: mean proportion correct = .681, t(19) = 8.678, p < .001] and they appeared to use a strategy of the optimal type. In contrast, most participants in both low-contingency conditions showed no evidence of learning. A few participants in both low-contingency conditions did appear to learn. However, even these ‘successful’ participants performed more poorly than their counterparts in the high-contingency conditions. Thus, degrading feedback contingency appeared to have a catastrophic effect on learning – in both RB and II conditions. To our knowledge, this is the first demonstration that state-feedback contingency plays such a critical role in category learning.

Experiment 2

In all conditions of Experiment 1, an ideal observer would respond incorrectly to 20% of the stimuli. We refer to these as the discrepant stimuli. One possible confound with Experiment 1 is that the high-contingency conditions included more discrepant stimuli near the optimal decision bound than the low-contingency conditions. Because of this, an ideal observer operating in the presence of perceptual noise will perform better in the high-contingency conditions than in the low-contingency conditions. This is because noise is more likely to move a discrepant stimulus to the opposite side of the decision bound in the high-contingency condition (since more discrepant stimuli are near the bound). Thus, the ideal observer would respond correctly to more discrepant stimuli in the high-contingency conditions than in the low-contingency conditions. This effect is not large⁴. Without noise, an ideal observer responds identically in the high- and low-contingency conditions. As noise levels increase, the ideal observer begins to show an accuracy advantage in the high-contingency conditions, and this advantage increases to a maximum value of about 4.4% at an unrealistically large noise level (i.e., when the perceptual noise is about equal to the variability within each category on the relevant dimension). As noise levels increase even higher, the accuracy advantage of the high-contingency conditions slowly decreases to 0 (at infinite noise levels).

The human observer always operates in the presence of perceptual noise (Ashby & Lee, 1993), although human perceptual noise will be much less than the variability level at which the ideal observer shows a maximum accuracy advantage in the high-contingency conditions of Experiment 1. So at human-like levels of perceptual noise, an ideal observer will perform less than 4% better in the high-contingency conditions than in the low-contingency conditions. Humans are not ideal observers, so we expect the high-contingency advantage of the best human to be less than this and Figures 2 and 3 show that the observed human high-contingency advantage is much larger than 4%. Therefore, this factor alone does not account for our results. Even so, because the ideal observer shows a small accuracy advantage in the high-contingency conditions, it is difficult to determine how much of the observed high-contingency accuracy advantage is due to a contingency difference, rather than to this difference in ideal observer performance.

Experiment 2 was designed to address this issue. Our solution was simple. Basically, we replicated all four conditions of Experiment 1, except we created a no-stimulus zone on either side of the optimal decision bound simply by moving (i.e., translating) the coordinates of all stimuli away from the bound by a fixed distance. This distance was chosen to be about equal to the perceptual variability exhibited by the Experiment 1 participants – that is, to the mean standard deviation of perceptual noise from the best-fitting decision bound models in Experiment 1. Figure 6 shows the resulting stimuli for the II conditions. The stimuli in the RB conditions were just 45° rotations of the II categories (as in Experiment 1). Because of the no-stimulus zone on either side of the optimal bound, an ideal observer displaying the same amount of perceptual noise as the Experiment 1 participants would perform identically⁵ in the high- and low-contingency conditions of Experiment 2.

Figure 6.

The high- and low-contingency II categories used in Experiment 2.

Methods

Participants and Design

Experiment 2 included 101 participants recruited from the University of California, Santa Barbara student community divided as follows among the same four experimental conditions as in Experiment 1 as follows: RB high contingency: 25 participants, RB low contingency: 30 participants, II high contingency: 22 participants, and II low contingency: 24 participants. A priori power calculations using G*Power 3.1.9 (Faul et al., 2007) suggest that with this sample size, power is again greater than 0.8 for a moderate effect size (f = 0.25) with α = 0.05 and a between-measure correlation of 0.25.

Stimuli and Apparatus

The stimuli were generated in a two-step procedure. First, the stimuli from all conditions were generated exactly as in Experiment 1. Second, in each condition, a no-stimulus region was created on both sides of the optimal decision bound by translating the coordinates of every stimulus away from the bound 3.5 units in the direction orthogonal to the bound. The resulting coordinates of every stimulus were then used to created a stimulus disk following the same procedures as in Experiment 1.

Procedures

All procedures were identical to Experiment 1.

Results

Accuracy-based Analyses

Figure 7 shows the proportion of correct responses in each 30-trial block for the RB and II conditions. Visual inspection suggests that average accuracy improved over the course of the experiment for the RB high-contingency condition, improved slightly for the II high-contingency condition, but hovered slightly above chance (50%) with no improvement over the course of the experiment for both low-contingency conditions.

Figure 7.

Accuracy for each block of trials in the RB (top panel) and II (bottom panel) conditions of Experiment 2.

To test these conclusions more rigorously and to examine whether there were any differences in how well participants learned the category structures in each condition, a two-factors repeated measures ANOVA (high contingency versus low contingency by block) was performed separately for the RB and II conditions. For the RB conditions, there was a significant effect of condition, [F(1, 53) = 28.53, p < .001, η² = .321], a significant effect of block, [F(19, 1007) = 2.442, p < .001, η² = .029], and no significant interaction between block and condition [F(19, 1007) = 1.301, p = .173, η² = .016]. This indicates that there was a significant difference in performance between RB high-contingency and RB low-contingency conditions. In the II conditions, there was a significant effect of condition, [F(1, 44) = 20.67, p < .001, η² = .140], no significant effect of block, [F(19, 836) = 0.785, p = 0.727, η² = .014], and a significant interaction between block and condition [F(19, 836) = 1.945, p < .01, η² = .036]. Similar to the RB results, this also indicates that there was a signiificant difference in performance between the II high-contingency and II low-contingency conditions.

As another test of learning, post hoc repeated measures t-tests were performed to compare accuracy in the last block to accuracy in the first block. The results showed a significant increase in the RB high-contingency condition [t(24) = 2.846, p < .01], but not in the other three conditions [RB: t(29) = .310, p = .759; II high contingency: t(21) = .816, p = .424; II low contingency: t(23) = −.175, p = .863].

Model-based Analyses

Statistical analyses of the accuracy data suggested that participants performed significantly better in both high-contingency conditions than in either corresponding low-contingency condition. Furthermore, we found no evidence of learning in either low-contingency condition. However, before interpreting these results further, it is important to determine the decision strategies that participants adopted, and especially whether participants in the high-contingency conditions were using strategies of the optimal type. To answer these questions, we fit decision bound models to the last 100 responses of each participant in the experiment. Just as in Experiment 1, three different types of models were fit to each participant's responses: models assuming an explicit rule-learning strategy, models assuming a procedural strategy, and models that assume random guessing.

The results are shown in Figure 8. Note that in both high-contingency conditions, most participants used a strategy of the optimal type. In contrast, in the low-contingency conditions, 40% of the RB participants and half of the II participants resorted to guessing. Figure 9 shows the best-fitting decision bounds for each participant in every condition, except for those participants whose responses were best accounted for by a guessing strategy (in these cases, there is no decision bound to plot). This figure clearly shows that degrading feedback contingency increased the number of participants who adopted suboptimal bounds. In both the RB and II conditions, the decision strategies of more participants in the high-contingency condition were closer to the optimal strategy than in the low-contingency condition. As in Experiment 1, the figure underestimates this effect because it does not show participants who responded as if they were guessing. Whereas, there were no guessers in the RB high-contingency condition and only 3 guessers in the II high-contingency condition, there were 12 guessers in each low-contingency condition.

Figure 8.

Number of participants whose responses were best fit by a model that assumed a rule-learning, procedural-learning, or guessing strategy in each of the four experimental conditions of Experiment 2.

Figure 9.

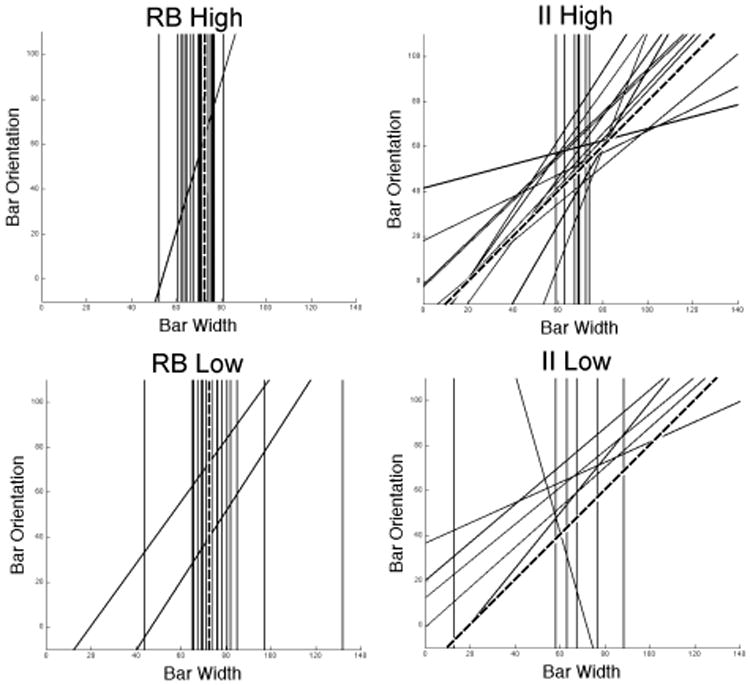
Best-fitting decision bounds for each participant in every condition of Experiment 2. The broken lines denote the optimal boundaries. Note that participants whose responses were best accounted for by a guessing strategy are not represented in this figure.

As in Experiment 1, we also computed the Eq. 2 probabilities for every participant to assess the quality of the DBM fits. For both RB and II categories, the quality of the DBM fit (relative to guessing) is significantly better when contingency is high than when it is low [RB Eq. 2 means: high-contingency = .998, low-contingency = .644, t(53) = 3.785, p < .01; II Eq. 2 means: high-contingency = .853, low-contingency = .516, t(44) = 2.793, p < .01].

Discussion

The Experiment 2 results closely matched the results of Experiment 1. Learning was good in both high-contingency conditions, whereas the learning curves were essentially flat in both low-contingency conditions with a mean accuracy during each of the last three blocks of training below 60% correct. Even so, for both RB and II categories, mean accuracy over the last 100 trials was significantly above chance in the low-contingency conditions [RB: percent correct = .574, t(29) = 2.877, p < .05; II: percent correct = .581, t(23) = 4.802, p < .01]. To understand why, we need to look more closely at the data of each individual participant.

In the case of RB categories, 5 of the 30 low-contingency participants learned well. Their mean accuracy was 76.6% correct, they all used the appropriate one-dimensional rule, and they all used this rule reliably (Eq. 2 mean = 1). When these 5 participants are removed from the low-contingency analysis, the mean accuracy of the remaining 25 participants is 53.6% correct, which is not significantly different from chance [t(24) = 1.47, p = .077]. So the story for the RB low-contingency condition is fairly simple – 5 participants learned well and 25 participants showed no (statistical) evidence of any learning. In contrast, in the RB high-contingency condition, 22 of 25 participants had an accuracy of 70% correct or better (and the accuracies of the other three were all above 60%), and the mean accuracy of all participants during the last block was significantly greater than chance [mean proportion correct = .720, t(25) = 12.547, p < .001].

In the II conditions, only 1 of 24 participants exceeded 70% correct during the last 100 trials in the low-contingency condition, and this single participant only achieved an accuracy of 72% correct. In contrast, 8 of the 22 high-contingency participants exceeded 70% correct and the mean accuracy of all high-contingency participants during the last block was significantly greater than chance [mean proportion correct = .679, t(22) = 9.626, p < .001]. Furthermore, the responses of 6 of the 24 low-contingency participants were best fit by a procedural strategy model, in contrast to 12 of the 22 high-contingency participants. The accuracy of the low-contingency procedural strategy participants was 67.2% correct, which is considerably higher than the accuracy of the low-contingency rule users (58.9%) or guessers (53.2%). So it appears that the most important reason that the low-contingency accuracy was above chance is because 6 of the 24 participants exhibited some procedural learning. Even so, it is important to note that the accuracy of the low-contingency procedural strategy participants was marginally lower than the accuracy of the high-contingency procedural strategy participants [high-contingency = 70.1% correct, low-contingency = 67.2%, t(16) = 1.357, p = .097].

In summary, the results of Experiment 2 closely matched the results of Experiment 1. Learning was good in both high-contingency conditions, whereas most participants in both low-contingency conditions showed no evidence of any learning. On the other hand, a few participants did appear to learn in both low-contingency conditions, and in general these few learners seemed to perform better than the few learners found in Experiment 1. Much more important however, is that the results of Experiment 2 provide strong evidence that the poor performance of the Experiment 1 low-contingency participants was not because the high-contingency categories in Experiment 1 included more discrepant stimuli near the category bound than the low-contingency categories. Instead, the two experiments together strongly support the hypothesis that contingency degradation greatly impairs both RB and II learning.

General Discussion

The present article describes the first known investigation of the effects of feedback contingency on human category learning. The results were dramatic. In two different experiments, and in both RB and II tasks, learning was good when state-feedback contingency was high, but degrading feedback contingency seemed to abolish all learning in most participants, even though our high- and low-contingency conditions used exactly the same stimuli, had exactly the same optimal strategies, and exactly the same optimal accuracies.

Whereas most low-contingency participants showed no evidence of any learning, a small group (between 10% and 20%) of participants did show evidence of learning in every low-contingency condition. In most cases, the participants who did show evidence of learning in the low-contingency conditions performed worse than their high-contingency counterparts, so even in this group contingency degradation seemed to impair learning. The exception was in the RB low-contingency condition of Experiment 2. Five of the 30 participants in that condition performed as well as the 25 participants in the Experiment 2 RB high-contingency condition. Thus, at least with the levels of contingency degradation studied here, it appears that normal RB learning is possible in at least some participants.

The results of Experiments 1 and 2 are incompatible with almost all current theories of learning. For example, as mentioned earlier, standard reinforcement learning models generally predict either better learning in the low-contingency conditions, or at worst, no difference between the low- and high-contingency conditions. By definition, noncontingent rewards are unpredictable. As such, they generate large reward prediction errors (RPEs) – in fact, for any given positive feedback rate, noncontingent rewards induce the largest possible RPEs. Reinforcement learning models predict that the amount of learning that occurs on each trial increases with the RPE, and because the feedback reinforces the optimal response on 80% of the trials in all conditions, the standard reinforcement learning model should predict better learning in our low-contingency conditions – a prediction that is strongly incompatible with our results.

Crossley, Ashby, and Maddox (2013) proposed a modification to the standard reinforcement learning model that does correctly predict our II results. Specifically, they proposed that II category learning is impaired when feedback contingency is degraded because the amount of dopamine release that occurs to an unexpected reward is modulated by feedback contingency. Working within the framework of the COVIS theory of category learning (Ashby et al., 1998), they proposed that when rewards are contingent on behavior, dopamine fluctuations with RPE are large, whereas if rewards are noncontingent on behavior, then dopamine fluctuations will be low (regardless of the RPE). This hypothesis is supported by functional magnetic resonance imaging studies in humans that have identified activity in the dorsal striatum that is correlated with RPE when feedback is contingent on behavior, but not when feedback is independent of behavior (Haruno & Kawato, 2006; O'Doherty et al., 2004). In addition, Crossley et al. (2013) also presented behavioral data that indirectly supported this hypothesis. An adaptive justification for this assumption is that when rewards are not contingent on behavior, then changing behavior cannot increase the amount or probability of reward. As a result, there is nothing of benefit to learn. If dopamine fluctuates under such conditions, then reinforcement learning models predict that learning will occur, but it will be of behaviors that have no adaptive value. Thus, this hypothesis predicts that the dopamine fluctuations that occur to feedback in the low-contingency II condition will be smaller than the fluctuations that occur in the high-contingency II condition, and as a result, learning will be better with highly contingent feedback. Our results support this prediction of the Crossley et al. (2013) hypothesis.

One interesting result that was observed both in Experiments 1 and 2 was that the effects of degrading contingency were similar in the RB and II conditions. This might be considered somewhat of a surprise because, as mentioned earlier, probabilistic category learning is thought to defeat the explicit learning strategies that succeed in deterministic RB tasks and instead to favor striatal-mediated procedural learning (Knowlton et al., 1996). Furthermore, our low-contingency conditions are more like the probabilistic tasks that motivated this hypothesis (which used binary-valued stimulus dimensions) than our high-contingency conditions. For this reason, one might have expected better performance in the II low-contingency condition than in the RB low-contingency condition.

Given that the RB and II results were so similar, one might naturally ask whether the mechanism responsible for the failure of participants to learn in the low-contingency conditions is the same in the RB and II tasks. As described earlier, there are so many qualitative differences in the role of feedback during RB and II learning and performance that a common mechanism can not be assumed. Unfortunately, none of our results speak to this question. Even so, there is theoretical reason to expect that the failures are due to different underlying causes.

The COVIS theory of category learning assumes separate explicit reasoning and procedural-learning categorization systems that compete for access to response production (Ashby et al., 1998; Ashby, Paul, & Maddox, 2011). The explicit system uses executive attention and working memory to select and test simple verbalizable hypotheses about category membership. The procedural system uses dopamine-mediated reinforcement learning to gradually associate categorization responses with regions of perceptual space. COVIS assumes that the explicit system dominates in RB tasks and the procedural system dominates in II tasks.

COVIS suggests that the impaired RB and II learning we saw when contingency was degraded was likely due to different causes. As mentioned earlier, the Crossley et al. (2013) generalization of the COVIS procedural system predicts that learning was poor in the low-contingency II condition because low state-feedback contingency dampens the dopamine response to feedback. The COVIS explicit system learns by constructing and testing explicit hypotheses about category membership. If feedback indicates that the current hypothesis is incorrect, then a new rule or hypothesis is selected and attention is switched from the old rejected rule to the newly selected rule. In the high-contingency condition, a participant using the correct rule will receive negative feedback only for stimuli for which response confidence is low. The correct rule in our RB task, was “Respond A if the bars are thin and B if the bars are thick.” In the high-contingency condition, a participant using this rule would receive negative feedback only (or almost only) when the presented stimulus had bars of nearly equivocal width. A participant receiving such negative feedback is likely to attribute the error to misperceived bar width or the use of an inaccurate response criterion, and is unlikely to conclude that the rule was wrong. In the low-contingency condition however, negative feedback would sometimes be received when the stimulus had bars of an extreme width. In this case, the error is unlikely to be due to misperception or a faulty criterion, so an obvious inference is that the rule was wrong. For these reasons, participants who generate and test explicit rules seem more likely to switch away from the correct rule in the low-contingency condition than in the high-contingency condition, leading to impaired learning when contingency is degraded. The original version of COVIS switched rules with equal probability on all error trials. Thus, that model predicts no difference between our RB low- and high-contingency conditions. But an obvious modification, which would seemingly account for our results, is that following negative feedback, the probability of switching from the current rule to a new rule is inversely related to response confidence. An important goal of future research should be to determine why learning is so poor in RB and II tasks when feedback contingency is degraded.

Another important question raised by our results is why have so many articles reported what appears to be good learning in probabilistic categorization tasks that used stimuli that varied on binary-valued dimensions (e.g., Estes, 1986; Estes et al., 1989; Gluck & Bower, 1988; Knowlton et al., 1994; Medin & Schaffer, 1978)? Given that the use of binary-valued stimuli should, in general, cause state-feedback contingency to be lower than in our high-contingency conditions, then an extrapolation of our results might lead one to expect poor learning of probabilistic categories when the stimuli vary on binary-valued dimensions. Our experiments were not designed to answer this question. Nevertheless, some interesting hypotheses come to mind. First, with binary-valued dimensions there are only a few stimuli, so explicit memorization strategies could succeed, whereas such strategies are useless in our experiments since participants never saw the same stimulus twice. Second, with binary-valued dimensions, all stimuli are typically the same distance from the optimal categorization boundary, which means that all stimuli are typically equally difficult to categorize. State-feedback contingency is essentially a correlation – between response confidence (i.e., the predictor) and feedback valence (i.e., the outcome). A correlation can only be computed when there are multiple values of the predictor. Perceptual noise could cause participants to assume there are multiple predictors in experiments with binary-valued stimuli, in which case a low value of feedback contingency would be computed. But it also seems possible that participants in such experiments might realize that there are only two values on each stimulus dimension, in which case state-feedback contingency is impossible to compute. So another possibility could be that with binary-valued stimulus dimensions, people are poor at estimating state-feedback contingency. Obviously, more research on this interesting issue is needed.

In summary, our results suggest that feedback contingency is a critically important variable during category learning. This novel finding has both important practical and theoretical implications. On the practical side, our results suggest that in any real-world feedback-based training, conditions should always be arranged so that feedback contingency is maximized. Theoretically, the Crossley et al. (2013) proposal that reducing contingency reduces the gain on dopamine fluctuations should be tested, and more theoretical proposals are needed about other possible ways in which feedback contingency can affect learning.