Object-Oriented Regression for Building Predictive Models with High Dimensional Omics Data from Translational Studies

Abstract

Maturing omics technologies enable researchers to generate high dimension omics data (HDOD) routinely in translational clinical studies. In the field of oncology, The Cancer Genome Atlas (TCGA) provided funding support to researchers to generate different types of omics data on a common set of biospecimens with accompanying clinical data and to make the data available for the research community to mine. One important application, and the focus of this manuscript, is to build predictive models for prognostic outcomes based on HDOD. To complement prevailing regression-based approaches, we propose to use an object-oriented regression (OOR) methodology to identify exemplars specified by HDOD patterns and to assess their associations with prognostic outcome. Through computing patient’s similarities to these exemplars, the OOR-based predictive model produces a risk estimate using a patient’s HDOD. The primary advantages of OOR are twofold: reducing the penalty of high dimensionality and retaining the interpretability to clinical practitioners. To illustrate its utility, we apply OOR to gene expression data from non-small cell lung cancer patients in TCGA and build a predictive model for prognostic survivorship among stage I patients, i.e., we stratify these patients by their prognostic survival risks beyond histological classifications. Identification of these high-risk patients helps oncologists to develop effective treatment protocols and post-treatment disease management plans. Using the TCGA data, the total sample is divided into training and validation data sets. After building up a predictive model in the training set, we compute risk scores from the predictive model, and validate associations of risk scores with prognostic outcome in the validation data (p=0.015).

1. Introduction

The advent of next generation sequencing technologies ^{1; 2} enables clinical researchers to routinely process hundreds of biospecimen samples collected from patients, assessing, e.g., genomewide expression levels ³, methylation levels⁴, or somatic mutations ⁵, referred to here as high dimensional omics data (HDOD). Despite the usually limited available sizes of clinical samples, the numbers of observed variables on each sample can be in the thousands or millions. The affordability of these technologies has moved the bottleneck of clinical research from sample acquisitions to data management and data analytics. While there are numerous analytic objectives contemplated by biomedical informatics researchers, one of them, the focus of this manuscript, is to build predictive models for specific clinical outcomes, utilizing HDOD along with other clinical variables.

Building predictive models has been a long-standing research interest shared by quantitative researchers in several disciplines. Computer scientists have been actively developing predictive models with large data sets from databases^{6; 7}. Methods include support vector machines ⁸, genetic algorithms ⁹, and many other machine learning algorithms ^{10; 11}. Additionally, taking full advantage of their intimate familiarity with database technologies and visualization tools, computer scientists have been effective in organizing HDOD, scaling up computing power to analyze HDOD, and presenting HDOD-derived results visually so that biomedical researchers can interact with HDOD and can intuitively comprehend results. Recent successes with these applications in biomedical research partially contribute to the growth of bioinformatics.

Building predictive models has been a long-standing interest for statisticians. A literature review is not attempted here. It suffices to note several major milestones in this area. Given the nature of predicting an outcome with multiple variables, regression-based predictive models are commonly built, and most are special cases within generalized linear models (GLM) ¹². Relaxing the parametric assumption, Hastie and Tibshirani described a generalized additive model (GAM), synthesizing results from decades of research on nonparametric regression methods ¹³. In recent years, statisticians have been developing penalized likelihood techniques to automate the covariate selections from HDOD ¹⁴, including LASSO ^{15; 16}, GBM ¹⁷, Elastic-Net ¹⁸, Ridge regression ¹⁹ and Radom Forests²⁰. These methods are commonly used tools for analyzing HDOD in translational research.

While there is some crossbreeding of methods between computer sciences and statistics, one fundamental difference in our opinion is that computer scientists often explore patterns with multiple variables from a systemic perspective, while statisticians tend to identify a few covariates following the parsimony principle. A major challenge facing statisticians is how to control the overly inflated false positive error rate in selecting predictors from HDOD, so that discoveries are reproducible in independent samples. In contrast, computer scientists or bioinformaticians, with primary interest in patterns of HDOD, often desire to quantify observed patterns in a robust manner, in hope that discovered patterns are reproducible on independent data sets.

To frame the “big picture”, consider what would be a clinician’s intuition in dealing with complex medical information. Clinicians typically gather multifaceted information from medical records, from physical examinations, and from diagnostic laboratory tests, a version of HDOD, and then make a clinical judgement based on the evidence plus their experiences of past cases. Mentally, an experienced clinician would compare the new patient with previously treated patients or those typical cases in textbooks or in literature, and would reduce the mental comparison to an intuitive clinical judgement with a sample size of one. In essence, the clinician’s assessment is holistic by comparing individual’s HDOD with those HDOD profiles of known subjects, like exemplars.

Being motivated by this clinician’s intuition, we propose a hybrid approach of integrating data pattern discovery and regression analytics, to retain desired features of both analytic approaches. This approach has two steps. At the first step, the goal is to identify a group of “exemplars” that are representative of subjects’ HDOD patterns, typically observed through clustering analysis of unsupervised learning ^{14; 21; 22}. To have cluster patterns represented, one could choose centroids of clusters as exemplars. To represent those samples under-represented by clusters, one could choose singletons to be exemplars. In essence, a HDOD pattern characterizes an exemplar. The number of exemplars (q) is generally smaller than the sample size (n), unless exemplars are derived externally (see discussion below). With reference to each exemplar, one can compute a similarity measurement with each subject, resulting in a matrix of similarity measurements with the dimension (n × q). Typically, p >> n > q. Effectively, this step transforms high dimension and sparse HDOD (n × p) into a “dense data matrix” (n × q). Then, at the second step, we use penalized likelihood methods to select those exemplars that are predictive of the outcome. Because of the substantially reduced dimensionality from p to q, the penalized likelihood can readily picks up informative exemplars, at much reduced penalty. The dual step procedure relies on exemplars from “unsupervised learning” and then selects informative exemplars with their associations with outcome via “supervised learning”. Because of regressing outcome on exemplar-specific similarities, this method is referred to as “object-oriented regression” or OOR for short. In contrast, most of regression-based methods mentioned above are known as covariate-specific regression methods (CSR).

2. Methodology

2.1 Motivation

The Statement of Problem

Consider a sample of n subjects (i = 1, 2,…, n) in a clinical follow-up database. On each ith subject, we observe a set of high dimensional and sparse covariates, denoted as X_i = (x_i1, x_i2, ⋯, x_ip), where the number of covariates is typically much greater than the sample size(p >> n), typical of HDOD. Also observed on each ith subject is time-to-event outcome variable of interest Y_i = (δ_i,t_i), in which binary indicator δ_i is for, e.g., alive or death, at the observed time t_i. The likelihood of all observed data may be written as

$$L\left(Y_i,X_i,\forall i\right)=-\sum _i\log f\left(Y_i\mid X_i\right)-\sum _i\log f\left(X_i\right),$$ (1)

where the summation is over n subjects, f(Y_i ∣ X_i) the conditional density of Y_i given covariates X_i, and f(X_i) is the multivariate distribution of covariates²³. To capture association of the time-to-event outcome with covariates, it is a common practice to model a hazard function²⁴, which may be written as

$$\lambda \left(t\mid X_i,\theta \right)={\lambda }_0\left(t\right)\text{exp}\left[h\left(X_i,\theta \right)\right],$$ (2)

where λ₀(t) is the baseline hazard function independent of covariates, and h(X_i, θ) is an arbitrary function indexed by a vector of unknown parameters θ to be estimated from a data set. Correspondingly, the distribution function f(Y_i ∣ X_i) is specified by the hazard function via

$$f\left(Y_i\mid X_i\right)={\left[\lambda \left(t_i\mid X_i,\theta \right)\right]}^{{\delta }_i}\text{exp}[-\underset{0}{\overset{t_i}{\int }}\lambda \left(u\mid X_i,\theta \right)\mathit{du}].$$ (3)

The analytic objective is to establish the outcome (Y_i) association with covariates (X_i) via modeling the arbitrary function h(X_i, θ).

The Representer Theorem

When the covariate function is unknown and is left unspecified, Kimeldorf and Wahba (1971) have shown that given the observed samples (X₁,X₂,…,X_n), the above arbitrary function h(X_i,θ) in the equation [2] can be generally represented by

$$h\left(X,\theta \right)=\sum _{k=1}^n{\theta }_{k}K\left(X,X_k\right),$$ (4)

where θ_k is a sample-specific and unknown parameter, and K(X,X_i) is known as the kernel function and needs to be semi-positive definite²⁵. One class of kernel function is the similarity measure that quantifies the similarity of X with X_k. For an observation X identical to X_k, the corresponding term is θ_kK(X,X_k) = θ_k. If X is completely different from X_k, θ_kK(X, X_k) = 0. Further, if X_k and X_k' are identical or nearly identical, corresponding terms can be merged as θ_kK(X, X_k) + θ_k'K(X, X_k',) ≈ (θ_k + θ_k')K(X, X_k) = α_kK(X, X_k). Lastly, one expects that the coefficient θ_k, quantifying outcome association with similarity measure K(X, X_k) with the kth individual, is likely to equal zero, if the covariate profile of the kth individual is not associated with the corresponding outcome. Zhu and Hastie used some of these observations to describe an import vector machine approach by grouping some K(X, X_k) terms²⁶.

The Representer theorem, together with above observations, forms the theoretical foundation for us to propose OOR by modeling this arbitrary function via

$$h\left(X_i,\alpha ,{\beta }^{\prime }s\right)=\alpha +\sum _{k=1}^q{\beta }_k{s}_k\left(X_i\right),$$ (5)

where s_k(X_i) = K(X_i, Z_k) is the similarity measurement of X with the kth unique HDOD Z_k, and (α, β_k) are unknown regression coefficients to be estimated. Formally, HDOD vector Z_k represents a pattern of HDOD or HDOD profile, and is referred to as an exemplar. Use of the new notation Z_k implies that the exemplar can be internally chosen from (X₁,X₂,…,X_n), or chosen externally from other sources. The regression coefficient β_k, if it does not equal zero, implies that anyone whose HDOD profile is similar to Z_k associates with the outcome via the above OOR [5].

Instead of regressing on HDOD as covariates, OOR regresses the outcome on the subject’s similarity with exemplars. As expected, the interpretation of regression coefficients is specific to similarity with exemplars. Naturally, such an interpretation is reminiscent of data queries used frequently by computer scientists. As expected, OOR provides a “holistic interpretation” of exemplar-specific associations, as opposed to covariate-specific associations.

2.2 An OOR Framework

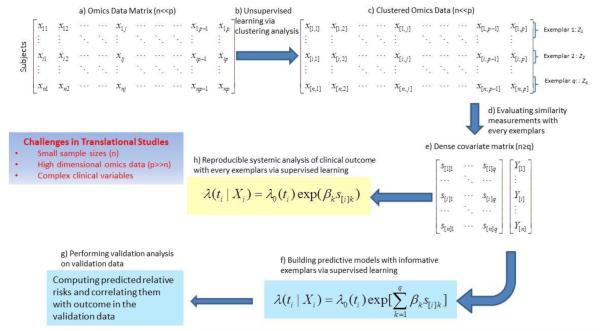
Figure 1 provides a schematic illustration of the OOR process. The HDOD as the input data are a large covariate matrix, with individual continuous elements (Fig 1a). Note that it is important to filter out those covariates that are noisy or unlikely informative, a usual requirement for any meaningful cluster analysis^27-29. Without outcome data, OOR first organizes HDOD to identify exemplars Z_k via unsupervised cluster analysis (Figure 1b and c). The result from the unsupervised learning is an array of q exemplars (Z₁,Z₂,…,Z_q). Based on a chosen similarity measurement K(X_i,Z_k) (see Discussion below), one computes the similarity measurements for each ith subject with every kth exemplar (Figure 1d). By treating similarity measurements as covariates, one now has a dense covariate matrix (Figure 1e). Under the proportional hazard model [2] and [5], one can then select informative exemplars to form a predictive model (Figure 1f). Using the predictive model, we compute predicted relative risks, and validate their associations with the survival outcome on an independent validation data set (Figure 1g). Besides building predictive models, OOR lends itself naturally to examine systemic association of the time-to-event outcome with HDOD profiles via their exemplar-specific association (Figure 1h). One may consider both univariate and multivariate association analysis. The following sections center on key components of OOR framework.

Figure 1.

A schematic flow of object-oriented regression, a) A omics data as a covariate matrix, b) organizing omics data via an unsupervised learning method, c) Clustered omics, resulted from two-way clustering analysis, leading to identification of exemplars, d) Computing similarity measurements with every exemplars and treating them as covariates, e) Dense covariate matrix of similarity measurements, useful for building a predictive model, f) Under the model, one can use penalized likelihood to select informative exemplars to build predictive models, g) One can perform validation analysis by assessing associations of predicted risk scores with clinical outcome, and h) Under a proposal hazard model for time-to-death, one can perform systemic association with individual exemplars

Without referring to outcome data, the aim of unsupervised learning process explores correlation structure of HDOD covariates across genes and across subjects. Purely from the statistical perspective, one utilizes the second portion of log likelihood function [1] without referring to the outcome, and hence the unsupervised learning exercise is inconsequential to the supervised learning later³⁰. Conventionally, clustering analysis organizes genes and/or samples ^27-29 by their correlations, and resulted clusters of samples allow one to identify centroids of interest. Centroids tend to have relatively high correlations (or similarities) with the group of samples within the cluster, and, as exemplars, represent multiple samples.

When dealing with HDOD, there are often many subjects with relatively unique HDOD profiles, distant from observed clusters. Operationally, we define these “unique subjects” as those whose HDOD profiles that are not represented by centroids or their combination. One may also want to include these unique subjects as exemplars. To identify these subjects, we use the following regression approach. Suppose that we have identified an initial set of t centroids as exemplars, denoted as [1],[2],…, and [t]. To start, we regress all subjects’ HDOD, other than those in clusters represented by HDOD, on the centroids’ covariates via

$$X_i={\vartheta }_{i0}+\sum _{k=1}^t{\vartheta }_{i,\left[k\right]}{X}_{\left[k\right]}+{\epsilon }_i,$$ (6)

where ϑ’s are regression coefficients, and ε_i is a vector of residuals. One evaluates the sum of residual squares (SRS) from the above linear regression, for each individual, and computes the fraction of residual variations explained by those informants. Then, the ith individual may be added to the set of exemplars if it satisfies

$$i=\text{argmax}\left({\mathrm{SRS}}_i∕{\mathrm{SRS}}_0\right),\text{subject to}\left({\mathrm{SRS}}_i∕{\mathrm{SRS}}_0\right)\ge f,$$ (7)

where SRS₀ is the SRS without exemplars, and f is a pre-selected threshold value (e.g., 0.5). Note that the analysis of selecting exemplars without referring to the outcome, does not affect any downstream supervised learning (below).

By the nature of clustering analysis, a subjective element is the choice of cluster numbers, typically assigned by visualization. To minimize the impact of this choice, one can start the analysis by treating everyone as “unique subjects”. By the iterative procedure [5] described above, one can automate the selection of exemplars, with a pre-selected threshold value f. If so, one skips the clustering analysis. Besides deriving exemplars internally, one can certainly include exemplars that are derived from external sources and the choice can improve the interpretability. Note that one should treat threshold value f as a tuning parameter to seek an optimal determination for the specific problem on hand. Further, for translational studies with exceptionally large sample sizes (e.g., >2000), one may have to adjust this tuning parameter, so that the dimensionality of “dense covariate matrix” is manageable.

2.3 Supervised Learning

Following identification of exemplars, the next step is to assess if the similarity to these exemplars is in any way associated with the outcome of interest. As noted above, we use the proportional hazard model [2] and [5] to capture relationship between the HDOD and the clinical outcome. For variable selection, we propose to use the penalized likelihood methods to control the over-fitting problem, in particular, the least absolute shrinkage and selection operator (LASSO) to select informative exemplars ^{15; 16}. Conceptually, LASSO is a version of penalized likelihood estimation, and the estimated regression coefficients $\left(\widehat{\alpha },{\widehat{\beta }}_1,{\widehat{\beta }}_2,\dots ,{\widehat{\beta }}_q\right)$ in OOR model [5] maximize the following penalized likelihood function:

$$\left(\widehat{\alpha },{\widehat{\beta }}_1,{\widehat{\beta }}_2,\dots ,{\widehat{\beta }}_q\right)=\underset{\alpha ,{\beta }_1,\dots ,{\beta }_q}{\text{argmax}}\left(\sum _{i=1}^n\log \left[f\left(Y_i\mid X_i,\alpha ,{\beta }_1,\dots ,{\beta }_q\right)\right]+\lambda \sum _{k=1}^q\mid {\beta }_k\mid \right),$$ (8)

where the first summation is over all random samples as a usual log-likelihood function, the second summation is over all absolute values of q regression coefficients, and λ is a tuning parameter to determine the magnitude of penalty on those non-zero regression coefficients. Following convention, the tuning parameter λ is estimated to give a minimum prediction error based on cross-validation.

2.4 Similarity Measures

Choosing an appropriate metric to measure similarity is crucial for OOR, as it dictates how similarities are computed, how clusters are identified, how exemplars are identified, and the extent of similarity between subjects and exemplars. In general, this choice should depend on the nature of HDOD and interpretation of results. Here we consider several common similarity measures. Note that by convention, the similarity measure is an inverse of distance, i.e., similarity of 1 and 0 are equivalent to the zero and infinitive distances, respectively.

Euclidean distance function

Consider two subjects with HDOD covariate vectors (X_i, X_i' ), all elements in which are numerical. Their Euclidean distance can be written as

$$D_{{\mathit{ii}}^{\prime }}=\Vert X_i-X_{i^{\prime }}\Vert ,$$ (9)

where ∥ • ∥ represents the square-root of sum of difference squares. When covariates are normalized by mean and standard deviation, the Euclidean distance has a monotonic relationship with the correlation coefficient, which is commonly used to measure similarity. Recently, Frey and Dueck have used a negative squared Euclidean distance, i.e., − ∥ X_i − X_i' ∥², as a similarity measure ³¹.

Radial basis kernel function

Another common conversion from the above distance to similarity measurement is via the following kernel function

$$S_{{\mathrm{ii}}^{\prime }}=\text{exp}(-\Vert X_i-X_{i^{\prime }}{\Vert }^2∕2{\widehat{\sigma }}^2),$$ (10)

where $\widehat{\sigma }$ is chosen to be a tuning parameter, depending on smoothness requirements, and may be chosen to be the standard deviation of all pairwise distances ²⁷.

Cosine similarity function

In information theory ³², a common measure between two vectors (X_i, X_i') is the cosine similarity, which may be written as

$$S_{{\mathit{ii}}^{\prime }}=\frac{X_i\otimes X_{i^{\prime }}}{\Vert X_i{\Vert }^{\ast }\Vert X_{i^{\prime }}\Vert },$$ (11)

where ⊗ is the inner product of two vectors. Despite its seemingly different representation, this similarity measure is identical to correlation coefficient between two vectors, if different covariate observations are treated as “sample values”.

Besides the above commonly used metrics of distances or similarities, there are other measures that are domain-specific. In the context of genetics, geneticists have used “identity-by-descent”, “identity-by-state” or kinship-coefficient as a measure of genetic similarity ³³. When dealing with text, there are many measures for semantic similarity measures ³⁴. There is enormous flexibility in choosing the similarity measure most suitable for a given application in OOR.

2.5 Comparison of OOR with CSR

As noted above, commonly-used methods from statistics are CSR, in the sense that these methods are to assess clinical associations with a vector of covariates (or features). These methods stem from reductionist perspective, reducing many covariates down to a few informative covariates. In contrast, OOR was rationalized to capture clinical associations with HDOD patterns via similarities of all subjects with those of exemplars, i.e., holistic associations. Given complementary perspectives, CSR and OOR have several fundamental differences in analytic objectives, application areas, result interpretations and analytic powers. In the following, we highlight several key differences between two regression approaches. It is important to realize that computer scientists have developed many methodologies, some of which are regression-based and are related to CSR methods mentioned above, but many others are heuristic methods customized for various domains of interest³⁵. Some of these heuristic methods, with some modifications, could be applied to analyze HDOD from biomedical research as well, and should be pursued through close collaboration with computer scientists.

CSR is generally designed in such a way that one can assess the association of an outcome with one or more covariates ^{12; 36}. The desirable feature of CSR is that one can isolate a covariate-specific association, after controlling other covariates in the regression. For this reason and others, CSR has been a “workhorse” for most statistical applications in last few decades. In the era of “big data” with many variables, Simon et al (2011) have described regularization paths to select covariates, in the context of the Cox proportional hazard model³⁷, the procedure implemented as a “glmnet” function in R and is used frequently for selecting covariates. When applied to data with excessively high dimension, application of CSR encounters some challenges. First, in dealing with HDOD, a typical application of CSR is unable to analyze all covariates simultaneously, because of p>>n. Use of LASSO has been helpful, but still pays “statistical costs” that are proportional to number of covariates in analysis. Secondly, one intrinsic assumption, required by CSR, is that covariate effects are additive in the regression model. When multiple correlated covariates are included, this assumption allows CSR to extrapolate outcome association with covariates where there are few or even no observations. When the assumption holds, CSR gains power. Otherwise, CSR’s extrapolations could be misleading. Thirdly, CSR is suitable for analyzing numerical HDOD covariates, and its application to unstructured data, such as genomic sequences or text data, may be limited.

Overcoming these limitations is the major impetus for developing OOR. OOR transforms the covariate matrix (n*p) into the similarity score matrix (n*q), where the q is much smaller than the sample size n (Figure 1). This transformation allows OOR to process HDOD. Admittedly, OOR addresses a different association question from CSR, and its primary objective is not to identify which covariates are significantly associating with outcome but to identify which patient or alike are likely to associate with the outcome. Through using similarity measures, OOR is suitable for correlating outcomes with HDOD of any dimension.

Aside from these differences, CSR and OOR have another important difference that makes these approaches complementary to each other in HDOD analysis. As noted above, CSR aims to screen through all individual covariates, and to identify a small subset of covariates that are predictive for the outcome, that is, CSR achieves parsimony with respect to the number of predictive covariates. In contrast, OOR screens through all of exemplars for a small subset of informative exemplars for the outcome, i.e., OOR achieves parsimony with respect to the number of predictive exemplars, but each exemplar is still characterized by all elements of HDOD. In the traditional biomarker research framework, CSR is clearly advantageous, because the resulted predictive model uses only a small set of selected predictors. In the era of systems biology (or systems medicine), future precision medicine likely will obtain HDOD routinely for various clinical indications without depending on a pre-specified panel of biomarkers. In such an application, OOR may be preferred, because of its robustness.

3. An Application to TCGA Lung Cancer Study

Lung cancer accounts for more deaths than any other cancer in both men and women, about 28 percent of all cancer deaths. The prognosis for lung cancer is poor, since many cases are diagnosed at advanced stages. The prognosis of early stage lung cancer is better, but the five-year survival rate is approximately 60%. Even among Stage I patients, some patients still have relatively short survival. It is of interest to stratify all stage I patients, based on prognostic survival probabilities. For patients with poorer survival probability, oncologists may design more aggressive treatment plans to improve prognosis. In contrast, those patients with much better prognosis may be treated with options that are more conservative.

3.1 Data Source

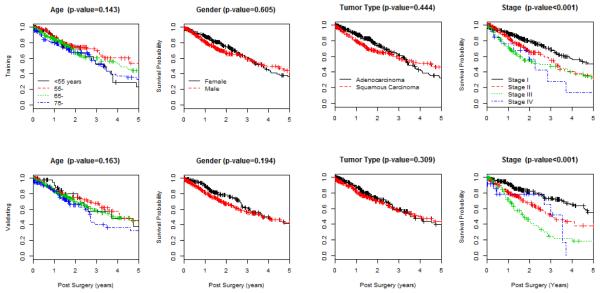
To address this question, we downloaded clinical phenotype and RNA-seq data from Xena (http://xena.ucsc.edu/). The 2015-06-10 release includes data 1,299 samples. After linking the two files and conducting basic quality control and excluding samples with missing data, our study includes 1,124 lung cases (571 adenocarcinoma cases and 553 squamous cell carcinoma), where both clinical phenotype data and gene expression data are complete. We randomly assigned the entire data set into training and validation sets, and kept completely separated for all downstream analyses, to retain the integrity of the validation results. Figure 2 shows the distributions of age at diagnosis for all patients in training and validation data sets, suggesting that patients in both sets have comparable age distributions. Further examination of gender, tumor type and stage reveals that their frequencies are largely comparable between training and validation sets (Table 1). With respect to survivorship, estimated Kaplan-Meier (KM) curves associated with four covariates are also comparable between training and validation sets (Figure 3).

Figure 2.

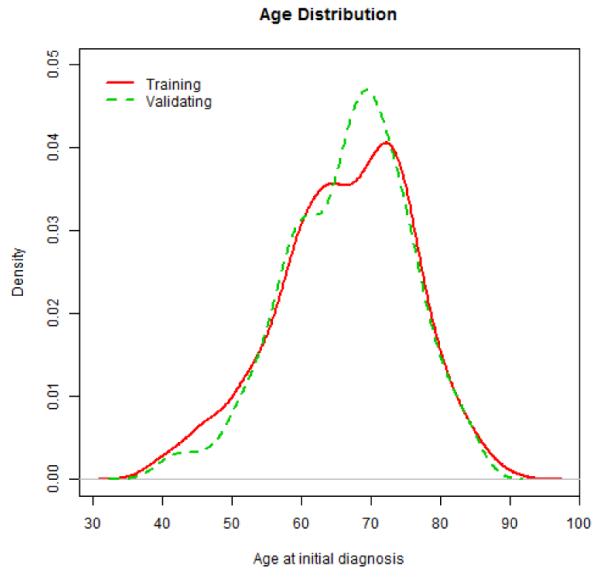
Distributions of age at diagnosis for all patients in training and validation data sets

Table 1.

Distribution of gender, stage and tumor type in training and validation set (data set is obtained from TCGA)

		Training	Validating	P-value
Gender	Female	238	208	0.10
	Male	318	343
	Missing	6	11
Stage	Stage I	296	277	0.15
	Stage II	144	160
	Stage III	102	87
	Stage IV	13	23
	Missing	7	15
Tumor	Adenocarcinoma	286	285	1.00
	Squamous Carcinoma	276	277
Total		562	562

Figure 3.

Kaplan-Meier curves, with Log-Rank test, are used to explore marginal associations of age, gender, tumor type and stage with prognostic survival over five years, in the training set (top panels) and the validation set (lower panels).

3.2 Prognostic Survivorship

In the current combined data set, including both adenocarcinoma and squamous cell carcinoma patients, it appears that the survivorship does not significantly associate with age (P-value=0.143), or with gender (P-value=0.605), or with tumor type (P-value=0.444). Instead, survivorship is significantly associated with tumor stage (P-value<0.001). Our primary goal is to create a predictive model that can predict prognostic survival probabilities for stage I patients. In the training set, there are 296 stage I patients. To maintain the sample size for building the predictive model, we will not stratify the training samples over tumor type, or gender, or age, since none of them is significantly associated with the survivorship.

3.3 RNA-seq Data

TCGA researchers used the Illumina HiSeq 2000 Sequencing platform to produce short reads from mRNAs and then integrated these into assessments of gene expression levels for 20,531 genes (https://support.illumina.com/sequencing/sequencing_instruments/hiseq_2000.html). For this illustrative exercise, we ordered gene expression values and replaced expression values with their corresponding ranks. While quantitative information in RNA-seq is lost, rank-based transformation eliminates sample-to-sample heterogeneity.

3.4 Gene Filtering

Prior to initiating OOR analysis, we filter out genes from the list of 20,531 genes in the training set. To retain the empirical nature of this exploration, we consider “stage” as a pivotal variable, since the stage clearly associates with the survivorship, and stage change from I to III represents a progression from early stage cancer to late stage cancer. As expected, many genes are up- or down-regulated as the cancer progresses. Presumably, progressions are occurring even among early stage cancers, except that their morphological features may not be observable yet. By correlating gene expression levels with stage I versus other stages, we computed Z-scores and associated p-values for every gene (Figure 4). Interestingly, there is a little peak right to the value 1, indicating that there may be possibly a mixture of two groups of genes: one group of genes associate with the outcome, while the majorities have no associations. Using the threshold value of p-value=0.01 (which is chosen to include any gene that would meet the traditional significance level if a single gene is considered), we selected 831 genes. After eliminating a few highly correlated genes among all stage I patients, we ended up with a final list of 789 genes as an input data for OOR analysis.

Figure 4.

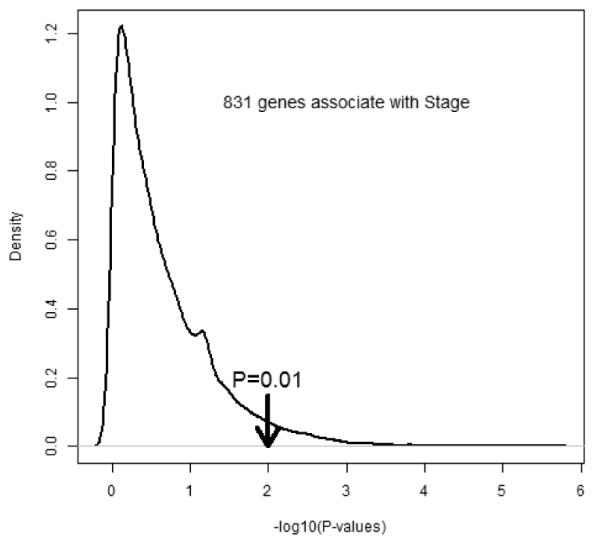
Estimated distribution of logarithmic p-values that measures associations of gene expressions that associate with indicator of stage I

3.5 Patterns with Selected Genes

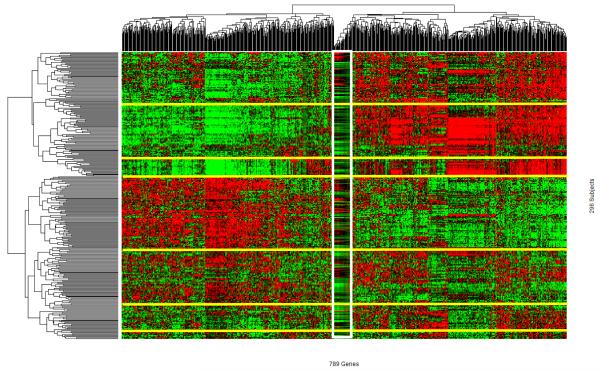
Using the Euclidean distance and complete linkage options in the heatmap.2 function of the R package ‘gplots’ (https://www.r-project.org/). we performed two-way clustering on the input data (Figure 5). The gene (columns) dendrogram indicates the presence of multiple groups of co-varying genes. Note that one vertical block (white lines) indicates a group of highly co-varying genes. Given the primary interest in identifying exemplars, the hierarchical clustering of samples (rows) implies the presence of multiple groups, among which seven large clusters are highlighted and separated by six yellow lines. The visual patterns give a strong qualitative impression that there are multiple groups of subjects with distinct gene expression profiles. While appreciating the visual impression of data, there are challenges to synthesizing data to generate reproducible results. First, perceptions of visual patterns vary from individual to individual. Second, presented visual patterns depend on choice of visualization parameters, such as color choices, color depths, etc.. Third, it is nearly impossible to separate systematic and random patterns visually. Indeed, we have performed “simulated experiments” in which we randomly choose 1000 genes and performed clustering analysis (not shown). In these experiments, one can occasionally see some patterns resulted from two way clustering. Largely, observed patterns are much less distinct from the pattern observed here (Figure 5).

Figure 5.

High dimensional omics data (HDOD) with 789 genes observed among 296 subjects in the training set are organized by two-way hierarchical clustering analysis. Graded green and red colors, respectively, correspond to below and above zero for gene-specific normalized expression values, i.e., lower and higher than averaged expression values, respectively.

3.6 Pathway Analysis

Besides visual impression of patterns, one could expect that selected genes, based on the pivotal stage I indicator, should include biologically meaningful elements. Of course, it is expected that some genes are selected purely by random chance, because of the liberal choice of p-value at 0.01. To check on biological significance of these 789 selected genes, we perform a pathway analysis, using TargetMine, a web tool for pathway analysis (http://targetmine.mizuguchilab.org/targetmine/begin.do). Ten pathways are found to include corresponding genes with the gene enrichment p-value less than 5% (Supplementary Table S1). The first panel of Table 2 lists these pathways, including cell cycle, mitotic cell cycle, M phase, and meiotic recombination, all of which are consistent with accelerated cellular growth of cancerous cells from stage I to higher stage. Even more interesting is that all involved tissues seem to connect with epithelial cells in airway, except for fallopian tube epithelium (Table 2). Gene lists in various tissues are shown in the supplementary table (Table S1).

Table 2.

Identified pathways and tissues from a set of 789 genes that have been selected from association analysis of genes with stage (I versus other higher stages)

ID	Pathway Identified	P-values
1	M Phase	1.094E-03
2	Cell Cycle	1.480E-03
3	Cell Cycle, Mitotic	1.999E-03
4	Chromosome Maintenance	4.139E-03
5	Systemic lupus erythematosus	4.391E-03
6	RHO GTPase Effectors	5.645E-03
7	Deposition of new CENPA-containing nucleosomes at the centromere	7.092E-03
8	Nucleosome assembly	7.092E-03
9	HDACs deacetylate histones	2.345E-02
10	Meiotic recombination	4.142E-02

ID	Tissue Involved
1	airway epithelial cells	1.341E-06
2	bronchial epithelial cells	7.214E-06
3	endobronchial epithelial lining fluid	6.094E-05
4	sinus mucosa	3.307E-04
5	trachea	7.683E-04
6	fallopian tube epithelium	1.280E-02

3.7 Exploration of Exemplars

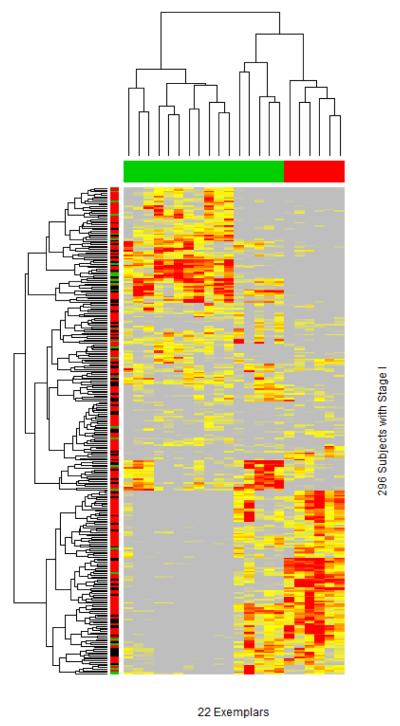
Gene expression pattern of 789 selected genes among 296 subjects clearly indicates the presence of clustered subjects who share expression profiles, and that there are not identical subjects with respect to these 789 genes. Given that the training set includes only 296 subjects, we choose all of them as exemplars, without relying on the clustering analysis for this application. As an initial exploration of exemplar-specific association with prognostic survivorship, we perform marginal association of individual exemplars with the survival outcome, and retain those exemplars that have marginal associations, which is a commonly used strategy to screen variables. By the association p-value at 0.05, we select 22 exemplars that are subject to the further selection by LASSO. Table 3 lists estimated coefficients, hazard ratios, standard errors, and p-values from the univariate association analysis of the clinical outcome with one exemplar a time. Subjects, who are similar to exemplar 1-16, appear to be at much elevated risks (>0) with their p-values less than 0.05. On the other hand, subjects who are similar to exemplar 17-22 appear to be at reduced risks (<0) with p-value less 0.05.

Table 3.

Estimated regression coefficients associated with each exemplar in the univariate OOR analysis by Cox regression model (estimated coefficient, hazard ratio, standard error, Z-score and P-value) and in the LASSO-based multivariate OOR analysis with Cox regression model (estimated coefficient only)

ID	Exemplars	Univariate OOR					OOR
		Coef	HR	SE	Z	P-value
1	TCGA_22_4609_01	2.91	18.29	0.76	3.81	1.399E-04	0.00
2	TCGA_56_5897_01	4.06	57.82	1.08	3.74	1.837E-04	1.17
3	TCGA_77_8131_01	2.61	13.53	0.78	3.32	8.865E-04	1.34
4	TCGA_22_1016_01	2.18	8.89	0.69	3.19	1.428E-03	1.33
5	TCGA_77_7338_01	2.75	15.72	1.00	2.76	5.719E-03	0.98
6	TCGA_18_3407_01	2.44	11.48	0.94	2.60	9.408E-03	0.28
7	TCGA_60_2707_01	1.89	6.64	0.74	2.55	1.083E-02	0.00
8	TCGA_77_8138_01	2.07	7.90	0.81	2.55	1.089E-02	0.61
9	TCGA_44_2668_11	1.73	5.62	0.72	2.41	1.584E-02	1.72
10	TCGA_56_6545_01	2.39	10.90	0.99	2.41	1.594E-02	0.00
11	TCGA_55_8299_01	1.92	6.84	0.85	2.26	2.396E-02	0.00
12	TCGA_85_8048_01	2.34	10.40	1.10	2.13	3.348E-02	0.00
13	TCGA_52_7622_01	1.66	5.26	0.79	2.10	3.576E-02	0.00
14	TCGA_56_8626_01	2.03	7.59	0.98	2.06	3.944E-02	0.66
15	TCGA_66_2773_01	2.12	8.29	1.05	2.02	4.375E-02	0.97
16	TCGA_66_2777_01	1.84	6.32	0.94	1.97	4.904E-02	0.00
17	TCGA_55_A492_01	−1.90	0.15	0.93	−2.03	4.215E-02	0.00
18	TCGA_78_7163_01	−1.81	0.16	0.86	−2.11	3.473E-02	−0.72
19	TCGA_78_7153_01	−2.99	0.05	1.41	−2.12	3.399E-02	0.00
20	TCGA_95_7948_01	−3.00	0.05	1.36	−2.20	2.781E-02	0.00
21	TCGA_71_6725_01	−3.04	0.05	1.36	−2.24	2.516E-02	0.00
22	TCGA_64_5778_01	−3.47	0.03	1.37	−2.52	1.162E-02	−0.25

Now given the selected 22 exemplars, we compute a similarity matrix of each subject with every exemplar, resulting in a “dense covariate matrix” illustrated in Figure 1e. Figure 6 shows the similarity matrix with 296 rows by 22 columns. Grey, yellow and red correspond to weak, modest and strong similarity of a subject to exemplar, respectively. Clustering helps to organize the 296 subjects and 22 exemplars into distinct subsets. The 22 exemplars are clustered into two main clusters. The color bar for the column represents the marginal associations with each exemplar: red for protective associations and green for risk associations. Interestingly, two sub-clusters on the right branch appear to have risk (green) and protective (red) associations, respectively, even though their overall similarities to exemplars are comparable.

Figure 6.

Selected 22 exemplars (based on 789 genes) among 296 patients of stage I in the training data set with the grey, yellow and red representing, respectively, weak, modest and high similarities of each subject with 22 exemplars. The column-specific color-coded bar indicates directionalities of exemplar-specific associations (red for protective association, green for risk association). The row-specific color-coded bar indicates the status of one year survival status (red for alive, black for censored, and green for death).

3.8 Building a Risk Score Calculator with Selected Exemplars

With carefully selected exemplars, we proceed to select informative exemplars from the “dense covariate matrix” by LASSO. The first step of LASSO is to estimate the penalty parameter by the cross-validation, leading to the estimate (λ = 0.021) (see Section 3.9 and 3.10 on stability of estimation by cross-validation). With the fixed penalty parameter value, the second step of LASSO is to select informative exemplars and to estimate associated regression coefficients. Result is shown in the last column of Table 3, in which 11 exemplars, with non-zero coefficients, are selected as informative exemplars for the prognostic outcome (shown in Figure 7). Estimated regression coefficients are listed. Interestingly, estimated regression coefficients in the 8^th column tend to be smaller than their counterparts in the 3^rd column from univariate regression analysis, probably reflecting that LASSO has distributed marginal associations to associations with multiple exemplars, while penalizing some unstable exemplars like the first exemplar (e.g., Ex 1: TCGA_22_4609_01).

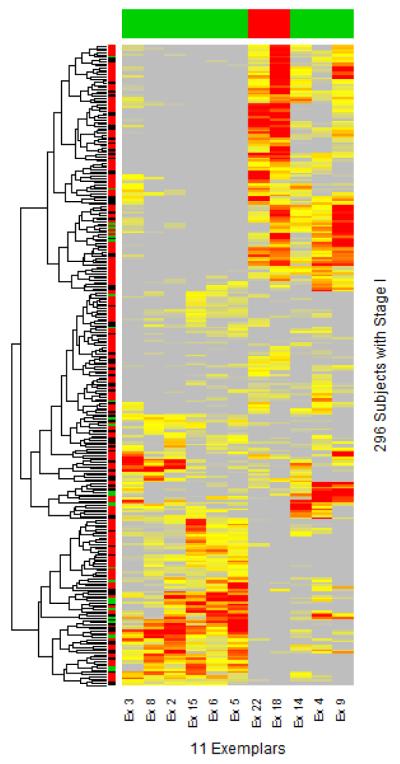
Figure 7.

Selected 11 exemplars with high dimensional omics data (HDOD) of 789 genes in the training data set. Graded grey, yellow and red colors represent, respectively, weak, modest and high similarities of each subject with 11 informative exemplars. The column-specific color-coded bar indicates directionalities of exemplar-specific associations (red for protective association, green for risk association). The row-specific color-coded bar indicates the status of one year survival status (red for alive, black for censored, and green for death).

With estimated regression coefficients, one can now proceed to construct a risk score calculator via

$${\text{Risk Score}}_i=\text{exp}[\sum _{k=1}^q{\widehat{\beta }}_k{s}_k\left(X_i\right)],$$ (12)

where ${\widehat{\beta }}_k$ is the estimated coefficient for the kth informative exemplar. Based on the proportional hazard model, the risk score, calculated for the ith subject, is the relative risk of the current subject in comparison with a “reference subject” who has zero similarity to any selected exemplars. Together with the baseline hazard function, one can build a predictive model based on the proportional hazard model [2] and [3].

For clinical practitioners, we have simpler interpretation. The similarity function s_k (X_i) measures the degree of similarity of the ith patient with the kth exemplar. Given the degree of the similarity, the coefficient ${\widehat{\beta }}_k$ dictates the weight contributing to the overall risk score. Collectively, cumulating weighted contributions lead to the overall risk score, and the exponential transformation puts the risk score onto the scale of relative risk, which is more familiar to many clinical investigators.

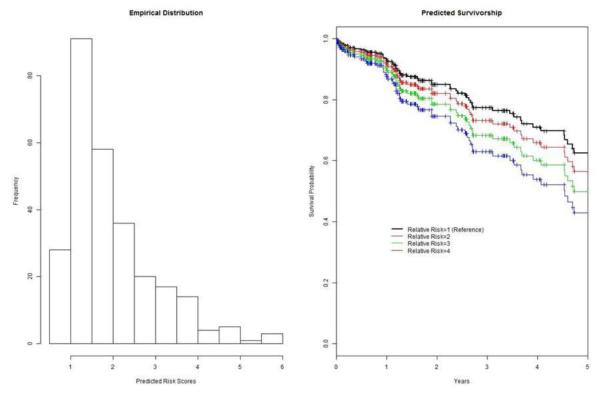
3.9 Validating the Risk Score Calculator

Using the validation data, we compute risk scores for every patients by the risk score calculator [11]. Figure 8a shows the distribution of risk scores, ranging from the minimum 0.71 to the maximum 5.65. Clearly, large portion of subjects have relative risks around one, while the distribution is skewed to the right tail. To validate its association with the survival outcome, we regress the outcome on the risk score on log scale, and find that the association with the risk score is statistically significant (p-value of 0.015, in Table 4). Hence, it is concluded that the risk score is positively predictive of the survival outcome. For the result interpretation, Figure 8b shows four survival curves, computing four expected survival curves, given different risk scores of 1, 2, 3 and 4, respectively. For patients at stage I at the baseline, their prognostic survival declines from 1 to 0.62 over five years. However, for those with risk score of 4, the five-year survival declines from 1 to 0.41 in five years.

Figure 8.

Evaluation of risk scores computed by the risk score calculator: a) Distribution of predicted risk scores in the validation set , and b) Estimated survivorships with risk score of 1 (reference), 2, 3 and 4 in the validation set.

Table 4.

Estimated coefficient, standard error, Z-score and P-value from applying the Cox regression model to estimated predicted risk scores in the validation set obtained by OOR, LASSO, Ridge regression, Elastic net, Random forest, and generalized boosting models.

Method	Coef	SE	Z-score	p-value
Object-Oriented Regression	0.584	0.24	2.435	0.015
LASSO	0.712	0.716	0.995	0.320
Ridge Regression	0.000	0.001	0.218	0.827
Elastic Net	0.166	0.128	1.295	0.195
Random Forest	0.011	0.018	0.629	0.529
Generalized Boosting	0.676	0.334	2.026	0.043

3.10 Monte Carlo Stability Analysis of the Penalty Parameter

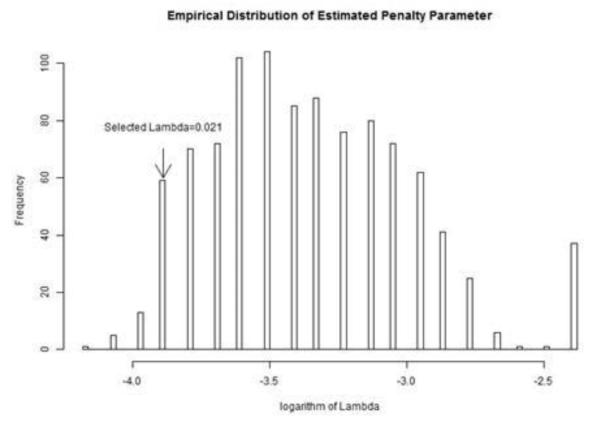
When applying OOR, one has to estimate a penalty parameter (λ) required by LASSO, and the choice of this parameter has a profound impact on variable selection. In the absence of knowing true value, the common approach is to use the cross-validation method to estimate this penalty. Unfortunately, cross-validation produces a randomly estimated penalty parameter. In this study, we ran a cross-validation, resulting in an estimate of 0.021. The question is ‘how stable is the estimated penalty parameter?’ For this purpose, we performed a Monte Carlo simulation experiment with 1,000 replicates. In each replicate, we used the ‘cv.glmnet’ function of the R ‘glmnet’ package (https://cran.r-project.org/web/packages/glmnet/index.html) to estimate the penalty parameter with 10 fold cross-validation ¹⁹. Figure 8 shows the empirical distribution of estimated penalty parameter values on a logarithmic scale. Interestingly, there are a total of 20 unique penalty values, ranging from 0.016 to 0.091. The smaller the penalty the value, the more exemplars are selected. In the current application, the penalty value of 0.091 leads to a null model with no exemplars selected. Without any prior choice, our analysis selected penalty value (λ = 0.021) that is marked in the Figure 9. Retrospectively, this is a somewhat smaller penalty value compared to the model (λ = 0.030).

Figure 9.

Distribution of estimated penalty parameter values from 1,000 Monte Carlo simulations. Selected penalty value (lambda=0.021) is marked.

3.11 Stability of Selecting Exemplars by Bootstrap Analysis

In recognition of the range of penalty parameter values, we anticipate that selected exemplars can be variable. To assess the stability of selected exemplars, we conducted a bootstrap analysis with 1,000 replicates. In each bootstrap sample, we randomly sample, with replacement, observed gene expression values and corresponding survival outcome, to form an analytic data set with the same sample size as the training set. With 20 fixed penalty values, we selected exemplars by LASSO from the same analytic data set. Table 5 lists estimated concordances of selected exemplars with different choices of penalty parameter values, via computing Kappa values ^{38; 39}. Kappa values range from 0 (no concordance) to 1 (perfect concordance). Given 1000 replicates, each element in the upper triangle represents the mean Kappa value, while the corresponding element in the lower triangle the standard deviations of estimated Kappa means. Clearly, concordances with adjacent penalty values are close to one. The concordance decreases as corresponding penalty values diverge. To gain insight into concordance at a quantitative level, we computed averaged estimates of coefficients associated with all 22 exemplars over 1,000 replicates. Then, we also visually examined pairwise concordances (not shown). Again, concordances are largely consistent between qualitative and quantitative assessments. Examining the XY plot for the upper right hand corner, i.e., with two extreme penalty values, we note that average coefficients of most exemplars remain concordant.

Table 5.

Estimated Kappa averages between selected exemplars by LASSO with different penalty values (top right triangle) and their standard deviations (lower triangle) with 1000 bootstrap samples

log(λ)	−4.163	−4.07	−3.977	−3.884	−3.791	−3.698	−3.605	−3.512	−3.419	−3.326	−3.233	−3.14	−3.047	−2.954	−2.861	−2.768	−2.675	−2.582	−2.488	−2.395
−4.163	-	0.94	0.89	0.84	0.79	0.75	0.71	0.67	0.64	0.61	0.58	0.54	0.50	0.46	0.42	0.38	0.33	0.28	0.24	0.19
−4.07	0.07	-	0.95	0.90	0.85	0.80	0.76	0.72	0.69	0.65	0.62	0.58	0.54	0.50	0.46	0.41	0.36	0.31	0.26	0.21
−3.977	0.10	0.07	-	0.95	0.90	0.85	0.81	0.77	0.73	0.70	0.66	0.62	0.58	0.54	0.49	0.44	0.39	0.33	0.28	0.23
−3.884	0.11	0.09	0.06	-	0.95	0.90	0.85	0.81	0.77	0.74	0.70	0.66	0.62	0.57	0.52	0.47	0.42	0.36	0.30	0.25
−3.791	0.12	0.11	0.09	0.07	-	0.95	0.91	0.86	0.82	0.79	0.75	0.71	0.66	0.61	0.56	0.50	0.45	0.39	0.32	0.27
−3.698	0.13	0.12	0.11	0.09	0.07	-	0.95	0.91	0.87	0.83	0.79	0.75	0.70	0.65	0.60	0.54	0.48	0.41	0.35	0.29
−3.605	0.14	0.14	0.12	0.11	0.09	0.07	-	0.95	0.91	0.87	0.83	0.79	0.74	0.69	0.64	0.57	0.51	0.44	0.37	0.31
−3.512	0.15	0.14	0.13	0.12	0.11	0.09	0.07	-	0.96	0.92	0.88	0.83	0.78	0.73	0.67	0.61	0.54	0.47	0.40	0.33
−3.419	0.15	0.15	0.14	0.13	0.12	0.11	0.09	0.07	-	0.96	0.92	0.87	0.82	0.77	0.71	0.64	0.58	0.50	0.42	0.35
−3.326	0.15	0.15	0.15	0.14	0.13	0.12	0.11	0.09	0.06	-	0.96	0.91	0.86	0.80	0.74	0.68	0.61	0.53	0.45	0.37
−3.233	0.15	0.15	0.15	0.15	0.14	0.13	0.12	0.11	0.09	0.07	-	0.95	0.90	0.85	0.78	0.71	0.64	0.56	0.48	0.40
−3.14	0.15	0.16	0.15	0.15	0.15	0.14	0.14	0.13	0.11	0.09	0.07	-	0.94	0.89	0.83	0.76	0.68	0.60	0.51	0.43
−3.047	0.15	0.16	0.16	0.16	0.15	0.15	0.15	0.14	0.13	0.12	0.10	0.08	-	0.95	0.88	0.81	0.73	0.64	0.55	0.46
−2.954	0.15	0.15	0.16	0.15	0.15	0.15	0.15	0.14	0.14	0.13	0.12	0.10	0.08	-	0.93	0.86	0.78	0.69	0.59	0.50
−2.861	0.15	0.15	0.15	0.15	0.15	0.16	0.16	0.15	0.15	0.14	0.13	0.13	0.11	0.09	-	0.92	0.84	0.74	0.64	0.54
−2.768	0.14	0.15	0.15	0.15	0.16	0.16	0.16	0.16	0.16	0.16	0.15	0.15	0.14	0.13	0.10	-	0.91	0.81	0.71	0.60
−2.675	0.14	0.14	0.15	0.15	0.15	0.16	0.16	0.17	0.17	0.17	0.17	0.16	0.16	0.16	0.14	0.12	-	0.89	0.78	0.67
−2.582	0.13	0.14	0.14	0.15	0.15	0.15	0.16	0.17	0.17	0.17	0.17	0.17	0.17	0.17	0.17	0.16	0.13	-	0.88	0.75
−2.488	0.12	0.13	0.13	0.14	0.14	0.15	0.16	0.16	0.16	0.17	0.17	0.17	0.18	0.18	0.18	0.18	0.17	0.15	-	0.86
−2.395	0.11	0.12	0.12	0.13	0.13	0.14	0.15	0.15	0.16	0.16	0.16	0.17	0.18	0.19	0.19	0.20	0.20	0.19	0.16	-

3.12 Comparison with Covariate-Specific Regression Analysis

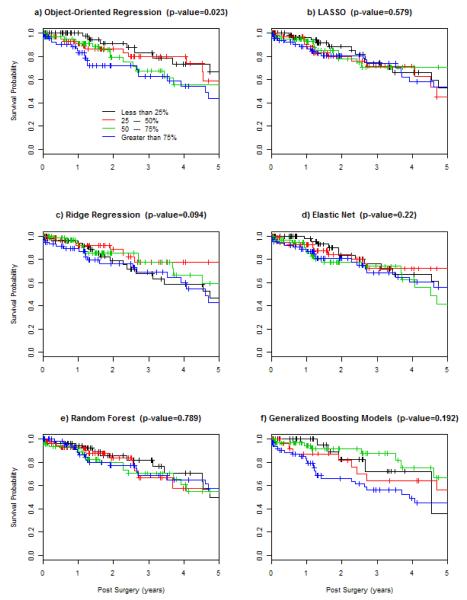
As noted above, many CSR methods have been developed for building predictive models, and are commonly applied to HDOD arising from biomedical research. While it is not possible to compare OOR method with all of them, we chose five commonly used CSR methods, i.e., LASSO-based method by regularization paths³⁷, Ridge regression designed for highly correlated data¹⁹, Elastic-Net to balance between LASSO and Ridge methods¹⁸, Random Forests from machine learning literature²⁰ and Generalized Boosting Models optimized for building predictive models¹⁷. All five methods are applicable to censored outcome, and are available as R packages. We use recommended default values for building predictive models on the training data set. To ensure a fair comparison, we apply these five methods to the same set of 789 filtered genes, to produce predictive models on the training set, without any refinement. Then, we use their corresponding “predict” functions, to compute “predicted values” in the validation data. Because these methods are diverse and their predicted values are not on the same scale, we regress survival outcome on their predicted values, to examine if these predicted values associate with the outcome. Table 4 lists estimated coefficient, its standard error, Z-score and p-value. It appears that the predicted values from GBM are significantly associated with the survival outcome in the validation data set (p=0.043). Predicted scores from four other methods appear not to reach their critical significance level. In fact, the result from Ridge regression falls on the null hypothesis entirely (p=0.827) with the coefficient of zero.

To gain further insights into potential values of these predicted scores, we convert predicted values into three categories: less than 25%, 25-50%, 50-75%, and greater than 75% of predicted values. For subjects within each category, we compute and draw KM curve in Figure 10. Figure 10a shows KM curves for risk scores in <25% (black), 25-50% (red), 50-75% (green) and 75%- (blue). Additionally, we compute the p-value using the nonparametric log-rank statistic, to measure the significance of differences among three groups. For OOR, the differences among three groups are significant (p-value=0.023). For LASSO, Ridge regession, Elastic net, and Random forest, patterns of KM curves are mixed without clear and meaningful separation. For GBM, it is interesting to note that the group with the highest risk scores have clearly worse survival than three groups. Collectively, however, the log rank test fails to reach the significance level (p=0.192).

Figure 10.

Computed Kaplan-Meier curves, with the p-value from log rank test, for patients whose predicted values are less than 15%, 25-50%, 50-75%, and greater than 75% percentile, where predicted values are produced by predictive models constructed by six different methods, in the validation data set.

4. Discussion

Increasing use of omics technologies in translational biomedical research presents an unprecedented challenge to data scientists, regardless of their academic roots in biomedical informatics, computer sciences, or biostatistics. A common and defining feature, shared by HDOD from translational research, is that the sample sizes are relatively small while the covariate dimension is very high. To address this challenge, we introduce OOR methodology as a hybrid of unsupervised and supervised learning methods. The key idea underlying OOR is to transform large and sparse HDOD matrix into a dense covariate matrix, through similarity measurement of subjects’ HDOD with exemplars’ HDOD, and then to assess their association with clinical outcome. This transformation is crucial, enabling one to assess systemic association of clinical outcome with HDOD profiles, and to reduce the curse of high dimensionality. The theoretical foundation in support for this transformation is the Representer theorem. As a result, OOR provides a rigorous statistical framework to assess systemic association of clinical outcome with HDOD useful for systems medicine, a spin off from system biology. More importantly, OOR methodology, the focus of this manuscript, provides a framework to build predictive models with HDOD for precision medicine practice.

To illustrate OOR, we applied it to a lung cancer study, with gene expression data obtained from TCGA. We built a predictive model for stratifying patients who have been diagnosed with stage I lung cancer (either adenocarcinoma or squamous cell carcinoma), and yet variable survival times. Through applying OOR, our analysis identified 11 exemplars from the training set. Similarity to nine exemplars appears to decrease the overall survival, while that with remainder two exemplars increase the overall survival. Applying the risk score [11] to the validation data, we assess its association with the prognostic survival, and find that the association is statistically significant (p=0.015). Upon stratifying all patients into four quarters, we use the non-parametric log rank statistic to evaluate differences of four survival curves, and conclude that computed risk scores are able to separate stage I patients into subgroups (p-value=0.023). Inspecting KM curves for four different strata, one notice that there are two groups of patients, separated by 50% percentile. Those patients with higher risk scores tend to have poorer survival over the five-year post-surgery. This result, if being further validated, may provide a rationale for providing these patients with adjuvant therapies, to improve their survival.

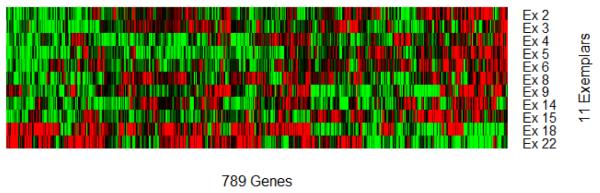
At this early stage of precision medicine, it is expected that clinical practitioners, with limited expertise in data science, are probably interested in understanding the rationale behind a risk score calculator [11]. First, we need to explain what are informative exemplars. Visually, we would like to show patterns of gene expression values associated with each informative exemplar (Figure 11), with a list of selected genes. For example, Ex 2 has some expression levels below average (green), while others are above average (red). Together with gene annotations for these 789 genes, one may gain an insight into what genes in concert tend to associate with poor survival. Indeed, Ex 18 and Ex 22 appear to have distinct patterns from those of the other nine exemplars, and associate positively with survival outcome. Finally, assigning appropriately calibrated weights to similarity with each exemplar, one can evaluate the overall risk score.

Figure 11.

Patterns of 11 informative exemplars characterized by 789 selected genes. Graded green and red colors, respectively, correspond to gene expression values that below and above averaged values for every gene.

While appreciating the attractions of OOR, it is equally important to recognize one potential weakness: the choice of metric in measuring similarity is somewhat arbitrary. In the literature of clustering analysis or unsupervised learning, multiple similarity metrics are in use, and they have their pros and cons, depending on the application context. From this perspective, OOR provides a level of flexibility in choosing similarity metrics that is appropriate for the application on hand.

OOR conceptually is connected with other analytic approaches. One class of approaches is the k-nearest neighbor methods (kNN), which are widely used in data mining literature of the computer sciences ^{40; 41}. The key idea is that objects in a relatively “close neighborhoods” defined by certain characteristics, tend to have similar outcomes. The kNN can be used to make predictive models, without making any modeling assumption, and are thus known sometimes as nonparametric predictive models. However, kNN does not take into account the fact that many neighborhoods have equivalent outcome associations (under either the null or alternative hypothesis). In this regard, OOR may be thought of as an extension to kNN or the nearest neighbor regression functional estimates ⁴². Direct comparison is not amenable with current version of kNN, since it is developed for binary classification problem.

Another closely related method is the grade of membership analysis, abbreviated as GoM ^43-45. Conceptually, GoM models the joint distribution of outcome and covariates through introducing a set of latent membership variables, under which a sensible distributional assumption is justifiable and, the likelihood, after integrating over all GoM latent membership variables, is computable. One can interpret GoM parameters as properties associated with individuals, rather than specific marginal interpretations of individual covariates. While GoM and OOR share the same conceptual goal, extracting information about an individual’s or object’s properties, OOR focuses on empirical observations of observed outcomes and covariates, without invoking any latent random variables.

The third closely related method is the principle component regression (PCR) ^{46; 47}. The key idea of PCA, shared with OOR, is to reduce the dimensionality of the covariate matrix through principal component analysis. After synthesizing a matrix of highly correlated covariates into a matrix of principal components, PCR correlates individual principle components with the outcome of interest. PCR is readily applicable to HDOD when p<n. In the event that p>n, one can still apply PCR, given that one applies the generalized inverse to perform single value decomposition⁴⁸. Resulted principle components, unfortunately, are not reproducible, depending on arbitrary order of covariates in HDOD. Hence, PCR is not recommended, unless the reproducibility of principal components is not important. In contrast, OOR seeks to identify a few exemplars that are representative of covariate matrix, and to correlate the outcome of interest with similarities to these exemplars.

The idea of using similarity measures by OOR is also connected with multiple methods developed and used in statistical genetics ^{49; 50}. While tracing these connections is not intended here, it suffices to note that classical and modern genetics aim to discover outcome-associated susceptibility genes that often cause similarity among related individuals who share more genetic variants than unrelated individuals. In the early days of genetics, segregation and linkage methods were used to characterize and discover genes through familial aggregations. In modern genetics, several research groups have proposed to assess the similarity of genetic markers and use similarity regression as a way to discover disease genes ⁵¹. While sharing similar scientific objectives, OOR uses similarity scores as a proxy to discover what exemplars have higher risk for disease, rather than discovering which SNPs associate with the disease.

OOR has another intrinsic connection with a recently popular method, known as the Sequence Kernel Association Test (SKAT)^{52; 53}, because OOR and SKAT share the representer’s theorem as their theoretical foundation. In brief, SKAT uses the representer’s theorem to represent the penetrance of all SNPs in combinations or their interactions, makes a sensible multivariate assumption about all regression coefficients, and tests their departure under the null hypotheses. Recently, Pan (2011) showed that the SKAT test is intrinsically equivalent to the similarity regression tests mentioned above ⁵⁴. OOR takes a further step beyond SKAT, regressing outcomes on similarity scores, rather than assuming them as random variables.

In conclusion, we have introduced a new analytic framework for analyzing HDOD. Beyond technical derivations and various connections with existing methods, what OOR brings to us is an introduction of an analytic framework for exploring the “systemic relationship” of HDOD with a clinical outcome, paving a way for serving systems medicine in the future. This approach is complementary to the usual covariate-specific exploration that has served the “reductionist perspective” well for decades. In the era of big data and systems biology and systems medicine, having a systemic framework should facilitate systematic investigations of HDOD and generate “reproducible patterns” of HDOD with omics data. Before leaving this section, it is important to recognize that OOR shares analytic objectives with many existing data analytics from both computational statistics and computer sciences. Systematic comparisons, by both theoretical explorations and numerical simulations, are necessary to identify situations where either existing methods or OOR are preferred and where they are complementary.