Direct measurement of correlation responses in Drosophila elementary motion detectors reveals fast timescale tuning

Abstract

Animals estimate visual motion by integrating light intensity information over time and space. The integration requires nonlinear processing, which makes motion estimation circuitry sensitive to specific spatiotemporal correlations that signify visual motion. Classical models of motion estimation weight these correlations to produce direction-selective signals. However, the correlational algorithms they describe have not been directly measured in elementary motion detecting neurons (EMDs). Here, we employed stimuli to directly measure responses to pairwise correlations in Drosophila’s EMD neurons, T4 and T5. Activity in these neurons was required for behavioral responses to pairwise correlations and was predictive of those responses. The pattern of neural responses in the EMDs was inconsistent with one classical model of motion detection, and the timescale and selectivity of correlation responses constrained the temporal filtering properties in potential models. These results reveal how neural responses to pairwise correlations drive visual behavior in this canonical motion detecting circuit.

eTOC

Salazar-Gatzimas et al. investigated the tuning properties of elementary motion detectors by measuring behavioral and neural responses to specific spatiotemporal correlations. They found neural tuning to fast correlation timescales, which constrained models of motion detection and predicted features of behavior.

Introduction

Animals across many taxa use visual motion information to guide behavior. In many visual circuits, direction-selective (DS) signals are computed locally in space by elementary motion detectors (EMDs) before they are pooled across the visual field (Barlow and Hill, 1963; Britten et al., 1992; Buchner, 1976; Franz and Krapp, 2000; Gabbiani et al., 1999; Hubel and Wiesel, 1962; Rust et al., 2006). These EMDs serve as canonical examples of neural computation. DS circuits have been the subject of intense study, from flies (Silies et al., 2014) to vertebrate retina (Demb, 2007; Wei and Feller, 2011) and cortex (Born and Bradley, 2005; Sincich and Horton, 2005), and these studies have resulted in a strong modeling framework for understanding motion computations.

Correlations are central to motion estimation. When an image moves across a field of photoreceptors, it generates correlations in light intensity over space and time. These correlations contain information that can be used to determine the direction and speed of the image’s motion (Fitzgerald et al., 2011; Potters and Bialek, 1994). Motion generates many kinds of correlations (Nitzany and Victor, 2014), but the strongest indicators of motion are frequently pairwise correlations in intensity over time and space (Clark et al., 2014; Fitzgerald and Clark, 2015; Fitzgerald et al., 2011; Potters and Bialek, 1994). Useful information about the direction of motion is carried by both positive and negative pairwise correlations (Clark et al., 2011; Fitzgerald and Clark, 2015). Negative correlations, often called “reverse-phi” (Anstis, 1970), generate motion percepts in the opposite direction of positive correlations in beetles (Hassenstein and Reichardt, 1956), fruit flies (Clark et al., 2011; Tuthill et al., 2011), fish (Orger et al., 2000), and humans (Anstis, 1970; Bours et al., 2009). Where negative correlation signals are processed remains unclear in these visual systems.

Models of motion computation detect spatiotemporal correlations using delays and nonlinearities (Adelson and Bergen, 1985; Borst and Egelhaaf, 1989). They weigh correlations to enhance responses to motion in the preferred direction (PD) relative to responses to motion in the null direction (ND). In particular, the Barlow-Levick model (BLM), first proposed to account for DS signals in vertebrate retina, suppresses signals when there is ND motion (Barlow and Levick, 1965). In contrast, the Hassenstein-Reichardt correlator (HRC) (Hassenstein and Reichardt, 1956), originally proposed to explain insect behavior, uses a multiplication step to enhance signals when there is PD motion. Both models respond to positive and negative pairwise correlations. These models are often written in opponent form, in which the output motion signal is the difference between signals from two EMDs with opposite PDs, leading to oppositely signed responses to motion in the PD and ND. Variants of these models provide stronger biological plausibility or account for details of response properties (Behnia et al., 2014; Eichner et al., 2011; Kim et al., 2014; Mo and Koch, 2003; Van Santen and Sperling, 1985).

In flies, the HRC model predicts a variety of neural and behavioral phenomena (Buchner, 1976; Egelhaaf and Borst, 1989; Haag et al., 2004). The HRC has been so successful in part because any nonlinear combination of two inputs is likely to have a large component that can be described mathematically as a simple product (Poggio and Reichardt, 1973) (see SI). Despite this success, the purely multiplicative HRC model in Drosophila has been excluded by several lines of evidence, including the fly’s ON and OFF motion pathways (Behnia et al., 2014; Clark et al., 2011; Joesch et al., 2010; Maisak et al., 2013) and DS responses to higher-order correlations (Clark et al., 2014). Other proposed models are HRC-like, in that they amplify signals to PD motion, but differ by not invoking pure multiplication (Behnia et al., 2014; Eichner et al., 2011; Serbe et al., 2016). When anatomical measurements of the spatial receptive field of EMD neuron T4 were compared with physiological measurements of delays in T4’s inputs, the combined results suggested that a BLM-like mechanism might apply in that EMD (Behnia et al., 2014; Takemura et al., 2013). Historically, distinguishing HRC- and BLM-like models has been difficult because they make similar predictions for opponent signals, such as those measured in the downstream neuron HS or in behavior.

Much is known about the circuits that compute visual motion in Drosophila. After light is detected by photoreceptors, signals split into parallel circuits that code selectively for the motion of light edges (ON pathway) and dark edges (OFF pathway) (Clark et al., 2011; Joesch et al., 2010; Silies et al., 2014). The EMD neurons T4 and T5, the earliest known DS neurons in the circuit, serve as the outputs of retinotopic light and dark edge pathways (Maisak et al., 2013). The DS outputs from T4 and T5 are averaged over space and subtracted opponently in VS and HS neurons (Mauss et al., 2015). Electron microscopy reconstruction has suggested which relay neurons provide inputs to T4 and T5 (Shinomiya et al., 2014; Takemura et al., 2013). Functional studies of those relay neurons have shown that they rectify signals, transmitting information about either contrast increments (ON pathway) or contrast decrements (OFF pathway) (Behnia et al., 2014; Meier et al., 2014; Strother et al., 2014). These relays impose small differential temporal delays, which could act as delays in the motion detecting circuit (Behnia et al., 2014). Silencing experiments have shown that there may be more than two input relays to T4 (Ammer et al., 2015) and there are at least 4 inputs to the neuron T5 (Fisher et al., 2015a; Serbe et al., 2016). Despite this detailed knowledge of the circuit and previous studies of the EMDs (Fisher et al., 2015b; Maisak et al., 2013), the response properties of T4 and T5 remain incompletely understood.

In this study, we first characterize the fly’s behavioral responses to pairwise visual correlations, and show that those responses require the neurons T4 and T5. We then image calcium activity in T4 and T5 to characterize their responses to visual stimuli with both stochastic and imposed correlations. We found that both T4 and T5 respond more strongly to PD correlations than to ND correlations, a result inconsistent with a BLM mechanism. Moreover, the neurons respond precisely to fast timescale correlations in a pattern that constrains temporal filtering steps and predicts the peak timing and direction of the fly’s behavioral responses.

Results

We confirmed that Drosophila optomotor rotational behavior was elicited by pairwise correlations using a psychophysical rig (Fig. 1A), in which a tethered fly walking on a spherical treadmill was presented with panoramic movies (Fig. 1B). By monitoring the rotation of the treadmill, we could measure the fly’s turning behavior while the tether ensured that the fly did not rotate.

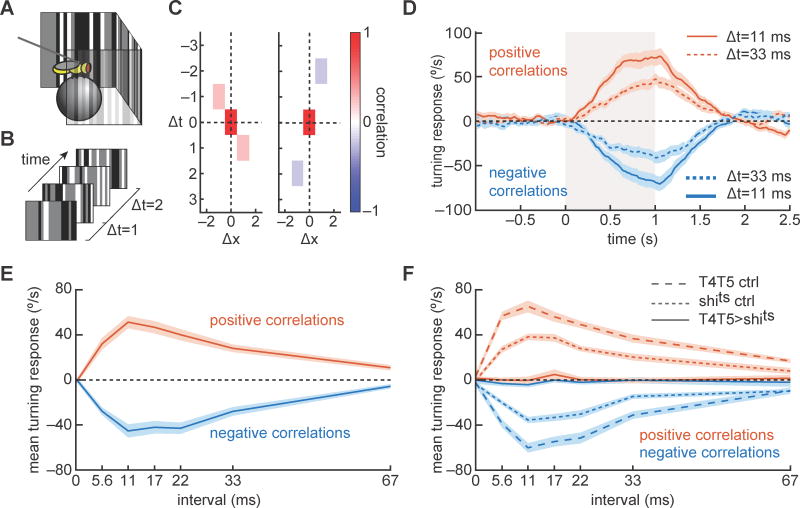
Figure 1.

Psychophysical responses to correlated noise stimuli map the correlation interval receptive field (CIRF) of Drosophila’s optomotor response. (A) We obtained psychophysical responses in Drosophila by tethering a fly above an air-suspended ball and examining the fly’s attempted rotation in response to visual stimuli displayed on a panoramic screen around it. (B) On the screens, we displayed correlated noise stimuli, which elicited turning behavior in the flies. (C) Correlated noise stimuli contain correlations at specific offsets in time and space (see SI). Example space-time correlograms show a rightward offset and positive correlation with temporal offset of 1 frame (left), and a negative correlation with a leftward displacement and a temporal offset of 2 frames (right). The red rectangles at the origins exist because the stimulus is perfectly correlated with itself when there is no offset in time or space. (D) Correlated noise stimuli were presented for 1 second beginning at time 0 (marked by gray box). Flies turned steadily in response to these stimuli, and modulated the strength of their response with the correlation sign and interval. Intervals times are reported as the time in milliseconds between correlations. (E) Mean turning responses were computed to the different signs and intervals of correlations. Flies responded most strongly to correlations with intervals of 11–22 ms. N=15 flies. Curves are mean ± SEM. (F) When neurons T4 and T5 were silenced using shibire^ts, turning in response to correlated noise stimuli was abolished. Genetic control flies responded in patterns similar to wild-type. N=15, 15, 20 flies for the T4T5>shi^ts, T4T5/+, and +/shi^ts curves. Curves are mean ± SEM. (See also Figure S1.)

The HRC model predicts that motion should be perceived in pairwise correlations of contrast. Based on previous work (van Steveninck et al., 1996), we designed a stochastic stimulus that enforced correlations in contrast between pairs of points in space and time. This generates a stimulus containing pairwise correlations at a defined spatiotemporal interval (Fig. 1C, see SI). These pairwise correlations produce motion percepts whose strength depends on the time interval between correlated pixels and on the sign of the correlation (see Supp. Movie 1). These noisy stimuli are similar to ‘glider’ stimuli that have been used to study responses to specific spatiotemporal correlations (Clark et al., 2014; Hu and Victor, 2010). However, the stimuli in this study have the advantage that they do not contain pairwise correlations at longer intervals, as gliders do (Hu and Victor, 2010). We will refer to these stimuli as correlated noise stimuli. We developed binary (black and white) and ternary (black, white, and gray) versions of this stimulus, which share precise correlational properties and elicit similar behaviors (Fig. S1A, see SI). The ternary version was used throughout this study except in Figure 1F, which used the binary version. Because the correlated noise stimulus generates continuous fast timescale correlations, sensitivity to these correlations is visible in sustained responses.

We presented correlated noise stimuli to flies and measured their turning responses. The stimuli elicited sustained turning responses that depended on both the sign and the time interval of the correlation (Fig. 1D). By varying this interval in the stimulus correlation, we mapped the correlation interval receptive field (CIRF) of the behavior (Fig. 1E). The CIRF measures the mean response to persistent correlations at different intervals. Flies responded maximally to correlated noise stimuli with correlation intervals of just 10 to 20 ms. CIRF tuning did not depend strongly on stimulus duration (Fig. S1B). Consistent with previous results, flies turned in the direction of the displacement for positive correlations, and in the direction opposite the displacement for negative correlations (Clark et al., 2011; Clark et al., 2014; Hassenstein and Reichardt, 1956; Tuthill et al., 2011) (Fig. 1E). Interestingly, the responses to positive and negative correlations had almost identical dependencies on the correlation interval.

We corroborated these results with an independent stimulus. We measured turning responses to purely stochastic stimuli and used reverse correlation to extract filters describing the response to (random) pairwise products of contrast in the stimulus. The interval dependence of those responses matched the ones found for correlated noise stimuli (Fig. S1).

We wished to identify the neural underpinnings of correlation detection in the fly. Recent studies have shown that the neurons T4 and T5 are DS, are required for DS responses in downstream neurons, and are required for flies to turn in response to a variety of motion stimuli (Maisak et al., 2013; Schnell et al., 2012). To determine whether these two neuron types were required to sense fast timescale pairwise correlations, we silenced them using the protein shibire^ts, which dominantly suppresses synaptic transmission (Kitamoto, 2001). Consistent with previous experiments, we found that when T4 and T5 were silenced, flies showed no detectable responses to the correlated noise stimuli (Fig. 1F). At least one of these cell types is therefore required for the fly to respond to these correlations.

The neurons T4 and T5 act as outputs for two parallel motion detection pathways selective for moving light and dark edges, respectively (Clark et al., 2011; Joesch et al., 2010; Maisak et al., 2013) (Fig. 2A). Based on the silencing result, we hypothesized that the response properties of T4 and T5 might confer on the fly its responses to fast correlations. Using in vivo 2-photon imaging, we measured the calcium responses of these neurons to visual stimuli presented on a panoramic screen around the fly (Fig. 2B, see SI). We expressed the protein GCaMP6f (Chen et al., 2013) simultaneously in both T4 and T5 and measured their responses in the lobula plate, where their axon terminals stratify into layers that respond selectively to motion in the four cardinal directions (Buchner et al., 1984; Maisak et al., 2013) (Fig. 2C). When imaging in the lobula plate, we observed punctate expression with a typical diameter of ~1 micron, the approximate size of single axon terminals (Takemura et al., 2013). Signals from these small puncta often responded selectively to only light or only dark edges (Fig. 2D, see SI). In those cases, this suggested the puncta were from only T4 or only T5 axons (Fisher et al., 2015b; Maisak et al., 2013). Among these puncta, many responded primarily to a single direction of motion, corresponding to their layer in the lobula plate (Fig. 2E). We focused on the progressive and regressive layers, which would drive optomotor rotational behavior.

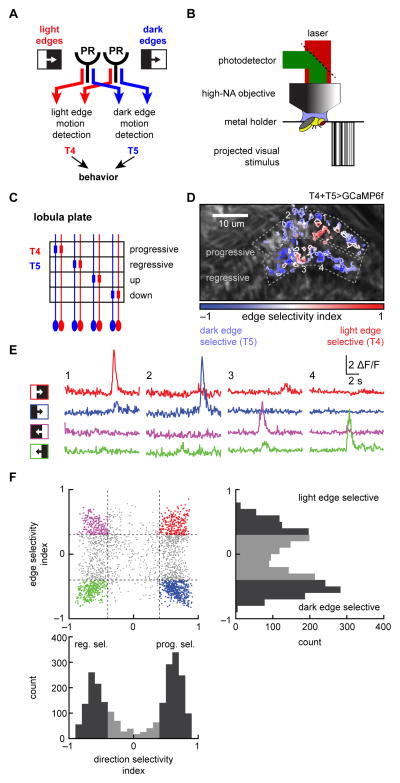
Figure 2.

Distinguishing T4 and T5 by their response properties. (A) Different circuitry detects light and dark edge motion in the fly eye. Distinct neural substrates relay information from photoreceptors (PR) to the neurons T4 and T5, which respond selectively to light and dark edges in each of the 4 cardinal directions. (B) Two-photon microscopy was used to image the calcium activity of T4 and T5 in the lobula plate, while the fly was presented with visual stimuli. (C) In the lobula plate, the neurons T4 and T5 stratify into four layers, each of which responds to one cardinal direction of motion. (D) Individual puncta selected in the progressive and regressive layers of the lobula plate are color coded according to their edge selectivity (see SI). The direction-selective layers are outlined. (E) Calcium traces of four sample puncta (numbered in (D)) responding to progressive and regressive light and dark edges. The edges swept through the fly’s full visual field at 30°/s. (F) Puncta were assigned both a progressive/regressive direction selectivity index (DSI) and a light/dark edge selectivity index (ESI), which indicated the directional tuning and edge tuning of each punctum (see SI). A punctum with a DSI = 1 (−1) responded solely to progressive (regressive) moving edges. Likewise, a punctum with ESI = 1 (−1) responded solely to light (dark) edges. Thresholds for ESI and DSI were used to classify axon terminals into progressive and regressive T4 and T5. Histograms at bottom and side show the distribution of DSI and ESI values. This panel contains 2242 puncta from 48 flies. (See also Figure S2.)

We measured the response properties of each punctum, and categorized them on the basis of direction-selectivity and edge polarity-selectivity: progressive (front-to-back) vs. regressive (back-to-front) edge selective and light vs. dark edge selective (Fig. 2F, Fig. S2A, see SI). We measured this selectivity by two indices: the edge selectivity index (ESI), which is positive/negative for light/dark edge selective puncta; and the direction-selectivity index (DSI), which is positive/negative for progressive/regressive selective puncta (see SI). By thresholding ESI and DSI, as well as response-repeatability, we selected puncta that consisted of progressive or regressive T4 or T5 axon terminals (Fig. S2A). The ESI thresholds were chosen to match ESIs measured in T4 and T5 dendritic arbors (Fig. S2B), where neuron type can be unambiguously determined based on anatomy. These selection criteria typically resolved almost twice as many T5 as T4 puncta, for reasons we do not understand. For statistical purposes, flies were considered the independent samples, and fly responses were calculated as the average response of all puncta of a certain type within each fly.

To quantify the response properties of these punctum-types, we presented flies with spatiotemporally uncorrelated stochastic visual stimuli using vertical bars as pixels (see SI). We used reverse correlation to fit each T4 or T5 punctum’s response to a linear model. We then selected statistically significant filters and averaged them after spatially aligning them to find average linear receptive fields for the four punctum-types (Fig. 3A, see SI). These linear receptive fields, which are not predicted by purely multiplicative models like the HRC, describe how each punctum responded to visual contrasts at different points in time and space in the preceding second. The responses to uncorrelated noise inputs had low signal-to-noise (~0.01, ratio of powers in the signal to the noise), making it difficult to assess how well these receptive field models predicted signals in T4 and T5 (see SI).

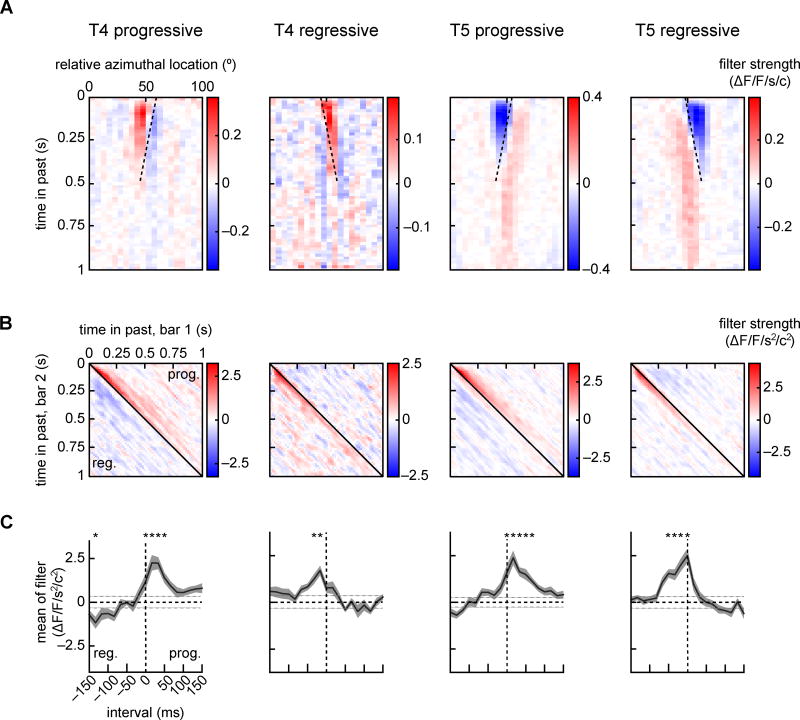
Figure 3.

Linear and second order receptive fields (RFs) of T4 and T5 progressive and regressive puncta. (A) Average linear RFs of the four puncta types, aligned to center each punctum’s receptive field at 50° azimuth before averaging. Dotted lines align with the preferred direction for the cell type. Pixels are vertical bars, so there is only one spatial dimension in this filter. (B) For each of the four puncta types, average second order receptive fields for nearest neighbor pixel pairs (see SI). Second order receptive fields showed strong responses to correlations with short intervals (near the diagonal) and with displacements in the punctum’s preferred direction. Progressive displacements are above the diagonal and regressive ones below. (C) Elements along each diagonal of the second order receptive field correspond to responses to a single correlation interval. These diagonal elements were averaged over the earliest 333 ms to quantify responses to different correlation intervals (see SI). These averages show significant responses to 17 or 33 ms intervals in the preferred direction in all four cell types (*p < 0.01, Bonferroni corrected, z-test relative to shuffled filters). The gray horizontal dotted lines represent one standard deviation of the shuffled filter controls. From left to right, throughout the plot, the number of flies (number of puncta) is 14 (37), 12 (26), 23 (127), 27 (103). (See also Figure S3.)

The linear receptive fields in both cell types showed a spatiotemporal orientation, which aligned with the direction-selectivity of the neuron (Fig. 3A, dotted lines) and were space-time inseparable (Fig. S3A). The linear receptive fields of both T4 and T5 contained both positive and negative weightings. T4 had a positive weighting of the most recent inputs, and lower amplitude negative weighting of less recent inputs. T5 neurons were oppositely weighted, with recent inputs weighted negatively. This difference in the filter signs is consistent with the complementary responses of the two cell types to light and dark edges (Maisak et al., 2013). These filter shapes are therefore consistent with both the direction- and the edge-selectivity of the T4 and T5 neurons.

In principle, it is possible that an instantaneous nonlinearity applied after this linear filter could generate DS signals (Adelson and Bergen, 1985; Borst and Egelhaaf, 1989) using the framework of a linear-nonlinear (LN) model (Dayan and Abbott, 2001). However, there are two reasons to measure the DS nonlinear response directly, rather than fit this data to an LN model. First, any LN model that relies on our measured linear filter would also include a ~200ms low-pass filter imposed by the calcium indicator. Models that include calcium indicator kinetics are unlikely to account for the behavioral correlation interval timescales of 10–20ms (Fig. 1 and Fig. S1). Second, LN models make substantial assumptions about the structure of the computation. They can be difficult to interpret when nonlinearities also act on inputs to a cell. For example, an LN model can produce DS outputs when fit to a non-DS synthetic model neuron that linearly adds two rectified inputs (see SI). In this example, the non-DS synthetic model neuron has a nonlinear-linear structure, but an LN model can shoehorn the data into its linear-nonlinear structure, creating direction-selectivity. This suggests that DS predictions of LN models should not be considered sufficient for such models to be adopted, especially when some input signals to T4 and T5 are rectified (Behnia et al., 2014; Meier et al., 2014; Serbe et al., 2016; Strother et al., 2014).

We opted to directly measure the second order DS nonlinear neural responses by measuring responses of T4 and T5 to pairwise correlations in the same stochastic stimuli used to extract the linear receptive fields. For all puncta associated with significant linear receptive fields, we computed the mean second order filters between nearest neighbor pixels in space (Fig. 3B) (see SI) (Marmarelis, 2004). These second order receptive fields show how each of the four neuron types responded to products of contrasts of neighboring pixels with different time intervals, at different times in the past. Just as the linear receptive fields may be thought of as responses to impulses of contrast at different points in space, the second order receptive fields can be transformed to emphasize that they represent the impulse responses to products of contrasts with specific time intervals (Fig. S3BC, see SI). The red regions indicate positive weightings, and occur in response to correlations on short time intervals in the PD of each neuron.

We measured the tuning to specific correlation intervals by averaging along the diagonals of these filters, which generates measurements proportional to the steady state response to correlations with a specific interval between pixels (Fig. 3C). These averages show strong enhancements of the signal in response to PD correlations on the timescale of ~17 ms, similar to the peak response interval of behavioral second order filters (Fig. S1). They also show high precision in distinguishing between intervals separated by just 17 ms. To observe the advantage of measuring the second order response directly, we computed the second order receptive fields that would arise from a quadratic nonlinearity following the measured linear receptive fields (Fig. S3). Those predicted second order receptive fields are less direction-selective, less precise, and sensitive to correlations on longer intervals than the measured second order receptive fields.

To distinguish responses to positive and negative correlations, we measured T4 and T5 responses to correlated noise stimuli. We found that progressive T4 and T5 neurons responded to the uncorrelated noise stimulus with sustained activity (Fig. 4AB), and modulated their responses relative to this baseline when presented with correlated noise stimuli. We measured the CIRF as we did with behavior, averaging neural responses over time to calculate an average response to each correlation interval (Fig. 4CD). Responses in both T4 and T5 were significantly enhanced by positive correlations in the PD, and significantly suppressed by negative correlations in the PD. This inversion of the modulation is consistent with an algorithm sensitive to pairwise correlations. When responses were averaged only over the second half of the presentation, the pattern of responses was largely unchanged, showing that potential initial transients in the response do not qualitatively affect the measured tuning (Fig. S4AB).

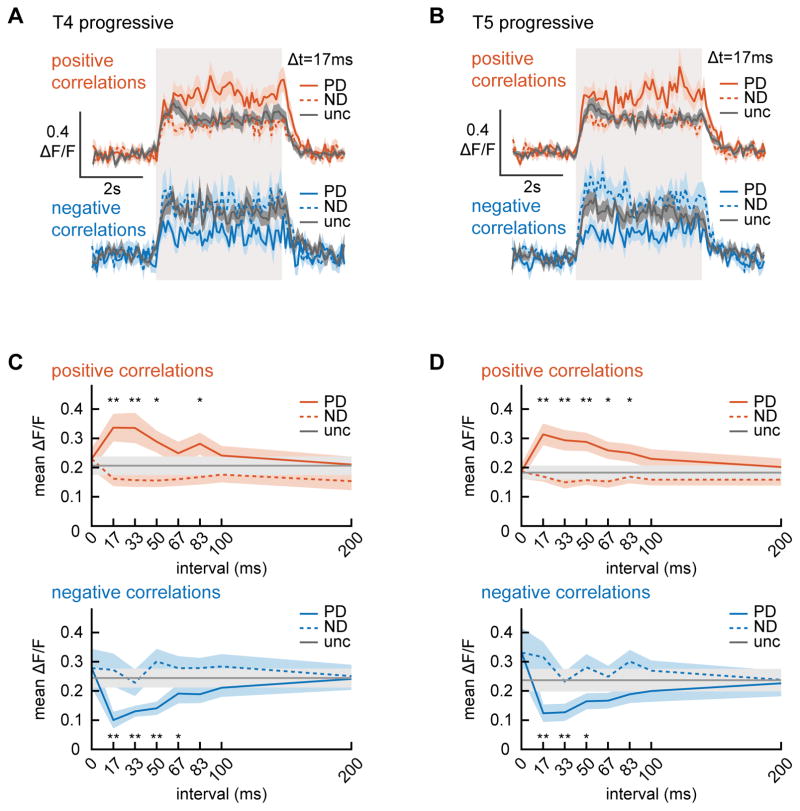
Figure 4.

Correlation interval receptive fields (CIRFs) for progressive layer T4 and T5 puncta. (A, B) Flies were shown correlated noise stimuli (Fig. 1, SI) for durations of 4 seconds (marked by gray box) and the responses of progressive T4 (A) and T5 (B) puncta were measured. Traces are averages over flies. The puncta responded strongly to uncorrelated stimuli and this response was enhanced/suppressed by positive/negative correlations in the preferred direction. The number of flies (number of puncta) is 17(102), 18(85), 19(148), 15(140) for T4 positive correlations, T4 negative correlations, T5 positive correlations, and T5 negative correlations. (C, D) Mean responses of progressive T4 (C) and T5 (D) to positive (top) and negative (bottom) correlations with varying intervals in the preferred and null directions (PD and ND). For both neurons, responses showed significant differences in the preferred direction compared to the uncorrelated stimulus (* p<0.05, ** p<0.01, Bonferroni corrected, Wilcoxon signed rank test). (See also Figure S4.)

The maximum modulation in both neuron types occurred for correlations on an interval of 17 ms, and extended to ~80 ms. The shape of these curves is quite similar to those predicted by the measured second order receptive fields (Fig. 3C). If the system were completely described by filters up to second order, one would expect a perfect match (see SI). Differences between the two may reflect the impact of non-second order correlations. In the measured CIRF, virtually no modulation occurred at intervals of 0 ms, demonstrating that the neurons compute correlation intervals precisely. This pattern of responses held for regressive T5 neurons, but regressive T4 neurons did not respond strongly with this assay (Fig. S4CD), though they did show correlation responses in their second order receptive fields (Fig. 3BC). Importantly, the response pattern in progressive T4 and T5 was not sensitive to varying the ESI and DSI thresholds for selecting puncta (Fig. S4EF), indicating that puncta selection criteria did not bias this pattern of results.

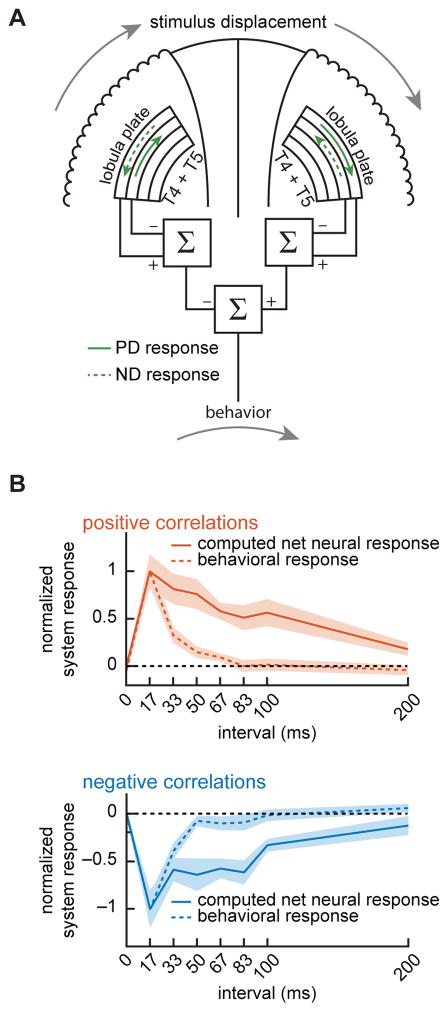
We next asked whether the neural responses in T4 and T5 could explain the behavioral responses to the same correlated noise stimuli. To calculate a net neural signal for rotational stimuli presented to both eyes, we computed the net motion response of progressive and regressive layers to binocular correlated noise stimuli. Rotational stimuli are progressive on one eye and regressive on the other, so this computed neural motion signal consisted of first adding T4 and T5 signals together (Maisak et al., 2013), subtracting the regressive from progressive layer signals (Mauss et al., 2015), and subtracting one eye from the other to create a net signal across the eyes (Fig. 5A). The computed neural motion signal and the behavioral signal both peaked at 17 ms, and diminished at longer intervals (Fig. 5B). Importantly, this net neural response also predicted a ‘reverse-phi’ response: the reverse-direction turning behavior in response to negative correlation stimuli. However, as the correlation interval increased, the behavioral responses attenuated faster than the neural responses in T4 and T5. One explanation for this difference is that another pathway, outside of T4 and T5, may influence the strength of the behavioral response. It is known that pathways parallel to T4 and T5 contribute to rotational behavior (Bahl et al., 2015). Another explanation for the difference is that the measured calcium signals may not reflect a straightforward ‘strength’ of the signal, as it relates to downstream circuitry (Schnell et al., 2014).

Figure 5.

Computed net neural signal compared to behavioral responses. (A) A net neural response was computed by combining PD and ND T4 and T5 responses from progressive and regressive layers. This combination computed first the opponent response within each eye, and then took the difference between eyes to generate the net neural response. (B) The behavioral correlation interval receptive field (CIRF) and the computed net neural CIRF both responded positively to positive correlations and negatively to negative correlations. Neural and behavioral curves are normalized to have a maximum response magnitude of 1. Positive correlation neural data: 11 flies (400 puncta); negative correlation neural data: 10 flies (473 puncta); positive correlation behavioral data: 12 flies; negative correlation behavioral data: 9 flies.

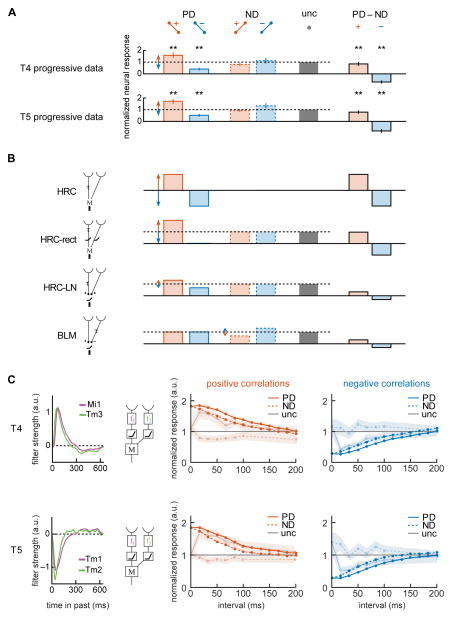
We wished to examine whether the response properties constrained potential circuit mechanisms, encapsulated by proposed models of motion estimation. We first re-plotted the data from Fig. 4C and 4D (time interval of 17 ms) to show how T4 and T5 responses were modulated in response to specific correlations (Fig. 6A). Both T4 and T5 modulate to correlations oriented in the PD more strongly than to correlations in the ND (p<0.05, Wilcoxon sign test, comparing response modulation in PD vs. ND for T4 and T5 progressive and regressive layers). The opponent signals derived from these responses show positive net responses to positive correlations, and negative net responses to negative correlations.

Figure 6.

Comparing correlation responses to circuit models of motion estimation. (A) Progressive layer T4 and T5 responses to correlated noise stimuli at an interval of 17 ms showed significant modulation in the preferred direction relative to uncorrelated (data from Fig. 4C,D). Opponent responses (PD–ND) were calculated for positive and negative correlations. Red and blue arrows highlight major deviations from the uncorrelated response, which is normalized to a value of 1. (* p<0.05, ** p<0.01, Bonferroni corrected for multiple comparisons in Fig. 4; Wilcoxon signed rank test for comparisons to uncorrelated; Wilcoxon sign test for opponent responses.) (B) We computed the responses of 4 simple models of motion estimation to correlated noise stimuli (see SI). For each model, individual layer signals were computed in addition to opponent signals. Responses of all but the HRC model were normalized so the uncorrelated response had a value of 1. (C) An HRC model was constructed using measured input filters to T4 (top) and T5 (bottom) cells (Behnia et al., 2014). The model responses were computed to positive (left) and negative (right) PD and ND correlated noise stimuli. The faded responses show data replotted from Fig. 4, normalized by the uncorrelated response. (See also Figure S5.)

To see how the modulation pattern in T4 and T5 constrained models of motion detection, we considered how four simple DS models responded to correlated noise in their preferred and null directions, compared to their responses to uncorrelated noise (Fig. 6B, see SI). These simple models ignore many of the complexities of the real EMD circuitry: lateral inhibition in the inputs (Freifeld et al., 2013; Meier et al., 2014; Srinivasan et al., 1982); multiple input pathways to the EMDs (Ammer et al., 2015; Serbe et al., 2016); interactions between ON and OFF pathways in the circuit periphery (Fisher et al., 2015a; Meier et al., 2014; Silies et al., 2013); and known neurotransmitters within the circuits (Hasegawa et al., 2011; Shinomiya et al., 2014). Nonetheless, these simple models provide useful intuition for the organization of the motion detection computation, which is why they persist as models for understanding motion detection (Behnia et al., 2014; Fisher et al., 2015b; Kim et al., 2014; Serbe et al., 2016; Shinomiya et al., 2014; Takemura et al., 2013)

In all four simple models, opponent responses (PD minus ND) to correlations were equal and opposite. The model responses to PD and ND positive and negative correlations, before the opponent subtraction, were qualitatively different (Fig. 6B). The HRC family of models strongly modulated their responses to PD correlations, while the BLM strongly modulated its response to ND correlations. This difference is fundamentally due to the location of the delayed input relative to the preferred direction in the two models of motion detection. The different patterns of response are not due to the simple filters in the models: the patterns remain with more realistic temporal filters and spatial filters (Fig. S5). The neural measurements in both T4 and T5 agree best with the HRC-like models, which respond to uncorrelated inputs and modulate signals to correlations in the PD. In these two models, signals are either rectified before multiplication or are generated by an HRC-like LN model. The T4 and T5 progressive responses to correlations on fast timescales are not consistent with the BLM, which modulates signals in the ND more than in the PD, though EMDs could have response properties that are a mixture of the two model classes.

When input filters to the EMD generate both positive and negative weightings, as real filters appear to do (Behnia et al., 2014), it becomes more difficult to categorize models simply as HRC or BLM (Kim et al., 2014). We therefore tested whether more realistic filters proposed in recent models could account for the pattern of correlation responses in T4 and T5. One recent study carefully measured calcium responses of four verified inputs to the T5 neuron, and fitted each input to a filtering and rectifying function, similar to the HRC-rect model, but with an additional temporal filtering step before multiplication (Serbe et al., 2016). These inputs were combined into a detailed and comprehensive motion detection model for T5, which included calcium indicator dynamics in the input arms. We simulated the responses of non-opponent multipliers using the architecture and parameters of this fitted model. It did not reproduce T5’s measured DS responses to correlated noise stimuli (Fig. S5B). This is a result of the model’s temporal filters, with timescales of hundreds to thousands of milliseconds. Models that include calcium indicator dynamics before the nonlinear step are unlikely to produce selective responses to fast-timescale correlations.

A second study used electrophysiological measurements rather than calcium indicators to characterize the filters of putative input arms to the T4 and T5 motion detectors (Behnia et al., 2014). In that study, the peak filter weights of the input arm pairs occurred 15–20 ms apart, consistent with the peak correlation interval measured here. We tested whether these high time-resolution filters could explain the observed responses when incorporated into a model that rectifies before multiplying, as the model in that paper did (Fig. 6C). When presented with correlated noise stimuli, these models showed a peak response in the PD at ~17 ms, but they also responded positively to ND positive correlations, which was not observed in T4 or T5 (Fig. 3C, 4CD). Therefore, while these filters predicted the interval of peak correlation response, they did not predict the precision with which that peak is computed by the circuit.

The models presented above do not fit the CIRF data well in T4 or T5, demonstrating that correlation responses provide a strong constraint on potential models of motion detection. Still, it is possible for a simple 2-input model to fit the CIRF data, though CIRF data does not constrain simple models so much that it uniquely defines a filter set to account for it. To show this, we built two distinct HRC-rect models that each reproduce measured CIRFs with some fidelity, yet which possess quite different temporal filters (Fig. S5C). More realistic models, which might include more than two inputs (Ammer et al., 2015; Serbe et al., 2016), allow even more freedom to choose filter sets to explain correlation responses.

Discussion

In this study, we used precisely correlated stimuli to investigate the response properties of the fly’s earliest-known DS neurons, T4 and T5. Psychophysical tests and genetic silencing showed that the neurons were required for the fly’s perception of pairwise correlations (Fig. 1). In vivo 2-photon calcium imaging revealed the linear and nonlinear response properties of the neurons (Fig. 3, 4). The response properties of T4 and T5 predicted the peak and sign of the fly’s perceptual tuning when shown identical stimuli (Fig. 5). Together, these results imply that the activity of the neurons T4 and T5 drives turning behavior in response to these pairwise correlation stimuli. The neurons responded to fast correlations and precisely discriminated between correlations with different intervals, strongly constraining the temporal filtering that precedes motion detection. Previously measured inputs to these neurons are sufficient to explain responses to short interval correlations, but not the precise discrimination of the neural responses (Fig. 6). Overall, at these fast timescales, the neural responses were most sensitive to pairwise correlations in the neuron’s PD, which is consistent with HRC-like models, and inconsistent with the BLM (Fig. 6). Moreover, the activity in these two neurons reveals neural origins of the famous “reverse-phi” motion illusions that helped inspire the correlational theory of motion detection (Hassenstein and Reichardt, 1956).

Fast timescale correlations

Both behavioral psychophysics (Fig. 1) and T4 and T5 recordings (Fig. 3, 4) showed peak responses to fast timescale correlations with intervals of ~17 ms. This timescale for the delay, derived from direct measurements of correlation responses, is faster than delay filters considered in earlier work (Brinkworth and O’Carroll, 2009; Eichner et al., 2011; Shoemaker et al., 2005), but is consistent with other measurements, often made using methods similar to those used here (Clark et al., 2011; Harris et al., 1999; Marmarelis and McCann, 1973). It is also consistent with some measurements of the response properties of neural inputs to T4 and T5, which show differences in peak response timing of ~20 ms (Behnia et al., 2014).

Since our pixels were 5° apart, the observed peak correlation intervals correspond to velocities of ~250–500 °/s. This is near the scale for peak responses in HS/VS to single moving light or dark edges (Ammer et al., 2015). It is also approximately the peak spontaneous rotational speed measured on our behavioral rig (where the 99^th percentile of rotational speed during gray stimulus presentation was ~380°/s), and is at the tail of the turning speed distribution for freely walking flies (Katsov and Clandinin, 2008). It is therefore a relevant timescale for walking flies.

A recent study used a different stimulus protocol to show DS amplification in T4 and T5 on timescales up to 100 ms (Fisher et al., 2015b). Our data highlight responses to correlations on faster timescales (Figs. 3, 4). Differences in these results may be due to different stimulus protocols, which can affect measurements of the delay in the circuit (Harris et al., 1999). The correlated noise stimulus used here adds noise to the stimulus in exchange for a precisely defined correlation interval, while other stimulus protocols introduce less noise, but exhibit more varied correlations over time. Stimuli with different timescales or lengthscales may reveal different processing regimes, for instance enhancing null-direction modulation, which was small but visible in our protocols (Figs. 3, 4).

The methods in this study measured perceptual and neural tuning to fast timescale correlations using slow readouts like behavior and calcium indicators. In the case of reverse correlation to stochastic inputs (Figs. 3B, S1), the smearing of the slow readout is orthogonal to the correlation interval, so that it does not affect the average signal for the interval measurements (see SI, Fig. S3BC). In the case of the correlated noise stimulus, which allows us to measure the CIRF (Figs. 1 and 4), the fast timescales are in the stimulus structure, and the readout is simply the steady state response, which is related to the second order receptive field measurements (see SI). These approaches may be useful in probing other neuron types, like starburst amacrine cells in vertebrate retina, where calcium is the primary indicator of direction selectivity (Euler et al., 2002).

Precise discrimination of correlations

Behavioral signals showed precise tuning to correlation intervals: flies distinguished between correlation intervals different by as little as 5 ms (Fig. 1). Opponent motion detection systems, as are thought to govern behavior, can distinguish between a small interval and a zero interval by subtracting signals from motion detectors with opposite direction-selectivity. In opponent systems, the motion detectors need only respond slightly more to motion in the PD than the ND. However, our data suggests that the neurons T4 and T5 are capable of strongly distinguishing PD motion from ND motion prior to the opponent layer subtraction (Mauss et al., 2015), even when the correlation intervals differ by as little as 33 ms (Figs. 3C, 4CD). In fact, our data suggests that these neurons distinguish between correlation intervals of 0 ms and 17 ms in the PD (Fig. 4CD).

The CIRFs showed little modulation at 0 ms intervals, indicating that the motion detector is not responding to instantaneously correlated inputs. Rejecting instantaneous correlations enhances EMD selectivity for correlations that signify motion by ignoring correlations that are not directional. Instantaneously correlated inputs could arise naturally from spatial correlations in the visual world or from input pathways with overlapping spatial receptive fields, which are suggested by connectomic and physiological data (Behnia et al., 2014; Takemura et al., 2013). Behaviors like escape responses to looming stimuli (Card and Dickinson, 2008; de Vries and Clandinin, 2012; Schilling and Borst, 2015), which may not rely on opponent motion signals, could benefit from this precision prior to the opponent subtraction.

Both the correlation delay timescale and the precision of responses in T4 and T5 are similar to those recorded by similar means in DS cells in cortical areas V1 (Livingstone and Conway, 2003) and MT (Livingstone et al., 2001). The similarities in the correlation responses in these two visual systems suggest that there may be similar computational requirements or constraints for the two motion detection systems, in contrast to the two systems’ clear anatomical and functional differences.

Similarities and differences in T4 and T5 responses

In this study, it was remarkable that T4 and T5 had similar correlation response properties, despite clear separation in their responses to light and dark edge stimuli (Fig. 2F). In particular, their second order receptive fields appear similar (Fig. 3B), as do their responses to a suite of different correlation intervals (Figs. 3C, 4). The exception was the T4 regressive layer, where the correlated noise stimuli did not elicit strong responses. Both T4 and T5 modulated their signal more to fast correlations in the PD than in the ND. These similarities are in spite of the different circuits that feed into T4 and T5. The neuron T4 has at least two input cell types (Ammer et al., 2015; Takemura et al., 2013), while T5 has 4 functional inputs, which are all cholinergic (Serbe et al., 2016; Shinomiya et al., 2014). The neuron T4 receives ON signals as inputs, while T5 receives OFF signals as inputs (Behnia et al., 2014; Meier et al., 2014; Serbe et al., 2016; Strother et al., 2014).

The most salient difference between T4 and T5 function is their selective response to different edge polarities. The pairwise correlations employed in this study exist equally in light and dark moving edges. In general, even-ordered correlations in contrast do not change when stimulus contrast is inverted, so to respond differently to light and dark edges, models (and neurons) must be sensitive to odd-ordered correlations (Clark et al., 2014). These higher order correlations occur frequently in the natural world (Nitzany and Victor, 2014), and motion estimation can be improved by detecting these signifiers of motion (Clark et al., 2014; Fitzgerald and Clark, 2015; Fitzgerald et al., 2011). Third order correlations are perceived as motion in both flies and humans (Clark et al., 2014; Hu and Victor, 2010). Future studies could investigate how higher order correlations are incorporated into the motion estimate (Clark et al., 2014; Fitzgerald and Clark, 2015). In this study, the largest differences between T4 and T5 properties showed up not in the pairwise correlation responses, but rather in the linear receptive field measured in each cell type.

Linear responses in motion detectors

In the fly EMDs, we observed spatiotemporally oriented linear filters to contrast changes on the screen (Fig. 3). The measured receptive fields extended up to 15 to 20° in space. This is broader than might be expected from classic psychophysical experiments (Buchner, 1976), but in line with the circuit connectome (Shinomiya et al., 2014; Takemura et al., 2013) and with functional studies of the EMD inputs (Behnia et al., 2014; Fisher et al., 2015a).

Linear responses are not predicted by a purely multiplicative model of motion detection, like the HRC, which responds only to products of pairs of contrasts. Linear filters likely be observed in an LN model of motion computation, similar to the HRC-LN in Figure 6. However, linear filters can also be obtained from multiplicative HRC-like models when input signals possess a non-zero mean immediately prior to multiplication (see SI). This would occur for HRC-rect-like models in which a multiplication step acts on rectified inputs (Behnia et al., 2014; Eichner et al., 2011; Serbe et al., 2016). Therefore, the existence of a linear receptive field is consistent with several models of motion detection.

The measured linear receptive fields (RFs) were oriented in the cells’ PD, and the light and dark selective cells had oppositely signed linear RFs (Fig. 3). If this linear, oriented RF were acted on by a nonlinearity, then this system might look similar to models of simple cells in cortical area V1 (Heeger, 1992; Movshon et al., 1978). Moreover, the linear RFs in T4 and T5 look similar in shape to those measured in OFF retinal ganglion cells (Kim et al., 2008) and to those suggested in starburst amacrine cells in the vertebrate retina (Kim et al., 2014). The data in this paper does not argue explicitly against an LN operation originating motion signals. Rather, acknowledging the difficulty in unambiguously identifying such a computational hierarchy, this study directly measured the second order DS nonlinear response.

Negative correlations in motion detection

Responses to negative correlations were among the earliest evidence of correlational motion detection in insects (Hassenstein and Reichardt, 1956). Negative correlations have been shown to be useful in estimating motion of natural scenes (Fitzgerald and Clark, 2015), and motion percepts in response to negative correlations, also known as “reverse-phi” stimuli, are pervasive in sighted animals (Anstis, 1970; Bours et al., 2009; Clark et al., 2011; Hassenstein and Reichardt, 1956; Orger et al., 2000; Tuthill et al., 2011). The recordings of T4 and T5 in this study show a neural basis for the negative correlation motion percept by revealing how EMD neurons modulate their signal strength based on the sign of the input correlation. Interestingly, although negative correlation responses motivated the sign-correct multiplication in the HRC (Hassenstein and Reichardt, 1956), our data and models show how behavioral responses to negative correlations can occur without hyperpolarizing neural responses (Figs. 4, 5). In T4 and T5 and in behavior (Fig. 1), the CIRF for positive and negative correlations each peaked at 17 ms intervals before falling towards baseline at longer intervals. This symmetry between positive and negative correlations is reminiscent of symmetries in human response thresholds to visual correlations (Bours et al., 2009).

The two simple models in this study that best matched the gross patterns of activity in T4 and T5 were HRC-like, but used rectification instead of or in addition to multiplication (Fig. 6). Though these two models can account for the correlated noise responses to both positive and negative correlations, they cannot account for some other known responses to negative correlations. For instance, black and white contrast pairings in sequentially presented bars yield behavioral (Clark et al., 2011) and neural responses (Eichner et al., 2011), which are not predicted by these two simple models. Models with bilobed temporal filters and incomplete rectification have predicted these responses (Eichner et al., 2011).

This study has shown that fly EMDs respond precisely to fast timescale pairwise correlations in their preferred direction, with a tuning that concurs with the fly’s behavior. These neural and behavioral measurements characterize the motion detector’s second order algorithm. The speed and precision of this algorithm will inform future measurements of the circuit’s physiology and connectivity, which can in turn refine the algorithmic description of motion detection.

Short Methods

Fly psychophysical responses were obtained from the responses of tethered flies to panoramic visual stimuli (Clark et al., 2011; Clark et al., 2014) (see SI). Visual stimuli were stochastic or possessed pairwise spatiotemporal correlations at only one interval in time and space (see SI). Behavioral responses to correlated noise with different intervals were averaged over time to generate correlation interval receptive fields (CIRFs). Second order filters were computed using standard methods (Marmarelis, 2004) (see SI).

Calcium activity was measured in vivo with a 2-photon microscope while flies were presented with visual stimuli (Clark et al., 2011) (see SI). Images were segmented into small puncta, whose signals were classified by selectivity to direction of motion and to light/dark edges (see SI). Receptive fields were found by standard reverse correlation methods (Chichilnisky, 2001; Dayan and Abbott, 2001; Marmarelis, 2004) (see SI). Neural responses to correlated noise with different intervals were averaged over time to generate the CIRFs.

Models (Fig. 6, S5) were implemented in Matlab, and the model responses were averaged over time (see SI). Code used in simulations is available on modelDB.

All statistics were computed by first averaging over puncta, then over flies. P-values were computed between groups of flies using a Wilcoxon signed rank test.

Highlights.

• Neural and behavioral responses to visual correlations were measured directly

• Both neural and behavioral responses are precisely tuned to fast correlations

• Neural signals predict behavioral responses to ‘reverse-phi’ illusory motion

• Responses to correlations constrain circuit models of motion detection