The Virtual Intestine: in-silico modeling of small intestinal electrophysiology and motility and the applications

Abstract

The intestine comprises a long hollow muscular tube organized in anatomically and functionally discrete compartments, which digest and absorb nutrients and water from ingested food. The intestine also plays key roles in the elimination of waste and protection from infection. Critical to all of these functions is the intricate, highly-coordinated motion of the intestinal tract, known as motility, which is co-regulated by hormonal, neural, electrophysiological and other factors. The Virtual Intestine encapsulates a series of mathematical models of intestinal function in health and disease, with a current focus on motility, and particularly electrophysiology. The Virtual Intestine is being cohesively established across multiple physiological scales, from sub/cellular functions to whole organ levels, facilitating quantitative evaluations that present an integrative in-silico framework. The models are also now finding broad physiological applications, including in evaluating hypotheses of slow wave pacemaker mechanisms, smooth muscle electrophysiology, structure-function relationships, and electromechanical coupling. Clinical applications are also beginning to follow, including in the pathophysiology of motility disorders, diagnosing intestinal ischemia, and visualizing colonic dysfunction. These advances illustrate the emerging potential of the Virtual Intestine to effectively address multi-scale research challenges in interdisciplinary gastrointestinal sciences.

Introduction

The efficient transport and uptake of nutrients through the gastrointestinal (GI) tract are essential for the maintenance of health, yet also underpins obesity, a major epidemic of modern Western society. Investigating the physiology and pathophysiology underlying intestinal functions presents a significant research challenge. One must not only consider the multiple participating cell types (e.g., smooth muscle, various mucosal cells, neurons and interstitial cells of Cajal (ICC)), but also their overlapping control systems, including hormonal, neural, electrophysiological and intracellular mechanisms.¹ Moreover, as in all physiological systems, intestinal functions must be understood separately and collectively across vast spatiotemporal scales, from milliseconds and micrometers for intracellular events, to minutes and centimeters for organ-level events, presenting a daunting analytical task.²

The purpose of this review is to discuss an in-silico framework to quantitatively link all physiological activities contributing to the function of the small and large intestines, which we term the Virtual Intestine. Relative to modeling work in cardiac and neural fields, in-silico research in the GI field is relatively limited, although many studies have appeared from multiple groups world-wide in recent years. This review follows on from, and advances, previous interdisciplinary reviews of the GI tract and the Virtual Stomach,^{3, 4} to present analysis focused on recent experimental investigations and mathematic models of intestinal structure and function. The review has a particular focus on motility, and particularly on electrophysiology, including motor control activities by smooth muscle cells, ICC, and, to a lesser extent neural circuits, because this is an area where modeling has been productively applied to date. Brief attention is also given to other example areas of applied intestinal modeling.

The review begins with an overview of several key anatomical considerations that are fundamental to the mathematical modeling approach in the intestines. Relevant cell, tissue and organ physiology and mathematical models are then discussed at each scale, with examples of works by a variety of groups and inter-disciplinary teams. Finally, some emerging clinical applications of the Virtual Intestine are considered. Throughout, the principle focus of the review is on the small intestine, whereas much less attention is given to colonic physiology and modeling, being an area where current knowledge remains comparatively under-developed.

FUNCTIONAL AND ANATOMICAL CONSIDERATIONS

The general structure of the GI tract is of a long continuous muscular tube, however, different regions are anatomically and functionally discreet, and are considered separately. Following ingestion and mastication in the mouth, food boluses are transported by muscular “peristalsis” (a wave-like propulsive motor activity) through the esophagus to the stomach. The stomach is a highly distensible acidic chamber, responsible for the physical and chemical breakdown of food particles into “chime” – a slurry-like substance, followed by delivery at a carefully controlled rate through the pyloric valve to the small intestine. Absorption occurs as chyme is moved slowly through the small intestine, facilitated by coordinated segmenting and peristaltic motor activities, and enabled by the high-surface area of the lining mucosa. The large intestine, i.e., colon and rectum, is responsible for the absorption of water and salts and the compaction and excretion of waste, while also hosting a vast number and range of microbiota, the symbiotic and pathological roles of which has become an intense area of current research.⁵

The total transit time through the intestines is an important contributor to, and indicator of, digestive health. Rapid transit may contribute to diarrhea, dehydration and malnourishment, and prolonged transit may contribute to constipation, bacterial overgrowth and chronic symptoms of abdominal discomfort. Transit time and overall motility are therefore tightly regulated throughout the GI tract.

The small intestine begins beyond the pylorus and ends at the ileocaecal valve. Three parts are recognized, based on a gradient of structure and function: the duodenum, jejunum and ileum, together spanning ^~4-5 meters in humans. The duodenum is mostly retroperitoneal (lying beneath the abdominal cavity's posterior lining), whereas the jejunum begins at the ligament of Treitz, and lies free in the infracolic abdominal compartment in continuity with the ileum, hanging off a “curtain” of fat and blood vessels known as the mesentery.

Within the intestine, contents are generally propelled distally at a typical overall transit time of 3-5 hours,⁶ with a number of distinct motility patterns playing key roles.⁷ The most well-known pattern is peristalsis, which involves coordinated circular and longitudinal contractions, and which generates propulsion of chyme.⁸ Pendular and segmenting contractions also continuously occur in the fed state as non-propulsive contractions that are important for the mixing of chyme and enabling efficient absorption. Pendular contractions occur in longitudinal muscles, generating a ‘to-and-fro’ motion with the rhythm and direction determined by the underlying slow wave activity.^{9, 10} Segmental contractions, by contrast, are mediated by circular muscles,^{8, 11} and induce mixing of the digesta by splitting boluses without overall propulsion. In the post-prandial state, when vagal influence is high, these mixing motions become dominant.

At the cellular level, intestinal contractions are, in part, enabled by dihydropyridine-senstitive Ca²⁺ channels (Ca_v1.2).¹² In addition, neural and hormonal regulations, as well as stretch sensitivity,¹³ play key regulatory roles in GI smooth muscle activation. At the tissue level, pendular contractions are proposed to result from slow-wave initiated spike activities, which induce localized “patches” of smooth muscle activation, thereby limiting the propagation to a succession of narrow fixed functional domains.^{9, 10} Segmental contractions, on the other hand, were recently suggested to be facilitated by the summation of slow waves occurring within both the myenteric plexus and the deep muscular plexus, resulting in an elegant interplay that induces an overall waxing and waning of the amplitude of slow wave activity.¹¹

The large intestine (or colon) forms the last section of the digestive tract, and is relatively dilated compared to the small intestine, and with substantially slower transit of contents.¹⁴ Anatomically, the large bowel is divided into the cecum, ascending, transverse, descending and sigmoid colons, followed by the rectum and anal canal, at an overall length of approximately 1.5 m. In general, the proximal colon is principally concerned with fluid and salt absorption, while the distal colon is concerned with the compaction, storage and expulsion of feces.

THE VIRTUAL INTESTINE: A REVIEW OF CURRENT PROGRESS

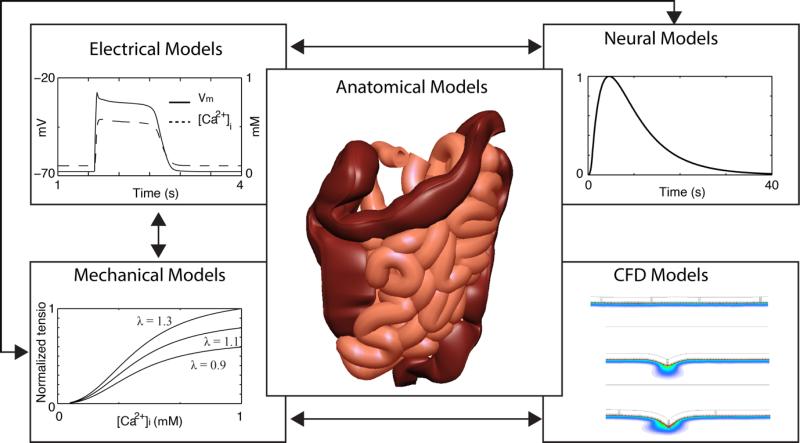
In many physiological fields, mathematical modeling studies have emerged as powerful platforms for investigating and integrating the structure, function and interactions of the underlying biological constituents. The need for such an integrative framework is now greater than ever. In the GI field, as is typical elsewhere, the vast outputs of reductionist biomedical science have continued to accelerate in volume and scope, necessitating a rational, systematic framework that can allow them to be quantitatively reintegrated to understand whole-organ function.¹⁵ In this review, a modeling framework of the Virtual Intestine is presented as illustrated in Fig. 1.

Figure 1.

The Virtual Intestine modeling framework. The arrows indicate directions of influence and links between the major components of the framework. Electrophysiological models are capable of simulating intestinal slow waves and calcium dynamics, which can be linked to electro-mechanical models to calculate intestinal motility. Neural models should also present a fundamental level of control, directly and indirectly co-regulating mechanical contractions, reproduced from Chambers et al.⁷⁷ Computational fluid dynamics (CFD) models can be linked to three different motility patterns to simulate flow of tracer inside a segment of intestine.¹⁰⁷ Further explanations of this simulation are provided in Figure 4. Finally, all functional models can be linked to geometric models with realistic anatomy.

Cellular Scale

Electrophysiological Models

Among the several factors co-regulating intestinal motility, a particular area of development in modeling has been electrophysiology, and especially regarding “slow wave activity”, a rhythmic electrical depolarization arising intrinsically within the gut wall. It is now well established that slow waves are generated and propagated by ICC, a class of electrically active pacemaker cells distributed in and between smooth muscle layers as an inter-connected syncytium.^{1, 16} The pattern, timing, and frequency of slow waves provides one key controlling influence of the patterns of GI motility, and there have been longstanding attempts to monitor and/or manipulate slow waves as a means to diagnose and treat digestive disorders, including in chronic nausea and vomiting, irritable bowel syndrome, and post-operative ileus.^17-20

GI electrophysiology has a rich history of slow wave modeling, with models directly informing understanding of control mechanisms for several decades.²¹ Early approaches employed “phenomenological” methods, i.e., chains of coupled relaxation-oscillators, which elegantly evaluated and explained excitation/refractory periods, “entrainment” or phase-locking among populations of cells, and the slow wave frequency gradient (discussed below).²¹ Indeed, coupled-oscillator models continue to be an informative tool for explaining emergent properties of ICC networks.²²

However, since the role of ICC became clearer, a more descriptive and fundamental type of model emerged - biophysically-based mathematical cell models, which explicitly quantify the mechanisms giving rise to slow wave activity, giving a new foundation to the Virtual Intestine.²³ Although Aliev et al. attempted to generate the first physiologically-realistic cell model, by adding meaningful parameters to coupled-oscillator models,²⁴ the first comprehensive biophysically-based model (based on specific ion current and intracellular formulations) was presented by Youm et al. in 2006.²⁵ Biophysically-based models are not only important for simulating the integrated functions of all cellular events, in order to understand whole-cell function, but they can also be used to test in-silico hypotheses regarding specific interventions such as electrolyte concentrations, drug effects, ion channel mutations, or electrical stimulation, and can be directly incorporated into multi-scale models (see sections below).^26-28

One of the major focuses of cellular models in recent years has been on interrogating the exact pacemaking mechanisms within ICC that generate slow waves.²³ This has allowed quantified assessment of ICC pacemaking theories, and/or has helped to identify the gaps in knowledge of the proposed mechanisms, providing an excellent example of applied mathematical cellular modeling.

Following Youm et al., a number of biophysically-based ICC models were developed based on the “non-selective cation channel” (NSCC) hypothesis.^29-32 This hypothesis detailed a close localized association between voltage-dependent NSCC channels and Ca²⁺ channels, and multiple “pacemaker units” (PMUs)^{23, 31}. The framework further suggested that calcium release from IP₃ operated stores in ER increases uptake of calcium in mitochondria, which then leads a localized reduction in calcium near the PMU, activating Ca²⁺-inhibited NSCC.²⁹ The activation of NSCC then led to the generation of a “unitary potential”, a fundamental pacemaker event that summates to generate the plateau period of slow waves.³⁰

In general, most of the recently proposed ICC models included a PMU mechanism to drive the self-excitatory behaviors of slow waves, and the coupling of the PMUs to underpin the entrainment of slow waves. The Corrias and Buist ICC model used a single PMU coupled with ER and mitochondria to present an aggregate of all the small PMUs in the ICC cytoplasm.³² The key PMU mechanism is a calcium-inhibited NSC current, I_NSCC, which is activated by a falling concentration of calcium in the PMU. Because the cell model used a single PMU, no unitary potentials were simulated in this model. The PMU model was coupled to nine specific ionic currents to simulate the whole-cell slow wave potentials.

Generation and entrainment of unitary potentials were studied by Faville et al. in a two component cell model.^{29, 30} The first component of the model was a unitary potential PMU model governed by an inward calcium current and I_NSCC, a plasma membrane calcium-ATPase and an onward sodium pump.³⁰ The calcium dynamic of the unitary potential model was adapted from the IP₃ model proposed by Sneyd et al., to simulate calcium release from the endoplasmic reticulum (ER) into the cytoplasm.³³ Four additional intracellular calcium fluxes, a mitochondrial calcium uniporter, sodium/calcium exchanger and cytosolic subspace calcium flux were coupled to the PMU model to simulate unitary potentials. The second component of the model proposed by Faville et al. was a whole-cell model incorporating multiple unitary potential PMUs to simulate summative intestinal slow waves.²⁹ Using ten PMUs, the Faville cell model was capable of simulating intestinal slow waves at a physiologically realistic frequency for small animal models of 17.4 cycles/minute.

Ultimately, however, the feasibility of the NSCC hypothesis was critically interrogated by Means et al. using a detailed mathematical model of spatiotemporal calcium dynamics between PMU, ER and mitochondria, and the hypothesis was found to be unrealistic.³⁴ The model introduced, for the first time, a sub-cellular geometric component of the three compartments to the analysis, coupled to calcium fluxes and diffusion between the compartments. To test the NSCC hypothesis, the authors tested a range of the densities (and hence the total rate of transport) of the various calcium transporters, particularly the SERCA pumps and the mitochondrial uniporters. The key result was that the calcium concentration in the PMU could not be reduced below the baseline levels under normal biophysical conditions.³⁴ It was only possible to achieve activation of NSCC by changing the mitochondrial uptake of calcium as a non-physiological, time-dependent uniporter. The simulation results of the restrictive conditions under which NSCC could be activated implied that I_NSCC is unlikely to be the major current responsible for the generation of slow waves in ICC.^{23, 34}

A more likely candidate for a key pacemaker current in ICC has emerged in recent years – a specific anoctamin 1 (Ano1, also termed TMEM16A) calcium-activated-chloride current.³⁵ Ano1 is abundantly expressed in all classes of ICC in human and murine GI tracts, and Ano1 knock-out mice demonstrate an absence of slow waves.³⁶ Ano1 currents are slow activating and outwardly rectifying at low concentrations of calcium, but at high concentrations of calcium, Ano1 activate rapidly with a linear voltage-current relationship. The Ano1 mechanism was recently incorporated into a mathematical cell model by Lees-Green et al., with microelectrode data recorded specifically from calcium-activated-chloride channels.³⁷ The modeled pacemaker cycle begins with calcium release from ER, which leads to activation of store-operated Ca²⁺ entry (SOCE) via SOC channels. Ano1 channels co-localized with SOC channels are simultaneously activated by increase in calcium in the micro-domains near the activated SOC channels, causing depolarization of membrane potential of ICC. The depolarization initiates the whole-cell slow wave activation via six ion currents. The pacemaker cycle concludes when influx of calcium via SOC and SERCA pump is sufficient to restore ER stores, resulting in the deactivation of Ano1 and SOC channels. The model has been applied to explore the dependence of the morphology of slow waves on E_Cl and identified potential candidates for currents supporting the plateau phase of slow waves.

The impressive scope of these developments, by several teams of investigators, from early coupled-oscillator approaches to detailed biophysically-based models incorporating the latest experimental data exemplify the critical role that integrative mathematical modeling can play in quantifiably testing hypotheses and theories, and in providing predictive in-silico data to inform experimental efforts.

Electromechanical Models

Beyond the experimental investigations and modeling efforts focused on ICC, a number of models have also now been developed to study mechanisms occurring within smooth muscle cells (SMC). As well as an ICC model, Corrias and Buist also presented a detailed model of gastric SMC activation, including the conductances contributing to membrane potential fluctuations (predominantly Ca²⁺ and K⁺), and intracellular Ca²⁺ dynamics.³⁸ Poh et al. also adapted the Corrias & Buist SMC model to simulate whole-cell slow waves in human jejunal SMC.³⁹ The SMC model included six ionic currents, one Ca²⁺/Na⁺ exchanger, one Na⁺/K⁺ pump, and the effects of two calcium buffering proteins, calmodulin and calreticulin. The SMC model was driven by a fitted slow wave representing the depolarizing effects of ICC.

Contraction of intestinal SMC has also now been explored in electromechanical modeling studies, evaluating intracellular calcium dynamics, with calcium binding to calmodulin and activation of myosin-light-chain kinase (MLCK).¹² To model these events, a quantitative description of active force generation in SMC was developed by Gajendiran and Buist by incorporating a two-module approach.⁴⁰ The first module models the activation of MLCK with its interactions with calcium and calmodulin, and the second module presents a four-state scheme describing myosin phosphorylation and cross-bridge formation between actin and myosin.⁴⁰ This model is able to relate force generation within SMC to a prescribed intracellular calcium activity. Du et al. later modified this model by coupling the intracellular calcium output from the Corrias and Buist ICC model to simulate a coupled electrometrical activation of SMC in a simple two-dimensional finite-element model.⁴¹

In a separate study, Young et al., recently applied the calcium and MLCK models in a discretized two-dimensional elliptical-shaped SMC with cytoskeletal and actin-myosin fibers.⁴² The total force experienced by the intestinal SMC was modeled using Newton's second law as the sum of the forces at each discreet point on the cell model. The model was applied to simulate the effects of edema on motility of SMC by decreasing the stimulus parameters of the IP₃ dynamic in the model.⁴³ The simulations predicted that edema could reduce motility by approximately 63-72%, which was validated by experimental measurements of rat intestinal tissue.⁴²

Tissue Scale

Tissue-Level Electrophysiology

Electrical recordings of GI slow waves have been conducted at the tissue and organ level since the early 1900's,⁴⁴ traditionally by applying a limited number of extracellular electrodes in linear configurations at sparse intervals along the intestine.^44-46 Foundational studies using this method outlined how slow waves normally conduct in-vivo in large animal models and humans, including describing how slow wave propagation is organized according to a “hierarchy’ of cellular frequencies, within “frequency plateaus” (explained further below).^{46, 47} However, due to a lack of spatial resolution in these methods, the conduction dynamics of slow waves, including pacemaker descriptions, and interactions between wavefronts at frequency plateau boundaries, as well as disease abnormalities, could not be reliably addressed.

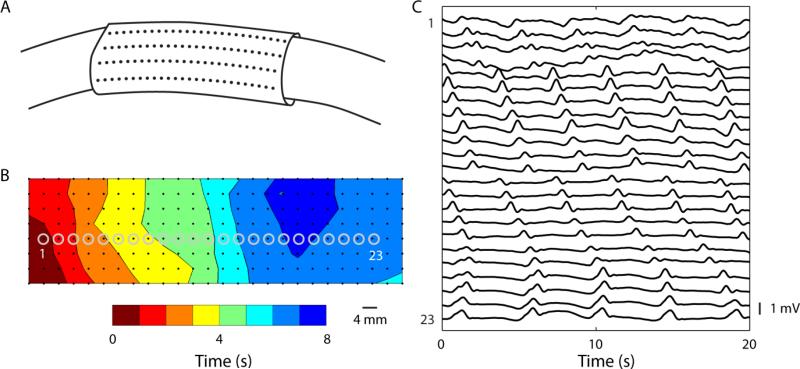
To overcome this limitation, Lammers et al. adapted high-resolution (HR) electrical mapping from the cardiac field to the GI field, whereby multi-electrode arrays were applied to map slow wave patterns in spatiotemporal detail.^48-51 Recent advances in HR mapping devices, amplifiers, and signal processing methods have been considerable, enabling greater efficiency in experimental outputs, and deeper insights into how intestinal slow wave patterns contribute to motility - although large knowledge gaps still exist, particularly in humans. The first intestinal HR mapping studies were performed with silver-wire electrode arrays encased in epoxy resin,⁴⁸ while flexible printed circuit (FPC) electrode arrays have more recently been used to study in-vivo slow wave events, enabling mapping around the intestinal circumference,^{50, 52} and paving the way for human translation.⁵³ Data is acquired from the multiple channels (typically >200 electrodes) at high sampling frequencies,^{48, 50} with semi-automated software packages playing an essential role in identifying and processing slow wave events (Fig. 2), including in diseased states.^54-57 Online visualization, classification and identification analytical tools are also becoming available, which have been applied during gastric studies, and are yet to be adapted to intestinal experiments.⁵⁸ Novel wireless recording techniques are under investigations, and have recorded intestinal slow wave activity,⁵⁹ which provide promise for long term monitoring of chronic slow wave activity.

Figure 2.

High-resolution mapping from (26×8 electrodes) from the porcine jejunum, distal to the ligament of Treitz. (A) The flexible electrodes were wrapped around the circumference of the intestinal serosa. (B) Intestinal slow waves were processed and displayed as activation (times) map, with red indicating early activation and each isochrone representing a 1 s interval of propagation. (C) Electrograms at 23 selected recording sites at locations labeled in B.

A particular area of focus concerning intestinal function, which has long been a focus of virtual models, has been the organization of the intestinal “frequency gradient”. Using extracellular electrodes, it has been shown that slow wave activity is arranged as a series of plateaus, with events in each plateau being “entrained” to the site of highest frequency, with stepwise frequency decrements then occurring from duodenum to terminal ileum (range in humans: ^~12 to 8 cycles/minute).^{47, 60, 61} Unlike gastric slow waves, which are entrained to a single frequency, the intestinal slow waves are organized into a series of plateaus of entrained frequencies with multiple pacemakers along the small intestine.^{45, 62, 63} The first intestinal pacemaker is located in the proximal duodenum, which is followed by additional pacemakers located in the distal portions of the intestine.^{45, 47, 51} Each pacemaker is capable of entraining a limited segment of the intestine, before entrainment ceases and the intrinsic activity of the next ICC takes over as a new pacemaker.⁴⁷ Dynamic interactions at the boundary between two adjacent entrained segments may contribute to an irregular “waxing and waning” of slow waves observed in recordings.^{22, 45}

Although the intestinal slow wave frequency gradient has been investigated for many years, the exact mechanisms of the gradient remain a source of enquiry. In an in-vitro analysis, Lammers et al. showed that slow waves could propagate the full length of the feline intestine, with frequency decrements due to “drop-out” of slow waves en-route, as conduction blocks occurred due to lengthening refractory periods in the aboral direction.⁶³ In-vivo, however, other mapping studies have demonstrated interacting peripheral pacemakers as the cause of frequency steps.^{22, 50, 51} In other recent work, intestinal slow wave dysrhythmias have also been described in detail in a number of animal species.^{48, 50, 51, 54, 63} These activities include conduction block, and functional re-entry, and a novel type of “circumferential re-entry”, i.e. re-entry occurring continuously around the anatomical circumference of the small bowel.^{49, 54}

Associated with the reduction in entrainment frequency in the aboral direction is a concomitant reduction in velocity of extracellular recordings.⁵⁰ For example, intestinal slow wave propagation velocity from the duodenum to the terminal ileum has been shown to decrease by approximately 90% in canines and by approximately 40% in pigs.^{50, 51} The decrease in velocity is not uniform, for example, a steep decrease in velocity was observed in the canine duodeno-jejunal junction,⁵¹ whereas the velocity was relatively more consistent over the long length of the distal porcine jejunum.⁵⁰ Similar to gastric slow waves,⁶⁴ intestinal slow wave also demonstrate anisotropy in propagation, with faster propagation in the circumferential direction than in the longitudinal direction.^{49, 65} A reduction in extracellular amplitudes is also correlated with the reduction in frequency and velocity, by approximately 70-75% over the length of the intestine^{50, 51}, although this may be partly a secondary phenomenon to the velocity gradient.⁶⁴

Another type of electrophysiological event in the intestine is known as spikes, which are true action potentials, superimposed during the plateau-phase of slow waves.⁶⁶ HR mapping studies by Lammers et al. have shown that spikes, or their corresponding events at the tissue level, can propagate independent of the direction of slow wave propagation, as “patches” within muscle layers themselves,^{67, 68} with highly accentuated propagation anisotropy.⁶⁹ Multiple HR mapping studies have demonstrated that the propagation of spikes is much faster than slow waves.^{63, 69} Furthermore, spatiotemporal mapping of contractions in the intestine reported that the length of contractile waves were consistent with the dimensions of spike patches, while the frequency was consistent with slow waves.⁷⁰ It has also been shown that multiple patches may occur simultaneously in a segment and lead summatively to motility in that segment.^{69, 71} Recent advances in detection and assessment of spike events may promote more investigations into these interesting, and partly unexplained, phenomena in future.⁵⁵

The enteric nervous system (ENS) also plays an essential role in modulating small intestinal motility patterns, however, a comprehensive discussion of these events is outside the scope of the present review, which is mainly focused on ICC and SMC electrophysiology. Based on previous spatiotemporal analyses, it is likely that one of the many functions of the ENS is to play a permissive role by causing smooth muscles to reach excitation in the presence of slow wave coupling to neighboring ICC.⁷⁰ Furthermore, it is also likely that different populations of ICC may mediate ENS innervation under different motility conditions. For example, in the colon, the sub-mucosal ICC play a mediating role with the enteric neurons that generate the haustral motility pattern, while the intracellular ICC play a role in mediating peristalsis.⁷

Previous attempts at using mathematical modeling to investigate the interactions between neurons and motility reflexes have been reviewed by Furness et al.⁷² Since then a number of detailed modeling studies have been conducted to simulate the interactions between after-hyperpolarization (AHP) and slow excitatory post synaptic potentials (EPSP) in large-scale networks of neurons,⁷³ detailed morphological features of enteric neurons, ⁷⁴ and further models of EPSP suitable for large-scale simulations.^75-77

A recent spatiotemporal imaging study by Janssen et al. used a cross-correlation technique to quantify the tangential and radial components of motility in a segment of intestine, in vivo.⁷⁰ Based on their findings, the authors concluded that neural inputs have a large degree of influence on the generation of spontaneous non-propagating segmental and pendular activities in the intestine.⁷⁰ Furthermore, the technique allowed detailed quantification of the frequency and propagation velocity of the contractile waves, which were in agreement with a previous electrical HR mapping study.⁴⁹

To better inform modeling, there is currently a critical need to translate all of the above types of investigations, concerning frequency gradients and plateaus, and slow wave velocities and amplitudes, and interactions between enteric nerves, slow waves, and motility, to humans, where detailed research is currently lacking. Another particular significant motility pattern, which has not yet received much attention in modeling, is the migrating motor complex (MMC), a multiple-phasic and high-amplitude sweeping contraction that occurs in the intestine during the fasted state, likely as a method to transport residual luminal debris distally.⁷⁸

Tissue Structural-functional Models

Another major recent focus of in-silico electrophysiological investigations at the tissue level has concerned the structure-function relationship between myenteric ICC networks and slow wave propagation. In a recent representative study, some of the aforementioned cell models have been applied in finite-element models of ICC-MY network structures reproduced from detailed images of ICC-MY network, obtained from the intestines of wild-type mice, and 5HT_2B receptor KO mice where ICC-MY populations are depleted.⁷⁹ The simulations predicted the degraded network in the KO had a significant impact on the direction and conduction pattern of slow wave propagation, as well as on current-density output and generated calcium concentrations,⁷⁹ which would together imply reduced and/or uncoordinated motility. These results are concordant with experimental observations noted in the stomachs of human patients with gastroparesis, with loss of ICC.⁸⁰

Until recently, one challenge in micro-structural ICC modeling was a lack of structural metrics to quantify normal and abnormal ICC networks. To overcome this problem, Gao et al. introduced six numerical metrics: density, thickness, hole size, contact ratio, connectivity and anisotropy.⁸¹ These metrics were applied to quantify the spatial rearrangement of ICC, finding that ICC networks in depleted samples from 5HT_2B receptor KO mice underwent remodeling with preferential alignment in the longitudinal direction,⁸¹ and also showed a novel pruning effect in ICC networks during post-natal development.⁸¹

Another challenge associated with realistic ICC network models approached by Gao et al. has been the limited spatial scale of imaged networks. This is particularly relevant to tissue-scale electrophysiological events, as development of intestinal dysrhythmias are shown to occur over a scale of tens of millimeters,^{49, 54, 82} whereas the typical field-of-view of confocal images are around 0.3 × 0.3 mm².^{79, 81} To overcome this problem, a stochastic algorithm (SNESIM) was introduced to generate virtual networks based on training from actual ICC networks.⁸³ The resulting virtual networks contained statistically the same structural information as the training network images and could in theory be extended to any spatial scales and ICC depletion levels.⁸⁴ A productive next step would be to apply these models to large scale questions arising from HR mapping studies concerning the genesis and maintenance of slow wave dysrhythmias.

A number of in-silico investigations have also focused on extended spatial analyses of intestinal slow waves. Lammers et al. developed an automata-based model to simulate the effects of ICC depletion on slow wave propagation in diabetic rats.⁸² When ICC depletion progressed, the delay in the time for intestinal slow wave propagation increased non-linearly, until it was completely blocked at 38% depletion.⁸² Interestingly, this value is roughly consistent with an apparent level of ICC decline determined in humans to be significant for inducing delayed gastric emptying in the stomach, although slow wave block does not occur uniformly at that level.¹⁷ More complex intestinal dysrhythmia formations, such as re-entry, is also now being studied. Based on HR mapping analyses of anatomical and circumferential re-entry, Angeli et al. proposed a series of equations relating the time it takes for the re-entrant wave to travel around the circumference of the intestine, linked to frequency and propagation velocity of slow waves.⁴⁹ A re-entry model in a segment of the intestine has also been achieved by Gizzi et al., using a number of FitzHugh–Nagumo type cell models and thermal coupling.⁸⁵ A common theme emerging from these in-silico studies is the complexity between the interactions of structure, ICC distribution, physiological variables such as temperature, and the roles of slow waves in initiating and maintaining intestinal dysrhythmias. In future work, it will also be necessary to consider the roles of and interactions between the major classes of ICC networks within the intestine, which have very recently been shown to interact in a specific manner to generate segmenting motor patterns.^{11, 86}

Whole-organ Models

To date, whole-organ models of intestinal function have received limited attention from mathematical modelers. Coupled-oscillator models continue to provide the major models for understanding slow wave propagation over an extended segment of the intestine.^{87, 88} In a large-scale application of the coupled-oscillator framework, Parsons and Huizinga recently evaluated the mechanisms of small intestine frequency plateau boundaries in terms of “fork and slip dislocations”, and found that gap junction inhibition increases the number of boundaries and decreases the velocity of contractile waves.²² The utility of coupled oscillators was also discussed in relation to “trigger waves”, and velocity in the absence or presence of frequency gradients.²²

While these models broadly reproduce the ICC network activity, and provide a computationally-efficient way to model the basic organization of intestinal slow waves over a long segment of the intestine (Fig. 3A), as pointed out above, they are limited in their ability to reproduce the detailed underlying physiology of slow waves due to their phenomenological nature, and cannot provide predictive responses to realistic experimental variables. Therefore, in future it will be important to promote alternative frameworks that also model the detailed and specific physiological events within ICC, as is being achieved in the stomach.⁸⁹

Figure 3.

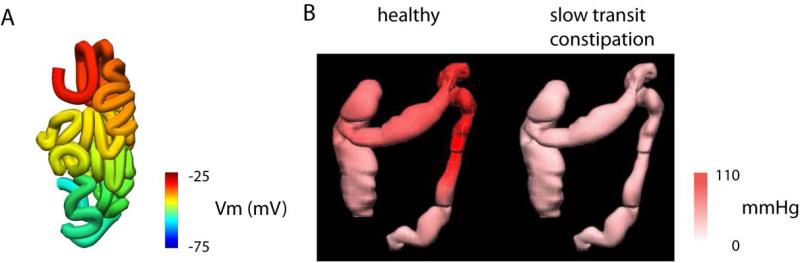
Small intestine and colon anatomically-based models. (A) A coupled-oscillator model applied in an anatomical model of the Visible Human small intestine.¹¹⁹ (B) A colonic model showing pressure information obtained using high-resolution manometric catheter from healthy subjects and slow transit constipation patients. In particular, the slow transit patients demonstrated lower pressures over time in the splenic flexure and descending colon compared to the healthy subjects.

Colonic Models

Colonic whole-organ electrophysiological modeling studies have been relatively limited to date, partly due to the added complexity of the organ. The colon involves a considerably more complex system than the small intestine, with greater co-regulation by enteric, autonomic, and central nervous system, offering fertile ground for applying modeling strategies to integrate function to quantitatively tests whole organ hypotheses.^90-92 The events underlying colonic pacemaking have recently been reviewed elsewhere,⁹³ and it is hoped that modeling may be productively applied in future to evaluate colonic organization hypotheses in future. Tissue-level electrophysiology studies will also have a useful role to play in the development of data to inform colonic models.⁹⁴

Models of Motility and Fluid Dynamics

Recent tissue-level in-silico investigations have been facilitated by the advances in extracellular recordings, and micro-structural and motility imaging techniques.^{22, 62, 83, 95,125} A productive next step will be to extend the spatial scales to longer segments and anatomically-realistic models of the intestine.⁹⁶ The new cell models detailed above,^{26, 37} and HR electrophysiological data, e.g., concerning propagation velocity and frequency gradient,⁴⁹ could be incorporated to represent a more physiologically-based sequence of intestinal slow wave propagations.

In emerging work, detailed models of slow wave propagation are also being applied to model gastrointestinal electromechanical coupling over large scales.^{97, 98} It would then be possible to use the mechanical deformations and force generations as boundary conditions to inform computational fluid dynamics (CFD) models of intestinal luminal mixing, generating horizontally-integrated multi-scale models of complete motility function.^{99, 100} For this to occur, it will also be necessary to develop and incorporate more realistic anatomical geometries, as has been achieved in the stomach.⁸⁹

In terms of understanding colonic motility, a recent and significant advance in humans has been the advent of high-resolution manometry, using fiber-optic sensor catheters, and video-analysis techniques.^{70, 101, 102} In particular, the use of high-resolution manometry and spatio-temporal imaging are leading to an improved understanding of intestinal function, and can therefore be expected to inform models of motility and fluid dynamics.¹⁰³ However, whereas high-resolution manometry was limited in its ability to identify segmental progression, the spatio-temporal technique on the colon could be used to distinguish both circumferential and longitudinal components of contraction. In another example of the application of whole-organ modeling, also in conjunction with high-resolution motility data, Davidson et al. applied an anatomically-realistic geometric model generated from the Visible Human Dataset (Fig 3B).^104,105 The finite element method was used to iteratively fit the surface of the colon to the data cloud digitized from the slices of cross-section images of the body, and manometry data was projected from the centerline of the model onto the surface of the colon model.¹⁰⁴ The modeling outcomes demonstrate highly effective integration of combined anatomical and physiological data, enabling rapid and intuitive representation of the complex overlay of colonic manometric data over time. One of the challenges is to relate the luminal pressure to deformation of intestinal wall, as captured by the high-resolution video analysis,⁷⁰ in a fully coupled mechanical model.

Computational fluid dynamics modeling has also already been applied to investigate intestinal luminal mixing. De Loubens et al used experimentally derived strain rate to simulate the mixing of the intestinal contents.⁸ The use of strain rates allows active contraction and passive stretch to be distinguished. Fullard et al., also used experimentally derived intestinal wall motions (or strain) to simulate the resultant luminal content flow.¹⁰⁶ This framework was then expanded to study the effects of combinations of longitudinal contractions and segmental contractions on luminal content, which was assumed to be incompressible and governed by the Navier-Stokes equation.¹⁰⁷

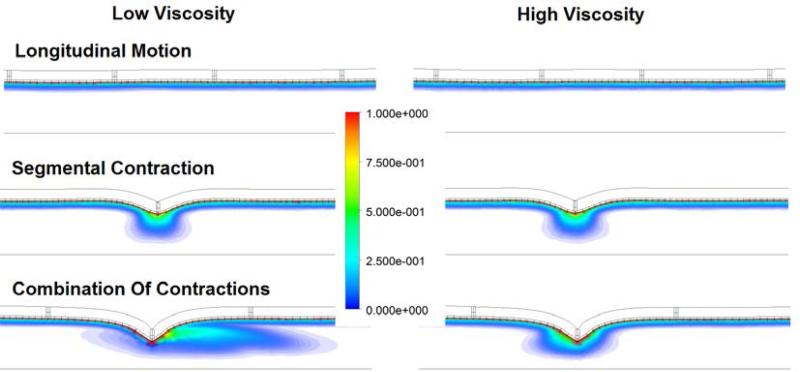
It was found that both the types of motion and viscosity of the content had a significant influence on mixing and transport (Fig. 4). Specifically, it was suggested by the authors that mixing of low viscous fluids was driven by intestinal wall motions, and mixing high viscous fluids was promoted mainly by segmental contractions of the intestine.¹⁰⁷ On the other hand, mesh-free methods, such as the smooth particle hydrodynamics (SPH) method, have also been applied to study luminal flow.¹⁰³ In the SPH method, each particle carries local deformation information in order to achieve coupling of fluid and luminal flow in the intestine. The deformation of the wall is then inferred from the integration, rather than being enforced. The model was used to show that descending inhibition could enable efficient transport for a compact region of content as well as reduced muscular work, even for partial occlusion of the lumen.¹⁰³ One potential way to validate these flow simulations is using particular image velocimetry to quantify movements of micro-particles, which better defines velocity gradients at the mucosa of the lumen.¹⁰⁸

Figure 4.

Numerical simulation of the diffusion of a tracer due to different types of contractions.¹⁰⁷ In each case, the tracer was initially located at the upper wall of the intestine. For a longitudinal contraction, the tracer was not transported any significant distance from the wall, regardless of viscosity. A segmental contraction was able to transport the tracer further into the lumen of the intestine, but there was little difference between a low or high viscous fluid. Finally, a combination of a segmental contraction and a longitudinal motion was the most efficient at transporting the tracer into the core of the organ, particularly in the case of a low viscous fluid. Figure courtesy of Drs. Luke Fullard, Wim Lammers and Maria Ferrua.

At a micro-scale level, Lim et al. used the lattice-Boltzmann method was to simulate and quantify flow and mixing of both Newtonian and non-Newtonian shear-thinning fluids at intestinal villi.¹⁰⁰ The simulation results demonstrated a significant increase in mixing and absorption of digesta as the displacement between the villi increased during longitudinal contraction. The dynamic formation of these micro-folds, as defined by Lentle et al.,¹¹⁰ could also influence intestinal content flow and mixing near the center of the lumen.¹⁰⁰ The lattice-Boltzmann method was also used to simulate flow of Newtonian fluid in the duodenum based on experimental imaging evidence.¹¹¹ The experimental data and CFD simulation in this case demonstrated that the pendular motility pattern best approached a continuously stirred tank reactor configuration rather than a plug flow reactor configuration.¹¹¹

Another factor influencing the CFD studies of intestinal flow is the actions of sphincters. To date most of the CFD models assumed simple sphincter conditions or fixed boundary conditions.^{106, 107} Sphincters serve important controlling functions to the transport of luminal content through the GI tract. Similarly, the gastro-duodenal junction and anal sphincter are tightly regulated by neuromuscular functions. Heldoom and Marani provided a detailed review of the common urethral sphincter models developed in the past.¹⁰⁹ These models mostly related flow rate or pressure parameters to the rate of change in volume or cross-sectional area. Incorporation of a more realistic sphincter boundary condition is an important next step in intestinal CFD analysis.

Non-invasive Recording and Modeling Techniques

In-silico investigations have also closely complemented the development of far-field recording techniques of intestinal slow waves. In particular, the use of cutaneous electrodes to measure the “electroenterogram” (EENG) and the use of non-contact magnetic field sensors (the superconducting quantum interference device, or SQUID) to measure the “magnetoenterogram” (MENG).^{112, 113} Both of these techniques have yet to achieve significant clinical translation, primarily because of the relatively low-signal to noise ratio of these recordings, and the limited ability to directly relate the recorded events occurring within the intestine; however, they remain an interesting ongoing focus of applied research.

At present, detection of dominant frequency component remains the standard analysis technique for these non-invasive methods.^{114, 115} One approach is to analyze the spatial variation information provided by multi-sensor arrays (as has been conducted in stomach in 29 sensors) over the abdomen,^{116, 117} and the derived signals relate it to activation of the underlying organ.¹¹⁸ Another advance would be to compute the equivalent dipole of the intestinal slow wave activity and then calculate the resultant magnetic field in a forward approach.¹¹⁹ To date, the simulated magnetic field has only been compared to SQUID recordings of the stomach.¹²⁰. As more recordings have become available, anatomical information and gradients in membrane potentials have been shown to also exert a significant effect on the MENG.¹²¹

CONCLUSIONS AND CLINICAL IMPLICATIONS

Our knowledge of intestinal electrophysiology and motility has made major strides in the last two decades, facilitated by advances in experimental recording methods, but also increasingly enabled by advances in in-silico tools. Mathematical modeling offers a powerful tool to deeply integrate and interrogate cellular events, including ICC electrophysiology, and these models will continue to be refined as further experimental data are generated. Future directions also include applying such models in specific clinical investigations, such as the effects of channelopathies on cellular functions, which may play a role in irritable bowel syndrome.¹³ This approach was successfully pioneered in a recent study in which the effects of sodium channel mutations were quantitatively assessed in gastric ICC and SMC models,²⁶ with significant implications for the stretch-sensitive activation of these channels and therefore motility functions.¹²²

At the tissue and organ levels, key questions regarding the organization of intestinal slow waves remain relevant and could be further investigated, particularly in humans. The interactions between the different ICC networks and the resultant dynamics of slow wave propagation are challenging aspects to investigate experimentally, and models will prove helpful.⁸⁶ New electromechanical models and mechanical models will also offer a direct way to validate simulation results against experimental and imaging data. Once validated, such models can also be used to predict the impacts of slow wave dysrhythmias and/or altered neural input into motility disorders, and even the subsequent effects on mixing and transit through CFD studies. Furthermore, the CFD simulations can be validated using HR spatiotemporal imaging studies coupled with a chemical engineering dye tracing method.^{8, 10} These methods have been successfully integrated as a basis for modeling studies.^{10, 111} Such integrated models hold potential to contribute to the understanding of diverse diseases including irritable bowel syndrome, diabetic intestinal dysfunction and chronic mesenteric ischemia.^{54, 113}

Across larger tissue scales, there is an increasing need for a framework of large-scale simulations, similar to those applied in enteric nerves modeling,⁷³ and with simplified intestinal slow wave models to allow computational efficiency, similar to gastric slow wave modeling.¹²³ Furthermore, there is a need to utilize internet-based database to disseminate large-scale data sets and mathematical models,¹²⁴ which will facilitate medical science with inter-disciplinary teams. In addition, further experimental recordings and their analysis will continue to be a key tool to inform accurate in-silico modeling of the Virtual Intestine. An assortment of bio-electrical signals co-exists in the intestine, including slow waves and spikes, with varying morphology and frequency along the intestine. Signal processing and analysis techniques will need to take into account these variations, when methods are applied to quantify data for clinical translation or physiological applications.

In summary, these examples and other emerging work on intestinal functions not able to be covered in this review, demonstrate the emerging potential of the Virtual Intestine to address multi-scale modeling research challenges in interdisciplinary gastrointestinal sciences.

Further Reading

Szurszewski, J.H., 1998. A 100-year perspective on gastrointestinal motility. Am. J. Physiol., 274(3 Pt 1), pp.G447–53.

Lammers, W.J., 2013. Arrhythmias in the gut. Neurogastroenterol. Motil., 25(5), pp.353–357.

Cheng, L.K., Pullan, A.J. & Farrugia, G., New Advances in Gastrointestinal Motility Research. Springer Netherlands, 2013, 266.