Abstract
For children to build a knowledge base, they must integrate and extend knowledge acquired across separate episodes of new learning. Children’s performance was assessed in a task requiring them to self-generate new factual knowledge from the integration of novel facts presented through separate lessons in the classroom. Whether self-generation performance predicted academic outcomes in reading comprehension and mathematics was also examined. The 278 participating children were in grades K-3 (mean age 7.7 years; range 5.5–10.3 years). Children self-generated new factual knowledge through integration in the classroom; age-related increases were observed. Self-generation performance predicted both reading comprehension and mathematics academic outcomes, even when controlling for caregiver education.
Keywords: knowledge extension, academic performance, self-generation
A major goal of education is to accumulate a knowledge base. Educators employ many strategies to engage learners in knowledge acquisition, including direct tuition, project-based learning, and tests, to name a few. Importantly, to accumulate knowledge over the educational career, learners must not only learn from individual episodes of experience, but also integrate classroom lessons with one another across time and medium. Moreover, to accumulate knowledge quickly and efficiently and thereby foster academic achievement, they also must go beyond what is directly given in learning episodes to self-generate novel understandings. They also must retain the newly derived knowledge over time. It has been established that under controlled laboratory conditions, children as young as 4 years productively extend their knowledge base through integration of separate lessons of new learning (Bauer & San Souci, 2010). They also remember the new information over a delay (Varga, Stewart, & Bauer, 2016), as do 6-year-olds (Varga & Bauer, 2013). The assumptions that children engage in these processes across classroom learning episodes, and that the processes contribute to academic performance, have not been tested, however. Accordingly, in the present research, we tested 5- to 9-year-old children’s self-generation of new factual knowledge through integration of separate yet related episodes of new learning in the classroom, and how performance relates to academic achievement.
Both within and outside the classroom, learners of all ages engage in productive processes such as analogy, deduction, induction, and textual inference, for example (e.g., Gentner, Loewenstein, & Thompson, 2003; Goswami, 1992, 2011; Paris & Upton, 1976; Perret, 2015). Without these productive processes, learning would proceed slowly, as each and every bit of information is acquired individually. For example, in teaching addition, rather than explicate each specific equation individually, teachers instruct that addition is an operation applied to an infinite combination of numbers. Because of the capacity of productive processes to foster rapid and efficient accumulation of knowledge, they are assumed to be a major mechanism of cognitive development (Bauer, 2012; Bauer & Varga, 2016; Brown, 1982; Siegler, 1989).
Consistent with their status as mechanisms of cognitive development, productive processes have been observed even in very young children (e.g., Singer-Freeman & Bauer, 2008; see Goswami, 2011, for a review). For example, infants in the second year of life extend the properties “drinks from a cup” to novel animals but not to novel vehicles, and “starts with a key” to novel vehicles but not to novel animals (Mandler & McDonough, 1996). There also are age-related increases in the efficacy of productive processes, such that relative to younger children, older children engage in them more consistently (Goswami, 2011). Developmental changes are attributed in part to increases in general abilities such as working memory and inhibitory control (i.e., the ability to ignore distractors; Crone et al., 2009; Goswami, 2011).
In addition to increases in general cognitive abilities supporting productive processes, older children have had more experiences contributing to their knowledge base. Productive processes, such as transfer through analogy, are more likely when children understand the underlying concepts (Brown, 1989; Gentner, Loewenstein, & Thompson, 2003). For example, physics students who already understand how water flows can use that analogy to understand electricity concepts (Gentner & Gentner, 1982). This type of transfer is limited to situations in which there is an appropriate already well-known model that can be accessed and, like other productive processes, is highly dependent on surface similarity, especially in novice learners (Brown, 1989; Gentner, 1989; Gentner, Loewenstein, & Thompson, 2003).
Encouraging productive self-extension of knowledge is one of the foundations behind “discovery learning” models, in which children are active participants in building their own knowledge base through experience (Mayer, 2004; Sobel & Sommerville, 2010). A meta-analysis on discovery learning showed that unassisted discovery learning (i.e., when children are provided no guidance), does not have an advantage over explicit instruction (Alfieri, Brooks, Aldrich, & Tenenbaum, 2011). However, when discovery learning is guided with feedback and worked examples, children have higher rates of learning (Alfieri, Brooks, Aldrich, & Tenenbaum, 2011).
Importantly, in terms of the question of how a knowledge base accumulates over time, the existing literatures on productive extension of knowledge are not fully informative, for three primary reasons. First, in many cases, the material over which the processes are tested is not representative of the factual content of a knowledge base. Instead, it is of arbitrary relations that are not intended to correspond to real-world semantic knowledge. For example, in a study of inductive reasoning, Schulz, Goodman, Tenenbaum, and Jenkins (2008) showed preschool-age children a series of block combinations. Some block combinations emitted a sound (such as a train whistle) whereas others were inert. Immediately after the demonstration, children were tested to determine whether they could induce the composition of unseen block combinations based on whether they emitted a sound. The task taps children’s understanding of basic causal principles; the information used to induce the principles is not expected to add to factual knowledge of blocks or whistles or trains, however.
The second reason the existing literatures on productive processes are not fully informative of the question of how a knowledge base accumulates over time is that many studies test the processes within a single episode of experience. Prime examples are studies of inference in textual material, in which clauses or sentences within a single text are integrated in the service of making inferences regarding information that the text only implies (e.g., Cain & Oakhill, 1999; Graesser, Singer, & Trabasso, 1994; Paris & Upton, 1976). Some types of inferences maintain textual integrity through integration of information to understand anaphoric reference, for example. Other types of inferences permit filling of gaps in the text through recruitment of information from beyond it (i.e., background knowledge) to understand information only implicit in the text. Importantly, whereas these paradigms examine productive extension within an episode of experience (e.g., a single text passage), they do not test integration of information across separate learning episodes (e.g., across different text passages).
The final limitation of the existing literature in terms of the question of how a knowledge base accumulates over time is that studies do not test the persistence of newly-derived factual knowledge in memory. In some cases, such as textual inferences just discussed, newly-derived information is explicitly assumed to be short-lived. That is, most textual inferences are thought to survive in working memory only long enough to aid comprehension (McKoon & Ratcliff, 1992). In paradigms that test deductive, inductive, and analogical reasoning (e.g., Shafto, Kemp, Bonawitz, Coley, & Tenenbaum, 2008; Viskontas, Morrison, Holyoak, Hummel, & Knowlton, 2004), newly-derived information could in principle be retained over time and become incorporated into the knowledge base. Yet whether this potential is met has not been a focus of research attention.
A paradigm that has all three of the features to model accumulation of a knowledge base over time is one in which children are challenged to self-generate and retain new factual knowledge through integration of separate yet related episodes in which they learn true but previously unknown information. In the laboratory, this process has been operationalized in a story-passage paradigm in which children are read picture-book style text passages that have distinct characters, plots, and settings, and which are separated in time by other activities. Each story passage conveys a true but previously unknown fact (i.e., a “stem” fact – not to be confused with STEM facts: the “stem” facts in the story-passage paradigm are not necessarily facts from science, technology, engineering, and math). The children then are asked questions that can be answered by generating a novel fact based on integration of pairs of related text passages (i.e., an “integration” fact). In the first laboratory test of this productive process, Bauer and San Souci (2010) tested 4- and 6-year-old children in two within-subject conditions. In the 2-stem condition, children were read both members of a pair of related text passages, each of which contained a true but previously unknown fact (e.g., dolphins live in groups called pods; dolphins talk by clicking and squeaking). The facts were related to one another such that if integrated, they could be used to self-generate new factual knowledge (i.e., pods talk by clicking and squeaking). In a 1-stem condition, children were read only one member of the pair of text passages necessary to self-generate the integration fact. As a consequence, they were not expected to produce the novel integration facts.
In the 2-stem condition, in open-ended testing, 4-year-olds self-generated the novel integration facts on 13% of trials. They did not produce the novel integration facts on any of the 1-stem trials. Four-year-olds had higher levels of productive extension of knowledge in forced-choice testing in which they selected the novel integration facts on 62% of trials, compared to only 33% of trials in the 1-stem condition (3-alternative forced-choice: 33% expected by chance). In the 2-stem condition, in open-ended testing, 6-year-olds produced the integration facts 67% of the time compared to only 17% of the time in the 1-stem condition. The fact that children had low levels of performance in the 1-stem control condition—in which they had no opportunity for integration—makes clear that exposure to both stem-facts was necessary for production of the novel integration facts.
Subsequent research has confirmed age-related increases in self-generation of new knowledge through integration. Bauer and Larkina (2016) tested 4-, 6-, and 8-year-old children in both 2-stem and 1-stem conditions. In the 2-stem condition, in open-ended testing, 4-, 6-, and 8-year-olds generated the novel integration facts on 13%, 50%, and 75% of the trials, respectively. Open-ended performance in the 1-stem control condition was 0% for all three age groups. This study provided additional evidence of age-related increases in self-generation of new factual knowledge through integration of separate learning episodes. It also provided further confirmation that production of novel integration facts depends on exposure to both members of pairs of related stem facts.
Laboratory studies also make clear that newly self-generated information is retained over time and becomes incorporated into the knowledge base. In Varga and Bauer (2013), 6-year-olds self-generated novel integration facts on 63% of trials in open-ended testing. They returned to the laboratory 1 week later and were tested for recall of the self-generated facts. They recalled 60% of the facts, evidencing virtually no forgetting. A similar pattern was apparent among 4-year-olds when both open-ended and forced-choice testing was considered. That is, 4-year-olds generated or selected novel integration facts on 60% of trials. One week later, they had the same high level of performance, exhibiting no forgetting over time (Varga et al., 2016; Experiment 1). Finally, research with adults provides evidence that newly self-generated factual information rapidly becomes incorporated into the knowledge base. In Bauer and Jackson (2015), adults participated in an event-related potential (ERP) study in which, after exposure to stem facts, they read a series of declarative sentences, some of which conveyed information formed through stem-fact integration. Based on a 400ms presentation, ERP responses to the novel integration facts were intermediate between responses to well-known facts (e.g., “Washington DC is the capital of the USA”) and responses to entirely novel facts. Based on a second 400ms presentation, the response became indistinguishable from that to facts that were well-known. The rapid transition of newly self-generated facts to the status of “well-known” suggests that the new information had become incorporated into the knowledge base.
To date, the process of self-generation of new factual knowledge through integration of separate yet related episodes of new learning has been tested only in the laboratory. Critically, the demand for this productive process is high outside the laboratory as well, especially in the typical ecological niche of the child—the classroom setting. In the classroom, children routinely are posed with the challenge of acquiring new information embedded within rich episodic contexts, such as stories. Picture books are used as a teaching instrument because they are engaging and children learn from fictional stories and rapidly incorporate the material into the knowledge base (Walker, Gopnik, & Ganea, 2015). Children are expected to learn not only within a given story, but to integrate content across stories (or other sources) as well. In fact, requirements to integrate across texts and data representations, both within and across content areas, are part of the Common Core State Standards (adopted by 42 states, the District of Columbia, and 4 territories; www.corestandards.org). By Grade 3, students are expected to “integrate knowledge and ideas” across “two different texts on the same topic,” with similar expectations for data representations (e.g., graphs). Though educational episodes are distinct and separated in time by intervening activities, learners are expected to integrate the presented facts in the classroom, just as they are in the text passage paradigm utilized in the laboratory.
Learners also are expected to go beyond what was directly given to self-generate novel understandings. For example, having learned that the movement of tectonic plates produces jagged mountains, and that the Appalachians are jagged mountains, learners may be expected to infer that the Appalachians were produced by the movement of tectonic plates, a fact not previously directly learned. This type of productive extension likely is a key to academic success, contributing as it does to rapid and efficient accumulation of knowledge (Bauer, 2012). As such, individual variability in the process of self-generation through integration can be expected to relate to academic achievement. Indirect evidence consistent with this prediction comes from laboratory tests with 7- to 10-year-olds (Bauer, Blue, Xu, & Esposito, 2016). Children either read or were read facts by an experimenter in the process of a board game. As in the story-passage paradigm described above (Bauer & San Souci, 2010), members of pairs of related stem facts could be integrated to support self-generation of new factual knowledge. Children also completed the Woodcock Johnson III Test of Cognitive Abilities Passage Comprehension task (Woodcock, McGrew, & Mather, 2001). Performance on the self-generation through integration task was related to reading comprehension; the relation obtained regardless of whether the facts were self-read or other-read. The present research will provide a direct test of relations between self-generation of new factual knowledge through integration of separate learning episodes and a wider range of tests of academic performance used by schools to track progress and make decisions about promotion to higher grades.
In the present research, we examined the productive process of self-generation through integration in the classroom context. We tested children in kindergarten, first, second, and third grade classrooms (ages 5 to 9 years). Across this age range, we expected to observe both age-related and individual variability in performance. Based on the logical arguments above, we further expected to observe relations between the productive process and academic achievement. We selected the wide age (and grade) range because laboratory studies have found the period of early childhood to be one of rapid development in self-generation through integration performance (e.g., Bauer, Blue, et al., 2016; Bauer & Larkina, 2016; Bauer & San Souci, 2010). The period is also when formal instruction begins in the United States. This allowed us to examine self-generation through integration of separate episodes across the first years of formal education. As has been observed in the laboratory (e.g., Bauer & Larkina, 2016; Bauer & San Souci, 2010), we expected age-related variability in performance, such that older children would show high levels of self-generation relative to younger children. In light of the fact that classrooms feature greater variability relative to the typical laboratory samples, we were prepared to observe overall lower levels of performance. Specifically, whereas the laboratory research on self-generation through integration has been primarily with children from middle- to upper-middle socioeconomic status, the classroom environment in which the research was conducted features a wider range of economic and educational privilege. To test the hypothesis that self-generation of new factual knowledge through integration of separate episodes of new learning relates to academic achievement, we collected academic performance data utilized by the schools to assess academic achievement in two different areas of performance: reading comprehension and mathematics.
The present work expands the existing literature by moving examination of self-generation of new factual knowledge through integration of separate episodes of new learning into the classroom and assessing the relations between self-generation of new factual knowledge and academic performance. The racially and ethnically diverse community sample extends the work not only beyond the laboratory, but also into a demographic that is representative of the general population.
Method
Participants
The participants were 278 (145 female; 133 male) typically developing students in kindergarten (n = 56; M = 6.08 years; range = 5.5–6.92 years), first grade (n = 72; M = 7.17 years; range = 6.58–7.92 years), second grade (n = 80; M = 8.17 years; range = 7.58–9.83 years), or third grade (n = 70; M = 9.17 years; range = 8.58–10.33). The children all attended school in a rural public school system in the southeastern United States. The children in kindergarten and 1st grade attended one school and the children in 2nd and 3rd grades attended a different school in the same district. Consent forms were sent home through parent communication folders (the typical means of communication between the school system and students’ parents/guardians). Only the children whose parents/guardians returned signed consent forms were included (approximately 52% of the population). Reflecting the diversity of the community, based on parental report, the sample was 45% African-American, 40% Caucasian non-Hispanic, 11% Caucasian Hispanic children; the racial/ethnic background of the remaining 4% was unknown. Approximately 87% of children in the community qualify for federally funded school lunch assistance. Of the 129 participants whose families reported caregiver education, 22% had a high school education or less, 33% had some training beyond high school, 20% had a technical or associates degree, and 20% had a college bachelor degree. Participating parents and teachers were thanked with a $10 gift card to a local merchant and participating children were thanked with a small school supply item (e.g., eraser). The institutional review board reviewed and approved all study protocol and procedures.
Stimuli
The stimuli were two novel “stem” facts from each of four domains: dolphins, palm trees, volcanos, and kangaroos. Within each domain, the two novel stem facts were related and could be combined to generate a novel integration fact. The stem and integration facts all had been used in prior related research in the laboratory (e.g., Bauer & Larkina, 2016; Bauer & San Souci, 2010; Varga et al., 2016); the present research was the first use of the stimuli and paradigm in the grade-school classroom. All facts were accurate and determined by prior research to be novel for children in the target age range.
The stem facts were featured in text passages resembling picture stories (see Bauer & San Souci, 2010, for an example text passage). The passages were 81 to 89 words in length, distributed over 4 pages. Each page consisted of a hand-drawn illustration depicting the main actions of the text; the text was not featured on the page. The passages were similar in structure: in each passage, a character (e.g., a ladybug) learned a true but novel fact in the course of a short story. Only the stem facts were included in the passages; the integration facts were not presented. For classroom use, the text passages were presented in digital book format. Each illustration was scanned into a PowerPoint® slide. The text passages were recorded by a native English speaker.
There were two different versions of the stimuli; the versions differed only in terms of the story characters (i.e., the content of the stories was the same). Children in Grades K and 1 had high surface similarity text passages, such that, within a pair of related stem-fact story passages, the characters that learned the novel facts were the same (e.g., a ladybug as the character in two text passages conveying 2 stem facts about dolphins). Children in Grades 2 and 3 had low surface similarity text passages, such that, within a pair of related stem-fact story passages, the characters that learned the novel facts were different (e.g., a ladybug in one text passage about dolphins and a lamb in the other text passage about dolphins). The two levels of surface similarity were constructed to ensure optimal levels of challenge for the age groups. Young children often depend on surface similarities while acquiring new information whereas older children are less likely to need this assistance (Brown, 1989; Gentner, 1989). Based on prior laboratory research, the design would avoid floor and ceiling effects (Bauer, King, Larkina, Varga, & White, 2012; Bauer & Larkina, 2016).
Measures
The school provided demographic information on each participating child whose parents provided consent. Information provided was gender, birthdate, race/ethnicity, and native language. Parents had the option to complete a questionnaire that provided information on household demographics, including caregiver education, a critical socio-economic component for development (e.g., Hoff, 2013).
Guidance counselors provided the year-end reading comprehension and math assessment results in June of the year of classroom and individual data collection. The reading comprehension measure used in the school system is the mCLASS: Text Reading Comprehension (TRC), an individually administered measure of reading fluency and comprehension of leveled readers. This measure was chosen for analyses because it is obtained in each of the grade levels of this study and represents a global reading performance evaluation. It is also a continuous measure in which higher grades have higher scores than lower grades, showing growth from K-3. The measure also has high ecological validity in that grade-level performance on the measure is one option for meeting the state requirement to show proficiency in reading. The school system did not have a math achievement measure that is consistent for all grade levels. For children in grades K-3, we recorded the cumulative score on final assessments based on mastery of Common Core State Standards. The score is not continuous and is reported as percentage of mastery of the Common Core State Standards for that grade. For 3rd grade, we also recorded the performance on the North Carolina End-of-Grade standardized math test. This assessment has a range of 421–473.
Procedure
Children were tested in groups in their classrooms. All testing was done by the first author, accompanied by a research assistant. The 45-minute classroom sessions were divided into three phases: (1) exposure to the first set of true but previously unknown stem facts, (2) exposure to the second set of true but previously unknown stem facts, and (3) test for self-generation of new factual knowledge through integration of pairs of related stem-facts.
In Phase 1 (exposure to the first set of true but previously unknown facts), students heard 1 text passage from each of 4 domains (dolphins, palm trees, volcanos, and kangaroos). Each text passage conveyed a stem fact that was true and was unlikely to be known by the students. The illustrations conveying the main actions of the passages were projected onto the classroom screen (approximately 4′ by 6′). The pre-recorded audio tracks were played through speakers. After exposure to four stem-fact passages, children engaged in an unrelated buffer activity for approximately 10 minutes.
Phase 2 commenced after the buffer activity. The children heard the second member of each stem-fact story pair, one from each of the 4 domains. For both Phase 1 and Phase 2, the slides and audio were advanced automatically, ensuring consistent timing across classrooms. The text passages within domains were counterbalanced and domains were presented in one of 4 predetermined random orders; each order was used approximately equally often across classrooms. Following Phase 2, children engaged in a second 10 min buffer activity.
Phase 3 tested for generation of new factual knowledge and recall of stem facts. All children were provided with a test packet. Each portion of the testing procedure was presented on one page of the packet. The first page tested production of integration facts through open-ended questions (a blank space was provided for children to write their answers). The second page tested open-ended recall of the individual stem facts. The third and fourth page asked the same integration and stem fact questions, respectively, in forced-choice format. Each question had three answer choices from which children were to choose by circling their preferred answer. The first author read each question aloud while she and a research assistant circulated through the classroom to ensure students were following along, not moving backwards through the test material, and recording their answers. The integration and stem fact questions were presented in one of 4 pre-determined random orders; each order was used approximately equally often across classrooms and text passage orders.
In advance of the test, students were told to do their best on spelling and that incorrect spelling would not count against them. To prevent students from seeing one another’s answers during the test, students worked behind desk shields commonly used in the classroom. Although the researchers anticipated students might speak aloud during testing, no student did. We also anticipated that children, especially in the lower grade levels, would need assistance in writing their answers. However, the instructions to “write the sounds you hear” were sufficient such that only a few children asked for assistance, with even the kindergarten children able to provide enough information for the answers to be scored with confidence (e.g., “clking and swkeeking” for “clicking and squeaking”).
Scoring
Children received 1 point for each correct response. Thus they could score up to a 4 in open-ended testing of the integration fact questions and up to 4 in forced-choice testing of integration fact questions. They could score up to 8 in each of open-ended and forced-choice testing of the stem-fact memory questions.
Results
The results are reported in three sections. First, we describe students’ self-generation of new factual knowledge through integration and memory for stem facts, both open-ended and forced choice. Second, we report correlations between self-generation of new factual knowledge through integration and academic performance. Third, we present regression models predicting academic performance. All analyses were conducted using SPSS Statistics package (Version 23). For all effects described as significant, statistical tests were two-tailed and p < .05.
Self-generation and stem fact memory performance
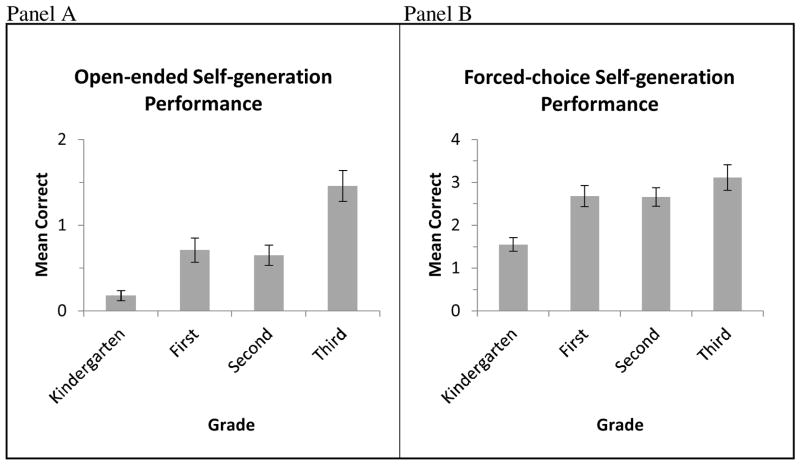
Levels of self-generation of new factual knowledge through integration of separate yet related episodes of new learning are depicted in Figure 1. The mean numbers of novel integration facts produced in open-ended testing by grade are depicted in Figure 1, Panel A. Kindergarten performance was nearly at floor whereas 3rd graders were correct on an average of 1.5 of 4 trials. The observed range was 0–4 in all grade levels with the exception of K, where it was 0–2. To examine the patterns statistically, we conducted a MANOVA with Grade predicting dependent variables derived from the self-generation through integration and stem fact test (open-ended and forced choice). However, significant results of both Levene’s and Box’s test indicated that the assumption of homogeneity of variances and covariances were violated.
Figure 1.
Mean correct open-ended (Panel A) and forced-choice (Panel B) production of novel integration facts. Error bars are standard error.
We employed the non-parametric Kruskal-Wallace H test that analyzes rank score, with follow-up Dunn’s tests as an appropriate replacement for ANOVA with Bonferroni corrections that does not have the assumption of normality or equivalent distributions (Dinno, 2015; Dunn, 1961; Kruskal & Wallace, 1952). The test showed there was a statistically significant difference in open-ended performance on the self-generation task between grade levels, χ2(3) = 33.75, p < 0.001, with a mean rank score of 105.62 for kindergarten, 134.40 for 1st grade, 135.41 for 2nd grade, and 176.54 for 3rd grade. Follow-up comparisons were made with Dunn’s test to control for familywise error. Third graders had significantly higher performance than children in all other grades, which did not differ from each other, zs < −41.13, ps < .002.
Children’s performance in forced-choice testing by grade is depicted in Figure 1, Panel B. A paired sample t-test revealed significantly higher performance in forced-choice testing (M = 2.55, SD = 1.27) compared to open-ended (M = 0.77, SD = 1.20), t(277)= −23.51, p < .001. The observed range in performance was 0–4 at all grade levels. As suggested by inspection of the figure, performance differed by grade, χ2(3) = 49.80, p < 0.001, with a mean rank score of 78.11 for kindergarten, 149.28 for 1st grade, 144.86 for 2nd grade, and 174.29 for 3rd grade. Dunn’s follow-up comparisons revealed that kindergarteners had significantly lower performance than all other grades, which did not differ from each other, zs < −66.75, ps < .001. Moreover, whereas for Grades 1, 2, and 3, forced-choice performance was significantly different from chance (33% or 1.33), ts > 8.76, ps < .001, for children in kindergarten, performance did not differ from chance, t(55) = 1.55, p = .13. In summary, performance on open-ended self-generation through integration questions was variable but generally low, especially in grades K-2. Children had higher performance in the forced-choice condition at all grade levels, but performance in K was lower than the other grades and did not differ from chance.
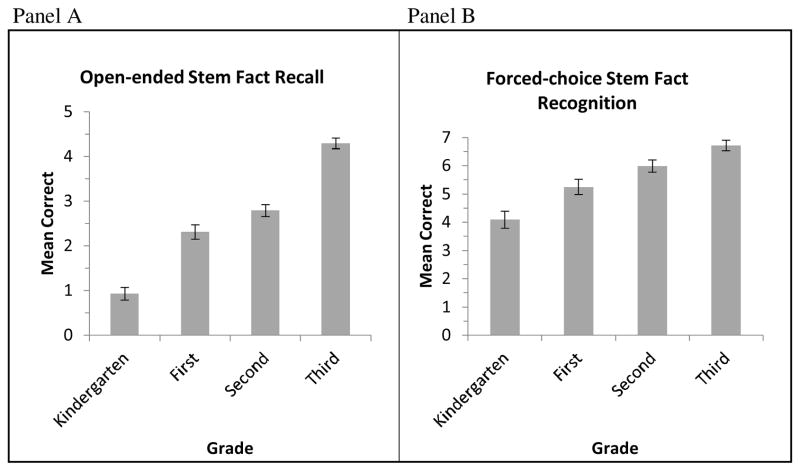
Stem fact performance by grade is reflected in Figure 2, Panel A (open-ended) and Panel B (forced-choice). Children’s scores on open-ended recall of the stem facts in Grades 1 and 3 encompassed the full range of the measure, 0–8. The range for K performance was 0–4 and 2nd grade performance was 0–7. Children’s open-ended recall of the stem facts differed by grade, χ2(3) = 67.40, p < 0.001, with a mean rank score of 76.06 for kindergarten, 128.51 for 1st grade, 148.91 for 2nd grade, and 190.80 for 3rd grade. Dunn’s follow-up comparisons revealed kindergarteners had significantly lower performance than all other grades, zs < −52.44, ps <= .001, whereas third graders had significantly higher performance than all other grades, zs < −20.41, ps <= .008. First and second graders did not differ from each other.
Figure 2.
Mean correct open-ended (Panel A) and forced-choice (Panel B) memory for stem facts. Error bars are standard error.
Forced-choice stem fact performance encompassed the full range of the measure at all grade levels, 0–8. Children’s forced-choice recognition of the stem facts differed by grade, χ2(3) = 48.38, p < 0.001, with a mean rank score of 76.44 for kindergarten, 117.52 for 1st grade, 142.08 for 2nd grade, and 170.46 for 3rd grade. Dunn’s comparisons revealed kindergarteners had significantly lower performance than all other grades, zs < −41.09, ps < .02. In addition, whereas first graders did not differ from second graders, they had significantly lower performance than third graders, z = −52.94, p < .001. The performances of second and third graders did not differ. All grade levels performed significantly higher than chance, ts > 9.35, ps < .001. In summary, K children had low levels of recall of and relatively low levels of recognition of stem facts compared to other grades. Third graders did well in both recall for and recognition of stem facts.
Correlations
We examined correlations between open-ended stem fact performance and self-generation through integration performance to determine whether memory for stem facts related to self-generation performance. The correlation between open-ended stem fact performance and self-generation through integration performance by grade is reported in Table 1. Kindergarten participants are not included due to low open-ended self-generation performance (13%) and thus restricted variance. Memory for the stem facts was correlated to self-generation through integration performance at all grade levels. To test whether there were differences by grade in utilization of the stem facts to self-generate new factual knowledge through integration, we utilized Fisher’s z-transformation and tested the null hypotheses that the correlations did not differ by grade level (Mudholkar, 1983). The 1st grade correlation did not differ from 2nd or 3rd grade correlations, Zs < 1.73. The 2nd grade correlation was significantly lower than the 3rd grade correlation, Z = 2.36. Third graders were more likely to utilize the stem facts to self-generate through integration than 2nd graders.
Table 1.
Open-ended Stem Fact and Self-generation Performance Correlation by Grade
Note:
indicates p < .001.
Correlations between self-generation variables and academic variables were analyzed using Z-scores (calculated within grade) so that the relations could be examined independent of age-related differences found above. Raw academic performance scores are reported in Table 2. Correlations between self-generation variables and academic performance are shown in Table 3. Kindergarten participants were not included in correlations reported for Self-generation due to low open-ended performance and thus restricted range, and chance levels of forced-choice performance. As predicted, self-generation through integration and stem fact memory performance, both open-ended and forced choice, were positively correlated to both reading and math academic performance.
Table 2.
Raw Academic Performance Scores by Grade.
| Grade | Reading Comprehension (SD) | Math Classroom (SD) | Math EOG (SD) |
|---|---|---|---|
| Kindergarten | 5.53 (3.44) | 86.78 (13.13) | |
| 1st | 16.48 (6.34) | 82.77 (12.99) | |
| 2nd | 22.15 (8.39) | 71.16 (13.94) | |
| 3rd | 35.71 (10.21) | 446.38 (8.79) |
Note: The reading comprehension score is based on the mCLASS: Text Reading Comprehension. Math classroom measure is the grade assigned based on classroom performance. The Math EOG, only available for 3rd grade, is the state standardized end-of-grade math test.
Table 3.
Correlations between self-generation performance variables and academic performance.
| Measure | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1. Open-ended Self-generation | |||||
| 2. Open-ended Stem Fact | .61** | ||||
| 3. Forced-choice Self- generation | .40** | .38** | |||
| 4. Forced-choice Stem Fact | .48** | .63** | .59** | ||
| 5. Reading Comprehension | .38** | .55** | .19* | .41** | |
| 6. Math | .28** | .45** | .17* | .43** | .62** |
Note:
indicates p < .001;
indicates p < .01.
Kindergarten data are not included in self-generation correlations due to low variance. Z-scores were analyzed to account for differences between grade and academic measures by grade.
Regression models predicting academic performance
To further examine relations between self-generation through integration and academic performance, we tested regression models predicting academic outcomes in two different areas of performance: reading comprehension and math. We tested the predictive utility of both open-ended and forced-choice self-generation through integration in separate models. The data from children in Kindergarten were not included due to restricted range of open-ended performance and chance performance in forced-choice. We also conducted the models with the full sample and with the subset for which caregiver education level was reported based on evidence that caregiver education is a predictor of academic achievement (Caro, McDonald, & Willms, 2009; Hoff, 2013). We conducted a preliminary two-way between-subjects (caregiver education information available, caregiver education information not available) MANOVA to test whether there were differences in performance on the self-generation through integration variables and the academic performance variables. All dependent variables analyzed were z-scores calculated within grade. There were no differences between groups on the open-ended self-generation through integration measure, F(1, 214) = .29, p = .59. Forced-choice performance did differ between groups, F(1, 214) = 4.24, p = .04, η2=.02, such that families who returned caregiver information tended to have children with higher forced-choice performance. There were no differences between groups in reading comprehension, F(1, 214) = 2.26, p = 0.13. However, mathematics scores approached significance, such that the families that completed and returned caregiver education information tended to have higher mathematics scores, F(1, 214) = 3.94, p = .048, η2=.02.
Reading Comprehension
The results for the hierarchical regression models predicting reading comprehension are shown in Table 4. For the full sample models (Panel A), Grade was included in Step 1. Grade significantly predicted performance in both full-sample models. In the model with open-ended performance predicting reading comprehension, open-ended self-generation through integration performance added significantly to the model explaining reading comprehension. The results were replicated in the forced-choice self-generation through integration model.
Table 4.
Hierarchical Regression (standardized coefficients) Predicting Reading Comprehension
| Panel A: Full Sample
|
Panel B: Subset with Caregiver Education
|
|||||||
|---|---|---|---|---|---|---|---|---|
| Open-ended | Forced-choice | Open-ended | Forced-choice | |||||
|
|
|
|
|
|||||
| Predictor | Step 1 | Step 2 | Step 1 | Step 2 | Step 1 | Step 2 | Step 1 | Step 2 |
| Grade | .67** | .58** | .67** | .64** | .68** | .58** | .68** | .66** |
| Caregiver Education | - | - | - | - | .34** | .20* | .34** | .32** |
| Self-generation Through Integration | - | .36** | - | .18** | - | .33** | - | .17* |
| R2 | .44** | .56** | .44** | .48** | .52** | .60** | .52** | .55** |
| ΔR2 | .12** | .03** | .08** | .03* | ||||
Note:
indicates p < .05,
indicates p ≤ .001.
Full sample indicates all participating children regardless of whether caregiver education information was available. Subset includes only children for whom caregiver information was available. Kindergarten is not included in models.
For the subset of the sample for whom caregiver education information was available (n = 127; Panel B), both Grade and caregiver education were included in Step 1. Both Grade and caregiver education significantly predicted reading performance across both models (open-ended and forced-choice). In both the open-ended model and the forced-choice model, self-generation through integration added significantly to the model predicting reading comprehension. Thus, the results replicated in the subset including caregiver education level.
Math Performance
The results for a hierarchical regression predicting math academic performance are shown in Table 5. As noted above, the math performance measures were not continuous across grade: 3rd grade was on a different scale from grades K-2. We thus used Z-scores for both math and self-generation performance so that the measures could be examined on the same scale. Grade was not included in the model because the Z-scores account for grade. For the full sample (Panel A), both the open-ended and forced-choice measures of self-generation of new factual knowledge through integration predicted math performance. However, in the subset of the sample for which caregiver education information was available (Panel B), the effects did not hold for either open-ended or forced choice. Thus once the variance associated with caregiver education was taken into account, self-generation through integration no longer explained significant variance in math achievement.
Table 5.
Hierarchical Regression (standardized coefficients) Predicting Math Performance
| Panel A: Full Sample
|
Panel B: Subset with Caregiver Education
|
|||||
|---|---|---|---|---|---|---|
| Open-ended | Forced-choice | Open-ended | Forced-choice | |||
|
|
|
|
|
|||
| Predictor | Step 1 | Step 1 | Step 1 | Step 2 | Step 1 | Step 2 |
|
|
|
|
|
|||
| Caregiver Education | - | - | .32* | .24* | .32* | .32* |
| Self-generation Through Integration | .29** | .16* | - | .20 | - | .07 |
| R2 | .08** | .03* | .10* | .14* | .10* | .11* |
| ΔR2 | .03+ | .006 | ||||
Note:
indicates p = .05;
indicates p < .01,
indicates p ≤ .001.
All coefficients are standardized. Full sample indicates all participating children regardless of whether caregiver education information was available. Subset includes only children for whom caregiver information was available. Kindergarten is not included in models.
The 3rd grade math performance measure is a state normed test and had more variance than the measure for K-2 which was based on classroom performance. To take advantage of the stronger measure, we conducted a separate regression analysis for 3rd grade only. The results are reported in Table 6. With the state normed test as the outcome measure, caregiver education was not a significant predictor of math performance. Importantly, self-generation through integration was a significant predictor in the model using open-ended measures of self-generation of new factual knowledge through integration; forced-choice performance was not a significant predictor.
Table 6.
Hierarchical Regression (standardized coefficients) Predicting Math Performance in Third Grade within the Subset with Caregiver Education
| Open-ended | Forced-choice | |||
|---|---|---|---|---|
|
| ||||
| Predictor | Step 1 | Step 2 | Step 1 | Step 2 |
| Caregiver Education | .32 | .07 | .32 | .30 |
| Self-generation Through Integration | - | .54* | - | .23 |
| R2 | .10 | .33* | .10 | .16 |
| ΔR2 | .23* | .05 | ||
Note:
indicates p < .01.
All coefficients are standardized.
Discussion
Not all entries into the knowledge base are the result of explicit lessons. One other means of accumulation of knowledge was demonstrated in this study—namely, children added to their knowledge base through self-generation of new factual knowledge through integration of separate episodes of new learning in the classroom. The finding is notable because it is the first test of this productive process beyond the controlled conditions of the laboratory. Moreover, the children’s performance predicted their academic achievement as represented by standardized measures of reading comprehension and math performance. The measures have high ecological validity in that they are used to track academic progress in the classroom.
The pattern of results found in the classroom was similar to the pattern of results found in the laboratory setting, despite modifications to the procedure. Moving the existing paradigm into the classroom required several modifications to the typical lab procedure to allow presentation to 25 children at once rather than to one child at a time. Performance differed by grade, as expected, and the full range of possible scores was represented for all grades with the exception of kindergarten (open-ended performance encompassed only the lower end of the possible range). Indeed, kindergarteners did not show evidence of self-generating either in open-ended or forced-choice format. Self-generation was, however, evident among children in Grades 1, 2, and 3. In general, classroom performance was lower than reported in laboratory studies. Although we cannot determine the precise reason(s) for the difference, we may speculate that it could be due to differences in sample demographics, to methodological differences, or both. Previous laboratory samples have been drawn from predominantly upper-middle class populations. The greater diversity of the present sample, including children from less advantaged families, may have contributed to lower performance (Caro, McDonald, & Willms, 2009). As well, classroom testing with groups of up to 30 children per class may have contributed to lower performance, even as it increased the ecologically validity of the paradigm. It will be left to future research to evaluate possible contributors to variability in levels of performance. In summary, although this task proved difficult for the youngest cohort, this investigation confirmed the assumption that children engage in this productive process in the classroom environment.
As predicted, self-generation through integration of separate episodes was related to reading comprehension as measured by classroom teachers. Self-generation performance contributed significantly to the model predicting reading comprehension scores in both the full sample and in the subset including caregiver education level. The effect was present for both open-ended and forced choice performance. Children with higher performance on the self-generation through integration task also had higher reading comprehension scores. Previous studies of reading comprehension have pointed out the need to make inferences from text for immediate text comprehension such as within a paragraph or even within a sentence (e.g., Cain & Oakhill, 1999; Graesser, Singer, & Trabasso, 1994; Paris & Upton, 1976). However, self-generation of factual knowledge through integration of separate episodes of learning requires integration of material across different sources and episodes, then extending that material to create a factual representation that was not stated. Children’s proficiency at making connections and extending understanding predicted their reading comprehension as measured within a text. Comprehending the primary text may be a necessary, though not sufficient, step to drawing connections between and extending beyond different texts.
The relation between reading comprehension and self-generation of new knowledge through integration found in this study replicates a previous laboratory examination with different measures of both self-generation through integration and reading comprehension. In Bauer, Blue, Xu, and Esposito (2016), self-generation of new factual knowledge through integration of separate episodes of new learning was evidenced in a paradigm in which children were required to integrate across separate sentences conveying true but novel facts. Self-generation was related to reading comprehension as tested using the Woodcock Johnson Test of reading comprehension. The difference in procedures and measures with similar results supports the generalizability of this finding.
Self-generation of new factual knowledge through integration of separate yet related episodes of new learning was also a significant predictor of math performance. However, when the model was conducted on the subset of the sample on which caregiver educational level was available, self-generation through integration fell below the level of statistical significance. This could be a reflection of the measures available for classroom K-2 math performance. The math measure indicating K-2 performance is based on teacher-administered assessments throughout the year and is intended to be a reflection of mastery of grade-level content. As the goal is for all children to master grade level content, the measure is positively skewed and the grade does not reflect growth in mathematical ability or knowledge across years.
Support for the possibility that the measure of math achievement for Grades K-2 obscured underlying relations comes from analysis based on standardized measure available only for Grade 3. The measure of 3rd grade math performance is standardized based on state performance expectations. We included caregiver education level in this model because it was established as a significant contributor in the previous regression models. Open-ended self-generation through integration was a significant predictor of performance on the state standardized math test even when controlling for caregiver education. In fact, caregiver education dropped out of the model as a significant predictor. The results indicate that self-generation through integration can predict math performance, but that this is subject to the specific measures employed.
The sample in this study differed from previous studies on self-generation of factual knowledge through integration of separate episodes of new learning. The majority of students participating in the current study were low income based on the percentage qualifying for federally subsidized meals. This is in contrast to the laboratory studies with primarily upper middle class participants (e.g., Bauer & San Souci, 2010; Varga & Bauer, 2013). The findings of this study support self-generation through integration of separate episodes as a productive process utilized across socio-economic groups and add to the generalizability of the current and past findings regarding this productive process.
Interestingly, although there was a general effect of grade, there was no grade-level improvement from 1st to 2nd grade and 1st graders did not differ from 3rd graders in the ability to utilize the stem facts to self-generate. This appears counter to a developmental pattern. However, in order to avoid ceiling affects, we chose to increase the difficulty of the task between the primary and intermediate schools so that K and 1st grade were read text passages with high surface similarity within each domain, such that they had the same character across related text passages. Second and 3rd grade children were read text passages with low surface similarity, such that the characters differed between related text passages from the same domain. This effectively prevented students from reaching ceiling performance, but also appears to have taxed the 2nd grade students’ ability to recognize that the text passages were related, possibly affecting integration and manifesting in lower-than-expected self-generation performance. In laboratory based studies, performance fell when the character changed between related text passages compared to when the character remained the same and could be used as a resource to guide integration (Bauer, King, Larkina, Varga, & White, 2012). The dependence on surface similarity, especially in novice learners, is also evident in other productive processes such as analogical transfer and deductive reasoning (Gentner, 1989; Goswami, 2011).
Posing a similar challenge to recognizing that text passages were related, Bauer and Larkina (2016) presented children aged 4, 6, and 8 with integratable text passages as well as related or unrelated text passages that could not be used to answer the subsequent self-generation through integration questions. Four-year-old children were challenged to recognize that passages could be integrated when other related, but not relevant, text passages were included. Six-year-olds were successful only under forced-choice test conditions, whereas 8-year-olds were successful in both open-ended and forced-choice conditions. In the current study, the 3rd graders were more successful than 2nd graders at integrating and self-generating new knowledge under the challenge of different characters. Similar to added information that was not relevant to the questions posed in Bauer and Larkina, changing the characters between text passages challenged children and made it more difficult to recognize that the text passages contained related content.
The results reported here should be interpreted with a degree of caution because they are based on cross-sectional work and thus have all the limitations inherent to cross-sectional studies. Future longitudinal research will more thoroughly delineate the development of self-generation through integration skills and relations with academic performance. In addition, although the low socio-economic status and rural nature of the sample was a strength given the majority of the laboratory work included an upper middle class urban sample, interpretation should keep the specifics of this sample in mind.
Future work should explore the component cognitive abilities underlying self-generation through integration, such as working memory and executive functions. In addition, self-generation through integration involves several steps including recognizing that separate units of information are related, integrating the units into a coherent representation, and accessing the necessary information to correctly answer the integration question (see Bauer & Larkina, 2016, for discussion). Future studies should examine the specific components of the process that relate to academic performance, so as to partition the variance. Such studies would be useful in determining what is responsible for the differences found in this study of classroom performance in an area of poverty compared to the laboratory and would inform possible interventions.
Another area for future research is identification of the level of surface similarity necessary to support integration and self-generation, across development. As noted earlier, especially for novice learners, high levels of surface similarity support productive processes (Bauer et al., 2010; Brown, 1989; Clark, 2009). Yet it is also clear that varied learning environments promote concept formation and transfer (Brown, 1989; Clark, 2009). Future research will be necessary to determine the balance between encouraging transfer and providing conditions for self-generative processes, with the expectation that the balance may shift over the course of development, as expertise is accrued, or both.
Self-generation and retention of new factual knowledge through integration of separate yet related episodes of new learning is unique in several ways that make this cognitive process especially relevant to education. Specifically, self-generation of new knowledge through integration tests the factual information acquired by extending new information presented through separate episodes that persists over time. Rather than testing arbitrary associations that are unlikely and not advantageous to retain, the current study tested factual knowledge that could reasonably become part of the knowledge base. As in school context, the new episodes of learning were separated by intervening activities and were embedded in rich episodic contexts. In the current study, the newly derived knowledge need only be retained for a period of 10–15 minutes. In lab studies, retention has been documented over a one-week delay (Varga & Bauer, 2013; Varga et al., 2016). Future research should test the assumption of retention of the newly formed knowledge in the classroom after a longer delay to assess the degree to which this information becomes incorporated into the knowledge base when attained through this productive process in the school context.
Conclusions
Children self-generated new factual knowledge through integration of separate yet related episodes of new learning in a classroom setting. Performance on this task predicted academic achievement in both reading and math. Self-generation through integration predicted a significant amount of variance over and above caregiver education level. Future research should investigate retention, both concurrent and cross-lagged component cognitive abilities, and the relation with academic performance over time, and seek to elucidate classroom practices that encourage the development of this productive process.
Children self-generated through integration of separate episodes in the classroom.
Self-generation of knowledge predicted academic achievement in reading and math.
Self-generation predicted academic performance above caregiver education level.
Acknowledgments
Funding and Acknowledgements
The work was supported by NICHD HD067359, and by NSF BCS1528091, to Patricia J. Bauer, and by Emory College of Arts and Sciences. The authors also thank the Spencer Foundation and the NCSU Teach for support for collection of portions of the data. The authors also thank Ruth Sirkin for assistance with participant testing, and other members of the Memory at Emory laboratory group for help at various stages of the research. They also thank the Greene County School System, North Carolina, and the children and parents who took part in the research.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alfieri L, Brooks PJ, Aldrich NJ, Tenenbaum HR. Does discovery-based instruction enhance learning? Journal of Educational Psychology. 2011;103(1):1. [Google Scholar]
- Bauer PJ. Chapter 3 Facilitating Learning and Memory in Infants and Young Children. Infants, Toddlers, and Families in Poverty: Research Implications for Early Child Care. 2012:49. [Google Scholar]
- Bauer PJ, Blue SN, Xu A, Esposito AG. Productive Extension of Semantic Memory in School-aged Children: Relations with Reading Comprehension and Deployment of Cognitive Resources. Developmental Psychology. 2016 doi: 10.1037/dev0000130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer PJ, Jackson FL. Semantic elaboration: ERPs reveal rapid transition from novel to known. Journal Of Experimental Psychology: Learning, Memory, And Cognition. 2015;41(1):271–282. doi: 10.1037/a0037405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer PJ, King JE, Larkina M, Varga NL, White EA. Characters and clues: Factors affecting children’s extension of knowledge through integration of separate episodes. Journal of Experimental Child Psychology. 2012;111:681–694. doi: 10.1016/j.jecp.2011.10.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer PJ, Larkina M. Realizing relevance: The influence of domain-specific information on generation of new knowledge through integration in 4- to 8-year-old children. Child Development. 2016 doi: 10.1111/cdev.12584. [DOI] [PubMed] [Google Scholar]
- Bauer PJ, San Souci P. Going beyond the facts: Young children extend knowledge by integrating episodes. Journal of Experimental Psychology. 2010;107:452–465. doi: 10.1016/j.jecp.2010.05.012. doi.org/10.1016/j.jecp.2010.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bauer PJ, Varga NL. The developmental cognitive neuroscience of memory: Implications for education. In: Tardif E, Doudin P, editors. Collective work on the topics of neuroscience, cognition and education. Oxford, UK: De Boeck; 2016. pp. 135–164. [Google Scholar]
- Brown AL. Learning and development: The problems of compatibility, access and induction. Human Development. 1982;25(2):89–115. [Google Scholar]
- Brown AL. Analogical learning and transfer: What develops. Similarity and analogical reasoning. 1989:369–412. [Google Scholar]
- Cain K, Oakhill JV. Inference making ability and its relation to comprehension failure in young children. Reading and Writing. 1999;11(5–6):489–503. doi: 10.1023/A:1008084120205. [DOI] [Google Scholar]
- Caro DH, McDonald JT, Willms JD. Socio-economic status and academic achievement trajectories from childhood to adolescence. Canadian Journal of Education. 2009;32(3):558–590. [Google Scholar]
- Clark RE. How much and what type of guidance is optimal for learning from instruction. Constructivist instruction: Success or failure. 2009:158–183. [Google Scholar]
- Common Core State Standards Initiative; Preparing America’s Students for College and Career. Retrieved from www.corestandards.org on March 20th, 2016.
- Crone EA, Wendelken C, Van Leijenhorst L, Honomichl RD, Christoff K, Bunge SA. Neurocognitive development of relational reasoning. Developmental science. 2009;12(1):55–66. doi: 10.1111/j.1467-7687.2008.00743.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dinno A. Nonparametric pairwise multiple comparisons in independent groups using Dunn’s test. 2015. [Google Scholar]
- Dunn OJ. Multiple comparisons among means. Journal of the American Statistical Association. 1961;56:52–64. [Google Scholar]
- Gentner D, Gentner DR. Flowing Waters or Teeming Crowds: Mental Models of Electricity. BOLT BERANEK AND NEWMAN INC; CAMBRIDGE MA: 1982. (No. BBN-4981) [Google Scholar]
- Gentner D, Loewenstein J, Thompson L. Learning and transfer: A general role for analogical encoding. Journal of Educational Psychology. 2003;95(2):393. [Google Scholar]
- Goswami UC. Analogical reasoning in children. Hove: Erlbaum; 1992. [Google Scholar]
- Goswami UC. Inductive and deductive reasoning. In: Goswami U, editor. Childhood cognitive development. Oxford, UK: Wiley–Blackwell; 2011. pp. 399–419. doi.org/10.1016/j.tics.2010.10.001. [Google Scholar]
- Graesser AC, Singer M, Trabasso T. Constructing inferences during narrative text comprehension. Psychological review. 1994;101(3):371. doi: 10.1037/0033-295x.101.3.371. [DOI] [PubMed] [Google Scholar]
- Hoff E. Interpreting the early language trajectories of children from low-SES and language minority homes: Implications for closing achievement gaps. Developmental Psychology. 2013;49(1):4–14. doi: 10.1037/a0027238. http://doi.org/10.1037/a0027238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruskal WH, Wallis WA. Use of ranks in one-criterion variance analysis. Journal of the American Statistical Association. 1952;47:583–621. [Google Scholar]
- Mandler JM, McDonough L. Drinking and driving don’t mix: inductive generalization in infancy. Cognition. 1996;59(3):307–335. doi: 10.1016/0010-0277(95)00696-6. [DOI] [PubMed] [Google Scholar]
- Mayer RE. Should there be a three-strikes rule against pure discovery learning? American psychologist. 2004;59(1):14. doi: 10.1037/0003-066X.59.1.14. [DOI] [PubMed] [Google Scholar]
- McKoon G, Ratcliff R. Inference during reading. Psychological review. 1992;99(3):440. doi: 10.1037/0033-295x.99.3.440. [DOI] [PubMed] [Google Scholar]
- Mudholkar GS. Fisher’s Z Transformation. Encyclopedia of Statistical Sciences 1983 [Google Scholar]
- Paris SG, Upton LR. Children’s Memory for Inferential Relationships in Prose. Child Development. 1976;47(3):660–668. http://doi.org/10.2307/1128180. [Google Scholar]
- Perret P. Children’s Inductive Reasoning: Developmental and Educational Perspectives. Journal of Cognitive Education and Psychology. 2015;14(3):389–408. [Google Scholar]
- Schulz LE, Goodman ND, Tenenbaum JB, Jenkins AC. Going beyond the evidence: Abstract laws and preschoolers’ responses to anomalous data. Cognition. 2008;109(2):211–223. doi: 10.1016/j.cognition.2008.07.017. [DOI] [PubMed] [Google Scholar]
- Shafto P, Kemp C, Bonawitz EB, Coley JD, Tenenbaum JB. Inductive reasoning about causally transmitted properties. Cognition. 2008;109(2):175–192. doi: 10.1016/j.cognition.2008.07.006. [DOI] [PubMed] [Google Scholar]
- Siegler RS. Connecting Formal and Informal Mathematical Knowledge. Contemporary Psychology: APA Review of Books. 1989;34(6):585–586. [Google Scholar]
- Singer-Freeman K, Bauer PJ. The ABCs of analogical abilities: Evidence for formal analogical reasoning abilities in 24-month-olds. British Journal of Developmental Psychology. 2008;26:317–335. [Google Scholar]
- Sobel DM, Sommerville JA. The Importance of Discovery in Children’s Causal Learning from Interventions. Frontiers in Psychology. 2010;1:176. doi: 10.3389/fpsyg.2010.00176. http://doi.org/10.3389/fpsyg.2010.00176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varga NL, Bauer PJ. Effects of delay on 6-year-old children’s self-generation and retention of knowledge through integration. Journal of Experimental Child Psychology. 2013;115:326–341. doi: 10.1016/j.jecp.2013.01.008. doi.org/10.1016/j.jecp.2013.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varga NL, Stewart RA, Bauer PJ. Effects of delay and reminders on the accessibility of self-generated knowledge in 4-year-old children. Journal of Experimental Child Psychology. 2016;145:48–63. doi: 10.1016/j.jecp.2015.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viskontas IV, Morrison RG, Holyoak KJ, Hummel JE, Knowlton BJ. Relational integration, inhibition, and analogical reasoning in older adults. Psychology and aging. 2004;19(4):581. doi: 10.1037/0882-7974.19.4.581. [DOI] [PubMed] [Google Scholar]
- Walker CM, Gopnik A, Ganea PA. Learning to learn from stories: children’s developing sensitivity to the causal structure of fictional worlds. Child development. 2015;86(1):310–318. doi: 10.1111/cdev.12287. [DOI] [PubMed] [Google Scholar]
- Woodcock RW, McGrew KS, Mather N. Woodcock-Johnson III tests of achievement. Itasca, IL: Riverside; 2001. [Google Scholar]