Postediting prostate magnetic resonance imaging segmentation consistency and operator time using manual and computer-assisted segmentation: multiobserver study

Abstract.

Prostate segmentation on T2w MRI is important for several diagnostic and therapeutic procedures for prostate cancer. Manual segmentation is time-consuming, labor-intensive, and subject to high interobserver variability. This study investigated the suitability of computer-assisted segmentation algorithms for clinical translation, based on measurements of interoperator variability and measurements of the editing time required to yield clinically acceptable segmentations. A multioperator pilot study was performed under three pre- and postediting conditions: manual, semiautomatic, and automatic segmentation. We recorded the required editing time for each segmentation and measured the editing magnitude based on five different spatial metrics. We recorded average editing times of 213, 328, and 393 s for manual, semiautomatic, and automatic segmentation respectively, while an average fully manual segmentation time of 564 s was recorded. The reduced measured postediting interoperator variability of semiautomatic and automatic segmentations compared to the manual approach indicates the potential of computer-assisted segmentation for generating a clinically acceptable segmentation faster with higher consistency. The lack of strong correlation between editing time and the values of typically used error metrics ($\rho <0.5$) implies that the necessary postsegmentation editing time needs to be measured directly in order to evaluate an algorithm’s suitability for clinical translation.

1. Introduction

In 2015, prostate cancer (PCa) was one of the most commonly diagnosed noncutaneous cancers and the second leading cause of death from cancer among men in North America.^1,2 Due to its high soft tissue contrast, magnetic resonance imaging (MRI) has demonstrated potential for detection, localization, and staging of PCa ^3–6 and is entering routine clinical use for PCa diagnosis, treatment planning, and therapy guidance.^3,6–8 Using an endorectal receiver (ER) coil during MRI acquisition yields images with higher resolution and improved signal-to-noise ratio, with reported positive impact on PCa diagnosis.^7,9,10

Delineation of the prostate gland on MRI is required for several clinical procedures in which MR images are employed; e.g., MRI-targeted transrectal ultrasound (TRUS)-guided biopsy, MRI-guided radiotherapy planning, and MRI-guided focal therapy. T2-weighted (T2w) prostate MRI plays an important role in anatomy description,^11,12 PCa detection and localization,¹³ and therefore, prostate contouring is usually performed on T2w MRI. However, three-dimensional (3-D) manual prostate contour delineation is laborious and time-consuming, and subject to substantial interoperator variability.¹⁴

Several algorithms have been presented in the literature for 3-D segmentation of the prostate on T2w MRI, as described in a recent survey.¹⁵ However, a minority of these methods has been validated for use on T2w MRI acquired using an ER coil (ER MRI). Although ER MRI can improve PCa detection, its improved contrast results in the presence of additional high-frequency details in the images. This makes automatic segmentation more challenging, especially for algorithms designed for use on non-ER MRI, where the intraprostatic signal is more homogeneous. Furthermore, the ER coil deforms and displaces the prostate gland and produces MRI artifacts¹⁶ that further challenge automatic segmentation. We have previously reported on a semiautomatic segmentation algorithm and this method is based on prostate shape and appearance models learned from a training set.¹⁷ Segmentation is performed in two steps: coarse localization of the prostate, followed by 3-D segmentation boundary detection and refinement. In the semiautomated approach, coarse localization is performed by the operator with four mouse clicks requiring $\sim 30\mathrm{s}$ of user interaction time. In the automated approach, coarse localization is performed automatically within 3 s of computation time, with no requirement for user interaction.

A range of segmentation accuracy values has been reported in the literature for automated and semiautomated algorithms (Table 1). Typically, reported error metrics include the mean absolute distance (MAD) between the boundaries of the automatic and manual segmentations, and/or the Dice similarity coefficient (DSC). Reported MAD values range from 1.5 to 3.4 mm,^17–20 and reported DSC values range from 82% to 91%.^17–21 Reasons for the range of different error values reported include algorithm design, the use of single-operator manual reference segmentations for validation in most studies, and the use of different imaging datasets. These differences notwithstanding, the errors yielded by state-of-the-art segmentation methods are approaching the differences observed between human expert operators.¹⁴ It is thus timely to shift the focus of research in this area to studies aimed at enabling clinical translation of these techniques for routine clinical use.

Table 1.

Reported segmentation errors for prostate segmentation algorithms intended for use on T2w ER MRI.

Group	Method	Dataset size	Accuracy	Segmentation time
Our group17	Local appearance and shape model (semiautomatic)	42 (test and training)	Whole gland:MAD: $2.0\pm 0.5\mathrm{mm}$DSC: $82\%\pm 4\%$Recall: $77\%\pm 9\%$Precision: $88\%\pm 6\%$$\mathrm{\Delta }V$: $-4.6\pm 7.2{\mathrm{cm}}^3$	Operator interaction: $28\pm 14\mathrm{s}$. (across 10 images and 9 operators) Execution: $85\pm 20\mathrm{s}$. (across 42 images, one operator)
Cheng et al.21	Atlas-based (automatic)	100 (training) and 40 (test)	Whole gland:TP: 91.2%DSC: 87.6%$\mathrm{\Delta }V$: 8.4%	NA
Liao et al.18	Multi-atlas-based (automatic)	66 (test) 9 (atlas)	Whole gland:MAD: $1.8\pm 0.9\mathrm{mm}$DSC: $88\%\pm 3\%$	Execution: 2.9 min
Toth and Madabhushi19	Active appearance model (semiautomatic)	108	Whole gland:MAD: $1.5\pm 0.8\mathrm{mm}$DSC: $88\%\pm 5\%$	Execution: 150 s
Vikal et al.22	Shape model (semiautomatic)	3	Has not reported for whole gland	Execution: 23 s
Martin et al.20	Atlas-based (semiautomatic)	1 (reference) 17 (test)	Whole gland:MAD: $3.4\pm 2.0\mathrm{mm}$Recall: $89\%\pm 6\%$Precision: $78\%\pm 12\%$	NA

Note: MAD, mean absolute distance; DSC, Dice similarity coefficient; $\mathrm{\Delta }V$, volume difference; TP, true positive.

For reasons of diagnostic accuracy and patient safety, the integration of any computer-assisted segmentation algorithm, fully automatic or otherwise, into clinical use will require that an expert reviews (and edits) the segmentation before proceeding. This will always be necessary since regardless of the reported accuracy of a given segmentation algorithm, variations in anatomy or image acquisition will occur in the clinic that could result in aberrant computer-assisted segmentations, with potentially adverse consequences to the patient if such segmentations were used to guide treatment without correction. Therefore, the clinical utility of a method will depend not only on its accuracy metric values (based on the final segmentation), such as the MAD and DSC, but also on the amount of editing deemed necessary by expert physicians in order to render the segmentation suitable for clinical use. This editing can be measured spatially using standard metrics, such as MAD and DSC, to compare the segmentation as output by the algorithm to the segmentation after editing, and these metrics can be computed on anatomically distinct regions to learn about the portions of the prostate requiring the most editing. Potentially of even greater importance, the amount of required editing time can be measured. For a segmentation algorithm to have clinical utility, it must allow the expert physician to obtain a segmentation deemed clinically acceptable by him/her in less time than would be required to perform a manual segmentation. This statement holds true regardless of the reported segmentation accuracy metrics (e.g., MAD, DSC) for an algorithm in the literature. Mahdavi et al. presented a semiautomatic prostate segmentation algorithm for TRUS images and reported the accuracy, repeatability, and the total segmentation time including user interaction, algorithm execution, and expert editing times for their method and compared them to the corresponding measurements for manual segmentation. They showed that semiautomatic segmentation approaches after manual editing could be an appropriate replacement for fully manual segmentation due to their relatively shorter segmentation times, higher consistency, and less reliance on operator experience.^23,24 However, to the best of our knowledge, questions of editing magnitude and time have not been extensively studied for ER MRI prostate segmentation algorithms reported in the literature. Ultimately, segmentation tools need to be integrated with other tools in user friendly clinical contouring platforms; such integration is beyond the scope of this work.

In this paper, we conducted a user study to answer four research questions related to our segmentation algorithm. (1) How much spatial segmentation editing do expert operators perform to obtain clinically useful segmentations? (2) What is the interoperator variability in segmentation with and without the use of the tool? (3) How much segmentation editing time do expert operators require to obtain clinically useful segmentations? (4) Can the necessary time requirement for segmentation editing be predicted from spatial segmentation error metrics? Questions (1), (2), and (3) were answered and compared under three conditions, in which the segmentations provided to the operators for editing came from (a) our automatic segmentation algorithm, (b) our semiautomatic segmentation algorithm, and (c) manual segmentation performed by another expert operator. As the scope of question (4) is limited to evaluation of computer-assisted segmentation algorithms, it was answered under conditions (a) and (b) only.

2. Materials and Methods

2.1. Materials

Our sample consisted of 10 axial T2w fast spin echo ER MRI acquired at 3.0-T field strength, all from patients with biopsy-confirmed PCa. Images were acquired with $\mathrm{TR}=4000$ to 13,000 ms, $\mathrm{TE}=156$ to 164 ms, $\mathrm{NEX}=2$. The voxel sizes were $0.27\times 0.27\times 2.2\mathrm{mm}$ as is typically seen in clinical prostate MRI. The images were acquired using a Discovery MR750 (General Electric Healthcare, Waukesha, Wisconsin). The study was approved by the research ethics board of our institution, and written informed consent was obtained from all patients prior to enrolment. All 10 MR images were segmented manually by three operators: one radiologist, one radiation oncologist, and an expert radiology resident with $>3$ years’ experience reading $>100$ prostate MRI studies in tandem with a board-certified radiologist as part of a trial conducted at our center. Editing was conducted by four radiation oncologists with genitourinary specialization and the same expert radiology resident. The ITK-SNAP software tool²⁵ was used for manual segmentation.

2.2. Study Design

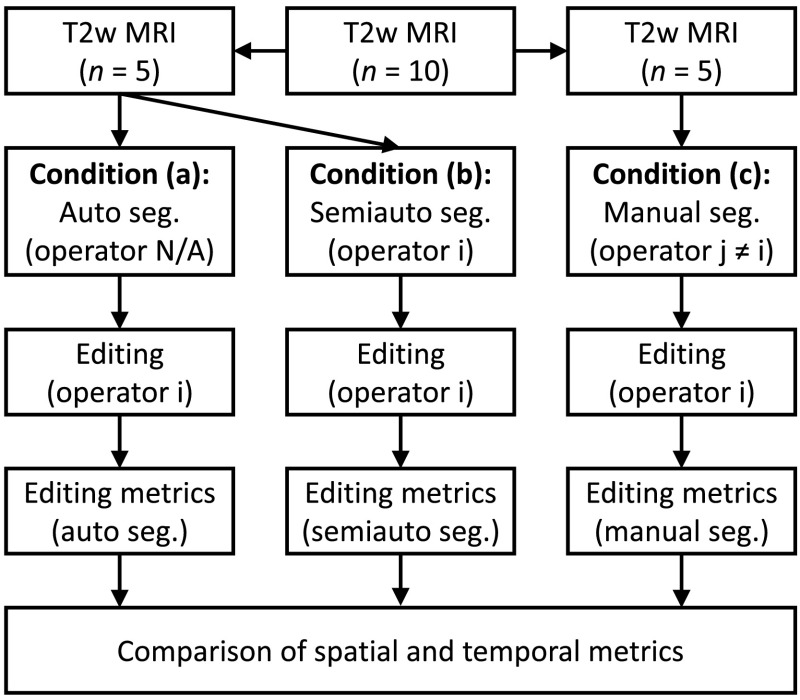
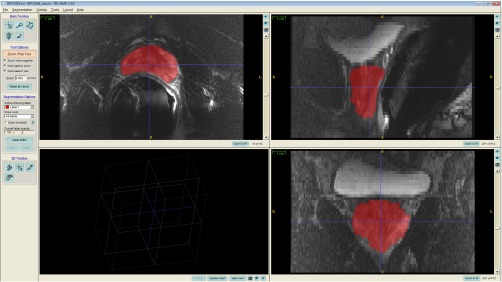
Our study design is shown in Fig. 1. Each operator #i edited a total of 15 segmentations under three conditions: (1) five automatic segmentations (performed using an automated version of our semiautomatic segmentation algorithm, described in Appendix), (2) five semiautomatic segmentations performed based on the operator’s own inputs as the semiautomatic segmentation algorithm operator, and (3) five manual segmentations performed by a different expert operator #j. Operator #j was the same individual throughout the entire experiment; operator #j provided only manual reference segmentations and did not take part in this editing study in any other way. Editing was performed in slice-by-slice mode using the ITK-SNAP²⁵ version 2.4.0 interface on axially oriented slices. Changes were applied only on the axial slices but sagittal and coronal views were also provided to the operator during editing, so the operator could check for spatial coherence of the segmentations in these views (Fig. 2). The operators used the adjustable-size paint brush tool in ITK-SNAP to add/remove area to/from the segmentation labels. They were able to adjust window and level and zoom in and out during editing. Spatial and temporal metrics were collected for each of the three conditions to compare the editing that was performed within each operator and between operators. To enable direct comparison of the editing of the automatic and semiautomatic segmentations, we used the same subset of five MRI scans for each operator for these two conditions. To mitigate possible effects of the order of MRI scan presentation on the experiment, the 15 segmentations were presented in a different randomized order for each operator, with a constraint that between any two presentations of the same MRI scan to the operator (i.e., once for automatic segmentation, and again with the same scan for semiautomatic segmentation), there were at least six MRI scans from other patients presented. Training in the use of ITK-SNAP and practice was provided in advance of the measured editing sessions.

Fig. 1.

Study design showing the workflow for a particular operator #i. The operator edited three sets of segmentations: five automatic segmentations, five semiautomatic segmentations performed by the operator, and five manual segmentations performed by a different operator #j. Spatial and temporal segmentation metrics were collected to measure the editing task and compared across the three conditions.

Fig. 2.

A snapshot of ITK-SNAP interface used for editing the segmentation labels.

2.3. Spatial Editing Magnitude and Interoperator Variability

We compared the pre-editing segmentations to the postediting segmentations in each of the three conditions shown in Fig. 1, “answering research question (1).” We used five different metrics, including MAD, DSC, recall, precision, and volume difference ($\mathrm{\Delta }V$), to perform comparisons in terms of surface disagreement, regional misalignment, and volume difference. Where applicable, the postediting segmentation was defined as the reference segmentation. These metrics are defined in detail below.

2.3.1. Mean absolute distance

The MAD metric measures the disagreement between two 3-D surfaces as the average of a set of Euclidean distances between corresponding surface points of two shapes. For each point on one surface, the closest point on the other surface is defined as the corresponding point. Equation (1) shows the MAD of $X$ and $Y$ as two surface point sets, where $D(p,q)$ is the Euclidean distance between points $p$ and $q$. A MAD of zero indicates ideal agreement between two shapes:

$$\mathrm{MAD}(X,Y)=\frac{1}{N}\sum _{p\in X}\underset{q\in Y}{\min }D(p,q).$$ (1)

The MAD calculation needs to consider one of the shapes as the reference (e.g., point set $Y$ is the reference in Eq. (1)]. Therefore, when two segmentations are to be compared and there is no reference segmentation, we use the bilateral MAD, which is the average of the two MAD values obtained using each segmentation as the reference.

2.3.2. Dice similarity coefficient

The DSC is a region-based metric that measures the proportion of the volume of the overlap region between two shapes and the average of their volumes in 3-D [Eq. (2)]. The DSC is a unitless metric and will be 100% in the case of ideal segmentation and 0% when there is no overlap.

2.3.3. Recall and precision rates

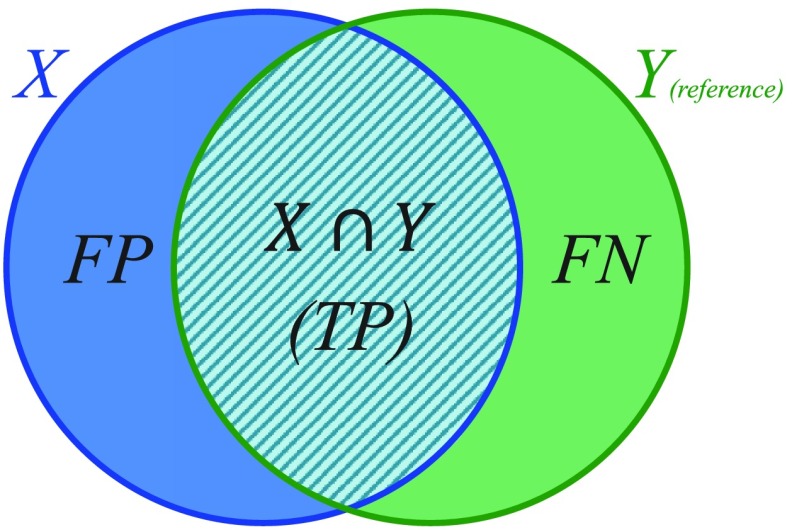
Recall (or sensitivity) and precision are also unitless error metrics that measure the regional misalignment in terms of the overlap region with 100% and 0% as the ideal and worst-case measurement values, respectively. To calculate recall and precision, we need to consider one shape as the reference. Recall measures the proportion of the reference that is within the segmentation [Eq. (3)] and precision measures the proportion of the segmentation that is within the reference [Eq. (4)]:

$$\mathrm{DSC}(X,Y)=\frac{2(X\cap Y)}{X+Y}=\frac{2\mathrm{TP}}{\mathrm{FP}+2\mathrm{TP}+\mathrm{FN}}\times 100,$$ (2)

$$\text{Recall}(X,Y)=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}\times 100,$$ (3)

$$\text{Precision}(X,Y)=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}}\times 100,$$ (4)

where TP is the true positive or correctly identified region, FP is the false positive or incorrectly identified region, and FN is the false negative or incorrectly ignored region (see Fig. 3).

Fig. 3.

Elements used to compute the DSC, recall, and precision validation metrics.

2.3.4. Volume difference

To calculate $\mathrm{\Delta }V$, we subtract the reference shape volume from the segmentation shape volume. Therefore, $\mathrm{\Delta }V$ is a signed error metric; i.e., negative values of $\mathrm{\Delta }V$ show that the segmentation is smaller than the reference and positive values of $\mathrm{\Delta }V$ show that the segmentation is larger than the reference.

2.4. Interoperator Variability

To quantify interoperator variability in segmentation and editing [answering research question (2)], we calculated simultaneous truth and performance level estimation (STAPLE)²⁶ consensus segmentations from the five operator segmentations before and after editing under all three conditions, with two exceptions. In the case of the pre-editing automatic segmentations, no operators were involved, so no STAPLE segmentation was calculated. In the case of the pre-editing manual segmentations, only the segmentations of a single operator #j were edited in this study. To obtain a measure of interoperator variability in pre-editing manual segmentations, we computed a STAPLE segmentation from manual segmentations performed by three of our operators on the same five images that were used for manual segmentation editing in our study. There were five sets, each containing five segmentations performed by different operators, with accompanying STAPLE consensus segmentation: (1) pre-editing semiautomatic, (2) postediting semiautomatic, (3) postediting automatic, (4) pre-editing manual, and (5) postediting manual. Within each of these five sets, our five segmentation error metrics were computed to compare each operator’s segmentation to the corresponding STAPLE segmentation, with the means of the metric values indicating the amount of interoperator variability. We used a one-way ANOVA test followed by one-tailed pairwise heteroscedastic $t$-tests to test for statistical significance of differences in these interoperator variability measurements between paired elements of the five sets. This allows us, for instance, to measure whether there is a statistically significant reduction of interoperator variability in edited semiautomatic segmentations, versus edited automatic segmentations.

2.5. Required Editing Time and Correlation with Spatial Error Metrics

For each label, we recorded the interaction time that was required to have a clinically acceptable segmentation using manual, semiautomatic, and automatic segmentation methods, answering research question (3). The time was documented from the moment when the operator began reviewing and editing the segmentation until the moment the operator verbally confirmed that the segmentation was ready to be used in clinic. The editing time included browsing through the slices in the 3-D volume, reviewing the segmentation, adding to and removing from the segmentation, window and level adjustment, editing tool selection and adjustment, and zooming in and out. For each of the three conditions, the mean and standard deviation of the interaction time was calculated across the five presented MRI scans separately for each operator, and also in aggregate across all five operators. For the semiautomatic algorithm, we measured the interaction time required for algorithm operation and included this interaction time as part of the time required for the condition involving semiautomatic segmentation.

We evaluated the degree to which measured spatial error metric values can be used as surrogates for the amount of editing time needed to achieve a segmentation that is satisfactory to the operator, answering research question (4). To do this, all five of our error metrics were calculated for the whole gland, apex, mid-gland, and base, comparing the pre-editing segmentation to the postediting segmentation for the automatic and semiautomatic segmentations (conditions 1 and 2 in Fig. 1), using the postediting segmentation as the reference where applicable. We measured the monotonicity of the relationship between each metric value and editing time using Spearman’s rank-order correlation ($\rho$). We tested the statistical significance of the correlation coefficients using the null hypothesis that there was no association between the error metric values and editing time values. For all tests, the sample size was 50 (10 images each contoured by 5 operators).

3. Results

3.1. Spatial Editing Magnitude and Interoperator Variability

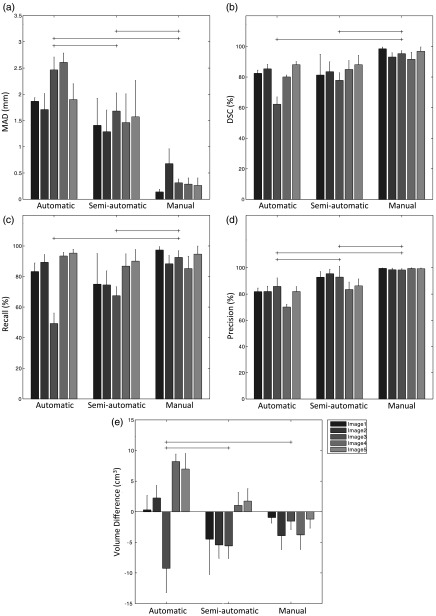
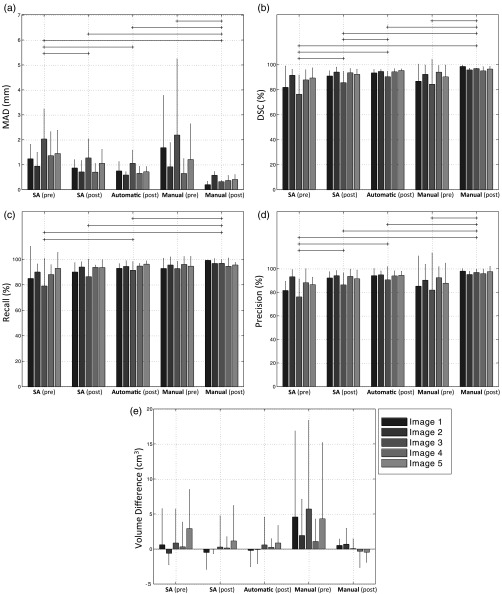
Figure 4 shows the spatial magnitude of editing required for automatic, semiautomatic, and manual segmentations for operators to achieve final edited segmentations suitable for clinical use. As might be expected, the general trend is that the automatic segmentations required the most editing, followed by the semiautomatic and manual segmentations. However, this trend was not reflected in all of the error metrics. For instance, looking at the DSC and recall metrics, we detected no significant difference in the amount of editing applied to the automatic versus semiautomatic segmentations based on these two metrics. Operator editing of manual segmentation consistently decreased segmentation volume without substantially affecting precision. This suggests that the manual pre-editing segmentations were deemed by the operators to be oversegmentations, and editing drew the boundaries inward by an amount reflected by the MAD metric values in Fig. 4 ($\mathrm{MAD}<1\mathrm{mm}$, in general). Figure 5 shows the interoperator variability in segmentation before and after editing, reported using the mean of each segmentation error metric across all operators for each image, with respect to a STAPLE reference standard. This analysis revealed significant differences in interoperator variability for most of the conditions, for all metrics except for the volume difference. Note the substantial interoperator variability in manual segmentation (reflected by large mean metric values and large variability indicated by the whiskers) for many metrics, relative to the interoperator variability in semiautomatic and automatic segmentations, even when manual editing is applied (e.g., compare the “manual-pre” measurements to the other measurements for the MAD metric in Fig. 5). Overall, postediting variability is lower than pre-editing variability, with postediting automatic and semiautomatic segmentations having similar variability. The MAD, DSC, and precision metrics revealed that editing reduced the amount of interoperator variability for the semiautomatic segmentation condition [compare SA (pre) to SA (post) in Fig. 5 for these three metrics]. Interestingly, a similar pattern was observed for the manual segmentations. No significant differences were found between pre-editing manual segmentations and computer-assisted segmentations for any of the conditions or metrics. Postediting automatic segmentation consistently demonstrated lower variability than pre-editing semiautomatic segmentation. No significant differences were found between postediting automatic segmentation and postediting semiautomatic segmentation.

Fig. 4.

Editing magnitude based on (a) MAD, (b) DSC, (c) recall, (d) precision, and (e) volume difference, showing the differences between the segmentations pre- and postediting for each of the three conditions. Each bar shows the average metric value for one image across five operators. The error bars indicate one standard deviation. The horizontal lines indicated statistically significant differences on the averages of the groups across all the five operators and five images ($p<0.05$).

Fig. 5.

Interoperator variability based on (a) MAD, (b) DSC, (c) recall, (d) precision, and (e) volume difference. Each bar shows the average metric value for one image across five operators. The error bars indicate one standard deviation. The horizontal lines indicated statistically significant differences on the averages of the groups across all the five operators and five images ($p<0.05$). SA, semiautomatic.

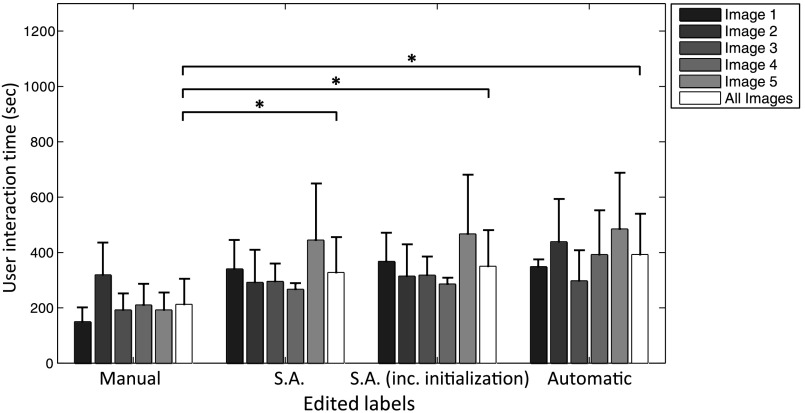
3.2. Required Editing Time and Correlation with Spatial Error Metrics

Table 2 shows the $\text{mean}\pm \text{standard deviation}$ of the recorded time required for each of the three conditions. For the semiautomatic condition, the time required only for editing, as well as the time required for editing plus the time required to interact with the semiautomated algorithm are reported separately. Figure 6 shows the breakdown of these editing times for each image. Significant differences were found among editing times for all conditions, except when comparing automatic segmentation to semiautomatic segmentation. To provide context for these editing times, according to the literature, the time required for manual prostate delineation on MRI can range from $\sim 5$²⁷ to 20 min per patient,²⁸ or about 1.6 min for each 2-D slice.²⁹ Our experience is concordant with this reported time range; timing of manual segmentation on the five images used in conditions (a) and (b) for one expert operator yielded a $\text{mean}\pm \text{standard deviation}$ segmentation time of $564\pm 162\mathrm{s}$ ($9:20\pm 2:42\min$). Based on Table 2, we observe that operators spent $\sim 2$ to 3 additional minutes editing computer-assisted segmentations, compared to the amount of time spent editing manual segmentations performed by a different expert operator.

Table 2.

User manual interaction time for ready to use prostate segmentation in T2w MRI.

Segmentation labels	No. of images	No. of Operators	User interaction time
Manual	5	5	$213\pm 90\mathrm{s}$ ($3:33\pm 1:30\min$)
Semiautomatic	5	5	$328\pm 126\mathrm{s}$ ($5:28\pm 2:06\min$)
Semiautomatic (user interaction time included)	5	5	$351\pm 128\mathrm{s}$ ($5:51\pm 2:08\min$)
Automatic	5	5	$393\pm 146\mathrm{s}$ ($6:33\pm 2:26\min$)

Fig. 6.

User manual interaction time on manual, semiautomatic (S.A.) and automatic segmentations. The statistically significant differences indicated with * on the averages of the groups across all the five images ($p<0.05$).

3.3. Correlation of Editing Time with the Metric Values

Table 3 shows the correlations between editing time and spatial editing magnitudes as measured using our segmentation error metrics. There were few significant correlations and none had magnitude $>0.5$. Significant correlations were predominantly in the base of the gland. In the base, recall was positively correlated with editing time, and precision and volume difference were negatively correlated with editing time. This pattern was observed in the whole gland as well but only weakly in the mid-gland and not in the apex.

Table 3.

Correlation between editing time and spatial editing magnitude measured using five metrics. Each value is the Spearman’s correlation coefficient between the value of each error metric and editing time. The bold numbers indicate statistically significant correlations ($p<0.05$).

Anatomic region	MAD	DSC	Recall	Precision	$\mathrm{\Delta }V$
Whole gland	0.204	0.18	0.361	$-\mathbf{0.341}$	0.417
Apex	0.206	$-0.081$	$-0.194$	$-0.138$	0.092
Mid-gland	0.263	$-0.149$	0.149	$-\mathbf{0.282}$	0.312
Base	$-0.14$	0.367	0.428	$-\mathbf{0.305}$	0.406

4. Discussion

4.1. Spatial Editing Magnitude and Interoperator Variability

As shown in Fig. 4, there was a nonzero difference between pre-editing and postediting expert manual segmentations for all metrics. The amount of editing performed on the manual segmentations provides valuable perspective on the amount of editing performed on the automatic and semiautomatic segmentations. One might expect that improvements to computer-assisted segmentation algorithms would require amounts of editing asymptotically approaching the amounts of editing that operators deem necessary for expert manual segmentations provided by other experts (i.e., expert operators would elect to edit outputs from even an ideal computer-assisted segmentation algorithm). For studies of computer-assisted segmentation algorithms using single-operator manual reference standard segmentations for validation, this observation is especially important; this suggests that algorithms yielding segmentation error metric values within the range observed in expert editing of manual expert segmentations could be considered to have essentially the same performance. For instance, Fig. 4 would suggest that two algorithms reporting DSC values of 94% and 96% would be considered to perform equally, as these values are well within the range of manual editing of manual segmentations. This observation could have ramifications for the ranking schemes used for segmentation grand challenges (such as PROMISE12³⁰), suggesting a practical equivalence of some top-ranked algorithms and a potential means for deciding when top-ranked algorithms are ready to be moved to the next stage of translation to clinical use. Although some metrics revealed a significant difference in the amount of editing required for automatic versus semiautomatic segmentations, this significance (and the magnitude of the difference) varied across metrics. This observation emphasizes the need for multiple, complementary spatial metrics to comprehensively assess the performance of a segmentation algorithm.

Our analysis in Fig. 5 indicates that, in general, allowing operators to edit provided segmentations reduces interoperator variability in segmentation, compared to the interoperator variability resulting from manual segmentations performed from scratch. The trend held even when comparing manual segmentations performed from scratch to manual segmentations that have been edited to satisfaction by another operator. This result underscores the value of providing operators with a starting segmentation for editing as this could improve the reproducibility of prostate segmentation, which is important for multicenter clinical trials and consistency of patient care in clinical practice. While the lowest interoperator variability resulted from giving operators a starting segmentation performed manually by another expert, in clinical practice, this is clearly impractical. From this perspective, the automatic segmentation could be seen as a practical alternative approach to obtain the starting segmentation. Although the difference in interoperator variability between postediting manual segmentations and postediting automatic segmentations was statistically significant, inspection of Fig. 5 reveals that this difference is very small from a practical perspective ($<0.5\mathrm{mm}$ in terms of MAD; 5% in terms of DSC, recall and precision; and $1{\mathrm{cm}}^3$ in terms of volume difference). This leads to the hypothesis that providing operators with an automatic segmentation with accuracy metric values similar to ours (Table 1) as a starting point will yield superior interoperator reproducibility even after editing, compared to manual segmentations performed from scratch. This hypothesis needs to be tested in a larger study covering a broader range of segmentation algorithms, a larger dataset, and a larger pool of operators having different experience levels.

4.2. Required Editing Time and Correlation with Spatial Error Metrics

Our results suggest that the use of automatic or semiautomatic segmentation algorithms to provide a starting segmentation for editing should reduce the total amount of time required to achieve a clinically acceptable segmentation, relative to typical reported times required for manual segmentations performed from scratch. Our results also suggest that the difference in total time required to use our automatic versus semiautomatic segmentation algorithms for this purpose is small, when the time required to interact with the semiautomatic segmentation algorithm is taken into account. Thus, the choice in this regard may come down to operator preference; the semiautomatic segmentation algorithm allows the operator to specify the apex-to-base extent of the prostate, reducing the need for editing involving adding or removing entire slices in these regions. This comes at the cost of needing to wait for $<60\mathrm{s}$ for the segmentation to be computed online, whereas the automatic segmentations can be computed offline immediately after MRI scanning and thus would appear instantaneously to the operator at time of editing. Our results also showed that operators spent more time in editing the computer-assisted segmentations, compared to the time spent in editing manual segmentations by another expert operator. We posit that this difference in editing time is an important metric for determining the suitability of a computer-assisted segmentation algorithm for translation to clinical use in scenarios in which for safety or other reasons, expert operator verification for necessary editing will be performed on every segmentation. From this perspective, there is room for improvement in our semiautomatic and automatic algorithms of $\sim 2$ to 3 min of editing time per prostate in order to achieve concordance with the amount of editing performed on manual segmentations.

Table 3 indicates a consistent negative correlation of the precision metric value with editing time, with statistically significant correlations in all anatomic regions except for the apex. This implies that the greater the false positive area in a computer-assisted segmentation, the greater the time that will be required to edit the segmentation to a clinically acceptable level. This is corroborated by the consistent positive correlation with the volume difference metric (again, significant everywhere except the apex), implying that the greater the amount of oversegmentation performed by computer-assisted segmentation algorithm, the more editing time that will be required. Comparing the correlation coefficients for precision and volume difference within the apex, mid-gland, and base, the strongest correlations were found in the base region. This implies that the above relationships are especially applicable for false-positive regions and oversegmentation of the base. However, based on these observations, one could make only a weak recommendation that the amount of necessary editing time could be estimated based on the precision and volume difference spatial error metric values; although the correlation coefficients are statistically significant in many cases, they do not have high magnitude.

The lack of strong correlations in Table 3 implies weak relationships between editing time and spatial editing magnitudes, as measured by our segmentation error metrics. The observations in the previous paragraph notwithstanding, this implies that in general, one cannot use spatial metrics such as the MAD, DSC, precision, recall, and volume difference to estimate the amount of time that an operator will require to produce a clinically acceptable segmentation using the output of a segmentation algorithm as a starting point. This is an important observation since in most clinical workflows, time is a scarce and valuable resource; if it takes (nearly) as long to edit a segmentation from an algorithm as it does to perform a manual segmentation from scratch, the clinician may be inclined toward the simpler approach of performing manual segmentation. We surmise that this issue is a major contributor to the present state of affairs, in which the academic literature has produced many hundreds of computer-assisted segmentation algorithms and yet very few of them have moved forward to clinical use. This leads to the conjecture that the most important metrics to compute when evaluating the suitability of an algorithm for clinical translation are operator variability, measured using spatial metrics, such as MAD, DSC, and so on, and editing time, measured directly using a sample of multiple operators. Viewed through this lens, the ideal segmentation algorithm would yield low operator variability and low editing time. This suggests that a potential reevaluation of the use spatial metrics for measuring segmentation “accuracy” may be in order, since in most practical clinical workflows, the final segmentation as edited and approved by the clinician will be used for its clinical purpose and could be considered 100% “accurate” for practical purposes. This observation supports engineers and computer scientists aiming for the concrete goal of “producing a clinically useful segmentation in a minimum amount of time,” in lieu of setting our aims according to the nebulous notion of accuracy, with all of its attendant issues (e.g., differing expert opinions on what constitutes a correct segmentation, issues regarding whether “gold standard” expert segmentations truly delineate the histologic boundary of the target of interest).

4.3. Limitations

This work must be considered in the context of its strengths and limitations. We acknowledge that given our image sample size and number of operators participating in the study, this is a descriptive, hypothesis-generating study that points the way to potentially fruitful studies on larger sample sizes with sufficient statistical power to draw firmer conclusions. We also acknowledge that although the editing interface we used, involving a mouse-driven variable-sized paintbrush tool, is concordant in its mode of operation with the interfaces used in many clinical workflows, it does constitute only a single mode of performing segmentation editing. Thus, our study generates no knowledge about the impact of the choice of editing tool on editing times, and this would be a subject of valuable further study. Finally, in this user study, we tested only two computer-assisted segmentation algorithms; a more comprehensive future study involving a broader cross-section of current algorithms is warranted.

4.4. Conclusions

In this paper, we conducted a user study measuring the amount of spatial editing performed by expert users on segmentations generated manually, semiautomatically, and automatically. We measured the interoperator variability in segmentation before and after editing, and measured the relationship between editing magnitude and time spent editing. With reference to the enumerated research questions in Sec. 1 of this paper, we have reached four main conclusions, with the acknowledgment that our sample size implies that these conclusions should be considered as hypotheses to test in future, larger studies. (1) As would be expected, the operators performed the most spatial segmentation editing on the automatic segmentations, followed by the semiautomatic segmentations, and the least amount of editing on the manual segmentations. The measured editing magnitudes varied according to the error metric used, reinforcing the value of using multiple, complementary error metrics in segmentation studies, rather than focusing on one or two typically used metrics (e.g., the MAD and DSC). (2) Providing operators with a starting segmentation for editing, either performed manually by another operator or (semi-)automatically through an algorithm, yielded lower interoperator variability in the final segmentation, compared to interoperator variability in manual segmentations performed from scratch (as is frequently performed in clinical workflows currently). Interoperator variability resulting from using our automatic algorithm to generate starting segmentations was not substantially higher than that resulting from using expert manual segmentations as starting segmentations, suggesting a role for our automated segmentation algorithm in this context. (3) The use of our automatic or semiautomatic segmentation algorithms to generate starting segmentations for editing is expected to decrease the total required segmentation time, compared to the time required to perform manual segmentations from scratch, and the choice of automatic versus semiautomatic segmentation for this purpose comes down to operator preference. (4) The necessary time requirement for segmentation editing cannot be reliably predicted from spatial segmentation error metrics in all anatomic regions of the prostate. Thus, for the many clinical workflows, where manual segmentation review and editing will be performed for safety and other reasons, and minimization of editing time is a primary goal, the fact that one algorithm outperforms another in terms of spatial metrics such as the MAD and DSC does not imply that the algorithm is more suitable for clinical translation. In such contexts, where the medical expert’s final edited segmentation is taken as correct for practical purposes, the ideal segmentation algorithm supports the expert’s obtaining a clinically acceptable segmentation in a minimum amount of time while minimizing interoperator segmentation variability. This increases the volume of patients that can be treated and simultaneously supports consistent quality of the intervention patients receive.

Biographies

Maysam Shahedi is a postdoctoral fellow in the Department of Medical Biophysics at Western University in London, Canada. He completed his PhD in biomedical engineering at Western University. He also holds BSc and MSc degrees in electrical engineering from Isfahan University of Technology, Iran.

Derek W. Cool is a research assistant at Robarts Imaging Research Laboratories and a radiology resident at Western University in London, Canada. He has received his BSc in computer science from the University of North Carolina in Chapel Hill, United States, and his MD-PhD in medical biophysics and radiology from Western University in London, Canada.

Cesare Romagnoli is an associate professor in the Department of Medical Imaging at Western University in London, Canada, and a radiologist at London Health Science Centre in London, Canada.

Glenn S. Bauman is a radiation oncologist specializing in genitourinary and central nervous system malignancies. He is also a professor of oncology at Western University and is an associate scientist at Lawson Health Research Institute in London, Canada. He received his BSc and MD from Western University, where he also completed his residency in radiation oncology. He also completed a clinical fellowship in radiation oncology at the University of California at San Francisco, United States.

Matthew Bastian-Jordan is an adjunct professor of imaging at Western University in London, Canada. He is also a radiologist at Queensland X-Ray in Queensland, Australia. He has completed a fellowship in musculoskeletal at Queensland X-Ray and a fellowship in abdominal and cross sectional imaging at Western University.

George Rodrigues is a clinician scientist and radiation oncologist at the Lawson Health Research Institute and London Health Sciences Centre in London, Canada. He has graduated from the University of Toronto Radiation Oncology Residency Program and attained his MSc in clinical epidemiology and biostatistics and his PhD in medicine.

Belal Ahmad is an associate professor of radiation oncology at Western University in London, Canada. He holds a BSc in human biology from the University of Toronto in Toronto, Canada, and an MD from Queen’s University Medical School in Kingston, Canada. He pursued his residency in radiation oncology at McMaster University in Hamilton, Canada, and a fellowship at Western University in London, Canada. He is a physician at the London Regional Cancer Program in London, Canada.

Michael Lock is an associate professor of medicine and medical biophysics at Western University in London, Canada. He is a staff radiation oncology consultant in the Department of Oncology at Western University and an associate scientist with the Lawson Health Research Institute in London, Canada.

Aaron Fenster is the director of the Imaging Research Laboratories at the Robarts Research Institute and a professor of medical biophysics, biomedical engineering, and radiology at Western University in London, Canada. He received his PhD degree in medical biophysics from the University of Toronto in Toronto, Canada. He holds a Canada Research Chair-Tier 1 in biomedical engineering.

Aaron D. Ward is an associate professor of medical biophysics, biomedical engineering, and oncology at Western University in London, Canada. His research focuses on development and clinical translation of computational techniques for diagnosis, therapy guidance, and treatment response assessment in oncology. He has received funding from the Natural Sciences and Engineering Research Council of Canada, the Canadian Institutes of Health Research, the Ontario Institute for Cancer Research, Prostate Cancer Canada, and Cancer Care Ontario.

Appendix.

The automatic segmentation method consists of two main steps: training and segmentation. The training step is identical to the training step used in the semiautomatic method and fully described in Ref. 17. At a high-level, during training, the algorithm learns (1) the local appearance of the prostate border through extracting a set of locally defined mean intensity image patches and (2) the prostate shape variation across the training image set by extracting 2-D statistical shape models for the prostate at each axial cross-section.

To segment a new prostate MR image, the algorithm first coarsely localizes the prostate region by automatically positioning a polygonal template shaped similarly to a typical prostate shape on the mid-sagittal plane. Then, the algorithm searches within a region defined based on the template position to find the prostate border on the axial slices. The segmentation is described in detail below.

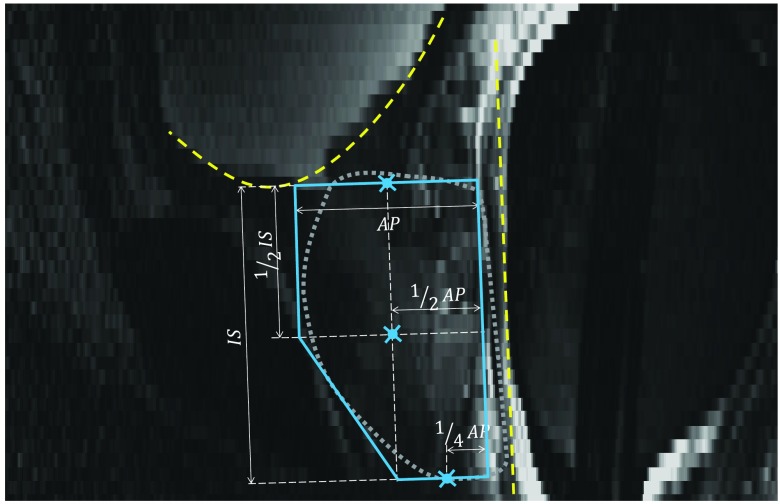
Anterior rectal wall boundary determination: The first step for positioning of the template was to fit a line to the anterior rectal wall boundary on the mid-sagittal slice of the image. To define the line, we extracted 10 equally spaced line intensity profiles (every second line) on the mid-sagittal image slice, parallel to the axial planes, and nearest to the mid-axial slice. Along each line, running from anterior to posterior, we selected a candidate point at the minimum of the first derivative (the point of sharp intensity transition from bright to dark at the rectal wall). We reduced the search space along each profile by covering 50% of the mid-sagittal plane width in the anteroposterior direction, starting from a 30% offset from the anterior-most extent of the plane. We tuned an optimizer to treat 40% of the points as outliers by computing a least-trimmed squares fit³¹ line to the candidate points. The dashed line in Fig. 7 shows the resulting rectal wall boundary line.

Fig. 7.

Automatic coarse localization of the prostate. The dashed line shows the estimated rectal wall line. The dashed curve shows the estimated bladder boundary. The solid line polygon is the prostate shape template used to select the center points for base, apex, and mid-gland. The manually delineated prostate border has been overlaid in dotted line as a reference. AP and IS are, respectively, anterioposterior and inferior–superior dimensions of the prostate. The three indicated points on the shape template define the estimated center points for base, apex, and mid-gland.

Inferior bladder boundary determination: The next step was to define the inferior boundary of the bladder on the mid-sagittal plane. We defined a set of lines oriented parallel to the rectal boundary line defined in the previous step. We extracted the intensity profile along each line and running from superior to inferior, we selected loci of minimum first derivative of the intensities, corresponding to the sharp intensity transition from bright to dark at the bladder border. We defined the parallel lines with 2 mm spacing starting 5 mm anterior to the rectal wall and limited the search space along the lines to the segments lying within the superior half of the image. We removed the points forming a local concave shape near the posterior end of the curve (i.e., inconsistent with bladder inferior aspect anatomy). Then, we computed a least-trimmed squares fit³¹ polynomial curve (second-order curve when the candidate point configuration yielded a convex shape and first-order curve otherwise) to the points with the optimizer tuned to treat 20% of the points as outliers. The dashed curve in Fig. 7 shows the determined bladder boundary.

Coarse prostate localization by template fitting: A prostate shape template (described in Fig. 7) was defined based on prostate dimensions readily available from the prostate ultrasound examination performed prior to MRI. The prostate template was positioned inferior to the bladder boundary curve, parallel to the rectal wall line and 3 mm anterior to it along a line perpendicular to the rectal wall line. The template was positioned to have a single contact point between the template and bladder boundary curve (Fig. 7).

3-D prostate boundary localization: The final segmentation step was to define the surface of the prostate in 3-D. The template position defined the center points for the base-most slice, the apex-most slice, and the mid-gland slice equidistant to the base- and apex-most slices. By interpolation of these three points using piecewise cubic interpolation, we estimated the center points for all the axial slices between base and apex. Then, we used the approach described in detail in Ref. 17 for prostate boundary localization. At a high level, for each slice, we defined 36 equally spaced rays emanating from the center point. Each ray was corresponded to one of the mean intensity image patches extracted during training. We translated the image patch along the ray to select a point on the ray whose circular image patch had the highest appearance similarity to the mean intensity patch, using the normalized cross-correlation similarity metric. After selecting 36 prostate border candidate points for each slice, 2-D shape regularization was performed using the corresponding shape model extracted during training. 3-D boundary localization was finalized by 3-D shape regularization. Full details are available in Ref. 17.

This method was tested using leave-one-out cross validation using a dataset of 42 images. The segmentations given by the algorithm were compared to segmentations performed by a single human expert operator. This experiment yielded a MAD of $3.2\pm 1.2\mathrm{mm}$, DSC of $71\%\pm 11\%$, recall of $69\%\pm 15\%$, precision of $76\%\pm 12\%$, and $\mathrm{\Delta }V$ of $-3.6\pm 1.4{\mathrm{cm}}^3$. Execution time was $54\pm 13\mathrm{s}$.