Mg²⁺ differentially regulates two modes of mitochondrial Ca²⁺ uptake in isolated cardiac mitochondria: implications for mitochondrial Ca²⁺ sequestration

Abstract

The manner in which mitochondria take up and store Ca²⁺ remains highly debated. Recent experimental and computational evidence has suggested the presence of at least two modes of Ca²⁺ uptake and a complex Ca²⁺ sequestration mechanism in mitochondria. But how Mg²⁺ regulates these different modes of Ca²⁺ uptake as well as mitochondrial Ca²⁺ sequestration is not known. In this study, we investigated two different ways by which mitochondria take up and sequester Ca²⁺ by using two different protocols. Isolated guinea pig cardiac mitochondria were exposed to varying concentrations of CaCl₂ in the presence or absence of MgCl₂. In the first protocol, A, CaCl₂ was added to the respiration buffer containing isolated mitochondria, whereas in the second protocol, B, mitochondria were added to the respiration buffer with CaCl₂ already present. Protocol A resulted first in a fast transitory uptake followed by a slow gradual uptake. In contrast, protocol B only revealed a slow and gradual Ca²⁺ uptake, which was approximately 40 % of the slow uptake rate observed in protocol A. These two types of Ca²⁺ uptake modes were differentially modulated by extra-matrix Mg²⁺. That is, Mg²⁺ markedly inhibited the slow mode of Ca²⁺ uptake in both protocols in a concentration-dependent manner, but not the fast mode of uptake exhibited in protocol A. Mg²⁺ also inhibited Na⁺-dependent Ca²⁺ extrusion. The general Ca²⁺ binding properties of the mitochondrial Ca²⁺ sequestration system were reaffirmed and shown to be independent of the mode of Ca²⁺ uptake, i.e. through the fast or slow mode of uptake. In addition, extra-matrix Mg²⁺ hindered Ca²⁺ sequestration. Our results indicate that mitochondria exhibit different modes of Ca²⁺ uptake depending on the nature of exposure to extra-matrix Ca²⁺, which are differentially sensitive to Mg²⁺. The implications of these findings in cardiomyocytes are discussed.

Introduction

Mitochondria have the capacity to take up and sequester large amounts of Ca²⁺ (Vasington and Murphy 1962). For decades it was believed that mitochondrial Ca²⁺ was a necessary means to maintain proper energy balance in the heart. However, recent mitochondrial Ca²⁺ uniporter (MCU) knockout studies in mice have contested the importance of Ca²⁺ in mitochondrial energy homeostasis (Pan et al. 2013). Cardiac specific MCU knockout studies using a mouse model reveal that cardiac mitochondrial Ca²⁺ is only essential during high stress conditions, but not for routine activities (Kwong et al. 2015; Luongo et al. 2015; Wu et al. 2015). Whereas the role of mitochondria as a Ca²⁺ sink against cytosolic Ca²⁺ overload is well recognized (Szabadkai and Duchen 2008; Nicholls 2005; Rasola and Bernardi 2011), their role in shaping the cytosolic Ca²⁺ transients during physiological conditions is still debated (Boyman et al. 2014; Lu et al. 2013). Moreover, the precise mechanisms and consequences by which mitochondria take up, extrude, and sequester cytosolic Ca²⁺ remain obscure.

It has been suggested that mitochondrial Ca²⁺ uptake consists of different components that result in different matrix free Ca²⁺ dynamics. One possible component constitutes the rapid and beat-to-beat changes in the concentration of matrix free Ca²⁺ ([Ca²⁺]_m) (Dedkova and Blatter 2013; Huser et al. 2000). This fast mode of Ca²⁺ uptake is proposed to be responsible for regulating ATP production (Dedkova and Blatter 2013; Carafoli 2010; Tarasov et al. 2012) by altering activities of Ca²⁺-sensitive dehydrogenases and other Ca²⁺-sensitive processes. However, this idea, as noted above, is controversial based on recent data obtained from MCU knockout mice (Pan et al. 2013; Kwong et al. 2015). Another possible component that has been proposed is the slow mode of Ca²⁺ uptake, which functions as a low-pass filter of the cytosolic Ca²⁺ transient while gradually accumulating matrix Ca²⁺ (Dedkova and Blatter 2013; Sedova et al. 2006). It is also thought to be a significant source of Ca²⁺ uptake during periods of sustained elevation of cytosolic Ca²⁺ (Carafoli 2010; Dorn and Maack 2013), such as in ischemia and reperfusion (IR) injury (Varadarajan et al. 2001).

The MCU is the primary pathway for Ca²⁺ uptake (Baughman et al. 2011; De Stefani et al. 2011) and may possess multiple conductance modes (Kirichok et al. 2004; Wei et al. 2012; Csordas et al. 2013). The recent identities of the MCU channel and its regulatory proteins (e.g. MICU1 and MICU2) involved in modulating mitochondrial Ca²⁺ uptake are now characterized as sensors of extra-matrix [Ca²⁺] ([Ca²⁺]_e) that stimulate or inhibit MCU, respectively. This would allow for a rapid response of mitochondria to Ca²⁺ signals generated in the cytoplasm (Marchi and Pinton 2014). Previous studies suggest that there exist additional potential Ca²⁺ uptake modes: the mitochondrial ryanodine-like receptor (Beutner et al. 2001; Tewari et al. 2014) and the rapid-mode (RaM) of Ca²⁺ uptake (Buntinas et al. 2001; Gunter et al. 1998; Sparagna et al. 1995). These fast modes of Ca²⁺ uptake were postulated, but not conclusively shown, to be responsible for transduction of physiological Ca²⁺ transients to match oxidative phosphorylation with energetic demands (Huser et al. 2000; O’Rourke and Blatter 2009).

Pharmacological inhibitors and/or modeling approaches have been used to identify the different modes of Ca²⁺ uptake, but the conclusions drawn from these studies have been disputed. For example, recent studies show relatively little mitochondrial Ca²⁺ uptake during physiological Ca²⁺ transients (Boyman et al. 2014; Lu et al. 2013), which implies that in the physiological setting, MCU might play only a negligible role in shaping physiological Ca²⁺ dynamics in the beating heart. Moreover, when mitochondria are loaded with sufficient Ca²⁺, changes in matrix free Ca²⁺ are difficult to detect due to the higher buffering power associated with higher mitochondrial Ca²⁺ loads (Bazil et al. 2013; Blomeyer et al. 2013). Regardless, the MCU becomes most relevant when cytosolic [Ca²⁺] is abnormally elevated, such as during IR, oxidative stress, sarcoplasmic reticulum stress, or Ca²⁺ overload (Varadarajan et al. 2001; An et al. 2001a; Rhodes et al. 2003; An et al. 2001b).

Excess Ca²⁺ uptake by mitochondria is sequestered in a phosphate-dependent reaction that forms amorphous calcium phosphate (CaPi) granules (Chalmers and Nicholls 2003; Greenawalt et al. 1964; Kristian et al. 2007). The exact composition of these CaPi granules is unknown, but they are presumed to consist of mixtures of Ca₃(PO₄)₂, Ca₈H₂(PO₄)₆, and Ca₁₀(PO₄)₆(OH)₂ (Thomas and Greenawalt 1968). The properties of this sequestration system are a current area of interest because the buffering system alters both Ca²⁺ uptake and release dynamics (Blomeyer et al. 2013), and may regulate mitochondrial permeability transition (mPTP) (Szabadkai and Duchen 2008; Wei et al. 2012), which in turn may regulate mitochondrial Ca²⁺ transients (Sareen et al. 2007). In the heart and other excitatory tissues, the mitochondrial Na⁺/Ca²⁺ exchanger (mNCE) is the primary pathway for Ca²⁺ extrusion (Boyman et al. 2013; Cai and Lytton 2004; Palty et al. 2004). Therefore, [Ca²⁺]_m is primarily maintained by a balance of Ca²⁺ uptake facilitated by the MCU, Ca²⁺ extrusion by the mNCE, and Ca²⁺ buffering by the sequestration system. The sequestration system acts as a Ca²⁺ reservoir so that the activities of MCU and mNCE establish a set point that helps maintain sub-lethal thresholds of cytosolic Ca²⁺ during Ca²⁺ loading conditions.

Thus, the modes of mitochondrial Ca²⁺ uptake and their regulation remain obscure. Interestingly, in a recent study, we reported that mitochondrial Ca²⁺ uptake displays two different profiles of matrix Ca²⁺ transient when CaCl₂ was added to mitochondrial suspension: a fast uptake of Ca²⁺ followed by a slower and more gradual uptake as matrix Ca²⁺ plateaus to a steady state (Boelens et al. 2013). Addition of Mg²⁺ to the respiration buffer appeared to have a differential effect on the two phases of the Ca²⁺ transient, with the slow phase attenuated more than the fast uptake phase. However, the impact of Mg²⁺ on mitochondria buffering of Ca²⁺ is not known. In the present study, we used a non-pharmacological approach to distinguish a slow and fast mode of mitochondrial Ca²⁺ uptake and determine the impact of extra-matrix Mg²⁺ on the modes of Ca²⁺ uptake and the mitochondrial buffering capacity or sequestration power of Ca²⁺. To further delineate the two modes of Ca²⁺ uptake, mitochondria were exposed to two different protocols based on the order by which mitochondria or CaCl₂ were first added to the respiration buffer with and without added MgCl₂.

Methods

Mitochondrial isolation

All experiments conformed to the Guide for the Care and Use of Laboratory Animals, and were approved by the Medical College of Wisconsin Institutional Animal Care and Use Committee. Mitochondria from guinea pig hearts were isolated as previously described (Blomeyer et al. 2013; Boelens et al. 2013; Aldakkak et al. 2013; Haumann et al. 2010). Briefly, guinea pigs (250–350 g) were anesthetized with intraperitoneal injection of 30 mg ketamine, and 700 units of heparin for anticoagulation. Hearts were excised and minced in ice-cold isolation buffer containing 200 mM mannitol, 50 mM sucrose, 5 mM KH₂PO₄, 5 mM MOPS, 1 mM EGTA and 0.1 % bovine serum albumin (BSA). Buffer pH was adjusted to 7.15 with KOH. The minced pieces were suspended in 2.65 ml ice-cold buffer with 5 U/ml protease (from Bacillus licheniformis) and homogenized at low speed for 30 s. Afterwards, 17 ml of ice-cold isolation buffer was added, and the suspension was again homogenized for 30 s and centrifuged at 8000 g for 10 min. The supernatant was discarded, and the pellet was re-suspended in 25 ml of ice-cold isolation buffer and centrifuged at 900 g for 10 min. The supernatant was recovered and centrifuged once more at 8000 g to yield the final mitochondrial pellet, which was re-suspended in isolation buffer and kept on ice (4 °C) for experiments after fluorescent dye loading to measure matrix Ca²⁺ transients.

The mitochondrial protein concentration was measured using the Bradford method (1976) and diluted with isolation buffer to a protein concentration of 5 mg/ml and incubated with the appropriate fluorescent dye or the vehicle (DMSO). Incubated mitochondria were re-suspended in 25 ml of ice-cold isolation buffer and re-centrifuged at 8000 g. Subsequently, the dye-loaded pellet was re-suspended in cold isolation buffer, and the protein concentration was measured again using the Bradford method and diluted finally to 12.5 mg/ml. The final mitochondrial suspension was kept in packed ice (4 °C), and all subsequent experiments were conducted within 6 h after the last step of the isolation procedure.

Experimental groups and protocols

Isolated mitochondria were exposed to five different concentrations of CaCl₂ and three different concentrations of MgCl₂. In addition, each of these groups was exposed to two different Ca²⁺ loading protocols, resulting in 30 groups overall. The only difference between the two experimental protocols (A and B) was the order of addition of mitochondria and CaCl₂ to the respiration buffer containing pyruvic acid. Extra-matrix (buffer) free Ca²⁺ ([Ca²⁺]_e) and matrix free Ca²⁺ ([Ca²⁺]_m) were monitored under identical experimental conditions for both protocols, except for the order of addition of CaCl₂ or mitochondria to the buffer. For the NADH and ΔΨ_m measurements, the number of experimental groups was reduced to eight for each experimental protocol (A and B). Each experiment was conducted with mitochondria pooled from 2 hearts and repeated 3–4 times on different days. Respiration buffer, which was adjusted to pH 7.15 with KOH, contained 130 mM KCl, 5 mM K₂HPO₄, 20 mM MOPS, 0.1 % BSA, and 40 μM EGTA (Blomeyer et al. 2013; Haumann et al. 2010). The mitochondrial concentration for all experiments was 0.5 mg/mL. The pH of the respiratory buffer remains at 7.15 after the addition of CaCl₂ and other substances, which was verified using a self-calibrating pH meter at the end of each experiment.

All experiments were conducted at room temperature (25 °C) using the cuvette-based fluorescence spectrophotometer described in our previous studies (Blomeyer et al. 2013; Boelens et al. 2013; Haumann et al. 2010; Agarwal et al. 2012, 2014; Aldakkak et al. 2011). Pyruvic acid (PA, 0.5 mM), cyclosporine A (CsA, 0.5 μM) and MgCl₂ (0, 0.5, 1.0 mM) were always present in the buffer. Ruthenium red (RR, 1 μM) was added at 300 s after all of the Ca²⁺ bolus was taken up. The volume of the experimental buffer in the cuvette containing no added EGTA, and before adding any substance was 910 μL. The volume of added substances (PA, MgCl₂, CaCl₂, CsA, NaCl) to the cuvette was 10 μL each and the volume of the mitochondrial suspension added to the cuvette was 40 μL resulting in a total volume of 1000 μl for each experiment in protocols A and B. At a final volume of 1000 μL, the dilution factor after the addition of mitochondria was 25 times. Since the initial concentration of mitochondria following isolation was 12.5 mg/mL, the final mitochondrial suspension was 0.5 mg/mL in each experiment. The addition of a 40 μL volume of mitochondrial suspension, which had a concentration of 1 mM EGTA from the original mitochondrial suspension (12.5 mg/mL), resulted in a final EGTA concentration of approximately 40 μM for the mitochondrial suspension in the cuvette. The experimental buffer had a [Ca²⁺]_e of approximately 50 nM that was similar to [Ca²⁺]_m before adding any CaCl₂.

The protocols (A and B) used to assess differences in [Ca²⁺] dynamics are shown in Fig.1. In protocol A at t = 30 s, 40 μL mitochondrial suspension was added to the experimental buffer. At t = 60 s, 0, 10, 20, 30 or 40 μM total CaCl₂ (10 μL of concentrated solution) was added to the mitochondrial suspension. In protocol B at t = 30 s, 0, 10, 20, 30 or 40 μM total CaCl₂ (10 μL of concentrated solution) was added first to the experimental buffer followed by addition of 40 μL mitochondrial suspension at t = 60 s. A high-speed magnetic stirring bar was turned on at the onset of each experiment to ensure prompt and rapid continuous mixing of the cuvette contents. With this approach, the effect of high initial localized boluses of [CaCl₂] on mitochondria in protocol A was minimized. In both protocols at t = 300 s, 1 μM RR was added to block the MCU and to prevent Ca²⁺ re-uptake after its release via the NCE. At t = 360 s, 10 mM NaCl was added to induce Ca²⁺ efflux. The respiration buffer including the added PA was Na⁺-free, except for the NaCl added at the end of each protocol to elicit Ca²⁺ release via mNCE activation. To avoid differences in buffer volume, the vehicle (deionized H₂O) was used for 0 mM MgCl₂ and 0 μM CaCl₂. Some additional experiments (not shown) were conducted in the presence of the mNCE inhibitor, CGP-37,157 (25 μM; Tocris Bioscience, Minneapolis, MN), to verify that the observed Na⁺-induced Ca²⁺ efflux was due only to mNCE activity. All chemicals were obtained from Sigma-Aldrich (St. Louis, MO) unless noted otherwise.

Fig. 1.

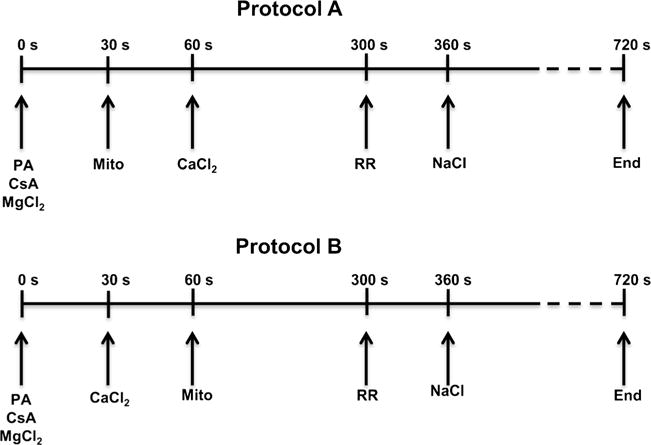
Timelines show the two experimental protocols used to characterize and quantify mitochondrial Ca²⁺ handling (influx, efflux, sequestration) in isolated guinea pig cardiac mitochondria. In protocol A, mitochondria were added to the experimental buffer before CaCl₂ was added. In protocol B, mitochondria were added to respiration buffer with CaCl₂ already present. All other additions were identical between protocols. 40 μM EGTA was present in all the experimental buffers; 0.5 μM CsA was added to all mitochondrial suspensions. Inset axes are the same as the main figure panels

Assessment of mitochondrial functional integrity

Before and after fluorescence measurements were made using the PTI spectrofluorometer, mitochondrial functional integrity/viability was assessed by measuring the respiratory control index (RCI) with a Clark type O₂ electrode (MT200A, Strathkelvin Instruments, Glasgow, UK). The RCI of mitochondria energized with 0.5 mM PA was calculated by dividing the rate of state 3 respiration (250 μM ADP) by the rate of state 4 respiration. Before the start of fluorescent measurements, RCI values were above 12 and at the end of the measurements (after approximately 6 h) RCI values were revaluated and remained above 8. This strong RCI after 6 h indicates that the mitochondria were viable and well coupled for the duration of the experiments.

Fluorescence measurements

Fluorescence spectrophotometry (Qm-8, Photon Technology International, Birmingham, NJ) was used to assess levels of [Ca²⁺]_e and [Ca²⁺]_m, ΔΨ_m, and NADH. Fura-4F (Invitrogen™, Eugene, OR) was used to measure either [Ca²⁺]_m (AM form) or [Ca²⁺]_e (penta-potassium salt). For [Ca²⁺]_m measurements, mitochondria were incubated for 30 min at room temperature (25 °C) with Fura-4F AM (5 μM) dissolved in DMSO. A final spin and resuspension of mitochondria were performed to remove any residual dye. To measure [Ca²⁺]_e, Fura-4F penta-potassium (1 μM) was added to the respiration buffer. ΔΨ_m was measured using the lipophilic dye TMRM (1 μM, Invitrogen™, Eugene, OR) in a ratiometric excitation approach (Scaduto and Grotyohann 1999). NADH was measured by its autofluorescence (Blomeyer et al. 2013; Boelens et al. 2013; Haumann et al. 2010). To ensure identical conditions as for the [Ca²⁺]_m measurement, mitochondria were incubated with the appropriate concentration of DMSO for 30 min at 25 °C before measuring [Ca²⁺]_e, ΔΨ_m, and NADH. [Ca²⁺]_e and ΔΨ_m were measured by directly adding the appropriate dye to the respiration buffer.

Measurement of free Ca²⁺

The Ca²⁺ measurements in this study represent the free matrix and extra-matrix Ca²⁺ for both protocols whereas the added CaCl₂ (10–40 μM) represents the total amount of CaCl₂ added to the cuvette. The molecular dye Fura-4F was used to measure concentrations of both matrix and extra-matrix free Ca²⁺. The vendor specified dissociation constant (K_d) of Fura-4F is 770 nM. However, when loaded in mitochondria, we determined a K_d of 890 nM. At an emission wavelength (λ_em) of 510 nm, the peak of the excitation wavelength (λ_ex) of Fura-4F shifted from 380 nm to 340 nm on binding Ca²⁺ to the dye molecules. Measuring Ca²⁺ at these wavelengths was not influenced by background noise (e.g. NADH autofluorescence), so a background subtraction was unnecessary. For calibration, ratios were obtained when all Fura-4F had become bound to Ca²⁺ (R_max) and when no Ca²⁺ was bound to Fura-4F (R_min). To determine these ratios, experiments were conducted in PA energized mitochondria using 500 nM CsA, 500 μM CaCl₂ for R_max, and A23187 (Ca²⁺-ionophore) in the presence of 2.5 mM EGTA for R_min. The [Ca²⁺]_m was calculated using the following equation (Grynkiewicz et al. 1985):

$${\left[{\text{Ca}}^{2=}\right]}_{\mathrm{m}}=K_d·\frac{S_{f2}}{S_{b2}}·\frac{R-R_{\text{min}}}{R_{\text{max}}-R}$$ (1)

K_d is 890 nM, S_f2 is the signal intensity of free Fura-4F measured at 380 nm, and S_b2 is the signal intensity of Ca²⁺-saturated Fura-4F measured at 380 nm. Their values were obtained from the R_max and R_min experiments, which were done for each preparation. For details, see Supplemental Figs. S1 and S2 for the fluorescence spectra in the presence of various amounts of Ca²⁺ and calibration of Fura-4F, respectively. Calibration of the Fura-4F penta-potassium signal in the presence of mitochondria was slightly different from the one used for Fura-4F AM. R_min was measured in respiration buffer with added 100 μM EGTA without added CaCl₂ to chelate all the Ca²⁺, while R_max was determined in the respiration buffer containing 1 mM CaCl₂. Ca²⁺ fluorescent measurements and calculation of [Ca²⁺]_e were conducted in the same manner as described above for [Ca²⁺]_m. Free [Mg²⁺] was not measured in this study. Our previous study showed that the calculated buffer [Mg²⁺] after adding MgCl₂ was nearly identical to the [Mg²⁺] measured using Mag-Fura-2 fluorescence (Boelens et al. 2013).

Measurement of NADH

NADH autofluorescence signals were measured at λ_ex of 350 nm and λ_em of 456 nm. For calibration, the NADH pool was either fully oxidized (0 %) with the respiratory uncoupler carbonyl cyanide 3-chlorophenylhydrazone (CCCP, 4 μM), or fully reduced (100 %) with the complex I blocker rotenone (10 μM).

Measurement of ΔΨ_m

Fluorescence changes using TMRM were detected by two λ_ex (546 and 573 nm) and one λ_em (590 nm). Using the ratio of the emission at both excitation wavelengths (573/546) has the advantage of a higher dynamic range when compared to a single wavelength technique (Scaduto and Grotyohann 1999). At the end of each protocol at t = 720 s, CCCP (4 μM) was added to fully depolarize mitochondria.

Statistical analyses

The data from four hearts were pooled separately for each of the four fluorescence measurements. Data were transferred from PTI FelixGX (Version 3) into Microsoft® Excel® (2007). IBM® SPSS® (Version 19) was used to execute statistical analysis, which was performed using one-way analysis of variance followed by post hoc Tukey’s range test to examine differences among individual groups. Changes were considered statistically significant when the p-value was set at ≤0.05. Data for analyses were collected at the times given below and are presented as means ± SEM. For some analyses, results are presented as means ± standard deviation. Statistical tests were performed to compare changes in [Ca²⁺]_m averaged from 60 to 70 s of all 30 possible treatment combinations for the five [CaCl₂], three [MgCl₂], and two protocol effects.

Calculation of mitochondrial Ca²⁺ buffering power

Initial rates of Ca²⁺ flux for both the uptake and extrusion phases were derived from the data and converted from d[Ca²⁺]_e/dt to d[Ca²⁺]_tot/dt using the method outlined in Bazil et al. (2013). Briefly, non-linear trend lines were fitted to the data shown in Figs. 2 and 4, and the analytical derivatives were used to compute the rate of change in free Ca²⁺. Trend line fits to the extra-matrix and matrix dynamics are shown in Supplemental Figs. S4 and S5, respectively. The extra-matrix rates were converted to total Ca²⁺ flux by using the known buffering power of EGTA. For simplicity, all Ca²⁺ uptake rates were assumed to be through the MCU and all Ca²⁺ release rates were assumed to be via the NCE. To compute the mitochondrial Ca²⁺ buffering power, the approach described in Bazil et al. (2013) was used. Specifically, the buffering power was calculated using the Ca²⁺ extrusion phase of the free Ca²⁺ dynamics profiles. The calculated Ca²⁺ buffering power was expressed as:

$${\beta }_{Ca,m}=1+{\displaystyle \sum _i\frac{n_i^2{\left[C{a}^{2+}\right]}_m^{n_i-1}{\left[B_{Ca,i}\right]}_m}{K_{Ca,i}^{n_i}{\left(1+{\left[C{a}^{2+}\right]}_m^{n_i}/K_{ca,i}^{n_i}\right)}^2}}$$ (2)

Fig. 2.

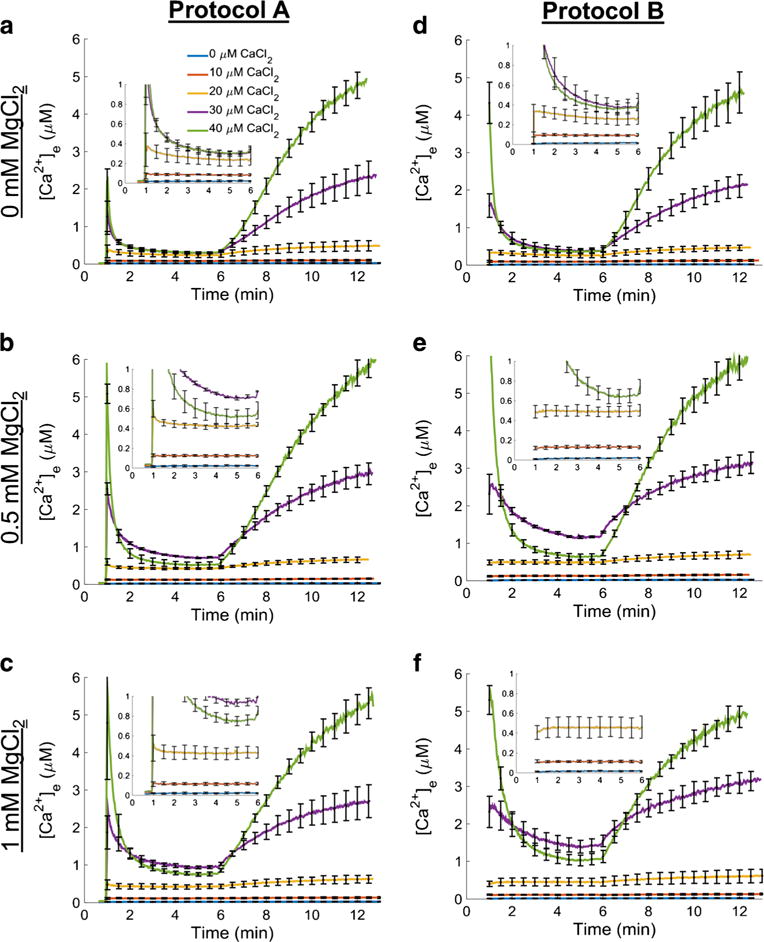
Extra-matrix free Ca²⁺ ([Ca²⁺]_e) dynamics. Ca²⁺ uptake and Ca²⁺ release for each combination of CaCl₂ and MgCl₂ concentrations are shown using the protocol depicted in Fig. 1. CaCl₂ was added to respiring mitochondrial suspension (left column; protocol A) or mitochondria were added to the buffer containing a given CaCl₂ concentration (right column; protocol B) at 60 s followed by ruthenium red (RR) at 300 s and NaCl at 360 s. The results for protocol A are shown in the left column and the results for protocol B are shown in the right column. Each row corresponds to the buffer MgCl₂ indicated on the left of each row. Insets show [Ca²⁺]_e dynamics for 0, 10, and 20 μM CaCl₂ in more detail. The axes are the same as the axes in the main figure panels. Error bars signify standard error of the mean

Fig. 4.

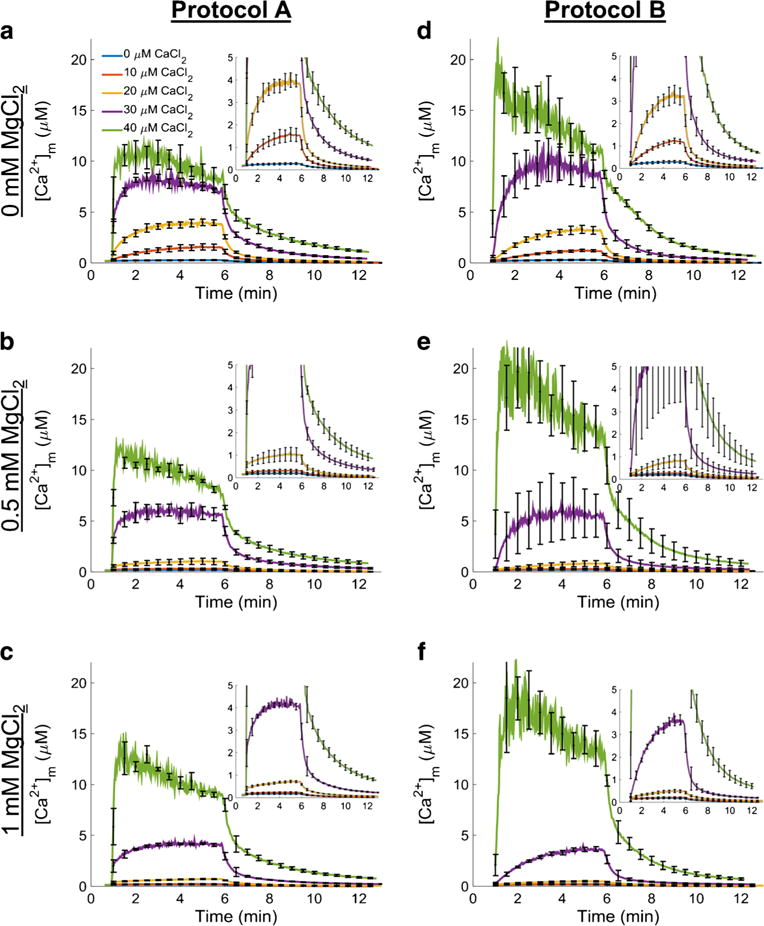
Matrix free Ca²⁺ ([Ca²⁺]_m) dynamics. Ca²⁺ uptake and Ca²⁺ release for each combination of CaCl₂ and MgCl₂ concentrations are shown using the protocol depicted in Fig. 1. CaCl₂ was added to the respiring mitochondrial suspension (left column; protocol A) or mitochondria were added to the buffer containing a given CaCl₂ concentration (right column; protocol B) at 60 s followed by ruthenium red (RR) at 300 s and NaCl at 360 s. The results for protocol A are shown in the left column and the results for protocol B in the right column. In protocol B when CaCl₂ was 40 μM, the fluorescent signal was close to Rmax, so the calculated [Ca²⁺]_m is likely an overestimation of the true value of [Ca²⁺]_m. Each row corresponds to the buffer MgCl₂ indicated on the left of each row. Insets show [Ca²⁺]_m dynamics for 0, 10, and 20 μM CaCl₂ in more detail. The axes are the same as the axes in the main figure panels. Error bars signify standard error of the mean

Results

Changes in extra-matrix ionized Ca²⁺

The dynamics of extra-matrix free Ca²⁺ for each protocol (A and B) and experimental conditions are shown in Fig. 2. Fluorescence ratios were converted to concentrations using Eq. 1. Each panel consists of five different traces representing one concentration of CaCl₂ added (0, 10, 20, 30, or 40 μM) at one of three fixed MgCl₂ concentrations (0, 0.5, or 1.0 mM) in the presence of 40 μM EGTA. The dynamics of lower CaCl₂ concentrations (0, 10, and 20 μM) are illustrated in more detail in the insets that show axes with the same labels seen in the main figure panels. Panels a–c show the Ca²⁺ dynamics profile using Protocol A, whereas panels d–f depict the Ca²⁺ dynamics profile using protocol B.

On a gross scale, the rates of decrease in [Ca²⁺]_e (Ca²⁺uptake rates), magnitude of uptake before addition of RR, and the rates of increase in [Ca²⁺]_e (Ca²⁺ efflux rates) after addition of NaCl, were similar in each protocol for the same [CaCl₂] and [MgCl₂] combination (Fig. 2). And as expected, Ca²⁺ uptake was attenuated when MgCl₂ was included in the buffer. However, distinct differences in the rates of Ca²⁺ uptake between each protocol were revealed by careful analysis. Double exponential functions fit to the Ca²⁺ uptake dynamics for protocol A revealed that the overall dynamics consisted of two time scales as shown in Fig. 3. These trend lines were fit between 60 and 150 s of the early phase of the uptake as shown in Supplemental Fig. S4. A single exponential function was sufficient to characterize the Ca²⁺ uptake dynamics for protocol B for all [CaCl₂] and [MgCl₂] combinations except for 40 μM CaCl₂ (data not shown). For this concentration of CaCl₂, a double exponential function was a better fit with similar time constants for the 40 μM CaCl₂ condition in protocol A. For additions of CaCl₂ of 10 μM and below, the dynamics of [Ca²⁺]_e were at or below detectable limits and were not used in the analysis. Furthermore, adding 40 μM CaCl₂ in the presence of 0.5 or 1.0 mM MgCl₂ in either protocol induced a faster Ca²⁺ uptake rate compared to 30 μM CaCl₂, which resulted in lower levels of [Ca²⁺]_e before addition of RR and NaCl.

Fig. 3.

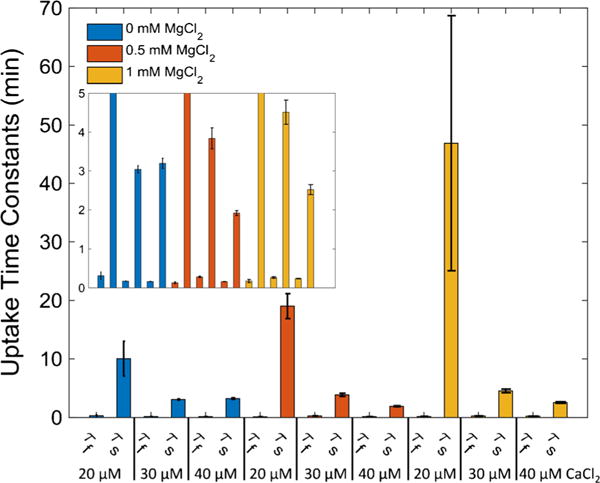
Two modes of Ca²⁺ uptake. For CaCl₂ concentrations of 20 μM and greater, a double exponential function was fit between 65 s and 150 s to the [Ca²⁺]_e dynamics observed in protocol A (Fig. 2). The fit time constants show that there was a fast and slow component of Ca²⁺ uptake associated with each bolus of CaCl₂ administered. The inset axes labels are the same as the main figure panel. Error bars signify propagated standard deviations

Changes in matrix ionized Ca²⁺

Using the same protocols (A and B) shown in Fig. 1, CaCl₂ was added and [Ca²⁺]_m was measured. As with the extra-matrix Ca²⁺, the fluorescent ratios were converted to concentrations using Eq. 1. Fura-4F AM loading and washout was confirmed by ensuring that [Ca²⁺]_m did not change after adding EGTA to the buffer (not shown). The results are displayed in Fig. 4 with a similar layout of the figure panels (a–f) shown in Fig. 2. Note that a very high [Ca²⁺]_m was attained because CsA had been added to the buffer in all experiments. Panels a–c and d–f show [Ca²⁺]_m dynamics at 0, 0.5 and 1.0 mM MgCl₂ using protocol A and protocol B, respectively. Matrix free Ca²⁺ dynamics were quantitatively and qualitatively different for each protocol and CaCl₂/MgCl₂ combination. For protocol A (Fig. 4, panels a–c), adding CaCl₂ (10, 20, 30, or 40 μM) induced an abrupt and rapid uptake of Ca²⁺. Adding lower [CaCl₂] (10 and 20 μM, see insets) caused smaller increases in peak [Ca²⁺]_m compared to the higher [CaCl₂] (30 and 40 μM). Nonetheless, even at lower [CaCl₂] (10 and 20 μM), there was an abrupt increase in Ca²⁺ uptake when CaCl₂ was added to mitochondria. Note that in protocol A the Ca²⁺ uptake at any [CaCl₂] showed an initial fast Ca²⁺ uptake phase followed by a slower gradual Ca²⁺ uptake phase. This fast uptake was not observed in protocol B.

Figure 5 shows the measured [Ca²⁺]_m recorded over a few seconds (averaged from 60 to 70 s) for protocols A and B. For the 20 and 30 μM CaCl₂ additions across all MgCl₂ conditions using protocol A, there were statistically significant differences in [Ca²⁺]_m when compared to the same CaCl₂ and MgCl₂ combination using protocol B (p ≤ 0.05). The presence of added MgCl₂ in the respiration buffer attenuated the maximal [Ca²⁺]_m in a concentration-dependent manner at each [CaCl₂] except for the 40 μM CaCl₂. For protocol B (Fig. 4, panels d–f), mitochondrial Ca²⁺ uptake was slower and more gradual at the lower [CaCl₂] (10, 20, and 30 μM) as shown in the insets of Figs. 2 and 4. However, in the 40 μM CaCl₂ group, adding mitochondria to respiration buffer with CaCl₂ already present (protocol B) showed a similar fast Ca²⁺ uptake rate as observed in protocol A. After adding 40 μM CaCl₂ in protocol B, the fluorescent signal was close to R_max; thus the calculated [Ca²⁺]_m was very noisy and likely not representative of the true value of [Ca²⁺]_m. For protocol A and during exposure to low CaCl₂ (10–30 μM), the [Ca²⁺]_m attained during the slow uptake, but not the initial fast uptake phase, was significantly different among the MgCl₂ additions for a given [CaCl₂]. Overall, a comparison of these protocols shows that there exists a Mg²⁺-insensitive, fast component of Ca²⁺ uptake that appears only when CaCl₂ is added to buffer already containing mitochondria, or when the [CaCl₂] is high enough. The addition of RR (1 μM) completely inhibited Ca²⁺ uptake in both protocols A and B. Furthermore, at 40 μM CaCl₂ the similarity in the rate of uptake between the two protocols is a verification to the equivalent rapidity of mixing of substances added to the cuvette.

Fig. 5.

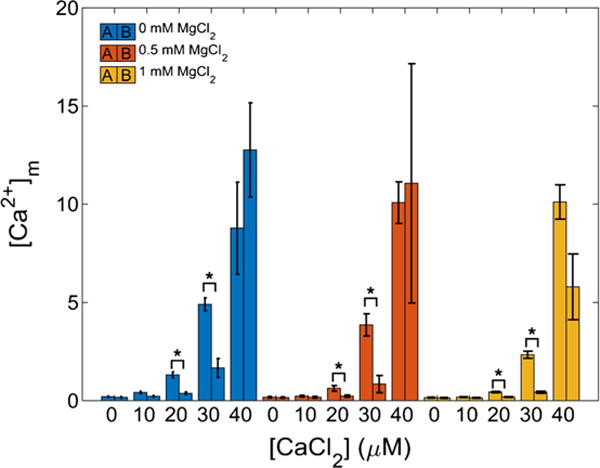
Ca²⁺ uptake by mitochondria. The amount of Ca²⁺ uptake by mitochondria depends on method of CaCl₂ delivery. The bar plots show [Ca²⁺]_m just after addition of CaCl₂ to mitochondria (protocol A, left bar) or after addition of mitochondria to buffer containing CaCl₂ (protocol B, right bar). These data correspond to a time of approximately 65 s. For all 20 and 30 μM CaCl₂ conditions, the rate of Ca²⁺ uptake in protocol A was significantly different from that of protocol B (p ≤ 0.05) for most of the [CaCl₂] and even in the presence of Mg²⁺. Error bars signify standard error of the mean

Changes in ΔΨ_m and NADH

In parallel studies, ΔΨ_m and NADH were measured to confirm that the differences observed in Ca²⁺ uptake dynamics were not due to changes in bioenergetics. Experimental conditions were simplified to consist of 0 and 1.0 mM MgCl₂ and 0 and 40 μM CaCl₂ combinations. Figure 6, panels a and b, and panels c and d, summarize changes in ΔΨ_m and NADH, respectively during protocol A and protocol B. Note that the starting point for the two variables in the figure were slightly different, with the start point at 30 and 60 s for protocols A and B, respectively. There were no significant differences observed in either ΔΨ_m or NADH between the two protocols. In addition, ΔΨ_m and NADH were not significantly affected by adding 40 μM CaCl₂ (protocol A and B) in either the presence or absence of 1 mM MgCl₂, which indicates that mitochondrial bioenergetics was not affected by the nature of mitochondrial exposure to CaCl₂ (protocol A vs. protocol B) or MgCl₂.

Fig. 6.

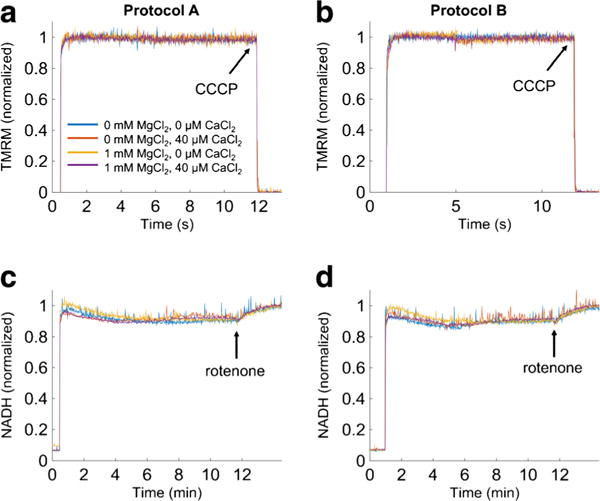
ΔΨ_m and NADH dynamics. The bioenergetics responses during protocols A and B were monitored in parallel using the ΔΨ_m sensitive dye TMRM and NADH autofluorescence. Traces are individual recordings. In averaged data there were no significant differences between the two MgCl₂ and CaCl₂ groups. The increases in signals mark the addition of mitochondria at 30 s (protocol A) and at 60 s (protocol B). The number of experimental groups was reduced to consist of only 0 and 1 mM MgCl₂ and 0 and 40 μM CaCl₂

Mitochondrial Ca²⁺ buffering power

The Ca²⁺ uptake dynamics obtained under protocols A and B that are shown in Figs. 2 and 4 were used to calculate the mitochondrial Ca²⁺ buffering power (βCa²⁺_m) as a function of [Ca²⁺]_m using Eq. 2 and shown in Fig. 7. At low [Ca²⁺]_m, βCa²⁺_m was nearly 3000:1 (total matrix [Ca²⁺]:free matrix [Ca²⁺]) but rose to 10,000:1 as [Ca²⁺]_m was increased beyond 5 μM. The calculated βCa²⁺_m values for [Ca²⁺]_m below 500 nM were highly variable due to the [Ca²⁺]_m measurement limitations discussed above. When MgCl₂ was present, βCa²⁺_m no longer increased as much and began to decrease as [Ca²⁺]_m increased further in a concentration-dependent manner. Based on a two component-buffering model for matrix Ca²⁺, this decrease in βCa²⁺_m is likely due to an effect of Mg²⁺ to reduce the Ca²⁺ binding capacity for the class 2 buffers. The effect of [Mg²⁺]_e on the sequestration parameters is summarized in Table 1. Although higher [Ca²⁺]_m were attained with protocol A due to increased MCU activity triggered by the activation of both fast and slow modes of Ca²⁺ uptake, βCa²⁺_m was invariant with respect to either protocol A or B and was uniquely set both by [Ca²⁺]_m and by [Mg²⁺]_e.

Fig. 7.

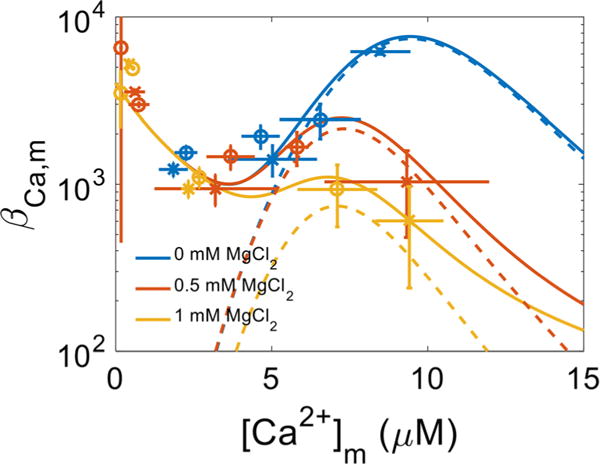
Mitochondrial Ca²⁺ buffering power. The Ca²⁺ sequestration system consists of at least two classes of buffers that bind Ca²⁺ with a differential affinity and capacity. Class 1 buffers are of the prototypical type whereby a single Ca²⁺ ion binds to a single site in an uncooperative manner. Class 2 buffers are atypical and bind multiple Ca²⁺ ions in a cooperative fashion. Class 1 buffers are not affected by Mg²⁺; however, in the presence of Mg²⁺, both the binding capacity and affinity of the Class 2 buffers are compromised. The blue, yellow and red colors correspond to the added 0 mM MgCl₂, 0.5 mM MgCl₂ and 1 mM MgCl₂ conditions, respectively. The circles (O) and x’s (x) represent rates obtained using the data from Protocols A and B, respectively. The lines correspond to model simulations of the two classes of Ca²⁺ buffers using Eq. 2 with the parameters listed in Table 1. Error bars signify propagated standard deviations. Dashed lines represent contributions to mitochondrial buffering power from the class 2 buffers only

Table 1.

Mitochondrial Ca²⁺ sequestration system model parameters

Parameter	Definition	Value
Class 1
[BCa,1]tot	Total Ca2+ buffer	12 mM
KCa,1	Buffer Ca2+ affinity	3 μM
n1	Hill coefficient	1
Class 2		0 Mg2+	0.5 mM Mg2+	1 mM Mg2+
[BCa,2]tot	Total Ca2+ buffer	8 mM	1.8 mM	0.6 mM
KCa,2	Buffer Ca2+ affinity	10 μM	7.75 μM	7.5 μM
n2	Hill coefficient	6

Mg²⁺ attenuates both Ca²⁺ uptake and efflux

The data shown in Figs. 2 and 4 were also used to calculate the rates for the slow mode Ca²⁺ uptake by MCU and extrusion by mNCE under the experimental conditions used in this study. Note that these transport rates were calculated using J_Ca2+,tot = (d[Ca²⁺]m/dt)*β_Ca2+,m within 10 s of CaCl₂ or NaCl-induced perturbations. Mg²⁺ was found to attenuate both the slow mode of Ca²⁺ uptake by MCU (Fig. 8a) and the release by mNCE (Fig. 8b). The slow mode Ca²⁺ uptake rates in protocol B were about 40 % of the slow mode Ca²⁺ uptake rates in protocol A for all three extra-matrix MgCl₂ levels. The extrusion rates were independent of the Ca²⁺ loading protocol, i.e. protocol A vs. protocol B. These rates were estimated from the [Ca²⁺]_e dynamics by averaging the rates between 75 and 90 s and 360–390 s for Ca²⁺ uptake and extrusion, respectively.

Fig. 8.

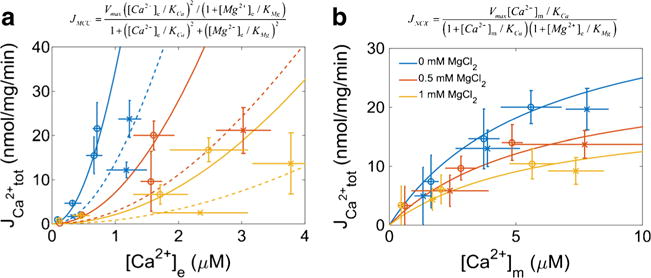
Mg²⁺ inhibition of Ca²⁺ uptake and extrusion. Panel 8a shows slow mode of Ca²⁺ uptake (via MCU) was attenuated by extra-matrix Mg²⁺ in the physiological concentration range. The model parameters for the simplified MCU model are: V_max, 900 nmol/mg/min; K_Ca, 6 μM; and K_Mg, 0.3 mM. Solid lines correspond to slow mode of MCU rates observed during protocol A, and dotted lines correspond to the slow mode of MCU rates observed during protocol B. The rates of Ca²⁺ uptake in protocol B were approximately 40 % of the rates observed in protocol A. Panel 8b shows buffer Mg²⁺ in the physiological range used in this study also affected the rate of Ca²⁺ efflux (via mNCE). The model parameters for the simplified NCE are: V_max, 40 nmol/mg/min; K_Ca, 5 μM; and K_Mg, 1 mM. The blue, yellow and red colors correspond to the 0 mM MgCl₂, 0.5 mM MgCl₂ and 1 mM MgCl₂ conditions, respectively. Extra-matrix [Na⁺] was assumed constant (10 mM) and thus not included in the equation. The circles (O) and x’s (x) represent rates obtained using the data from Protocols A and B, respectively. The lines correspond to model simulations with the equations given above their respective panels. Error bars signify propagated standard deviations

Discussion

Mitochondrial Ca²⁺ uptake modes

In our examination of factors that affect mitochondrial Ca²⁺ handling (influx, efflux and sequestration), we measured extra-matrix and matrix free Ca²⁺ dynamics in isolated cardiac mitochondria using various combinations of [CaCl₂] and [MgCl₂] under two different Ca²⁺ loading protocols (Fig. 1). The order of addition, i.e. mitochondria before CaCl₂ or mitochondria after CaCl₂, resulted in significant differences in mitochondrial Ca²⁺ uptake dynamics. In protocol A, mitochondria displayed a fast Ca²⁺ uptake profile at each [CaCl₂] that was followed by a slower and more gradual Ca²⁺ uptake profile when CaCl₂ was added first as a bolus and mitochondria after that in the presence or absence of MgCl₂. These two modes are evident from the time constant analyses summarized in Fig. 3 and the degree of Ca²⁺ uptake depicted in Fig. 5. In protocol B, when mitochondria were exposed to the buffer containing CaCl₂ already present with or without MgCl₂, Ca²⁺ uptake was slower and more gradual at CaCl₂ concentrations below 40 μM. Therefore, when compared to protocol A, only the slower mode of Ca²⁺ uptake was apparent at the lower [CaCl₂] in protocol B. These differences in Ca²⁺ uptake between the two protocols were not due to differences in ΔΨ_m as indicated in Fig. 4a, b. This finding is further supported by the data of Supplemental Fig. S3, which shows that in the absence of PA before adding CaCl₂ first or mitochondria first, the different uptake modes remained evident as in the original two main protocols in which PA was present. The presence of extra-matrix MgCl₂ markedly attenuated the slow, but not the fast, component of Ca²⁺ uptake and altered mitochondrial Ca²⁺ buffering (sequestration) power (Figs. 7 and 8). This is also evident by the decreasing effect of Mg²⁺ on the slow time constants shown in Fig. 3. Also, note that the fast time constants were relatively insensitive to Mg²⁺, which further supports the Mg²⁺ independent nature of the fast uptake shown in Fig. 5. These two potential modes of Ca²⁺ uptake are consistent with our recent computational modeling report on the dynamics of Ca²⁺ uptake (Tewari et al. 2014). Interestingly, the analysis also revealed that the slow mode was inhibited in protocol B reaching only 40 % of the rate observed during protocol A regardless of [Mg²⁺]_e as shown in Fig. 8a (compare dashed lines vs. solid lines). We suggest that there are two distinct modes of Ca²⁺ uptake that occur at physiological levels of cytosolic Ca²⁺ and Mg²⁺. One mode is a fast, Mg²⁺-insensitive Ca²⁺ uptake pathway that could be modeled as a RyR-type channel (Tewari et al. 2014) and the other is a slower Mg²⁺-sensitive Ca²⁺ uptake pathway (Pradhan et al. 2011), that is also modulated by the mode of Ca²⁺ delivery. Moreover, the Mg²⁺-insensitive nature of the fast mode we found in the present study is compatible with the data on Mg²⁺-insensitive RaM of Ca²⁺ uptake reported by Gunter et al. (1998). Our findings are also consistent with the attenuating effect of Mg²⁺ on the slow mode of Ca²⁺ uptake reported earlier by our group (Boelens et al. 2013).

The focus of this study was not to characterize the regulatory action of the molecular components of the MCU complex; however, it suffices to note that the differences in uptake could be attributed to a differential regulation of MCU during exposure to different CaCl₂ with and without MgCl₂. It is possible that the marked differences in the two modes of Ca²⁺ uptake we found are attributable to the MCU complex and its regulatory subunits, e.g. MICU1 and MICU2 (Marchi and Pinton 2014; Patron et al. 2014; Mallilankaraman et al. 2012). MICU1 appears to act in response to high cytosolic [Ca²⁺] by stimulating Ca²⁺ uptake by MCU, whereas MICU2 appears to inhibit MCU functions at a lower cytosolic [Ca²⁺] (Patron et al. 2014; Kamer and Mootha 2014). However, major controversies abound in these observations, with conflicting results reported (Marchi and Pinton 2014; Patron et al. 2014; Mallilankaraman et al. 2012). Some of the discrepancies might be due to the composition of the buffer. For example, in one report Mg²⁺, an allosteric modulator of MCU activity was present, whereas in another study it was absent (Csordas et al. 2013; Mallilankaraman et al. 2012). And while incontrovertible evidence of MCU inhibition by Mg²⁺ exists (see, for example, Kirichok et al. 2004), the molecular components responsible remain unidentified. The ability of the Ca²⁺ delivery method to unmask different modes of MCU activity could be attributed to its effect on the state of the EF-hands located on the MICU1 and/or MICU2 regulatory subunits. For example, if the MICU1 and MICU2 subunits act in conjunction as a Ca²⁺-sensitive break mechanism (Patron et al. 2014; Kamer and Mootha 2014), a rapid change in Ca²⁺ near the subunits may temporarily release the break and result in a brief, rapid uptake of Ca²⁺. That said, the present study is focused on the observation of a fast and slow mode of Ca²⁺ uptake that is dependent on the manner by which mitochondria are exposed to a bolus of CaCl₂, and not specifically on the regulation by MICU1, MICU2, and other regulatory proteins. Future elaborate studies in the contribution of these proteins to these two modes of Ca²⁺ in the presence and absence of Mg²⁺, and the impact on the mitochondrial Ca²⁺ buffering capacity should be undertaken.

It is evident that mitochondria took up Ca²⁺ in a quick and robust manner when CaCl₂ was added to the mitochondrial suspension (protocol A). In contrast, the matrix free Ca²⁺ dynamics data showed that when mitochondria were added to respiration buffer with CaCl₂ already present, the fast uptake mode was abolished for all CaCl₂ concentrations except for the highest [CaCl₂] (40 μM). Note that the order of adding 40 μM CaCl₂ and mitochondria to the respiration buffer resulted in similar Ca²⁺ uptake profile for both protocols. This indicates that the rapid mixing of the cuvette content assured near instantaneous homogenous mixture, and that the difference in Ca²⁺ uptake between the two protocols was mostly due to the different modes of uptake in mitochondria and not to an uneven mix of the added CaCl₂. The order of adding mitochondria or CaCl₂ also did not affect the ΔΨ or redox state indicating that mitochondria were fully energized in the presence of PA when mitochondria were added before or after adding CaCl₂. These observations provide further evidence that the method of exposure to Ca²⁺, and not bioenergetic differences such as ΔΨ, is the regulatory mechanism behind the vastly different uptake modes observed in our study. In addition, this difference in Ca²⁺ uptake was more apparent when MgCl₂ was included in the respiration buffer of either Ca²⁺ loading protocol. This difference in the mode of Ca²⁺ uptake was also not dependent on the mitochondrial redox state because the NADH autofluorescence data (Fig. 6) showed no observable difference between the two protocols (A and B), in the presence or absence of added CaCl₂ or MgCl₂.

Based on these observations, we can conclude that Mg²⁺ regulates bulk Ca²⁺ uptake by attenuating mainly the slow component of the MCU-mediated Ca²⁺ uptake in a concentration-dependent manner. This conclusion is supported by our previous findings (Boelens et al. 2013) and recent computational models (Tewari et al. 2014; Bazil and Dash 2011) and indicates that the MCU is capable of operating in multiple conductance modes. In addition, the data revealed another intriguing aspect of the Ca²⁺-dependent regulation of mitochondrial Ca²⁺ uptake. As shown in Fig. 2, the 40 μM CaCl₂ bolus resulted in a lower [Ca²⁺]_e at the time of RR addition compared to the 30 μM CaCl₂ bolus for either protocol. In other words, a higher bolus of CaCl₂ resulted in more Ca²⁺ being taken up by mitochondria, which was inhibited by Mg²⁺ in a concentration-dependent manner. We speculate that this phenomenon is due to differential regulation or modulation of MCU conductance/open probability times by other components of the protein complex (e.g. MICU1 and MICU2) (Kamer and Mootha 2014; Harrington and Murphy 2015).

The Mg²⁺-sensitivity of the MCU complex likely plays a role in heart failure, ischemia and reperfusion injury, and other related events in the myocardium (for review see Douban et al. 1996; Kolte et al. 2014; Levitsky and Takahashi 2013). For example, cytosolic [Mg²⁺] is known to rise during ischemia due to net ATP hydrolysis. This rise in [Mg²⁺] would help mitigate mitochondrial Ca²⁺ loading via MCU, but the Ca²⁺ buffering system would be compromised, which could counter the Mg²⁺ effect and contribute to mitochondrial Ca²⁺ overload. In heart failure, the net decrease in cellular Mg²⁺ content would lead to more mitochondrial Ca²⁺ uptake via the MCU. Based on our results reported herein, the decrease in cytosolic [Mg²⁺] levels observed in these pathophysiological conditions, e.g. heart failure, would likely result in elevated [Ca²⁺]_m. This would likely induce Ca²⁺-mediated mitochondrial dysfunction, and if the local cytosolic [Ca²⁺] is high, also possibly trigger mPTP opening with concomitant cell death. Indeed, it has been reported that the cardiovascular consequences of Mg²⁺ deficiency in clinical studies include multifocal necrosis with Ca²⁺ accumulation in mitochondria in a pattern suggestive of myocardial infarction (Seelig 1989).

MgCl₂ and mitochondrial mNCE-induced Ca²⁺ efflux

The well-known effect of Mg²⁺ to attenuate Ca²⁺ uptake and its extrusion is demonstrated in greater detail by our data. The rate of increase in [Ca²⁺]_m significantly decreased as a function of [Mg²⁺]_e with an apparent K_i of 0.25 mM (Fig. 8a). This value is similar to that of our previously determined computational model of Ca²⁺ uptake (Pradhan et al. 2011). At 1 mM [Mg²⁺]_e, close to the physiological extra-matrix level, the MCU complex was inhibited by greater than 15-fold at the peak of a 1 μM cytosolic Ca²⁺ transient. Despite this, [Ca²⁺]_m reached close to 1 μM with addition of 20 μM CaCl₂ (Fig. 4c) due to the rapid uptake mode by the MCU complex. Incidentally, [Mg²⁺]_e also inhibits Na⁺-dependent Ca²⁺ efflux (Wingrove and Gunter 1986), which is consistent with some of our current findings (Fig. 8b). Here, it is shown that Mg²⁺ with a K_i of 1 mM inhibited the rate of decrease in [Ca²⁺]_m. Moreover, the maximal rate of Ca²⁺ efflux was reduced to half when [Mg²⁺]_e was increased from 0 mM to 1 mM. So not only is Ca²⁺ uptake slowed when there is an increase in [Mg²⁺]_e, but also the rate of Ca²⁺ extrusion is impeded. Whereas it appears to be clear that [Mg²⁺]_e regulates the slower phase of Ca²⁺ uptake, the Mg²⁺-insensitive rapid component of the MCU complex can lead to net Ca²⁺ uptake when mitochondria are presented with sufficiently high, pulse-like Ca²⁺ transients.

Mitochondrial Ca²⁺ buffering

The data from this study also corroborates previous reports that the mitochondrial Ca²⁺ sequestration system consists of at least two classes of buffers (Wei et al. 2012; Bazil et al. 2013; Blomeyer et al. 2013) (Fig. 7) and challenges recent findings (Wei et al. 2012; Tewari et al. 2014) that suggest the manner in which Ca²⁺ is loaded into mitochondria (fast vs. slow) modulates the degree of Ca²⁺ buffering. In our prior study, we used indo-1 to monitor [Ca²⁺] in both the extra-matrix and matrix compartments and mitochondrial Ca²⁺ buffering (Blomeyer et al. 2013). In contrast, in the current study we used Fura-4F because it can register higher [Ca²⁺] than indo-1 without saturating. Consequently, we also added CsA to the experimental buffer to prevent mPTP opening induced by high [Ca²⁺]_m. As a result of using a different Ca²⁺ indicator dye and different experimental conditions, we observed somewhat different buffering parameters between the current and previous studies (Bazil et al. 2013; Blomeyer et al. 2013) that can be explained by the different extent of dye loading, cation binding properties between each type of Ca²⁺ fluorescence dye, and experimental conditions. Despite these differences, the general properties of the sequestration system identified in this study are identical to our previous reports (Bazil et al. 2013; Blomeyer et al. 2013). That is, the class 1 buffers are of the prototypical type and consist of binding sites that bind a single Ca²⁺ ion, whereas the class 2 buffers are capable of binding multiple Ca²⁺ ions at a single site in a cooperative fashion.

There is strong supporting evidence that the class 2 buffers consist of complexes formed by the annexin class of proteins in conjunction with acidic phospholipids in the membrane that promote or facilitate the formation of CaPi granules on the inner leaflets of the inner mitochondrial membrane (IMM) (for discussion, see Bazil et al. 2013). In our present study, we show that Mg²⁺ also modulates this class of Ca²⁺ buffers but does not regulate the class 1 buffers (Fig. 7). The mechanisms by which Mg²⁺ alters Ca²⁺ sequestration is unclear but may involve two mechanisms: i) extra-mitochondrial Mg²⁺ alters the class 2 buffer affinity for Ca²⁺ or ii) matrix Mg²⁺ encumbers the formation of CaPi complexes in the matrix on the surface of the IMM. We propose that latter is more likely. Based on earlier reports by Brierley et al. (1962, 1963, 1964), Mg²⁺ is actively loaded into energized mitochondria in a Pi-dependent and -independent manner. Therefore, Pi levels might modulate Mg²⁺ uptake during Ca²⁺ loading which would result in an increase in matrix Mg²⁺ content. However, Boelens et al. (2013) reported that increasing buffer MgCl₂ did not change [Mg²⁺]_m appreciably over time. In that study, Ca²⁺ uptake was absent, and the internal mechanisms regulating matrix Mg²⁺ were already in homeostasis. A plausible hypothesis is that Mg²⁺ enters mitochondria concomitantly with Ca²⁺ and interferes with CaPi granule formation. This is consistent with the observation that Mg²⁺ prevents and slows the spontaneous transition of CaPi from an amorphous state to a crystalline state (Wu et al. 2008, 2009). Nevertheless, our results demonstrate that when [Mg²⁺]_e is elevated, the ability of mitochondria to sequester large amounts of Ca²⁺ is hindered.

Summary and perspective

The mechanism by which isolated mitochondria take up and sequester Ca²⁺ is a complex function not only of how much Ca²⁺ mitochondria are exposed to, but also the experimental conditions. In one scenario, when added CaCl₂ exceeds a threshold, a rapid, Mg²⁺-insensitive mode of Ca²⁺ uptake is activated. In another scenario, when mitochondria are added to the buffer with low concentrations of EGTA and CaCl₂ already present, the rapid mode of Ca²⁺ uptake is not activated, that is unless the buffer concentration of CaCl₂ is sufficiently high. Thus, the MCU appears to consist of multiple conductance modes, which are differentially modulated by extra-matrix Mg²⁺.

Mitochondrial Ca²⁺ homeostasis plays important roles in cellular physiology, regulation of cellular bioenergetics, reactive oxygen species signaling and Ca²⁺ signaling. Agonist-induced intracellular Ca²⁺ signals can be rapidly transduced to the matrix because mitochondria can exist in close apposition to sites of Ca²⁺ release where local cytosolic [Ca²⁺] can be higher than in the rest of the cytoplasm (Mallilankaraman et al. 2012). The physiological implications of the different modes of Ca²⁺ uptake in this study are unclear but allude to a process whereby mitochondria can rapidly accumulate and sequester Ca²⁺ to prevent catastrophic cytosolic Ca²⁺ overload, mPTP opening and cell death. Therefore, a better understanding of the Ca²⁺ dynamics and how it is modulated by physiological [Mg²⁺] could provide new insights into the potential molecular mechanisms that regulate Ca²⁺ fluxes in and out of mitochondria under both physiological and pathophysiological conditions.