Fine-mapping cellular QTLs with RASQUAL and ATAC-seq

Abstract

When cellular traits are measured using high-throughput DNA sequencing quantitative trait loci (QTLs) manifest as fragment count differences between individuals and allelic differences within individuals. We present RASQUAL (Robust Allele Specific QUAntitation and quality controL), a novel statistical approach for association mapping that models genetic effects and accounts for biases in sequencing data in a single, probabilistic framework. RASQUAL substantially improves fine-mapping accuracy and sensitivity of association detection over existing methods in RNA-seq, DNaseI-seq and ChIP-seq data. We illustrate how RASQUAL can be used to maximise association detection by generating the first map of chromatin accessibility QTLs (caQTLs) in a European population using ATAC-seq. Despite a modest sample size, we identified 2,707 independent caQTLs (FDR 10%) and demonstrate how combining RASQUAL and ATAC-seq can provide powerful information for fine-mapping gene regulatory variants and for linking distal regulatory elements with gene promoters. Our results highlight how combining between-individual and allele-specific genetic signals improves the functional interpretation of noncoding variation.

Introduction

Association mapping of cellular traits is a powerful approach for understanding the function of genetic variation. Cellular traits that can be quantified by sequencing are particularly amenable for association analysis because they provide highly quantitative information about the phenotype of interest and can easily be scaled genome-wide. Population scale studies using sequencing-based cell phenotypes such as RNA-seq, ChIP-seq and DNaseI-seq have revealed an abundant QTLs for gene expression and isoform abundance^1–4, chromatin accessibility⁵, histone modification, transcription factor binding (TF)^6–9 and DNA methylation¹⁰, providing precise information on the molecular functions of human genetic variation. However the effect sizes of many common variants are modest meaning that association analysis typically requires large sample sizes, which can be problematic when assays are labour intensive or cellular material is difficult to obtain. Furthermore, even well-powered studies can struggle to accurately fine-map causal variants.

One advantage of sequencing-based cell phenotyping is the ability to identify allele-specific (AS) differences in traits between maternal and paternal chromosomes¹¹. AS differences can arise when a sequenced individual is heterozygous for a cis-acting causal variant and several studies have highlighted abundant AS changes in a variety of cell traits^1,2,5,7. AS signals provide information both about the existence of a QTL and the likely causal variants because individuals showing allelic imbalance must also be heterozygous at the causal site¹². However, although both between-individual and AS signals provide complementary information about genetic associations, principled approaches for combining them are lacking. In part this is because AS signals are challenging to analyse: allele-specificity can also be produced by a wide variety of technical factors including reference mapping bias ¹³, the presence of collapsed repeats¹⁴, PCR amplification bias^15,16 and sequencing errors¹⁷. Biological phenomena such as imprinting or random allelic inactivation^6,15 can also produce allelic imbalance when no cis-QTL exists. Genotyping errors can also be a serious problem, particularly in cases where homozygous SNPs located within a sequenced feature (feature SNPs, fSNPs) are miscalled as heterozygous⁶. Effective use of AS information must take account of these biases to avoid high false positive rates¹⁵. Previous strategies to address these problems have included the creation of personal reference genomes for read mapping, read masking, genomic blacklists or simulation strategies to compute genome-wide mapping probabilities that account for reference bias effects. However, it is challenging to set sensible values for the thresholds that these strategies rely on: overly conservative settings can lead to a loss of power while overly liberal settings may inflate the false positive rate. Additionally, genome wide simulations, custom read filtering and alignment steps significantly increase the time, complexity and computational burden required for analysis.

Here we describe a novel statistical method, RASQUAL (Robust Allele Specific QUAntitation and quality controL), that integrates between-individual differences, allele-specific signals and technical biases in sequencing-based cell phenotypes into a single, probabilistic framework for association mapping of cis-QTLs. RASQUAL can be applied to existing data sets without requiring data filtering, masking or the creation of personalised reference genomes. When applied to RNA-seq, ChIP-seq and DNaseI-seq data sets, RASQUAL significantly outperformed existing methods, both in its ability to detect QTLs and to fine-map putatively causal variants. We explored how RASQUAL and ATAC-seq could be used to improve fine-mapping of causal regulatory variants by generating the first map of chromatin accessibility QTLs (caQTLs) in a European population¹⁸. Despite a modest sample size of 24 individuals, RASQUAL detected over 2,700 independent caQTLs (FDR 10%) providing a rich resource for the functional interpretation of human noncoding variation.

Results

Rationale and statistical overview of RASQUAL

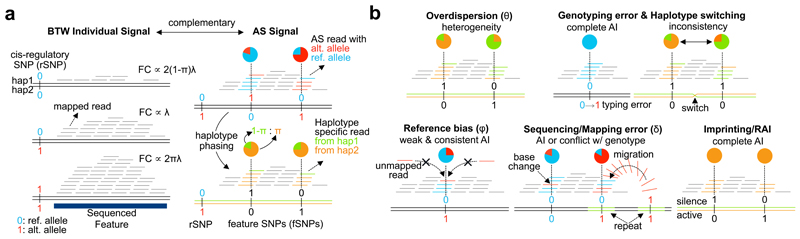
If a sequenced feature, such as a ChIP-seq peak, is affected by a single cis-regulatory SNP (rSNP) the total number of fragments mapped onto the feature correlates with rSNP genotype (the between-individual signal; Fig. 1a). When sequenced reads overlap fSNPs located inside the sequenced feature, AS differences can be detected by comparing the numbers of reads that map to one or other allele of the fSNP (the AS signal; Fig. 1a; Supplementary Fig. 1). RASQUAL models each sequenced feature and considers all genotyped variants within a given distance of the feature (the cis-window). For simplicity, RASQUAL assumes a single causal variant at each feature, although multiple causal variants can be tested for by conditioning on the lead SNP genotype.

Figure 1.

Schematic of RASQUAL approach. Throughout, reference and alternate alleles are coloured blue and red and coded 0 or 1, respectively, while alternative haplotype are coloured orange and green, respectively. (a) Plot illustrates the two sources of input data to RASQUAL: between-individual and AS signals, as observed from sequence data. Left panel shows the fragment count (FC) is proportional to rSNP genotype and right hand panel illustrates how those two signals are connected by the cis-regulatory effect π after conversion of AS counts into haplotype specific expression (see Main text for details). (b) Visual representation of the key RASQUAL features and parameters. Overdispersion introduces greater heterogeneity in the AS count than would be expected under binomial assumption. RASQUAL models the overdispersion in AS counts and total fragment counts with a single parameter θ. Genotyping error introduces complete allelic imbalance when homozygote is miscalled as heterozygote. Haplotype switching produces inconsistency of allelic imbalance among SNPs within an individual. Reference bias occurs when sequence reads containing the alternative allele(s) are unmappable to the correct location. RASQUAL employs a parameter φ that captures the excess of allelic imbalance beyond the genetic effect π. Sequencing/mapping error introduces additional allelic imbalance or genotype inconsistency. RASQUAL explicitly models the proportion of reads that are erroneously sequenced or mapped from incorrect genomic location by parameter δ to allow imperfect sequencing results. Imprinting introduces strong allelic imbalance that can confounds with genetic effects.

The model consists of two components: (1) between-individual signals are captured by regressing the total fragment count, Y_i, onto the number of alternative alleles at the rSNP, G_i(G_i = 0,1,2), assuming fragment counts follow a negative binomial distribution (p_NB) with a scaling parameter, λ, for absolute mean of coverage depth at the feature, and (2) allele-specific signals are modelled assuming the alternative fragment count $Y_{il}^{\left(1\right)}$ at the lth fSNP given the total number of fragments overlapping that fSNP, Y_il, follows a beta binomial distribution (p_BB). These model components are connected by the single cis-regulatory effect parameter (π) such that the expected fragment count is proportional to {2(1 − π) λ, λ, 2πλ} for G_i = 0,1,2 and the expected allelic ratio in an individual heterozygous for the putative causal SNP becomes {1 − π, π} at heterozygous fSNPs (Fig. 1a); otherwise {0.5,0.5} for a homozygous individual. The likelihood of RASQUAL model is written as

$$ℒ\left(\pi ,\delta ,\phi ,\lambda ,\theta \right)\propto \prod _{\begin{array}{l}i=1\\ \text{sample}\end{array}}^N{\displaystyle \sum _{G_i}\underset{\text{between}-\text{individual}\text{signal}}{\underbrace{p\left(G_i\right)p_{\text{NB}}\left(Y_i|G_i;\pi ,\lambda ,\theta \right)}}}\prod _{\begin{array}{l}l=1\\ \text{fSNP}\end{array}}^L{\displaystyle \sum _{D_{il}}\underset{\text{allele}-\text{specific}\text{signal}}{\underbrace{p\left(D_{il}|G_i\right)p_{\text{BB}}\left(Y_{il}^{\left(1\right)}|Y_{il},D_{il};\pi ,\delta ,\phi ,\theta \right)}}}$$

where D_il denotes the diplotype configuration in individual i between the putatively causal variant and the lth fSNP, p(G_i) and p(D_il|G_i) denote prior probabilities of genotype and diplotype configuration (obtained from SNP phasing and imputation). In addition to the cis genetic effect (π), the allelic ratio depends upon δ, the probability that an individual read maps to an incorrect location in genome and φ, the reference mapping bias (where φ = 0.5 corresponds to no reference bias). Overdispersion in both Y_i and $Y_{il}^{\left(1\right)}$ is captured by a single shared parameter θ (see Supplementary Methods for details). For simplicity, our model assumes that Y_i, the feature count, is independent of δ and φ. When this assumption was relaxed we found that the model performed similarly to the original model (see Supplementary Methods, section 3.13 for details). Parameter estimation and genotypes are iteratively updated during model fitting by an expectation-maximisation (EM) algorithm¹⁹ to arrive at the final QTL call for each sequenced feature (Supplementary Fig. 2). For each feature, RASQUAL outputs a likelihood ratio test statistic for the hypothesis of a single QTL as well as estimated over-dispersion, reference allele mapping bias, sequencing/mapping error rate at each tested SNP and posterior probabilities for each genotype at the lead rSNP and fSNPs. RASQUAL also performs a separate likelihood ratio test for imprinting in the given feature. Although the software presently handles only SNPs, the model could be extended in future to also incorporate indel mutations. We anticipate that this will require modification of the model to handle the additional uncertainty in the alignment of indel mutations.

RASQUAL improves causal variant localisation

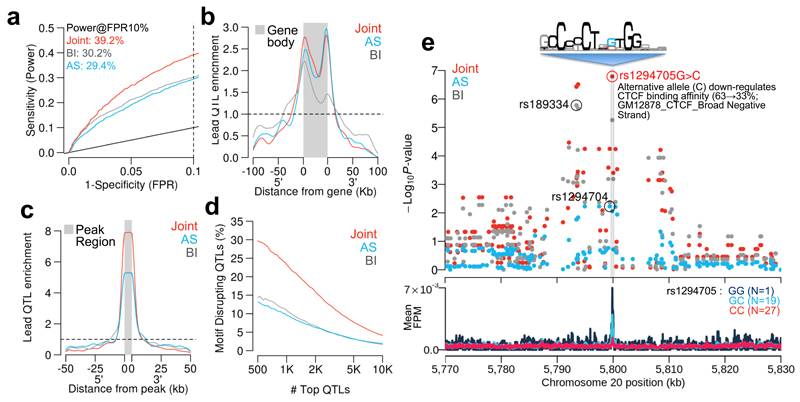
We first investigated the relative importance of the AS and between-individual components of the RASQUAL model. We assessed power using an RNA-seq data set from 373 lymphoblastoid cell lines (LCLs) in European individuals generated by the gEUVADIS project³ (Supplementary Table 2). Our analysis used a challenging test of model performance: how many QTLs mapped using the full data set could our model detect in a small subsample of the same data? We compared the numbers of eQTLs detected by RASQUAL in a subsample of 24 individuals of RNA-seq data with the set of “true positive” eQTLs provided by gEUVADIS project (see Online Methods). Our results clearly show that RASQUAL’s combined allele-specific and between-individual level information significantly outperformed either source alone with the joint model detecting, for example, 40% of eQTLs in the true positive set at false positive rate (FPR) at 10% compared with 32% and 29% for the between-individual and allele-specific only models (Fig. 2a, b). Our analysis also suggested that eQTLs detected by the joint model are strongly enriched at both the 5’ and 3’ ends, while those found using only allele-specific signals are more enriched towards the 3’ end of the gene body (Fig. 2b). We also note that our power was not significantly reduced in weakly expressed genes (Supplementary Fig. 3). This partly because count-based models more accurately capture uncertainty for low expressed genes, but may also reflect a limitation of our model testing, because eQTLs are challenging to map in weakly expressed genes even in large samples such as that published by the gEUVADIS project.

Figure 2.

Comparing between-individual only (BI), allele-specific only (AS) and combined models. In panels a-d, red curves indicate the joint RASQUAL model, blue indicates the AS only signal and grey indicates the between-individual only signal. (a) ROC curves for detecting known eQTL genes (see Online Methods) for the three different models in a random subset of 24 individuals from gEUVADIS RNA-seq data¹. Dotted line indicates FPR=10%. (b) Density plot shows the enrichment of top 1,000 lead eQTLs relative to the gene body and 5’/3’ flanking regions. (c) Density plot showing positional enrichment of the lead CTCF QTL SNPs near the CTCF peak, relative to all SNPs, aggregated over the top 1,000 detected CTCF QTLs. (d) The percentage of motif-disrupting lead SNPs in top N CTCF binding QTLs. Motif-disrupting SNPs were defined as SNPs located within a CTCF peak and putative CTCF motif, whose predicted allelic effect on binding, computed using CisBP position weight matrices², corresponded to an observed change in CTCF ChIP-seq peak height in the expected direction (see Online Methods). Ordering of the top QTLs was based on their statistical significance independently measured by the three models. (e) Regional plot of P-values around an example CTCF binding QTL (top panel) and CTCF ChIP-seq coverage plot stratified by the lead SNP detected by the joint model (rs1294705) (bottom panel). The sequencing logo (Accession M4325) was derived by the CisBP database analysis of ENCODE CTCF ChIP-seq for GM12878 conducted by Broad Institute.

Next we examined how RASQUAL’s combined model could improve the accuracy of fine-mapping. Here, we used a set of 47 ChiP-seq samples for CCCTC-binding factor (CTCF) in LCLs derived from European individuals ⁹ (Supplementary Table 2). The availability of population scale CTCF ChIP-seq data provided a unique opportunity to test fine mapping performance because causal CTCF QTLs are expected to frequently occur within a well-defined region: the relatively long and informative canonical CTCF binding motif. We defined a high confidence set of “motif-disrupting” putatively causal variants by identifying those SNPs that fulfilled three criteria: (i) they were located within CTCF peak regions (ii) they were located inside CTCF motif matches and (iii) there was concordance between the predicted and observed allelic effect on binding, where predicted allelic effects were computed using the CTCF position weight matrix from the CisBP database²⁰ (see Online Methods for details). RASQUAL’s combined model dramatically improved causal variant localisation. CTCF lead SNPs detected by a combined model were over twice as likely to be motif-disrupting: 29% of lead SNPs in our top 500 CTCF QTLs from the combined model occurred within the CTCF motif, compared with 14% and 13% of lead SNPs from the allele-specific or between-individual only models (Fig. 2c,d). An example of a putatively causal CTCF SNP that was successfully colocalised only by the combined model is shown in (Fig. 2e).

RASQUAL outperforms existing methods

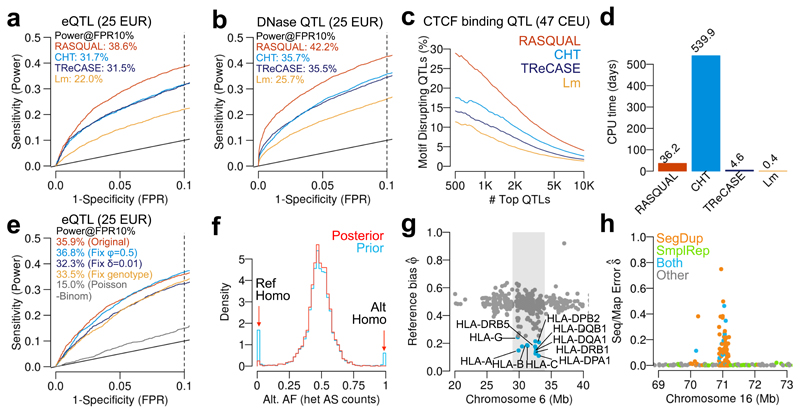
We next compared RASQUAL with three other methods: simple linear regression of log-transformed, principal component-corrected FPKM values, TReCASE²¹ and CHT as implemented in the WASP package⁶. A brief summary of the mathematical differences between TReCASE, CHT and RASQUAL is presented in the Supplementary Methods. For this comparison, in addition to the RNA-seq and ChIP-seq data sets, we also analysed DNaseI-seq data from 70 Yoruban individuals⁵ (Supplementary Table 2) where we again compared QTLs detected in a subsample with a set of “true positive” DNase QTLs mapped using the full data (see Online Methods for details). Across all sample sizes in all data sets, RASQUAL significantly outperforms the other two methods (Fig. 3a-b, Supplementary Fig. 4). At a false positive rate (FPR) of 10% RASQUAL detected between 50 and 130% more eQTLs and between 60 and 150% more DNase QTLs than simple linear regression and between 14 and 30% more eQTLs and between 9 and 24% more DNase QTLs than the next best performing method. We also briefly tested how well RASQUAL performed on larger data sets, and analysed 100 samples of RNA-seq data from the gEUVADIS data set. Unfortunately we were unable to get CHT to converge quickly enough to provide a comparison but, consistent with our results for smaller sample sizes, RASQUAL also detected substantially more QTLs than either linear regression (2,106 more QTLs at FDR 5%) or TReCASE (597 more at FDR 5%) (Supplementary Fig. 5).

Figure 3.

Comparison of RASQUAL with the combined haplotype test (CHT), TReCASE and simple linear regression of log-transformed, principal component-corrected FPKM values (Lm). Dotted line indicates FPR=10% throughout. (a) ROC curves for detecting known eQTL genes (see Online Methods) in a random subset of 25 individuals from gEUVADIS RNA-seq data. (b) ROC curves for detecting known DNaseI QTLs in a random subset of 25 individuals from DNaseI-seq data ³. (c) Percentage of motif-disrupting SNPs in top N lead CTCF-binding QTLs. Ordering of the top QTLs was based on their statistical significance independently measured by the four models. (d) CPU time in days required by each method to finish mapping CTCF QTLs genome-wide. (e) ROC curves for detecting known eQTL genes in a random subset of 25 individuals from gEUVADIS RNA-seq data. The original RASQUAL model (red) is compared to a model with fixed reference bias φ = 0.5 (light blue), fixed mapping/sequencing error δ = 0.01 (dark blue), fixed genotype likelihood (yellow) and no overdispersion θ (poisson-binomial model; grey). (f) Allelic imbalance at heterozygous fSNPs (coverage depth > 20). Heterozygous fSNPs are called as maximum “a priori” genotype (blue) and maximum “a posteriori” genotype (red) (g) The reference bias parameter φ̂ for RNA-seq data estimated by RASQUAL in the MHC region (chr6:28,477,797-33,448,354). Genes with φ̂ < 0.25 are coloured in blue. (h) Example of a genomic distribution of the sequencing/mapping error (δ̂) estimated by RASQUAL for the CTCF ChIP-seq data. Colours represent known segmental duplications (orange), simple repeats (green) or both (blue).

The improvement in variant localisation was even more pronounced with, for example, RASQUAL lead SNPs in the top 500 CTCF QTLs 2.5-fold more likely be “motif-disrupting” compared with simple linear regression and 50% more likely than next best performing method (Fig. 3c). In the majority of cases the next best performing method was CHT, although it performed significantly worse than both RASQUAL and TReCASE for larger sample sizes (Supplementary Fig. 4). Fixing the overdispersion parameter of CHT to the default value rather than estimating it from the data improved performance slightly for the eQTL data (Supplementary Fig. 6), but hampered performance in the CTCF and DNase data, where very few QTLs were detected with the default overdispersion parameter. Across all data sets CHT also took significantly longer to run than RASQUAL, for example requiring 542 days of CPU time to analyse the CTCF ChIP-seq data set, compared with 36.2 CPU days for RASQUAL (Fig. 3d). In part, this difference is likely to arise because RASQUAL is written in C to maximise computational efficiency. Another popular package, Matrix eQTL²², optimises standard linear regression for QTL mapping. For example, in our tests Matrix eQTL finished QTL mapping in our CTCF ChIP-seq data within 0.028 CPU days. However, Matrix eQTL does not use allele-specific information and so will perform identically to linear regression in all other respects.

Simulations

In addition to the analysis of real data, we also explored the performance of RASQUAL using simulations. Our power estimates from simulated data for a range of sample sizes (5, 10, 25, 50 and 100 samples) were qualitatively similar to those estimated from real data (Supplementary Fig. 7a), and analysis of data simulated under the null hypothesis also suggested our model P-values were well-calibrated (Supplementary Fig. 7b-c). We also found that parameter estimates were highly correlated with their simulated values in all cases (Supplementary Fig. 8-10). In a small number of cases (<10% of genes) we noticed that the mapping/sequencing error parameter (δ) was over or underestimated. This occurred because sequencing and mapping errors are infrequent and typical read coverage can sometimes be too low for accurate estimation of δ. However, analysis of genes where δ was inconsistently estimated (Online Methods) suggest that our power and FPR were not significantly affected (Supplementary Fig. 7d-f).

Overdispersion and genotyping error

We next examined the ability of RASQUAL to handle two common features of high-throughput sequence data that are problematic for AS analysis: read overdispersion and genotyping error. Although overdispersion of read count data is well appreciated in the literature on differential expression (e.g., Anders et al.²³), it is sometimes overlooked in AS analysis^24–30. RASQUAL models overdispersion in total read counts and allele specific counts using a single parameter shared between the AS and between-individual components of the model. Modelling overdispersion in this way provided a very substantial increase in power and variant localisation over a Poisson-binomial model for both real and simulated data (Fig 3e; Supplementary Fig. 11). This result suggests that using non-overdispersed distributions to model AS signals may inflate the false positive rate, because random fluctuations in allelic ratios may not be properly accounted for (e.g., Supplementary Fig. 12a).

RASQUAL also employs a novel, iterative approach to genotyping error that refines imperfect genotype calls from genome imputation. Prior to model fitting, we observed an excess of heterozygous SNPs exhibiting complete monoallelic expression in both the RNA-seq data (Fig. 3f, Supplementary Fig. 13) and in other data sets (Supplementary Fig. 14, 15). Although a small fraction of extreme monoallelic expression is expected to be real, the majority of this excess is likely to result from homozygous individuals that have been miscalled as heterozygotes (e.g., Supplementary Fig. 12b). In addition to genotyping errors, RASQUAL can also correct for haplotype switching in heterozygous individuals for rSNPs with large effects (Supplementary Fig. 16). After fitting RASQUAL the frequency of monoallelic expression at heterozygous SNPs was significantly reduced (Fig. 3f). Compared with a model where genotypes and haplotype phase were fixed, the full model also exhibited a significant increase in power in real and simulated data (Fig. 3e; Supplementary Fig. 11).

Reference bias and mapping error

AS signals can be affected by mapping bias towards the reference genome. Previous approaches, such as the WASP pipeline ⁶, have used a filtering strategy to remove reads suspected of being influenced by reference bias. In contrast, RASQUAL uses a feature-specific parameter φ (where φ = 0.5 denoting no bias towards the reference) to detect individual regions where mapping is biased towards the reference. We found that <1% of all features exhibited extreme reference bias (φ < 0.25) in all data sets (Supplementary Table 3), suggesting that reference bias has a minor impact at most genomic loci. Genes with high reference bias tended to cluster in specific genomic locations and were strongly enriched for genes in the MHC region (OR = 39.0; P = 6.7 × 10⁻²²) including most known MHC class I and II genes (Fig. 3g and Supplementary Fig. 12c).

An additional problem for allele-specific analysis are reads that map to incorrect genomic locations, due to problems in the reference assembly or from sequencing errors (Supplementary Fig. 12d). The δ parameter in RASQUAL captures mapping errors by comparing genotype calls with the observed read sequences during model fitting. We next tested RASQUAL’s ability to model read mapping errors in sequenced features. Features exhibiting large δ estimates in the RNA-seq data were enriched in pseudogenes (OR = 7.6; P = 7.5 × 10⁻¹¹⁵) (Supplementary Fig. 17), and for repeat regions and segmental duplications overlapping within CTCF ChIP-seq peaks (OR = 3.0; P < 10⁻³⁰⁰) (Fig. 3h and Supplementary Fig. 18). Analysis of real data suggested that modelling reference bias and mapping errors had a small effect on power (Fig. 3e) although, in the case of the DNase data, the impact of reference bias will be reduced (Supplementary Table 3) because we followed the protocol published by Degner et al.⁵, which used a variant aware aligner.

Simulations suggested that modest impact of modelling reference bias and mapping error occurred because, when these parameters were not estimated from data, a small increase in sensitivity was offset by a similar decrease in specificity, as a result of inflation of test statistic both under the null and alternative hypotheses (Supplementary Fig. 11b-c). However, our simulations also illustrated that not accounting for reference bias significantly increased the chances that a feature SNP would be falsely identified as causal under the null (Supplementary Fig. 11f). Additionally, a major advantage of modelling reference bias and mapping errors is the ability to identify and filter associations following QTL mapping.

Imprinting

Genomic imprinting is characterised by extreme allele-specific bias ^31,32 and can sometimes confound QTL mapping. An additional quality control feature of RASQUAL is the ability to highlight potentially imprinted regions. In RASQUAL, imprinting is detected by searching for sequenced features where all samples show allelic imbalance but, unlike a true cis-acting QTL, the identity of the silenced allele varies randomly between individuals (see Supplementary Methods). RASQUAL provides an additional P-value that corresponds to the test for imprinting that can be used to remove putatively imprinted genes from the analysis. To test the performance of this QC filter, we identified putatively imprinted genes in 24 RNA-seq samples and compared these to the lists recently published in Baran et al.³¹ from the analysis of LCLs in over 639 LCLs. We detected 16 putatively imprinted genes, of which 8 were also found Baran et al using a much larger sample size, a highly significant enrichment (OR = 4,049; P < 10⁻²⁴). When we applied the impriting test to the CTCF ChIP-seq data (see Supplementary Table 3) we identified three putatively imprinted peaks 1kb downstream and upstream of H19 (lincRNA) a known imprinted lincRNA^33,34.

Mapping caQTLs with RASQUAL and ATAC-seq

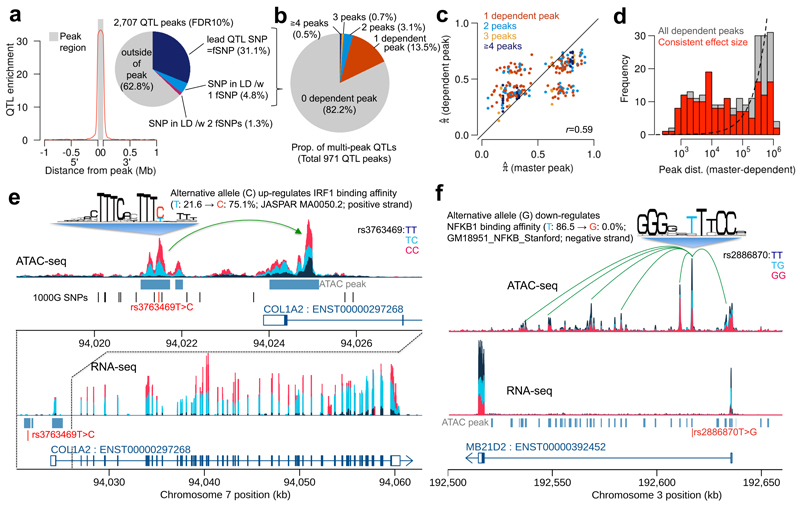
We next sought to combine the increased fine-mapping accuracy of RASQUAL with ATAC-seq, a high-resolution experimental assay to identify regions of open chromatin¹⁸, and generated genome-wide chromatin accessibility landscapes in 24 LCLs from the 1000 Genomes GBR population¹⁸. Despite the modest sample size RASQUAL detected 2,707 caQTLs at FDR 10% using a permutation test. Lead SNPs detected by RASQUAL were very highly enriched within the ATAC peak itself (841 peaks; OR = 42; P < 10⁻¹⁶) (Fig. 4a), with a smaller number in perfect LD with one or more fSNPs within the peak (130 in perfect LD with a single fSNP, and 34 with 2 fSNPs). In the set of 971 lead SNPs within a peak or in perfect LD with an fSNP, the majority (666) overlapped a known transcription factor binding motif that was disrupted by one of the SNP alleles (Supplementary Fig. 19).

Figure 4.

ATAC-QTL mapping with RASQUAL. (a) Positional enrichment of ATAC-QTL lead SNPs, relative to all SNPs, across all 2,707 FDR 10% significant associations detected; inset shows proportion of lead SNPs located inside, outside and in perfect LD (r² > 0.99) with a SNP inside the ATAC peak. (b) Breakdown of multipeak caQTLs in terms of the number of dependent peaks. (c) Comparison of effect sizes (π̂) between master and dependent peaks. (d) Distribution of peak distance between master and dependent peaks. (e) Example of a multipeak ATAC-QTL (rs3763469) that perturbs a putative enhancer-promoter interaction in the COL1A2, also driving variation in gene expression (RASQUAL eQTL P = 3.4 × 10⁻⁴² on gEUVADIS 343 EUR samples). Sequence logo illustrates the IRF1 position weight matrix from JASPAR (f) Example of a multipeak QTL (rs2886870) disrupting the NFKB motif drives associations at 6 peaks in the intron and promoter of the MB21D2 gene. The SNP is also an eQTL of this gene (gEUVADIS project P = 5.2 × 10⁻⁵⁴ on 373 EUR samples).

We also detected a small number (173) of “multipeak” caQTLs where the lowest P-value SNP was shared across more than 1 peak in a 2Mb window (see Online Methods). For each multipeak caQTL, we classify peaks into a master and dependent peaks. The number of dependent peaks ranged from 1 to 9 (Fig. 4b) with a median of one dependent peak per window. Of these 173, 119 showed a consistent direction of effect between master and dependent peaks (Fig. 4c). The distribution of distances between the master and dependent peaks suggested that we find many more interactions over distances of less than 100kb than expected by chance (Fig. 4d). We were less confident of the interactions over longer distances given the increased the greater number of discrepant effect directions we observed between master and dependent peaks, consistent with a greater rate of phasing errors over larger scales. Using the same procedure in permuted data we detected 56 multipeak caQTLs, of which 47 contained 1 dependent peak and 9 contained 2 dependent peaks suggesting that we find almost twice as many multipeak caQTLs as might expected under the null (OR = 2.3; P = 7.1 × 10⁻⁷). In some cases, these multipeak associations appeared to result from enhancer-promoter interactions that are perturbed by a genetic variant. For example, rs3763469 is the lead caQTL SNP for a region of open chromatin located approximately 2.5kb upstream of the promoter of the COL1A2 gene (Fig. 4e) with the alternative allele predicted to increase binding affinity of the transcription factor IRF1. However, we observed that this SNP is also a caQTL for the adjacent ATAC peak located over the promoter region of COL1A2 gene, for which no other common SNPs were annotated in the 1000 Genomes database. In other striking examples, we observed genetic associations spanning a large number of additional peaks spread over many tens of kilobases (Fig. 4f).

Fine-mapping disease and cell trait associations

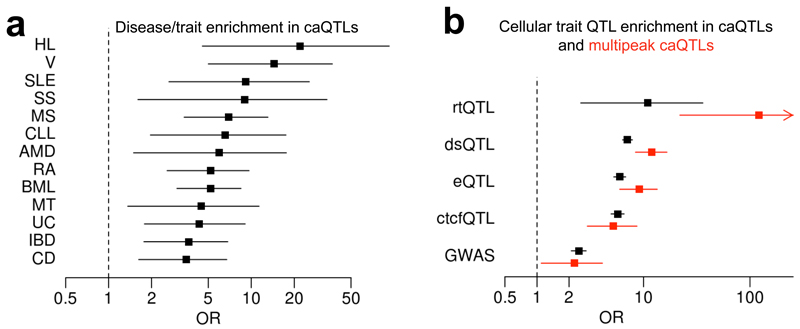
Our results suggest that, combined with ATAC-seq, RASQUAL is a potentially powerful tool for fine-mapping causal regulatory variants because many putatively causal caSNPs are found in a small genomic space (the ATAC peak itself). Our caQTLs significantly overlapped GWAS associated SNPs for a range of traits (see Online Methods for details), most significantly rheumatoid arthritis (OR = 5.2; P = 1.1 × 10⁻⁵) (Fig. 5a). As one example, our analysis highlighted the RA-associated SNP rs909685³⁵, which is both a strong caQTL and eQTL for the SYNGR1 gene, as a likely causal variant located within an ATAC peak downstream of the promoter (Supplementary Fig. 20). In other cases, our analysis pinpointed instances of multiple, putatively causal variants located within the same ATAC peak. For example we found a suggestive chronic lymphocytic leukemia susceptibility SNP (rs2521269³⁶) in perfect LD with two putatively causal ATAC variants (Supplementary Fig. 21) that appear to alter the expression of the two adjacent genes, C11ORF21 and TSPAN32 (Supplementary Fig. 22).

Figure 5.

Enrichment of caQTLs and multipeak caQTLs for SNPs associated with other cellular and organismal traits from GWAS. (a) Disease/traits in GWAS catalogue that are enriched in caQTLs (Fisher exact P<0.01). The dot shows the odds ratio between each disease/trait and caQTL, and black line shows its 95% confidence interval. (b) Cellular trait QTL enrichment in caQTL (black) and multipeak caQTL (red). The dot shows the odds ratio between each disease/trait and caQTL, and the black line shows its 95% confidence interval. The red arrow shows the confidence interval continues toward 451. Hodgkin’s lymphoma (HL); Vitiligo (V); Systemic lupus erythematosus (SLE); Systemic sclerosis (SS); Multiple sclerosis (MS);Chronic lymphocytic leukemia (CLL); Age-related macular degeneration (AMD); Rheumatoid arthritis (RA); Blood metabolite levels (BML); Metabolic traits (MT); Ulcerative colitis (UC); Inflammatory bowel disease (IBD); Crohn’s disease (CD); DNA replication timing QTL (rtQTL); DNaseI hypersensitive QTL (dsQTL); CTCF binding QTL (ctcfQTL); expression QTL (eQTL).

The caQTLs we detected were also significantly enriched for other cellular QTLs detected in LCLs including DNaseI-seq, CTCF ChIP-seq and RNA-seq data sets (Fig. 5d), with multipeak QTLs more than twice as likely to be associated with gene expression than normal caQTLs. Our caQTLs were most strongly enriched in a set of replication timing QTLs (rtQTLs) (OR = 11.0; P = 10⁻³) recently mapped in LCLs³⁷. This enrichment was even more extreme when we considered multipeak caQTLs, which were 10 times more likely to be associated (OR = 177.6; P = 1.26 × 10⁻⁶) (Fig. 5d) than normal caQTLs. The example multipeak QTL SNP rs2886870 (Fig. 4f) is in perfect LD with the rtQTL SNP (rs6786283) detected in Koren et al.³⁷ in Europeans.

Discussion

We have developed a novel statistical model, RASQUAL, for mapping associations between genotype and sequence-based cellular phenotypes. In our tests, RASQUAL consistently outperformed existing methods across a range of sequence data types. We generated a novel ATAC-seq data set in LCLs from European individuals and illustrated how RASQUAL can be used for fine-mapping disease-associated variants and for uncovering fundamental mechanisms of gene regulation.

A major difference between RASQUAL and the other methods we have tested is that RASQUAL handles bias and detection of genetic signals in a single statistical framework, using information from all individuals and without relying on data filtering. This strategy leads to better numerical stability and parameter estimation, improving power and fine-mapping accuracy. RASQUAL also employs novel modelling strategies compared with other methods, including iterative genotype correction and the use of a single overdispersion parameter shared across the between-individual and allele-specific model components to further improve model stability. The relative importance of different parameters varied: power and fine-mapping were mostly impacted by better estimation of overdispersion and by genotype correction while sequencing error primarily improved RASQUAL’s fine-mapping performance. We found that reference bias had a minor impact on both fine-mapping and power, as also suggested by other recent work³⁸. Additional performance might be achieved by the use of variant-aware aligners or alternative modeling strategies to further minimise reference bias.

The integrative approach employed by RASQUAL also improves usability. Users of RASQUAL are not required set arbitrary thresholds for data quality control, or perform computationally intensive read remapping or simulations. Although users can set prior distributions for certain model parameters, our analysis suggests that the default values perform well (see Online Methods). RASQUAL can also highlight genomic regions with problematic AS signals, enabling more informed downstream analysis. Additionally, by minimising the amount of data removed, RASQUAL avoids inadvertant removal of real signal, which may be a problem for filtering strategies. For example, although we found WASP successfully reduced reference bias (Supplementary Fig. 23), it also removed between 22 and 31% of reads in our RNA-seq subset analysis while making a relatively minor difference in power for association detection and fine-mapping (Supplementary Fig. 24). We note, however, that WASP is being actively developed and these results will likely improve the pipeline continues to be refined. One caveat of our analysis is that the “true” positive QTL calls from the gEUVADIS project and Degner et al.⁵ could also be influenced by similar biases to those we have modelled within RASQUAL. However, our results from real and simulated data are extremely similar, suggesting that the impact of many biases on our “true” positive QTL calls is small, probably because neither gEUVADIS or Degner et al.⁵ used allele-specific information to call QTLs. Finally, although our results suggest that RASQUAL improves fine-mapping for sequencing based traits, further work is required to combine cellular QTL studies with those from disease studies.

We now briefly consider the experimental settings in which RASQUAL’s performance is likely to be optimised. Dense genotyping, either from imputation or whole genome sequencing, is critical because this ensures that sequenced features contain as many variable sites as possible. It is also important that genotype likelihoods are available to enable RASQUAL to perform genotype error correction and poor quality imputation or phasing information is likely to significantly impair RASQUAL’s ability to detect QTLs. This will be particularly problematic when the distance between the true rSNP and fSNP is large, due greater likelihood of haplotype switching errors. RASQUAL will also be sensitive to the depth of read coverage at feature SNPs, as greater coverage will enable more accurate quantification of allele-specific signals. As one example, the mean read coverage per sample in our ATAC-seq data was 68.8 million fragments. For individual features, we expect the most dramatic improvements in sensitivity and fine-mapping to be observed for large features, containing many heterozygous SNPs with high read coverage. We note that, while dense genotyping information is preferable, it is not essential and it is possible to also run RASQUAL in in a “genotype-free” mode. Here, only SNPs located inside sequenced features are considered, genotypes are learned from the read data and SNP locations are specified using, for example, dbSNP. Although lack of genotype information will reduce power substantially, it can enable analysis of sequence data sets where genotype data are absent and standard QTL analysis is not possible³⁹.

We found that all methods that use allele-specific information showed a enrichment of lead eQTL SNPs towards the 3’ end of the transcript. One explanation for this result is that allele-specific analysis is more sensitive to changes in splicing of gene 3’ UTRs, which often accounts for a large fraction of the total reads mapped to many genes. Some evidence for this comes from the fact that eQTLs detected using only allele-specific signals are enriched for exon QTLs (Supplementary Fig. 25c, f). While changes in splicing are legitimate biological signals, we note that eQTLs detected using any allele-specific method should not immediately be interpreted as “classical” eQTLs and that examination of the location of the lead SNP may assist functional interpretation.

Our results also illustrate how RASQUAL can be used to extract meaningful genetic signals from data sets of a modest size. For example, our analysis of ATAC-seq data demonstrates how genetic variation can be leveraged to connect distal regulatory elements with gene promoters or with other regulatory elements. A strength of this approach, compared with experimental techniques such as Hi-C or CHiAPET, is that these interactions are linked to specific genetic changes enabling potential characterisation of causal relationships between regulatory elements and their target genes. We expect that genetic analysis of long-range regulatory interactions will be a powerful complement to standard experimental techniques in future, more well-powered studies.

RASQUAL’s performance with modest sample sizes will potentially enable researchers to collect and analyse multiple complementary sequence data sets, rather than being forced to maximise the sample size for an single phenotype. Combined with RASQUAL’s improved ability to localise causal variants we suggest that a major future application of our model will be the fine-mapping of causal regulatory variants to better understand the molecular mechanisms underlying phenotypic variation.

Online methods

Hypothesis testing for inference of QTL

For statistical hypothesis testing of QTL, all five parameters for each SNP-feature combination in the cis-regulatory window are estimated independently to get the maximum likelihood under alternative hypotheses. Under the null hypothesis, all parameters except π are estimated for each feature independently, while π is set to 0.5 and we use a likelihood ratio test to compare the null and alternative hypotheses for each SNP-feature combination using the χ² distribution with one degree of freedom (for π). We use an EM algorithm to obtain the maximum likelihood estimators of the parameters⁴. We do not introduce any common parameters across features estimated a priori, but instead introduced prior distributions for all the parameters (see Supplementary Methods for details) to increase the stability and usability of RASQUAL. A detailed description of the derivation of statistical model and the EM algorithm is available in the Supplementary Methods.

Data preprocessing of sequencing traits

The gEUVADIS RNA-seq data was downloaded from ArrayExpress (Accession E-GEUV-3), CTCF CHIP-seq data was downloaded from the European Nucleotide Archive (Accession ERP002168) and the DNaseI-seq was downloaded from the Gene Expression Omnibus (Accession GSE31388). All data sets were realigned to human genome assembly GRC37. RNA-seq data were aligned using Bowtie 2⁵ and reads mapped to splice junctions using tophat 2⁶, with ENSEMBL human gene assembly 69 as the reference transcriptome. CTCF ChIP-seq data was realigned using bwa⁷ and the DNaseI-seq was realigned using the alignment method described in Degner et al.³. Following alignment, we removed reads with a quality score of <10 from all three data sets.

For the CTCF ChIP-seq and DNaseI-seq data, we generated genome wide read coverage depths from either the fragment midpoints or cut site data respectively. Peaks were called by comparing two Gaussian kernel densities with bandwidths of 100 and 1,000 bp, corresponding to a “peak” and “background” model respectively. We then defined a peak as a region where the peak kernel coverage exceeded the background kernel coverage, and where the peak coverage was greater than 0.001 fragments per million.

For RNA-seq data, we counted the number of sequenced fragments of which one or other sequenced end overlaps with an union of annotated Ensembl gene exons. For CTCF ChIP-seq and ATAC-seq data, we counted the number of sequenced fragments of which one or other sequenced end overlaps with the annotated peak. For DNaseI-seq data, we simply counted the number of reads that are overlapping with the annotated peak. For the computation of principal components we also calculated FPKM and RPKM values for these data sets (see Supplementary Methods). All sequence data sets were corrected for between library variation in amplification efficiencies of different GC content reads. For each sample, all features were binned based on their GC content, the relative over-representation of features of a given GC content for a given sample relative to all other samples was estimated using a smoothing spline. This value was then either included as a covariate, in the comparison of CHT, TReCASE and RASQUAL, or to correct RPKM or FPKM values for the linear model.

SNP genotype data preparation

We downloaded VCF files for the 1000 Genomes Phase I integrated variant set from the project website. Because RNA-seq and ATAC-seq samples completely overlapped with the 1000 Genomes samples, we used the subsamples from the VCF files. For CTCF ChIP-seq and DNaseI-seq data, samples were completely overlapped with the HapMap samples (except for NA12414 in CEU population and NA18907 in YRI population) but not 1000 Genomes samples. Therefore we downloaded the HapMap phase II & III genotypes from the project website and imputed with the 1000 Genomes Phase I haplotypes using IMPUTE2⁸. For the two samples which are not in HapMap samples, we obtained genotypes from the 1000 Genomes data at HapMap SNP loci and merged before the imputation. We adopted the common 2-step imputation approach to phase HapMap genotypes first and then impute haplotypes. Note that, to apply whole genome imputation, we split each chromosome in 20Mb bins with 100kb overlaps.

For any cellular trait mapping, we used SNP loci with minor allele frequency greater than 5% and imputation quality score (MaCH R² or IMPUTE2 I²) greater than 0.7 for candidate rSNP. For fSNPs, we used all SNPs overlapping with the target feature with at least one individual being heterozygote. For TReCASE analysis, we merged AS counts at those fSNPs with heterozygous genotypes for each feature according to the phased haplotype information. Indels and other structural variants were discarded.

Definition of true QTLs

The eQTL/exon-QTL lists detected using the entire gEUVADIS European data set (N=373) at FDR 5% were downloaded from the EBI website (see URLs section). dsQTLs were downloaded from the University of Chicago eQTL browser (see URLs section) and used the UCSC liftover tool to transfer genome coordinates to hg19. We then obtained peaks (in our annotation) that overlapped with the reported dsQTL regions as a gold standard dsQTL peak set.

CTCF motif-disrupting SNPs

At each CTCF peak, a lead SNP was defined by each method as the SNP with the lowest P-value. In cases where there were multiple lead SNPs, a lead SNP was selected at random from the set of lowest P-value SNPs. Motif-disrupting SNPs were defined as SNPs located within a CTCF peak and putative CTCF motif, whose predicted allelic effect on binding (computed using CisBP ² position weight matrices (PWMs)) corresponded to an observed change in CTCF ChIP-seq peak height in the expected direction.

The predicted allelic effect is calculated from a PWM as follows. Let S_a:b be the reference sequence at chromosomal position between a and b on a chromosome. We assume a SNP locus at chromosomal position c. For a PWM with motif length m, we calculate the binding affinity score

$$w\left(S_{a:b}\right)=\frac{1}{{0.25}^m}{\displaystyle \sum _{j=c-m+1}^c\left[PWM\left(S_{i:j+m-1}\right)+PWM\left({\tilde{S}}_{i:j+m-1}\right)\right]},$$

where PWM(·) denotes the PWM score for S_a:b and ${\tilde{S}}_{a:b}$ denotes the reverse complement sequence of S_a:b. We also calculated the affinity score for the sequence $S_{a:b}^{\left(c\right)}$ where the reference sequence at position c, that is S_c:c, is replaced by the alternative allele of the SNP. We compared w(S_a:b) with $w\left(S_{a:b}^{\left(c\right)}\right)$ to determine which SNP allele is over-represented at the putative binding site involving the SNP locus at c.

For CTCF-binding motifs, there exist multiple PWMs (N=67) reported in Weirauch et al.². We simply took the average affinity score $\overline{w}\left(S_{a:b}\right)$ across all PWMs. Then we considered only SNPs that gave either $\overline{w}\left(S_{a:b}\right)>0$ or $\overline{w}\left(S_{a:b}^{\left(c\right)}\right)>0$ as a SNP in a CTCF motif starting at chromosomal position $\widehat{J},$ such that

$$\widehat{J}=\underset{j=c-m+1,\dots ,c}{\text{argmax}}PWM\left(S_{j:j+m-1}\right)+PWM\left({\tilde{S}}_{j:j+m-1}\right)+PWM\left(S_{j:j+m-1}^{\left(c\right)}\right)+PWM\left({\tilde{S}}_{j:j+m-1}^{\left(c\right)}\right).$$

Multiple testing correction

Following Battle et al.⁹, we implemented a two-stage multiple testing correction to determine which features contain a significant QTL. First, because SNP density varies between genomic regions, QTL mapping for different features involves testing different number of SNPs. This results in lead P-values that are incomparable across features because more SNP dense regions will involve greater numbers of tests and therefore smaller P-values observed by chance under the null hypothesis. As in Battle et al.⁹ we used a Bonferroni correction to correct for multiple tests within windows.

After P-values for each feature have been corrected for the number of tests in the cis-window, they are used to set the false discovery rate (FDR) threshold for the number of features tested genome-wide. Here we used a permutation strategy as in Pickrell et al.¹⁰. Specifically, we drew random permutations {(i)} for total fragment count and {(i_l)} for AS counts at each fSNP l independently. Then we maximise the following likelihood

$${ℒ}_{\text{perm}}(\Theta )={\displaystyle \prod _{i=1}^N{\displaystyle \sum _{G_i}p\left(G_i\right)p_{\text{NB}}\left(Y_{\left(i\right)}|G_i\right)}}{\displaystyle \prod _{l=1}^L{\displaystyle \sum _{D_{\left(i_l\right)l}}p\left(D_{\left(i_l\right)l}|G_i\right)p_{\text{BB}}\left(Y_{\left(i_l\right)l}^{\left(1\right)}|Y_{\left(i_l\right)l},D_{\left(i_l\right)l}\right)}}$$

with respect to Θ = {π, φ, δ, λ, θ} to obtain the likelihood ratio statistic (between π = 0.5 and π ≠ 0.5). Here, $D_{\left(i_l\right)l}$ denotes the diplotype configuration between G_i and permuted fSNP $G_{\left(i_l\right)l}.$ P-values obtained from permuted data were corrected for multiple tests within each feature as described for real data. Then the permutation P-values $\left\{p_j^{\text{perm}};j=1,\dots ,J\right\}$ for total J features were compared with the real P-values {p_j; j = 1, …, J} to calibrate genome-wide P-value threshold α under the false-discovery rate

$$\text{FDR}=\frac{\#\left\{k|p_k^{\left(\text{perm}\right)}<\alpha \right\}}{\#\left\{k|p_k<\alpha \right\}}.$$

ATAC-seq in LCLs

The ATAC-seq method used was as described in Buenrostro et al.¹¹, but with some modifications: (1) 100,000 LCL nuclei obtained from sucrose and Triton X-100 treatment were tagmented using the Illumina Nextera kit and then subject to limited PCR amplification, incorporating indexing sequence tags (2) ATAC libraries were purified and size selected before pooling (3) index tag ratios were balanced using a MiSeq (Illumina) run before deep sequencing with 75bp paired-end reads on a HiSeq 2500 (Illumina). For more details, see Supplementary Methods.

Mapping multi-peak caQTLs

For the 971 caQTLs whose lead SNPs are found in the peak or in perfect LD (R² > 0.99) with one fSNP, we asked how many of those caQTL SNPs are appeared to be the lead SNP for other peaks (not necessarily significant). We found 173 out of the 971 caQTL SNPs were shared with other peaks or in perfect LD with the lead SNP of those other peaks. We defined the peaks involved those caQTL SNPs as “master” caQTL peaks and other peaks sharing those lead caQTL SNPs as “dependent” peaks. If there are two or more caQTL SNPs in perfect LD, we picked up the peak with the most significant lead caQTL SNP as the master peak. We further filtered out dependent peaks whose effect sizes are inconsistent with those of the master peaks. We obtained 119 caQTL peaks which have one or more dependent peaks with consistent effect sizes $\left({\widehat{\pi }}_{\text{master}},{\widehat{\pi }}_{\text{dependent}}>0.5\text{or}{\widehat{\pi }}_{\text{master}},{\widehat{\pi }}_{\text{dependent}}<0.5\right).$ Note that if two lead SNPs are in LD but negatively correlated (i.e., R = −1), the effect size was subtracted from 1 for the dependent peak (i.e., ${\widehat{\pi }}_{\text{dependent}}\leftarrow 1-{\widehat{\pi }}_{\text{dependent}}).$

Disease enrichment analysis for ATAC QTLs

We obtained the publicly available GWAS catalogue data¹² from the UCSC website created on Mar 2015. We only included studies that had at least 10 hits that were genome-wide significant of P < 5 × 10⁻⁸ that overlapped with the SNPs tested in ATAC QTL mapping (5,703,168 loci as a total) and were based on European populations with the sample sizes greater than 1,000. The resulting data set contained GWAS on 101 diseases and other traits. Because of tight LD, different index SNPs in the same locus were reported by multiple GWA studies for a single disease/trait. Likewise, multiple LD SNPs were significantly associated with a single ATAC peak. To merge these LD SNPs, we assigned the lead ATAC peak with the minimum P-value for each SNP locus and counted the number of lead peaks (instead of SNPs) that are significantly associated with a disease/trait and/or ATAC QTLs (Supplementary Fig. 26). The disease/trait enrichment was assessed using a Fisher’s exact test. The number of tested peaks is different across SNPs because multiple testing correction has been applied for each lead P-value and SNPs with the corrected lead P-values less than FDR 10% were called as significant ATAC QTL SNPs.