Network dismantling

Significance

Many systems of interest can be represented by a network of nodes connected by edges. In many circumstances, the existence of a giant component is necessary for the network to fulfill its function. Motivated by the need to understand optimal attack strategies, optimal spread of information, or immunization policies, we study the network dismantling problem (i.e., the search for a minimal set of nodes in which removal leaves the network broken into components of subextensive size). We give the size of the optimal dismantling set for random networks, propose an efficient dismantling algorithm for general networks that outperforms by a large margin existing strategies, and provide various insights about the problem.

Abstract

We study the network dismantling problem, which consists of determining a minimal set of vertices in which removal leaves the network broken into connected components of subextensive size. For a large class of random graphs, this problem is tightly connected to the decycling problem (the removal of vertices, leaving the graph acyclic). Exploiting this connection and recent works on epidemic spreading, we present precise predictions for the minimal size of a dismantling set in a large random graph with a prescribed (light-tailed) degree distribution. Building on the statistical mechanics perspective, we propose a three-stage Min-Sum algorithm for efficiently dismantling networks, including heavy-tailed ones for which the dismantling and decycling problems are not equivalent. We also provide additional insights into the dismantling problem, concluding that it is an intrinsically collective problem and that optimal dismantling sets cannot be viewed as a collection of individually well-performing nodes.

A network (a graph G in the discrete mathematics language) is a set V of N entities called nodes (or vertices), along with a set E of edges connecting some pairs of nodes. In a simplified way, networks are used to describe numerous systems in very diverse fields, ranging from social sciences to information technology or biological systems (reviews are in refs. 1 and 2). Several crucial questions in the context of network studies concern the modifications of the properties of a graph when a subset S of its nodes is selected and treated in a specific way. For instance, how much does the size of the largest connected component of the graph decrease if the vertices in S (along with their adjacent edges) are removed? Do the cycles survive this removal? What is the outcome of the epidemic spreading if the vertices in S are initially contaminated, constituting the seed of the epidemic? On the contrary, what is the influence of a vaccination of nodes in S preventing them from transmitting the epidemic? It is relatively easy to answer these questions when the set S is chosen randomly, with each vertex being selected with some probability independently. Classical percolation theory is nothing but the study of the connected components of a graph in which some vertices have been removed in this way.

A much more interesting case is when the set S can be chosen in some optimal way. Indeed, in all applications sketched above, it is reasonable to assign some cost to the inclusion of a vertex in S: vaccination has a socioeconomic price, incentives must be paid to customers to convince them to adopt a new product in a viral marketing campaign, and incapacitating a computer during a cyber attack requires resources. Thus, one faces a combinatorial optimization problem: the minimization of the cost of S under a constraint on its effect on the graph. These problems thus exhibit both static and dynamic features, the former referring to the combinatorial optimization aspect and the latter referring to the definition of the cost function itself through a dynamical process.

In this paper, we focus on the existence of a giant component in a network: that is, the largest component containing a positive fraction of the vertices (in the $N\to \infty$ limit). On the one hand, the existence of a giant component is often necessary for the network to fulfill its function (e.g., to deliver electricity or information bits or ensure possibility of transportation). An adversary might be able to destroy a set of nodes with the goal of destroying this functionality. It is thus important to understand what an optimal attack strategy is, possibly as a first step in the design of optimal defense strategies. On the other hand, a giant component can propagate an epidemic to a large fraction of a population of nodes. Interpreting the removal of nodes as the vaccination of individuals who cannot transmit the epidemic anymore, destroying the giant component can be seen as an extreme way of organizing a vaccination campaign (3, 4) by confining the contagion to small connected components [less drastic strategies can be devised using specific information about the epidemic propagation model (5, 6)]. Another related application is influence maximization as studied in many previous works (7–9). In particular, optimal destruction of the giant component is equivalent to selection of the smallest set of initially informed nodes needed to spread the information into the whole network under a special case of the commonly considered model for information spreading (7–9).

To define the main subject of this paper more formally, following ref. 10, we call S a C-dismantling set if its removal yields a graph with the largest component that has size (in terms of its number of nodes) at most C. The C-dismantling number of a graph is the minimal size of such a set. When the value of C is either clear from the context or not important for the given claim, we will simply talk about dismantling. Typically, the size of the largest component is a finite fraction of the total number of nodes N. To formalize the notion of destroying the giant component, we will consider the bound C on the size of the connected components of the dismantled network to be such that $1\ll C\ll N$. It should be noted that we defined dismantling in terms of node removal; it could be rephrased in terms of edge removal (11), which turns out to be a much easier problem. The dismantling problem is also referred to as fragmentability of graphs in graph theory literature (12–14) and optimal percolation in ref. 15.

Determining whether the C-dismantling number of a graph is smaller than some constant is nondeterministic polynomial (NP)-complete decision problem (a proof is in SI Appendix). The concept of NP completeness concerns the worst case difficulty of the problem. The questions that we address in this paper are instead the following. What is the dismantling number on some representative class of graphs (in our case, random graphs)? What are the best heuristic algorithms, how does their performance compare with the optimum, and how do they perform on benchmarks of real world graphs? Simple heuristic algorithms for the dismantling problem were considered in previous works (16–18), where the choice of the nodes to be included in the dismantling set was based on their degrees (favoring the inclusion of the most connected vertices) or some measure of their centrality. More recently, a heuristic for the dismantling problem has been presented in ref. 15 under the name “collective” influence (CI), in which the inclusion of a node is decided according to a combination of its degree and the degrees of the nodes in a local neighborhood around it. Ref. 15 also attempts to estimate the dismantling number on random graphs.

Our Main Contribution

In this paper, we provide a detailed study of the dismantling problem, with both analytical and algorithmic outcomes. We present very accurate estimates of the dismantling number for large random networks, building on a connection with the decycling problem [in which one seeks a subset of nodes with removal that leaves the graph acyclic; also an NP-complete problem (19)] and recent studies of optimal spreading (20–23). Our results are the one-step replica symmetry broken estimate of the ground state of the corresponding optimization problem.

On the computational side, we introduce a very efficient algorithm that outperforms considerably state of the art algorithms for solving the dismantling problem. We show its efficiency and closeness to optimality on both random graphs and real world networks. The goal of our paper is closely related to the one of ref. 15; we present an assessment of the results reported therein on random as well as real world networks.

Our dismantling algorithm, which has been inspired by the theoretical insight gained on random graphs, is composed of three stages.

• i)Min-Sum message passing for decycling. This part is the core of the algorithm, using a variant of a message-passing algorithm developed in refs. 20 and 21. A related but different message-passing algorithm was developed for decycling in ref. 22 and later applied to dismantling in ref. 24; it performs comparably with ours.
• ii)Tree breaking. After all cycles are broken, some of the tree components may still be larger than the desired threshold C. We break them into small components, removing a fraction of nodes that vanishes in the large size limit. This operation can be done in time $O\left(N\log N\right)$ by an efficient greedy procedure (detailed in SI Appendix).
• iii)Greedy reintroduction of cycles. As explained below, the strategy of first decycling a graph before dismantling it is the optimal one for graphs that contain few short cycles (a typical property of light-tailed random graphs). For graphs with many short cycles, we improve considerably the efficiency of our algorithm by reinserting greedily some nodes that close cycles without increasing too much the size of the largest component.

The dismantling problem, as is often the case in combinatorial optimization, exhibits a very large number of (quasi)optimal solutions. We characterize the diversity of these degenerate minimal dismantling sets by a detailed statistical analysis, computing in particular the frequency of appearance of each node in the quasioptimal solutions, and conclude that dismantling is an intrinsically collective phenomenon that results from a correlated choice of a finite fraction of nodes. It thus makes much more sense to think in terms of good dismantling sets as a whole and not about individual nodes as the optimal influencers/spreaders (15). We further study the correlation between the degree of a node and its importance for dismantling, exploiting a natural variant of our algorithm, in which the dismantling set is required to avoid some marked nodes. This study allows us to show that each of the low-degree nodes can be replaced by other nodes without increasing significantly the size of the dismantling set. Contrary to claims in ref. 15, we do not confirm any particular importance of weak nodes, apart from the obvious fact that the set of highest-degree nodes is not a good dismantling set.

To give a quantitative idea of our algorithmic contribution, we state two representative examples of the kind of improvement that we obtain with the above algorithm with respect to the state of the art (15).

• i)In an Erdős–Rényi (ER) random graph of average degree 3.5 and size $N=5^7$, we found $C=\mathrm{1,000}$ dismantling sets removing $17.8\text{\%}$ of the nodes, whereas the best known method (adaptive eigenvalue centrality for this case) removes $20.2\text{\%}$ of the nodes, and the adaptive CI method of ref. 15 removes $20.6\text{\%}$ of the nodes. Hence, we provide a $13\text{\%}$ improvement over the state of the art. Our theoretical analysis estimates the optimum dismantling number to be around $17.5\text{\%}$ of the nodes; thus, the algorithm is extremely close to optimal in this case.
• ii)Our algorithm managed to dismantle the Twitter network studied in ref. 15 (with $\mathrm{532,000}$ nodes) into components smaller than $C=\mathrm{1,000}$ using only $3.4\text{\%}$ of the nodes, whereas the CI heuristics of ref. 15 needs $5.6\text{\%}$ of the nodes. Here, we thus provide a $60\text{\%}$ improvement over the state of the art.

Not only does our algorithm show beyond state of the art performance, but it is also computationally efficient. Its core part runs in linear time over the number of edges, allowing us to easily dismantle networks with tens of millions of nodes.

Relation Between Dismantling and Decycling

We begin our discussion by clarifying the relation between the dismantling and decycling problems. Although the argument below can be found in ref. 10, we reproduce it here in a simplified fashion. The decycling number (or more precisely, fraction) ${\theta }_{\text{dec}}\left(G\right)$ of G is the minimal fraction of vertices that have to be removed to make the graph acyclic. We define similarly the dismantling number ${\theta }_{\text{dis}}\left(G,C\right)$ of a graph G as the minimal fraction of vertices that have to be removed to make the size of the largest component of the remaining graph smaller than a constant C.

For random graphs with degree distribution $q={\left\{q_k\right\}}_{k\ge 0}$, in the large size limit, the parameters ${\theta }_{\text{dec}}$ and ${\theta }_{\text{dis}}$ will enjoy concentration (self-averaging) properties; we shall thus write their typical values as

$${\theta }_{\text{dec}}\left(q\right)=\underset{N\to \infty }{\text{lim}}\mathbb{E}\left[{\theta }_{\text{dec}}\left(G\right)\right],$$ [1]

$${\theta }_{\text{dis}}\left(q\right)=\underset{C\to \infty }{\text{lim}}\underset{N\to \infty }{\text{lim}}\mathbb{E}\left[{\theta }_{\text{dis}}\left(G,C\right)\right],$$ [2]

where $\mathbb{E}[•]$ denotes an average over the random graph ensemble. For the dismantling number, we allow the connected components after the removal of a dismantling set to be large but subextensive because of the order of limits. It was proven in ref. 10 that, for some families of random graphs, an equivalent definition is ${\text{lim}}_{\mathit{ϵ}\to 0}{\text{lim}}_{N\to \infty }\mathbb{E}\left[{\theta }_{\text{dis}}\left(G,\mathit{ϵ}N\right)\right]$ (i.e., connected components are allowed to be extensive but with a vanishing intensive size).

The crucial point for the relation between dismantling and decycling is that trees (or more generically, forests) can be efficiently dismantled. It was proven in ref. 10 that ${\theta }_{\text{dis}}\left(G,C\right)\le 1/\left(C+1\right)$ whenever G is a forest. This inequality means that the fraction of vertices to be removed from a forest to dismantle it into components of size C goes to zero when C grows.

This observation brings us to the following two claims concerning the dismantling and decycling numbers for random graphs with degree distribution q: (i) for any degree distribution, ${\theta }_{\text{dis}}\left(q\right)\le {\theta }_{\text{dec}}\left(q\right)$; and (ii) if q also admits a second moment (we shall call q light tailed when this is the case), then there is actually an equality between these two parameters, ${\theta }_{\text{dis}}\left(q\right)={\theta }_{\text{dec}}\left(q\right)$.

The first claim follows directly from the above observation on the decycling number of forests. After a decycling set S of G has been found, one can add to S additional vertices to turn it into a C-dismantling set, the additional cost being bounded as ${\theta }_{\text{dis}}\left(G,C\right)\le {\theta }_{\text{dec}}\left(G\right)+1/\left(C+1\right)$. Taking averages of this bound and the limit $C\to \infty$ after $N\to \infty$ yields directly i.

To justify our second claim, we consider a C-dismantling set S of a graph G. To turn S into a decycling set, we need to add additional vertices to break the cycles that might exist in $G\mathrm{\backslash }S$. The lengths of these cycles are certainly smaller than C, and removing at most one vertex per cycle is enough to break them. We can thus write ${\theta }_{\text{dec}}\left(G\right)\le {\theta }_{\text{dis}}\left(G,C\right)+n_C\left(G\right)/N$, with $n_C\left(G\right)$ denoting the number of cycles of G of length at most C. We recall that the existence of a second moment of q implies that $n_C\left(G\right)$ remains bounded when $N\to \infty$ with C fixed. Considering the limit $N\to \infty$ and property i, property ii follows.

Network Decycling

In this section, we shall explain the results on the decycling number of random graphs that we obtained via statistical mechanics methods and how they can be exploited to build an efficient heuristic algorithm for decycling arbitrary graphs.

Testing the Presence of Cycles in a Graph.

The 2-core of a graph G is its largest subgraph of minimal degree 2; it can be constructed by iteratively removing isolated nodes and leaves (vertices of degree 1) until either all vertices have been removed or all remaining vertices have degree at least 2. It is easy to see that a graph contains cycles if and only if its 2-core is nonempty. To decide if a subset S is decycling, we remove the nodes in S and perform this leaf removal on the reduced graph. To formalize this procedure, we introduce binary variables $x_i^t\left(S\right)\in \left\{\mathrm{0,1}\right\}$ on each vertex $i\in V$ of the graph, t being a discrete time index. At the starting time $t=0$, one marks the initially removed vertices by setting $x_i^0\left(S\right)=1$ if $i\in S$ and 0 otherwise, and let the x variables evolve in time according to

$$x_i^{t+1}\left(S\right)=\{\begin{array}{ll}1\hfill & \text{if}\hspace{0.17em}{x}_i^t\left(S\right)=1,\hfill \\ \mathbb{I}\hspace{0.17em}\hspace{0.17em}\left[{\displaystyle \sum _{j\in \partial i}\left(1-x_j^t\left(S\right)\right)\le 1}\right]\hfill & \text{if}\hspace{0.17em}{x}_i^t\left(S\right)=0,\hfill \end{array}$$ [3]

where $\partial i=\left\{j:\left(ij\right)\in E\right\}$ denotes the local neighborhood of vertex I, and $\mathbb{I}$ denotes the indicator function (that is, one if its argument is true and zero otherwise). One can check that the $x_i$ s are monotonous in time (they can only switch from zero to one); hence, they admit a limit $x_i^{\ast }\left(S\right)$ when $t\to \infty$. At this fixed point, $x_i^{\ast }\left(S\right)=0$ if and only if i is in the 2-core of $G\mathrm{\backslash }S$; hence, the sufficient and necessary condition for S to be a decycling set of G is $x_i^{\ast }\left(S\right)=1$ for all vertices i.

Note that the leaf removal procedure can be equivalently viewed as a particular case of the linear threshold model of epidemic propagation or information spreading. By calling a removed vertex infected (or informed), one sees that the infection (or information) of node i occurs whenever the number of its infected (or informed) neighbors reaches its degree minus one. This equivalence, which was already exploited in refs. 15 and 23, allows us to build on previous works on minimal contagious sets (20, 21, 23) and influence maximization (7–9).

Optimizing the Size of Decycling Sets.

From the point of view of statistical mechanics, it is natural to introduce the following probability distribution over the subsets S to find the optimal decycling sets of a given graph

$$\widehat{\eta }\left(S\right)=\frac{1}{Z\left(\mu \right)}{e}^{\mu \left|S\right|}{\displaystyle \prod _{i\in V}\mathbb{I}\left[x_i^{\ast }\left(S\right)=1\right]},$$ [4]

where $\left|S\right|$ denotes the number of vertices in S, μ is a real parameter to be interpreted as a chemical potential (or an inverse temperature), and the partition function $Z\left(\mu \right)$ normalizes this probability distribution. From the preceding discussion, this measure gives a positive probability only to decycling sets, and their minimal size can be obtained as the ground-state energy in the zero-temperature limit:

$${\theta }_{\text{dec}}\left(G\right)=\frac{1}{N}\underset{\mu \to -\infty }{\text{lim}}\frac{1}{\mu }\ln \hspace{0.17em}Z\left(\mu \right).$$ [5]

The computation of this partition function remains at this point a difficult problem; in particular, the variables $x_i^{\ast }$ depend on the choice of S in a nonlocal way. One can get around this difficulty in the following way: because the evolution of $x_i^t$ is monotonous in time, it can be completely described by a single integer, $t_i\left(S\right)=\text{min}\left\{t:x_i^t\left(S\right)=1\right\}$, the time at which i is removed in the parallel evolution described above. Note that $t_i\left(S\right)=0$ if and only if $i\in S$ and $t_i\left(S\right)>0$ otherwise. We use the natural convention $\min \hspace{0.17em}ø=\infty$; hence, the nodes i in the 2-core of $G\mathrm{\backslash }S$ are precisely those with an infinite removal time $t_i\left(S\right)=\infty$. The crucial advantage of this equivalent representation in terms of the activation times is its locality along the graph. Indeed, the dynamical evolution rule (Eq. 3) can be rephrased as static equations linking the times $t_i$ on neighboring vertices:

$$t_i\left(S\right)=\{\begin{array}{ll}0\hfill & \text{if}\hspace{0.17em}\hspace{0.17em}i\in S,\hfill \\ {\varphi }_i\left({\left\{t_j\right\}}_{j\in \partial i}\right)\hfill & \text{if}\hspace{0.17em}\hspace{0.17em}i\in V\mathrm{\backslash }S,\hfill \end{array}$$ [6]

$$\text{with}\hspace{0.17em}\hspace{0.17em}{\varphi }_i\left({\left\{t_j\right\}}_{j\in \partial i}\right)=1+{\text{max}}_2\left({\left\{t_j\left(S\right)\right\}}_{j\in \partial i}\right),$$ [7]

where we denote ${\text{max}}_2$ the second largest of the arguments [reordering them as $t_1\ge t_2\ge \dots \ge t_n$, one defines ${\text{max}}_2\left(t_1,\dots ,t_n\right)=t_2$]. In the leaf removal procedure, one vertex is removed in the first step after the time at which all but one of its neighbors has been removed, making it a leaf. Eq. 6 admits a unique solution for each S; hence, the partition function can be rewritten as

$$Z\left(\mu \right)={\displaystyle \sum _{\left\{t_i\right\}}{e}^{\mu {\displaystyle \sum _i{\psi }_i\left(t_i\right)}}}{\displaystyle \prod _{i\in V}\mathbb{I}\left[t_i<\infty \right]}{\displaystyle \prod _{i\in V}\mathrm{\Phi }\left(t_i,{\left\{t_j\right\}}_{j\in \partial i}\right)},$$ [8]

with ${\psi }_i\left(t_i\right)=\mathbb{I}\left[t_i=0\right]$, and $\mathrm{\Phi }\left(t_i,{\left\{t_j\right\}}_{j\in \partial i}\right)=\mathbb{I}\hspace{0.17em}\left[t_i=0\right]+\mathbb{I}\hspace{0.17em}\left[t_i={\varphi }_i\left({\left\{t_j\right\}}_{j\in \partial i}\right)\right]$. We have thus obtained an exact representation of the generating function counting the number of decycling sets according to their size as a statistical mechanics model of variables (the $t_i$ s) interacting locally along the graph G. We transformed the nonequilibrium problem of leaf removal into an equilibrium problem, where the times of removal play the role of the static variables. Note that ref. 22, which also estimates the decycling number, uses a simpler but approximate representation, where one cycle may remain in every connected component, and the correspondence between microscopic configurations and sets of removed vertices is many to one. The domain of the variables $t_i$ should include all integers between zero and the diameter of G and the additional $\infty$ value. For practical reasons, in the rest of this paper, we restrict this set to $\left\{\mathrm{0,1},\dots ,T,\infty \right\}$, where T is a fixed parameter, and project all $t_i$ s greater than T to $\infty$. This restriction means not only that we require $G\mathrm{\backslash }S$ to be acyclic but that its connected components are trees of diameter at most T. For large-enough values of T, this additional restriction is inconsequential.

The exact computation of the partition function (Eq. 8) for an arbitrary graph remains an NP-hard problem. However, if G is a sparse random graph, the large size limit of its free energy density $\ln Z\left(\mu \right)/\left(N\mu \right)$ can be computed by the cavity method (25, 26). The latter has been developed for statistical mechanics models on locally tree-like graphs, such as light-tailed random graphs, for which the exactness of the cavity method has been proven mathematically on several problems. The starting point of the method is based on the fact that light-tailed random graphs converge locally to trees in their large size limit; hence, models defined on them can be treated with belief propagation (BP; also called Bethe Peierls approximation in statistical mechanics). In BP, a partition function akin to Eq. 8 is computed via the exchange of messages between neighboring nodes. In this case, where an interaction in Eq. 8 includes node i and all of its neighbors $j\in \partial i$, we obtain a tree-like representation if we let pairs of variables $t_i,t_j$ live on the edges and add consistency constraints on the nodes. The BP message ${\eta }_{ij}\left(t_i,t_j\right)$ from i to $j\in \partial i$ is then a function of both the activation times $t_i$ and $t_j$. This message is interpreted as the marginal probability law of the local variables $t_i$ and $t_j$ in an amputated (cavity) graph, in which the interaction between i and j has been removed. Thanks to the locally tree-like character of the graph, some correlation decay properties are verified and allow a node’s incoming messages to be treated as independent. Under this assumption, the iterative BP equations (20, 21, 23) for decycling are written as

$${\eta }_{ij}\left(t_i,t_j\right)\propto {\displaystyle \sum _{{\left\{t_k\right\}}_{k\in \partial i\mathrm{\backslash }j}}{e}^{\mu {\psi }_i\left(t_i\right)}\mathrm{\Phi }\left(t_i,{\left\{t_k\right\}}_{k\in \partial i}\right)}{\displaystyle \prod }_{k\in \partial i\mathrm{\backslash }j}{\eta }_{ki}\left(t_k,t_i\right),$$ [9]

where the $\propto$ symbol includes a multiplicative normalization constant. The free energy can then be computed as a sum of local contributions depending on the messages solution of the BP equations.

Better parametrizations with a number of real values per message that scale linearly with T (rather than quadratically) can be devised (21, 23). A parametrization with $2T$ real values per message was introduced in ref. 23 and used to obtain improved results for the minimum decycling set on regular random graphs by extending the cavity method to the so-called first level of the replica symmetry breaking (1RSB) scheme. The extension of this calculation to random graphs with arbitrary light-tailed degree distributions is reported in SI Appendix (along with expansions close to the percolation threshold and at large degrees and a lower bound on ${\theta }_{\text{dec}}$ valid for all graphs). The 1RSB predictions for the decycling fraction ${\theta }_{\text{dec}}\left(d\right)$ of ER random graphs with average degree d, obtained by solving numerically the corresponding equations and extrapolating the results in the large T limit, are presented for a few values of d in Table 1.

Table 1.

The (1RSB) cavity predictions for the decycling number of ER random graphs of average degree d and the decycling number reached by the Min-Sum algorithm on graphs of size $N={10}^7$ nodes

d	${\theta }_{\text{dec}}\left(d\right)$	${\theta }_{\text{dec}}^{\text{MS}}\left(d\right)$
1.5	0.0125	0.0135
2.5	0.0912	0.0936
3.5	0.1753	0.1782
5	0.2789	0.2823

Min-Sum Algorithm for the Decycling Problem.

We turn now to the description of our heuristic algorithm for finding decycling sets of the smallest possible size. The above analysis shows the equivalence of this problem with the minimization of the cost function ${\displaystyle {\sum }_i{\psi }_i\left(t_i\right)}$ over the feasible configurations of the activation times $\left\{t_i\right\}\in {\left\{0,\dots ,T\right\}}^V$, where feasible means that, for all vertices i, either $t_i=0$ (then i is included in the decycling set S) or if $t_i>0$, it obeys the constraint $t_i=1+{\text{max}}_2\left({\left\{t_j\right\}}_{j\in \partial i}\right)$. Because this minimization is NP hard, we formulate a heuristic strategy in the following manner. We first consider a slightly modified cost function with ${\psi }_i\left(t_i\right)=\mathbb{I}\left[t_i=0\right]+{\epsilon }_i\left(t_i\right)$, where ${\epsilon }_i\left(t_i\right)$ is a randomly chosen infinitesimally small cost associated with the removal of node i at time $t_i$. The minimum $\left\{t_i^{\ast }\right\}$ of this cost function is now unique with probability one and can be constructed as $t_i^{\ast }=\text{argmin}\hspace{0.17em}{h}_i\left(t_i\right)$, where the field $h_i\left(t_i\right)$ is the minimum cost among the feasible configurations with a prescribed value for the removal time $t_i$ of site i. From the solution of this combinatorial optimization problem, we construct one of the minimal decycling sets S by including vertex i in S if and only if $t_i^{*}=0$. It remains now to find a good approximation for $h_i$; we compute it by the Min-Sum algorithm, which corresponds to the $\mu \to -\infty$ limit of BP and is similarly based on the exchange of messages $h_{ij}\left(t_i,t_j\right)$ between neighboring vertices, an analog of ${\eta }_{ij}\left(t_i,t_j\right)$, but interpreted as a minimal cost instead of a probability. We defer to SI Appendix for a full derivation and implementation details, stating here the final equations.

$$h_i\left(t_i\right)={\psi }_i\left(t_i\right)+{\displaystyle \sum _{k\in \partial i}{L}_{ki}\left(t_i\right)}+M_i\left(t_i\right),$$ [10a]

$$h_i\left(0\right)={\psi }_i\left(0\right)+{\displaystyle \sum _{k\in \partial i}{R}_{ki}\left(0\right)},$$ [10b]

$$M_i\left(t_i\right)=\min \left\{0,\underset{k\in \partial i}{\text{min}}\left\{R_{ki}\left(t_i\right)-L_{ki}\left(t_i\right)\right\}\right\},$$ [11]

for T ≥ t_i > 0, where $L_{ij}$, $R_{ij}$, $M_{ij}$, $h_{ij}^0$, and $h_{ij}^1$ form a solution of the following system of fixed point equations for messages defined on each directed edge $i\to j$ of the graph:

$$L_{ki}\left(t_i\right)=\underset{t_k<t_i}{\text{min}}{h}_{ki}^0\left(t_k\right)\hspace{0.17em},$$ [12a]

$$R_{ki}\left(t_i\right)=\min \left\{h_{ki}^0\left(t_i\right),\underset{t_k>t_i}{\text{min}}{h}_{ki}^1\left(t_k\right)\right\},$$ [12b]

$$M_{ij}\left(t_i\right)=\min \left\{0,\underset{k\in \partial i\mathrm{\backslash }j}{\text{min}}\left\{R_{ki}\left(t_i\right)-L_{ki}\left(t_i\right)\right\}\right\},$$ [12c]

$$h_{ij}^0\left(t_i\right)\propto {\psi }_i\left(t_i\right)+{\displaystyle \sum _{k\in \partial i\mathrm{\backslash }j}{L}_{ki}\left(t_i\right)}\hspace{0.17em},$$ [12d]

$$h_{ij}^1\left(t_i\right)\propto {\psi }_i\left(t_i\right)+{\displaystyle \sum _{k\in \partial i\mathrm{\backslash }j}{L}_{ki}\left(t_i\right)}+M_{ij}\left(t_i\right),$$ [12e]

$$h_{ij}^0\left(0\right)\propto {\psi }_i\left(0\right)+{\displaystyle \sum _{k\in \partial i\mathrm{\backslash }j}{R}_{ki}\left(0\right)},$$ [12f]

where $\propto$ includes now an additive normalization constant. An intuitive interpretation of all of these quantities and equations is provided in SI Appendix; let us only mention at this point that the message $h_{ij}^0\left(t_i\right)$ [respectively $h_{ij}^1\left(t_i\right)$] is the minimum feasible cost on the connected component of i in $G\mathrm{\backslash }j$ under the condition that i is removed at time $t_i$ in the original graph, assuming that j is not removed yet (respectively assuming that j is already removed from G).

This system can be solved efficiently by iteration. The computation of one iteration takes $O\left(\left|E\right|T\right)$ elementary ($+$, $-$, $\times$, $\text{min}$) operations, where $\left|E\right|$ denotes the number of edges of the graph, and a relatively small number of iterations is usually sufficient to reach convergence. In principle, one should take the cutoff T on the removal times to be greater than N to solve the decycling problem. We found, however, that using large but finite values of T (i.e., constraining the diameter of the tree components after the node removal) did not increase extensively the size of the decycling set; in the simulations presented below, we used $T=35$. Note that our algorithm is very flexible, and many variations can be implemented by appropriate modifications of the cost function. For example, we exploited the possibility to forbid the removal of certain marked nodes i by setting ${\psi }_i\left(t_i=0\right)=\infty$ for them.

Results for Dismantling

Results on Random Graphs.

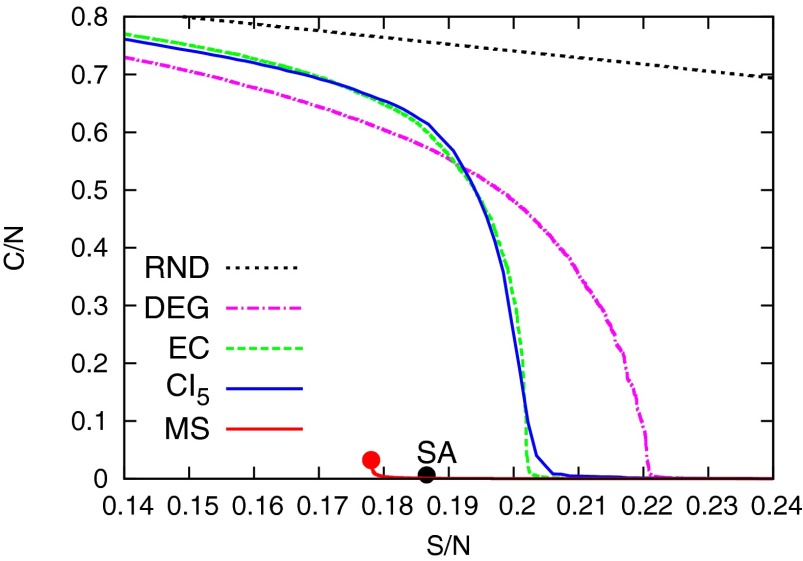
The outcome of our algorithm applied to an ER random graph of average degree 3.5 is presented in Fig. 1. Here, the red circle corresponds to the output of its first stage (decycling with Min-Sum), which yields, after the removal of a fraction 0.1781 of the nodes, an acyclic graph in which the largest components contain a fraction 0.032 of the vertices. The red line corresponds to the second stage, which further reduces the size of the largest component by greedily breaking the remaining trees. We compare with simulated annealing (SA; black circle) as well as several incremental algorithms that successively remove the nodes with the highest scores, where the score of a vertex is a measure of its centrality. Other than a trivial function that gives the same score to all vertices [hence removing the vertices in random order (RND)] and the score of a vertex equal to its degree, we used the eigenvector centrality (EC) measure and the recently proposed CI measure (15). We used all of these heuristics in an adaptive way, recomputing the scores after each removal. Additional details on all of these algorithms can be found in SI Appendix.

Fig. 1.

Fraction of nodes in the largest component as a function of the fraction of removed nodes for an ER random graph of average degree $d=3.5$ and size $N=\mathrm{78,125}$. We compare the result of our Min-Sum algorithm (MS) with random (RND), adaptive largest degree (DEG), adaptive EC, adaptive CI centrality, and SA.

We see from Fig. 1 that the Min-Sum algorithm outperforms the others by a considerable margin: it dismantles the graph using $13\text{\%}$ fewer nodes than the CI method. The Monte Carlo-based SA algorithm performs rather well but is considerably slower than all of the others.

In Fig. 2, we zoom in on the results of the second stage of our algorithm and perform a finite size scaling analysis, increasing the size of the dismantled graphs up to $N={10}^8$. In this way, we identify a threshold for decycling (and thus, for dismantling) by the Min-Sum algorithm that converges toward the value ${\theta }_{\text{dec}}^{MS}\approx 0.1782$, which is close but not equal to the theoretical prediction of the 1RSB calculation ${\theta }_{\text{dec}}^{1\text{RSB}}\approx 0.1753$ (vertical arrow in Fig. 2). Fig. 2, Inset shows a remarkable scaling that indicates that the size of the largest component after dismantling by removing a given fraction of nodes does not depend on the graph size.

Fig. 2.

Fraction of nodes in the largest component $C/N$ as a function of the fraction of nodes removed by the Min-Sum algorithm followed by the greedy tree breaking for the ER random graph of average degree $d=3.5$ and a range of sizes. (Inset) Same plot for the size of the largest component. The collapse of the curves suggests that, to reduce the largest component to a given constant size C, it is sufficient to remove $S=sN$ nodes, where $s=s\left(C\right)$ does not depend on N.

Combinatorial optimization problems typically exhibit a very large degeneracy of their (quasi)optimal solutions. We performed a detailed statistical analysis of the quasioptimal dismantling sets constructed by our algorithm, exploiting the fact that the Min-Sum algorithm finds different decycling sets for different realizations of the random tie-breaking noise ${\epsilon }_i\left(t_i\right)$.

For a given ER random graph of average degree 3.5 and size $N=\mathrm{78,125}$, we ran the algorithm for 1,000 different realizations of the tie-breaking noise ${\epsilon }_i\left(t_i\right)$ and obtained 1,000 different decycling sets, all of which had sizes within 40 nodes of one another. Randomly chosen pairs among these 1,000 decycling sets coincided, on average, on 82% of their nodes. For each node, we computed its frequency of appearance among the 1,000 decycling sets that we obtained. We then ordered nodes by this frequency and plotted the frequency as a function of this ordering in Fig. 3. We see that some nodes appear in almost all found sets, that about $60\text{\%}$ of nodes do not appear in any sets, and that a large portion of nodes appears only in a fraction of the decycling sets. We compare the frequencies of nodes belonging to one typical set found by Min-Sum and the CI heuristics.

Fig. 3.

Frequencies with which vertices appear in different decycling sets on an ER graph with $N=\mathrm{78,125}\hspace{0.17em}\text{and}\hspace{0.17em}d=3.5$. The y axis gives the frequency with which a given vertex appears in close to optimal decycling sets found by the Min-Sum (MS) algorithm. We ordered the vertices by this frequency and depict their ordering divided by N on the x axis. The different curves correspond to all vertices, vertices appearing in one randomly chosen decycling set found by the MS algorithm, and one found by the CI algorithm.

An important question to ask about dismantling sets is whether they can be thought of as a collection of nodes that are in some sense good spreaders or whether they are a result of highly correlated optimization. We use the result of the previous experiment and remove the nodes that appeared most often (i.e., have the highest frequencies in Fig. 3). If the nature of dismantling was additive rather than collective, then such a choice should further decrease the size of the discovered dismantling set. This scenario is not what happens; with this strategy, we need to remove $20.1\text{\%}$ of nodes to dismantle the graph compared with the $17.8\text{\%}$ of nodes found systematically by the Min-Sum algorithm. From this observation, we conclude that dismantling is an intrinsically collective phenomenon, and one should always speak of the full set rather than a collection of influential spreaders.

We also studied the degree histogram of nodes that the Min-Sum algorithm includes in the dismantling sets and saw that, as expected, most of the high-degree nodes belong to most of the dismantling sets. Each of the dismantling sets also included some nodes of relatively low degrees; for instance, for an ER random graph of average degree $d=6$ and size $5^7$, a typical decycling set found by the Min-Sum algorithm has around 460 (i.e., around $17\text{\%}$ of the decycling set) nodes of degree 4 or lower. To assess the importance of low-degree nodes for dismantling, we ran the Min-Sum algorithm under the constraint that only nodes of degree at least 5 can be removed, and we find decycling sets almost as small (only about 50 nodes; i.e., $0.2\text{\%}$ larger) as without this constraint. From this observation, we conclude that none of the low-degree nodes (even those with high CI centrality) are indispensable for dismantling, going against a highlight claim of ref. 15.

More General Graphs.

Up to this point, our study of dismantling relies crucially on the relation to decycling. For light-tailed random graphs, these two problems are essentially asymptotically equivalent. However, for arbitrary graphs that contain many small cycles, the decycling number can be much larger than the dismantling one. We argue that, from the algorithmic point of view, decycling still provides a very good basis for dismantling. For instance, consider a portion of $N=\mathrm{532,000}$ nodes of the Twitter network already analyzed in ref. 15. The decycling solution found by Min-Sum improves considerably the results obtained with the CI and EC heuristics (Fig. 4).

Fig. 4.

Fraction $C/N$ taken by the largest component in the Twitter network achieved after removing a fraction $S/N$ of nodes using the Min-Sum (MS) algorithm and the adaptive versions of CI and EC measures. The red circle marks the result obtained by decycling using MS (followed by the curve from the optimal tree-breaking process). The branches at lower values of $S/N$ are obtained after the application of the RG strategy from the graph obtained when the largest component has $C=100$ nodes. The black circle denotes the dismantling fraction obtained by SA.

In a network that contains many short cycles, decycling removes a large proportion of nodes expressly to destroy these short cycles. Many of these nodes can be put back without increasing the size of the largest component. For this reason, we introduce a reverse greedy (RG) procedure, in which starting from a dismantled graph with dismantling set S, maximum component size C, and a chosen target value $C\prime >C$ for the maximum allowed component size, removed nodes are iteratively reinserted. At each step, among all removed nodes, the one that ends up in the smallest connected component is chosen for reinsertion (details are in SI Appendix). The computational cost of this operation is bounded by $k_{\text{max}}C\prime \log \left(k_{\text{max}}C\prime \right)$, where $k_{\text{max}}$ is the maximal degree of the graph; the update cost is thus typically sublinear in N.

In graphs where decycling is an optimal strategy for dismantling, such as the random graphs, a vanishing fraction of nodes can be reinserted by the RG procedure before the size of the largest component starts to grow steeply. For real world networks, the RG procedure reinserts a considerable number of nodes, negligibly altering the size of the largest component. For the Twitter network in Fig. 4, the improvement obtained by applying the RG procedure is impressive: $32\text{\%}$ fewer nodes for the CI method and $20\text{\%}$ fewer nodes for the Min-Sum algorithm, which ends up being the best solution that we found, removing only $3.4\text{\%}$ of nodes to dismantle into components smaller than $C=\mathrm{1,000}$ nodes. RG makes it possible to reach, and even improve, the best result obtained with SA that solves the dismantling problem directly and is not affected by the presence of short loops (SI Appendix has details on SA). Qualitatively similar results are achieved on other real networks [e.g., on the YouTube network with 1.13 million nodes (27), the best dismantling set that we found with Min-Sum + RG included $4.0\text{\%}$ of nodes; this result is a $22\text{\%}$ improvement with respect to the CI heuristics].

The RG procedure is introduced as a heuristic that provides a considerable improvement for the examples that we treated. The theoretical results of this paper are valid only for classes of graphs that do not contain many small cycles, and hence, our theory does not provide a principled derivation or analysis of the RG procedure. This point is an interesting open direction for future work. More detailed study (both theoretical and algorithmic) of dismantling of networks for which decycling is not a reasonable starting point is an important direction of future work.