When machine vision meets histology: A comparative evaluation of model architecture for classification of histology sections

Abstract

Classification of histology sections in large cohorts, in terms of distinct regions of microanatomy (e.g., stromal) and histopathology (e.g., tumor, necrosis), enables the quantification of tumor composition, and the construction of predictive models of genomics and clinical outcome. To tackle the large technical variations and biological heterogeneities, which are intrinsic in large cohorts, emerging systems utilize either prior knowledge from pathologists or unsupervised feature learning for invariant representation of the underlying properties in the data. However, to a large degree, the architecture for tissue histology classification remains unexplored and requires urgent systematical investigation. This paper is the first attempt to provide insights into three fundamental questions in tissue histology classification: I. Is unsupervised feature learning preferable to human engineered features? II. Does cellular saliency help? III. Does the sparse feature encoder contribute to recognition? We show that (a) in I, both Cellular Morphometric Feature and features from unsupervised feature learning lead to superior performance when compared to SIFT and [Color, Texture]; (b) in II, cellular saliency incorporation impairs the performance for systems built upon pixel-/patch-level features; and (c) in III, the effect of the sparse feature encoder is correlated with the robustness of features, and the performance can be consistently improved by the multi-stage extension of systems built upon both Cellular Morphmetric Feature and features from unsupervised feature learning. These insights are validated with two cohorts of Glioblastoma Multiforme (GBM) and Kidney Clear Cell Carcinoma (KIRC).

1. Introduction

Although molecular characterization of tumors through gene expression analysis has become a standardized technique, bulk tumor gene expression data provide only an average genome-wide measurement for a biopsy and fail to reveal inherent cellular composition and heterogeneity of a tumor. On the other hand, histology sections provide wealth of information about the tissue architecture that contains multiple cell types at different states of cell cycles. These sections are often stained with hematoxylin and eosin (H&E) stains, which label DNA (e.g., nuclei) and protein contents, respectively, in various shades of color. Furthermore, morphometric abberations in tumor architecture often lead to disease progression, and it is therefore desirable to quantify tumor architecture as well as the corresponding morphometric abberations in large cohorts for the construction of predictive models of end points, e.g., clinical outcome, which have the potential for improved diagnosis and therapy.

Despite the efforts by some researchers on reducing inter- and intra-pathologist variations (Dalton et al., 2000) during manual analysis, this approach is not a scalable solution, and therefore impedes the effective representation and recognition from large cohorts for scientific discoveries. With its value resting on capturing detailed morphometric signatures and organization, automatic quantitative analysis of a large collection of histological data is highly desirable, and is unfortunately impaired by a number of barriers mostly originating from the technical variations (e.g., fixation, staining) and biological heterogeneities (e.g., cell type, cell state) always presented in the data. Specifically, a histological tissue section refers to an image of a thin slice of tissue applied to a microscopic slide and scanned from a light microscope, and the technical variations and biological heterogeneities lead to significant color variations both within and across tissue sections. For example, within the same tissue section, nuclear signal (color) varies from light blue to dark blue due to the variations of their chromatin content; and nuclear intensity in one tissue section may be very close to the background intensity (e.g., cytoplasmic, macromolecular components) in another tissue section.

It is also worth to mention that alternative staining (e.g., fluorescence) and microscopy methods (multi-spectral imaging) have been proposed and studied in order to overcome the fundamental limitations/challenges in tissue histology (Stack et al., 2014; Levenson et al., 2015; Rimm, 2014; Huang et al., 2013; Ghaznavi et al., 2013); however, H&E stained tissue sections are still the gold standard for the assessment of tissue neoplasm. Furthermore, the efficient and effective representation and interpretation of H&E tissue histology sections in large cohorts (e.g., The Cancer Genome Atlas dataset) have the potential to provide predictive models of genomics and clinical outcome, and are therefore urgently required.

Although many techniques have been designed and developed for tissue histology classification (see Section 2), the architecture for tissue histology classification remains largely unexplored and requires urgent systematical investigation. To fulfil this goal, our paper provides insights to three fundamental questions in tissue histology classification: I. Is unsupervised feature learning preferable to human engineered features? II. Does cellular prior knowledge help? III. Does the sparse feature encoder contribute to recognition? The novelty of our work resides in three folds: (i) architecture design: we have systematically experimented the system architecture with various combinations of feature types, feature extraction strategies and intermediate layers based on sparsity/locality-constrained feature encoders, which ensures the extensive evaluation and detailed insights on impact of the key components during the architecture construction; (ii) experimental design: our experimental evaluation has been performed through cross-validation on two independent datasets with distinct tumor types, where both datasets have been curated by our pathologist to provide examples of distinct regions of microanatomy (e.g., stromal) and histopathology (e.g., tumor, necrosis) with sufficient amount of technical variations and biological heterogeneities, so that the architecture can be faithfully tested and validated against important topics in histopathology (see Section 4 for details). More importantly, such an experimental design (combination of cross- validation and validation on independent datasests), to the maximum extent, ensures the consistency and unbiasedness of our findings; and (iii) outcome: the major outcome of our work are well-justified insights in the architecture design/construction. Specifically, we suggest that the sparse feature encoders based on Cellular Morphometric Feature and features from unsupervised feature learning provide the best configurations for tissue histology classification. Furthermore, these insights also led to the construction of a highly scalable and effective system (CMF-PredictiveSFE-KSPM, see Section 4 for details) for tissue histology classification. Finally, we believe that our work will not only benefit the research in computational histopathology, but will also benefit the community of medical image analysis at large by shedding lights on the systematical study of other important topics.

Organization of this paper is as follows: Section 2 reviews related works. Section 3 describes various components for the system architecture during evaluation. Section 4 elaborates the details of our experimental setup, followed by a detailed discussion on the experimental results. Lastly, Section 5 concludes the paper.

2. Related work

Current work on histology section analysis is typically formulated and performed at multiple scales for various end points, and several outstanding reviews can be found in Demir and Yener (2009); Gurcan et al. (2009). From our perspective, the trends are: (i) nuclear segmentation and organization for tumor grading and/or the prediction of tumor recurrence (Basavanhally et al., 2009; Doyle et al., 2011). (ii) patch level analysis (e.g., small regions) (Bhagavatula et al., 2010; Kong et al., 2010), using color and texture features, for tumor representation. and (iii) detection and representation of the auto-immune response as a prognostic tool for cancer (Fatakdawala et al., 2010).

While our focus is on the classification of histology sections in large cohorts, in terms of distinct regions of microanatomy (e.g., stromal) and histopathology (e.g., tumor, necrosis), the major challenge resides in the large amounts of technical variations and biological heterogeneities in the data (Kothari et al., 2012), which typically leads to techniques that are tumor type specific or even laboratory specific. The major efforts addressing this issue fall into two distinct categories: (i) fine-tuning human engineered features (Bhagavatula et al., 2010; Kong et al., 2010; Kothari et al., 2012; Chang et al., 2013a); and (ii) applying automatic feature learning (Huang et al., 2011; Chang et al., 2013c) for robust representation. Specifically, the authors in Bhagavatula et al. (2010) designed multi-scale image features to mimic the visual cues that experts utilized for the automatic identification and delineation of germ-layer components in H&E stained tissue histology sections of teratomas derived from human and nonhuman primate embryonic stem cells; the authors in Kong et al. (2010) integrated multiple texture features (e.g., wavelet features) into a texture-based content retrieval framework for the identification of tissue regions that inform diagnosis; the work in Kothari et al. (2012) utilized various features (e.g., color, texture and shape) for the study of visual morphometric patterns across tissue histology sections; and the work in Chang et al. (2013a) constructed the cellular morphometric context based on various cellular morphometric features for effective representation and classification of distinct regions of microanatomy and histopathology. Although many successful systems have been designed and developed, based on human engineered features, for various tasks in computational histopathology, the generality/applicability of such systems to different tasks or to different cohorts can sometimes be limited, as a result, systems based on unsupervised feature learning have been built with demonstrated advantages especially for the study of large cohorts, among which, both the authors in Huang et al. (2011) and Chang et al. (2013c) utilized sparse coding techniques for unsupervised characterization of tissue morphometric patterns.

Furthermore, tissue histology classification can be considered as a specific application of image categorization in the context of computer vision research, where spatial pyramid matching(SPM) (Lazebnik et al., 2006) has clearly become the major component of the state-of-art systems (Everingham et al., 2012) for its effectiveness in practice. Meanwhile, sparsity/locality-constrained feature encoders, through dictionary learning, have also been widely studied, and the improvement in classification performance has been confirmed in various applications (Yang et al., 2009; Wang et al., 2010; Chang et al., 2013a).

The evolution of our research on the classification of histology sections contains several stages: (i) kernel-based classification built-upon human engineered feature (e.g., SIFT features) (Han et al., 2011); (ii) independent subspace analysis for unsupervised discovery of morphometric signatures without the constraint of being able to reconstruct the original signal (Le et al., 2012); (iii) single layer predictive sparse decomposition for unsupervised discovery of morphometric signatures with the constraint of being able to reconstruct the original signal (Nayak et al., 2013); (iv) combination of either prior knowledge (Chang et al., 2013a) or predictive sparse decomposition (Chang et al., 2013c) with spatial pyramid matching; and (v) more recently, stacking multiple predictive sparse coding modules into deep hierarchy (Chang et al., 2013d). And this paper builds on our longstanding expertise and experiences to provide (i) extensive evaluation on the model architecture for the classification of histology sections; and (ii) insights on several fundamental questions for the classification of histology sections, which, hopefully, will shed lights on the analysis of histology sections in large cohorts towards the ultimate goal of improved therapy and treatment.

3. Model architecture

To ensure the extensive evaluation and detailed insights on impact of the key components during the architecture construction, we have systematically experimented the model architecture with various combinations of feature types, feature extraction strategies and intermediate layers based on sparsity/locality-constrained feature encoders. And this section describes how we built the tissue classification architecture for evaluation. Tables 1 and 2 summarize the aberrations and important terms, respectively, and detailed descriptions are listed in the sections as follows.

Table 1.

Annotation of abbreviations in the paper, where FE stands for feature extraction; SFE stands for sparse feature encoding; and SPM stands for spatial pyramid matching. Here, we also provide the dimension information about (i) original features (outcome of FE); (ii) sparse codes (outcome of SFE); (iii) final representation (outcome of final spatial pooling, i.e., SPM); and (iv) final prediction (outcome of architectures as a one-dimensional class label.).

Category	Abbreviation	Description	Dimension
FE	CMF	Cellular Morphometric Feature	15
	DSIFT	Dense SIFT	128
	SSIFT	Salient SIFT	128
	DCT	Dense [Color,Texture]	203
	SCT	Salient [Color,Texture]	203
	DPSD	Dense PSD	1024
	SPSD	Salient PSD	1024
SFE	SC	Sparse Coding	1024
	GSC	Graph Regularized Sparse Coding	1024
	LLC	Locality-Constraint Linear Coding	1024
	LCDL	Locality-Constraint Dictionary Learning	1024
SPM	KSPM	Kernal SPM	(256, 512, 1024)
	LSPM	Linear SPM	(256, 512, 1024)
Architecture	FE-KSPM	Architectures without the sparse feature encoder	1
	FE-SFE-LSPM	Architectures with the sparse feature encoder	1

Table 2.

Annotation of important terms used in this paper.

Term	Description
Human Engineered Features	Refers to features that are pre-determined by human experts, with manually fixed filters/kernels/templates during extraction.
Cellular Prior Knowledge	Refers to the morphometric information, in terms of shape, intensity, etc., that are extracted from each individual cell/nucleus
Cellular Saliency	Refers to perceptually salient regions corresponding to cells/nulei in tissue histology sections.
Multi-Stage System	Specifically refers to the architectures with multiple stacked feature extraction/abstratcion layers.
Single-Stage System	Specifically refers to the architectures with a single feature extraction layer.

3.1. Feature extraction modules (FE)

The major barrier in tissue histology classification, in large cohorts, stems from the large technical variations and biological heterogeneities, which requires the feature representation to capture the intrinsic properties in the data. In this work, we have evaluated three different features from two different categories (i.e., human-engineered feature and unsupervised feature learning). Details are as follows.

Cellular Morphometric Feature – CMF

The cellular morphometric features are human-engineered biological meaningful cellular-level features, which are extracted based on segmented nuclear regions over the input image. It has been recently shown that tissue classification systems based on CMF are insensitive to segmentation strategies (Chang et al., 2013a). In this work, we employ the segmentation strategy proposed in Chang et al. (2013b), and simply use the same set of features as described in Table 3. It is worth to mention that although generic cellular features, e.g., Zernike monments (Apostolopoulos et al., 2011; Asadi et al., 2006), have been successfully applied in various biomedical applications, we choose to use CMF due to (i) its demonstrated power in tissue histology classification (Chang et al., 2013a); and (ii) the limited impact by including those generic cellular features on both evaluation and understanding of the benefits introduced by the sparse feature encoders.

Table 3.

Cellular morphometric features, where the curvature values were computed with σ = 2.0, and the nuclear background region is defined to be the region outside the nuclear region, but inside the bounding box of nuclear boundary.

Feature	Description
Nuclear Size	#pixels of a segmented nucleus
Nuclear Voronoi Size	#pixels of the voronoi region, where the segmented nucleus resides
Aspect Ratio	Aspect ratio of the segmented nucleus
Major Axis	Length of Major axis of the segmented nucleus
Minor Axis	Length of Minor axis of the segmented nucleus
Rotation	Angle between major axis and x axis of the segmented nucleus
Bending Energy	Mean squared curvature values along nuclear contour
STD Curvature	Standard deviation of absolute curvature values along nuclear contour
Abs Max Curvature	Maximum absolute curvature values along nuclear contour
Mean Nuclear Intensity	Mean intensity in nuclear region measured in gray scale
STD Nuclear Intensity	Standard deviation of intensity in nuclear region measured in gray scale
Mean Background Intensity	Mean intensity of nuclear background measured in gray scale
STD Background Intensity	Standard deviation of intensity of nuclear background measured in gray scale
Mean Nuclear Gradient	Mean gradient within nuclear region measured in gray scale
STD Nuclear Gradient	Standard deviation of gradient within nuclear region measured in gray scale

Dense SIFT – DSIFT

The dense SIFT features are human-engineered features, which are extracted from regularly-spaced patches over the input image, with the fixed patch-size (16 × 16 pixels) and step-size (8 pixels).

Salient SIFT – SSIFT

The salient SIFT features are human-engineered features, which are extracted from patches centered at segmented nuclear centers (Chang et al., 2013b) over the input image, with a fixed patch-size (16 × 16 pixels).

Dense [Color, Texture] – DCT

The dense [Color,Texture] features are human engineered features, and formed as a concatenation of texture and mean color with the fixed patch-size (20 × 20 pixels) and step-size (20 pixels), where color features are extracted in the RGB color space, and texture features (in terms of mean and variation of filter responses) are extracted via steerable filters (Young and Lesperance, 2001) with 8 directions $(\theta \in \{0,\frac{\pi }{8},\frac{\pi }{4},\frac{3\pi }{8},\frac{1\pi }{2},\frac{5\pi }{8},\frac{3\pi }{4},\frac{7\pi }{8}\left\}\right)$ and 5 scales (σ ∈ {1, 2, 3, 4, 5}) on the grayscale image.

Salient [Color,Texture] – SCT

The salient [Color,Texture] features are human-engineered features, which are extracted on patches centered at segmented nuclear centers (Chang et al., 2013b) over the input image, with a fixed patch-size (20 × 20 pixels).

Dense PSD – DPSD

The unsupervised features are learned by predictive sparse decomposition (PSD) on randomly sampled image patches following the protocol in Chang et al. (2013c), and the dense PSD features are extracted from regularly-spaced patches over the input image, with the fixed patch-size (20 × 20 pixels), step-size (20 pixels) and number of basis functions (1024). Briefly, given X = [x₁, …, x_N] ∈ ℝ^m×N as a set of vectorized image patches, we formulated the PSD optimization problem as:

$$\begin{array}{l}\underset{\mathbf{B}\mathbf{,}\mathbf{Z}\mathbf{,}\mathbf{W}}{min}{\Vert \mathbf{X}-\mathbf{B}\mathbf{Z}\Vert }_F^2+\mathrm{\lambda }{\Vert \mathbf{Z}\Vert }_1+{\Vert \mathbf{Z}-\mathbf{W}\mathbf{X}\Vert }_F^2\\ \mathrm{s.t.}{\Vert {\mathbf{b}}_i\Vert }_2^2=1,\forall i=1,\dots ,h\end{array}$$ (1)

where B = [b₁, …, b_h] ∈ ℝ^m×h is a set of the basis functions; Z = [z₁, …, z_N] ∈ ℝ^h×N is the sparse feature matrix; W ∈ ℝ^h×m is the auto-encoder; λ is thee regularization constant. The goal of jointly minimizing Eq. (1) with respect to the triple <B, Z, W> is to enforce the inference of the regressor WX to be resemble to the optimal sparse codes Z that can reconstruct X over B (Kavukcuoglu et al., 2008). In our implementation, the number of basis functions (B) is fixed to be 1024, λ was fixed to be 0.3, empirically, for the best performance.

Salient PSD – SPSD

The salient PSD features are extracted on patches centered at segmented nuclear centers (Chang et al., 2013b) over the input image, with the fixed patch-size (20 × pixels) and fixed number of basis functions (1024).

The properties of aforementioned features are summarized in Table 4. Note that salient features are not included, given the fact that they only differ from their corresponding dense versions with extra saliency information. It is clear that, different from SIFT and CT, which are generic features designed for general purposes, both CMF and PSD can encode biological meaningful information, where the former works in a pre-determined manner while the latter has the potential to capture biological meaningful patterns in an unsupervised fashion. Therefore, within the context of tissue histology classification, CMF and PSD have the potential to work better due to these intrinsic properties, as shown in our evaluation.

Table 4.

Properties of various features in evaluation. Note, all human-engineered features are pre-determined and dataset independent; while features from unsupervised feature learning are task/dataset-dependent, and are able to capture task/dataset-specific information, such as potentially meaningful morphometric patterns in tissue histology.

FE	Design	Target	Biological Information
CMF	Human-Engineered	Cell (dataset independent)	Cellular morphometric information
SIFT	Human-Engineered	Generic (dataset independent)	NA
CT	Human-Engineered	Color and texture patterns (dataset independent)	NA
PSD	Learned	Generic (dataset dependent)	Dataset dependent

3.2. Sparse feature encoding modules (SFE)

It has been shown recently (Yang et al., 2009; Wang et al., 2010) that the impose of the feature encoder through dictionary learning, with sparsity or locality constraint, significantly improves the efficacy of existing image classification systems. The rationale is that the sparse feature encoder functions as an additional feature extraction/abstraction operation, and thus adds an extra layer (stage) to the feature extraction component of the system. Therefore, it extends the original system with multiple feature extraction/abstraction stages, which is able to capture intrinsic patterns at the higher-level, as suggested in Jarrett et al. (2009). To study the impact of the sparse feature encoder on tissue histology classification, we adopt three different sparsity/locality-constrained feature encoders for evaluation. Briefly, let Y = [y₁, …, y_M] ∈ ℝ^a×M be a set of features, C = [c₁, …, c_M] ∈ ℝ^b×M be the set of sparse codes, and B [b₁, …, b_b] ∈ ℝ^a×b be a set of basis functions for feature encoding, the feature encoders are summarized as follows.

Sparse Coding – (SC)

$$\begin{array}{cc}\underset{\mathbf{B}\mathbf{.}\mathbf{C}}{min}{\displaystyle \sum _{i=1}^M{\Vert {\mathbf{y}}_i-\mathbf{B}{\mathbf{c}}_i\Vert }^2}+\mathrm{\lambda }{\Vert {\mathbf{c}}_i\Vert }_1;& \mathrm{s.t.}\Vert {\mathbf{b}}_i\Vert \le 1,\forall i\end{array}$$ (2)

where ‖b_i‖ is a unit ℓ₂ -norm constraint for avoiding trivial solutions, and ‖c_i‖₁ is the ℓ₁ -norm enforcing the sparsity of c_i. In our implementation, the number of basis functions (B) is fixed to be 1024, λ is fixed to be 0.15, empirically, for the best performance.

Graph Regularized Sparse Coding – (GSC) (Zheng et al., 2011)

$$\begin{array}{cc}\underset{\mathbf{B}\mathbf{,}\mathbf{C}}{\min }{\displaystyle \sum _{i=1}^M{\Vert {\mathbf{y}}_i-\mathbf{B}{\mathbf{c}}_i\Vert }^2+\mathrm{\lambda }{\Vert {\mathbf{c}}_i\Vert }_1+\alpha \mathbf{T}\mathbf{r}(\mathbf{C}\mathbf{L}{\mathbf{C}}^{\mathbf{T}});}& \mathrm{s.t.}\Vert {\mathbf{b}}_i\Vert \end{array}\le 1,\forall i$$ (3)

where ‖b_i‖ is a unit ℓ₂-norm constraint for avoiding trivial solutions, and ‖ c_i‖₁ is the ℓ₁ -norm enforcing the sparsity of c_i, Tr (·) is the trace of matrix ·, L is the Laplacian matrix, and the third term encodes the Laplacian regularizer (Belkin and Niyogi, 2003). Please refer to Zheng et al. (2011) for details of the formulation. In our implementation, the number of basis functions (B) is fixed to be 1024, the regularization parameters, λ and α are fixed to be 1 and 5, respectively, for the best performance.

Locality-Constraint Linear Coding – (LLC) (Wang et al., 2010)

$$\begin{array}{cc}\underset{\mathbf{B}\mathbf{,}\mathbf{C}}{min}{\displaystyle \sum _{i=1}^M{\Vert {\mathbf{y}}_i-\mathbf{B}{\mathbf{c}}_i\Vert }^2+\mathrm{\lambda }{\Vert {\mathbf{d}}_i\odot {\mathbf{c}}_i\Vert }_1;}& \mathrm{s.t.}{\mathbf{1}}^{\top }{\mathbf{c}}_i\end{array}=1,\forall i$$ (4)

where ⊙ denotes the element-wise multiplication, and d_i ∈ ℝ^b encodes the similarity of each basis vector to the input descriptor y_i, Specifically,

$${\mathbf{d}}_i=\text{exp}(\frac{\text{dist}({\mathbf{y}}_i,\mathbf{B})}{\sigma })$$ (5)

where dist (y_i, B) = [dist (y_i, b₁), …, dist (y_i, b_b)], dist(y_i, b_j) is the Euclidean distance between y_i and b_j, σ is used to control the weight decay speed for the locality adaptor. In our implementation, the number of basis functions (B) is fixed to be 1024, the regularization parameters λ and σ are fixed to be 500 and 100, respectively, to achieve the best performance.

Locality-Constraint Dictionary Learning – (LCDL) (Zhou and Barner, 2013)

The LCDL optimization problem is formulated as:

$$\begin{array}{l}\underset{\mathbf{B}\mathbf{,}\mathbf{C}}{min}{\Vert \mathbf{Y}-\mathbf{B}\mathbf{C}\Vert }_F^2+\mathrm{\lambda }{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=1}^K\left[c_{\mathit{ji}}^2{\Vert {\mathbf{y}}_i-{\mathbf{b}}_j\Vert }_2^2\right]}+}\mu {\Vert \mathbf{C}\Vert }_F^2\\ \mathrm{s.t.}\{\begin{array}{llll}{\mathbf{1}}^{\mathrm{T}}{\mathbf{c}}_i=1\hfill & \forall i\hfill & \hfill & (\ast )\hfill \\ c_{\mathit{ji}}=0\hfill & \text{if }{\mathbf{b}}_j\notin {\mathrm{\Omega }}_{\tau }({\mathbf{y}}_i)\hfill & \forall i,j\hfill & (\ast \ast )\hfill \end{array}\end{array}$$ (6)

where Ω_τ(y_i) is defined as the τ-neighborhood containing τ nearest neighbors of y_i, and λ, μ are positive regularization constants. $\mu {\Vert \mathbf{C}\Vert }_F^2$ is included for numerical stability of the least–squares solution. The sum-to-one constraint (*) follows from the symmetry requirement, while the locality constraint (**) ensures that y_i is reconstructed by atoms belonging to its τ-neighborhood, allowing c_i to characterize the intrinsic local geometry. In our implementation, the number of basis functions (B) is fixed to be 1024, the regularization parameters λ and μ are fixed to be 0.3 and 0.001, respectively, and the neighborhood size τ is fixed to be 5, empirically, to achieve the best performance.

The major differences of aforementioned sparse feature encoders reside in two folds:

1. Objective:

   1. SC: Learning sets of over-complete bases for efficient data representation, originally applied to modeling the human visual cortex;
   2. GSC: learning the sparse representations that explicitly take into account the local manifold structure of the data;
   3. LLC: generating descriptors for image classification by using efficient locality-enforcing term;
   4. LCDL learning a set of landmark points to preserve the local geometry of the nonlinear manifold;
2. Locality Enforcing Strategy:

   1. SC: None;
   2. GSC: using graph Laplacian to enforce the smoothness of sparse representations along the geodesics of the data manifold;
   3. LLC: using a locality adaptor which penalizes far-way samples with larger weights. During optimization, the basis functions are normalized after each iteration, which could cause the learned basis functions deviate from the original manifold and therefore lose locality-preservation property;
   4. LCDL deriving an upper-bound for reconstructing an intrinsic nonlinear manifold without imposing any constraint of the energy of basis functions;

It is clear that SC is the most general approach for data representation purpose. Although various locality-constrained sparse coding techniques have demonstrated success in many applications (Zheng et al., 2011; Wang et al., 2010; Zhou and Barner, 2013), their distance metric in Euclidean Space has imposed implicit hypothesis on the manifold of the target feature space, which might potentially impair the performance, as reflected in our evaluation.

3.3. Spatial pyramid matching modules (SPM)

As an extension of the traditional Bag of Features (BoF) model, SPM has become a major component of state-of-art systems for image classification and object recognition (Everingham et al., 2012). Specifically, SPM consists of two steps: (i) vector quantization for the construction of dictionary from input; and (ii) histogram (i.e., histogram of dictionary elements derived in previous step) concatenation from image subregions for spatial pooling. Most recently, the effectiveness of SPM for the task of tissue histology classification has also been demonstrated in Chang et al. (2013a); 2013c). Therefore, we include two variations of SPM as a component of the architecture for tissue histology classification, which are described as follows.

Kernel SPM (KSPM Lazebnik et al., 2006)

The nonlinear kernel SPM that uses spatial-pyramid histograms of features. In our implementation, we fix the level of pyramid to be 3.

Linear SPM (LSPM Yang et al., 2009)

The linear SPM that uses the linear kernel on spatial-pyramid pooling of sparse codes. In our implementation, we fix the level of pyramid to be 3, and choose the max pooling function on the absolute sparse codes, as suggested in Yang et al. (2009); Chang et al. (2013a).

The choice of spatial pyramid matching module is made to optimize the performance/efficiency of the entire classification architecture. Experimentally, we find that (i) FE-KSPM outperforms FE-LSPM; and (ii) FE-SFE-LSPM and FE-SFE-KSPM have similar performance, while the former is more computationally efficient than the latter. Therefore, we adopt FE-SFE-LSPM and FE-KSPM during the evaluation.

As suggested in Jarrett et al. (2009), the vector quantization component of SPM can be seen as an extreme case of sparse coding, and the local histogram construction/concatenation component of SPM can be considered as a special form of spatial pooling. As a result, SPM is conceptually similar to the combination of sparse coding with spatial pooling, and therefore is able to serve as an extra layer (stage) for feature extraction. Consequently, FE-KSPM can be considered as a single-stage system, and FE-SFE-LSPM can be considered as a multi-stage system with two feature extraction/abstraction layers.

3.4. Classification

For architecture: FE-SFE-LSPM, we employed the linear SVM for classification, the same as in Wang et al. (2010); Yang et al. (2009). For architecture: FE-KSPM, the homogeneous kernel map (Vedaldi and Zisserman, 2012) was first applied, followed by linear SVM for classification.

4. Experimental evaluation of model architecture

4.1. Experimental setup

Our extensive evaluation is performed based on the cross-validation strategy with 10 iterations, where both training and testing images are randomly selected per iteration, and the final results are reported as the mean and standard error of the correct classification rates with various dictionary sizes (256,512,1024) on the following two distinct datasets, curated from (i) Glioblastoma Multiforme (GBM) and (ii) Kidney Renal Clear Cell Carcinoma (KIRC) from The Cancer Genome Atlas (TCGA), which are publicly available from the NIH (National Institute of Health) repository. The curation is performed by our pathologist in order to provide examples of distinct regions of microanatomy (e.g., stromal) and histopathology (e.g., tumor, necrosis) with sufficient amount of biological heterogeneities and technical variations, so that the classification model architecture can be faithfully tested and validated against important studies. Furthermore, the combination of extensive cross-validation and independent validation on datasets with distinct tumor types, to the maximum extent, ensures the consistency and unbiasedness of our findings. The detailed description of our datasets as well as the corresponding task forumulation are described as follows.

GBM Dataset

In brain tumors, necrosis, proliferation of vasculature, and infiltration of lymphocytes are important prognostic factors. And, some of these analyses, such as the quantification of necrosis, have to be defined and performed as classification tasks in histology sections. Furthermore, necrosis is a dynamic process and different stages of necrosis exist (e.g., from cells initiating a necrosis process to complete loss of chromatin content). Therefore, the capability of identification/classification of these end points, e.g., necrosis-related regions, in brain tumor histology sections, is highly demanded. In this study, we aim to validate the model architecture for the three-category classification (i.e., Tumor, Necrosis, and Transition to Necrosis) on the GBM dataset, where the images are curated from the whole slide images (WSI) scanned with a 20X objective (0.502 micron/pixel). Representative examples of each class can be found in Fig. 1, which reveal a significant amount of intra-class phenotypic heterogeneity. Such a highly heterogenous dataset provides an ideal test case for the quantitative evaluation of the composition of model architecture and its impact, in terms of performance and robustness, on the classification of histology sections. Specifically, the number of images per category are 628, 428 and 324, respectively, and most images are 1000 × 1000 pixels. For this task, we train, with various model architectures, on 160 images per category and tested on the rest, with three different dictionary sizes: 256, 512 and 1024.

Fig. 1.

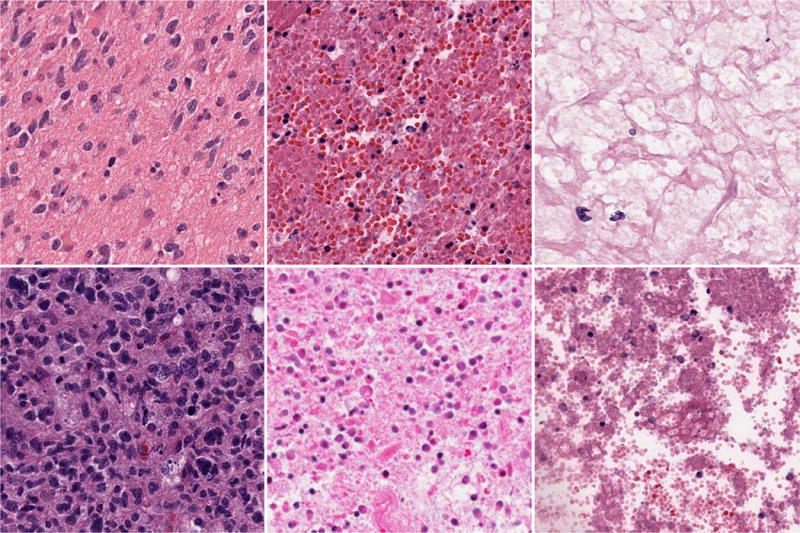
GBM Examples. First column: Tumor; Second column: Transition to necrosis; Third column: Necrosis. Note that the phenotypic heterogeneity is highly diverse in each column.

KIRC Dataset

Recent studies on quantitative histology analysis (Lan et al., 2015; Rogojanu et al., 2015; Huijbers et al., 2013; de Kruijf et al., 2011) reveal that the tumor-stroma ratio is a prognostic factor in many different tumor types, and it is therefore interesting and desirable to know how such an index plays its role in KIRC, which can be fulfilled with two steps as follows, (i) identification/classification of tumor/stromal regions in tissue histology sections for the construction of tumor-stroma ratio; and (ii) correlative analysis of the derived tumor-stroma ratio with clinical outcome. Therefore, in this study, we aim to validate the model architecture for the three-category classification (i.e., Tumor, Normal, and Stromal) on the KIRC dataset, where the images are curated from the whole slide images (WSI) scanned with a 40X objective (0.252 micron/pixel). Representative examples of each class can be found in Fig. 2, which (i) contain two different types of tumor corresponding to clear cell carcinoma, with the loss of cytoplasm (first row), and granular tumor (second row), respectively; and (ii) reveal large technical variations (i.e., in terms of staining protocol), especially in the normal category. The combination of the large amount of biological heterogeneity and technical variations in this curated dataset provides an ideal test case for the quantitative evaluation of the composition of model architecture and its impact, in terms of performance and robustness, on the classification of histology sections. Specifically, the number of images per category are 568, 796 and 784, respectively, and most images are 1000 × 1000 pixels. For this task, we train, with various model architectures, on 280 images per category and tested on the rest, with three different dictionary sizes: 256, 512 and 1024.

Fig. 2.

KIRC examples. First column: Tumor; Second column: Normal; Third column: Stromal. Note that (a) in the first column, there are two different types of tumor corresponding to clear cell carcinoma, with the loss of cytoplasm (first row), and granular tumor (second row), respectively; and (b) in the second column, staining protocol is highly varied. The cohort contains a significant amount of tumor heterogeneity that is coupled with technical variation.

4.2. Is unsupervised feature learning preferable to human engineered features?

Feature extraction is the very first step for the construction of classification/recogonition system, and is one of the most important factors that affect the performance. To answer this question, we evaluated four well-selected features based on two vastly different tumor types as described previously. The evaluation was carried out with the FE-KSPM architecture for its simplicity, and the performance was illustrated in Fig. 3 for the GBM and KIRC datasets. It is clear that the systems based on CMF (CMF-KSPM) and PSD (PSD-KSPM) have the top performances, which are due to i) the critical role of cellular morphometric context during the pathological diagnosis, as suggested in Chang et al. (2013a); and ii) the capability of unsupervised feature learning in capturing intrinsic morphometric patterns in histology sections.

Fig. 3.

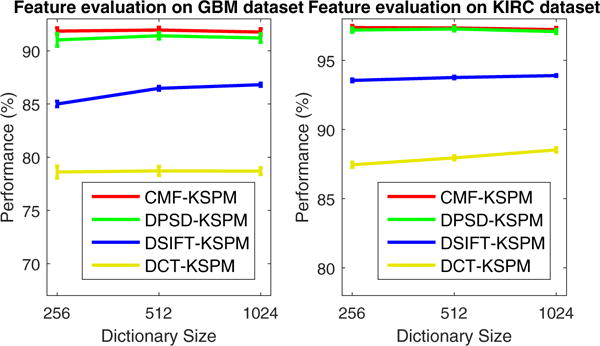
Evaluation of different features with FE-KSPM architecture on both GBM (left) and KIRC (right) datasets. Here, the performance is reported as the mean and standard error of the correct classification rate, as detailed in Section 4.

4.3. Does cellular saliency help?

CMF differs from DSIFT, DCT and DPSD in that (1) CMF characterizes biological meaningful properties at cellular-level, while DSIFT, DCT and DPSD are purely pixel/patch-level features without any specific biological meaning; (2) CMF is extracted per nuclear region which is cellular-saliency-aware, while DSIFT, DCT and DPSD are extracted per regularly-spaced image patch without using cellular information as prior. An illustration of aforementioned feature extraction strategies can be found in Fig. 4. Recent study (Wu et al., 2013) indicates that saliency-awareness may be helpful for the task of image classification, thus it will be interesting to figure out whether SIFT, [Color,Texture] and PSD features can be improved by the incorporation of cellular-saliency as prior. Therefore, we design salient SIFT (SSFIT), salient [Color,Texture] and salient PSD (SPSD) features, which are only extracted at nuclear centroid locations. Comparison of classification performance between dense features and salient features, with the FE-KSPM architecture, is illustrated in Fig. 5 for GBM and KIRC datasets, which show that, for SIFT, [Color,Texture] and PSD features, cellular-saliency-awareness plays a negative role for the task of tissue histology classification. One possible explanation is that, different from CMF, which encodes specific biological meanings and summarizes tissue image with intrinsic biological-context-based representation, SIFT, [Color,Texture] and PSD lead to appearance-based image representation, and thus require dense sampling all over the place in order to faithfully assemble the view of the image.

Fig. 4.

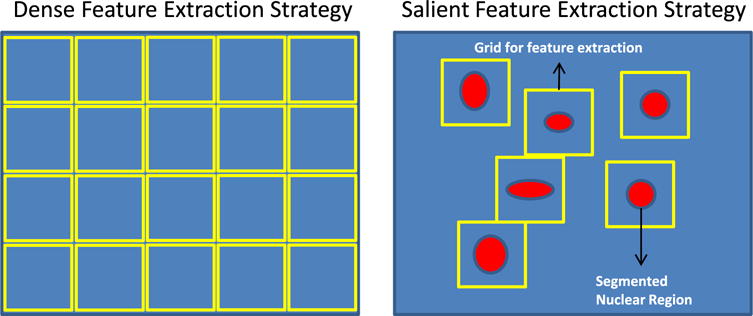
Illustration of dense feature extraction strategy (left) and salient feature extraction strategy (right), where dense features are extracted on regularly-spaced patches, while salient features are extracted on patches centered at segmented nuclear centers. Here, yellow rectangle and red blob represent feature extraction patch/grid and segmented nuclear region, respectively.

Fig. 5.

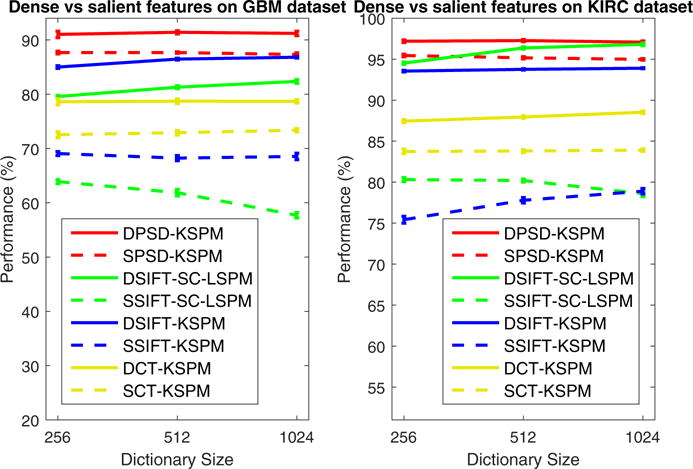
Evaluation of dense feature extraction and salient feature extraction strategies with the FE-KSPM architecture on both GBM (left) and KIRC (right) datasets, where solid line and dashed line represent systems built upon dense feature and salient feature, respectively. Here, the performance is reported as the mean and standard error of the correct classification rate, as detailed in Section 4.

4.4. Does the sparse feature encoder help?

The evaluation of systems with the sparse feature encoder is carried out with the configuration FE-SFE-LSPM, where LSPM is used instead of KSPM for improved efficiency. Classification performance is illustrated in Fig. 6 and Fig. 7 for the GBM and KIRC datasets, respectively; and the results show that, compared to FE-KSPM,

1. For FE =CMF and SFE ∈ {SC,GSC,LLC,LCDL}, FE-SFE-LSPM consistently improves the classification performance for both GBM and KIRC datasets;

2. For FE ∈ {SIFT,[Color,Texture]} and SFE ∈ {SC,GSC,LLC,LCDL}, FE-SFE-LSPM improves the performance for KIRC dataset; while impairs the performance for GBM dataset;

3. For FE =PSD, FE-SFE-LSPM improves the performance for both GBM and KIRC datasets, with SFE = SC; while, in general, impairs the performance for both datasets, with SFE ∈ {GSC,LLC,LCDL}.

Fig. 6.

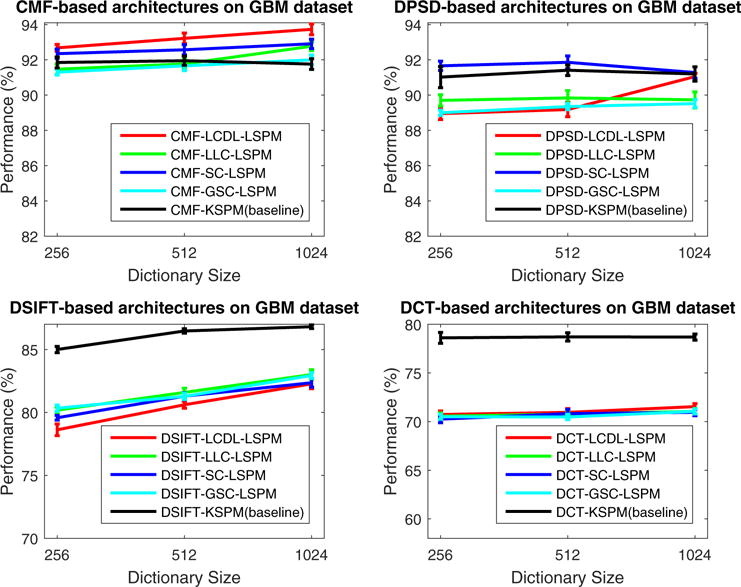
Evaluation of the architectures with sparse feature encoders (FE-SFE-LSPM) on GBM dataset. Here, the performance is reported as the mean and standard error of the correct classification rate, as detailed in Section 4.

Fig. 7.

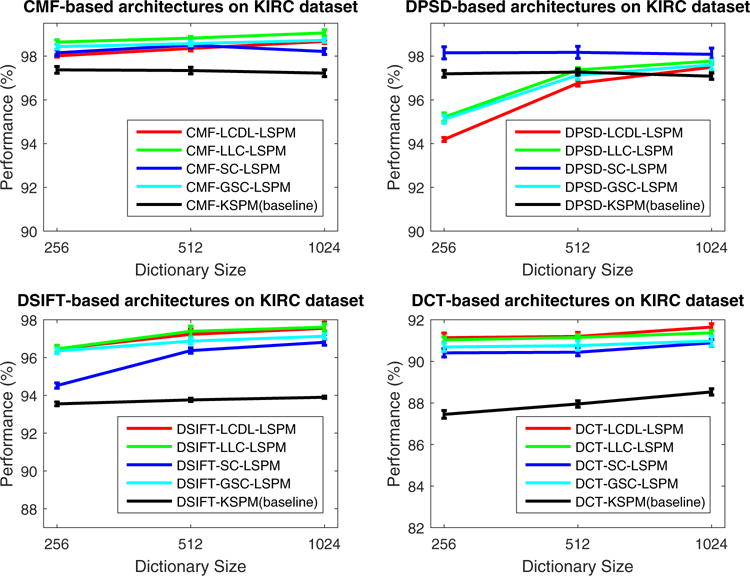
Evaluation of the architectures with sparse feature encoders (FE-SFE-LSPM) on KIRC dataset. Here, the performance is reported as the mean and standard error of the correct classification rate, as detailed in Section 4.

The observations above suggest that, the effect of the sparse feature encoder highly correlates with the robustness of the features being used, and significant improvement of performance can be achieved consistently across different datasets with the choice of CMF. It is also interesting to notice that, with the choice of PSD, the sparse feature encoder only helps improve the performance with sparse coding (SC) as the intermediate feature extraction layer. A possible explanation is that, compared to CMF which has real physical meanings, the PSD feature resides in a hyper space constructed from unsupervised feature learning, where Euclidean-distance, as a critical part of GSC, LLC and LCDL, may not apply.

Furthermore, it is also interesting and important to know the effect of incorporating deep learning for feature extraction. Therefore, for further validation, we have also evaluated two popular deep learning techniques, namely Stacked PSD (Chang et al., 2013d) and Convolutional Neural Networks (CNN) (Lecun et al., 1998; Huang and LeCun, 2006; Krizhevsky et al., 2012). Specifically,

1. StackedPSD-KSPM: for the evaluation of Stacked PSD, the same protocol as in Chang et al. (2013d) is utilized. Briefly, two layers of PSD, with 2048 (first layer) and 1024 (second layer) basis functions, respectively, are stacked to form a deep architecture for the feature extraction on 20 × 20 image-patches with a step-size fixed to be 20, empirically, for best performance. After the patch-based extraction, the same protocol as shown in FE-KSPM is utilized for classification.

2. AlexNet-KSPM: for the evaluation of CNN, we adopt one of the most powerful deep neural network architecture: AlexNet (Krizhevsky et al., 2012) with the Caffe (Jia et al., 2014) implementation. Given (i) the extremely large scale (60 million parameters) of the AlexNet architecture; (ii) the significantly smaller data-scale of GBM and KIRC, compared to ImageNet (Deng et al., 2009) with one thousand categories and millions of images, where AlexNet is originally trained; and (iii) the significant decline of performance due to over-fitting that we experience with the end-to-end tuning of AlexNet on our dataset as a result of (i) and (ii), we simply adopt the pre-trained AlexNet for feature extraction on 224 × 224 image-patches with a step-size fixed to be 45, empirically, for best performance. After the patch-based extraction, the same protocol as shown in FE-KSPM is utilized for classification. It is worth to mention that such an approach falls into the categories of both deep learning and transfer learning.

Experimental results, illustrated in Fig. 8, suggest that,

1. Both sparse feature encoders and feature extraction strategies based on deep learning techniques consistently improve the performance of tissue histology classification;

2. The extremely large-scale convolutional deep neural networks (e.g., AlexNet), pre-trained on extremely large-scale dataset (e.g., ImageNet), can be directly applicable to the task of tissue histology classification due to the capability of deep neural networks in capturing transferable base knowledge across domains (Yosinski et al., 2014). Although the fine-tuning of AlexNet towards our datasets shows significant performance drop due to the problem of over-fitting, the direct deployment of pretrained deep neural networks still provides a promising solution for tasks with limited data and labels, which is very common in the field of medical image analysis.

Fig. 8.

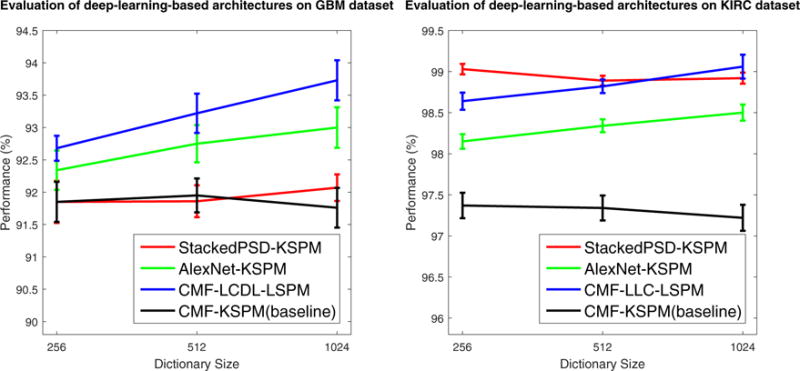
Evaluation of the effect of incorporating deep learning for feature extraction on both GBM and KIRC datasets. Note that, given the various combinations of FE-SFE-LSPM, CMF-LCDL-L SPM and CMF-LLC-L SPM are chosen for GBM and KIRC datasets, respectively, for their best performance. Here, the performance is reported as the mean and standard error of the correct classification rate, as detailed in Section 4.

4.5. Revisit on spatial pooling

To further study the impact of pooling strategy, we also provide extensive experimental evaluation on one of the most popular pooling strategies (i.e., max pooling) in place of spatial pyramid matching within FE-SFE-LSPM framework, which is defined as follows,

$$\mathit{max}\mathrm{:}{f}_j=max\{|c_{1j}|,|c_{2j}|,\dots .,|c_{Mj}|\}$$ (7)

where C = [c₁, …., c_M] ∈ ℝ^b×M is the set of sparse codes extracted from an image, c_ij is the matrix element at i-th row and j-th column of C, and f = [f₁, …, f_b] is the pooled image representation. The choice of max pooling procedure has been justified by both biophysical evidence in the visual cortex (Serre et al., 2005) and researches in image categorization (Yang et al., 2009), and the derived architecture is described as FE-SFE-Max. In our experimental evaluation, we focus on the top-two-ranked features (i.e., DPSD and CMF), where the corresponding comparisons of classification performance are illustrated in Fig. 9. It is clear that systems with SPM pooling consistently outperforms systems with max pooling with various combinations of feature types and sparse feature encoders. A possible explanation is that the vector quantization step in SPM can be considered as an extreme case of sparse coding (i.e., with a single non-zero element in each sparse code); and the local histogram concatenation step in SPM can be considered as a special form of spatial pooling. As a result, SPM is conceptually similar to an extra layer of sparse feature encoding and spatial pooling, as suggested in Jarrett et al. (2009), and therefore leads to an improved performance, compared to the architecture with max pooling.

Fig. 9.

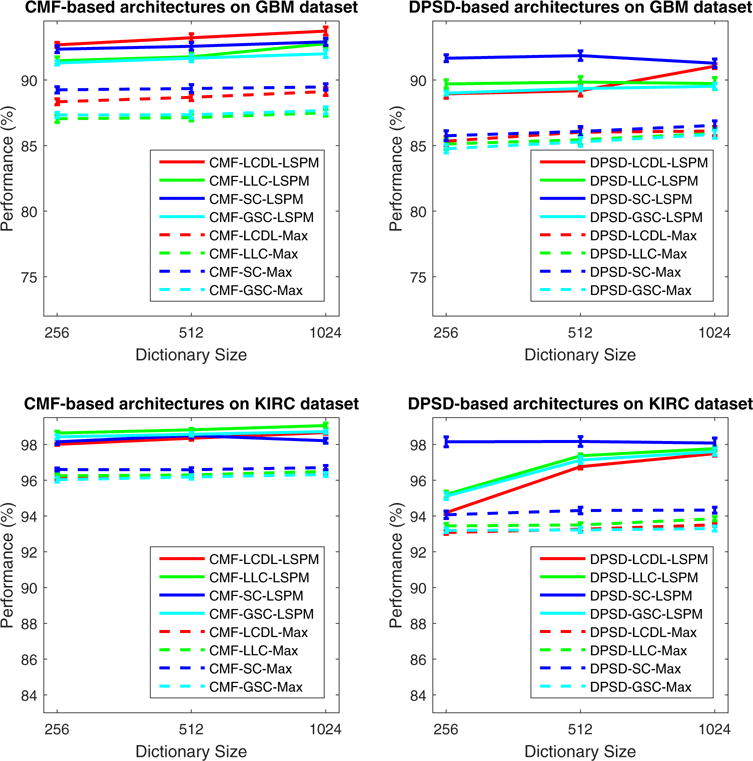
Evaluation of the impact of different spatial pooling strategies with the FE-SFE-LSPM framework on both GBM and KIRC datasets. Note that, given many of the popular spatial pooling strategies, max pooling is chosen due to the extensive justification by both biophysical evidence in the visual cortex and researches in image categorization tasks. The derived architecture is described as FE-SFE-Max, and only the top-two-ranked features (i.e., DPSD and CMF) are involved during evaluation. Here, the performance is reported as the mean and standard error of the correct classification rate, as detailed in Section 4.

4.6. Revisit on computational cost

In addition to classification performance, another critical factor, in clinical practice, is the computational efficiency. Therefore, in this section, we provided a detailed evaluation on computational cost of various systems. Given the fact that (i) training can always be carried out off-line; (ii) the classification of the systems in evaluation are all based on linear SVM, our evaluation on computational efficiency focuses on on-line feature extraction (including sparse feature encoding), which is the most time-consuming part during the testing phase. As shown in Table 5,

1. SIFT features are the most computational efficient features among all the ones in comparison. However, the systems built on SIFT features greatly suffer from the technical variations and biological heterogeneities in both datasets, and therefore are not good choices for the classification of tissue histology sections;

2. Given the fact that the nuclear segmentation is a prerequisite for salient feature extraction (e.g., SPSD, SSIFT and SCT), systems built upon salient features may not be necessarily more efficient than systems built upon dense features. Furthermore, since the salient features typically impair the tissue histology classification performance, they are therefore not recommended;

3. The gain in performance of sparse feature encoders in our evaluation is at the cost of computational efficiency. And the scalability of derived systems can be improved by (i) the development of more computational-efficient algorithms, which was demonstrated in Table 6; and (ii) the deployment of advanced computational techniques, such as cluster computing or GPU acceleration for clinical deployment, which was demonstrated in Table 5 for AlexNet.

4. Most interestingly, the sparse feature encoder, based on CMF-SFE, is much more efficient even compared to many shallow architectures based on PSD or CT features; and, it is only 5% slower compared to its corresponding shallow version, based on CMF. The computational efficiency are due to (i) the high sparsity of nuclei compared to dense image patches (e.g., 350 nuclei/image v.s. 2000 patches/image); and (ii) the extremely low dimensionality of cellular morphometric features compared to other features (e.g., 15 nuclear morphometric features v.s. 128 SIFT features, 203 CT features and 1024 PSD features). Furthermore, in computational histopathology, both nuclear-level information (based on nuclear segmentation) and patch-level information (based on tissue histology classification) are very critical components, which means the nuclear segmentation results can be shared across different tasks for the further improvement of the efficiency of multi-scale integrated analyses.

Table 5.

Average computational cost (measured in second) for feature extraction (including sparse feature encoding) on images with size 1000 × 1000 pixels. The evaluation is carried out with Intel(R) Xeon(R) CPU X5365 @ 3.00GHz, and GeForce GTX 580.

Feature Extraction Component(s)	Average Computational Cost (in second)
Nuclear Segmentation	40
CMF-SFE	42 = Nuclear-Segmentation-Cost(40) + SFE-Cost(2)
DPSD-SFE	115 = DPSD-Cost(95) + SFE-Cost(20)
SPSD-SFE	70 = SPSD-Cost(60) + SFE-Cost(10)
DSIFT-SFE	16 = DSIFT-Cost(10) + SFE-Cost(6)
SSIFT-SFE	47 = SSIFT-Cost(45) + SFE-Cost(2)
DCT-SFE	90 = DCT-Cost(80) + SFE-Cost(10)
SCT-SFE	108 = SCT-Cost(105) + SFE-Cost(3)
CMF	40 = Nuclear-Segmentation-Cost(40)
DPSD	95
SPSD	60 = Nuclear-Segmentation-Cost(40) + PSD-Cost(20)
DSIFT	10
SSIFT	45 = Nuclear-Segmentation-Cost(40)+SIFT-Cost(5)
DCT	80
SCT	105 = Nuclear-Segmentation-Cost(40) + SCT-Cost(65)
StackedPSD	100
AlexNet	1200/180 (CPU-Only/GPU-Acceleration)

Table 6.

PredictiveSFE achieved 40X speed-up, compared to SFE, in sparse cellular morphometric feature extraction. The evaluation was carried out with Intel(R) Xeon(R) CPU X5365 @ 3.00GHz.

Sparse Cellular Morphometric Feature Extraction	Average Computational Cost (in second)
PredictiveSFE	0.05
SFE	2

To further improve the scalability of systems built-upon CMF-SFE, as a demonstration of algorithmic-scaling-up of sparse feature encoders, we constructed a predictive sparse feature encoder (PredictiveSFE) in place of SFE as follows, to approximate the morphometric sparse codes, specifically, provided by Eq. 2,

$$\begin{array}{l}\underset{\mathbf{B}\mathbf{,}\mathbf{C}\mathbf{,}\mathbf{G}\mathbf{,}\mathbf{W}}{min}{\Vert \mathbf{Y}-\mathbf{B}\mathbf{C}\Vert }_F^2+\mathrm{\lambda }{\Vert \mathbf{C}\Vert }_1+{\Vert \mathbf{C}-\mathrm{G}\sigma (\mathbf{W}\mathbf{Y})\Vert }_F^2\\ \mathrm{s.t.}{\Vert {\mathbf{b}}_i\Vert }_2^2=1,\forall i=1,\dots ,h\end{array}$$ (8)

where Y = [y₁, …, y_N] ∈ ℝ^{m × N} is a set of cellular morphometric descriptors; B = [b₁,…,b_h] ∈ ℝ^m×h is a set of the basis functions; C = [c₁, …, c_N] ∈ ℝ^{h × N} is the sparse feature matrix; W ∈ ℝ^{h × m} is the auto-encoder; σ(·) is the element-wise sigmoid function; G = diag (g₁, …, g_h) ∈ ℝ^h×h is the scaling matrix with diag being an operator aligning vector, [g₁, …, g_h], along the diagonal; and λ is the regularization constant. Joint minimization of Eq. (8) w.r.t the quadruple <B, C, G, W>, enforces the inference of the nonlinear regressor Gσ(WY) to be similar to the optimal sparse codes, C, which can reconstruct Y over B (Kavukcuoglu et al., 2008). As shown in Algorithm 1, optimization of Eq. (8) is iterative, and it terminates when either the objective function is below a preset threshold or the maximum number of iterations has been reached. In our implementation, the number of basis functions (B) was fixed to be 128, and the SPAMS optimization toolbox (Mairal et al., 2010) is adopted for efficient implementation of OMP to compute the sparse code, C, with sparsity prior set to 30. The end result is a highly efficient (see Table 6) and effective (see Fig. 10) system, CMF-PredictiveSFE -KSPM, for tissue histology classification.

Fig. 10.

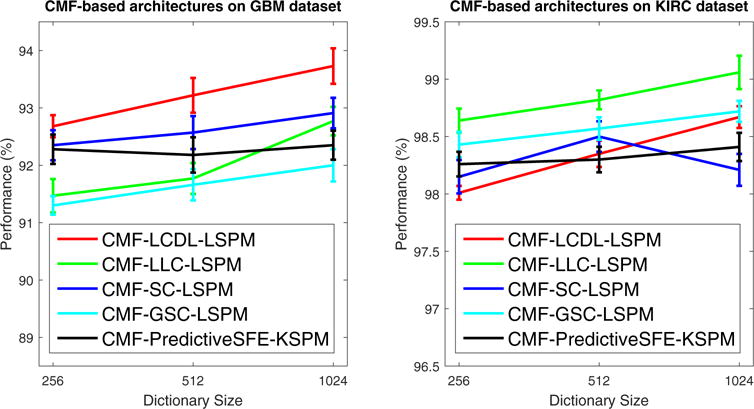
Systems built-upon CMF-PredictiveSFE provide very competitive performance compared to systems built-upon CMF-SFE. Here, the performance is reported as the mean and standard error of the correct classification rate, as detailed in Section 4.

Algorithm 1.

Construction of the Predictive Sparse Feature Encoder (PredictiveSFE).

Require: Training set Y = [y1, …, yN ] ∈ ℝm×N
Ensure: Predictive Sparse Feature Encoder W ∈ ℝh×m
1:	print Randomly initialize B, W, and G
2:	repeat
3:	Fixing B, W and G, minimize Eq. (8) w.r.t C, where C can be either solved as a ℓ1-minimization problem Lee et al. (2007) or equivalently solved by greedy algorithms, e.g., Orthogonal Matching Pursuit (OMP) Tropp and Gilbert (2007).
4:	Fixing B, W and C, solve for G, which is a simple least-square problem with analytic solution.
5:	Fixing C and G, update B and W, respectively, using the stochastic gradient descent algorithm.
6:	until Convergence (maximum iterations reached or objective function ≤ threshold)

5. Conclusions

This paper provides insights to the following three fundamental questions for the task of tissue histology classification:

1. Is unsupervised feature learning preferable to human engineered features? The answer is that, CMF and PSD work the best, compared to SIFT and [Color,Texture] features, on two vastly different tumor types. The reasons are that (i) CMF encodes biological meaningful prior knowledge, which is widely adopted in the practice of pathological diagnosis; and (ii) PSD is able to capture intrinsic morphometric patterns in histology sections. As a result, both of them produce robust representation of the underlying properties preserved in the data.

2. Does cellular saliency help? The surprising answer is that cellular saliency does not help improve the performance for systems built upon pixel-/patch-level features. Experiments on both GBM and KIRC datasets confirm the performance-drop with salient feature extraction strategies, and one possible explanation is that both pixel-level and patch-level features are appearance-based representations, which require dense sampling all over the place in order to faithfully assemble the view of the image.

3. Does the sparse feature encoder contribute of recognition? The sparse feature encoder significantly and consistently improves the classification performance for systems built upon CMF; and meanwhile, it conditionally improves the performance for systems built upon PSD (PSD-SC-LSPM), with the choice of sparse coding (SC) as the intermediate feature extraction layer. It is believed that the consistency of performance highly correlates with the robustness of the feature being used, and the improvement of performance is due to the capability of the sparse feature encoder in capturing complex patterns at the higher-level. Furthermore, this paper provides a clear evidence that deep neural networks (i.e., AlexNet), pre-trained on large scale natural image datasets (i.e., ImageNet), is directly applicable to the task of tissue histology classification, which is due to the capability of deep neural networks in capturing transferable base knowledge across domains (Yosinski et al., 2014). Although the fine-tuning of AlexNet towards our datasets shows significant performance drop due to the problem of over-fitting, the direct deployment of pre-trained deep neural networks still provides a promising solution for tasks with limited data and labels, which is very common in the field of medical image analysis.

Besides the insights in the aforementioned fundamental questions, this paper also shows that the superior performance of the sparse feature encoder is at the cost of computational efficiency. However, the scalability of the sparse feature encoder can be improved by (i) the development of more computational-efficient algorithms; and (ii) the deployment of advanced computational techniques, such as cluster computing or GPU acceleration. As a demonstration, this paper provides an accelerated version of CMF-SFE, namely CMF-PredictiveSFE, which falls into the category of algorithmic-scaling-up and achieves 40X speed-up during sparse feature encoding. The end result is a highly scalable and effective system, CMF-PredictiveSFE-KSPM, for tissue histology classification.

Furthermore, all our insights are independently validated on two large cohorts, Glioblastoma Multiforme (GBM) and Kidney Clear Cell Carcinoma (KIRC), which, to the maximum extent, ensures the consistency and unbiasedness of our findings. To the best of our knowledge, this is the first attempt that systematically provides insights to the fundamental questions aforementioned in tissue histology classification; and there are reasons to hope that the configuration: FE-SFE-LSPM (FE ∈ {CMF,PSD}) as well as its accelerated version: FE-PredictiveSFE-KSPM (FE {CMF,PSD}), can be widely applicable to different tumor types.