Conformal Invariants for Multiply Connected Surfaces: Application to Landmark Curve-Based Brain Morphometry Analysis

Abstract

Landmark curves were widely adopted in neuroimaging research for surface correspondence computation and quantified morphometry analysis. However, most of the landmark based morphometry studies only focused on landmark curve shape difference. Here we propose to compute a set of conformal invariant-based shape indices, which are associated with the landmark curve induced boundary lengths in the hyperbolic parameter domain. Such shape indices may be used to identify which surfaces are conformally equivalent and further quantitatively measure surface deformation. With the surface Ricci flow method, we can conformally map a multiply connected surface to the Poincaré disk. Our algorithm provides a stable method to compute the shape index values in the 2D (Poincaré Disk) parameter domain. The proposed shape indices are succinct, intrinsic and informative. Experimental results with synthetic data and 3D MRI data demonstrate that our method is invariant under isometric transformations and able to detect brain surface abnormalities. We also applied the new shape indices to analyze brain morphometry abnormalities associated with Alzheimer’s disease (AD). We studied the baseline MRI scans of a set of healthy control and AD patients from the Alzheimer’s Disease Neuroimaging Initiative (ADNI: 30 healthy control subjects vs. 30 AD patients). Although the lengths of the landmarks in Euclidean space, cortical surface area, and volume features did not differ between the two groups, our conformal invariant based shape indices revealed significant differences by Hotelling’s T² test. The novel conformal invariant shape indices may offer a new sensitive biomarker and enrich our brain imaging analysis toolset for studying diagnosis and prognosis of AD.

Graphical Abstract

1. Introduction

Shape analysis is a key research topic in anatomical modeling and involves statistical comparisons of anatomy and medical image registration. In the computational analysis of brain anatomy, volumetric or surface feature measures of structures identified on 3D MRI have been used to study group differences in brain structure and also to predict diagnosis (Botino et al., 2002; Li et al., 2014). In research studies that analyze brain morphometry, many shape analysis methods have been proposed, such as spherical harmonic analysis (SPHARM) (Gerig et al., 2001; Chung et al., 2008), medial representations (M-reps) (Pizer et al., 1999), point distribution models (PDM) (Cootes et al., 1995; Shen et al., 2004), minimum description length approaches (Davies et al., 2003), spectral methods (Shi et al., 2010; Seo and Chung, 2011; Wachinger et al., 2015) and cortical thickness and gyrification indices (Batchelor et al., 2002; Luders et al., 2006), etc. These methods may be applied to analyze shape changes or abnormalities in brain cortical and subcortical structures. Even so, a stable method to compute transformation-invariant shape descriptors would be highly advantageous to this research field.

Landmark based statistical shape analysis is a technique that has been adopted by a variety of fields, including anthropology, genetics, and evolutionary biology (e.g. Boyer et al., 2011) and now has been widely used for brain imaging research (e.g. Thompson et al., 2004; Van Essen, 2005; Glaunès et al., 2004). Although many prior approaches have tried to build cortical correspondence by aligning curvature, sulcal depth or other geometric maps (e.g. Fischl et al., 1999c; Argall et al., 2006; Lyttelton et al., 2007; Tosun and Prince, 2008; Yeo et al., 2010), there is increasing evidence that good relationships can be created between primary sulci and the boundaries of cytoarchitectonic fields in primary cortices (Fischl et al., 2008) and it suggests that a landmark-based method may provide better results for cortical surface shape analysis. Since the manual labeling of landmark curves is time-consuming and error-prone, a variety of cortical landmark identification algorithms have been developed to delineate landmark curves rather than rely upon manual landmark placement (e.g. Le Goualher et al., 1999; Lohmann and von Cramon, 2000; Cachia et al., 2003; Van Essen, 2005; Shattuck et al., 2009; Im et al., 2010; Zhong et al., 2010).

In addition to serving as common geometric constraints to help shape analysis of cortical surfaces, brain landmark curves are often directly analyzed to illustrate brain morphometry changes (e.g. Joshi et al., 2012; Chollet et al., 2014). For example, Mangin et al. (2003) has studied sulcal patterns by enforcing rotational as well as scale invariance. Some prior work (e.g. Tao et al., 2001; Vaillant and Davatzikos, 1997) studied and compared landmark curves via unit speed parameterizations of active contours for constructing Procrustes shape average for sulci. With the current-based diffeomorphic approach, Durrleman et al. (2007) focused on detecting variability in the sulcal patterns without pursuing explicit point correspondences. Fillard et al. (2007) proposed a statistical representation for sulcal curves and measured variability by extrapolating a covariance tensor field to the whole brain. Joshi et al. (2012) further developed a reparametrization invariant shape space of sulcal curves and built statistical models intrinsically on the shape space. However, most of the prior landmark curve analysis frameworks mainly focused on the landmark curves themselves. Missing at this time is an algorithm that studies the global brain morphometry changes through the landmark curve analysis. Here we propose a novel and intrinsic method to compute conformal invariants (shape indices) on multiply connected surfaces and apply it to study brain morphometry by analyzing statistics based on landmark curves. Our conformal invariants are based on the surface conformal structure and can be accurately computed using the surface hyperbolic Ricci flow method.

All oriented metric surfaces have conformal structures. If there exists a conformal map between two surfaces, then they are conformally equivalent. All surfaces can be classified by the conformal equivalence relation. Any two conformally equivalent surfaces have the same coordinates in the Teichmüller shape space (Luo, 1998) and the coordinates are invariant to conformal maps. We call them conformal invariants. By computing and studying conformal invariants and their statistical behavior, we may develop a promising approach for measuring local and global changes or identifying abnormalities in anatomical morphometry due to neurodegenerative diseases. We hypothesize that the heterogeneous changes caused by some neurodegenerative diseases, such as Alzheimer’s disease (AD), may dramatically alter surface conformal structure so that measuring the conformal invariant changes may offer a set of stable and accurate shape indices for brain morphometry that may enrich our understanding of AD effects and enhance our image analysis schemes. Furthermore, our system may be complementary to other brain shape analysis techniques and advance further the use of imaging biomarkers for preclinical AD research (Sperling et al., 2011; Caselli and Reiman, 2013).

In this work, we develop a conformal invariant-based brain morphometry system based on hyperbolic Ricci flow (Hamilton, 1988) and Teichmüller space coordinate theorem (Luo, 1998). Here we automatically trace six landmark curves on each cortical surface with the FreeSurfer (Fischl et al., 1999a) and Caret software (Van Essen et al., 2001) to represent major anatomical and functional features. After slicing a cortical surface along these landmarks, we convert it to a multiply connected surface. We then compute its hyperbolic uniformization metric with the hyperbolic Ricci flow method (Zeng et al., 2010; Shi et al., 2015) and isometrically embed it onto the 2D Poincaré disk. The lengths of the landmarks in the hyperbolic parameter space form the proposed shape indices, which are the Teichmüller space coordinates of the multiply connected cortical surface. We validate the proposed method on some synthetic and longitudinal brain image data. We further apply our system to study brain cortical structural differences associated with baseline T1-weighted brain images from the ADNI dataset, including 30 healthy control subjects and 30 AD patients. Here we set out to test whether our new system can compute reliable shape indices and whether the new shape indices are able to capture brain morphometry abnormalities.

2. Methods and Materials

2.1. Theoretical Background

In this section, we briefly introduce the most relevant theoretical background in conformal geometry, hyperbolic geometry, surface Ricci flow (Hamilton, 1988) and Teichmüller space theory (Gardiner and Lakic, 2000).

Conformal Deformation

Let S be a surface in ℝ³ with a Riemannian metric g (defined in Appendix .1). Suppose u : S → ℝ is a scalar function defined on S. It can be verified that ḡ = e^2ug is also a Riemannian metric on S and angles measured by ḡ are equal to angles measured by g, which means the deformation of metrics from g to ḡ is angle-preserving. Then ḡ is called the conformal deformation of g and u is the conformal factor. Furthermore, when surface metric changes, surface Gaussian curvature K (defined in Appendix .2) will change accordingly to K̄ = e^−2u(−Δ_gu + K), where Δ_g is the Laplace-Beltrami operator under the metric g.

Uniformization Theorem

Given a surface {S, g}, there exist an infinite number of metrics that are conformal to g. The uniformization theorem states that, among all the conformal metrics, there exists a unique representative, which induces constant Gaussian curvature everywhere on S. Furthermore, the constant will be one of {1, 0, −1}. The corresponding metric is called the uniformization metric of S. Therefore, using the uniformization metric, one can embed the universal covering space of any closed surface onto one of three canonical spaces: the unit sphere 𝕊² for genus-zero surfaces that have positive Euler characteristics; the plane 𝔼² for genus-one surfaces that have Euler characteristic zero; the hyperbolic space ℍ² for high-genus surfaces that have negative Euler characteristics.

Fundamental Group and Universal Covering Space

Let S be a closed surface and q ∈ S is a base point. Two loops through q are homotopic if one of them can deform to the other without leaving S. The concatenation of two loops is called their product. All homotopy classes of loops form the fundamental group of S, denoted as π₁(S, q). By slicing S along the fundamental group of loops, we obtain a simply connected domain of S, i.e., a genus-zero surface with a single boundary, denoted as S̃. For multiply connected surfaces, their fundamental groups consist of paths that connect existing boundaries. An example of the fundamental group on a multiply connected cortical surface is illustrated in Fig. 2 (d), where the fundamental group of paths are labeled as τ_i. The detailed computation process is introduced in Sec. 2.2.1. The projection ϕ : S̃ → S is a local homeomorphism, which maps paths on S̃ to their endpoints. The pair (S̃, ϕ) is called the universal covering space of S.

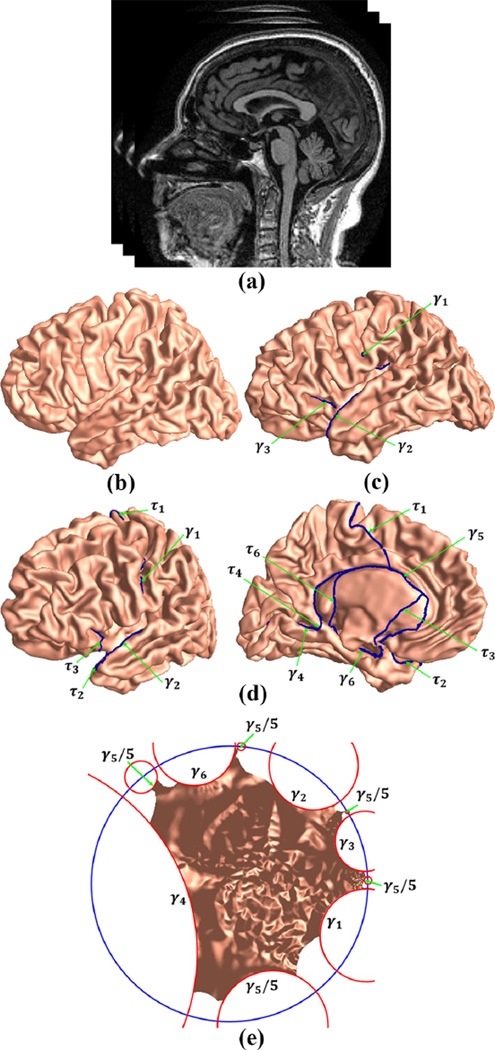
Figure 2.

Algorithm pipeline. Given an MRI (a), the cortical surfaces (b) are reconstructed with the FreeSurfer (Fischl et al., 1999b). Six landmarks are then traced on each cortical surface using the Caret tool (Van Essen et al., 2001). With topology optimization, each cortical surface is converted to a multiply connected surface (c). We then compute the fundamental group (d) of the multiply connected surface. Finally, with the hyperbolic Ricci flow, we map each cortical surface onto the Poincaré disk (e).

Surface Ricci Flow

The hyperbolic uniformization metric of a multiply connected surface can be computed by the hyperbolic Ricci flow (Zeng et al., 2010; Shi et al., 2015). Given a Riemannian manifold {S, g}, the normalized surface Ricci flow is defined as $\frac{d\mathbf{g}(t)}{dt}=2(\frac{2\pi \chi (S)}{A(0)}-K(t))\mathbf{g}(t)$, where A(0) is the total area of S at time 0 and K(t) is the Gaussian curvature induced by metric g(t). If χ(S) < 0, the solution to the normalized Ricci flow equation exists for all t > 0 and converges to a metric with constant Gaussian curvature $\frac{2\pi \chi (S)}{A(0)}$ (Hamilton, 1988). With conformal mapping, which requires g(t) = e^2u(t)g(0), we obtain a simplified Ricci flow equation

$$\frac{du(t)}{dt}=-2K(t)$$ (1)

The derivation of Eq. (1) can be found in (Wang et al., 2012).

Hyperbolic Geometry

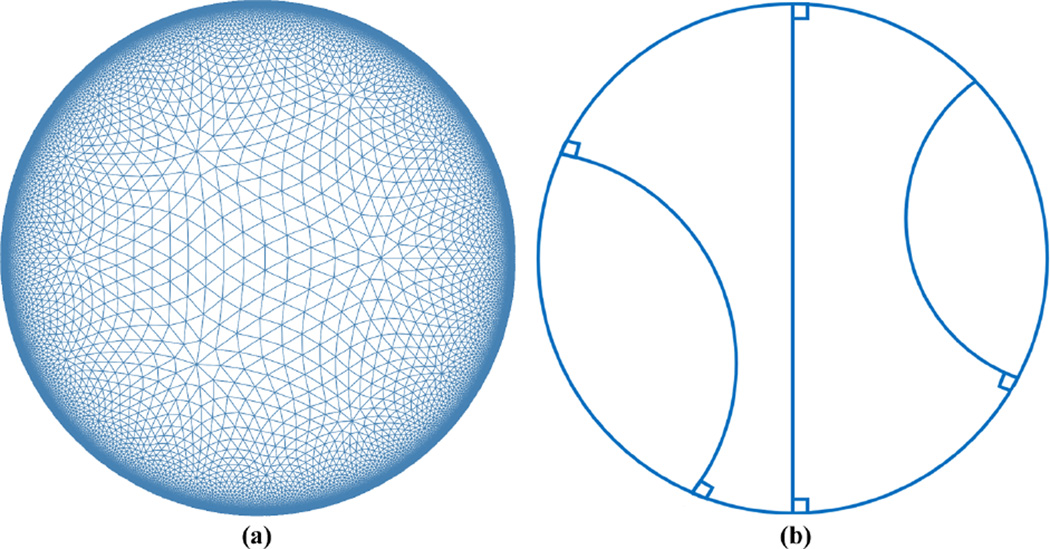
Suppose S is a surface, given its hyperbolic uniformization metric and S̃, we can isometrically embed its universal covering space onto the hyperbolic space ℍ². The hyperbolic space cannot be realized in ℝ³, thus we use the Poincaré disk model to visualize it. Figure 1 (a) is an illustration of the Poincaré disk model. The Poincaré disk is the unit disk |z| < 1, z = x + iy in the complex plane ℂ with the metric $d{s}^2=\frac{4dzd\overline{z}}{{(1-z\overline{z})}^2}$. The rigid motion in the Poincaré disk is the Möbius transformation

$$z\to e^{i\theta }\frac{z-z_0}{1-\overline{z_0}z}$$ (2)

With a conformal mapping computed by the surface Ricci flow, all open boundaries on S are mapped to geodesics in the Poincaré disk model. Geodesics in the Poincaré disk are hyperbolic lines, which are circular arcs that are perpendicular to the unit circle, as shown in Fig. 1 (b).

Figure 1.

Illustration of the hyperbolic geometry. (a) The Poincaré disk model; (b) geodesics in the Poincaré disk model.

Teichmüller Space

Given two surfaces {S₁, g₁} and {S₂, g₂}, a map ϕ : S₁ → S₂ is conformal, if the pull back metric induced by ϕ is a conformal deformation of g₁, i.e., ϕ*g₂ = e^2ug₁. Two surfaces are conformally equivalent if there is a conformal map between them. Fixing the topology, all conformal equivalence classes of surfaces form a finite-dimensional Riemannian manifold, which is called the Teichmüller space (Gardiner and Lakic, 2000). Each point in the Teichmüller space represents a class of conformally equivalent shapes and a curve segment represents a deformation from one class to another. The Riemannian metric in Teichmüller space is well defined and it measures the angle distortion between shapes. The Teichmüller space coordinates of surfaces are invariant to conformal maps and if two surfaces have the same Teichmüller coordinates, they are conformally equivalent. Therefore, the Teichmüller coordinates can be used to index shapes (Wang et al., 2009a,b; Zeng et al., 2010).

Teichmüller Space Coordinates on Multiply Connected Surfaces

Genus-zero surfaces with more than two open boundaries are called multiply connected surfaces. Multiply connected surfaces have negative Euler characteristics and can be conformally mapped to the hyperbolic space ℍ² with their hyperbolic uniformization metric. The lengths of the open boundaries on the multiply connected surfaces under the hyperbolic uniformization metric are the Teichmüller coordinates of the surfaces (Luo, 1998; Wang et al., 2009b). The obtained Teichmüller space coordinates, i.e. conformal invariants, are invariants with conformal structures, computationally simple and stable. We use them as the shape indices to characterize multiply connected surfaces.

2.2. Computational Algorithms

This section introduces the computational algorithms of the proposed shape indices in details. Specifically, we build an integrated and automated framework to compute the shape indices for cortical surfaces. Major steps are summarized in Alg. 1 and Fig. 2.

2.2.1. Cortical Surface Reconstruction and Brain Landmark Curve Tracing

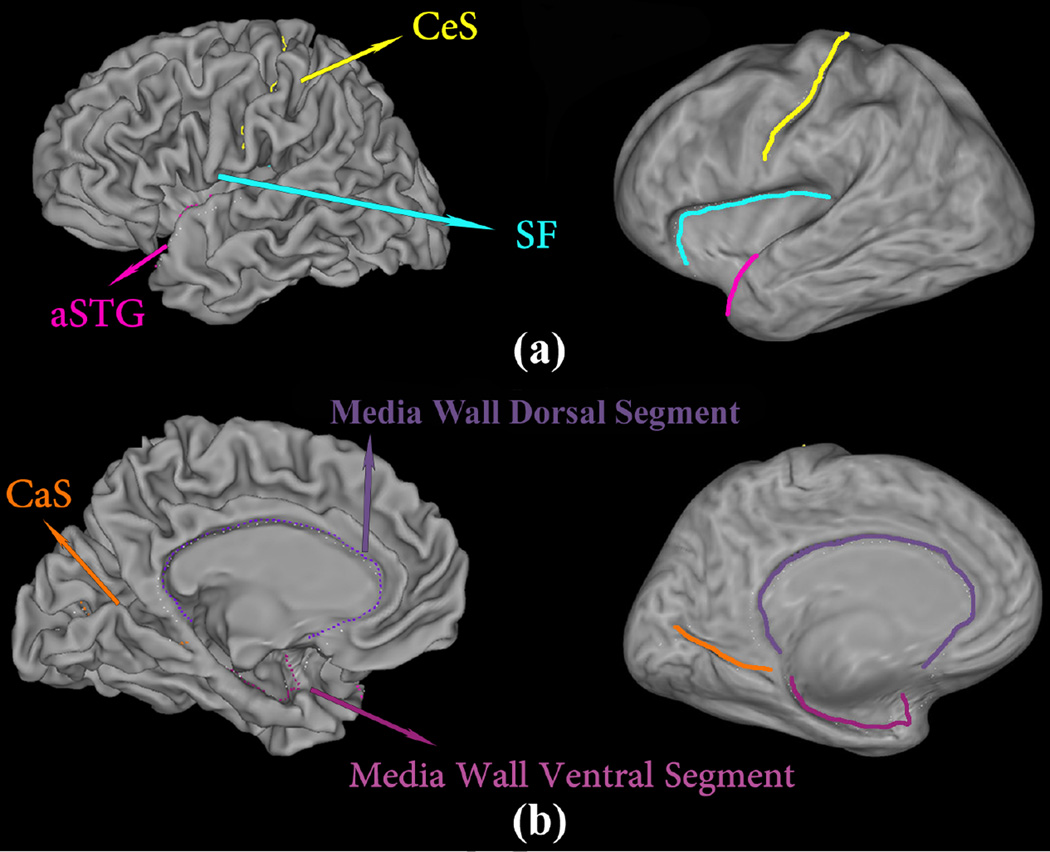
Given a structural MR image, the image segmentation and cortical surface reconstruction are automatically performed with the FreeSurfer software package (Fischl et al., 1999b). A reconstructed left hemispherical surface is illustrated in Fig. 2 (b). Then, a set of ‘Core 6’ landmark curves, including the Central Sulcus (CeS), Anterior Half of the Superior Temporal Gyrus (aSTG), Sylvian Fissure (SF), Calcarine Sulcus (CaS), Medial Wall Ventral Segment, and Medial Wall Dorsal Segment, are automatically traced on each cortical surface using the Caret package (Van Essen et al., 2001). In Caret software, the PALS-B12 atlas is used to delineate the “core 6” landmarks, which are well-defined and geographically consistent,

Algorithm 1.

Surface Conformal Invariants Computation Pipeline.

	Input: A structural MR image.
	Output: Shape indices, which is a set of conformal invariants of the cortical surfaces.
1	The structural MRI (Fig. 2 (a)) is segmented and the cortical surfaces (Fig. 2 (b)) are reconstructed automatically using the FreeSurfer software (Fischl et al., 1999b).
2	Six landmark curves are automatically traced on each cortical hemisphere surface using the Caret software (Van Essen et al., 2001).
3	With topology optimization, each cortical surface is converted to a multiply connect surface. Open boundaries γ1, γ2, γ3 are shown in Fig. 2 (c).
4	The fundamental group of each cortical surface is computed and the simply connected domain is obtained by slicing each surface along the fundamental group of paths (Fig. 2 (d)).
5	Compute the hyperbolic uniformization metric of the multiply connect surface and embed it onto the Poincaré disk with the simply connect domain (Fig. 2 (e)).
6	Compute the conformal invariants, i.e. shape indices, with the hyperbolic uniformization metric.

when compared with other gyral and sulcal features on human cortex. The stability and consistency of the six landmarks was validated in (Van Essen, 2005).

An illustration of the landmark curves on a left cortical surface is shown in Fig. 3 with two views. We show the landmarks with both the original and inflated cortical surfaces for clarity.

Figure 3.

A left cortical surface with six landmark curves, which are automatically labeled with Caret (Van Essen et al., 2001), showing in two different views on both the original and inflated surfaces. The inflated surface is obtained with FreeSurfer (Fischl et al., 1999b).

2.2.2. Topology Optimization

After we identify six landmark curves on a cortical surface, we further slice open the mesh along them. Basically, each vertex on the landmark curve split into two vertices with the same geometry position except the two ending vertices. The new vertices form two new boundaries that are connected by the two ending vertices so we get a closed boundary. Geometrically the surface is still closed but we create a topological hole. We call this process topology optimization. The key idea is that, with the topology optimization, we convert some significant surface curves into open boundaries and each cortical surface is converted to a multiply connected surface. As a result, we may apply practical algorithms which are suitable to deal with genus zero surfaces with open boundaries to specifically process these curves. In our prior work (Wang et al., 2012, 2013), by converting brain landmark curves into open boundary, we enforced landmark curve matching by boundary matching conditions for cortical surface registration research. Similarly, after the topology optimization, here we analyze the intrinsic conformal invariants of the obtained multiply connected surfaces for brain morphometry study.

As shown in Fig. 2 (c), we label the open boundary CeS as γ₁, aSTG as γ₂, SF as γ₃, CaS as γ₄, Medial Wall Ventral Segment as γ₅, and Medial Wall Dorsal Segment as γ₆, respectively. Then we compute the fundamental group of the cortical surface by tracing paths to connect the Medial Wall Dorsal Segment (γ₅) to every other landmark curve boundary. Specifically, we choose 5 points on the Medial Wall Dorsal Segment and connect each point to the nearest endpoint of every other boundary. The paths are traced with Dijkstra’s algorithm with avoidance of collisions (Li et al., 2009). An example of the fundamental group on a cortical surface is shown in Fig. 2 (d), where the path connecting γ₅ with γ_i is labeled as τ_i. After slicing a cortical surface along with its fundamental group of paths, we obtain its simply connected domain. In the following section, we explain in details how we compute the hyperbolic uniformization metric with the multiply connected surface and embed it onto the Poincaré disk with the simply connected domain.

2.2.3. Discrete Hyperbolic Ricci Flow

In practice, smooth surfaces are often approximated by simplicial complexes (triangular meshes). We denote a triangular mesh as Σ, the vertex set as V, the edge set as E, and the face set as F. We use υ_i to represent a vertex, e_ij to represent the edge connecting vertices υ_i and υ_j, f_ijk to represent the face formed by vertices υ_i, υ_j, and υ_k, and ${\theta }_i^{jk}$ to represent the corner angle located at vertex υ_i in face f_ijk.

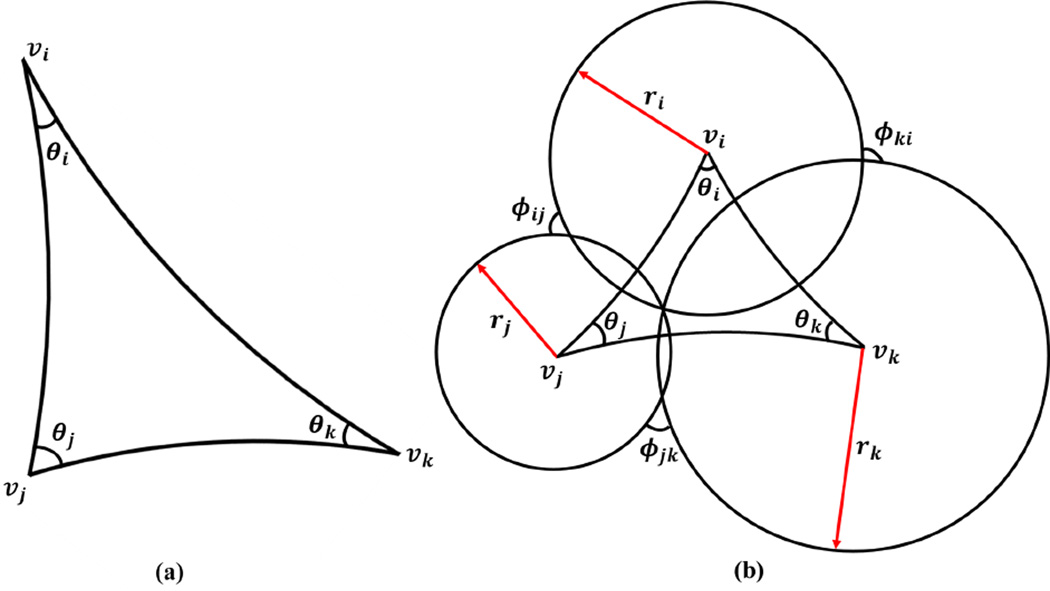
The discrete Riemannian metric defined on Σ is a function defined on each edge l : E → ℝ⁺, such that in each face f_ijk, the triangle inequality holds l_jk + l_ki > l_ij. Usually, it is the edge length. In hyperbolic geometry, we regard each triangle as a hyperbolic triangle, as shown in Fig. 4 (a). The corner angles in each face are computed with the hyperbolic cosine law

$${\theta }_i={\text{cos}}^{-1}\frac{\text{cos}\mathrm{h}{l}_{ij}\text{cos}\mathrm{h}{l}_{ki}-\text{cos}\mathrm{h}{l}_{jk}}{2\text{sin}\mathrm{h}{l}_{ij}\text{sin}\mathrm{h}{l}_{ki}}$$ (3)

Figure 4.

Illustration of a hyperbolic triangle (a) and the circle packing metric in the hyperbolic space (b).

The discrete Gaussian curvature K_i on vertex υ_i ∈ Σ can be computed using the angle deficit

$$K_i=\{\begin{array}{cc}2\pi -{\sum }_{f_{ijk}\in F}{\theta }_i^{jk},\hfill & {\upsilon }_i\notin \partial \mathrm{\Sigma }\hfill \\ \hfill \pi -{\sum }_{f_{ijk}\in F}{\theta }_i^{jk},& {\upsilon }_i\in \partial \mathrm{\Sigma }\hfill \end{array}$$ (4)

where ∂Σ represents the boundary of the mesh.

The concept of the circle packing metric was introduced by Thurston in (Thurston, 1976) for approximating conformal metric deformation. Conformal metric deformations, in the smooth case, preserve infinitesimal circles and the intersection angles among them. The discrete conformal deformation of metrics uses circles with finite radii to approximate infinitesimal circles. Let r be a function defined on the vertices, r : V → ℝ⁺, which assigns a radius r_i to the vertex υ_i. Similarly, let Φ be a function defined on the edges, $\mathrm{\Phi }:E\to [0,\frac{\pi }{2}]$, which assigns an acute angle ϕ_ij to each edge e_ij and is called a weight function on the edges. The set {r, Φ} is called the circle packing metric of the mesh Σ, which is illustrated in Fig. 4 (b) with a hyperbolic triangle. Two circle packing metrics (r₁, Φ₁) and (r₂, Φ₂) on the same mesh are conformally equivalent if Φ₁ ≡ Φ₂. A conformal deformation of a circle packing metric only modifies the vertex radii and preserves the intersection angles on the edges.

The edge length l_ij is given by the hyperbolic cosine law

$$l_{ij}=\text{cos}{\mathrm{h}}^{-1}(\text{cos}\mathrm{h}{r}_i\text{cos}\mathrm{h}{r}_j+\text{cos}{\varphi }_{ij}\text{sin}\mathrm{h}{r}_i\text{sin}\mathrm{h}{r}_j)$$ (5)

Suppose u : V → ℝ denotes the discrete conformal factor vector, u = {u₁, u₂, …, u_n}, where n is the number of vertices on Σ, and define (Zeng et al., 2010; Shi et al., 2015)

$$u_i=\text{log}\left(\text{tan}\mathrm{h}\frac{r_i}{2}\right)$$ (6)

The discrete Ricci flow is defined as follows:

$$\frac{d{u}_i(t)}{dt}=-2K_i(t),$$ (7)

The discrete Ricci flow is exactly the same form as the Ricci flow equation in the continuous setting (Eq. 1). Let the conformal factor vector be u₀ = {0, 0, …, 0} at time 0, the discrete hyperbolic Ricci energy is defined as in (Zeng et al., 2010)

$$f(\mathbf{u})={\int }_{{\mathbf{u}}_0}^{\mathbf{u}}\sum _{i=1}^n{K}_{i}d{u}_i,$$ (8)

It can be easily proved that $\frac{\partial {\theta }_i}{\partial u_j}=\frac{\partial {\theta }_j}{\partial u_i}$ using Eqs. 3, 5, and 6. Given the definition of Gaussian curvature K_i in Eq. 4, immediately we get $\frac{\partial K_i}{\partial u_j}=\frac{\partial K_j}{\partial u_i}$. Thus, the differential 1-form $\omega ={\sum }_{i=1}^n{K}_{i}d{u}_i$ is closed as dω = 0. This proves that the hyperbolic Ricci energy (Eq. 8) is convex and its unique global minimum corresponds to the hyperbolic metric with zero vertex Gaussian curvature. The discrete Ricci flow (Eq. 7) is the negative gradient flow of the hyperbolic Ricci energy. Thus, the hyperbolic Ricci energy can be minimized with the gradient descent method using Eq. 7.

Here, we use Newton’s optimization method, which is more efficient and stable than gradient descent (Zeng et al., 2010; Wang et al., 2012; Shi et al., 2015). The gradient of the hyperbolic Ricci energy (Eq. 8) is $\nabla f(\mathbf{u})=(\frac{\partial f}{\partial u_1},\frac{\partial f}{\partial u_2},\dots ,\frac{\partial f}{\partial u_n})=(K_1,K_2,\dots ,K_n)$. Then

Algorithm 2.

Hyperbolic Ricci Flow with Newton’s Optimization

	Input: A triangular mesh Σ(V, E, F).
	Output: Hyperbolic metric of Σ.
1	Compute the initial ri for each vertex υi and the weight ϕij for each edge eij.
2	Set the target Gaussian curvature as zero.
3	repeat Compute the edge lengths with Eq. 5, face corner angles with Eq. 3, and the Gaussian curvature with Eq. 4. For each vertex υi, compute $\frac{\partial K_i}{\partial u_i}$ and $\frac{\partial K_i}{\partial u_j}$ with Eq. 9 and construct the Hessian matrix H. Solve the linear system HΔu = −2K. Update ui for vertex υi with ui ← ui + Δui. Update ri for vertex υi with Eq. 6.
	until the resulting Gaussian curvature of all vertices is less than a user-defined threshold.

the elements in the Hessian matrix H are $h_{ii}=\frac{\partial K_i}{\partial u_i},h_{ij}=\frac{\partial K_i}{\partial u_j}$, i, j = 1, 2, …, n. Specifically, define τ_ij = sinh(r_i)cosh(r_j) + cosh(r_i)sinh(r_j)cos(ϕ_ij), we have

$$\frac{\partial K_i}{\partial u_i}=\text{sin}\mathrm{h}(r_i)\times {\mathrm{\Sigma }}_{f_{ijk}}\frac{CB-DA}{A\sqrt{A^2-B^2}},\frac{\partial K_i}{\partial u_j}=\text{sin}\mathrm{h}(r_j)\times {\mathrm{\Sigma }}_{f_{ijk}}\frac{EB-FA}{A\sqrt{A^2-B^2}}$$ (9)

where A = sinh(l_ij)sinh(l_ki), B = cosh(l_ij)cosh(l_ki) − cosh(l_jk), $C={\tau }_{ij}\text{sin}\mathrm{h}(l_{ki})\frac{\text{cos}\mathrm{h}(l_{ij})}{\text{sin}\mathrm{h}(l_{ij})}+{\tau }_{jk}\text{sin}\mathrm{h}(l_{ij})\frac{\text{cos}\mathrm{h}(l_{ki})}{\text{sin}\mathrm{h}(l_{ki})}$ , D = τ_ijcosh(l_ki) + τ_kicosh(l_ij), $E={\tau }_{ji}\text{sin}\mathrm{h}(l_{ki})\frac{\text{cos}\mathrm{h}(l_{ij})}{\text{sin}\mathrm{h}(l_{ij})}$, F = τ_jicosh(l_ki) − τ_jk.

Algorithm 2 summarizes the hyperbolic Ricci flow method with Newton’s optimization.

2.2.4. Embedding onto the Poincaré Disk and Conformal Invariants Computation

After computing the hyperbolic uniformization metric, we can embed the surface onto ℍ², as described in Alg. 3. An illustration of the cortical surface embedding onto the Poincaré disk is in Fig. 2 (e).

In the Poincaré disk, open boundaries on the mesh Σ are mapped to hyperbolic geodesics, as shown with red curves in Fig. 2 (e). Assume the edges on boundary b_k are counter-clockwisely ordered, as (e_i, e₂, …, e_m), and the two edges adjacent to vertex υ_i ∈ b_k are e_i and e_i+1. Then the length of each boundary is computed as

$${\text{len}}_{b_k}={\mathrm{\Sigma }}_{e_i\in b_k}|e_i|$$ (10)

where |e_i| is the length of edge e_i under the hyperbolic metric. The lengths of the geodesics are invariant to conformal mappings and they form the proposed shape indices for each surface.

Algorithm 3.

Embed the surface onto the Poincaré disk.

	Input: A multiply connected surface Σ with its hyperbolic uniformization metric and   its simply connected domain Σ̃.
	Output: The embedding of Σ̃ onto the Poincaré disk.
1	Copy the hyperbolic uniformization metric from Σ to Σ̃.
2	Select a seed face f012 = [υ0, υ1, υ2] ∈ Σ̃, map each vertex to the Poincaré disk as: p(υ0) = (0, 0), $p({\upsilon }_1)=\frac{e^{l_{01}}-1}{e^{l_{01}}+1}(1,0)$, and $p({\upsilon }_2)=\frac{e^{l_{02}}-1}{e^{l_{02}}+1}(\text{cos}{\theta }_0^{12},\text{sin}{\theta }_0^{12})$.
3	Put all the neighboring faces of f012 to a queue.
4	while the queue is not empty do
5		Pop the first face fijk from the queue;
6		if fijk has been embedded then
7			Continue;
8		else
9			Suppose υi and υj have been embedded, compute the intersections of two circles (center, radius): (p(υi), lik) and (p(υj), ljk).
10			Then p(υk) is chosen as the intersection point that keeps the face upward.
11			Put the neighboring faces of fijk in the queue.
12		end
13	end

2.3. Subjects

Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public private partnership. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.

The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California - San Francisco. ADNI is the result of efforts of many coinvestigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date, these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.

In this study, the T1-weighted images from 64 subjects were used. The structural MRI images were from the ADNI baseline (62 images) and 24-months dataset (2 images) (Mueller et al., 2005; Jack et al., 2008). We used FreeSurfer’s automated processing pipeline (Dale et al., 1999; Fischl et al., 1999a) for skull stripping, tissue classification, surface extraction, and cortical and subcortical parcellations. It also calculated volumes of individual grey matter parcellations in mm³ and surface area in mm², provided surface and volume statistics for about 34 different cortical structures, and computed geometric characteristics such as curvature, curvedness, local foldedness for each of the parcellations (Desikan et al., 2006). We further loaded the pial surface constructed by FreeSurfer to Caret (Computerized Anatomical Reconstruction and Editing Tooklit) software (Van Essen et al., 2001), which applies atlas based spherical registration and automatically trace the core 6 landmarks, including Central Sulcus (CeS), Anterior Half of the Superior Temporal Gyrus (aSTG), Sylvian Fissure (SF), Calcarine Sulcus (CaS), Medial Wall Ventral Segment, and Medial Wall Dorsal Segment. Details of Caret software on spherical deformation and landmark information are described in (Van Essen Lab, 2012).

Specifically, the subjects we studied included 30 AD (age: 76.67 ± 7.61), 30 healthy control subjects (age: 76.50 ± 7.51) and 2 MCI patients (for longitudinal illustration). The demographic information of 60 studied subjects in ADNI baseline dataset is in Table 1. Here MMSE is short for mini-mental state examination (Folstein et al., 1975). It is a brief cognitive assessment tool generally used for office-based clinical examinations. Full score is 30, lower means more impaired.

Table 1.

Demographic information of 60 studied subjects in ADNI baseline dataset.

	Gender(M/F)	Education	Age	MMSE at Baseline
CTL	13/17	15.1 ± 2.1	79.73 ± 3.73	29.94 ± 0.81
AD	14/16	15.4 ± 2.8	82.52 ± 6.12	24.82 ± 1.68

3. Experimental Results

3.1. A Synthetic Data Example

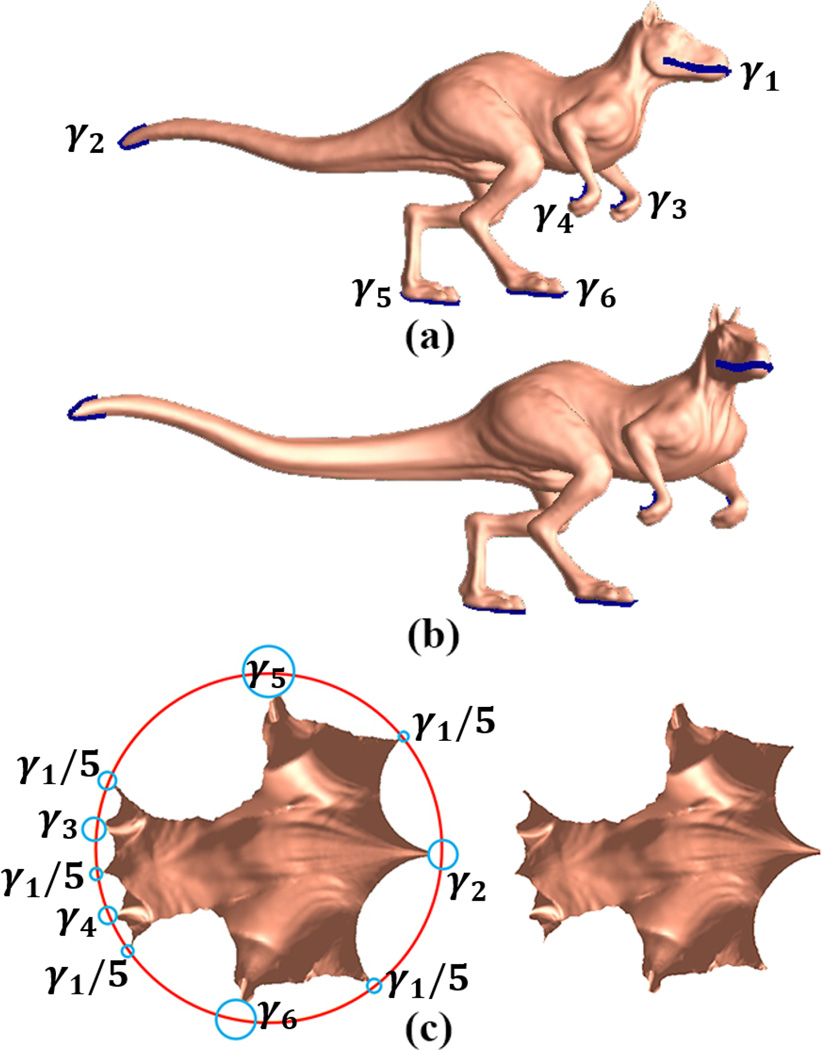
The proposed conformal invariant based shape indices are succinct, intrinsic, invariant under the rigid motions and scalings. To validate these properties, we conducted a synthetic experiment with two dinosaur surfaces, which differed by an isometric deformation. Fig. 5 (a) is a dinosaur surface with six open landmark curves, where the landmark curves are labeled as γ_i, i = 1, …, 6. They were chosen to represent the most salient shape information, including head, tail, and limbs, etc. We isometrically bent the surface into a different pose with an elongated tail, as shown in Fig. 5 (b). The two surfaces are isometrically equivalent so they are also conformally equivalent. After we sliced open them along six open landmark curves, both surfaces have the Euler characteristic −4. Following the uniformization theorem, they may be equipped by Riemannian metrics that induce constant negative Gaussian curvatures, i.e. their conformal parameterizations admit hyperbolic geometry. We applied our conformal invariant computation pipeline (Alg. 1) and computed the length of each boundary under the hyperbolic metric.

Figure 5.

Synthetic experiment to illustrate the stability of the proposed shape index under isometric deformations: (a) a dinosaur surface with six open boundaries after slicing along six open landmark curves; (b) an isometrically bent surface from (a); (c) the embedding of two surface parameterizations onto the hyperbolic Poincaré disk (a, left; b, right).

Fig. 5 (c) shows the embedding of two surfaces (a, left; b, right) onto the Poincaré disk. As indicated by the picture, we can see open boundaries, γ₁, …, γ₆ are mapped to the geodesic curves on the Poincaré disk. Among them, boundary γ₅ is mapped to several segments because of the way we generate the fundamental group of the multiply connected surfaces. We also computed the the hyperbolic lengths of the boundaries, i.e. the conformal invariant shape indices. They were: [1.85083, 0.404286, 1.04093, 0.93902, 0.536393, 0.54362] for (a) and [1.85083, 0.404287, 1.04093, 0.93902, 0.536393, 0.54362] for (b), respectively. The resulting shape indices and embedding were almost identical for both surfaces. This simple synthetic example shows that the proposed shape index is invariant between the synthesized conformal transformation and also demonstrates that the proposed algorithm is able to generate stable computational results.

3.2. Longitudinal Cortical Morphometry in Alzheimer’s Disease

In this experiment, we tested the feasibility of the proposed shape index in studying longitudinal cortical morphometry associated with AD. We randomly selected two mild cognitive impairment (MCI) patients from the ADNI database. One MCI patient converted to AD 36 months after the baseline screening, which we called the MCI converter subject, the other who did not convert to AD 36 months after the baseline screening was called the MCI stable subject.

In our experiments, we studied their structural MR images at two time points, the baseline and 24 months. Our hypothesis is that we may observe some different atrophy patterns associated with the conversion vs. stable progression paths. In this experiment, only the left hemispherical cortical surfaces were used. With the preprocessing with FreeSurfer (Fischl et al., 1999a) and Caret (Van Essen et al., 2001) software packages, two baseline brain cortical surfaces with the landmark curves are shown in Fig. 6 (a). We computed the lengths of the landmark curves under the hyperbolic metric in the same way as the above section. For each MCI patient, we obtained a shape feature matrix (B_i, T_i), i = 1, …, 6, where B represents the baseline cortical surface and T represents the 24-month cortical surface. Then we calculated the L² norm of the shape difference for a given subject over time as $d=\sqrt{{\sum }_{i=1}^6{(B_i-T_i)}^2}$. With the proposed method, the shape difference between the cortical surfaces of two time points is 0.3925 and 1.0438 for the MCI stable and converter subjects, respectively. We see some more differences on the MCI converter subject’s longitudinal image data than the MCI stable subject.

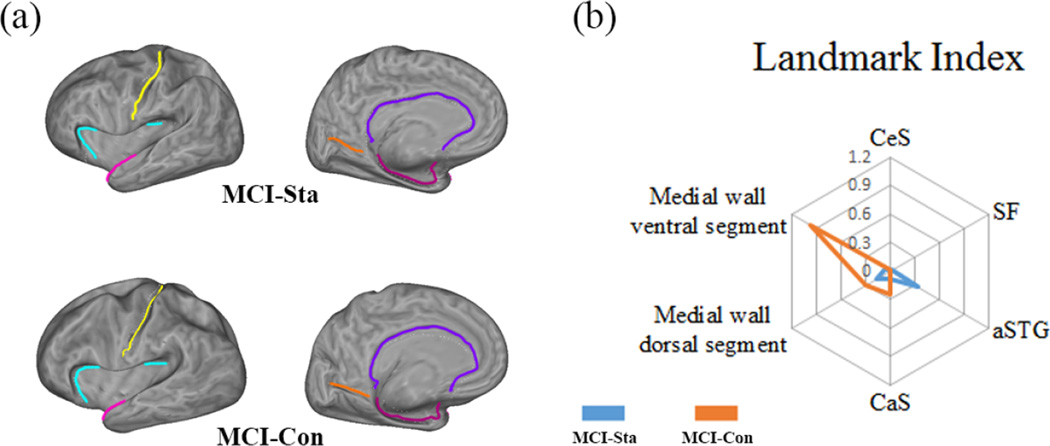
Figure 6.

Radar chart showing the variance of each landmark curve on multiply connected cortical surfaces. (a) two baseline flattened cortical surfaces with identified six landmark curves. (b) Radar chart on individual landmark conformal invariants between two MCI subjects. The landmark conformal invariants are computed on their left cortical surfaces. Each landmark is associated with a corner on a hexagon and six axes are connected them to the common origin point. The position on the axis is proportional to the absolute difference between two landmark conformal invariants computed on different time points. By connecting the six points from the same subject, we get two new hexagons. The blue line stands for MCI Stable (MCI-Sta) and the orange for MCI converter (MCI-Con). The radar chart provides a simple way to display multivariate data in the form of a two-dimensional chart.

Further, to illustrate the difference on each conformal invariant, we plotted the radar chart (Chambers et al., 1983) in Fig. 6 (b). Basically, a radar chart is a graphical method of displaying multivariate data in the form of a two-dimensional chart where three or more quantitative variables are represented on axes starting from the same point. In our case, six landmarks are associated with six corners on a hexagon and six axes connect them to the common origin point. The position on each axis is proportional to the absolute difference between the computed conformal invariants on two time points. The more different, the farther away the point is to the origin. Meanwhile, we used two different color lines to connect the longitudinal differences from two different subjects, the blue color is for the MCI stable subject while the orange color is for the MCI converter subject. From the radar chart, we find that there is a clear difference between these two subjects’ radar charts. Interestingly, we also found on the MCI converter radar chart, there are sharp differences associated with two landmark curves on the medial wall ventral segment and medial wall dorsal segment, especially on medial wall ventral segment. Since medial wall ventral segment runs along the medial margin of the hippocampal sulcus and medal wall dorsal segment runs along the corpus collosum (Fig. 3). It may be particularly consistent with prior observations that, for AD conversion, grey matter atrophy is more related to medial temporal lobe region and the posterior cingulate (Frisoni et al., 2010; Thompson et al., 2003; Buckner et al., 2008; Leech and Sharp, 2014; Matsuda, 2007). Although multi-subject studies are clearly necessary, this experiment demonstrates that our conformal invariants may potentially be used as a set of shape indices to compare and classify cortical surfaces of AD patients at different stages of disease progression. Our work may also provide a simple way to directly visualize the cortical morphometry changes related to different brain regions.

3.3. Application of Conformal Invariants to Multivariate Statistics on Population-based Group Difference Study

This experiment further investigates the variation patterns of the six landmarks to study brain shape morphometry in AD at the group-level population-based study. We hypothesize that the length of those six landmarks under hyperbolic metric may serve as useful shape indices to verify and predict degeneration of AD. In this experiment, we applied a group-wise statistical analysis to our proposed shape indices in left hemisphere cortex between AD and control subjects. Our data set consisted of 60 subjects which were randomly chosen from ADNI database, including 30 AD subjects and 30 matching normal controls. The demographic information of these subjects is shown in Table 1. The cortical surface of each subject was computed, from which six landmarks were extracted using the same method as that in the previous experiments. Similarly, we use the lengths of six landmarks in hyperbolic space as the conformal invariants to represent morphometric characteristics of cortical surfaces. Here, conformal invariants for each cortical surface for a given hemisphere was a vector υ = (υ₁,…, υ₆)^T, where υ_i is the length of a given landmark under hyperbolic metric.

Similar to our prior work (e.g. Wang et al., 2011), we performed the permutation based Hotelling’s T² test to evaluate group difference. Suppose there are two sets of feature vectors from two different groups, C = (x₁, x₂, …, x_m) and W = (y₁, y₂, …, y_n), where m and n are the number of subjects in AD and the control group respectively. The difference between two groups is measured by the Mahalanobis distance,

$$d(\upsilon )=\sqrt{{({\mu }_C-{\mu }_W)}^T{({\mathrm{\Sigma }}_W+{\mathrm{\Sigma }}_C)}^{-1}({\mu }_C-{\mu }_W)}$$ (11)

where μ_C, μ_W, Σ_C and Σ_W are the mean and covariance of two groups, respectively. We first compute the true group distance based on the true grouped samples. Then we randomly assigned the feature vectors into two groups each with the equal size number of 30 and recomputed group distance. The process was repeated 5000 times with the outcome of 5000 permutation values. Finally, a probability (p value) was computed as the ratio of the number of permutation values greater than the true group distance to the total permutation times. To evaluate if our proposed conformal invariant vector really helped to improve the detection power, we also computed group differences by using cortical surfaces area and cortex volume.

With this protocol, the prominent statistical result of conformal invariants was p = 0.0133 between AD and control groups. For comparison purpose, we also computed the natural lengths of the six landmark curves in the ambient space, as they are the counterpart of the proposed shape indices in the Euclidean domain. Similarly, we used Hotelling’s T² test to perform group comparison. With the same permutation test as above, the Euclidean lengths of the landmarks did not reveal significant difference between the two groups (p = 0.7844). Furthermore, we also conducted permutation based t tests using left cortical surface area and left cortex volume, respectively. Similarly, we conducted 5000 times of permutation and estimated the probability of the ground truth data happened in this random permutation results. Neither of the two statistical results reached significant level (p = 0.5888 and p = 0.1152 for left cortical surface area and left cortex volume, respectively). Our empirical results demonstrated that it may be possible to use our proposed shape indices to detect AD related morphometric variation on group-based studies.

4. Discussion

Application of the shape space concept to investigate brain morphometry changes can be used to evaluate disease burden, progression and response to interventions. In this paper, we introduced a novel Teichmüller shape space based automatic brain imaging system that focuses on studying six major landmark curves on human brain cortical surfaces. There are two main findings in our paper. First, this paper demonstrates the feasibility of applying the concept of Teichmüller shape space to study image based brain morphometry variance. The Teichmüller shape space is an abstract mathematical concept which reflects intrinsic surface conformal structure. Our prior work (Zeng et al., 2012) has shown that the Teichmüller shape space could be applied to study certain brain functional area morphometry changes. However, that work strongly depended on the specific areas to be studied. In this work, we focus on six common landmark curves and compute the Teichmüller shape space coordinates when modeling them as open curves. The proposed method is general and has the potential to provide an integrated simple morphometry descriptor to brain shape analysis research. Second, we built an efficient and practical imaging analysis pipeline by integrating surface Ricci flow, hyperbolic geometry methods and other popular neuroimaging software tools such as FreeSurfer and Caret. The obtained image indexing system is robust and automatic and defined on 6 most common landmarks in human brains. The obtained imaging indices practically encode information about intrinsic surface conformal structure, providing a unique way to study subtle brain morphometry changes that may enrich current state-of-the-art brain morphometry analysis algorithms.

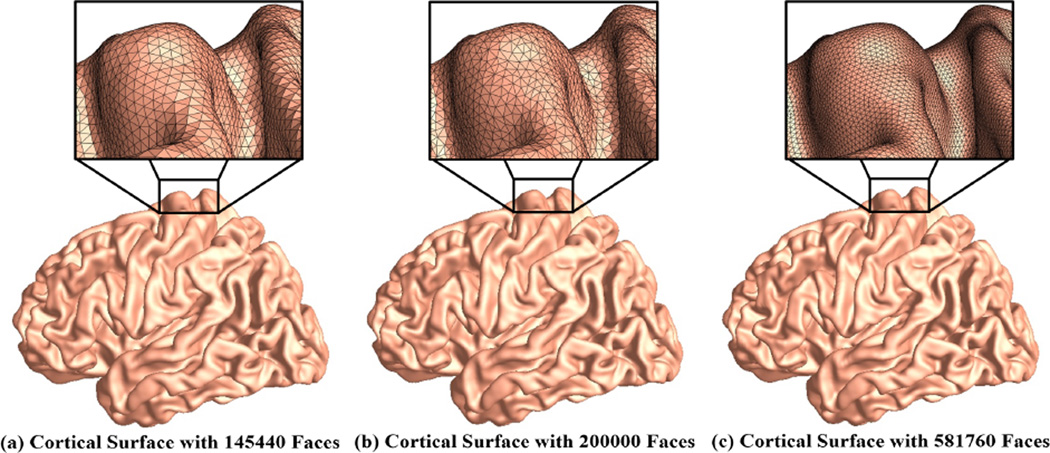
The proposed conformal invariant computation system is theoretically sound and numerically efficient (Jin et al., 2008; Wang et al., 2012; Zeng et al., 2010; Shi et al., 2015). To evaluate its numerical stability, we randomly selected a baseline brain image from a healthy control subject. With FreeSurfer and Caret, we identified 6 landmark curves on its left cortical surface. We further used Loop subdivision (Loop, 1987) to increase its face numbers and generated two additional surfaces. These three cortical meshes with some zoom-in snapshots are shown in Fig. 7. Then we applied the same computational pipeline on these three cortical surfaces to compute their conformal invariants. The computed conformal invariants for three meshes are [3.44536, 3.11303, 4.75132, 3.5008, 5.88926, 4.67419], [3.37195, 3.16175, 4.87988, 3.40043, 5.96301, 4.74933] and [3.46745, 3.10535, 4.7666, 3.48866, 5.83625, 4.75211] for three meshes with 145440, 200000, and 581760 faces, respectively. We can see the results are quite similar and difference are less than 2% of the the original values. The empirical results demonstrate that our computation is robust and independent of the mesh resolutions.

Figure 7.

Cortical surface meshes in different resolutions. The cortical mesh (a) was originally from a healthy control subject and reconstructed by FreeSurfer software. With Loop subdivision, we generated two other meshes, (b) and (c), with different resolutions. The inner pictures show the zoom-in snapshots of the mesh structures. Our empirical results show that the computational results are stable with different mesh resolutions.

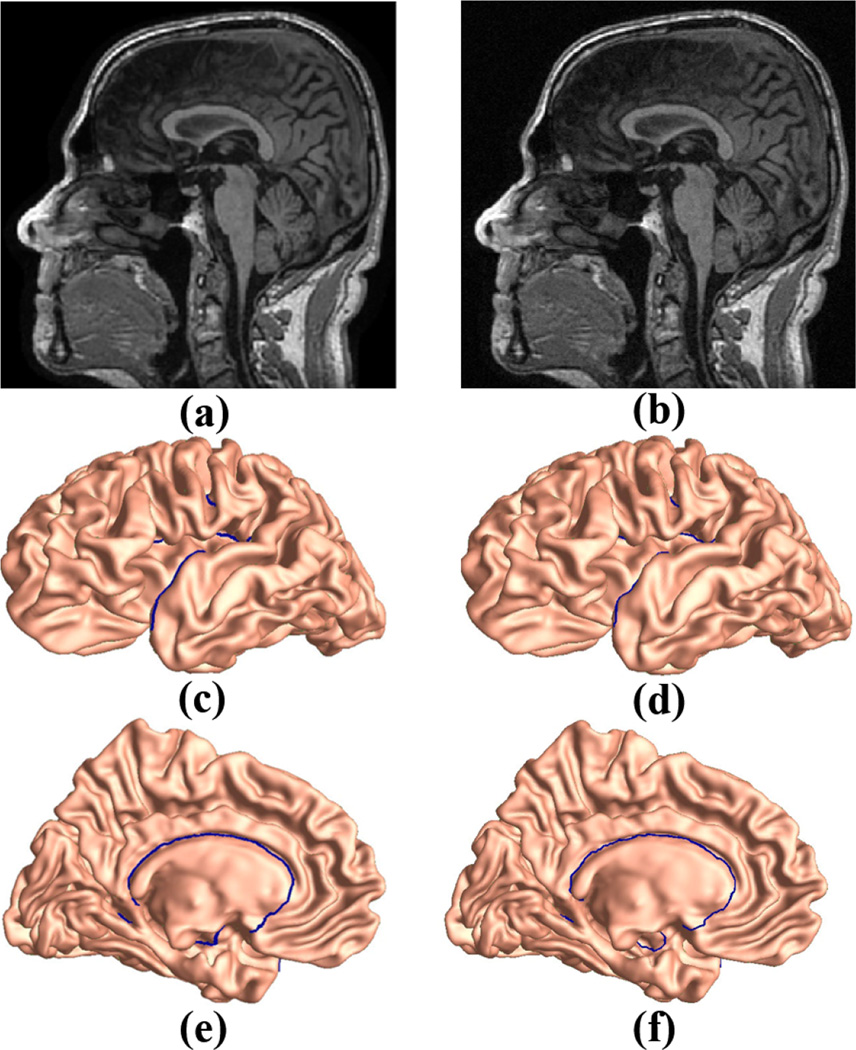
It is well known that noise in MR images has an important influence on brain imaging study and many denoising algorithms have been introduced (Wink and Roerdink, 2004; Nobi and Yousuf, 2011). Thus an MRI analysis tool that is robust to image noise will be highly advantageous. To study the sensitivity of our method to image noise, we randomly selected an MR image from the ANDI baseline control dataset. As studied in (Gudbjartsson and Patz, 1995), the image intensity in MR images with noise present is governed by a Rician distribution, we manually added the Racian noise to the original MR image with standard deviation of 35, using the method as in (Ridgway, 2007). The raw images without and with noise are shown in Fig. 8 (a) and (b), respectively. With FreeSurfer and Caret, the reconstructed cortical surfaces overlaid with landmark curves are shown in Fig. 8, where (c) and (e) are the front and back views of the left cortical surface from the image without noise, (d) and (f) are from the noisy image. We can see that the reconstructed cortical surfaces and the landmark curves are very similar to each other. Then we computed the conformal invariants with both multiply connected surfaces and the resulting shape indices are [3.44536, 3.11303, 4.75132, 3.5008, 5.88926, 4.67419] for Fig. 8 (c, e) and [3.46495, 3.1554, 4.81487, 3.53899, 5.84046, 4.67932] for Fig. 8 (d, f), respectively. We can see that the results are quite similar, even with a high image noise level. Although more carefully designed experiments are necessary, this simple experiment demonstrates that our method may be robust to noise in raw MR images.

Figure 8.

Sensitivity of the proposed shape indices to raw MR image noise. (a) an MR image without noise, (b) the same MR image as in (a) but with noise added, (c) front view of the cortical surface reconstructed from image (a), overlaid with landmark curves, (d) front view of the cortical surface reconstructed from image (b), overlaid with landmark curves, (e) back view of the cortical surface reconstructed from image (a), overlaid with landmark curves, (f) back view of the cortical surface reconstructed from image (b), overlaid with landmark curves.

The longitudinal MCI experiment presented in Sec. 3.2 serves as a quick illustration to justify the relevance of our proposed work with the AD research. It is not expected that such a simple comparison would bring any new insights to the AD research. To do so, more rigorous test-retest population based studies are certainly necessary. Even so, our work shows that the posterior cingulate area is one of the areas that has the drastic shape changes over the study period. In the literature, the posterior cingulate is among a few structures that are affected significantly by the early stages of AD (Buckner et al., 2008; Leech and Sharp, 2014; Matsuda, 2007). In our prior work (Shi et al., 2015), we also found that subregions on lateral ventricles that are adjacent to posterior cingulate demonstrated significant enlargement in MCI converters. Thus our observation is consistent with AD research results in the literature. It may indicate that our shape indices may be able to capture the brain shape morphometry that is associated with AD progress.

The current work is related to manifold shape space research, which was pioneered by Kendall (1977) and Bookstein (1978). In image analysis research, shape space was well studied for brain atlas estimation (Fletcher et al., 2009; Fletcher, 2013), shape analysis (Kurtek et al., 2011; Gutman et al., 2015; Su et al., 2015a), morphometry study (Younes et al., 2009; Boyer et al., 2011), and other applications. In a computational anatomy framework (Grenander and Miller, 1998), the space of diffeomorphisms was carefully studied (Miller et al., 2002; Miller and Younes, 2001; Trouvé, 1998; Younes, 2010). In Srivastava et al. (2005), Younes et al. (2008) and Srivastava and Jermyn (2009), shape space was defined as the space of orbits of the reparameterization group acting on the space of immersions. The reparameterization invariant (RI) metric constructed in Bauer et al. (2010) and Bauer et al. (2012) used the volume form and the mean curvature of the immersion f, and the metric in (Kurtek et al., 2012) used the area multiplication factor of f. Kurtek et al. (2013) extended the work in (Kurtek et al., 2012) by adding landmark constraints. Jermyn et al. (2012) simplified the RI metric computation and Gutman et al. (2015) recently built a Riemannian framework for an intrinsic comparison of the RI metric structure. Lipman and Daubechies (2011) introduced a metric for shape comparison based on conformal uniformization and optimal mass transport. The metric is invariant under Möbius transformation. Later, Lipman et al. (2013) provided a convergence analysis of the discrete approximation to the arising mass transport problems. Mémoli (2011) presented a modification and expansion of the original Gromov-Hausdorff notion of distance between metric spaces which considers probability measures defined on measurable subsets of metric spaces. Recently, Riemannian optimal mass transport (Ambrosio and Gigli, 2013; Su et al., 2015a) was introduced. It was used to compute Wasserstein distance on sphere (Su et al., 2015b) and hyperbolic domain (Shi et al., 2016)

There are two important caveats when applying Teichmüller shape space coordinates for brain morphometry research. First, it demands more investigations on how useful the conformal invariants are for brain morphometry study. Further, it may be beneficial to apply our method if the users have some prior knowledge on the brain deformations associated with a specific neurodegenerative disease. Otherwise, one may have to screen a set of candidate curves to find which are the most sensitive to certain disease states. It demands some computation time to make it clinically useful. Even so, it is a natural idea that one can expect certain neurodegenerative diseases would have distorted conformal structures so that one can use the conformal invariants to measure the severity and develop an imaging biomarker. Our work provides unique measurements to quantify cortical surface deformations and associate them with some brain cognitive measures. Second, Teichmüller shape space remains a fast growing research field, including some recent seminal work in the pure mathematics society (e.g. Mirzakhani, 2008). The current work presents our initial efforts to study the possibility for the Teichmüller shape space coordinates as a valid brain imaging biomarker. We hope our preliminary results could inspire new ideas on this topic and further advance brain morphometry research.

5. Conclusion and Future Work

In this paper, we propose a stable way to compute conformal invariants for multiply connected surfaces. With topology optimization, surface hyperbolic Ricci flow and hyperbolic embedding, we can conformally map a 3D surface with open boundaries onto the Poincaré disk. The lengths of the open boundaries on the multiply connected surfaces under the hyperbolic uniformization metric are the Teichmüller space coordinates, i.e. conformal invariants. The computed conformal invariants are robust to rigid-body transformations and conformal transformations of the surfaces from which they are derived. Local geometry is well preserved under conformal mapping so conformal invariants may be good candidate features for brain research on cortical and subcortical surface morphometries. The proposed method is part of our ongoing work on hyperbolic conformal geometry and its applications in brain imaging research. In (Shi et al., 2015), we studied ventricular enlargement in MCI converters using hyperbolic Ricci flow and surface tensor-based morphometry (TBM) (Chung et al., 2008). Based on this work, we developed a hyperbolic space sparse coding system (Zhang et al., 2016). In (Shi et al., 2016), we computed the hyperbolic Wasserstein distance and applied it to an AD-control cortical surface classification problem and achieved an accuracy rate of 76.7%. This demonstrates that we may use hyperbolic Wasserstein distance as a single shape index to characterize a unique brain surface. These promising results encourage us to further explore the power of hyperbolic geometry. In future, we will continue working on computing novel surface features from surface hyperbolic conformal structure and studying their applications in AD diagnosis. The proposed conformal invariant-based shape indices are an integral part of our future work. Specifically, first, we will further validate the method with more imaging data; second, by applying some popular statistical classifiers, such as the support vector machine (Cortes and Vapnik, 1995) and linear discriminant analysis (LDA) (Fisher, 1936), we plan to carefully study and validate these conformal invariants for MCI conversion prediction and AD prognosis. Furthermore, we will also study more shape space invariants, such as the period matrix of high-genus surfaces for conformal equivalence (Gu et al., 2004), heat kernel descriptors for isometry equivalence (Wang and Wang, 2015), etc. These invariants may provide new reliable and intrinsic shape features.

Highlights.

• A Teichmüller shape space approach to landmark curve-based brain morphometry study

• FreeSurfer/Caret used to reconstruct cortical surfaces and locate 6 landmark curves

• With topology optimization, cortical surfaces are equipped with hyperbolic metric

• Hyperbolic Ricci flow conformally maps multiply connected surfaces to Poincaré disk

• Experiments on synthetic and ADNI data showed promising results

Appendix. 1

Riemannian Metric

Suppose S is a surface embedded in ℝ³ and its parametric representation is r(x, y) with local coordinates (x, y). A tangent vector of S is dr = r_xdx + r_ydy, where (dx, dy) are coordinates of dr on the tangent plane. The length of the tangent vector is ds² =< dr, dr >= dx² < r_x, r_x > +2dxdy < r_x, r_y > +dy² < r_y, r_y >. Let E =< r_x, r_x >, F =< r_x, r_y >, and G =< r_y, r_y >, then ds² can be written as

$$d{s}^2=(\begin{array}{cc}\hfill dx\hfill & \hfill dy\hfill \end{array})\left(\begin{array}{cc}\hfill E\hfill & \hfill F\hfill \\ \hfill F\hfill & \hfill G\hfill \end{array}\right)\left(\begin{array}{c}\hfill dx\hfill \\ \hfill dy\hfill \end{array}\right).$$ (1)

The ds² is called the first fundamental form or Riemannian metric, which defines an inner product in the tangent space of S. Usually, we denote the Riemannian metric as the positive definite tensor $\mathbf{g}=\left(\begin{array}{cc}\hfill E\hfill & \hfill F\hfill \\ \hfill F\hfill & \hfill G\hfill \end{array}\right)$

Appendix .2

Gaussian Curvature

Given a surface S, the Gauss map G : S → 𝕊² projects each point p ∈ S to its normal n(p) on the unit sphere. The Gaussian curvature K(p) is defined as the Jacobian of the Gauss map, i.e., the ratio between the infinitesimal area around the Gauss image of p on the sphere and the infinitesimal area around p on the surface. Gaussian curvature is intrinsic surface property and invariant under isometries. According to the Gauss-Bonnet theorem (Carmo, 1976), the total Gaussian curvature of a surface is determined by its topology: ∫_S KdA = 2πχ(S), where dA is the surface area element and χ(S) is the Euler characteristic of S.