Computing Group Cardinality Constraint Solutions for Logistic Regression Problems

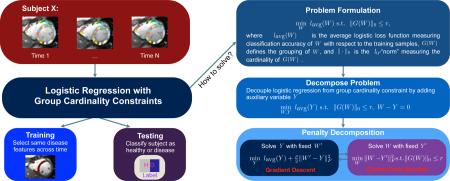
Abstract

We derive an algorithm to directly solve logistic regression based on cardinality constraint, group sparsity and use it to classify intra-subject MRI sequences (e.g. cine MRIs) of healthy from diseased subjects. Group cardinality constraint models are often applied to medical images in order to avoid overfitting of the classifier to the training data. Solutions within these models are generally determined by relaxing the cardinality constraint to a weighted feature selection scheme. However, these solutions relate to the original sparse problem only under specific assumptions, which generally do not hold for medical image applications. In addition, inferring clinical meaning from features weighted by a classifier is an ongoing topic of discussion. Avoiding weighing features, we propose to directly solve the group cardinality constraint logistic regression problem by generalizing the Penalty Decomposition method. To do so, we assume that an intra-subject series of images represents repeated samples of the same disease patterns. We model this assumption by combining series of measurements created by a feature across time into a single group. Our algorithm then derives a solution within that model by decoupling the minimization of the logistic regression function from enforcing the group sparsity constraint. The minimum to the smooth and convex logistic regression problem is determined via gradient descent while we derive a closed form solution for finding a sparse approximation of that minimum. We apply our method to cine MRI of 38 healthy controls and 44 adult patients that received reconstructive surgery of Tetralogy of Fallot (TOF) during infancy. Our method correctly identifies regions impacted by TOF and generally obtains statistically significant higher classification accuracy than alternative solutions to this model, i.e., ones relaxing group cardinality constraints.

Graphical abstract

1. Introduction

An important topic in medical image analysis is to identify image phenotypes by automatically classifying time series of 3D Magnetic Resonance Images (MRIs). For example, intra-subject MRI sequences are used to analyze cardiac motion (Osman et al., 1999; Sermesant et al., 2003; Chandrashekara et al., 2004; Huang et al., 2005; Besbes et al., 2007; Sundar et al., 2009; Zhang et al., 2010a; Margeta et al., 2012; Wang et al., 2012; Yu et al., 2014), and brain development (Chetelat et al., 2005; Zhang et al., 2010b; Aljabar et al., 2011; Serag et al., 2012; Toews et al., 2012; Bernal-Rusiel et al., 2013; Schellen et al., 2015). However, the automatic classification of medical images is generally challenging. First, the number of features extracted from medical images is usually much larger than the number of samples. This generally results in overfitting of the method to the data, i.e., much higher classification accuracy during training than on test data (Ryali et al., 2010; Marques et al., 2012; Deshpande et al., 2014). In addition, the image phenotypes identified by automatic classifiers are often difficult to relate to the medical literature (Qu et al., 2003). In this article, we propose an algorithm that addresses both issues by directly solving the so called logistic regression problem with group sparsity constraints.

Classifiers based on sparse models reduce the dense image data to a small number of features by counting the number of selected features via the l₀-“norm” and are configured so that the count is below a predefined threshold (Yamashita et al., 2008; Carroll et al., 2009; Rao et al., 2011; Liu et al., 2012; Lv et al., 2015). A generalization of that concept are group sparsity models, which first group image features based on predefined rules and then count the number of non-zero groupings (Ng et al., 2010; Wu et al., 2010; Ryali et al., 2010). To solve the underlying minimization problem, however, these methods relax the feature selection process from (group) cardinality constraints to weighting feature by, for example, replacing the l₀-“norm” with the l₂-norm (Meier et al., 2008; Friedman et al., 2010; Ryali et al., 2010; Li et al., 2012). The solution of those methods relates to the original sparse problem only under specific assumptions, e.g., the data entry matrix needs to satisfy the restricted isometry property in compressed sensing problem (Candes and Tao, 2005; Candès et al., 2006). However, matrices generally do not satisfy this property, such as those of the appendix of (Lu and Zhang, 2013), and most data matrices of medical image applications, e.g., matrices defined by the regional volume scores of subjects. Thus, with the exception of sparse models applied to compressed sensing, the solution obtained with respect to the relaxed norm generally does not recover the one of the original sparse model defined by the l₀-“norm”. In addition, the number of measures selected by the classifier depends now on the training data due to the soft selection scheme. One can select a predefined number by choosing measures whose weight is above a certain threshold. However, in the case of sparse logistic regression the corresponding classifier depends on the measures below the threshold and the relevance of those weights with respect to the disease under study is an ongoing topic of discussion (Haufe et al., 2014; Sabuncu, 2014). Alternatively, the upper bound associated with the sparse constraint is set so that the classifier returns the wanted number of measures for a given training data set (Vounou et al., 2012; Zhang and Shen, 2012; Ma and Huang, 2008; Zhang et al., 2012). The tuning is now data dependent, i.e., each training set is generally associated with a different upper bound so that selected number of scores is constant across training sets. Even comparing the patterns of different subsets of the same data set, i.e., folds, is none trivial as each pattern is the solution to a minimization problem, whose sparsity constraint is unique to a fold. Avoiding soft feature selection and thus these issues, our algorithm solves the original group sparsity constrained, logistic classification problem defined by the l₀-“norm” by extending the Penalty Decomposition (PD) method (Lu and Zhang, 2013). By doing so, our method uses a single model to not only classify samples but also directly select patterns (without thresholding or changing upper bounds) that potentially are image phenotypes meaningful to medical community.

To further investigate its potential, we now generalize PD from solving sparse logistic regression problems with group size one to more than one. Specifically, we assume that an intra-subject series of images represents repeated samples of the same disease patterns. In other words, selecting an image feature for disease identification needs to account for the entire series of measurements created by that feature across time. We model this assumption by combining each “feature series” into a single group. The proposed PD algorithm then derives a solution within that model by decoupling the minimization of the logistic regression function from enforcing the group sparsity constraint. Applying Block Coordinate Descent (BCD), the minimum to the smooth and convex logistic regression problem is determined via gradient descent while we derive a closed form solution for finding a sparse approximation of that minimum.

We apply our method to cine MRI of 38 healthy adults and 44 adult patients, that received reconstructive surgery of Tetralogy of Fallot (TOF) during infancy. The data sets fulfill the assumption of the group sparsity model as the residual effects of TOF mostly impact the shape of the right ventricle (Atrey et al., 2010; Bailliard and Anderson, 2009) so that the regions impacted by TOF should not change across the time series captured by a cine MRI. During training, we automatically set all important parameters of our approach by first training a separate regressor for each setting of the parameter space. We then reduce the risk of over-fitting by combining those classifiers into a single ensemble of classifiers (Rokach, 2010). This ensemble of classifiers correctly favors subregions of the ventricles most likely impacted by TOF. For most experiments, it also produces statistically significant higher accuracy scores than ensemble of classifiers that relax the group cardinality constraint.

We first proposed to generalize PD to group sparsity constraints at MICCAI 2015 (Zhang and Pohl, 2015). This article provides a more in-depth view of this idea. Specifically, we expand PD to guarantee convergence of the sparse approximation to a local minimum of the group-sparsity confined, logistic regression problem, which is the primary contribution of this manuscript. We also modify the experiments by replacing the morphometric encodings of heart regions based on the average of the Jacobian determinants with simple volumetric scores. This simplifies preprocessing as alignment of each cine MRI to a template is unnecessary. It also reduces the size of the parameter search space, which now omits the smoothing parameters associated with the alignment process. Moreover, we not only record a single accuracy score for each implementation but instead generate distributions of scores by modifying the number of training samples. For each training size, we apply the method to 10 different training and testing sets. Finally, we distinguish the ventricular septum from the left ventricle to refine our findings from the previous publication (Zhang and Pohl, 2015) and support those findings with new plots that visualize the selection of regions across the entire heart.

Beyond our MICCAI publication, a possible alternative regression approach for simultaneous classification and pattern extraction is the random forest method (Lempitsky et al., 2009). However, it is unclear how to expand this technology to group-wise selection schemes that enforce temporal consistency in selecting regions, i.e., the same regions are picked across all time points. Due to these difficulties most machine learning approaches applied to cine MRI just focus on disease classification, such as (McLeod et al., 2013; Afshin et al., 2014; Bai et al., 2015). They often improve results by manually selecting regions thought to be impacted by the disease before performing classification (Wald et al., 2009). An exception are (Qian et al., 2011; Ye et al., 2014; Bhatia et al., 2014), which seperately perform disease classification and weigh individual regions possibly impacted by disease. The disconnect between the two steps and the weighing of individual regions makes clinical interpretation of the findings more difficult as, in addition to the earlier mentioned issues associated with the interpretation of weights, it increases the risk of false positive findings compared to directly identifying patterns of regions. Our experimental results echo these issues, where logistic regression with relaxed sparsity constraints was generally significantly less accurate than our proposed solution to the original sparsity constraint. We conclude that our proposed approach is the first to solve a single optimization problem for simultaneous disease classification and group-based pattern identification based on segmentation of cine MRIs.

The rest of this paper is organized as follows. Section 2 provides an in-depth description of PD algorithm and its convergence properties. Section 3 summarizes the experiments on the TOF dataset and Section 4 concludes the paper with final remarks.

2. Solving Sparse Group Logistic Regression

We first describe the logistic regression model with group cardinality constraint, which accurately assigns subjects to cohorts based on features extracted from intra-subject image sequences. We then generalize the PD approach to find a solution within that model. We end the section deriving convergence properties of the resulting algorithm.

2.1. The Model

The input to our model are N subjects, their diagnosis {b₁,...,b_N} and features {Z¹,..., Z^N} extracted from 3D+t medical images with T time points. The diagnosis b_s ∈ {−1, +1} is +1 if subject ‘s’ is healthy and −1 otherwise. The feature matrix $Z^s≔\left[z_1^s{z}_2^s\dots z_T^s\right]\in {\mathbb{R}}^{M\times T}$ of subject s is composed of vectors $z_t^s\in {\mathbb{R}}^M$ encoding the t^th time point through M features. Our goal is now to accurately model the relationship between the labels {b₁,...,b_N} and the features {Z¹,...,Z^N}.

Given the large number of features and the relatively small number of samples, we make the model tractable by assuming that the disease is best characterized by the same ‘r’ features (subject to (s.t.) r ≤ M) at each time point, which means the same ‘r’ rows of each feature matrix Z^s. One way of modeling this relationship is via group-sparsity constraint solutions to a logistic regression problem. Weighing features according to their importance in separating the healthy from the disease group, the problem of logistic regression is to find the configuration that most accurately infers the diagnosis of each sample. Sparsity constraints simply confine the search space to those configurations that only select a subset of features, i.e, the weight of non-selected features is zero. Our model aims to identify ‘r’ rows of a feature matrix, which group-sparsity constraint does by first defining the features of a row as a group before enforcing the sparsity constraint on those groupings. In other words, if the model chooses a feature in one time point, the corresponding features in other time points should also be chosen since the importance of a feature should be similar across time.

To formally define this model, we now introduce

• the diagnosis-weighted feature matrix A^s := b_s · Z^s for s = 1,...,N,

• the weight matrix $W\in {\mathbb{R}}^{M\times T}$ defining the importance of each feature in correctly classifying subjects,

• $W^i≔(W_1^i,\dots ,W_T^i)$ being the i^th row of matrix W,

• the trace of a matrix Tr(·),

• the logistic function θ(y) := log(1 + exp(–y)), and

• the average logistic loss function with respect to the label weight $v\in \mathbb{R}$

$$l_{\mathrm{avg}}(v,W)=\frac{1}{N}\sum _{s=1}^N\theta (\mathrm{Tr}\left(W^{\mathsf{T}}{A}^s\right)+v\cdot b_s).$$ (1)

The logistic regression problem with group sparsity constraint is then defined as

$$(v^{\ast },W^{\ast })≔\underset{v\in \mathbb{R},W\in {\mathbb{R}}^{M\times T}}{\arg \min }{l}_{\mathrm{avg}}(v,W)\mathrm{s}.\mathrm{t}.{\Vert \tilde{W}\Vert }_0\le r,$$ (2)

where $\tilde{W}≔{({\Vert W^1\Vert }_2,\dots ,{\Vert W^M\Vert }_2)}^{\mathsf{T}}$ groups the weight vectors over time by computing the l₂-norm of the rows. Thus, ${\Vert \tilde{W}\Vert }_0$ equals the number of nonzero components of $\tilde{W}$, i.e., the non-zero rows of W. The sparsity constraint search space is then formally defined as

$$\mathcal{X}≔\{W\in {\mathbb{R}}^{M\times T}:{\Vert \tilde{W}\Vert }_0\le r\},$$

so that Eq. (2) shortens to

$$(v^{\ast },W^{\ast })≔\underset{v\in \mathbb{R},W\in \mathcal{X}}{\arg \min }{l}_{\mathrm{avg}}(v,W).$$ (3)

Note, that in the case of T = 1 or replacing ${\Vert \tilde{W}\Vert }_0$ with ${\Vert W\Vert }_0$ then Eq. (3) changes to the more common sparse logistic regression problem, which, in contrast, chooses individual features of W ignoring any temporal dependency. While the accuracy of this model might be similar to the proposed group-sparsity model, the selected features have limited meaning for diseases such as the residual effects of TOF. TOF impacts the morphometry and thus leads to changes in local shape patterns that are consistent across the cardiac cycle.

2.2. Approximating the Solution to the Group Sparsity Constraint, Minimization Problem

PD of (Lu and Zhang, 2013) estimates the sparse solution (T = 1) to logistic regression problems by decoupling the minimization of the logistic regression l_avg(·,·) from finding a solution within sparsity constraint space χ. It does so by defining a penalty function consisting of two components: (1) the logistic regression l_avg(·,·) dependent on v and an auxiliary variable $Y\in {\mathbb{R}}^{M\times T}$, and (2) a similarity measure S(Y,W) between the non-sparse solution Y and the approximated sparse solution W. In other words, the penalty function is defined as

$$q_{\varrho }(v,Y,W)≔l_{\mathrm{avg}}(v,Y)+\varrho S(W,Y),$$

where the penalty parameter ϱ < 0 weighs the importance of S (·,·). At each iteration, PD increase ϱ and then determines the $(\widehat{Y},\widehat{W})$ minimizing q_ϱ(·,·,·). Thus, as ϱ increases, the difference reduces between $\widehat{Y}$, the solution of the regularized logistic problem, and its sparse approximation $\widehat{W}$. Once the algorithm converges, $\widehat{W}$ is the approximated solution of the original sparse problem. In the remainder of this subsection, we generalized PD to approximate the group sparsity constraint solution (T ≥ 1) of the logistic regression problem defined by Eq. (3).

To adapt PD to our model, we first assume that our algorithm is initialized qith ϱ_i and (v_i, W_i), where $W_i\in \mathcal{X}$. Each iteration ‘p’ of our algorithm is then composed of three steps: define penalty function, minimize penalty function, and update and check convergences of results.

Step 1 - Define penalty function

Finding (v*, W*) of Eq. (3) is equivalent to solving

$$(v^{\ast },Y^{\ast },W^{\ast })≔\underset{v\in \mathbb{R},Y\in {\mathbb{R}}^{M\times T},W\in \mathcal{X}}{\arg \min }{l}_{\mathrm{avg}}(v,Y)\mathrm{s}.\mathrm{t}.W-Y=0.$$ (4)

Introducing the matrix Frobenius norm ∥ · ∥_F, the above equation is equivalent to

$$(v^{\ast },Y^{\ast },W^{\ast })≔\underset{v\in \mathbb{R},Y\in {\mathbb{R}}^{M\times T},W\in \mathcal{X}}{\arg \min }{l}_{\mathrm{avg}}(v,Y)\mathrm{s}.\mathrm{t}.{\Vert W-Y\Vert }_F^2=0$$ (5)

so that $S(W,Y)≔\frac{1}{2}{\Vert W-Y\Vert }_F^2$ is a natural metric to measure the similarity between W and Y for our PD algorithm. For the current penalty parameter ϱ_p, we define the PD characteristic penalty function as

$$q_{{\varrho }_p}(v,Y,W)≔l_{\mathrm{avg}}(v,Y)+\frac{{\varrho }_p}{2}{\Vert W-Y\Vert }_F^2.$$ (6)

Thus, the solution to the following non-convex and non-continuous minimization problem approximates the original sparse solution of Eq. (3):

$$({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)≔\underset{v\in \mathbb{R},Y\in {\mathbb{R}}^{M\times T},W\in \mathcal{X}}{\arg \min }{q}_{{\varrho }_p}(v,Y,W).$$ (7)

Step 2 - Determine local minimum point of Eq. (7) via BCD

To find a local minimum point of Eq. (7), BCD alternates between minimizing the penalty function (Eq. (6)) with respect to the non-sparse terms (v, Y) and updating the sparse term W. Specifically, let (v_b–1, Y_b–1, W_b–1) be the current estimate of BCD. The b^th iteration of BCD then determines (v_b, Y_b) by solving the smooth and convex problem

$$(v_b,Y_b)\leftarrow \underset{v\in \mathbb{R},Y\in {\mathbb{R}}^{M\times T}}{\arg \min }\left\{l_{\mathrm{avg}}(v,Y)+\frac{{\varrho }_p}{2}{\Vert W_{b-1}-Y\Vert }_F^2\right\},$$ (8)

which can be done via a gradient descent. To update W_b, minimizing the penality function with respect to W, i.e.,

$$W_b\leftarrow \underset{W\in \mathcal{X}}{\arg \min }{\Vert W-Y_b\Vert }_F^2,$$ (9)

can now be solved in closed form. We derive the closed form solution by assuming (without loss of generality) that the rows of Y_b are nonzero and listed in descending order according to their l₂-norm, i.e., let $Y_b^j$ be the j^th row of Y_b for j = 1,..., M then ${\Vert Y_b^1\Vert }_2\ge {\Vert Y_b^2\Vert }_2\ge \dots \ge {\Vert Y_b^M\Vert }_2>0$. Lemma A.1 (see Appendix for this and any proceeding lemmas and theorems) then shows that the closed form solution W_b is defined by the first ‘r’ rows of Y_b,

$$W_b^j=\{\begin{array}{cc}{Y}_b^j,\hfill & \text{if}j\le r;\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}\text{for}i=1,\dots ,M.$$ (10)

In theory, multiple global solutions W_b exist in case ${\Vert Y_b^r\Vert }_2={\Vert Y_b^{r+1}\Vert }_2$. In practice, we have not come across that scenario.

Denoting with ∥·∥_max the max norm of a matrix, i.e.,, ${\Vert A\Vert }_{\max }≔{\max }_{i,j}\left\{\Vert a_{ij}\Vert \right\}$, BCD stops updating the results when the relative change of each variable is smaller than a benchmark value ϵ_BCD, i.e.,

$$\max \left\{\frac{\mid v_b-v_b\mid }{\max (\mid v_b\mid ,1)},\frac{{\Vert Y_b-Y_b\Vert }_{\max }}{\max ({\Vert Y_b\Vert }_{\max },1)},\frac{{W_b-W_b\Vert }_{\max }}{\max ({\Vert W_b\Vert }_{\max },1)}\right\}\le {ϵ}_{BCD}.$$ (11)

We choose this criteria over the absolute change of the sequence (v_b, Y_b, W_b), i.e.,

$$\max \{\mid v_{b-1}-v_b\mid ,{\Vert Y_{b-1}-Y_b\Vert }_{\max },{\Vert W_{b-1}-W_b\Vert }_{\max }\}\le {ϵ}_{BCD},$$

as it is more robust when variables have large values, i.e.,

$$\max \{\mid v_b\mid ,{\Vert Y_b\Vert }_F,{\Vert W_b\Vert }_F\}$$

is large.

Step 3 - Update results, penalty parameter, and check the stopping criterion

Let BCD stop at the b′^th iteration, ${\widehat{Y}}_p$ is then set to Y_b′ and ${\widehat{v}}_p$ to v_b′. To update ${\widehat{W}}_p$, we first define an upper bound Γ = l_avg(v_i, W_i) with respect to the initialization, and then check whether

$$\underset{v\in \mathbb{R},Y\in {\mathbb{R}}^{M\times T}}{\min }{q}_{{\varrho }_{p+1}}(v,Y,W_{b^{\prime }})\le \Gamma .$$ (12)

In case the condition Eq. (12) holds, ${\widehat{W}}_p$ is set to W_b′ and otherwise to W_i. According to Lemma A.5, this check guarantees that in case PD converges ${\widehat{W}}_p$ also converges to ${\widehat{Y}}_p$, i.e., $\underset{p\to \infty }{\lim }{\widehat{W}}_p-{\widehat{Y}}_p=0$. Finally, PD stops updating the results when ${\widehat{Y}}_p$ and ${\widehat{W}}_p$ are similar enough according to the similarity parameter ϵ_PD, i.e.,

$${\Vert {\widehat{W}}_p-{\widehat{Y}}_p\Vert }_{\max }\le {ϵ}_{PD}.$$ (13)

Note, Algorithm 1 is the pseudocode of our PD approach (Step 1-3), whose corresponding software implementation used for this publication can be dowloaded via https://dx.doi.org/10.6084/m9.figshare.3398332 or the current version via https://github.com/sibis-platform/PDLG.

Algorithm 1.

Penalty Decomposition (PD) Applied to Eq. (3)

1:	Initialization: Choose a sparsity parameter $r\in \mathbb{N}$, scalar weight $v_i\in \mathbb{R}$ and a feasible sparsity constrained weights $W_i\in \mathcal{X}$ where
	$\mathcal{X}≔\{W\in {\mathbb{R}}^{M\times T}:{\Vert \tilde{W}\Vert }_0\le r\}$.
	Furthermore, set the following parameters
	• W0 ← Wi (initialize weight)
	• ϱ0 > 0 (initial penalty)
	• σ > 1 (penalty updating factor)
	• ϵBCD > 0 (upper bound for convergence of BCD)
	• ϵPD > 0 (upper bound for convergence of PD)
	• p ← 0 (PD index)
	• Γ = lavg(vi, Wi) (upper bound for qϱp(v, Y, W))
2:	repeat (PD Loop)
3:	% Step 1: Define the penalty function
4:	$q_{{\varrho }_p}(v,Y,W)≔l_{\mathrm{avg}}(v,Y)+\frac{{\varrho }_p}{2}{\Vert W-Y\Vert }_F^2$
5:
6:	% Step 2: Determine the local minimum point of qϱp via BCD
7:	b ← 0 (BCD index)
8:	repeat (BCD Loop)
9:	b ← b + 1
10:	% Solve the following via Gradient Descent
11:	$(v_b,Y_b)\leftarrow \underset{v\in \mathbb{R},Y\in {\mathbb{R}}^{M\times T}}{\arg \min }\{l_{\mathrm{avg}}(v,Y)+\frac{{\varrho }_p}{2}{\Vert W_{b-1}-Y\Vert }_F^2\}$
12:	$W_b^j=\{\begin{array}{cc}{Y}_b^j,\hfill & \text{if}j\le r;\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}\phantom{\}}\text{for}l=1,\dots ,M$.
13:	until $\max \{\frac{\mid v_b-v_{b-1}\mid }{\max (\mid v_b\mid ,1)},\frac{{\Vert Y_b-Y_{b-1}\Vert }_{\max }}{\max \left(\Vert Y_b\Vert {}_{\max },1\right)},\frac{{\Vert W_b-W_{b-1}\Vert }_{\max }}{\max ({\Vert W_b\Vert }_{\max },1)}\}\le {ϵ}_{BCD}$
14:
15:	% Step 3: Update results, penalty parameter, and check the stopping criterion
16:	ϱp+1 ← σ · ϱp (increase penalty parameter)
17:	if minv,Y qϱp+1(v, Y, Wb) ≤ Γ then
18:	W0 ← Wb
19:	else
20:	W0 ← Wi
21:	p ← p + 1, ${\widehat{v}}_p\leftarrow v_b$, ${\widehat{Y}}_p\leftarrow Y_b$ and ${\widehat{W}}_p\leftarrow W_0$
22:	until ${\Vert {\widehat{W}}_p-{\widehat{Y}}_p\Vert }_{\max }\le {ϵ}_{PD}$

2.3. Convergence Properties of Penalty Decomposition

For the interested reader, we now briefly derive the properties guaranteeing that the converged solution of our PD approach is a local minimum point of Eq. (3). Focusing just on one iteration of PD, we first show that if the BCD approach of Step 2 converges then the corresponding accumulation point is also a local minimum point of Eq. (7). Across iterations of PD, these local minima define another sequence, which is defined by Step 3. We then show if the sequence converges to an accumulation point with exact r nonzero rows then this point is a local minimum point of the original sparse problem defined by Eq. (3). Note, deriving these properties of our algorithm is non-trivial as the PD penalty function Eq. (6) is non-convex and the sparse space $\mathcal{X}$ is non-continuous. The Appendix contains the complete proofs of the properties of our method described below.

Convergence property of Step 2

In the p^th iteration of PD, let $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ be an accumulation point of the converged sequence (v₁, Y₁, W₁), (v₂, Y₂, W₂),... produced by BCD. To show that $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is a local minimum point of Eq. (7), the triple needs to be the minimum point of $q_{{\varrho }_p}$(·,·,·) with respect to a neighborhood of this triple. We confine the neighborhood to those triples (v, Y, W), where the sign of non-zero components of ${\widehat{W}}_p$ equals those of W. We formally express this constraint by introducing the set of indices corresponding to non-zero components of ${\widehat{W}}_p$

$${\Omega }_{{\widehat{W}}_p}≔\{i\in \{1,\dots ,M\}:{\Vert {\left({\widehat{W}}_p\right)}^i\Vert }_2\ne 0\},$$

so that the neighborhood is defined as

$$\mathcal{N}≔\left\{(v,Y,{\widehat{W}}_p+H)\in (\mathbb{R},{\mathbb{R}}^{M\times T},\mathcal{X}):{\Vert {\left(H\right)}^i\Vert }_2<{\Vert {\left({\widehat{W}}_p\right)}^i\Vert }_2,\forall i\in {\Omega }_{\widehat{W}}\right\}.$$ (14)

An interesting characteristic of that neighborhood is that for any triple $(v,Y,{\widehat{W}}_p+H)\in \mathcal{N}$ the following relation holds among H, ${\widehat{Y}}_p$ and ${\widehat{W}}_p$ (see also Lemma A.3)

$$H{({\widehat{Y}}_p-{\widehat{W}}_p)}^T=0,$$ (15)

where 0 is a matrix whose entries are all zero. We make use of this property in Theorem A.4, where we derive the following lower bound for $q_{{\varrho }_p}$(·,·,·) with respect to $(v,Y,{\widehat{W}}_p+H)\in \mathcal{N}$

$$q_{\varrho }(v,Y,{\widehat{W}}_p+H)\ge q_{\varrho }({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)+\mathrm{Tr}\left(H{({\widehat{Y}}_p-{\widehat{W}}_p)}^T\right)$$

so that applying Eq. (15) results in

$$=q_{\varrho }({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p).$$

In other words, $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is a local minimum point of Eq. (7).

Convergence property of Step 3

Let (v*, Y*, W*) be the accumulation point of the converging sequence $({\widehat{v}}_1,{\widehat{Y}}_1,{\widehat{W}}_1)$, $({\widehat{v}}_2,{\widehat{Y}}_2,{\widehat{W}}_2)$,... produced by Step 3. Furthermore, assume that W* has exact ‘r’ nonzero rows, i.e., ${\Vert \widetilde{W^{\ast }}\Vert }_0=r$, which has always been the case in our experiments. Lemma A.7 then states that (v*, W*) is a local minimum point of Eq. (3) if there exists a matrix ${\Lambda }_{\mathcal{K}}\in {\mathbb{R}}^{M\times T}$ so that the following holds:

$$\begin{array}{cc}\hfill {\frac{\partial l_{\mathrm{avg}}(v,W)}{\partial W}\mid }_{v=v^{\ast },W=W^{\ast }}+{\Lambda }_{\mathcal{K}}& =0,\hfill \\ \hfill {\frac{\partial l_{\mathrm{avg}}(v,W)}{\partial v}\mid }_{v=v^{\ast },W=W^{\ast }}& =0,\hfill \\ \hfill {\left({\Lambda }_{\mathcal{K}}\right)}^{\mathcal{K}}& =0,\hfill \end{array}$$ (16)

where $\mathcal{K}$ is a set of ‘r’ indices for which (W*)ⁱ ≠ 0 and f(x) |x=x′ is the value of f(·) at x′. To determine, ${\Lambda }_{\mathcal{K}}$, we note that Y* = W* (see also Lemma A.5). Theorem A.8 then states that the sequence

$$Z_p≔{\varrho }_p({\widehat{Y}}_p-{\widehat{W}}_p)$$ (17)

is a bounded and converges to Z*. The theorem furthermore notes that (v*, W*) fulfills the condition of Eq. (16) when ${\Lambda }_{\mathcal{K}}=Z^{\ast }$. In summary, if PD converges then it converges to a local minimum point of the original sparse problem is defined by Eq. (3).

3. Testing Algorithms on Correctly Classifying TOF

To better understand the strength and weakness of our proposed Algorithm 1, we compare the accuracy of our approach to alternative solver of sparsity constraint logistic regression problems on a data set consisting of regional volume scores extracted from cine MRIs of 44 TOF cases and 38 healthy controls. The dataset provides an ideal test bed for such a comparison as it contains ground-truth diagnosis, i.e., each subject received reconstructive surgery for TOF during infancy or not. Furthermore, refining the quantitative analysis of these scans could lead to improved monitoring of TOF patients, i.e., timing for follow-up surgeries. Finally, the residual effects of TOF reconstructive surgery mostly impact the morphometry, i.e., the shape of the right ventricle (Bailliard and Anderson, 2009; Atrey et al., 2010), so that the regional volume scores extracted from each time point of the image series are sample descriptions of the same phenomena, a core assumption of the group sparsity model. We not only show that our PD approach (Algorithm 1) reflects this manifestation of the disease by mostly weighing its decision based on regions within the right ventricle but also achieves significantly higher accuracy than alternative solutions to this model, such as solving logistic regression with relaxed sparsity constraints (Ryali et al., 2010) ¹.

3.1. Experimental Setup

Extracting Regional Volume Scores

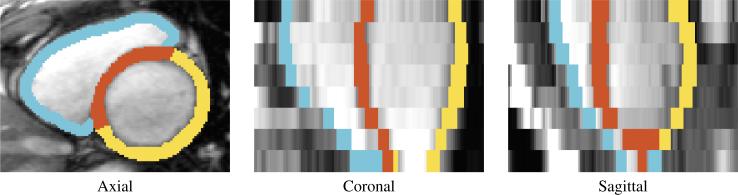
Each sample of the data set consists of a segmentation of each time point of a motion-corrected cine MRI, i.e., we corrected for slice misalignment due to breathing motion by detecting the center of the left ventricle via Hough transform (Duda and Hart, 1972) and then stacking the slices so that the center of the left ventricle aligns across the slices. Covering the basal, mid-cavity, and apical part with 8 slices, the segmentation outlines the right ventricular blood pool, the wall of the Left Ventricle (LV), and the Ventricular Septum (VS), which was done at end-diastole according to the semi-automatic procedure described in (Ye et al., 2014) and then propagated from end-diastole to the other time points via non-rigid registration (Avants et al., 2008). For the right ventricular blood pool, we reduce the maps to a 7mm band along its boundary, which is similar to the width of the wall of the other two structures, and name it RV (see Fig. (1)). For each time point and image slice, we then parcellate the three structures into smaller sections based on a predefined subtended angles from the center of mass (of the RV or LV&VS). More specifically, RV and LV are divided into the same number of sections, while the VS is divided into $\frac{1}{3}$ of that number reflecting its relative size to RV and LV. For example in Fig. (2), the VS is divided into six sections with respect to each slice and time point of the scan while the RV and LV are divided into 18 sections each. Finally, the input to our proposed solver is the volume of each section.

Figure 1.

Example segmentation of the RV (blue), VS (red), and LV (yellow)

Figure 2.

An example slice of the partitioning of the RV and LV into 18 sections and the VS into six sections at time point 1, 6, 13, 19, and 25.

Measure Classification Accuracy

We measure the accuracy of our approach with respect to correctly classifying samples just based on the sectional volumes scores of the RV alone, the LV alone, and the VS alone as well as using the scores of the whole heart (RV, LV&VS). We train our algorithm with different numbers of training samples, which are defined by the percentage {5%, 10%, . . . , 75%} of cases captured by the entire data set, i.e., 82 cases. For each training sample size, we run ten experiments to estimate a distribution of accuracy scores.

For each experiment, we randomly select the training samples from both groups and label the remaining cases as test subjects. For a fair comparison with other sparse logistic regression solvers, we initialize our algorithm according to (Lu and Zhang, 2013), i.e., ϱ = 0.1, σ = √10, ϵ_BCD = 10⁻⁴, ϵ_PD = 10⁻³, W_i = 0 and v_i = 1. For each training set, we then determine the optimal setting of our algorithm with respect to the broad parameter space of the remaining two parameters:

• the number of sections s ∈ {2, 3, . . . , 9} that each slice of the VS is divided into (so that each subject is represented by 3360 to 15120 volume scores)

• and the maximum percentage of regional values chosen by our approach ω ∈ {5%, 10%,... , 50%}. In other words, the sparsity constraint is defined as r := ceil(M · s · ω) where M · s is the total number of section that the heart cycle is divided into.

We determine the optimal setting by first experimenting with parameter exploration. Specifically, for each of the 80 unique parameter settings we define a regressor by computing the optimal weights W* of Algorithm 1 with respect to training data. In all experiments, PD then converged within 5 iterations and BCD converged within 500 iterations for each penalty parameter ϱ_p. After convergence, we compute the accuracy of the regressor with respect to the training set via the normalized accuracy (nAcc), i.e., we separately compute the accuracy for each cohort and then average their values to account for the imbalance in cohort size. The entire process of training and measuring the accuracy of the 80 regressors took less than 10 seconds on a single PC (Intel(R) Xeon(R) CPU E5-2603 v2 @1.80GHz and 32G memory). It also resulted in multiple settings, i.e., regressors, with 100% classification accuracy. In case of parameter exploration failing, a common solution (and the one we chose) is to train an ensemble of classifiers (Rokach, 2010). The final label of the ensemble is then defined by the weighted average across the set of regressors, where the weight of the regressor in the decision of the ensemble of classifiers is simply its training accuracy. Once trained, we then measure the accuracy of the resulting ensemble on correctly assigning test samples to the patient groups using the nAcc score. In the remainder of this section, we refer to this ensemble of classifier as L0-Grp.

Alternative Models

We compare our solver to alternative algorithm using the same mechanism as above, i.e., we create ensemble of classifiers with respect to the same parameter space and training data sets, and measure their accuracy on the same test data sets. Specifically, we use the algorithm by (Liu et al., 2009) to solve the logistic regression with the sparsity constraints relaxed via the l₂-norm, i.e.,

$$\underset{v\in \mathbb{R},W\in {\mathbb{R}}^{M\times T}}{\min }{l}_{\mathrm{avg}}(v,W)+\lambda \sum _{i=1}^M{\Vert W^i\Vert }_2$$ (18)

with λ being the sparse regularizing parameter. We refer to the corresponding ensemble as Rlx-Grp. Note, relaxing the sparsity constraint via the l₁-norm results in a optimization problem ignoring temporal consistency, which violates our initial assumption of the model.

In addition, we investigate the accuracy of PD and (Liu et al., 2009) when only applied to a single time point (T = 1). When T = 1, then Eq. (3) simplifies to

$$\underset{v\in \mathbb{R},W\in {\mathbb{R}}^M}{\min }{l}_{\mathrm{avg}}(v,W)\mathrm{s}.\mathrm{t}.{\Vert W\Vert }_0\le r,$$ (19)

i.e., the sparsity constrained problem solved by PD in (Lu and Zhang, 2013). We refer to the corresponding ensemble as L0-nGrp. Furthermore, for T = 1, Eq. (18) is equivalent to

$$\underset{v\in \mathbb{R},W\in {\mathbb{R}}^{M\times T}}{\min }{l}_{\mathrm{avg}}(v,W)+\lambda {\Vert W\Vert }_1,$$ (20)

whose corresponding ensemble of classifier we refer to Rlx-nGrp. Finally, we note that the sparsity parameter λ of Rlx-Grp and Rlx-nGrp is not directly related to the number of selected sections. For a fair comparison to the sparsity constrained methods, we therefore automatically tune the sparsity parameter λ of Eq. (18) and Eq. (20) so that the number of chosen sections r̄ were similar to those defined in Eq. (3), i.e., |r – r̄| ≤ 1.

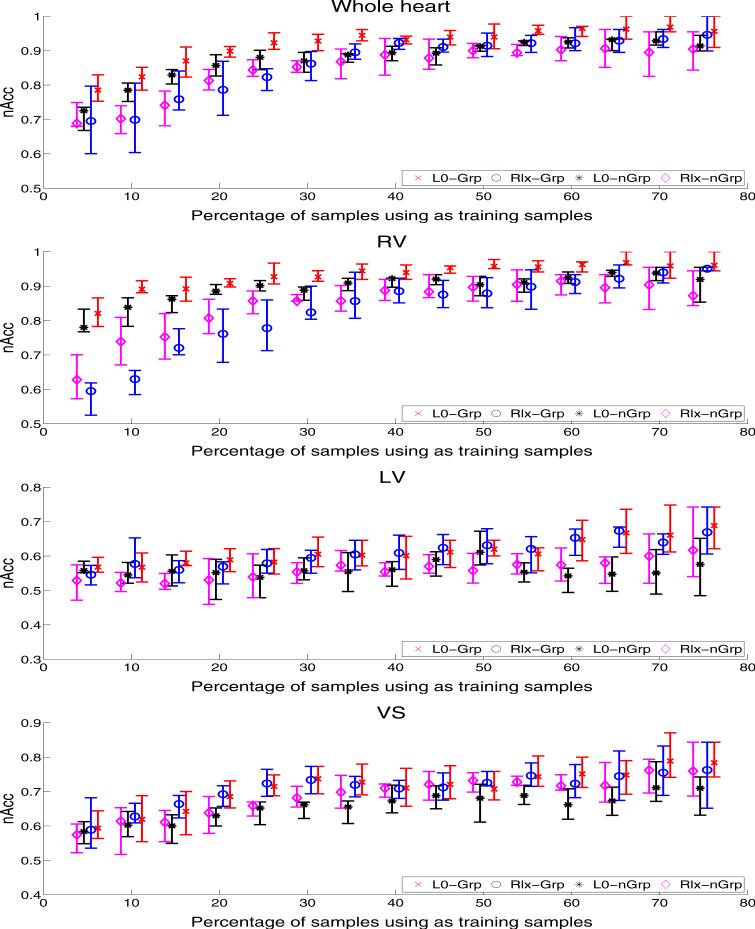
3.2. Experimental results

The box plots of Fig. (3) summarize the distribution of the accuracy scores associated with each implementation and structure by the average, the first quin-tile, and the fourth quintile of the nAcc scores across the 10 test data sets run for each training sample size. For all four implementations, the average nAcc scores generally increase with the number of training samples. For the RV and the whole heart (RV,LV&VS), the proposed L0-Grp implementation (red boxplots) generally achieves a higher average accuracy, first quintile, and fourth quintile scores than then other three approaches. The difference is especially large for smaller number of training samples, i.e., 5% to 35%. For large training samples, i.e., 70% and 75%, L0-Grp is the only method with a fourth quintile score of 100%. To follow up these observations, we computed the p-value of the paired-sample t-test (McDonald, 2009) between L0-Grp and other three implementations. Table 1 summarizes those computations. For the whole heart, L0-Grp is significantly better (p < 0.05) than Rlx-nGrp and L0-nGrp with respect to 13 out of the 15 training sample sizes, and 10 out of the 15 training sets with respect to the Rlx-Grp. For the RV, the counts for statically significant differences increase with respect to the implementations with relaxed constraints. However, this is not true for L0-nGrp implementation, in which case L0-Grp is significantly better in 8 experiments. In this experiment, we conclude that the impact of reducing the number of time points on the accuracy scores is less than relaxing the sparsity constraint. An explanation for this observation might lie in the fact that solution generated by solvers relaxing the sparsity constraint, i.e., Rlx-nGrp and Rlx-Grp, is only accurate with respect to the original problem Eq. (3) under certain conditions (Candès et al., 2006), which are not satisfied here and in medical image analysis in general.

Figure 3.

The boxplots of the average, first quintile, and fourth quintile nAcc scores for all four ensembles with respect to the percentage of the whole data set used for training and the encoding of the LV, RV, VS and the whole heart (RV,LV&VS). For the RV and whole heart, the proposed L0-Grp implementation (red box plots) generally achieves a higher average, first quintile, and fourth quintile scores than then other three approaches. With respect to the LV and VS, all four methods perform similarly with the average nAcc scores starting at around 55% and generally increasing with the number of training samples.

Table 1.

Significant: p ≤ 0.05; Trend: 0.05 < p ≤ 0.1; Indifferent: p > 0.1. Frequency of p-value of the paired-sample t-test between L0-Grp and the other three methods. In most tests, the results obtained by L0-Grp are significantly more accurate than the other three methods with respect to the paired-sample t-test (McDonald, 2009).

	RV			RV, LV & VS
	Significant	Trend	Indifferent	Significant	Trend	Indifferent
Rlx-Grp	13	0	2	10	2	3
L0-nGrp	8	4	3	13	2	0
Rlx-nGrp	15	0	0	13	2	0

With respect to the LV and VS, Fig. (3) reports insignificant differences between the accuracy of all four methods. The average nAcc scores start at around 55% and generally increase with the number of training samples. While the average scores of Rlx-Grp almost match those of L0-Grp, L0-Grp achieves the highest average sore with 69% for the LV and 74% for the VS indicating that the VS is slightly more impacted by TOF than the LV. This observation is also in alignment with the literature (Bailliard and Anderson, 2009; Atrey et al., 2010) reporting the residual effects of TOF impacting the RV, which the VS is attached to. Increasing the number of training samples also impacts the spread between the first and fourth quintile. This issue is partly due to the fact that the larger the training data set, the smaller the test set. From a statistical perspective, e.g. recording the outcome of flipping a biased coin several times, one expects this outcome as the first and fourth quintile scores deviate further from the average score compared to experiments with larger test sets. Interestingly enough, only the average scores of the L0-nGrp are not improving with large training sets as it peaks at a training size of 50% for the LV and gets unstable starting at 50% for the VS. In other words, adding more samples to the training is not more informative than adding more information of each individual sample by, for example, increasing the number of time points or including measurements from the RV, the structure most impacted by TOF.

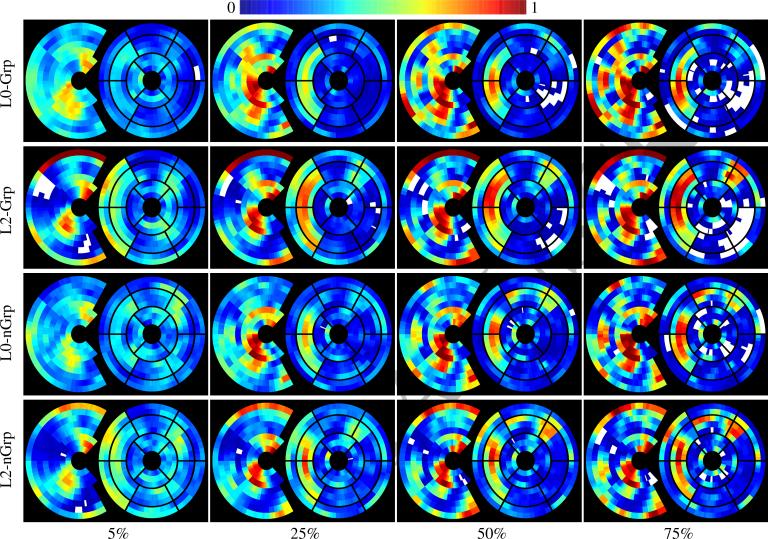
To gain a deeper understanding of the experimental results, Fig. (4) plots the importance of heart sections in distinguishing TOF from healthy controls based on the regional volume scores and with respect to the type of solver and percentage associated with the training sample size. The incomplete circle on the left represents the importance of sections of the RV and on the right the importance of sections of the LV and VS. Each ring of those (incomplete) circles represents a slice of the cine MRI with the outer circle representing the base of the heart. As it is common in the cardiac literature, we overlay the bullseye plot over the LV & VS maps. For each type and percentage, we infer the importance of a section from their average importance across the corresponding ensembles of classifiers, i.e., the number of times a section was selected by a sparse solver multiplied by the solvers’ training accuracy. Sections in white were never selected, those in blue had very low and those in red very high impact on the final classification. The ensembles were indifferent to sections labeled turquoise, green, yellow, and orange. We first note that across solvers the number of indifferent section reduces and the number of ignored section increases with larger number of training samples. This indicates a higher confidence of the ensembles in the importance of sections. Furthermore, the number of selected RV sections (left) increases, which is inline with the increase in testing accuracy. Of all methods, L0-Grp relies least on LV sections (right). This could explain its significantly higher accuracy scores compared to those other method in the majority of whole heart experiments. As noted in Section 1, one has to be careful when relating the weights of classifiers to biomedical landmarks. We are in this experiment as the importance maps of Fig. (4) are based on the number of times regions were selected by solvers (not their soft weights) and those of the L0-Grp are in accordance with the medical literature stating that residual effects of TOF mostly impact the RV.

Figure 4.

Importance of heart sections in distinguishing TOF from healthy controls with respect to the type of solver and percentage associated with the training sample size. The incomplete circle on the left represents the importance of sections of the RV and on the right the importance of sections of the LV and VS. Each ring of those (incomplete) circles represents a slice of the cine MRI. As it is common in the cardiac literature, we overlay the bullseye plot over the LV & VS maps. For each type and percentage, the importance of a section is inferred from its average importance across the corresponding ensembles of classifiers, which is based on the number of times a section was selected by a sparse solver. The number of white regions (never selected), blue (weight close to 0) and red (weight close to 1) is generally increasing with the number of training samples indicating that the confidence of the ensemble increases in the selection of the sections. Furthermore, all methods correctly emphasize more sections of the RV than the LV&VS. L0-Grp ignores the LV sections the most of all solvers. This could explain its significantly higher accuracy in most experiments of the whole heart compared to those other three methods.

4. Conclusion

We generalized the PD approach to directly solve group cardinality constraint logistic regression, i.e., simultaneously performing disease classification and temporal-consistent pattern identification. To do so, we assumed that an intra-subject series of images represents repeated samples of the same disease patterns. We modeled this assumption by combining series of measurements created by a feature across time into a single group. Unlike existing approaches, our algorithm then derived a solution within that model by decoupling the minimization of the logistic regression function from enforcing the group sparsity constraint. The minimum to the smooth and convex logistic regression problem was determined via gradient descent while we derived a closed form solution for finding a sparse approximation of that minimum. We applied our method to cine MRI of 38 healthy controls and 44 adult patients that received reconstructive surgery of Tetralogy of Fallot (TOF) during infancy. Our method correctly identified the RV to be most impacted by TOF and generally obtained statistically significant higher classification accuracy than alternative solutions to this model, i.e., ones relaxing group cardinality constraints or ones only applied to a single time point.

While the experiments were confined to regional volumes scores extracted from cine MRIs, the method could be applied to any features computed from intra-subject sequence of images. One only has to ensure that the assumption holds that series of images represent repeated samples of the same disease patterns. Furthermore, one has to be careful when relating the selected features to disease patterns. We did so on our experiments as the selcted features agreed with the medical literature.

Highlights.

• Model concurrent disease classification and temporal-consistent pattern selection

• Minimize model by directly solving logistic regression confined by group cardinality

• Correctly identify ROIs differentiating the cine MRs of 44 TOF from 38 controls

• Generally significantly more accurate than approaches relaxing group sparsity

Appendix A

Lemma A. 1

Given a matrix $A\in {\mathbb{R}}^{M\times T}$, let A^j be the j^th row of A for j = 1,..., M. Without loss of the generality, we assume that

$${\Vert A^1\Vert }_2\ge {\Vert A^2\Vert }_2\ge \dots \ge {\Vert A^M\Vert }_2>0.$$

Then the solution for the minimization problem

$$W^{\ast }≔\underset{W\in \mathcal{X}}{\arg \min }{\Vert W-A\Vert }_F^2,$$ (A.1)

within $\mathcal{X}≔\{W\in {\mathbb{R}}^{m\times T}:\tilde{W}≔{({\Vert W^1\Vert }_2,\dots ,{\Vert W^m\Vert }_2)}^{\mathsf{T}}and{\Vert \tilde{W}\Vert }_0\le r\}$ are the first r rows of A, i.e.,

$${\left(W^{\ast }\right)}^j=\{\begin{array}{cc}{A}^j,\hfill & ifj\le r;\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\phantom{\}}forj=1,\dots ,M.$$ (A.2)

Proof

Suppose there is a solution $\overline{W}$ to Eq. (A.1) which is different from W* defined in Eq. (A.2). We now show that the ${\Vert \overline{W}-A\Vert }_F^2\ge {\Vert W^{\ast }-A\Vert }_F^2$.

We know that for all $\Vert {\overline{W}}^j\Vert \ne 0$, the following is true ${\overline{W}}^j=A^j$ as otherwise $\overline{W}$ can not be an optimal solution for Eq. (A.1). To see that, simply replace ${\overline{W}}^j$ with A^j for any j such that $\Vert {\overline{W}}^j\Vert \ne 0$, which results in returns a smaller value for ${\Vert W-A\Vert }_F^2$. Since $\overline{W}$ is different from W′, there must exists i₁ > r such that ${\overline{W}}^{j_1}=A^{j_1}$. Given that $\overline{W}\in \mathcal{X}$, then there must exists a row ${\overline{W}}^{j_2}$ such that ${\Vert {\overline{W}}^{j_2}\Vert }_2=0$ for j₂ ≤ r. By using the definition of W*, we also have ${\Vert {\left(W^{\ast }\right)}^{j_2}-A^{j_2}\Vert }_2=0$ and (W*)^j1 = 0. In addition, ${\Vert A^{j_2}\Vert }_2\ge {\Vert A^{j_1}\Vert }_2$ according to the assumption that ${\Vert A^1\Vert }_2\ge {\Vert A^2\Vert }_2\ge \dots \ge {\Vert A^M\Vert }_2$. Then we have

$$\begin{array}{cc}\hfill {\Vert A^{j_1}-{\overline{W}}^{j_1}\Vert }_2^2+{\Vert A^{j_2}-{\overline{W}}^{j_2}\Vert }_2^2& ={\Vert A^{j_2}\Vert }_2^2\hfill \\ \hfill & \ge {\Vert A^{j_1}\Vert }_2^2\hfill \\ \hfill & ={\Vert A^{j_1}-{\left(W^{\ast }\right)}^{j_1}\Vert }_2^2+{\Vert A^{j_2}-{\left(W^{\ast }\right)}^{j_2}\Vert }_2^2,\hfill \end{array}$$

which implies that if we define

$${\left(W^{\prime }\right)}^j=\{\begin{array}{cc}{\overline{W}}^j,\hfill & \text{if}j\ne j_1,j_2;\hfill \\ {\left(W^{\ast }\right)}^j,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}\text{for}j=1,\dots ,M,$$

then ${\Vert \overline{W}-A\Vert }_F^2\ge {\Vert W^{\prime }-A\Vert }_F^2$. Continuing this procedure of replacing values results at some point W′ = W* and thus ${\Vert \overline{W}-A\Vert }_F^2\ge {\Vert W^{\ast }-A\Vert }_F^2$. Thus W* is an optimal solution of problem Eq. (A.1).

Lemma A. 2

Suppose that $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is an accumulation point of the sequence {(v_b, Y_b, W_b)} generated by BCD described in Section 2. Then it is also the block coordinate minimum point of Eq. (7), i.e.,

$$\begin{array}{cc}\hfill ({\widehat{v}}_p,{\widehat{Y}}_p)& ≔\underset{v\in \mathbb{R},Y\in {\mathbb{R}}^{M\times T}}{\arg \min }{q}_{{\varrho }_p}(v,Y,{\widehat{W}}_p),\hfill \\ \hfill {\widehat{W}}_p& ≔\underset{W\in \mathcal{X}}{\arg \min }{q}_{{\varrho }_p}({\widehat{v}}_p,{\widehat{Y}}_p,W).\hfill \end{array}$$ (A.3)

Proof

First, note that

$$\begin{array}{cc}\hfill q_{{\varrho }_p}(v_{b+1},Y_{b+1},W_b)& \le q_{{\varrho }_p}(v,Y,W_b)\forall v\in \mathbb{R},Y\in {\mathbb{R}}^{M\times T},\hfill \\ \hfill q_{{\varrho }_p}(v_{b+1},Y_{b+1},W_{b+1})& \le q_{{\varrho }_p}(v_{b+1},Y_{b+1},W)\forall W\in \mathcal{X}.\hfill \end{array}$$ (A.4)

It then follows that

$$q_{{\varrho }_p}(v_{b+1},Y_{b+1},W_{b+1})\le q_{{\varrho }_p}(v_{b+1},Y_{b+1},W_b)\le q_{{\varrho }_p}(v_b,Y_b,W_b)\forall b\ge 1.$$ (A.5)

Hence, the sequence {q_ϱp(v_b, Y_b, W_b)} is non-increasing. Since $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is an accumulation point of {(v_b, Y_b, W_b)}, there exists a subsequence L such that

$$\underset{b\in L\to \infty }{\lim }\left\{(v_b,Y_b,W_b)\right\}=({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p).$$

We then observe that {q_ϱp(v_b, Y_b, W_b)}_b∈L is bounded, which together with the monotonicity of {q_ϱp(v_b, Y_b, W_b)} implies that {q_ϱp(v_b, Y_b, W_b)} is bounded below and hence lim_b→∞ q_ϱp(v_b, Y_b, W_b) exists. This observation, Eq. (A.5), and the continuity of q_ϱp(·,·,·) yield

$$\begin{array}{cc}\hfill {\lim }_{b\to \infty }{q}_{{\varrho }_p}(v_{b+1},Y_{b+1},W_b)& ={\lim }_{b\to \infty }{q}_{{\varrho }_p}(v_b,Y_b,W_b)\hfill \\ \hfill & ={\lim }_{b\in L\to \infty }{q}_{{\varrho }_p}(v_b,Y_b,W_b)\hfill \\ \hfill & =q_{{\varrho }_p}({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p).\hfill \end{array}$$

Given that q_ϱp(·,·,·) is continuous, then taking limits on both sides of Eq. (A.4) with respect to b ∈ L → ∞ results in

$$\begin{array}{cc}\hfill q_{{\varrho }_p}({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)& \le q_{{\varrho }_p}(v,Y,{\widehat{W}}_p)\forall v\in \mathbb{R},Y\in {\mathbb{R}}^{M\times T},\hfill \\ \hfill q_{{\varrho }_p}({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)& \le q_{{\varrho }_p}({\widehat{v}}_p,{\widehat{Y}}_p,W)\forall W\in \mathcal{X}.\hfill \end{array}$$ (A.6)

Note that $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is the accumulation point of {(v_b, Y_b, W_b)}_b∈L→∞. Then according to the definition of $\mathcal{X}$, we have ${\Vert {\tilde{W}}_b\Vert }_0\le r$ which immediately implies ${\Vert {\tilde{\widehat{W}}}_p\Vert }_0\le r$. Thus, $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is a block coordinate minimum point of Eq. (7).

Lemma A. 3

Let $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ be a block coordinate minimum of Eq. (7) and $H\in {\mathbb{R}}^{M\times T}$ define a small feasible step of ${\widehat{W}}_p$, i.e., ${\widehat{W}}_p+H\in \mathcal{X}$. Then

$$H^i{({\widehat{Y}}_p^i-{\widehat{W}}_p^i)}^T=0,fori\in \{1,\dots ,M\}.$$ (A.7)

Proof

We note that if ${\Vert {\tilde{\widehat{Y}}}_p\Vert }_0\le r$ where ${\tilde{\widehat{Y}}}_p≔{({\Vert {\widehat{Y}}^1\Vert }_2,\dots ,{\Vert {\widehat{Y}}^m\Vert }_2)}^{\mathsf{T}}$, then according to Eq. (A.2), ${\widehat{W}}_p={\widehat{Y}}_p$. Thus, Eq. (A.7) is true. For ${\Vert {\tilde{\widehat{Y}}}_p\Vert }_0>r$, we observe from Eq. (A.2) that ${\left({\widehat{W}}_p\right)}^i={\left({\widehat{Y}}_p\right)}^i$ for all $i\in {\Omega }_{{\widehat{W}}_p}$ where ${\Omega }_{{\widehat{W}}_p}≔\{i\in \mathcal{I}:{\Vert {\left({\widehat{W}}_p\right)}^i\Vert }_2\ne 0\}$. Thus ${\left(H\right)}^i{({\widehat{Y}}_p^i-{\widehat{W}}_p^i)}^T=0$ for $i\in {\Omega }_{{\widehat{W}}_p}$. On the other hand, ${\Vert {\left(H\right)}^i\Vert }_2<{\Vert {\left({\widehat{W}}_p\right)}^i\Vert }_2$ for all $i\in {\Omega }_{{\widehat{W}}_p}$, so that ${({\widehat{W}}_p+H)}^i\ne 0$ for all $i\in {\Omega }_{{\widehat{W}}_p}$. From ${\widehat{W}}_p+H\in \mathcal{X}$, it follows that (H)ⁱ = 0 for all $i\notin {\Omega }_{{\widehat{W}}_p}$ and hence ${\left(H\right)}^i{({\widehat{Y}}_p^i-{\widehat{W}}_p^i)}^T=0$ for $i\notin {\Omega }_{{\widehat{W}}_p}$.

Theorem A. 4

Suppose that $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is an accumulation point of the sequence {(v_b, Y_b, W_b)} generated by BCD described in Section 2. Then, $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is a local minimum point of Eq. (7).

Proof

According to Lemma A.2, we have $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is a block coordinate minimum point of Eq. (7). Next we show that $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is also a local minimum point of Eq. (7).

Since l_avg(·,·) is a convex function, we know that q_ϱp(·,·,·) is also convex. It then follows from the first relation of Eq. (A.3), the partial derivative of q_ϱp(·,··) 1.1.1 in Bertsekas (1999)), that

$$\begin{array}{cc}\hfill {\phantom{\mid }\frac{\partial q_{{\varrho }_p}(v,Y,W)}{\partial Y}\mid }_{v={\widehat{v}}_p,Y={\widehat{Y}}_p,W={\widehat{W}}_p}& =0,\hfill \\ \hfill {\phantom{\mid }\frac{\partial q_{{\varrho }_p}(v,Y,W)}{\partial v}\mid }_{v={\widehat{v}}_p,Y={\widehat{Y}}_p,W={\widehat{W}}_p}& =0,\hfill \\ \hfill {\phantom{\mid }\frac{\partial q_{{\varrho }_p}(v,Y,W)}{\partial W}\mid }_{v={\widehat{v}}_p,Y={\widehat{Y}}_p,W={\widehat{W}}_p}& ={\varrho }_p({\widehat{Y}}_p-{\widehat{W}}_p).\hfill \end{array}$$ (A.8)

Let H be a “small” feasible step of ${\widehat{W}}_p,h\in \mathbb{R}$ and $G\in {\mathbb{R}}^{M\times T}$. Then using Lemma 3, Eq. (A.8) and the convexity of q_ϱp, we have

$$\begin{array}{cc}\hfill q_{{\varrho }_p}({\widehat{v}}_p+h,{\widehat{Y}}_p+G,{\widehat{W}}_p+H)& \stackrel{2}{\ge }{q}_{{\varrho }_p}({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)+h\left[{\phantom{\mid }\frac{\partial q_{{\varrho }_p}(v,Y,W)}{\partial v}\mid }_{v={\widehat{v}}_p,Y={\widehat{Y}}_p,W={\widehat{W}}_p}\right]+\mathrm{Tr}\left(G{\left[{\phantom{\mid }\frac{\partial q_{{\varrho }_p}(v,Y,W)}{\partial Y}\mid }_{v={\widehat{v}}_p,Y={\widehat{Y}}_p,W={\widehat{W}}_p}\right]}^T\right)+\mathrm{Tr}\left(H{\left[{\phantom{\mid }\frac{\partial q_{{\varrho }_p}(v,Y,W)}{\partial W}\mid }_{v={\widehat{v}}_p,Y={\widehat{Y}}_p,W={\widehat{W}}_p}\right]}^T\right)\hfill \\ \hfill & \stackrel{\mathrm{Eq}.\left(\mathrm{A}.8\right)}{=}{q}_{{\varrho }_p}({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)+{\varrho }_p\mathrm{Tr}\left(H{({\widehat{Y}}_p-{\widehat{W}}_p)}^T\right)\hfill \\ \hfill & \stackrel{\text{Lemma A.3}}{\ge }{q}_{{\varrho }_p}({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p),\hfill \end{array}$$

which together with the above choice of h, G and H implies that $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ is local minimum point of Eq. (7).

Lemma A.5

Let $\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}$ be the sequence generated by PD, ${\rho }_p=\rho \cdot {\sigma }^{p-1}$ and $\Gamma =l_{\mathrm{avg}}(v_i,W_i)$. Suppose (v*, Y*, W*) is an accumulation point of $\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}$. Then

$$Y^{\ast }=W^{\ast }.$$

Proof

Since (v_i, W_i) defined in Algorithm 1 is a feasible point of Eq. (3), we have

$$\underset{v,Y}{\min }{q}_{{\varrho }_{p+1}}(v,Y,W_i)\le q_{{\varrho }_{p+1}}(v_i,W_i,W_i)=l_{\mathrm{avg}}(v_i,W_i)=\Gamma .$$

By the specification of W₀ according to line 17-20 of Algorithm 1, we have

$$\underset{v,Y}{\min }{q}_{{\varrho }_{p+1}}(v,Y,W_0)\le \Gamma .$$

From Eq. (A.4), we know that the sequence of q_ϱp(v_b, Y_b, W_b) is non-increasing. Thus in view of Eq. (7) and the choice of $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ that is specified in line 21 of Algorithm 1, we observe that $\forall p$

$$l_{\mathrm{avg}}({\widehat{v}}_p,{\widehat{Y}}_p)+\frac{{\varrho }_p}{2}{\Vert {\widehat{W}}_p-{\widehat{Y}}_p\Vert }_F^2=q_{{\varrho }_p}({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\le \Gamma .$$

By the definition of $l_{\mathrm{avg}}({\widehat{v}}_p,{\widehat{Y}}_p)$, we have $l_{\mathrm{avg}}({\widehat{v}}_p,{\widehat{Y}}_p)>0$. Then we obtain that

$${\Vert {\widehat{W}}_p-{\widehat{Y}}_p\Vert }_F^2\le 2[\Gamma -l_{\mathrm{avg}}({\widehat{v}}_p,{\widehat{Y}}_p)]∕{\varrho }_p\le 2\Gamma ∕{\varrho }_p.$$ (A.9)

Since (v*, Y*, W*) is an accumulation point of $\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}$, there exists a subsequence ${\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}}_{k\in \mathcal{S}}\to (v^{\ast },Y^{\ast },W^{\ast })$. Then taking limits on both sides of Eq. (A.9) as $p\in \mathcal{S}\to \infty$, and using ϱ_p → ∞ as p → ∞, we see that ${\Vert W^{\ast }-Y^{\ast }\Vert }_F^2=0$. Thus, the conclusion holds immediately.

Lemma A. 6

Let $\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}$ be the sequence generated by PD, ${\mathcal{K}}_{{\widehat{W}}_p}=\{i_1^p,\dots ,i_r^p\}$ be a set of r district indices in $\mathcal{I}≔\{1,\dots ,M\}$ such that ${\left({\widehat{W}}_p\right)}^i=0$ for any $i\notin {\mathcal{K}}_{{\widehat{W}}_p}$. Suppose (v*, Y*, W*) is an accumulation point of $\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}$, then when k ∈ S is sufficiently large,

$${\mathcal{K}}_{{\widehat{W}}_p}={\mathcal{K}}_{W^{\ast }}$$

for some index set ${\mathcal{K}}_{W^{\ast }}\subseteq \mathcal{I}$.

Proof

Since (v*, Y*, W*) is an accumulation point of $\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}$, there exists a subsequence ${\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}}_{k\in \mathcal{S}}\to (v^{\ast },Y^{\ast },W^{\ast })$. Since ${\mathcal{K}}_{{\widehat{W}}_p}$ is an index set, ${\left\{(i_1^p,\dots ,i_r^p)\right\}}_{p\in \mathcal{S}}$ is bounded for all k. Thus, there exists a subsequence $S\subseteq \mathcal{S}$ such that ${\left\{(i_1^p,\dots ,i_r^p)\right\}}_{p\in S}\to (i_1^{\ast },\dots ,i_r^{\ast })$ for some r distinct indices $i_1^{\ast },\dots ,i_r^{\ast }$. Since $i_1^k,\dots ,i_r^k$ are r distinct integers, one can easily conclude that $(i_1^p,\dots ,i_r^p)=(i_1^{\ast },\dots ,i_r^{\ast })$ for sufficiently large p ∈ S. Let ${\mathcal{K}}_{W^{\ast }}=\{i_1^{\ast },\dots ,i_r^{\ast }\}$. It then follows that ${\mathcal{K}}_{{\widehat{W}}_p}={\mathcal{K}}_{W^{\ast }}$ when k ∈ S is sifficiently large, and moreover, ${\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}}_{k\in S}\to (v^{\ast },Y^{\ast },W^{\ast })$.

Lemma A. 7

Let (v*, W*) ∈ $(\mathbb{R},\mathcal{X})$ and the family of subsets of $\mathcal{I}$ with size ‘r’ and the sets’ complement only consisting of the zero rows of W* be defined as

$${\mathcal{I}}_{W^{\ast }}≔\{\mathcal{K}\subseteq \mathcal{I}:\mid \mathcal{K}\mid =r,{\left(W^{\ast }\right)}^{\overline{\mathcal{K}}}=0\},$$

where $\overline{\mathcal{K}}≔\mathcal{I}\backslash \mathcal{K}$. (v*, W*) is then a local minimum point of Eq. (3) if for each $\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}$ there exists a matrix ${\Lambda }_{\mathcal{K}}\in {\mathbb{R}}^{M\times T}$ so that the following holds:

$$\begin{array}{cc}\hfill {\frac{\partial l_{\mathrm{avg}}(v,W)}{\partial W}\mid }_{v=v^{\ast },W=W^{\ast }}+{\Lambda }_{\mathcal{K}}& =0,\hfill \\ \hfill {\frac{\partial l_{\mathrm{avg}}(v,W)}{\partial v}\mid }_{v=v^{\ast },W=W^{\ast }}& =0,\hfill \\ \hfill {\left({\Lambda }_{\mathcal{K}}\right)}^{\mathcal{K}}& =0\hfill \end{array}$$ (A.10)

with ${f\left(x\right)\mid }_{x=x^{\prime }}$ being the value of f(·) at x′.

Proof

The proof first determines the necessary condition for minima of Eq. (3) and then shows that any (v*, W*) fulfilling the necessary condition also fulfils the sufficient condition. To derive the necessary condition, let us assume that (v*, W*) is a local minimum point of Eq. (3). Now, we know that ${\mathcal{I}}_{W^{\ast }}$ may contain more than one component due to the inequal cardinality constraints in Eq. (3), i.e., ${\Vert {\tilde{W}}^{\ast }\Vert }_0\le r$. Then for any $\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}$, we observe that (v*, W*) also minimizes the following problem

$$\underset{v\in \mathbb{R},W\in {\mathbb{R}}^{M\times T}}{\min }{l}_{\mathrm{avg}}(v,W)s.t.W^{\overline{\mathcal{K}}}=0.$$ (A.11)

Then according to Proposition 3.1.1 of (Bertsekas, 1999), for any (v*, W*) being the solution of Eq. (A.11), it is necessary that there exists a matrix ${\Lambda }_{\mathcal{K}}\in {\mathbb{R}}^{M\times T}$ so that the following holds:

$$\begin{array}{cc}\hfill {\frac{\partial l_{\mathrm{avg}}(v,W)}{\partial W}\mid }_{v=v^{\ast },W=W^{\ast }}+{\Lambda }_{\mathcal{K}}& =0,\hfill \\ \hfill {\frac{\partial l_{\mathrm{avg}}(v,W)}{\partial v}\mid }_{v=v^{\ast },W=W^{\ast }}& =0,\hfill \\ \hfill {\left({\Lambda }_{\mathcal{K}}\right)}^{\mathcal{K}}& =0.\hfill \end{array}$$ (A.12)

Now any (v*, W*) that is a local minimum point of Eq. (3) also has to be a local minimum point of Eq. (A.11) for all $\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}$. Thus it has to fulfill Eq. (A.12) for all $\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}$ so that Eq. (A.12) is a first-order necessary condition of Eq. (3).

From now on, we call any (v*, W*) fulfilling Eq. (A.12) for all $\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}$ a stationary point. We now show that a first-order sufficient condition of Eq. (3) is the existence of a stationary point, i.e., any point fulfilling the necessary condition is also a local minimum point of Eq. (3). From Proposition 3.4.1 of (Bertsekas, 1999), we know that (v*, W*) is the global minimum point of Eq. (A.11) for all

$$\overline{\mathcal{K}}\in \{\mathcal{I}\backslash {\mathcal{K}}_{W^{\ast }}:{\mathcal{K}}_{W^{\ast }}\in {\mathcal{I}}_{W^{\ast }}\}.$$

Hence, there exists ϵ > 0 and neighborhoods of (v*, W*) for different $\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}$, i.e.,

$${\mathcal{N}}_{\mathcal{K}}(v^{\ast },W^{\ast };ϵ)≔\left\{v\in \mathbb{R},W\in {\mathbb{R}}^{M\times T}:W^{\overline{\mathcal{K}}}=0\text{and}\sqrt{{(v-v^{\ast })}^2+{\Vert W-W^{\ast }\Vert }_F^2}<ϵ\right\}$$

with ϵ > 0, such that for all members of the union of neighborhoods, i.e.,

$$\forall (v,W)\in {\cup }_{\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}}{\mathcal{N}}_{\mathcal{K}}(v^{\ast },W^{\ast };ϵ),$$

the following is true

$$l_{\mathrm{avg}}(v,W)\ge l_{\mathrm{avg}}(v^{\ast },W^{\ast }).$$

Now we define the neighborhood of (v*, W*) with respect to the sparse space as $\mathcal{X}$ as

$$\mathcal{N}(v^{\ast },W^{\ast };ϵ)≔\left\{v\in \mathbb{R},W\in \mathcal{X}:\sqrt{{(v-v^{\ast })}^2+{\Vert W-W^{\ast }\Vert }_F^2}<ϵ\right\}.$$

Since ${\cup }_{\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}}{\mathcal{N}}_{\mathcal{K}}(v^{\ast },W^{\ast };ϵ)=\mathcal{N}(v^{\ast },W^{\ast };ϵ)$, then for any $(v,W)\in \mathcal{N}(v^{\ast },W^{\ast };ϵ)$ there exists $\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}$ so that according to Eq. (A.11) $l_{\mathrm{avg}}(v,W)\ge l_{\mathrm{avg}}(v^{\ast },W^{\ast })$. Hence

$$l_{\mathrm{avg}}(v,W)\ge l_{\mathrm{avg}}(v^{\ast },W^{\ast }),\forall (v,W)\in \mathcal{N}(v^{\ast },W^{\ast };ϵ).$$

Thus, any stationary point (v*, W*) is a local minimum point of Eq. (3).

Theorem A. 8

Let (v*, Y*, W*) be an accumulation point of the sequence $\left\{({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)\right\}$ generated by PD. Assume that the solution $({\widehat{v}}_p,{\widehat{Y}}_p,{\widehat{W}}_p)$ obtained by BCD satisfies

$${\Vert \frac{\partial q_{{\varrho }_p}(v,Y,W)}{\partial v}{\mid }_{v={\widehat{v}}_p,Y={\widehat{Y}}_p,W={\widehat{W}}_p}\Vert }_F<{ϵ}_p$$ (A.13)

for ϵ_p → 0. If ${\Vert \widetilde{W^{\ast }}\Vert }_0=r$, then (v*, W*) is a local minimum point of problem Eq. (3).

Proof

We now prove the statement by first showing $Z_p≔{\varrho }_p({\widehat{Y}}_p-{\widehat{W}}_p)$ is bounded, then that converges to ${\Lambda }_{\mathcal{K}}$ for some $\mathcal{K}\in {\mathcal{I}}_{W^{\ast }}$ (the matrix defined in Eq. (A.12)), and finally the (v*, W*) have to be a minimum point of Eq. (3) when ${\Vert \widetilde{W^{\ast }}\Vert }_0=r$. Now let us assume that Z_p is not bounded. To contradict this results, let

$$P_p≔-\frac{\partial q_{{\varrho }_p}(v,Y,W)}{\partial v}{\mid }_{v={\widehat{v}}_p,Y={\widehat{Y}}_p,W={\widehat{W}}_p}.$$

It then follows from Eq. (A.13) that ${\Vert P_p\Vert }_F\le {ϵ}_p$ for all p. Thus for ${\lim }_{p\to \infty }{ϵ}_p=0$ follows ${\lim }_{p\to \infty }{P}_p=0$. Applying Eq. (17) and the definition of q_ϱp in Eq. (7), we have

$$-\frac{\partial l_{\mathrm{avg}}(v,Y)}{\partial Y}{\mid }_{v={\widehat{v}}_p,Y={\widehat{Y}}_p}-Z_p-P_p=0.$$ (A.14)

Now ${\left\{{\Vert Z_p\Vert }_F\right\}}_{k\in S}\to \infty$. Let ${\overline{Z}}_p=Z_p∕{\Vert Z_p\Vert }_F$. Obviously, the sequence $\left\{{\overline{Z}}_p\right\}$ is bounded. Then by using Bolzano-Weierstrass Theorem, there must exists an accumulation point $\overline{Z}$ such that ${\left\{{\overline{Z}}_p\right\}}_{p\in K\subseteq S}\to \overline{Z}$. Clearly ${\Vert \overline{Z}\Vert }_F=1$. Dividing both sides Eq. (A.14) by ∥Z_p∥_F, taking the limits with respect to p ∈ K → ∞, and using the relation ${\lim }_{p\in S\to \infty }{P}_p=0$, we obtain that

$$\stackrel{‒}{Z}=0,$$ (A.15)

which contradicts ${\Vert \overline{Z}\Vert }_F=1$. Therefore, the subsequence {Z_p}_p∈S is bounded. By applying Bolzano-Weierstrass Theorem Bartle and Sherbert (1982) and the boundness of {Z_p}_p∈S, there must exists an accumulation point Z* such that ${\left\{Z_p\right\}}_{p\in K\subseteq S}\to Z^{\ast }$. Taking limits on both sides of Eq. (A.14) as $p\in K\subseteq S\to \infty$, and using the relations ${\lim }_{k\in S\to \infty }{P}_p=0$, we see that the first two relations of Eq. (A.12) hold with Z* = Λ*. From Eq. (10) and the definitions of ${\mathcal{I}}_{{\widehat{W}}_p}$, we have ${\left({\widehat{W}}_p\right)}_p^{\mathcal{K}}={\left({\widehat{Y}}_p\right)}^{\mathcal{K}}$ for and hence ${\left(Z_p\right)}^{{\mathcal{K}}_{{\widehat{W}}_p}}=0$. In addition, we know from Lemma 6 that ${\mathcal{K}}_{{\widehat{W}}_p}={\mathcal{K}}_{W^{\ast }}$ when k ∈ S is sufficiently large. Hence ${\left(Z^{\ast }\right)}^{{\mathcal{K}}_{W^{\ast }}}=0$. This together with the definitions of ${\mathcal{K}}_{W^{\ast }}$ and $\overline{{\mathcal{K}}_{W^{\ast }}}$ implies that Z* satisfies

$${\left(Z^{\ast }\right)}^i=\{\begin{array}{cc}0\hfill & \text{if}i\in {\mathcal{K}}_{W^{\ast }},\hfill \\ {\left({\Lambda }_{{\mathcal{K}}_{W^{\ast }}}\right)}_i\hfill & \text{if}i\in \overline{{\mathcal{K}}_{W^{\ast }}}.\hfill \end{array}\phantom{\}}$$

Now ${\Vert \widetilde{W^{\ast }}\Vert }_0=r$ so that

$${\mathcal{I}}_{W^{\ast }}=\{{\mathcal{K}}_{W^{\ast }}\subseteq \mathcal{I}:\mid {\mathcal{K}}_{W^{\ast }}\mid =r,{\left(W^{\ast }\right)}^i=0,\forall i\notin {\mathcal{K}}_{W^{\ast }}\}$$

has only one unique component. Hence, Z* together with (v*, W*) satisfies Eq. (A.12) so that according to Lemma A.7 (v*, W*) is a local minimum point of Eq. (3).