Abstract
Aims
The objective of this study was to develop a population pharmacokinetic (PK) and pharmacodynamic (PD) model to quantitatively describe the antihypertensive effect of combined therapy with amlodipine and valsartan.
Methods
PK modelling was used with data collected from 48 healthy volunteers receiving a single dose of combined formulation of 10 mg amlodipine and 160 mg valsartan. Systolic (SBP) and diastolic blood pressure (DBP) were recorded during combined administration. SBP and DBP data for each drug alone were gathered from the literature. PKPD models of each drug and for combined administration were built with NONMEM 7.3.
Results
A two‐compartment model with zero order absorption best described the PK data of both drugs. Amlodipine and valsartan monotherapy effects on SBP and DBP were best described by an I max model with an effect compartment delay. Combined therapy was described using a proportional interaction term as follows: (D1 + D2) +ALPHA×(D1 × D2). D1 and D2 are the predicted drug effects of amlodipine and valsartan monotherapy respectively. ALPHA is the interaction term for combined therapy. Quantitative estimates of ALPHA were −0.171 (95% CI: −0.218, −0.143) for SBP and −0.0312 (95% CI: −0.07739, −0.00283) for DBP. These infra‐additive interaction terms for both SBP and DBP were consistent with literature results for combined administration of drugs in these classes.
Conclusion
PKPD models for SBP and DBP successfully described the time course of the antihypertensive effects of amlodipine and valsartan. An infra‐additive interaction between amlodipine and valsartan when used in combined administration was confirmed and quantified.
Keywords: amlodipine, blood pressure, interaction, NONMEM, valsartan
What is Already Known about this Subject
Due to differences in their mechanisms of action, amlodipine (CCB) and valsartan (ARB) are often used in combination to reduce blood pressure.
Combination therapy is known to be less effective than expected from adding two independent monotherapies (infra‐additive effect).
What this Study Adds
Predicted bp changes in healthy population from PKPD modelling are consistent with bp changes reported in patient population.
It is confirmed and quantitatively estimated that the interaction of combined administration leads to an infra‐additive effect.
Tables of Links
| TARGETS | |
|---|---|
| G protein‐coupled receptors 2 | Voltage‐gated ion channel 3 |
| angiotensin II type 1 receptors http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=2534 | Calcium channel |
These Tables list key protein targets and ligands in this article that are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY 1, and are permanently archived in the Concise Guide to PHARMACOLOGY 2015/16 2, 3
Introduction
The antihypertensive effectiveness of combined therapy with the calcium channel blocker (CCB) amlodipine, and the angiotensin II receptor blocker (ARB) valsartan, has been demonstrated in several large, randomized clinical trials 4. Amlodipine and valsartan are both effective antihypertensive agents 4, 5, 6. Amlodipine is a member of the class of dihydropyridine CCBs that directly blocks calcium influx into vascular smooth muscle and cardiac muscle thereby decreasing peripheral vascular resistance 4, 5, 7. Valsartan, on the other hand, blocks the vasoconstrictor and aldosterone‐secreting effects of angiotensin II by selectively inhibiting the binding of angiotensin II to angiotensin II type 1 receptors 4, 5, 7.
Because amlodipine and valsartan exert their effects through different pharmacological pathways, it is of interest to quantify the combined effects of these drugs. Combination therapy is known to be more effective in reducing blood pressure (BP) than therapy with amlodipine or valsartan given alone 4, 5, 6. But there are no studies that quantitatively describe the combined antihypertensive effect with co‐administration of valsartan and amlodipine in comparison to monotherapy.
With this background, the objectives of this analysis were: first to model the population pharmacokinetics of amlodipine and valsartan, and then to model the antihypertensive population pharmacodynamics (PD) of the two drugs and quantify the drug–drug interaction, based on data collected from a study of the combined administration of the two drugs 7 and the literature data for the single dose administration of each drug.
Methods
Data for combined administration
Combined administration data used in the analysis was derived from 48 healthy subjects enrolled in a comparative pharmacokinetic study to compare the pharmacokinetics of two fixed dose combination (FDC) tablets of valsartan and amlodipine 7.
In that study, the subjects were given a single dose of the FDC tablet of 160 mg valsartan/10 mg amlodipine besylate or a single dose of the FDC tablet of 160 mg valsartan/10 mg amlodipine orotate in a crossover fashion, with a 14‐day washout period. For PK analysis, blood samples were collected at 0 (predose) and 0.5, 1, 1.5, 2, 3, 4, 6, 8, 10, 12, 16, 24, 48, 72, 96, 144, and 192 h. Blood samples up to 48 h were collected for plasma concentration analysis of both amlodipine and valsartan and those sampled from 72 h to 192 h were collected for plasma concentration analysis of amlodipine only. For PD analysis, blood pressure (systolic SBP, diastolic DBP) was measured at 0 (predose) and 2, 4, 8, 12, 16, 24, 48, 72, 96, 144, 192 h after the dose for each tablet. BP was measured while subjects were in the sitting position 7. In this work, for PK analysis all data up to t = 192 h were used, and for PD analysis data only up to t = 24 h were used as blood pressure measurements after 24 h were obtained in the outpatient clinic after discharge and measurement conditions were different.
The study was approved by the Institutional Review Board of Yonsei University Severence Hospital (Seoul, Korea) and performed in accordance with the Declaration of Helsinki and Good Clinical Practice 7. All subjects gave written informed consent before study enrolment.
Data for monotherapy
Previous drug interaction studies for amlodipine and valsartan have shown that there is no clinically relevant pharmacokinetic interaction between the two drugs 4. Therefore, the combined administration PK data 7 was used to develop a PK model for each drug.
In order to develop a model for SBP and DBP time course after monotherapy, a search of the literature was used to obtain results in healthy subjects (Supplementary Table S2). The literature search included the keywords amlodipine, valsartan, healthy volunteers and phase I study. Two studies were considered suitable for further analysis 8, 9 (Supplementary Table S1). The studies for other CCBs and ARBs were similar (Supplementary Table S2). SBP and DBP time courses were obtained from the mean BP values recorded at each measured time point for t ≤ 24 h.
Pharmacokinetic data analysis and modelling
One and two compartment models with first order elimination were tested, allowing for various forms of absorption kinetics. For the two compartment model, the following parameters were estimated; apparent clearance (CL/F), inter‐compartmental clearance (Q/F) and the volume of distribution of central (V1/F) and peripheral compartment (V2/F). Each parameter is predicted in a subject whose weight (WT) (in kg) is based on a standard individual CLSTD, QSTD, V1STD or V2STD, whose size is WTSTD. WTSTD was set to 70 kg 10.
Theory based allometric scaling was applied and model parameters were described according to the following equations [10]:
| (1) |
| (2) |
FsizeCL (Equation (1)) is multiplied by CLSTD and QSTD to predict CL/F and Q/F and FsizeV (Equation (2)) is multiplied by V1STD and V2STD to predict V1/F and V2/F.
Covariate analysis for amlodipine and valsartan population PK models included age, serum creatinine, smoking and drinking status. Serum ALT, AST and GGT were also included in the covariate analysis of amlodipine as this drug is extensively metabolized in the liver and hepatic dysfunction may affect the pharmacokinetic characteristics of the drug 11. Stepwise covariate modelling (SCM) was performed using PsN at significance levels of P < 0.05 for forward selection and P < 0.001 for backward elimination 12. The selection procedure was conducted separately for each drug.
Pharmacodynamic modelling
Drug interactions can be labelled as “synergistic”, “additive” or “antagonistic” when the drugs' combined effect exceeds, equals or is less than that of the sum of the effects of the individual drugs, respectively 13. It is preferred to refer to “antagonistic” effects as “infra‐additive” when describing interactions that involve two agonists 14.
A population PKPD model for the time course of SBP and DBP changes in the healthy subject combination treatment study was developed using a sequential PKPD approach (PPP&D 15). The PPP&D method was used, where PD modelling was conducted with the PK data being incorporated in the model‐building process and population parameters of the PK model being fixed at their estimates 15.
A similar approach was used for the PKPD analysis of monotherapy but because only mean concentrations and blood pressures were available, this is a form of naïve pooled analysis. SBP and DBP data were modelled simultaneously.
The time course of blood pressure change from baseline caused by drug was predicted using Equation (3):
| (3) |
where BP is blood pressure, Baseline is baseline blood pressure, PD (Ce) represents different types of PD models as a function of drug concentration. Both immediate and delayed response models were tested. An effect compartment model was applied to describe the delayed onset of drug effect. Ce is either the predicted plasma concentration for the immediate effect or the predicted concentration in the effect compartment for the delayed onset PD model.
| (4) |
| (5) |
| (6) |
| (7) |
Several PD models including linear, log‐linear, I max and Sigmoid I max models (Equations (4), (5), (6) and (7), respectively) were explored. I max is the maximum inhibition effect, IC50 is the concentration which produces 50% maximum inhibition and γ refers to the steepness.
An empirical model was used to describe the pharmacodynamic interaction between amlodipine and valsartan. Each drug effect on blood pressure lowering is described using the predicted effect compartment concentration after monotherapy with amlodipine, PD(ACe) or valsartan, PD(VCe). The interaction is described by an empirical additive plus proportional model where the parameter α estimates the global interaction with combined therapy (Equation (8)):
| (8) |
Modelling tools
All PK and PD model analyses were done with NONMEM (Version 7.3, ICON, Hanover, MD) and the first order conditional estimation with the interaction option. Visual predictive checks (VPCs) were created using Wings for NONMEM 740 16.
Model selection and evaluation
Model selection was guided by the precision of parameter estimates, objective function value (OFV) and Akaike Information criterion (AIC). To evaluate the final PD models of monotherapies, predicted BP changes were compared to the reported BP changes found in the published literature. To verify that the final population PK and PD models adequately described the central tendency and spread of the data, the models were evaluated using a VPC given 1000 simulated datasets from the final models. Observed concentrations were overlaid with model predictions (mean, 5th and 95th percentiles) to detect the fraction of the data that lay within the model prediction intervals. For the PD interaction term model, VPC of the final model and the model with interaction term of 0 were compared for evaluation purposes. The significance of the interaction parameters were determined using the likelihood ratio test. A total of 200 bootstrap replications were used to estimate parameter imprecision and confidence intervals using a non‐parametric bootstrap approach 17.
Results
Participant demographics and data
Data were available from 48 participants for both amlodipine and valsartan pharmacokinetic analysis. A summary of the demographic characteristics of study subjects is reported in Supplementary Table S3. There were 816 measurements of amlodipine and 624 measurements of valsartan concentrations. For amlodipine, 0.61% of measured concentrations were below the limit of quantitation. For valsartan, there were 6.5% of measured concentrations below the limit of quantitation. There were 336 measurements of SBP and DBP with no missing values. There were no missing values in BP data.
The data from the literature was based on 24 subjects with 12 measurements of mean SBP and DBP for amlodipine and 12 subjects with six measurements of mean SBP and DBP for valsartan for t ≤ 24 h.
Pharmacokinetic model
Population pharmacokinetic analysis for amlodipine and valsartan
The pharmacokinetic data for amlodipine was best described by a two‐compartment model with zero order absorption and first order elimination. The OFV value of −387.497 for zero order absorption compared with −29.849 with first order absorption of amlodipine demonstrated that the zero order absorption model better described the data. This result is in accordance with the bi‐exponential decline seen in the plasma concentration vs. time plot of amlodipine (Supplementary Figure S1). Between‐subject variability for clearance, central volume and duration of zero‐order input for amlodipine were estimated along with correlation between clearance and central volume of distribution. Proportional and additive combined error model best described the residual unidentified variability in the data.
Pharmacokinetic model building for valsartan was conducted in a similar way as for amlodipine, leading to a two‐compartment disposition model with first order elimination based on the bi‐exponential plasma concentration vs. time curve (Supplementary Figure S1) and zero order absorption, which yielded a smaller OFV than first order absorption (7712.434 vs. 7874.858). Correlation between clearance and central volume of distribution was incorporated in the model and the residual unidentified variability was best described by a proportional and additive combined error model.
The estimated pharmacokinetic parameters for amlodipine and valsartan are listed in Supplementary Table S4. Apart from body weight, no other covariate factors were found to be significant (P > 0.001). The apparent clearance (CL/F) for a subject with a body weight of 70 kg was estimated to be 39.4 l h−1 for amlodipine and 6.18 l h−1 for valsartan.
The amlodipine and valsartan PK models were evaluated using VPC (Supplementary Figure S2 and Figure S3). The median peak concentration of both drugs was somewhat underpredicted but subsequently the median predictions adequately follow the median observations. Overall, the variability of the predictions was consistent with the variability of the observations. Therefore, we consider the PK models are acceptable to predict concentrations for the pharmacodynamic models of amlodipine and valsartan.
Pharmacodynamic model
bp lowering effect of amlodipine monotherapy
Plotting the SBP and DBP responses as a function of the measured plasma concentration curve for amlodipine provided some evidence of delayed effect (Figure 1). Therefore, both delayed and immediate response PD models were investigated. The data was best described with an effect compartment delay and an E max model for both SBP and DBP. The fit from an empirical linear pharmacodynamics model was similar to a pharmacodynamic theory‐based E max model. Therefore the theory‐based model was selected because of its better extrapolation properties. Estimated I max from valsartan monotherapy (0.164) was used as a fixed I max for amlodipine monotherapy, assuming that the amlodipine and valsartan monotherapy show similar efficacy.
Figure 1.

Literature data of mean concentration vs. mean blood pressure response plot after single dose of 10 mg amlodipine was given. SBP is shown on the left‐hand side and DBP is shown on the right‐hand side. Arrows indicate increasing time
A delayed response E max model with delay parameters for SBP and DBP decreased the OFV by 11.5 compared with an immediate response model. SBP and DBP were plotted as a function of the predicted amlodipine concentrations in the effect compartment. The hysteresis shown in Figure 1 is clearly reduced for both SBP and DBP (Figure 2).
Figure 2.
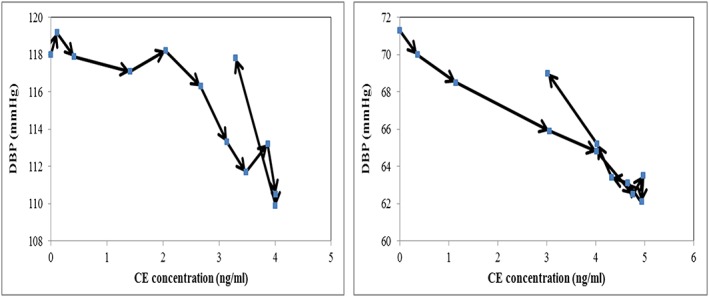
Predicted concentration in effect compartment vs. mean blood pressure response plot after a single dose of 10 mg amlodipine was given. The concentrations were predicted with an effect compartment delay and an I max pharmacodynamic model. SBP is shown on the left‐hand side and DBP is shown on the right‐hand side. Arrows indicate increasing time
The estimated PD parameters for amlodipine are listed in Table 1. SBP and DBP responses to amlodipine concentration are described according to the following equations where CE is the predicted effect compartment concentration of amlodipine:
| (9) |
| (10) |
Table 1.
PD estimates from mean healthy subject data of amlodipine monotherapy
| Amlodipine | |||
|---|---|---|---|
| PD model | Delayed I max | ||
| No. of parameters | 8 | ||
| Parameter | Estimate (RSE%) | Bootstrap estimate | 95% CI |
| SBP BSL (mmHg) | 119(1.03) | 115.32 | 113–118 |
| DBP BSL (mmHg) | 71.3 (2.04) | 65.79 | 63.29–68.9 |
| I max | 0.164 FIX | 0.164 FIX | |
| SBP IC 50 (ng ml −1 ) | 8.27 (32.2) | 10.80 | 0–13 |
| DBP IC 50 (ng ml −1 ) | 2.97 (36.8) | 4.79 | 0–6 |
| SBP Keq (/h) | 0.211 (Teq = 3.3 h) (38.3) | 0.133 | 0.1–0.211 |
| DBP Keq (/h) | 0.821 (Teq = 0.84 h) (104.7) | 0.316 | 0.1–0.821 |
| Residual variability | Estimate (RSE%) | Bootstrap estimate | 95% CI |
|---|---|---|---|
| σ SBP additive (mmHg) | 2.01 (17.4) | 2.92 | 0.91–3.65 |
| σ DBP additive (mmHg) | 1.36 (22.5) | 2.74 | 0.96–3.59 |
BSL, estimated baseline; DBP, diastolic blood pressure; SBP, systolic blood pressure; σ, sqrt(NONMEM SIGMA)
The PD models of amlodipine monotherapy were evaluated using VPCs and the predicted maximum BP changes from the PD models compared to reported maximum BP changes found in the literature. The confidence intervals of the SBP and DBP predictions were consistent with the median observations (Supplementary Figure S4). Predicted maximum BP changes of SBP and DBP are in accordance with the reported maximum BP changes from the literature 9 (Supplementary Table S5). Overall, we consider the PD models are acceptable to describe both SBP and DBP after monotherapy.
bp lowering effect analysis for valsartan monotherapy
Plotting the SBP and DBP responses as a function of the measured plasma concentrations of valsartan provided evidence of a delayed onset of effect as shown in Figure 3. Both delayed and immediate response PD models were investigated and the data was best described with an effect compartment delay and an I max model for both SBP and DBP. With one parameter increase, the OFV of the delayed response model was reduced by 8.4 compared to the immediate response model. The hysteresis shown in Figure 3 is reduced with SBP and disappeared with DBP (Figure 4). The estimated PD parameters for valsartan from the selected model are listed in Table 2. SBP and DBP response to valsartan administration was described according to the following equations where CE is the predicted effect compartment concentration of valsartan:
| (11) |
| (12) |
Figure 3.
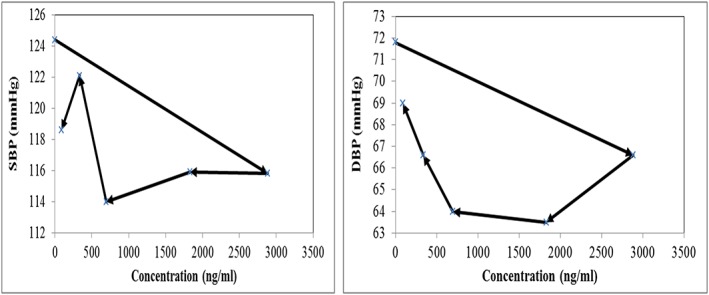
Literature data of mean concentration vs. mean blood pressure response plot after single dose of 160 mg valsartan was given. SBP is shown on the left‐hand side and DBP is shown on the right‐hand side. Arrows indicate increasing time
Figure 4.
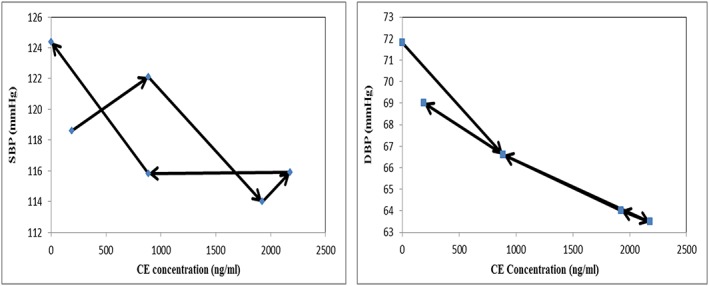
Predicted concentration in effect compartment vs. mean blood pressure response plot after single dose of 160 mg valsartan was given. The concentrations were predicted with the chosen final model, an effect compartment delay and an I max model. SBP is shown on the left‐hand side and DBP is shown on the right‐hand side. Arrows indicate increasing time
Table 2.
PD estimates from mean healthy subject data of valsartan monotherapy
| Valsartan | |||
|---|---|---|---|
| PD model | Delayed I max | ||
| No. of parameters | 7 | ||
| Parameter | Estimate (RSE%) | Bootstrap estimate | 95% CI |
| SBP BSL(mmHg) | 126 (1.58) | 119.6 | 117–125 |
| DBP BSL (mmHg) | 71.3 (2.52) | 67.52 | 65.1–71.8 |
| I max | 0.164 (102) | 0.228 | 0.0623–1 |
| IC 50 (ng ml −1 ) | 1200 (53.3) | 1823.05 | 1020–4000 |
| Keq (/h) | 0.542 (teq = 1.3 h) (59.5) | 0.403 | 0.1–0.777 |
| Residual variability | Estimate (RSE%) | Bootstrap estimate | 95% CI |
|---|---|---|---|
| σ SBP additive (mmHg) | 3.18 (33.0) | 2.82 | 0.228–4 |
| σ DBP additive (mmHg) | 0.41 (35.8) | 2.26 | 0–3.406 |
DBP, diastolic blood pressure; SBP, systolic blood pressure; σ, sqrt(NONMEM SIGMA)
I max (0.164) for both SBP and DBP was estimated relative to the BP baseline. When expressed in terms BP units, the I max for SBP is 20.7 mmHg (= 126 × 0.164) and for DBP 11.7 mmHg (= 71.3 × 0.164). SBP and DBP changes after monotherapy were plotted as a function of the predicted valsartan concentrations in the effect compartment (Figure 4).
The PD models of valsartan monotherapy were evaluated by VPCs and the predicted maximum BP changes from the PD models compared to the reported maximum BP changes found in the literature. The confidence intervals of the SBP and DBP predictions were consistent with the median observations (Supplementary Figure S5). Predicted maximum BP changes of SBP and DBP are in accordance with the reported maximum BP changes from the literature (Supplementary Table S6). Overall, the PD models are acceptable to predict both SBP and DBP and the estimated parameters to be used for the pharmacodynamic models of amlodipine and valsartan combined therapy.
Interaction term of bp lowering effect between amlodipine and valsartan
The interaction between amlodipine and valsartan was best described with a proportional term (Equation (8)). A second interaction model was also investigated to describe the interaction between amlodipine and valsartan (Supplementary Drug interaction models). The core assumption of this second model is that the two drugs compete with each other for occupancy of the same receptor which is not the case for amlodipine and valsartan. This common receptor model led to implausible parameter estimates (e.g. I max of 0.03 which is seven times smaller than expected) and was not investigated further. The estimated PD parameters for the proportional interaction model are reported in Table 3. The proportional interaction term for SBP was −0.171 and for DBP was −0.0312.
Table 3.
Population PD estimates and interaction term (ALPHA) of amlodipine and valsartan combined administration in healthy subjects
| SBP | |||
|---|---|---|---|
| Interaction type | Proportional | ||
| No. of parameters | 8 | ||
| Parameter | Estimate (RSE%) | Bootstrap estimate | 95% CI |
| BSL (mmHg) | 117 (1.10) | 116.8 | 114–119.0 |
| ALPHA | −0.171 (11.6) | −0.178 | −0.218–−0.143 |
| PPV | Estimate (RSE%) | Bootstrap estimate | 95% CI |
| BSL | 0.059 (18.8) | 0.055 | 0.035–0.074 |
| ALPHA | 0 FIX | ||
| IC 501 | 0.468 (84.3) | 0.341 | 0–0.872 |
| IC 502 | 1.732 (43.4) | 1.671 | 0–3.127 |
| AML Keq a | 1.319 (46.5) | 1.336 | 0–2.403 |
| VAL Keq a | 0.376 (37.9) | 0.371 | 0–0.613 |
| Residual variability | Estimate (RSE%) | Bootstrap estimate | 95% CI |
| σ additive (mmHg) | 7.84 (6.36) | 7.84 | 6.86–8.73 |
| DBP | |||
|---|---|---|---|
| Interaction type | Proportional | ||
| No. of parameters | 6 | ||
| Parameter | Estimate (RSE%) | Bootstrap estimate | 95% CI |
| BSL (mmHg) | 72.8 (1.33) | 72.9 | 71.2–74.7 |
| ALPHA | −0.0312 (57.8) | −0.0336 | −0.0774–−0.00283 |
| PPV | Estimate (RSE%) | Bootstrap estimate | 95% CI |
| BSL | 0.071 (15.9) | 0.07 | 0.046–0.092 |
| ALPHA | 0 FIX | ||
| ω IC 501 | 1.612 (33.1) | 1.674 | 0.907–2.819 |
| ω IC 502 | 1.131 (32.8) | 1.042 | 0.004–1.622 |
| Residual variability | Estimate (RSE%) | Bootstrap estimate | 95% CI |
| σ additive (mmHg) | 4.46 (5.22) | 4.45 | 3.95–4.90 |
ALPHA, interaction term for co‐administration of amlodipine and valsartan; BSL, estimated baseline; other parameters (I max, etc.) fixed to values estimated from combined administration PK models and single drug PD models. PPV value calculated from sqrt(NONMEM OMEGA estimate)
The SBP and DBP PD models of amlodipine and valsartan combined administration were evaluated by VPC. To evaluate the appropriateness of the interaction term in the model, the final interaction models for SBP and DBP were compared to models without interaction (Figures 5 and 6). A VPC using a model with the interaction term fixed to 0 for SBP showed a very poor fit between the predictions and the observations, with predicted SBP lower than the observations at all times,. In contrast, the proportional interaction model successfully described the time course of systolic blood lowering effect of the amlodipine and valsartan combined administration.
Figure 5.
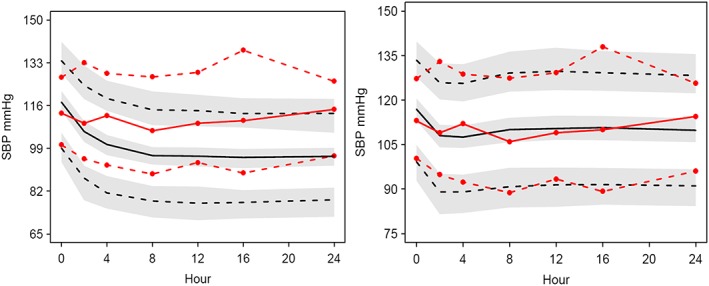
VPC plots of SBP without an interaction term model of combined therapy (left) and the same model with the interaction term (right). Observations and predictions are illustrated in red lines and black lines respectively. Solid lines represent median, lower and upper dashed lines represent 5th percentile and 95th percentile respectively. Shaded areas describe 95% confidence interval of the predictions
Figure 6.
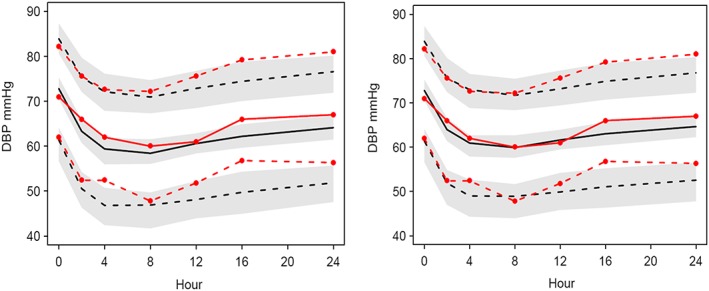
VPC plots of DBP without an interaction term model of combined therapy (left) and the same model with the interaction term (right). Observations and predictions are illustrated in red lines and black lines respectively. Solid lines represent median, lower and upper dashed lines represent 5th percentile and 95th percentile respectively. Shaded areas describe 95% confidence interval of the predictions
For DBP, the median predictions adequately follow the median observations. The discrepancy between the predictions and the observations were evident when the interaction term was fixed to 0 as shown in Figure 6. The model without interaction was not so markedly different for DBP but nevertheless the proportional interaction model for the combined therapy was better.
Discussion
In previous population PK studies of amlodipine, the absorption phase was often well described with first order absorption 18, 19, 20. Reported CL/F for amlodipine from other studies varied between 32 and 39 l h−1 20, 21, 22. The mean or median weight in these studies was near 70 kg. Estimated CL/F of amlodipine in this study for a 70 kg subject was 39.4 l h−1, which is in accordance with findings from previously reported clearance from both quantitative PK modelling and NCA analysis 20, 21, 22.
The population PK model of valsartan is in accordance with findings from a previously published population PK model for valsartan. Lim et al. reported estimates of CL/F, Q, Vc and Vp of 6.07 l h−1, 2.02 l h−1, 13.8 l and 14.2 l, respectively 23, and the mean weight for the study was near 70 kg.
Empirical effect compartment models adequately describe the observed hysteresis between the time course of plasma concentrations and time course of blood lowering effect. Figures 2 and 4 show that the hysteresis either shrinks or completely collapses when the blood lowering effect is plotted as a function of predicted concentration in the effect compartment. Pharmacodynamic effect often lags behind plasma concentration for various reasons such as drug distribution, slow equilibration with the target or changes in a physiological mediator.
It has been reported that amlodipine and valsartan show similar BP reduction in hypertensive patients 24, 25, 26, thus I max is fixed to the estimated value from valsartan monotherapy as the data is not informative about amlodipine. For amlodipine, estimated C50 of the SBP is about three times bigger than the C50 of DBP (Table 1).
In this work, the mechanism of the interaction could not be determined, so the interaction was described empirically. As a result, a proportional interaction term best described the blood pressure lowering effect of combined administration of amlodipine and valsartan. The interaction term (α) can be described in three categories; infra‐additive if α is less than 0, additive if α is equal to 0 and synergistic if α is greater than 0. We have demonstrated that the combined drug response of amlodipine and valsartan for both SBP and DBP is infra‐additive. Combined administration of amlodipine with valsartan exerts greater antihypertensive effects than that of either drug given alone but less than the sum of the two drugs as monotherapy. This outcome was in an accordance with other publications where the antihypertensive effect of the two drugs in hypertensive patients are greater than the either monotherapy given alone but the drug interaction is infra‐additive 4, 5.
One of the limitations of this study is that the interaction model was quantitatively analysed from healthy subject data, assuming that PK and PD parameters estimated in healthy subjects would be the same in hypertensive patients, with the only difference between these two groups being baseline SBP and DBP. However, as antihypertensive medications are given to patients with hypertension, this assumption was validated by testing if the healthy subject predictions were consistent with blood pressure changes in treated patients.
To this end, blood pressure changes relative to baseline were predicted for healthy subjects and compared with the mean observed changes in five patient studies (Supplementary Table S7). Both amlodipine and valsartan I max PD models gave similar predictions to changes reported in patients (Table 4), which supported the validity of our assumption.
Table 4.
Comparison between the calculated ratios of mean reported bp changes of patients and predictions from I max bp models of amlodipine and valsartan at steady state
| Amlodipine patients’ mean | Amlodipine healthy predicted | Valsartan patients’ mean | Valsartan healthy predicted | |
|---|---|---|---|---|
| RSBP (%) | 12 | 9 | 11 | 8 |
| RDBP (%) | 13 | 13 | 11 | 8 |
RSBP, RDBP; relative BP changes to SBP and DBP baseline respectively
The PD models are empirically developed to describe the time course of antihypertensive effects of combined therapy. The pharmacology of amlodipine and valsartan and their mechanisms of actions are widely known 4, 6, 25, 27, 28, 29. It would be valuable to develop mechanistic PD models to understand and describe the interaction observed with combined therapy.
Conclusion
An I max model with effect compartment delay adequately described the SBP and DBP data with both amlodipine and valsartan monotherapy. The quantitatively estimated interaction term of combined administration, defined on the basis of a model developed from monotherapy, is consistent with previous descriptions of an infra‐additive effect.
Competing Interests
All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare: no support from any organization for the submitted work; no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years; no other relationships or activities that could appear to have influenced the submitted work.
This work was supported by a grant from the Brain Korea 21 PLUS Project for Medical Science, Yonsei University.
Contributors
Y. A. H contributed to data interpretation, literature search, figure creation and writing, N. H. contributed to data interpretation and writing, Y. K. and M. S. contributed to study design, study conduct and data collection, and K. P. coordinated the entire study.
Supporting information
Table S1 Clinical trials used in the analysis of amlodipine and valsartan pharmacokinetics and pharmacodynamics analysis
Table S2 Summary of maximum BP changes after a single dose of calcium channel blockers or angiotensin II receptor blockers (ARBs) in normotensive subjects
Table S3 Demographic characteristics of study subjects for population PK analysis
Table S4 Final population PK estimates of amlodipine and valsartan
Table S5 Comparison between the predicted and the reported maximum BP changes with the final BP models and the literature of amlodipine monotherapy
Table S6 Comparison between the predicted and the reported maximum BP changes with the final BP models and the literature of valsartan monotherapy
Table S7 Summary of maximum BP changes after amlodipine or valsartan were given to patients with hypertension
Figure S1 Spaghetti plot of individual time concentration curves for amlodipine (A, left) and valsartan (B, right), superimposed with median (red dashed line)
Figure S2 VPC plot of population PK model of amlodipine. Inset shows the first 24 h after the dose. Observations and predictions are illustrated in red lines and black lines respectively. Solid lines represent median; lower and upper dashed lines represent 5th percentile and 95th percentile respectively. Shaded areas describe 95% confidence interval of predictions
Figure S3 VPC plot of final population PK model of valsartan. Inset shows the first 24 h after the dose. Observations and predictions are illustrated in red lines and black lines respectively. Solid lines represent median; lower and upper dashed lines represent 5th percentile and 95th percentile respectively. Shaded areas describe 95% confidence interval of predictions
Figure S4 VPC plots of SBP (left) and DBP (right) model of amlodipine monotherapy. Observations and predictions are illustrated in red and black line respectively
Figure S5 VPC plots of SBP (left) and DBP (right) model of valsartan monotherapy. Observations and predictions are illustrated in red and black line respectively
Supporting info item
Heo, Y. ‐A. , Holford, N. , Kim, Y. , Son, M. , and Park, K. (2016) Quantitative model for the blood pressure‐lowering interaction of valsartan and amlodipine. Br J Clin Pharmacol, 82: 1557–1567. doi: 10.1111/bcp.13082.
References
- 1. Southan C, Sharman JL, Benson HE, Faccenda E, Pawson AJ, Alexander SP, et al. The IUPHAR/BPS Guide to PHARMACOLOGY in 2016: towards curated quantitative interactions between 1300 protein targets and 6000 ligands. Nucl Acids Res 2016; 44: D1054–D1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Alexander SPH, Davenport AP, Kelly E, Marrion N, Peters JA, Benson HE, et al. CGTP CollaboratorsThe Concise Guide to PHARMACOLOGY 2015/16: G protein coupled receptors. Br J Pharmacol 2015; 172: 5744–5869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Alexander SPH, Catterall WA, Kelly E, Marrion N, Peters JA, Benson HE, et al. CGTP CollaboratorsThe Concise Guide to PHARMACOLOGY 2015/16: Voltage‐gated ion channels. Br J Pharmacol 2015; 172: 5904–5941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Frampton JE, Scott LJ. Amlodipine/valsartan single‐pill combination: a review of its use in the management of hypertension. Am J Cardiovasc Drugs 2009; 9: 309–330. [DOI] [PubMed] [Google Scholar]
- 5. Flack JM, Calhoun DA, Satlin L, Barbier M, Hilkert R, Brunel P. Efficacy and safety of initial combination therapy with amlodipine/valsartan compared with amlodipine monotherapy in black patients with stage 2 hypertension: the EX‐STAND study. J Hum Hypertens 2009; 23: 479–489. [DOI] [PubMed] [Google Scholar]
- 6. Plosker GL, Robinson DM. Amlodipine/valsartan: fixed‐dose combination in hypertension. Drugs 2008; 68: 373–381. [DOI] [PubMed] [Google Scholar]
- 7. Kim Y, Son M, Lee D, Roh H, Son H, Chae D, et al. Pharmacokinetic comparison of 2 fixed‐dose combination tablets of amlodipine and valsartan in healthy male Korean volunteers: a randomized, open‐label, 2‐period, single‐dose, crossover study. Clin Ther 2013; 35: 934–940. [DOI] [PubMed] [Google Scholar]
- 8. Czendlik C, Sioufi A, Preiswerk G, Howald H. Pharmacokinetic and pharmacodynamic interaction of single doses of valsartan and atenolol. Eur J Clin Pharmacol 1997; 52: 451–459. [DOI] [PubMed] [Google Scholar]
- 9. Kim BH, Kim JR, Kim MG, Kim KP, Lee BY, Jang IJ, et al. Pharmacodynamic (hemodynamic) and pharmacokinetic comparisons of S‐amlodipine gentisate and racemate amlodipine besylate in healthy Korean male volunteers: two double‐blind, randomized, two‐period, two‐treatment, two‐sequence, double‐dummy, single‐dose crossover studies. Clin Ther 2010; 32: 193–205. [DOI] [PubMed] [Google Scholar]
- 10. Holford N, Heo YA, Anderson B. A pharmacokinetic standard for babies and adults. J Pharm Sci 2013; 102: 2941–2952. [DOI] [PubMed] [Google Scholar]
- 11. Rohatagi S, Carrothers TJ, Kshirsagar S, Khariton T, Lee J, Salazar D. Evaluation of population pharmacokinetics and exposure‐response relationship with coadministration of amlodipine besylate and olmesartan medoxomil. J Clin Pharmacol 2008; 48: 823–836. [DOI] [PubMed] [Google Scholar]
- 12. Lindbom L, Pihlgren P, Jonsson N. PsN‐Toolkit – a collection of computer intensive statistical methods for non‐linear mixed effect modeling using NONMEM. Comput Methods Programs Biomed 2005; 79: 241–257. [DOI] [PubMed] [Google Scholar]
- 13. Hendrickx JF, Eger EI 2nd, Sonner JM, Shafer SL. Is synergy the rule? A review of anesthetic interactions producing hypnosis and immobility. Anesth Analg 2008; 107: 494–506. [DOI] [PubMed] [Google Scholar]
- 14. Minto C, Vuyk J. Response surface modelling of drug interactions. Adv Exp Med Biol 2003; 523: 35–43. [DOI] [PubMed] [Google Scholar]
- 15. Zhang L, Beal SL, Sheiner LB. Simultaneous vs. sequential analysis for population PK/PD data I: best‐case performance. J Pharmacokinet Pharmacodyn 2003; 30: 387–404. [DOI] [PubMed] [Google Scholar]
- 16. Holford NHG. Wings for NONMEM Version 740 for NONMEM 7.3 and NONMEM 7.2, 2015. Available at http://wfn.sourceforge.net (last accessed 1 September 2016).
- 17. Parke J, Holford NH, Charles BG. A procedure for generating bootstrap samples for the validation of nonlinear mixed‐effects population models. Comput Methods Programs Biomed 1999; 59: 19–29. [DOI] [PubMed] [Google Scholar]
- 18. Flynn JT, Nahata MC, Mahan JD, Portman RJ. Population pharmacokinetics of amlodipine in hypertensive children and adolescents. J Clin Pharmacol 2006; 46: 905–916. [DOI] [PubMed] [Google Scholar]
- 19. Kim KA, Park PW, Lee OJ, Choi SH, Min BH, Shin KH, et al. Effect of CYP3A5*3 genotype on the pharmacokinetics and pharmacodynamics of amlodipine in healthy Korean subjects. Clin Pharmacol Ther 2006; 80: 646–656. [DOI] [PubMed] [Google Scholar]
- 20. Son H, Lee D, Lim LA, Jang SB, Roh H, Park K. Development of a pharmacokinetic interaction model for co‐administration of simvastatin and amlodipine. Drug Metab Pharmacokinet 2014; 29: 120–128. [DOI] [PubMed] [Google Scholar]
- 21. Josefsson M, Zackrisson AL, Ahlner J. Effect of grapefruit juice on the pharmacokinetics of amlodipine in healthy volunteers. Eur J Clin Pharmacol 1996; 51: 189–193. [DOI] [PubMed] [Google Scholar]
- 22. Park JY, Kim KA, Lee GS, Park PW, Kim SL, Lee YS, et al. Randomized, open‐label, two‐period crossover comparison of the pharmacokinetic and pharmacodynamic properties of two amlodipine formulations in healthy adult male Korean subjects. Clin Ther 2004; 26: 715–723. [DOI] [PubMed] [Google Scholar]
- 23. Lim HS, Cho JY, Oh DS, Chung JY, Hong KS, Bae KS, et al. Angiotensin II type 1 receptor 1166 A/C polymorphism in association with blood pressure response to exogenous angiotensin II. Eur J Clin Pharmacol 2007; 63: 17–26. [DOI] [PubMed] [Google Scholar]
- 24. Smith TR, Philipp T, Vaisse B, Bakris GL, Wernsing M, Yen J, et al. Amlodipine and valsartan combined and as monotherapy in stage 2, elderly, and black hypertensive patients: subgroup analyses of 2 randomized, placebo‐controlled studies. J Clin Hypertens 2007; 9: 355–364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Corea L, Cardoni O, Fogari R, Innocenti P, Porcellati C, Provvidenza M, et al. Valsartan, a new angiotensin II antagonist for the treatment of essential hypertension: a comparative study of the efficacy and safety against amlodipine. Clin Pharmacol Ther 1996; 60: 341–346. [DOI] [PubMed] [Google Scholar]
- 26. Markham A, Goa KL. Valsartan. A review of its pharmacology and therapeutic use in essential hypertension. Drugs 1997; 54: 299–311. [DOI] [PubMed] [Google Scholar]
- 27. Boutouyrie P, Achouba A, Trunet P, Laurent S, Group ET. Amlodipine‐valsartan combination decreases central systolic blood pressure more effectively than the amlodipine‐atenolol combination: the EXPLOR study. Hypertension 2010; 55: 1314–1322. [DOI] [PubMed] [Google Scholar]
- 28. Murdoch D, Heel RC. Amlodipine. A review of its pharmacodynamic and pharmacokinetic properties, and therapeutic use in cardiovascular disease. Drugs 1991; 41: 478–505. [DOI] [PubMed] [Google Scholar]
- 29. Haria M, Wagstaff AJ. Amlodipine. A reappraisal of its pharmacological properties and therapeutic use in cardiovascular disease. Drugs 1995; 50: 560–586. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1 Clinical trials used in the analysis of amlodipine and valsartan pharmacokinetics and pharmacodynamics analysis
Table S2 Summary of maximum BP changes after a single dose of calcium channel blockers or angiotensin II receptor blockers (ARBs) in normotensive subjects
Table S3 Demographic characteristics of study subjects for population PK analysis
Table S4 Final population PK estimates of amlodipine and valsartan
Table S5 Comparison between the predicted and the reported maximum BP changes with the final BP models and the literature of amlodipine monotherapy
Table S6 Comparison between the predicted and the reported maximum BP changes with the final BP models and the literature of valsartan monotherapy
Table S7 Summary of maximum BP changes after amlodipine or valsartan were given to patients with hypertension
Figure S1 Spaghetti plot of individual time concentration curves for amlodipine (A, left) and valsartan (B, right), superimposed with median (red dashed line)
Figure S2 VPC plot of population PK model of amlodipine. Inset shows the first 24 h after the dose. Observations and predictions are illustrated in red lines and black lines respectively. Solid lines represent median; lower and upper dashed lines represent 5th percentile and 95th percentile respectively. Shaded areas describe 95% confidence interval of predictions
Figure S3 VPC plot of final population PK model of valsartan. Inset shows the first 24 h after the dose. Observations and predictions are illustrated in red lines and black lines respectively. Solid lines represent median; lower and upper dashed lines represent 5th percentile and 95th percentile respectively. Shaded areas describe 95% confidence interval of predictions
Figure S4 VPC plots of SBP (left) and DBP (right) model of amlodipine monotherapy. Observations and predictions are illustrated in red and black line respectively
Figure S5 VPC plots of SBP (left) and DBP (right) model of valsartan monotherapy. Observations and predictions are illustrated in red and black line respectively
Supporting info item


