On cavitation and macroscopic behaviour of amorphous polymer-rubber blends

Abstract

The macroscopic behaviour of rubber-modified polymethyl methacrylate (PMMA) was investigated by taking into account the microdeformation mechanisms of rubber cavitation. The dependence of the macroscopic stress–strain behaviour of matrix deformation on the cavitation of rubber particles was discussed. A phenomenological elastic-viscoplastic model was used to model the behaviour of the matrix material, while the rubber particles were modelled with the hyperelasticity theory. A two-phase composite material with a periodic arrangement of reinforcing particles of a circular unit cell section was considered. Finite-element analysis was used to determine the local stresses and strains in the two-phase composite. In order to describe the cavitation of the rubber particles, a criterion of void nucleation is implemented in the finite-element (FE) code. A comparison of the numerically predicted response with experimental result indicates that the numerical homogenisation analysis gives satisfactory prediction results.

Introduction

Polymers are used as engineering materials for a wide variety of applications. A serious limitation for the application of these materials is their propensity for brittle fracture, which is induced particularly by low temperatures and high strain rates [1]. A method of enhancing fracture toughness under these conditions is to introduce a disperse rubbery phase. The toughening effect is mainly based on the initiation of plasticity in the polymer matrix at many sites and at lower macroscopic stresses than in the homopolymer. As a consequence, energy dissipation takes place in a larger volume.

The rubber toughening of a polymeric matrix involves cavitation in the rubber phase and void growth or crazing in the viscoplastic matrix. According to experimental observations [2], there is a competition between plastic flow in the matrix, cavitation in the rubber particles, and crazing. Moreover, the volume change caused by void growth modifies the local stress field [3, 4]. However, for a greater understanding of the role that cavitation plays in the rubber toughening of plastics, it seems more appropriate to study the cavitation of rubber particles blended in a plastic matrix and give an accurate description of the deformation processes.

The consequence of cavitation is a local reduction in the bulk modulus and hydrostatic stress components in the vicinity of the void and a corresponding increase of the deviatoric component of stress. The onset of cavitation and the size of the process zone depend on the cavitation resistance of the rubbery phase. In fact, owing to higher cavitation resistance, particle cavitation is delayed, which results in the build up of a higher elastic energy prior to shear yielding of the matrix. Higher elastic energy may then cause a faster growth of shear bands and thus, a larger plastic zone forms and a higher toughness is obtained [5]. In this context, Lazzeri and Bucknall [6], considered cavitation as a promoter of shear yielding, and modelled the effect of cavitation on shear yielding in the form of dilatational bands.

The role and importance of void formation within the rubber particles in polymer blends are still not clear but have been a centre of interest and have recently become a subject of intensive discussion. Based on experimental measurements [4, 7] of the rubber cavitation phenomena occurring in appropriate polymer blend samples, several cavitation models for predicting the critical state that promotes the initiation of the cavity [3, 8–10] were developed. The macroscopic material response under loading conditions, taking into account the cavitation process, was studied [11].

Previous experiments on polymers have revealed that the application of sufficiently large tensile load can cause the appearance of holes that were not previously evident in the material. Upon further loading, these cavities grow in size and eventually coalesce. The cavitation phenomenon was first experimentally observed by Gent and Lindley [12] in rubber cylinders. The nonlinear theory of elasticity was used to explain the nucleation of such holes in elastomers. The critical stress for cavitation was found to be a linear function of the shear modulus. Although this theory is in good agreement with experimental results, a material that contains a large number of microvoids is extremely difficult to deal with from both an analytical and a computational perspective. In their theoretical study, Gent and Tompkins [13] reconfirmed the observation of Gent and Lindley, and concluded that higher stresses are necessary to cause the growth of microvoids, taking into account the surface energy, which provides an additional restraint upon expansion.

These difficulties were partially overcome by Ball [14], who used a nonlinear elastic analysis and described cavitation as a bifurcation problem. This variational approach does not require pre-existing holes. Later, Hou and Abeyaratne [10] examined the nucleation of a cavitation under multiaxial stress states in the case of nonlinear elasticity using the deformation theory of plasticity, for incompressible solids. On the basis of energy balance, several models have been developed by Lazzeri and Bucknall [6], and by Dompas and Groeninckx [9]. The formation of the cavity is stated to occur when the stored volumetric strain energy is greater than the energy required for the creation and expansion of the surface area of the void. The volume strain energy in the rubber particles can originate from two sources: mechanical loading and differential thermal contraction [15]. Fond et al [3] also developed a model based on energy conservation between the noncavitated state and the final damaged state.

There have been some attempts to use the finite-element method to model rubber-toughened materials [11, 16]. Moreover, the axisymmetric unit cell concept combined with the finite-element method was frequently used to investigate the behaviour of heterogeneous polymers related to cavitation and plastic shear yielding [17, 18]. These studies involved the analysis of simple unit cell model for blends with periodic array, representing regurlarly distributed particles in a continuous matrix.

In this study, the mechanical behaviour of rubber-toughened polymer is described using a finite-element approach. Assuming a periodic array of rubber particles, an axisymmetric unit cell model is designed. Finit-element analyses are performed using a recent hyper-elastic-viscoplastic material model [19] under finite strain formulation. To highlight how the void nucleation acts on yield behaviour, an earlier criterion for cavity nucleation was applied to rubber particle. The objective was to compare and analyse the influence of the occurrence of cavitation on macroscopic behaviour and discuss the information about rubber particle cavitation that could be obtained from these results.

Finite-element modelling of cavitation damage

Considering the heterogeneous nature of the studied material, which consists of a blend of two materials, stiff polymeric matrix and soft rubber particles, the homogenisation technique is used; it accounts for the large deformation behaviour on both microscopic and macroscopic levels.

A numerical homogenisation technique based on the classical concept of a local periodic representative volume element (RVE), and finite-element procedures are proposed. The composite is defined as a periodic three-dimensional array of hexagonal cylinders of matrix material, each containing a single spherical particle. Symmetry arguments are used to limit the RVE to 1/4 that of the axisymmetric cell (figure 1(a)). R is the initial radius of the unit cell, H, the initial height of the cell and r the initial radius of the particle. The boundary conditions at the different edges of the unit cell are written as

To ensure compatibility among all periodic representative cells, the face at x=R of the cylindrical cell is required to remain straight and parallel to the initial state after deformation. To satisfy this requirement, the displacement of all nodes on the line (x=R) in the x-direction are the same.

Figure 1.

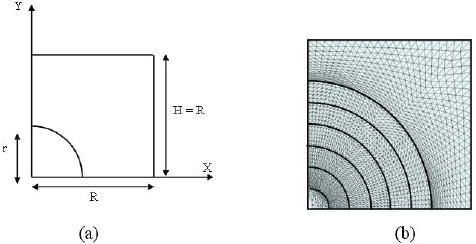
(a) The axisymmetric cell and geometrical parameters. (b) Finite-element meshes adopted for the unit cell of the composite.

The behaviour of the constituent phases of a composite was simulated using a nonlinear constitutive model described in detail by Benseddiq et al [19]. The behaviour of elastomeric particles is described by a hyperelastic Neo-Hookean model, whereas Perzyna's viscoplastic model is adopted to characterise the behaviour of the polymer matrix.

The macro-micro relation assumes that the macroscopic deformation and stress tensors are equal to the RVE averaged strain and stress tensors. The problem of rubber cavitation is studied through the framework of local criteria that modify the properties of the particle. This allows us to simulate the cavitation process by simply replacing the damaged particles by spherical voids in the computations. We assume that cavitation will occur only when the state of the hydrostatic stress is equal to or higher than a limit given by the considered model. Three models of cavitation, found and formulated in term of critical stress, were used in this study.

The criterion of void nucleation is written as

where σ_I and σ_C represent the actual hydrostatic stress in the particle and the critical stress given by the cavitation criterion, respectively. The value of σ_C represents the limit stress of three selected models. These cavitation criteria are given as follows.

• Gent model:

  

  where μ_r and E_r are, respectively, the shear and Young's modulus of the rubber.
• Hou and Abeyaratne model:

  

  where (σ₁, σ₂, σ₃) denotes calculated components of the stress tensor.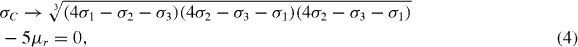
• Fond's model:

  

  where d₀ is the diameter of the rubber particle, Γ the rubber fracture energy, γ the rubber surface energy, and k_r the bulk modulus of the rubber. ν_m and μ_m are, respectively, Poisson's ratio and the shear modulus of the matrix.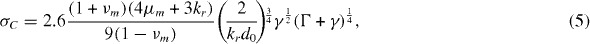

The three models are integrated in the material model for modelling the micromechanical behaviour with the cavitation damage of the particle. The cavitation damage is largely controlled by the hydrostatic tensile stress. Therefore, when hydrostatic tensile stress in any particle element exceeds the critical stress, the cavitation was assumed to occur in this element. To this end in the particle, a mesh with various surfaces corresponding to the various sizes of voids is considered (figure 1(b)). In each step of macroscopic loading, the criterion requires only the knowledge of the hydrostatic stresses for each node of the particle elements. Condition (2) must be checked systematically, and if it is satisfied for a specified surface, meaning that the particle has reached its stress limit at this location, then the stiffness of the given elements is degraded. All these elements are deactivated thereafter. The elements vanishing option through the finite-element code was used to deactivate selected elements. In fact, to deactivate the elements, their stiffness is multiplied by a severe reduction factor. To avoid numerical problems related to equilibrium, the stresses are calculated in several steps without incrementing loading. The cavitation is controlled by a critical hydrostatic stress, according to the assumption posed. The modelling of the damage progresses from the healthy particle case to the total degradation of the particle, jumping from one surface to another. The detailed computational steps for this damage analysis are given in figure 2. The numerical algorithm of the proposed damage model was implemented in the nonlinear finite-element code. The validity of the algorithm was checked with uniaxial loading and two different strain rates.

Figure 2.

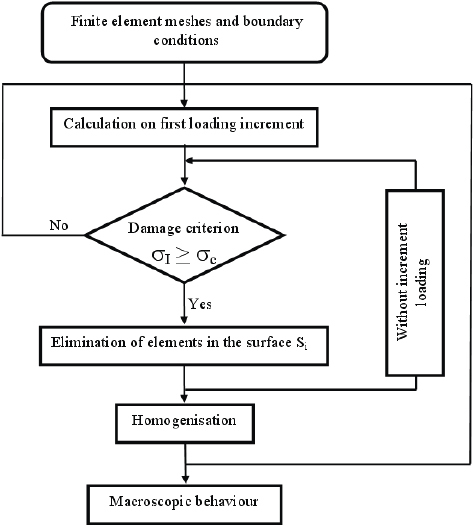
Cavitation modelling algorithm.

Experimental procedure

From brittle to ductile, it is known that some polymers can undergo a significant transition in the deformation behaviour by blending them with elastomers to improve their toughness. Thus, in addition to the cohesive deformation mechanisms, it has been shown that damage mechanisms are very active in rubber-toughened polymers under tension, namely, cavitation in the rubbery phase, crazing and matrix shear yielding at the nodule interface.

To gain a basic understanding of the deformation mechanisms, experiments were performed to examine the elastic-viscoplastic deformation behaviour of rubber-toughened polymethylmethacrylate (PMMA).

Material and specimens

The material used in the experiments was PMMA, with a weight-average molar mass of 60 000 g mol⁻¹. The homopolymer and blends containing, by volume, 30% core shell rubber particles were tested. The particles supplied had a hard shell, a soft polybutadienne core and overall diameters of about 270 nm. Plates 4 mm thick were prepared by compression moulding. Tensile specimens with gage section dimensions of 90 mm×10 mm×4 mm were machined from these plates (figure 3(a)).

Figure 3.

(a) Tensile sample geometry. (b) Tensile sample with ink marks for the video camera testing system.

Tensile test and measurements

All tensile tests over a range of strain rates and temperatures were conducted on an Instron machine to measure the stress–strain behaviour of the rubber-toughened PMMA. The introduction of the rubber phase into the matrix completely changes the deformation mechanisms of PMMA; the blend shows significant ductility [20]. At room temperature, specimens of RT-PMMA are strained under uniaxial tension and strain rates of 10⁻⁴, 10⁻³ and 5×10⁻³ s⁻¹.

The mechanical tests were performed on a tensile test machine. It is a strain measurement system based on a video camera system and enables us to assess volume changes in real time during deformation as well as measure the strain at a particular zone of yield initiation [21].

Gloaguen and Lefebvre [22] calculated the true stress–strain and volumetric strain behaviour of nylon and polypropylene by measuring the separation of pairs of ink marks on rectangular bar specimens. Two cameras were used to simultaneously measure the strain in all three directions. Later, G'Sell et al [21] developed an optical technique using rectangular bar specimens, where the assumption of constant volume plasticity is not required. The locations of seven dots (figure 3(b)) on the surface of the specimen were used to calculate the true axial and lateral strain at a particular axial location. These are the most successful endeavours used the video system to capture images of the specimen at various stages of deformation.

Assuming a transversely isotropic strain tensor, the total true volume strain ε_V is expressed as

where V and V₀ are the instantaneous and initial volumes. ε₁₁ and ε₂₂ are the axial and transverse true strains, respectively.

The plastic volume strain (volume changes due to cavitation [20]) is defined by

where ε_V^e is the elastic volume strain expressed as

where ν and E are Poisson's ratio and Young's modulus, respectively. The true stress is given by

where S and S₀ are the instantaneous and initial cross sections, respectively, and F is the applied force.

Results and discussion

We limit this study to the simulation of the material behaviour at room temperature, at which the cavitation mechanism is in effect and plays an important role in the ductile-brittle transition of the glassy polymer.

To determine the parameters of the chosen viscoplastic law describing the behaviour of the polymer matrix, we used experimental yield stress at different strain rates of the PMMA matrix. These yield stress points were deduced using the compression ones, and the relationship between compression yield and tensile behaviour to avoid the brittle nature of the PMMA matrix at room temperature. The set of parameters obtained is represented in table 1.

Table 1.

Viscoplastic parameters at room temperature.

E [MPa]	v	σ0[MPa]	m	γ[s−1]
2078	0.4	63.6589	0.443	0.1

The rubber is assumed to behave as a Neo-Hookean hyperelastic material. The corresponding coefficient is chosen from the literature [3], and is the shear modulus for an incompressible material (μ_r=0.333 MPa). From these parameters and the chosen equation defining the criterion of the appearance of cavitation, the critical stress is calculated and given in table 2. To calculate the critical stress of Fond's model [3] the diameter of the rubber particle is assumed to be 240 nm. The values of the fracture energy and surface tension used are Γ=0.05 and γ=0.03 J m⁻², respectively. Finally, simulations of tensile test are carried out for two different strain rates. In the comparison presented in figure 4, we used the Gent and Hou-Abeyaratne criterion to simulate the damage of the composite by rubber cavitation. The predictions show that the cavitation takes place very early in the elastic part at a total strain of approximately 0.3%.

Table 2.

The calculated critical stresses.

Gent (1956) (σC=5μr/2)	Hou & Abeyaratne (1992) (σC=5μr/2) (In hydrostatic case)	Fond et al (1996)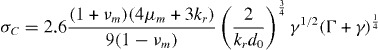
0.833 MPa	0.833 MPa	Kr=2500 MPa 8.92 MPa	Kr=2000 MPa 9.02 MPa	Kr=500 MPa 12.55 MPa

Figure 4.

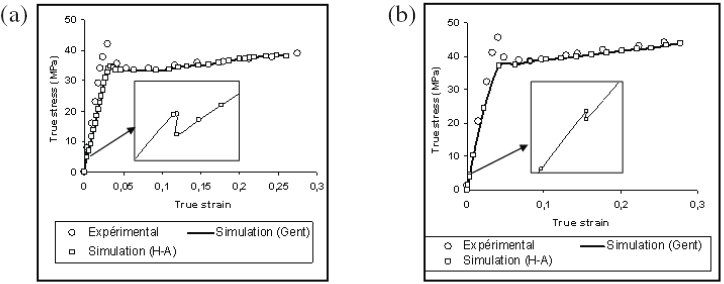
Model predictions (Gent and Hou et al criteria) and experimental measurements at room temperature and different strain rates of (a) 10^{- 3} s^-1 and (b) 10^-4 s^{- 1}.

The two models lead to the same result, because of the pure hydrostatic stress state in the particle. This is confirmed on figure 5, where the evolution of the ratio σ₁/σ₂ in the particle is found to be constant and equal to 1. Although these two models give good results for elastomers, they clearly underestimate the level of stress at which the cavity in the particle appears. This may be due to the surface energy effect which is not taken into account in the two models.

Figure 5.

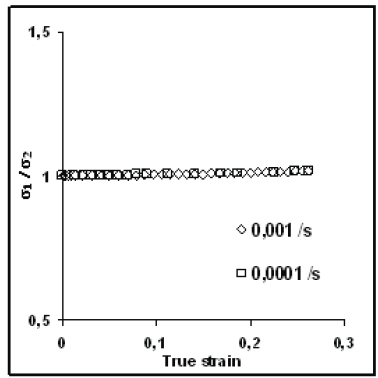
Triaxiality ratio σ₁/σ₂ in the rubber particle for different strain rates.

The same experimental results are shown with the results of simulations using the Fond criterion in figure 6. The level of stress at which cavitation appears depends on the bulk modulus Kr. For a value of 2500 MPa, the critical strain is 1%. It reaches 2% when Kr equals 2000 MPa.

Figure 6.

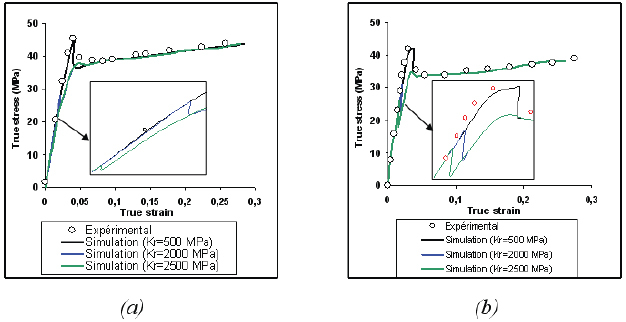
Model predictions (Fond's criterion) and experimental measurements at room temperature and different strain rates of (a) 10^-3 s^-1 and (b) 10^-4 s^-1.

The optimal value of Kr that gives the best agreement between the experiment and simulation is 500 MPa. In this case, the critical cavitation strain is about 4%. This critical strain also depends on strain rates. When Kr equals 500 MPa, it is 4.1% at 10⁻³ s⁻¹, and 3.8% at 10⁻⁴ s⁻¹.

At this stage of damage, plasticity of the matrix is present, but does not seem to play an important role. Matrix yielding is due entirely to the onset of rubber cavitation. This study of sensitivity would have been important if we had had the properties of the core-shell particle. The formulation used here is valid for a pure rubber particle. In figure 7, we show the capability of the model to reproduce the damage behaviour of polymeric composite and the sensitivity at the strain rates. A highly satisfactory agreement is obtained in term of the stress–strain response and plastic volume strain.

Figure 7.

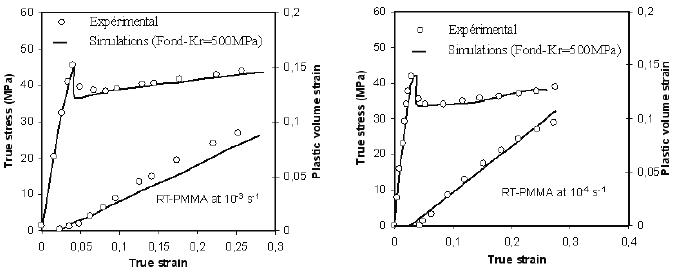
Experimental and numerical evolution of stresses and plastic volume strain with true strain.

Conclusion

The finite-element analysis on RT-PMMA was carried out to predict the macroscopic behaviour of this polymeric composite.

To account for the strain-softening-rate-dependent material behaviour of amorphous polymers, Perzyna's visco-plastic model was adopted. In addition, for large deformations typically exhibited by the rubbery phase of the composite, a hyperelastic Neo-Hookean model was used to model the particle behaviour. The strain softening and hardening was described by the combination of a viscoplastic model with multilinear isotropic hardening. The homogenisation technique adopted for the material in this study consists of a regular stacking of rubber particles in an amorphous polymer matrix; it was shown that this approach can be successfully applied to predict the macroscopic behaviour of the heterogeneous polymer materials with complex material behaviour and microstructure.

The effect of cavitated particles on the macroscopic response was also studied. One of the most important results of the finite-element simulations is the reduction in the stress level at the macroscopic scale when the void volume fraction increases. The hydrostatic stress which controls the initiation of cavitation is strongly dependent on the volume fraction of voids. The hydrostatic stress in the rubber particle is also influenced significantly by the bulk modulus of the rubber. The onset of cavitation takes place under loading conditions for which the hydrostatic stress reaches precisely the critical value, which corresponds to the yield stress of the material and prevents brittle fracture.