Smart optical coherence tomography for ultra-deep imaging through highly scattering media

Iterative time reversal overcomes multiple scattering and breaks the imaging-depth limit in optical coherence tomography.

Abstract

Multiple scattering of waves in disordered media is a nightmare whether it is for detection or imaging purposes. So far, the best approach to get rid of multiple scattering is optical coherence tomography. This basically combines confocal microscopy and coherence time gating to discriminate ballistic photons from a predominant multiple scattering background. Nevertheless, the imaging-depth range remains limited to 1 mm at best in human soft tissues because of aberrations and multiple scattering. We propose a matrix approach of optical imaging to push back this fundamental limit. By combining a matrix discrimination of ballistic waves and iterative time reversal, we show, both theoretically and experimentally, an extension of the imaging-depth limit by at least a factor of 2 compared to optical coherence tomography. In particular, the reported experiment demonstrates imaging through a strongly scattering layer from which only 1 reflected photon out of 1000 billion is ballistic. This approach opens a new route toward ultra-deep tissue imaging.

INTRODUCTION

The propagation of light in inhomogeneous media is a fundamental problem with important applications, ranging from astronomical observations through a turbulent atmosphere to deep tissue imaging in microscopy or light detection through a dense cloud in LIDAR (light detection and ranging) technology. Conventional focusing and imaging techniques based on Born approximation generally fail in strongly scattering media because of the multiple scattering (MS) events undergone by the incident wavefront. Recent advances in light manipulation techniques have allowed great progresses in optical focusing through complex media (1). Following pioneering works in ultrasound (2, 3), Vellekoop and Mosk (4) showed how light can be focused spatially through a strongly scattering medium by actively shaping the incident wavefront with a spatial light modulator (SLM). Subsequently, a matrix approach to light propagation through complex media was developed (5). This relies on the measurement of the Green’s functions between each pixel of an SLM and of a charge-coupled device (CCD) camera across a scattering medium. The experimental access to this transmission matrix allows taking advantage of MS for optimal light focusing (5–7) and communication (8, 9) across a diffusive layer or a multimode fiber.

MS is a much more difficult challenge with regard to imaging. On the one hand, imaging techniques such as diffuse optical tomography (10), acousto-optic imaging (11), or photoacoustic (12) imaging take advantage of the diffuse light to image scattering media in depth, but their resolution power is limited. More recently, the memory effect exhibited by the MS speckle (13, 14) was taken advantage of to image objects through strongly scattering layers with a diffraction-limited resolution (15–17). However, this only applies to thin opaque layers because the field of view is inversely proportional to the scattering medium thickness. On the other hand, conventional reflection imaging methods provide an optical diffraction-limited resolution but usually rely on a single scattering (SS) assumption. The imaging limit of conventional microscopy can be derived from the scattering mean free path l_s. This describes the average distance that a photon travels between two consecutive scattering events. In turbid media, MS starts to predominate beyond a few l_s’. To cope with the fundamental issue of MS, several approaches have been proposed to enhance the SS contribution drowned into a predominant MS background. The first option is to spatially discriminate SS and MS, as performed in confocal microscopy (18, 19) or two-photon microscopy (20). The second option consists of separating SS from MS photons by means of time gating (21–23). The most widely used coherence time-gated technique is probably optical coherence tomography (OCT) (24–26), which is analogous to ultrasound imaging. It combines scanning confocal microscopy with coherent heterodyne detection (27). OCT has drastically extended the imaging-depth limit compared to conventional microscopy. Nevertheless, its ability in imaging soft tissues remains typically restricted to a depth of 1 mm (28, 29).

Inspired by previous works in ultrasound imaging through strongly scattering media (30–32), we propose a matrix approach of optical imaging to push back the fundamental limit of MS. Experimentally, this approach, referred to as smart-OCT, relies on the measurement of a time-gated reflection matrix from the scattering medium. Unlike previous works (33, 34), the reflection matrix in this work is directly investigated in the focal plane on a point-to-point basis (35, 36). An input-output analysis of the reflection matrix allows for the removal of most of the MS contribution. Then, iterative time reversal (37–39) is applied to overcome the residual MS contribution as well as the aberration effects induced by the turbid medium itself. A proof-of-concept experiment demonstrates imaging through a strongly scattering paper layer from which only 1 reflected photon out of 1000 billion is associated to an SS event from the object hidden behind it. In a second experiment, our approach is successfully applied to optical imaging through a thick layer of biological tissues. Compared to OCT and related methods (34), we show, both theoretically and experimentally, an extension of the imaging-depth limit by a factor of 2. This means a multiplication by a factor of 2 of the sensitivity in decibel compared to existing OCT systems.

RESULTS

Measuring the time-gated reflection matrix

The smart-OCT approach is based on the measurement of the time-gated reflection matrix R from the scattering sample. Until now, optical transmission/reflection matrices have always been measured in the k space (plane-wave basis) (5, 6, 33, 34). Here, inspired by previous studies in acoustics (35, 36), the reflection matrix is directly investigated in the real space (point-to-point basis). The experimental setup and procedure are described in Fig. 1. A set of reflection coefficients, R(r_out,r_in), are measured between each point of the focal plane identified by the vectors r_in at the input and r_out at the output. These coefficients form the reflection matrix R. In the experiments described below, the reflection matrix is measured over a field of view of 40 × 40 μm², mapped with 289 input wavefronts.

Fig. 1. Measuring the time-gated reflection matrix.

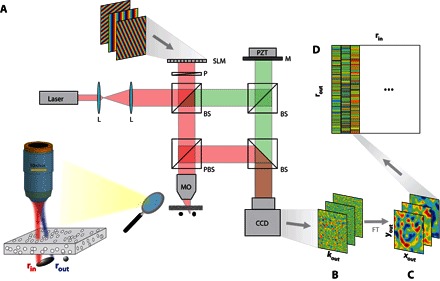
(A) A femtosecond laser beam (center wavelength, 810 nm; bandwidth, 40 nm) is shaped by an SLM acting as a dynamic diffraction grating. A set of incident plane waves is thus emitted from the SLM and focused at a different position in the focal plane of an MO (NA, 0.25). The backscattered wave field is collected through the same MO and interferes with a reference beam on an CCD camera. The latter one is conjugated with the back focal plane of the MO. The amplitude and phase of the wave field are recorded by phase-shifting interferometry (5). The time of flight t is controlled by the length of the interferometric arm and is matched with the position of the focal plane. Experimental setup: L, laser; P, polarizer; MO, microscope objective; BS, beam splitter; PBS, polarized beam splitter; PZT, piezo phase shifter; M, mirror. (B) For each input-focusing point r_in, the reflected wave field R(r_in,k_out) is recorded in the k space. (C) A two-dimensional Fourier transform yields the wave field in the real space R(r_in,r_out), where r_out represents the output-focusing point in the focal plane. (D) For each incident-focusing point r_in, the recorded wave field is stored along a column vector. Finally, the set of column vectors forms the reflection matrix R = [R(r_in,r_out)].

Reflection matrix in the SS regime

Figure 2A displays the reference reflection matrix R₀ measured for a ZnO bead with a diameter d = 10 μm, deposited on a microscope slide. R₀ contains two main contributions:

Fig. 2. Target detection in the deep MS regime.

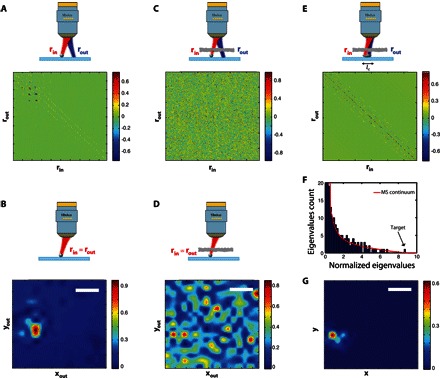
(A) The reference time-gated reflection matrix R₀ measured for a ZnO bead deposited on a glass slide. (B) En face OCT image deduced from R₀ (Eq. 1). (C) The time-gated reflection matrix R in the presence of a strongly scattering layer (L = 12.25l_s). (D) En face OCT image deduced from R (Eq. 1). (E) The SS matrix R_S deduced from R with l_c = 5 μm (Eq. 3). (F) The eigenvalue histogram of R_SR^†_S compared to the random matrix prediction (red line): the largest eigenvalue emerges from the MS noise. (G) Smart-OCT image deduced from the first eigenstate of R_S. Scale bars, 10 μm.

(1) The specular echo from the glass slide that emerges throughout the diagonal of R₀.

(2) The strong bead echo that arises for positions r_in ~ r_b, with r_b being the position of the bead in the focal plane. Because the bead diameter d is larger than the width δ of the point spread function, the bead also emerges along off-diagonal elements, for which |r_out − r_in| ≤ d.

The SS contribution thus only emerges along the diagonal and closed-diagonal elements of R₀. This is accounted for by the fact that a singly scattered wave field can only come from points illuminated by the incident focal spot. A time-gated confocal image can be deduced from R₀ by only considering its diagonal elements, such that

$${\mathit{I}}_0(\mathbf{r})=|{\mathit{R}}_0(\mathbf{r},\mathbf{r})|$$ (1)

The corresponding image displayed in Fig. 2B is equivalent to an en face OCT image. Not surprisingly, it shows a clear image of the target on the microscope glass slide.

Reflection matrix in the deep MS regime

In the second experiment, a stack of two paper sheets is placed between the MO (microscope objective) and the target bead (see Fig. 1). The thickness of each sheet is 82 μm, hence an overall thickness L = 164 μm for the scattering layer. The distance between the front surface of the scattering layer and the target is F ≃ 1 mm. The scattering and transport mean free paths in the paper sheet have been measured and estimated to be l_s ~ 13.4 μm and l_t ~ 19.9 μm, respectively (see section SI). This yields an optical thickness L ~ 12.25l_s ~ 8.2l_t. The ballistic wave has to go through 24.5l_s back and forth, thus undergoing an attenuation of exp(−24.5) ~ 2 × 10⁻¹¹ in intensity. The SS-to-MS ratio (SMR) of the reflected wave field is estimated to be 10⁻¹² in the MO back focal plane (see section SII). For an incident plane wave, this means that only 1 scattered photon out of 1000 billion is associated to an SS event from the target. As shown in fig. S3, the target is far to be detectable and imaged in this experimental configuration, whether it be by conventional microscopy (SMR, ~10⁻¹⁰), confocal microscopy (SMR, ~10⁻⁸), or OCT (SMR, ~10⁻⁵). This experimental situation is thus particularly extreme, even almost desperate, for a successful imaging of the target.

Figure 2C displays the reflection matrix R measured in the presence of the scattering layer. Contrary to the SS contribution that emerges along the diagonal and closed-diagonal elements of R (Fig. 2A), MS randomizes the directions of light propagation and gives rise to a random reflection matrix (30). Nevertheless, one can try to image the target by considering the diagonal of R (Eq. 1). The corresponding en face OCT image is shown in Fig. 2D. As theoretically expected (see fig. S3), MS still predominates despite confocal filtering and coherence time gating. An image of speckle is thus obtained without any enhancement of the intensity at the expected target location (see comparison with the reference image in Fig. 2B).

Matrix approach dedicated to target detection in the deep MS regime

An alternative route is now proposed to image and detect the target behind the scattering layer. The smart-OCT approach first consists in filtering the MS contribution in the measured reflection matrix R. To that aim, the R matrix is projected on a characteristic SS matrix S, whose elements are given by

$$\mathit{S}({\mathbf{r}}_{\mathbf{out}},{\mathbf{r}}_{\mathbf{in}})= \text{exp}(-{|{\mathbf{r}}_{\mathbf{out}}-{\mathbf{r}}_{\mathbf{in}}|}^2/{\mathit{l}}_{\mathrm{c}}^2)$$ (2)

l_c is a tunable parametric length that accounts for the fact that the ballistic signal does emerge not only along the diagonal of the R matrix but also along off-diagonal elements (Fig. 2A). l_c is governed by two factors:

(1) The coherence length of the ballistic wave field in the focal plane: In addition to ballistic attenuation and MS, the scattering layer also induces aberrations that degrade the focusing quality of the ballistic wavefront and enlarge the point spread function of the imaging system. (2) The size of the target: As shown by Fig. 2A, the target signal does not only emerge along the diagonal elements of R in the absence of the scattering layer. This is accounted for by the size of the target that is larger than the resolution cell.

Mathematically, the projection of R can be expressed as a Hadamard product with S

$${\mathbf{R}}_{\mathbf{S}}=\mathbf{R}·\mathbf{S}$$ (3)

which, in term of matrix coefficients, can be written as

$${\mathit{R}}_{\mathit{S}}({\mathbf{r}}_{\mathbf{out}},{\mathbf{r}}_{\mathbf{in}})=\mathit{R}({\mathbf{r}}_{\mathbf{out}},{\mathbf{r}}_{\mathbf{in}})\times \mathit{S}({\mathbf{r}}_{\mathbf{out}},{\mathbf{r}}_{\mathbf{in}})$$ (4)

This mathematical operation thus consists in keeping the diagonal and closed-diagonal coefficients of R, where the SS contribution arises, and filtering the off-diagonal elements of R mainly associated with the MS contribution. It can be seen as a digital confocal operation with a virtual pinhole mask of size l_c (40). In the present experiment, the SS matrix R_S is deduced from R by considering that l_c = 5 μm. The result is displayed in Fig. 2E. R_S contains the SS contribution as wanted, plus a residual MS contribution (see comparison with the reference matrix in Fig. 2A). This term persists because MS signals also arise along and close to the diagonal of R. Compared to an SS/MS separation performed in the far field (31, 34), an SS projection in a point-to-point basis (Eq. 3) is much more flexible because the tunable parameter l_c can be adapted as a function of the aberration level or the expected target size.

Once this SS matrix is obtained, one can apply the DORT method (French acronym for Decomposition of the Time Reversal Operator). Initially developed for ultrasound (37, 38), the DORT method takes advantage of the reflection matrix to focus iteratively by time reversal processing on each scatterer of a multitarget medium (39). Mathematically, the time reversal invariants can be deduced from the eigenvalue decomposition of the time reversal operator RR^† or, equivalently, from the singular value decomposition of R (the superscript † stands for transpose conjugate). A one-to-one association between each eigenstate of R and each scatterer exists. On the one hand, the eigenvectors of R allow selective focusing and imaging of each scatterer. On the other hand, the associated eigenvalue directly yields the scatterer reflectivity. Nevertheless, this one-to-one association is only valid under an SS approximation. Hence, the DORT method cannot be applied to the raw matrix R because it contains an extremely predominant MS contribution. The trick here is to take advantage of the SS matrix R_S.

A singular value decomposition of R_S is performed. This consists in writing R_S = UΣV^†. Σ is a diagonal matrix containing the real positive singular values σ_i in a decreasing order, σ₁ > σ₂ > ··· > σ_N. The square of the singular values, ${\mathrm{\sigma }}_{\mathit{i}}^2$, correspond to the eigenvalues of ${\mathbf{R}}_{\mathbf{S}}{\mathbf{R}}_{\mathbf{S}}^{†}$. U and V are unitary matrices whose columns correspond to the input and output singular vectors U_i and V_i, respectively. Figure 2F displays the histogram of the eigenvalues ${\mathrm{\sigma }}_{\mathit{i}}^2$ normalized by their average. This is compared to the distribution that would be obtained in a full MS regime (see section SIII). The histogram of ${\mathrm{\sigma }}_{\mathit{i}}^2/\langle {\mathrm{\sigma }}_{\mathit{i}}^2\rangle$ in Fig. 2F follows this distribution except for the largest eigenvalue$,{\mathrm{\sigma }}_1^2$, which is actually beyond the superior bound of the MS continuum of eigenvalues. This means that the first eigenspace is associated to the target (31, 32). The combination of the first input and output singular vectors, |U₁ ∘ V₁|, forms the smart-OCT image displayed in Fig. 2G. The image of the target is nicely recovered. The comparison with the en face OCT image displayed in Fig. 2D unambiguously demonstrates the benefit of smart-OCT in detecting a target in the deep MS regime (L = 12.25l_s). Note that the target image does not exactly match with the reference image (Fig. 2B). This difference can be accounted for by the residual aberration effects induced by the scattering layer itself.

The theoretical study developed in section SII confirms this experimental result. Under the conditions of the reported experiment, the imaging-thickness limit (SMR, ~1) is found to be of 1.5l_s for conventional microscopy, 3.5l_s for confocal microscopy, and 7l_s for OCT. This explains the failure of OCT in detecting the target (Fig. 2D). In contrast, the predicted imaging-thickness limit is of 12l_s for the smart-OCT approach. This accounts for the successful detection of the target in our experimental configuration (Fig. 2G).

Imaging in the deep MS regime

From the previous experiment, one could say that the smart-OCT approach is only a single-target detection method dedicated to the deep MS regime. To demonstrate that we can go beyond the detection and imaging of a single target, we investigated a configuration with three 5-μm-diameter ZnO beads deposited on a microscope slide. Figure 3 (A and B) displays the time-gated reflection matrix R₀ and the corresponding en face OCT image in the absence of any scattering layer. Both figures will serve as reference in the following discussion. A paper sheet is then placed between the MO and the focal plane. The corresponding reflection matrix R is shown in Fig. 3C. Not surprisingly, it displays a random feature characteristic of a predominant MS contribution. The en face OCT image built from the diagonal elements of R is displayed in Fig. 3D. Again, the MS speckle prevents clear and unambiguous detection of the three targets (see comparison with Fig. 3B). The MS filter is applied to the raw matrix R (l_c = 5 μm) (Eq. 3), yielding the SS matrix R_S displayed in Fig. 3E. Iterative time reversal is then performed. The first three eigenstates of R_S are displayed in Fig. 3F. A comparison with the reference image in Fig. 3B highlights the one-to-one association between each bead and each of these eigenstates. Finally, the combination of these eigenstates weighted by the corresponding eigenvalue provides the smart-OCT image. Comparison with the en face OCT image (Fig. 3D) demonstrates the success of the smart-OCT approach for imaging in the deep MS regime.

Fig. 3. Imaging in the deep MS regime.

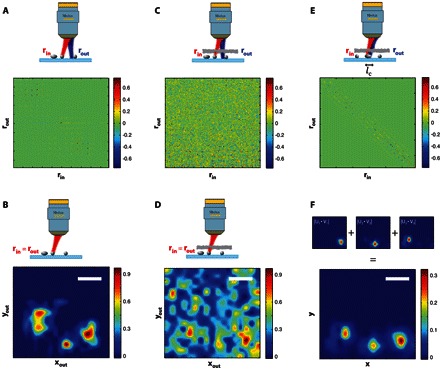
(A) The reflection matrix R associated to three 5-μm-diameter ZnO beads deposited on a glass slide. (B) Time-gated confocal image of the three beads in the absence of the scattering layer. (C) The reflection matrix R measured in the presence of a scattering layer (L = 6.2l_s) placed before the three beads. (D) Time-gated confocal image in the presence of the scattering layer. (E) The SS matrix R_s built from R using Eq. 3. (F) The three first eigenstates of R_s, |U_i ∘ V_i|, are combined to yield the smart-OCT image of the three beads in the presence of the scattering layer. Scale bars, 10 μm.

Imaging through thick biological tissues

Following this experimental proof of concept, we now apply our approach to the imaging of an extended object through biological tissues. A positive U.S. Air Force (USAF) 1951 resolution target placed behind an 800-μm-thick layer of rat intestine tissues is imaged through an immersion objective [40×, NA (numerical aperture), 0.8; Olympus] (see Fig. 4A). The reflection matrix R is measured over a field of view of 60 × 60 μm² (see the green square in Fig. 4A) with 961 input wavefronts. The diagonal of R yields the en face OCT image displayed in Fig. 4B. Because of the aberration effects and MS events induced by the biological tissues, the three bars of the USAF target cannot be recovered. A comparable result is obtained if the DORT method is directly applied to the raw matrix R (see fig. S4). To overcome these detrimental effects, the MS filter is applied to the raw matrix R (l_c = 8 μm) (Eq. 3), yielding the SS matrix R_S. Iterative time reversal is then performed. In previous experiments, the object being imaged consisted of one or a few beads. This sparsity implied that only a few eigenstates were needed to recover the image of the beads. In the present case, the USAF target is an extended object. It is thus associated with a large number M of eigenstates, with M scaling as the number of resolution cells contained in the object (41). To estimate the rank M of the object, one can compute the SD of the image, ${\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathrm{\sigma }}_{\mathit{i}}|{\mathbf{U}}_{\mathbf{i}}\circ {\mathbf{V}}_{\mathbf{i}}|$, as a function of the number n of eigenstates considered for the imaging process. The result is displayed in Fig. 4C. A maximum SD is found for M ~ 250 eigenstates. The corresponding image is displayed in Fig. 4E. The three bars of the USAF target are recovered nicely, and the comparison with the en face OCT image (Fig. 4B) is striking. This experimental result demonstrates the benefit of our approach for deep tissue imaging. To illustrate the importance of a correct determination of M, we also show for comparison the images built from the first 20 and 500 eigenstates of R (see Fig. 4, D and F, respectively). On the one hand, considering too few eigenstates only provides a partial imaging of the field of view (Fig. 4D). On the other hand, considering too many eigenstates blurs the image because the weakest eigenvalues are mainly associated with the MS background (Fig. 4F).

Fig. 4. Imaging through thick biological tissues.

(A) Schematic of the experimental configuration. A positive resolution target USAF 1951 is placed in the focal plane of an immersion MO, with an 800-μm-thick layer of rat intestine on top of it. The region of interest is surrounded by a green square in the bottom inset. DIC, differential interference contrast; WD, working distance. (B) En face OCT image of the resolution target. (C) SD of the smart-OCT image as a function of the number M of eigenstates of R_s considered to build the image. (D to F) Smart-OCT images of the resolution target obtained from the 20, 250, and 500 first eigenstates of R_S.

DISCUSSION

These experimental results demonstrate the benefit of the smart-OCT approach for optical imaging in strongly scattering media. In section SII, this superiority is confirmed by the theoretical investigation of the imaging-depth limit derived for different imaging techniques (conventional/confocal microscopy, OCT, and smart-OCT). In view of applications to deep tissue imaging, Fig. 5 shows the SMR evolution versus the optical depth F in biological tissues. The experimental parameters chosen for this figure are those typically encountered in full-field OCT (42) and are provided in table S1. The detection threshold is set at an SMR of 1. The imaging-depth limits expected in tissues are as follows: 1l_s for conventional microscopy, 8l_s for confocal microscopy, and 12l_s for OCT. The latter value is in agreement with the imaging-depth limit recently reached by Kang et al. (34), with an optical technique similar to OCT. This technique actually combines coherence time gating with a spatial input-output correlation of waves from the far field that allows a confocal discrimination of reflected photons. In contrast, our approach goes beyond OCT because it also involves a subsequent iterative time reversal processing of the reflection matrix. This results in an additional gain in SMR that scales with N, the number of input wavefronts (see section SII). This leads to an imaging-depth limit of 22l_s in Fig. 5, hence multiplying the current OCT limit by almost 2. This imaging improvement is drastic if we keep in mind that the ballistic contribution decreases by a factor of exp(−2L/l_s) in a reflection configuration. The smart-OCT approach is thus particularly suited for ultra-deep tissue imaging. Of course, a trade-off will have to be made in practice between the imaging depth and the measurement time that also scales linearly with N. Note also that the imaging depth can be limited by the dynamic range of the CCD camera. For instance, a dynamic range of 75 dB would be required to reach the theoretical imaging-depth limit under the experimental conditions of Fig. 5 (see table S1).

Fig. 5. Imaging-depth limit in human soft tissues.

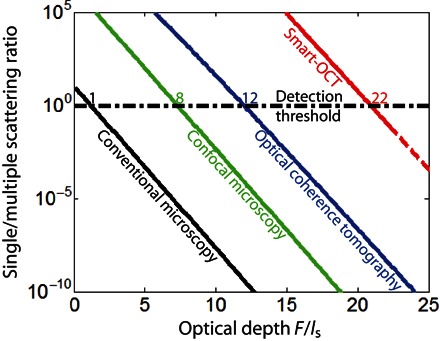
This graph compares the SMRs expected for conventional microscopy (black line), confocal microscopy (green line), OCT (blue line), and smart-OCT (red line) as a function of the optical depth F/l_s. The y axis is in log scale. These curves have been computed from the theoretical study developed in section SII, considering experimental parameters typical of full-field OCT (42). The detection threshold (SMR, ~1; black dashed horizontal line) yields the following imaging-depth limits: ~1l_s for conventional microscopy, ~8l_s for confocal microscopy, ~12l_s for OCT, and ~22l_s for smart-OCT.

A second point we would like to discuss is the resolution and sectioning capabilities of our approach. On the one hand, because the image is built from singly scattered photons, the transverse resolution is only diffraction-limited and does not depend on the penetration depth. On the other hand, the coherent time-gated detection scheme provides an axial resolution δz that is only governed by the coherence time τ_c of the light source: δz ~ cτ_c/(2n), where n is the refractive index of the medium. In the present experiment, the coherence time of the femtosecond laser is 50 fs. This yields an axial resolution of 5 μm in biological tissues (n ~ 1.4). By measuring a set of reflection matrices at successive depths, a three-dimensional image of the sample can thus be obtained as in conventional OCT, with the great advantage that the penetration depth is multiplied by a factor of 2. To reach a better axial resolution, the measurement of the reflection matrix can be made under a simple white light illumination. A recent study actually demonstrated the passive measurement of the time-dependent point-to-point reflection matrix from an incoherent illumination (43). As already demonstrated in full-field OCT (42), the temporal incoherence of the white light source would provide an excellent axial resolution (δz ~1 μm). Moreover, this device would comply with the noninvasive, low-cost, speed, and low-complexity specifications required for medical applications.

In summary, this study proposes a matrix approach of light propagation dedicated to optical detection and imaging through complex media. The so-called smart-OCT approach combines a matrix discrimination of ballistic waves with iterative time reversal. The first proof-of-concept experiment demonstrates the imaging of several microbeads in the deep MS regime, whereas existing imaging techniques, such as OCT, are shown to fail. The second experiment demonstrates the diffraction-limited imaging of an extended object (USAF target) through a thick layer of biological tissues. The theoretical investigation also demonstrates the significant superiority of our approach compared to confocal microscopy or OCT. In particular, an imaging-depth limit of 22l_s is predicted for smart-OCT in biological tissues, hence drastically pushing back the fundamental MS limit in optical imaging.

MATERIALS AND METHODS

The following components were used in the experimental setup (Fig. 1): a femtosecond laser (Femtosecond Fusion 20-400), an SLM (PLUTO-NIR-2, HOLOEYE), an objective lens (10×; NA, 0.25; Olympus), and a CCD camera (Dalsa Pantera 1M60) with a dynamic range of 60 dB. The incident light power was 10 mW in the experiment. Thus, the radiant flux was 10⁶ W cm⁻² at the focal spot in free space. For each wavefront input, the complex-reflected wave field was extracted from four intensity measurements. Hence, the measurement of each line of the reflection matrix can be done at 15 Hz. On the basis of the SMR, the reflected wave field has to be averaged over a given number n of measurements. In the imaging experiments through the paper layer (Figs. 2 and 3) and biological tissues (Fig. 4), the values of number n were fixed to 32 and 5, respectively. Hence, the duration time for the recording of the reflection matrix was ~10 min for the paper (289 input wavefronts) and ~5 min for the biological tissues (961 input wavefronts). The numerical postprocessing of the reflection matrix (SS projection and iterative time reversal) to get the final image took only a few seconds.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/11/e1600370/DC1

section SI. Optical characterization of the paper layers

section SII. SMR for various imaging techniques

section SIII. Eigenvalue distribution of the reflection matrix in the MS regime

fig. S1. Measurement of the scattering mean free path in the paper.

fig. S2. Measurement of the transport mean free path in the paper.

fig. S3. Theoretical prediction of the SMR in the experimental conditions of the article.

fig. S4. Iterative time reversal processing applied to the raw reflection and SS matrices measured through biological tissues.

table. S1. Experimental parameters used for the theoretical prediction of the SMR in Fig. 5 and fig. S3.

References (44–59)