Multicolor 3D meta-holography by broadband plasmonic modulation

High-quality multicolor 2D and 3D meta-holography is realized based on broadband plasmonic modulation.

Abstract

As nanofabrication technology progresses, the emerging metasurface has offered unique opportunities for holography, such as an increased data capacity and the realization of polarization-sensitive functionality. Multicolor three-dimensional (3D) meta-hologram imaging is one of the most pursued applications for meta-hologram not yet realized. How to reduce the cross-talk among different colors in broad bandwidth designs is a critical question. On the basis of the off-axis illumination method, we develop a novel way to overcome the cross-talk limitation and achieve multicolor meta-holography with a single type of plasmonic pixel. With this method, the usable data capacity can also be improved. It not only leads to a remarkable image quality, with a signal-to-noise ratio (SNR) five times better than that of the previous meta-hologram designs, but also paves the way to new meta-hologram devices, which mark an advance in the field of meta-holography. For example, a seven-color meta-hologram can be fabricated with a color gamut 1.39 times larger than that of the red, green, and blue (RGB) design. For the first time, a full-color meta-holographic image in the 3D space is also experimentally demonstrated. Our approach to expanding the information capacity of the meta-hologram is unique, which extends broad applications in data storage, security, and authentication.

INTRODUCTION

Holography provides a promising way to design and reconstruct electromagnetic waves with a desired phase and amplitude. It has a broad range of applications in microscopy, in beam shaping, and in the entertainment industry (1–11). One of the primary applications of holography is the lensless projection of two-dimensional (2D) graphs or 3D objects. Since the birth of the milestone Benton hologram technique, huge efforts were devoted to move toward multicolor holography that can preserve the imaging quality with a wide viewing angle (4, 6, 12). Conventional multicolor holography, such as the Denisyuk scheme, relies on the transparent light modulation plate with different types of photoresists to modulate the primary colors (13–16). Spatial light modulators based on the liquid crystal displays and digital mirror devices were then used to dynamically control the light amplitude and phase in the reconstruction process (17). In these techniques, the period of the pixel on the hologram is related to the viewing angle of the transmitted light, which can be described by the equation below (18)

$$\frac{1}{2\mathit{i}\mathrm{\lambda }}({\mathit{e}}^{\mathit{i}\mathrm{\theta }}-{\mathit{e}}^{-\mathit{i}\mathrm{\theta }})=\frac{1}{\mathrm{\Lambda }}$$ (1)

where λ is the wavelength of incident light, θ is the half-maximum viewing angle (which is defined as the angle between the wave vectors of the incident light and those of the transmitted light), and Λ is the period of the pixel. In these devices, the pixel size is huge; thus, the viewing angle is narrow, which limits its applications.

Metasurface, which is composed of subwavelength artificial structures to arbitrarily tailor the light properties, was recently proposed to be the constituent material of hologram owing to its reduced pixel size (19–25). Although the meta-hologram provides a sufficient viewing range, the new challenge is how to simultaneously multiplex multiwavelengths into one metasurface and to eliminate the cross-talk among different wavelengths. Recently, researchers demonstrated multicolor spectral modulation by integrating three plasmonic pixels with different sizes into one metasurface (4). These three plasmonic pixels independently respond to red, green, and blue (RGB) lights. However, further improvement of this method is challenging because of one fundamental limitation: larger bandwidth leads to more cross-talk. Besides, because the method is based on the resonance of the nanorods, several nanoantennas need to be grouped to obtain an effective response, which reduces the data density and the viewing angle of the hologram.

To solve these problems, we develop the off-axis illumination method into the meta-holography and create multicolor 2D and 3D meta-holograms using metasurfaces with a single type of plasmonic pixel. This approach represents a great advance for meta-holography for the following reasons. First, it provides a methodology to overcome the fundamental cross-talk limitation for multicolor meta-hologram. A schematic diagram of this methodology is shown in Fig. 1A. Laser beams with different wavelengths are obliquely irradiated upon the metasurface formed by nanoslit antennas. The outcoming light beams at designed angles are then superimposed to form the final multicolor image (17, 26). By this method, the cross-talk among different wavelengths is eliminated. As shown in Fig. 1B, the signal-to-noise ratio (SNR), defined as the ratio between the peak intensity in the image and the standard deviation (SD) of the background noise (10), can be markedly increased (up to 126.3). The reduced cross-talk also enables holography with more colors. For example, a full-color meta-hologram consisting of seven wavelengths is demonstrated for the first time, which represents a gamut area that is 39% larger than the traditional RGB holography. Second, compared to the conventional multicolor meta-holograms that rely on several types of plasmonic pixels, our approach uses one plasmonic pixel to modulate broad bandwidth wavelengths, which results in an increased viewing angle of the transmitted light because of the reduced pixel period on the metasurface. Third, a full-color meta-holographic image in the 3D space was experimentally demonstrated. It should be noted that the virtual object was displayed in the space, which has a volume of 324,000 μm³. It was the first realization of multicolor 3D meta-holography, which is one more step toward the realization of a matrix-free 3D display with a wide viewing angle that can be observed with the naked eye. Furthermore, our approach is also promising for a broad range of other applications, such as data storage, security, dynamic meta-hologram, and authentication (27–29).

Fig. 1. Schematic diagram of the methodology and achromatic phase shift.

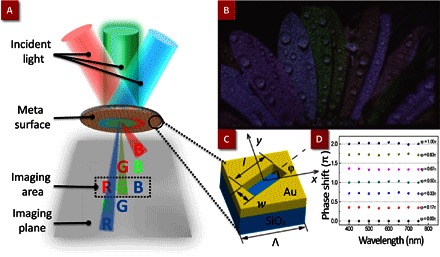
(A) Schematic diagram of the off-axis illumination method for meta-hologram. (B) Experimental results of a flower RGB image. (C) Structure of a plasmonic nanoslit antenna. (D) Simulation results for the phase shift performance of the antennas with different ϕ (unit in radians) from 400- to 750-nm wavelength. Simulation settings: material of the metal is Au; the thickness of the Au film is 120 nm; period Λ = 200 nm; length l =140 nm; width w = 60 nm.

RESULTS AND DISCUSSION

Hologram design principle

The building block to construct the meta-hologram is a set of nanoslit antennas, which is based on the Pancharatnam-Berry phase tuning (30–35) to modulate the transmitted light. These nanoantennas are made of metallic cells on the quartz substrate, as shown in Fig. 1C. (For different samples, the fabrication processes are different. Details of the fabrication and the dimensions of the nanoslit antenna can be found in section S1.) The slit is designed to be angled with respect to the x axis and to provide different phase shifts. According to the local phase shift associated with the spin-orbit interaction and propagating bounded wave exchange (22), the phase of the cross-polarized light (Φ) depends on the orientation angle (φ) of the nanoslit by the relation Φ = 2φ for circular polarization incident light, which is used to determine the angle of the nanoslit (34, 35). It is worth mentioning that such a nanoslit is efficient for a broadband wavelength covering the visible range (380 to 780 nm). Figure 1D shows the simulation results, demonstrating the phase modulation for the nanoslit antennas at different wavelengths. This achromatic feature is the key feature for our approach to achieve multicolor holography without cross-talk. We use this metasurface with broadband performance to design a single holographic image that contains all the image patterns corresponding to different colors. These images are separated and positioned at different spatial locations. Consequently, these individual image patterns are independent from each other so that the cross-talk among colors is eliminated.

With such nanoslit antennas, the meta-hologram is capable of reconstructing both multicolor 2D and 3D images. We first discuss the process in designing a multicolor 2D meta-hologram based on three primary colors (red, green, and blue). The recording and reconstruction principles are shown in Fig. 2 (A and B, respectively). To design the arrangement of the nanoslit antennas, we first divided a colorful image into its RGB components. The corresponding RGB components are shifted to different locations of the imaging plane to separate themselves from each other. These components then form one new holographic image. The phase distribution of the hologram is calculated by the Gerchberg-Saxton (GS) algorithm based on the image, with the termination condition defined by (36)

$$\text{SSE}=\frac{{\iint (|\mathit{g}(\mathit{u},\mathit{v})|-|\mathit{G}(\mathit{u},\mathit{v})|)}^2\mathit{d}\mathit{u}\mathit{d}\mathit{v}}{{\iint |\mathit{G}(\mathit{u},\mathit{v})|}^2\mathit{d}\mathit{u}\mathit{d}\mathit{v}}<\mathrm{\epsilon }$$ (2)

where SSE is the mean square error between the target image and the holographic image, g(u,v) is the Fourier transform of the incident light wave function, G(u,v) is the Fourier transform of the target image, and ε is the preset tolerance. In our calculation, the local minimum effect of the GS algorithm was not particularly taken care of, and the initialized phase of every pixel of the image is set to be zero.

Fig. 2. Design principle and experimental configuration of meta-holography.

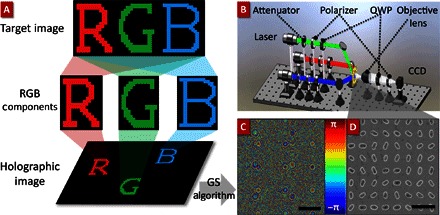
(A) Design principle for the holographic imaging. (B) Experimental setup for the reconstruction process. QWP, quarter-wave plate; CCD, charge-coupled device. (C) Phase diagram of the meta-hologram calculated by the GS algorithm corresponding to the flower holographic image. Scale bar, 500 μm. Color bar, phase shift. (D) Scanning electron microscope image of the nanoslit antennas. Scale bar, 1 μm.

The phase distribution of the hologram calculated by the GS algorithm is shown in Fig. 2C. Then, these phased pixels are substituted by the corresponding nanoslits to provide the desired phase shift. The nanoslit antennas are effective for all the wavelengths because of their broadband performance, as shown in Fig. 1D. In the reconstruction process, the individual color component, for example, the red light, obtains not only the red patterns but also the “unwanted” image patterns designed for green and blue light. The selection of the correct image patterns can then be achieved by the off-axis illumination. The GS algorithm relies only on the phase and amplitude of the transmitted light. It is possible to tune the k_x and k_y components of the transmitted light wave vector using Eq. 3 without affecting the holographic reconstruction (Fig. 3A). For example, the wave vector in the x direction can be calculated as

$${\mathit{k}}_{\mathit{x}}={\mathit{k}}_0\times \frac{{\mathit{e}}^{\mathit{i}{\mathrm{\theta }}_{\mathit{x}}}+{\mathit{e}}^{-\mathit{i}{\mathrm{\theta }}_{\mathit{x}}}}{2}$$ (3)

where k₀ is the transmitted light wave vector and θ_x is the incident angle with respect to the x axis (see fig. S1). As k_x and k_y are tuned, the holographic images are shifted on the imaging plane. The correct holographic images can be shifted and superimposed into the final image, whereas the unwanted patterns are moved out of the imaging region. By this reconstruction principle, a single type of the nanoslit antenna is used to control multiple wavelengths.

Fig. 3. k-space modulation.

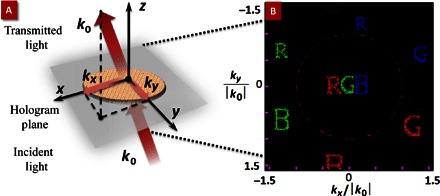
(A) Schematic diagram to demonstrate the modulation of the k space of incident light. (B) Simulation results for the hologram design that shifts all the unwanted images into the k space corresponding to evanescent waves.

It can be derived from Eq. 1 that the maximum viewing angle can be even larger than π for the metasurface plasmonic pixels, which has a period that is smaller than the wavelength. In this case, the $\sqrt{{\mathit{k}}_{\mathit{x}}^2+{\mathit{k}}_{\mathit{y}}^2}$ component is larger than |k₀|, and k_z becomes an imaginary number, which means that the transmitted light is converted into the evanescent waves on the metasurface plane. In such broad k space of the transmitted light, it is possible to design the unwanted patterns in the k space corresponding to the evanescent waves. The unwanted patterns then “disappear” in the far field and are hidden from the observer. Simulation results are shown in Fig. 3B to demonstrate such design (the method used for this simulation is the GS algorithm mentioned in the previous section). The red dashed lines in the figure mark the k-space boundary between the evanescent wave and the propagating wave. It is clear that the unwanted patterns corresponding to each color are located outside the k space of the propagating wave. The observer does not capture the near-field waves, and these patterns are hidden. This design strategy makes the imaging area to only consist of the desired image patterns. The holographic image stays “clean” and free from the interference of the unwanted image. Furthermore, the accessible data capacity of the subwavelength hologram can be increased with our approach. Traditionally, the information that existed in the evanescent domain (k_x,y > k₀) cannot be captured under the normal incidence condition. With off-axis illumination, all the data in 4k₀ × 4k₀ (k_x,y < 2k₀) can be accessed in the far field.

Optical characterization

The schematic diagram of the experimental setup of the holographic reconstruction is shown in Fig. 2B. The incident angles of the RGB lasers and the specifications of each component can be found in section S2. The image is captured by a CCD camera.

In this design, the nanoslits (1.6 × 10⁷) were fabricated on a total area of 4 mm². Figure 2D shows the image of the holographic metasurface characterized by a scanning electron microscope. The experimental holographic image for a multicolor “flower” pattern is shown in Fig. 4. Figure 4 (A to C) shows the simulation results individually corresponding to the RGB colors for comparison. The experimental results for each color and their superposition are presented in Figs. 1B and 4 (D to F). It is clear that the experimental results restore the features of the designed images. The images corresponding to the RGB colors are independent from each other, and the cross-talk among different wavelengths is eliminated. Therefore, the image details are clear, and the final image is vivid. It should be noted that in this experiment, a 405-nm laser is used to represent the blue color (450 to 495 nm). This wavelength mismatch is accountable for the difference between the simulation and experimental results.

Fig. 4. Multi-image meta-holography.

(A to C) Simulation results for the flower holography for the RGB image patterns. (D to F) Experimental results corresponding to the red, green, and blue image patterns, respectively. (G to I) RGB holographic images of map of China, which are reconstructed by the same hologram metasurface of the flower image with different light incident angles.

The SNR is calculated to be 126.3 from the experimental results, which is more than five times higher than that of the previous meta-hologram design (10). Such high-quality images are mainly attributed to the neglectable cross-talk between different colors. The off-axis illumination also reduces the noise from the copolarized light and contributes to the SNR. The nanoslit antenna is effective to all the wavelengths, and a single type of antenna can cover the entire metasurface. Compared to previous meta-hologram methodology that requires multiple types of plasmonic pixels to share the same metasurface (4), the pixel period for our approach can be smaller and the viewing angle of the meta-hologram can be larger.

The above off-axis illumination method has also been used to design various types of photonic devices with different functionalities, including the following.

Multi-image hologram.

Multi-image holography can be achieved. Because the position of the patterns on the image plane depends on |k_x| and |k_y| of the illumination light, multi-image hologram can be designed on one single metasurface. Switching among different images is achieved by tuning the incident angle of the illumination light. Using this method, we designed and fabricated a dual-image hologram consisting of the flower (Fig. 4, D to F) and “map of China” images (Fig. 4, G to I). The details of the fabrication process and characterization are summarized in sections S1 and S2, as well as in Materials and Methods. When the incident angle of the light is set as θ_x = 71.55° and θ_y = 71.55°, the red flower pattern appears in the imaging area. The image changes into the red map of China as the incident angle is set at θ_x = 71.58° and θ_y = 90°. The larger incident angle will affect the linearity between the phase shift of nanoslit antennas and the rotation angle φ to a certain extent. However, the performance of holography will not be obviously degraded because of the high tolerance of meta-hologram, which has been discussed in detail by Zhang et al. (11) and also demonstrated in our experiments. It is worth mentioning that, with proper design, superposition of even more images is achievable. An angle-tuned dynamic meta-hologram is even possible if the frames of dynamic images are compiled into the metasurface and each frame is switched by tuning the incident angle.

Seven-color meta-hologram.

With this new technique, a seven-color meta-hologram image is designed and fabricated for the first time, as shown in Fig. 5 (the simulation results are shown in section S3). It follows the similar design principle of the RGB hologram except that lasers at seven different wavelengths were used to reconstruct the image. The details of the design parameters, fabrication process, and characterization are summarized in sections S1 and S2, as well as in Materials and Methods. Compared to the RGB design, the key feature for such full-color holography is that the color gamut is increased by 1.39 times (details can be found in section S4). A larger color gamut describes a broader spectrum that the holography can be reproduced in in the color space (37). Human eyes can capture a broader spectrum beyond the colors mixed by the RGB components. Seven-color mixing extends the range of the colors available for the holography and provides a much improved capability to display a more colorful and superior image. Furthermore, the light sensors and retinas of animals are sensitive to a wide range of wavelengths, which requires a much larger color gamut than the one mixed by RGB (38). Our approach has great potential to satisfy these needs and even beyond. For the topic of authentication, it is possible to fabricate a super-thin meta-hologram, including both the visible and “invisible” image patterns at a specific wavelength, so the holographic image contains “secret” information invisible to the human eyes. Furthermore, for the data security applications, introducing more wavelengths is similar to increasing the length of the password, which increases the order of the complexity and enhances the security level.

Fig. 5. Seven-color meta-holography.

(A) Seven-color holographic image for the Sun Phoenix, a pattern discovered on an ancient artifact gold coil, made in the Chinese Shang dynasty 3000 years ago. (B to H) Patterns corresponding to purple, blue, cyan, red, orange, yellow, and green colors, respectively.

Multicolor 3D imaging.

Using this new method, we also design and fabricate a multicolor 3D object. A modified point source algorithm is adapted to design the metasurface (10, 39). The 3D object is represented by a collection of the RGB point sources. The complex amplitude at the hologram plane is then calculated as the superposition of the light fields from the entire 3D object consisting of all point sources. Different from the 2D holographic characterization setup, the 3D object needs to scan through the vertical direction (z dimension) of the imaging space. The details on the characterization setups are summarized in section S2 and in Materials and Methods. The results are presented in Fig. 6. A spiral helix pattern composed of 20 light spots is designed, which is denoted as a “stars” map. At different positions along the z axis, the holographic image is captured by the CCD camera. Stars with varying colors can be identified in these images. These stars are arranged in a space of 60 × 60 × 90 μm. The volume of this space is 324,000 μm³. A video is taken to present this 3D stars map, and it can be found in the Supplementary Materials. The realization of the matrix-free, full-color 3D display for the naked eye is a long-pursued dream not yet realized. To achieve this goal, it is very important to compile a great amount of information into the limited hologram surface to control all the pixels in a 3D space. Our approach provides a unique advantage for its enhanced data capacity and high density of plasmonic pixels on the metasurface.

Fig. 6. Multicolor 3D meta-holography.

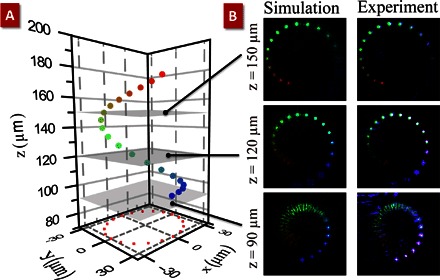
(A) Schematic diagram of the 3D object in the spatial coordinate. (B) Experimental results for the cross-sections at different z positions.

SUMMARY AND CONCLUSIONS

In summary, we present a unique methodology for meta-hologram. This approach not only overcomes the fundamental cross-talk limitation and improves the SNR in this field but also provides new opportunities to design functional devices that have never been realized before. The physics related to the pattern selection and k-space modulation are discussed. Our approach can use a broad k space, extending into the evanescent wave region. This feature extends the usable data capacity of the meta-hologram. We also demonstrate novel and interesting photonic devices, such as the multi-image hologram, the “Sun Phoenix” seven-color meta-hologram, and the stars map 3D imaging, which represent an advance for meta-hologram technology. It is worth mentioning that there are some aspects that could further improve this method. For example, the efficiency for the short wavelength is relatively low (section S5). Methods, such as the reflective (12, 40) or dielectric (41, 42) metasurface, are very promising to overcome this challenge. Furthermore, the illumination requires precise tuning compared with the existing methods based on on-axis illumination (4, 6, 24), and there is plenty of space to further improve the setup. The potential of our approach is not limited to the cases discussed above. It offers new routes for many exciting applications, such as the angle-tuned dynamic meta-hologram and matrix-free 3D display for the naked eye. Various fields, including data storage, security, and authentication, can also benefit from this technique. Furthermore, this approach requires relatively low fabrication accuracy and can be fabricated with a wide choice of materials, which makes it feasible to be linked to other techniques, such as the nanoimprint for mass production.

MATERIALS AND METHODS

Experimental setup of optical characterization

The characterization setup for the 2D holography is shown in Fig. 2B. In our setup, the laser from the light source passed through a tunable attenuator (maximum attenuation: optical density, 3; Daheng Optics) to control its amplitude. Then, the polarizer (10LP-VIS-B, Newport) and the achromatic Zero-Order QWP (10RP52-1, Newport) were used to convert the laser beam into a circular polarized light. The holographic image was captured with a CCD camera through an objective lens. The other pair of polarizer and QWP was used to filter out the noise.

The characterization setup for the 3D holography is slightly different from that for the 2D holography. One scanning system, which scans the xy imaging plane across the z axis, was added into the optical path, as shown in Fig. 2B. With this scanning system, the objective lens can capture the images at different planes along the z direction.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/11/e1601102/DC1

section S1. Plasmonic nanoantenna array fabrication

section S2. Experimental setup of optical characterization

section S3. Simulation results for the seven-color hologram

section S4. Calculation of the color gamut

section S5. Efficiency of the meta-hologram

fig. S1. Definition of incident angles.

fig. S2. Target pictures, simulation, and experimental results of the seven-color Sun Phoenix holography.

fig. S3. Efficiency of the meta-hologram.

table S1. Incident angles for “flower.”

table S2. Incident angles for “map of China.”

table S3. Incident angles for “seven-color hologram.”

table S4. Incident angles for “3D imaging.”

table S5. List of the wavelength versus colors.

movie S1. The evolution of the images at different elevations above the hologram for “3D imaging.”