Abstract
The genotype–phenotype (GP) map is a central concept in evolutionary biology as it describes the mapping of molecular genetic variation onto phenotypic trait variation. Our understanding of that mapping remains partial, especially when trying to link functional clustering of pleiotropic gene effects with patterns of phenotypic trait co-variation. Only on rare occasions have studies been able to fully explore that link and tend to show poor correspondence between modular structures within the GP map and among phenotypes. By dissecting the structure of the GP map of the replicative capacity of HIV-1 in 15 drug environments, we provide a detailed view of that mapping from mutational pleiotropic variation to phenotypic co-variation, including epistatic effects of a set of amino-acid substitutions in the reverse transcriptase and protease genes. We show that epistasis increases the pleiotropic degree of single mutations and provides modularity to the GP map of drug resistance in HIV-1. Moreover, modules of epistatic pleiotropic effects within the GP map match the phenotypic modules of correlated replicative capacity among drug classes. Epistasis thus increases the evolvability of cross-resistance in HIV by providing more drug- and class-specific pleiotropic profiles to the main effects of the mutations. We discuss the implications for the evolution of cross-resistance in HIV.
Keywords: mutation, genetic integration, M-matrix, G-matrix.
Introduction
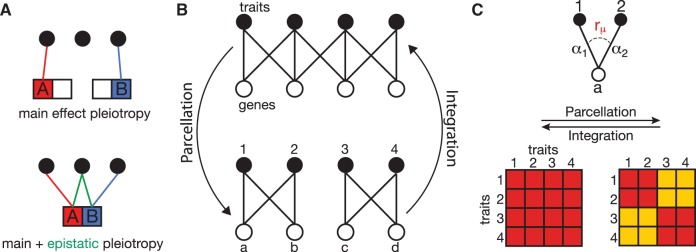
A central goal of evolutionary biology is to understand how genetic variation maps onto phenotypic variation, and ultimately fitness. Many phenotypic traits are complex traits affected by many genes, as for instance Alzheimer’s disease or type 2 diabetes in humans (Mackay et al. 2009; Plomin et al. 2009). The genes affecting such traits often affect other traits as well, and are thus pleiotropic. The way they affect trait variation also often depends on their interactions with other genes. There is thus pleiotropy and epistasis in the GP map (Hansen 2006; Phillips 2008). The way pleiotropic and epistatic gene effects are organized within the GP map is expected to play a capital role in the capacity of living organisms to adapt and evolve (Wagner and Altenberg 1996; Hansen 2006; Wagner et al. 2007; Armbruster et al. 2014). In particular, the modular clustering of pleiotropic effects among sets of traits allows phenotypic modules to respond to selection independently from each other, potentially increasing the evolvability of the organism (Wagner and Altenberg 1996; Wagner et al. 2007; Armbruster et al. 2014). Trait genetic integration (i.e., higher density of pleiotropic links within than between modules; fig. 1B) may be favored when coordinated changes at multiple traits are necessary, or disfavored when pleiotropic links act as genetic constraints on evolution (leading to parcellation, see fig. 1B). Indeed, when several traits are affected by a common set of pleiotropic loci, as within a module, they become less evolutionary independent because changes in allelic frequencies at those loci will affect all traits, and changes favorable to one trait may be detrimental to the other traits (Otto 2004). This would be the case if, for instance two traits are genetically correlated while selection acts to change only one of them, while keeping the other constant. Evolution may break such pleiotropic constraints, or build them up, if variation in pleiotropy exists at the underlying genes. Trait integration is often deduced from trait phenotypic or genetic correlations within a population (fig. 1C) and is expected to reflect the degree of genetic independence of the traits (Pigliucci 2003; Armbruster et al. 2014). Genetic correlations among traits are function of the correlation among pleiotropic mutational effects at the underlying genes (fig. 1C), among other more transient sources of genetic covariances (e.g., linkage disequilibrium, drift). Variation in genetic covariation among traits thus depends on variation in the pleiotropic degree and in the correlation of the effects of pleiotropic mutations. Which of these two properties of pleiotropic mutations is more likely to vary and to contribute to trait correlations in natural systems is mostly unknown.
Fig. 1.
(A) two mutations A and B affect each one trait when alone and affect each two traits when together on the same sequence. The epistatic interaction between A and B thus has pleiotropy one and adds one trait to the trait repertoire of both A and B. (B) Genotype–phenotype maps, with edges between genes (empty circles) and traits (solid circles) representing the pleiotropic effects of the genes. Parcellation results from the decrease of the number of edges between trait modules (1–2 and 3–4). Integration is the reverse process (re-drawn from Wagner and Altenberg 1996). (C) A mutation in gene a has effects α1 on trait 1 and α2 on trait 2. The genetic correlation between α1 and α2 is . The two square grids below represent the strength of the among-trait correlations (genetic or phenotypic) resulting from the two GP maps in (B). The modular phenotypes (on the right) have lower correlations between modules (yellow) than within (red).
What role does epistasis play in the evolution of the GP map? Epistasis may cause pleiotropy to vary at a locus because pleiotropy is also a property of a genetic interaction, be it between two mutations within or between genes. For instance, two mutations in a gene may have lower pleiotropic degree when alone than when together in the same sequence (fig. 1A). Epistasis may thus provide the genetic variation necessary for the evolution of pleiotropy (Guillaume and Otto 2012; Pavlicev and Wagner 2012; Rueffler et al. 2012) and restructure genetic correlations among traits to, for instance, match patterns of trait covariation favored by selection (Jones et al. 2014). These effects of epistasis may be even more important on the long run than its single trait effect of altering evolutionary paths to higher fitness peaks (Weinreich et al. 2006; Poelwijk et al. 2007; Franke et al. 2011) by alleviating pleiotropic constraints on trait evolution. Epistatic pleiotropy, whereby the pleiotropic degree of a mutation depends on its interaction with other mutations (Wolf et al. 2005, 2006), is indeed thought of as a potent source of variation in pleiotropy and thus an important factor affecting the evolution of the structure of the GP map of genetically correlated traits (Hansen 2006; Pavlicev et al. 2011; Pavlicev and Wagner 2012).
The goal of our work is to uncover both the distribution of the pleiotropic degree and the among-trait covariation of mutations and their pairwise interactions affecting multiple traits to understand the genetic basis and evolvability of phenotypic correlations. Access to such data is challenging but would enable us to ask how phenotypic modularity is reflected within the GP map, and vice-versa. We indeed have little evidence so far that the patterning of the pleiotropic effects within the GP map directly affects the correlational structure of the phenotypes. For instance, studies of mouse bone structures show little correspondence between pleiotropic modules of QTL affecting morphological traits and the genetic variance–covariance structure of those traits (Hallgrímsson and Lieberman 2008; Roseman et al. 2009). Within module integration of pleiotropic effects may not cause elevated trait genetic correlation if the underlying genes bear pleiotropic allelic values that cancel each other because sometimes positive and sometimes negative, compensating for each other’s effects (i.e., hidden pleiotropy). Simulations confirm that without correlation of the allelic pleiotropic effects within modules, no clear correlational pattern will emerge at the phenotypic level despite pleiotropy of the underlying loci (Polster 2013).
We use an extensive dataset of fitness measurements of 70,080 patient-derived viral particles of HIV-1B in 15 different antiretroviral (ARV, all abbreviations are listed in Table 4) drug environments that we treat as our phenotypic traits (Petropoulos et al. 2000). The fitness effects of the amino-acid variants occurring in two genes, the reverse transcriptase and the protease, have been previously estimated together with their pairwise interaction effects in each environment (Hinkley et al. 2011). We are thus able to describe the distribution of pleiotropy and epistatic pleiotropy of the mutations, and the genetic variance–covariance structure of their single and interaction effects on the 15 drug resistance traits. Previous studies have found pleiotropy and epistasis in all types of organisms, from bacteria and viruses to vertebrates and plants, including disease genes in humans (Moore 2003; Azevedo et al. 2006; Cordell 2009). Epistatic interactions have been shown to happen among mutations within (Weinreich et al. 2006; Ortlund et al. 2007; Hinkley et al. 2011) and between genes (reviewed in Phillips 2008), and a few studies have measured genome-wide distributions of epistasis, mostly in bacteria (Elena and Lenski 1997) and viruses (Bonhoeffer et al. 2004). Genome-wide distributions of whole-gene pleiotropy have also been described in model systems using gene knock-out/-down technique (Giaever et al. 2002; Dudley et al. 2005; Sönnichsen et al. 2005). Even so, we are still missing measurements of the mutational variation in pleiotropy and we only start to apprehend the extent of epistatic pleiotropy (Wolf et al. 2005, 2006) and its contribution to variation in trait correlations (Cheverud et al. 1997, 2004; Pavlicev et al. 2008). In contrast, in this study, we are able to link patterns of mutational variation in pleiotropy, epistasis, and the co-variation of their effect with patterns of phenotypic trait co-variation. In other words, we are able to fully describe the structure of the GP map of drug resistance in HIV-1, which has not been achieved before.
Table 4.
Abbreviations used in the Text.
| GP map | genotype–phenotype map |
| ARV | antiretroviral |
| a.-a. | amino-acid |
| PI | protease inhibitor |
| NRTI | nucleoside reverse transcriptase inhibitor |
| NNRTI | nonnucleoside reverse transcriptase inhibitor |
| RT | reverse transcriptase |
| PR | protease |
| GKRR | generalized kernel ridge regression |
| ME | main effects |
| EP | epistatic effects |
| PD | pleiotropic degree |
| pleiotropic degree of the main effects | |
| pleiotropic degree of the epistatic effects | |
| pleiotropic degree of the main and epistatic effects | |
| M-matrix | across-trait variance–covariance matrix of mutational effects |
| G-matrix | across-trait variance–covariance matrix of genotype values |
| SEQ | the G-matrix of observed genotypic values of samples viral a.-a. sequences |
| PCA | principal component analysis |
| PC1 | first principal component |
In HIV, pleiotropy and epistasis may play a fundamental role in the evolution of resistance to multiple drugs, or cross-resistance. Since the advent of ARV drug therapies, resistances to single and multiple drugs have appeared and cross-resistance mutations have been cataloged (Rhee et al. 2003; Bennett et al. 2009). The acquisition of cross-resistance mutations may compromise treatment options of combination ARV therapies and cause substantial threat to the health of HIV infected patients (Bartlett et al. 2006; Wittkop et al. 2011; WHO 2012). Understanding the genetic basis of cross-resistance is thus essential to evaluate its evolutionary potential. However, quantitative estimates of the evolvability of cross-resistance can only be provided by system-based approaches. Two such approaches have been applied to the HIV dataset used here (Petropoulos et al. 2000), which is arguably the largest dataset available. First, Hinkley et al. (2011) inferred the fitness landscape of HIV-1 in the 15 drug environments and showed that within-gene epistasis significantly contributes to the genetic variation in fitness, while between-gene epistasis contributes very little. Second, Martins et al. (2010) showed significant modular co-variation of fitness estimates in the different drug environments that matches the different ARV classes; the protease inhibitors (PIs), nucleoside reverse transcriptase inhibitors (NRTIs), and nonnucleoside reverse transcriptase inhibitors (NNRTIs). What they could not elucidate is the mutational origin of the clustering because their study remained at the phenotypic level. It is thus unclear whether phenotypic modularity is contributed by modularity of the main effects of single mutations or of the interaction effects of double mutations within the two ARV targeted genes, reverse transcriptase and protease. The structure of the GP map of drug resistance in HIV-1 is thus not elucidated yet.
In this study, we test whether the GP map of HIV drug resistance traits has a modular structure that corresponds to the modules of correlated phenotypes. Such a test has never been performed using concomitant single-gene mutational and phenotypic data. With the dataset at hand, we show that mutation interactions have modular epistatic pleiotropic effects that tend to increase the pleiotropy of single mutations, and confer modularity to mutational pleiotropic effects that match with the pattern of phenotypic co-variation.
Results
HIV Fitness Dataset
We use the estimates of fitness effects of mutations within the reverse transcriptase (RT) and protease (PR) genes of HIV-1 published by Hinkley et al. (2011), based on fitness measurements of 70,080 patient-derived viral particles of HIV-1B in 15 different ARV drug environments (described in Methods) and one drug-free environment (Petropoulos et al. 2000). Briefly, fitness is estimated as the replicative capacity of a test vector (NL4-3 HIV clone) engineered to undergo only one round of replication and into which the patient-derived HIV-1B sequences were inserted (full details in Petropoulos et al. 2000). These fitness values associated with the sequences were then used to estimate the single and double (pairwise interactions) mutation effects of amino-acid (a.-a.) substitutions within the two genes (511 in PR and 1,348 in RT). To this end, Hinkley et al. (2011) developed a machine learning approach, generalized kernel ridge regression (GKRR), to fit a model called MEEP that predicts the log-fitness of the sampled sequences (virions) as the sum of the main effects (ME) and pairwise epistatic effects (EP) of the set of a.-a. composing each sequence, for each environment separately (see “Methods” section for details). The GKRR provides estimates of fitness effects of 1,859 single mutations (main effects) and 1,090,889 possible pairwise combinations of those mutations (epistatic effects) (Hinkley et al. 2011). We reduced the epistatic dataset by excluding nonindependent interactions between nonpolymorphic sites and interactions present in less than 10 sequences, resulting in a net total of 556,125 epistatic effects per environment. Furthermore, we developed a method to estimate the pleiotropy of each single and double mutation from the GKRR data based on a bootstrapping approach (see “Methods” section for details). This step is necessary to infer the graph structure of the GP map from an estimate of the pleiotropic degree (PD) of the mutations and their interactions. A proxy of the PD of a mutation, or of a gene knock-out, is classically given by the number of discrete traits on which it has a significant effect (Dudley et al. 2005; Ohya et al. 2005; Ostrowski et al. 2005). We obtain the PD of each single and double mutation by counting their number of significant effects in the 16 environments (PD ) using their bootstrap confidence intervals in each environment.
Pleiotropy and Epistatic Pleiotropy
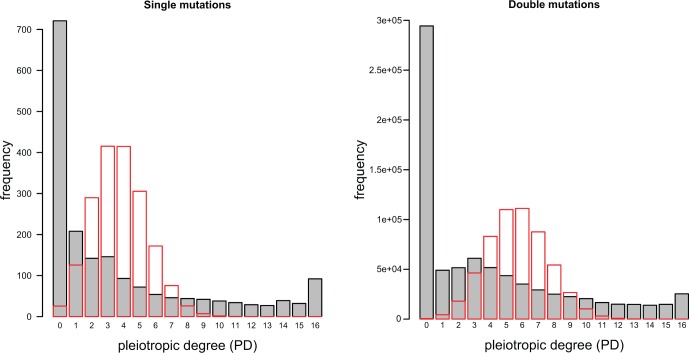
The distributions of the PD of single mutations () and of epistatic interactions () are shown in figure 2. The two distributions are fat-tailed and enriched for fully pleiotropic mutations, that is mutations having an effect in all 16 environments. They are also significantly different from random distributions obtained by permutation, as shown in figure 2 and by Kolmogorov–Smirnov tests (ME: D = 0.7059, P value; EP: D = 0.8235, P value).
Fig. 2.
Distributions of the pleiotropic degree (PD) of single (left) and double (right) mutations. Open bars with red lining represent the random expectations of the PD distributions obtained after 10,000 randomizations of significant main and epistatic effects (see “Methods” section).
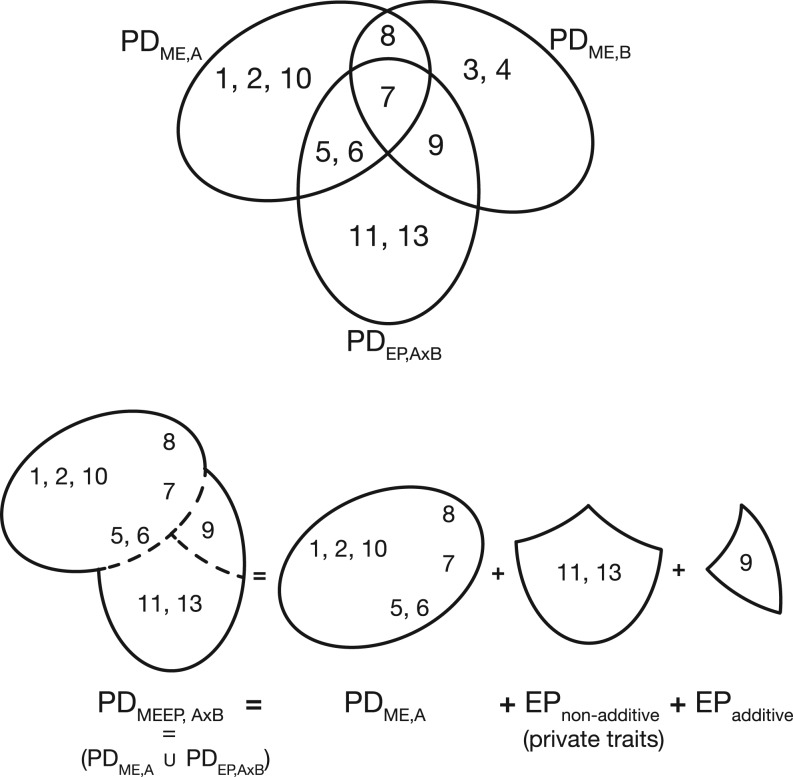
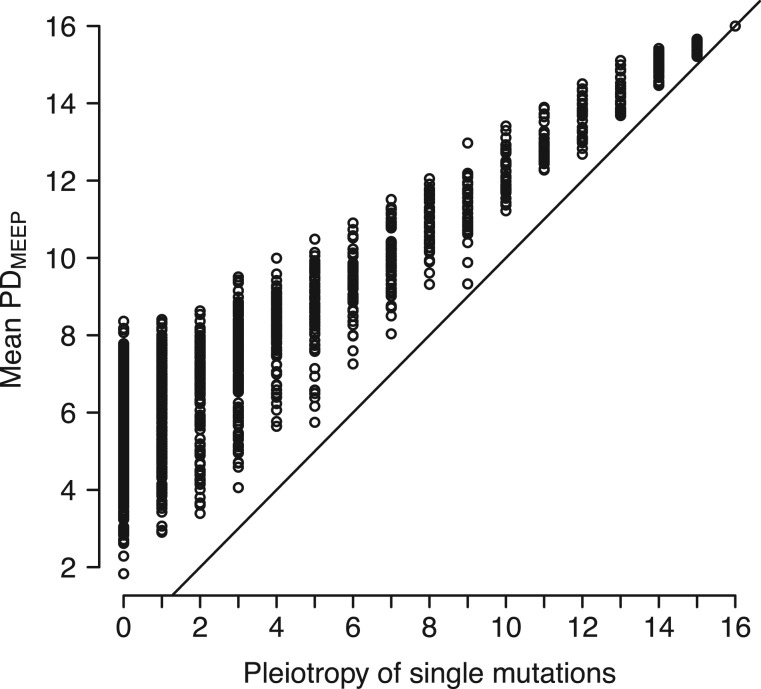
Epistasis modifies pleiotropy of single mutations by changing their trait repertoire, that is, by changing the set of traits they significantly affect as a single mutation () when in interaction with another modifier mutation. The epistatic repertoire is defined as (see fig. 3). We found that mutations have an average of 9.22 (±4.89), larger than the average or (6.14 and 6.45, respectively, see fig. 4). We expect to be larger than or because of the additive nature of the MEEP model (i.e., the total effect of a mutation in interaction with another mutation is the addition of the main and epistatic effect of that mutation, fig. 3). However, on an average, mutation interactions increase trait repertoires (fig. 4) above what is expected under pure additivity of the trait repertoires of the two mutations, for which we expect (Wilcoxon, ). The additive expectation is obtained as the union of the repertoires of the two interacting mutations: . Departures from this expectation are caused by addition of traits that are specific to the mutation interaction (i.e., the private traits of the interaction, see fig. 3), or subtraction of traits not affected by the interaction. Decomposition of into its additive and nonadditive components shows that, on an average, epistasis causes an additive increase of trait repertoires of 1.62 traits and a nonadditive increase of 2.42 private traits, thus summing to an average epistatic increase of about four traits. These changes are smaller than their random expectations (2.09 and 3.25 for additive and nonadditive increases, respectively) at P < 0.0001, obtained from 10,000 randomizations (see “Methods” section). The additive increase is also smaller than expected under complete additivity (3.63), showing that some traits are not affected in interaction. Finally, 68% of the 73% of mutations that show an increase of PD in interaction (or 50% of all mutations) do so by obtaining private traits from their interactions.
Fig. 3.
Venn diagrams of the trait repertoires of two mutations (A and B) and their interaction (A × B). Numbers represent traits (or environments) harboring a significant main or epistatic effect of mutation A and B. Mutation A is the focal mutation with and repertoire . Mutation B is the modifier mutation with and repertoire . The resulting interaction has with repertoire , which thus partially overlaps with the repertoires of A and B. The total pleiotropy of A in interaction with B is given by = , as shown on the second row. The repertoire of mutation A thus “gains” three traits in interaction with B, of which one gives an additive increase (trait 9, added from mutation B’s repertoire) and two give a nonadditive increase (traits 11 and 13). Traits 11 and 13 are called the private traits of the interaction because they pertain to the interaction’s repertoire only.
Fig. 4.
Relationship between the PD of single mutations and their average , that is the average number of environments they affect across all their significant interactions. The solid line represents the 1:1 relationship.
Structure of the GP Map of Fitness among Drugs
The structure of the GP map of phenotypic traits is often deduced from the pattern of trait genetic covariation under the premises that genetic covariation is a reflection of the underlying organization of pleiotropic allelic effects. To test for this correspondence, we, first, compare covariance matrices of main and epistatic effects of mutations with the observed covariance matrix of virion fitness values and, second, test whether allelic pleiotropic effects form modules similar to the modules of covariation of fitness values among genotypes, that is, at the phenotypic level. The covariation of mutational pleiotropic effects is conventionally reported as the M-matrix, the mutational variance–covariance matrix (Camara and Pigliucci 1999; Estes et al. 2005). We report estimates of the two M-matrices of main and epistatic effects calculated as the within environment variance (on the diagonal) and between-environment covariance (off-diagonal) of mutational effects (main or epistatic) and test whether the genetic covariation of the phenotypic traits stems directly from the pattern of mutational covariation. We thus compare M-matrices with the G-matrix holding the variance–covariance structure of the 70,080 fitness (genotypic) values in the 16 environments. G-matrices hold the within environment variances and between environment covariances of sequence fitness values on and off the diagonal, respectively. Furthermore, to better appreciate the importance of epistasis in structuring the GP map of drug resistance, we compare three G-matrices with each other: the SEQ G-matrix obtained from the original fitness estimates of the 70,080 sequences, the ME G-matrix obtained from the reconstructed fitness values of the sequences using estimated main effects only, and the MEEP G-matrix obtained from the predicted sequence fitness values using the full MEEP model.
Viral Fitness Is Modular among Drug Classes
Viral fitness clusters among drug classes, as shown by patterns of genetic correlations (fig. 5) and principal component analysis (PCA) of the G-matrices (see fig. 6 and supplementary figs. S5–S7, Supplementary Material online). The NRTI class has greater drug specificity with two submodules, one composed of the cytidine (3TC) and guanosine (ABC, ddI) analogs and the other of the thymidine (d4T, ZDV) and adenosine (TFV) analogs (see also Martins et al. 2010). Overall, correlations are high (table 1), particularly among NNRTIs (0.92) and PIs (0.89). The same modular pattern as in the SEQ G-matrix is found in the MEEP G-matrix (fig. 5). The ME sequence fitness G-matrix, however, shows much higher correlations among all drug classes, without clear modular structure, suggesting a larger integration of the GP map at the level of main effects.
Fig. 5.
Heatmaps of the correlation matrices of fitness measurements of observed sequence data (SEQ), estimates of main effects (ME), and estimates of main and epistatic effects (MEEP) for the 15 drug environments and the drug-free condition (ND). Drugs are ordered by class: ND (No Drug), NNRTIs (DLV, EFV, NVP), NRTIs (3TC, ABC, D4T, DDI, TFV, ZDV), and PIs (AMP, IDV, LPV, NFV, RTV, SQV).
Fig. 6.
Principal component analysis of the G-matrices of sequence viral fitness (SEQ), of the main effects only (ME), and of the main and epistatic effects (MEEP) of the mutations in reverse transcriptase and protease. Gray dots indicate the relative positions of data points (virus log-fitness) within the two principal components (PCs) and arrows symbolize the positions of the original traits (drug environments) in this new phenotypic space. Drug classes are highlighted with colors. ND, no-drug condition.
Table 1.
Mean Correlations Within and Between Drug Classes in Sequence Fitness.
| Sequence Data (SEQ) | Main Effects (ME) | MEEP | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PIs | NRTIs | NNRTIs | PIs | NRTIs | NNRTIs | PIs | NRTIs | NNRTIs | |
| PIs | 0.89 | 0.46 | 0.24 | 0.97 | 0.90 | 0.68 | 0.89 | 0.45 | 0.11 |
| NRTIs | 0.62 | 0.34 | 0.92 | 0.76 | 0.54 | 0.26 | |||
| NNRTIs | 0.92 | 0.88 | 0.89 |
The lack of modularity of the main effects and the similarity between the SEQ and the MEEP viral fitness are confirmed when using evolutionary metrics to compare the G-matrices (see “Methods” section). In particular, the autonomy of a G-matrix measures the degree of genetic modular integration of phenotypic traits: higher autonomy is reached when traits within modules are more strongly genetically related to each other than to other traits in other modules (Hansen and Houle 2008). We find that the MEEP and SEQ matrices have the highest autonomy and thus better integrated modules than the ME matrix (table 2a). Second, the effective dimensionality nD provides a weighted modularity measure representing the number of independent trait modules with equal variance (Kirkpatrick 2009). Here, the MEEP matrix has the highest number of independent trait dimensions, followed by SEQ and ME (table 2a). Finally, the random skewers approach provides a matrix similarity measure in the form of a vector correlation coefficient (Cheverud 1996) (see “Methods” section). This analysis shows that the MEEP and SEQ matrices are the most similar among the three matrices (table 2c). The MEEP matrix then captures most of the correlation structure present in the SEQ matrix and provides a good estimate of the multivariate trait structure of viral fitness, although it exacerbates the modularity found in the original fitness data.
Table 2.
Covariance Matrix Comparisons.
| (a) | G-matrices | ME | MEEP | SEQ |
| 1.16 (1.157, 1.161) | 2.08 (2.07, 2.09) | 1.90 (1.89, 1.92) | ||
| 0.07 (0.072, 0.074) | 0.16 (0.161, 0.163) | 0.16 (0.159, 0.164) | ||
| (b) | M-matrices | ME | EP | |
| 1.11 (1.072, 1.163) | 1.10 (1.079, 1.129) | |||
| 0.05 (0.033, 0.072) | 0.07 (0.066, 0.076) | |||
| (c) | Random skewers | ME vs. MEEP | ME vs. SEQ | MEEP vs. SEQ |
| vector correlation | 0.75 | 0.86 | 0.95 |
Note.— (a) Effective dimensionality (, a measure of modularity), and autonomy (, a measure of genetic independence) of the fitness covariance matrices. (b) Same metrics for the mutational covariance matrices of main (ME) and epistatic (EP) effects. (c) Similarity of the ME, MEEP and sequence (SEQ) fitness covariance matrices measured with Random skewers (see “Methods” section). When provided, values in parenthesis are the 2.5% and 97.5% bootstrap confidence limits of 10,000 bootstrap replicates (see Supp. Information, PCA stability section).
The PCA confirms the clustering among drug classes (fig. 6), although drug classes do not differentiate along the first PC, with roughly equal loadings of the 16 environments. PC1 explains 50% of total fitness variation in the SEQ dataset (fig. 6), and 84% and 47% for ME and MEEP, respectively. PC1 is similar to a size vector discriminating high versus low average fitness values of generally highly correlated sequence fitness values among drugs. PC2 nevertheless differentiates the NNRTIs from the other drug environments, especially within the SEQ dataset, whereas PC3 further differentiates the NRTIs from the PIs and NNRTIs, although mainly in SEQ and MEEP. Interestingly, that third PC differentiates among the two NRTI sub-groups in the MEEP dataset, where 3TC, ABC, and ddI have negative loadings on PC3. That general drug-class modular structure is largely confirmed by hierarchical clustering analysis (see supplementary figs. S5–S7, Supplementary Material online), which more clearly shows the two NRTIs sub-groups. The stability of the PCs is very high when tested by sub-sampling and bootstrapping (see Supplementary Information).
Mutational Covariation Is Less Modular than Viral Fitness Covariation
The modularity of trait covariation within the G-matrix may have two nonexclusive sources: (1) elevated correlation of pleiotropic allelic values among traits within modules and (2) clustering of pleiotropic effects within modules. The previous results suggest that EP should differ from ME in at least one of those two aspects, which we evaluate by comparing their M-matrix and by investigating the modularity of their respective GP map.
The M-matrix of the main effects is very close to its G-matrix (table 2a and b, first column), whereas the EP matrix has lower and autonomy than the MEEP matrix (table 2a and b, second column). The two M-matrices have similar modularity, although epistatic effects have slightly higher autonomy (table 2b). Epistatic effects are then much less modular than the modularity of the MEEP data would suggest. Consequently, the covariation of mutational epistatic effects cannot explain the modular covariation found among genotypes in the MEEP or SEQ G-matrices. We thus speculate that it is the combination of main and epistatic effects within the observed sequences that contributes to the higher modularity seen in the MEEP and SEQ data. That combinatorial aspect of the data is given by the graph structure of the GP map and thus depends on the distribution of pleiotropy of the main and epistatic effects among the traits, which we evaluate next.
Epistatic Pleiotropic Effects Are More Modular than Main Effects
To measure the clustering of main and epistatic effects within the GP map, we use the parcellation statistic of Mezey et al. (2000). measures the lack of pleiotropic effects between nonoverlapping sets of traits (modules). We found that the main effects are significantly less modular (, P = 0.0018) and the epistatic effects more modular (, P < 0.0001) than expected by chance, based on comparison with randomized sets of ME and EP within environments for a four-module partitioning of the data (see “Methods” section). Furthermore, epistatic effects have much larger standardized parcellation than main effects, with and (see “Methods” section). Among all possible clustering of the 15 drug traits, there will be some that maximize the parcellation of the ME data compared with randomized sets. Instead of conducting an exhaustive search, we tested two other trait combinations suggested by the clustering analysis: a two-module clustering {{NNTRIs}–{NRTIs + PIs}} and a three-module clustering {{NNTRIs}–{3TC, ABC, ddI}–{TFV, ZDV, d4T, + PIs}} (see supplementary fig. S7, Supplementary Material online). The parcellation of ME is significantly larger than expected by chance for the two-module case (P < 0.0001), but significantly smaller for the three-module case (P = 0.0003). The parcellation of EP is always significantly larger with P < 0.0001. Together, this shows that EP form well supported modules that match those found in the viral sequence fitness data, whereas ME cluster among a smaller partitioning of two modules, confirming that pleiotropy is less modular for main than for epistatic effects.
Epistatic Effects Trade-off More among Drug Classes
Fitness trade-offs among drug classes are not clearly apparent from the analysis of correlational patterns: the pairwise genetic correlations between drug environments are positive and often large. Trade-offs might, however, exist and explain part of the variation in genetic correlations. Indeed, the proportion of antagonistic EP between two drug environments (i.e., positive in one environment and negative in the other) is larger in drug pairs between (5.2%) than within (0.7%) drug classes, on an average (Wilcoxon: ). Main effects show lower proportions of antagonistic effects in drug pairs, with 1.5% between and 0.3% within drug classes on an average. The difference remains when accounting for the net effects of the mutations, calculated by summing main and epistatic effects of each interaction (1.5% between drug classes and 0.49% within, Wilcoxon: ). Interestingly, the higher proportion of antagonism between drug classes is largely caused by the NNRTI mutations with the other drug classes (8.8% and 2.5% for EPs and net effects, respectively), compared with the level of antagonism among PIs and NRTIs (1.6% and 0.55% for EPs and net effects, respectively). Moreover, the proportions of pairwise antagonistic EP are strongly negatively correlated to the pairwise correlations of fitness values in the SEQ matrix (). By introducing variation in the sign of pleiotropy in addition to variation in its extent, epistasis causes lower correlations among drug environments because of larger trade-offs in net mutational fitness effects.
More Highly Correlated Traits Are More Genetically Integrated Traits
Is the correlation of fitness values within drug classes (phenotypic integration) indicative of the degree of pleiotropy of the mutations (genetic integration)? We looked at two aspects of mutation pleiotropy: (1) the proportion of significant mutations that are fully pleiotropic in each drug class (i.e., have PD = 3 in NNRTIs, and PD = 6 in NRTIs and PIs) and (2) the average pleiotropic degree of the significant mutations relative to the maximum pleiotropy in each drug class (i.e., “relative” pleiotropy in table 3). Among the three classes, NNRTIs have the highest average correlation of fitness values, followed by PIs and NRTIs (table 1). Accordingly, single and double mutations with significant effects in NNRTIs are more fully pleiotropic and have a higher average pleiotropic degree than mutations in PIs, and in NRTIs (table 3). Therefore, more phenotypically correlated traits are here also more genetically integrated traits, with regards to the among-trait density of pleiotropy of their underlying mutations. Together with results from the previous section, phenotypic integration is supported by more pleiotropic links and less antagonistic mutational effects within than between drug classes.
Table 3.
Proportion of Significant Main and Epistatic Effects that are Fully Pleiotropic Within Drug Class, and the Average Pleiotropic Degree of Significant Mutations Relative to the Maximum Within-Class Pleiotropy (three for NNRTI, and six for NRTI and PI).
| Drug Class | Full Pleiotropy | Relative Pleiotropy | ||
|---|---|---|---|---|
| ME | EP | ME | EP | |
| NNRTI | 0.49 | 0.52 | 0.73 | 0.76 |
| NRTI | 0.23 | 0.18 | 0.55 | 0.53 |
| PI | 0.38 | 0.29 | 0.65 | 0.6 |
Intra versus Inter-Genic Epistasis
Until now we have kept all epistatic interactions within and between reverse transcriptase and protease. To our knowledge, it has not been investigated whether mutations within reverse transcriptase may affect the inhibitory effects of drugs targeting protease, and vice versa. Hinkley et al. (2011) tested for the effect of inter-protein epistasis but found little influence of inter-genic interactions on the overall variation in viral fitness within drug environments. By removing inter-genic interactions, we find that the intra-genic EP M-matrix has slightly lower modularity (; 95% CI = [1.064, 1.067]), with unchanged autonomy (; 95% CI = [0.067, 0.073]) compared with the full EP M-matrix (table 2). Recalculating sequence fitness with intra-genic interactions only in the MEEP model further shows that inter-genic EP have little effect on the modularity (; 95% CI = [2.06, 2.09]) and autonomy (; 95% CI = [0.132, 0.134]) of the MEEP G-matrix. The structure of the GP map of drug resistance is thus little affected by inter-genic epistasis between RT and PR.
Discussion
Our analysis of the genetic co-variation of fitness of HIV-1B among ARV drugs confirms that there exists high potential for the evolution of cross-resistance. Evaluation of the response of HIV to selection imposed by multiple ARV treatments can be conducted using quantitative genetics theory based on the genetic variance–covariance matrix (the G-matrix) of fitness in multiple environments (Falconer 1952; Lande 1979; Via and Lande 1985). As first noted by Falconer (1952), considering the genetic correlation between trait values in two different environments is not different from the genetic correlation of two different traits in the same environment. The differential environmental effects of the single and double mutations are thus rightly interpreted as pleiotropic effects structuring the GP map of fitness in multiple environments. In HIV, we expect a positively correlated response of cross-resistance to multiple ARV drugs because the majority of genetic variation in fitness lies along the first PC of the SEQ G-matrix, which is shared among all HIV fitness traits. This is even more true for within drug class cross-resistance, especially within NNRTIs and PIs, which are more correlated and can be seen as near-identical traits. Alternatively, a weaker cross-resistance is expected for HIV evolving under less correlated ARV treatments, as when taken from two different ARV classes or from the two different sub-modules within the NRTIs. It is indeed known that NRTIs have higher drug-specific resistance mutations than other ARV classes (Harrigan and Larder 2002; Martins et al. 2010; Arts and Hazuda 2012).
From the same token, drug combinations with the lowest potential for cross-resistance evolution are combinations with lowest pairwise or three-way correlations, when mimicking combination therapies. Based on our results, combinations of one NNRTI with a PI would have lowest potential for cross-resistance, as would one NNRTI with an NRTI. Within the NRTI class, combinations of TFV with either 3TC or ABC would also minimize the potential for cross-resistance. Interestingly, recommendations from the International AIDS Society (Hammer et al. 2008) precisely involve combinations of EFV (NNRTI) with two NTRIs such as TFV with 3TC or ABC, or one RTV-boosted PI (LPV) with two of these NRTIs. Our predictions are in line with those recommendations, although NNRTIs would seem more adequate in combination with PIs. Nevertheless, from our data, TFV is the NRTI with lowest correlations with the PIs. Of course, medical recommendations take more criteria in consideration than the potential for cross-resistance evolution from in vitro data. For instance, each drug has its own pharmacokinetics and side effects, and may elicit specific combinations of resistance mutations, especially among NRTIs (Ali et al. 2010; Cihlar and Ray 2010; Arts and Hazuda 2012). This, in part, justifies the fact that we kept all drug environments separate, although NNRTIs and PIs could be considered as single trait-environments based on their high within module average correlations, which would lower the average pleiotropic degree.
About Measures of Pleiotropy
We have measured pleiotropy by performing an environment-wise exclusion of nonsignificant mutational effects under the rational that nearly neutral mutations of small effects can be discarded because not significantly contributing to fitness variation in a given environment. This approach is expected to provide an acceptable proxy of the pleiotropic degree of a mutation, or a gene, when detection thresholds are not too low (Wagner and Zhang 2012). The advantage of this measure is to correspond to the definition of pleiotropy used in theoretical studies as being the number of discrete phenotypic traits that are affected by a mutation (Chevin et al. 2010; Lourenço et al. 2011). Its evolutionary properties are thus well understood. It may, nevertheless, lead to a downward-biased estimate of pleiotropy resulting in the characteristic L-shaped PD distribution found previously because of low detectability of mutational effects of otherwise fully pleiotropic mutations (Hill and Zhang 2012). Although our PD distributions may also be biased towards lower values, they drastically differ from previous distributions by their high frequency of fully pleiotropic mutations (fig. 2). That shape is not predicted as an outcome of detection bias, even when genetic correlations among traits are high (Hill and Zhang 2012). Furthermore, the shape of the PD distributions is robust to our significance filtering because not affected when using only the most or the least frequent mutations. A bias may exist because mutation frequency is strongly negatively correlated with the size of bootstrap confidence intervals (see “Methods” section) and more frequent mutations may thus be more pleiotropic. Yet, of the most frequent mutations (i.e., 403 out of 404 a.a. of the consensus sequence) has the same median of two traits and same distribution with a similar enrichment of fully pleiotropic mutations as the full distribution (supplementary fig. S1, Supplementary Material online). Similar PD distributions are found for less frequent mutations and for interactions (supplementary figs. S2 and S3, Supplementary Material online). In sum, given that nonpleiotropic mutations have lower absolute effect sizes than mutations with large PDs, we have effectively eliminated mutations that would, on an average, less affect fitness variation in the presence of selection than more pleiotropic mutations (supplementary fig. S4, Supplementary Material online). Altogether, this gives us confidence that our PD estimates are robust and biologically meaningful.
General Implications
Studying mutations within two essential genes of a virus allowed us to uncover a direct link between mutational variation in pleiotropy and the pattern of covariation among the phenotypes. This relationship is not expected to be as direct in higher organisms where the ontogeny of phenotypes involves multiple loci and intermingled developmental processes, which may rewrite the character relationships in slightly different ways at each developmental stage. In this “palimpsest” ontological model (Hallgrímsson and Lieberman 2008), the influence of the underlying genes is obscured by the constant rewriting of the phenotypes. The best known example is the mouse cranial and mandibular morphological traits, where pleiotropic effects of mapped QTL show significant modularity relative to basal developmental units (Mezey et al. 2000) but not to phenotypic units (Roseman et al. 2009). In a simpler organism like HIV, the influence of the genes is directly integrated into phenotypic variation avoiding being drowned out by a succession of developmental processes. Nevertheless, a similar direct relationship between GP map and phenotypic structures may be expected in higher organisms for more basal phenotypes. An example would be molecular phenotypes, such as gene expression traits where co-variation in expression may be a direct function of the activity of pleiotropic gene regulatory elements. Recent transcriptomics studies support that idea and have uncovered heritable variation of gene expression in a few organisms [e.g., Drosophila melanogaster (Ayroles et al. 2009); three-spine sticklebacks (Leder et al. 2015)], and indirectly suggest the presence of pleiotropy in gene regulation by reporting significant genetic covariance in gene expression (e.g., in D. serrata: McGuigan et al. 2014).
The extent of epistatic pleiotropy in other organisms is little known beside a few QTL studies in mice (Wolf et al. 2005, 2006), in which a small number of epistatic interactions among QTL for morphological traits were shown to contribute less to the phenotypic covariance of the traits than single pleiotropic QTL, and did not change the trait covariances. In contrast, we show a large effect of epistatic pleiotropy on trait covariation. Moreover, we found that although a large proportion of single mutations do not significantly affect fitness in any environments, they will gain significant effects in interaction and change the pleiotropic effects of their interacting partners. Such mutations can be viewed as modifiers of pleiotropy with potentially large effects on trait covariances (Pavlicev and Wagner 2012). Similar effects have been found by mapping loci that affect the relationship between traits but remain hidden to the analysis of single effects. Such relationshipQTL have been shown to affect the trait covariation of mice morphological traits (Cheverud et al. 2004; Pavlicev et al. 2008). Interestingly, although our study drastically differs in scope and scale, we show that the same phenomena take place in organisms as different as a virus and a mouse.
Our study contributes to better understand the relationship between M- and G-matrices. Little is known about their correspondence in living species, and direct estimates of M-matrices are scarce (but see Camara and Pigliucci 1999; Estes et al. 2005; Houle and Fierst 2013). The correlation of the allelic effects of pleiotropic genes encapsulated in the M-matrix has important evolutionary consequences because, if nonrandom, it creates stable patterns of genetic and phenotypic correlations among phenotypic characters (Jones et al. 2003) that override the effects of other sources of genetic covariance among pleiotropic allelic effects (e.g., linkage (Lande 1980), drift (Griswold et al. 2007), migration (Guillaume and Whitlock 2007), correlational selection (Jones et al. 2003)). The correlational pattern of phenotypes then depends on how much the structure of the M-matrix translates into heritable genetic covariation of the traits, encapsulated in the G-matrix. We show that the correlational structure within the M-matrices of main and epistatic effects are poor predictors of the covariation of fitness among drug environments. Therefore, patterns of trait integration here depend on the distribution of the pleiotropic effects among the traits within the GP map. This indicates that the precise structure of the GP map cannot be ignored as a cause of trait covariation or genetic constraints, and, hence, as a means of their evolution by modification of gene pleiotropy (Guillaume and Otto 2012; Pavlicev and Wagner 2012).
Conclusions
By studying phenotypic variation and its underlying mutational variation, we were able to link phenotypic with pleiotropic modularity. We showed that in HIV-1, a modular epistatic GP map leads to a modular phenotype. The main effects also play an important role by quantifying the effects that are shared among environments. They, however, lack modularity in the correlations and in the patterning of their pleiotropic effects within the GP map. Epistasis modulates these effects and although it increases pleiotropy, it does so in a modular fashion, and provides more drug-specific and class-specific profiles to viral fitness. Our findings have strong implications for our understanding of the evolutionary potential of drug resistance against multiple drugs in HIV. More generally, they suggest that epistasis may play a fundamental role in shaping the evolvability of living organisms by directly affecting the structure of the GP map and the strength of genetic correlations of phenotypic traits.
Materials and Methods
Experimental Data
Our analyses are based on a sample of 70,080 patient-derived HIV-1 sequences assayed for fitness in 16 different environments: one drug-free and 15 in presence of one antiretroviral drug (Petropoulos et al. 2000). The replicative capacity (fitness) of each sample was measured by inserting the full sequence of the protease gene (99 amino acids) and most of the reverse transcriptase gene (amino acids 1–305) of the patient-derived virion into the backbone of an HIV-derived test vector used for routine drug resistance testing. The test vector is based on the NL4-3 molecular HIV clone and has been modified such that it undergoes only one round of replication (full details are in Petropoulos et al. 2000). The fitness of each sequence is the number of virus progeny produced after one replication cycle relative to that of the base test vector, and provides an estimate of viral fitness in each environment. The 15 drugs used belong to three different classes: protease inhibitors (PIs), nucleoside reverse transcriptase inhibitors (NRTIs) and nonnucleoside reverse transcriptase inhibitors (NNRTIs). The six PI drugs are amprenavir (AMP), indinavir (IDV), lopinavir (LPV), nelfinavir (NFV), ritonavir (RTV), and saquinavir (SQV), the six NRTI drugs are abacavir (ABC), didanosine (ddI), lamivudine (3TC), stavudine (d4T), zidovudine (ZDV), and tenofovir (TFV), and the three NNRTI drugs are delavirdine (DLV), efavirenz (EFV), and nevirapine (NVP). For each drug, the replicative capacity of a virus on drugs was given by the interpolated value measured at the drug concentration at which the NL4-3 based control virus has 10% of its replicative capacity in the absence of drug (the IC90 for NL4-3 was used as the reference drug concentration for every subsequent measurement).
Estimates of Single and Double Mutation Effects
Amino acid sequences of the protease gene and the partial reverse transcriptase gene were obtained by population sequencing for all virus samples included in this analysis (Petropoulos et al. 2000). Because of this population sequencing, sequences are defined in terms of probabilities of allele occurrences for each locus. The effects of all single and double mutations present in the sequence dataset were then estimated using a generalized kernel ridge regression (GKRR) procedure (Hinkley et al. 2011). In brief, the GKRR is a machine learning approach fitting a general linear model in which the number of parameters to estimate by far outnumbers observation points. It avoids over-fitting of the model by using a training sub-dataset completely independent from the sub-dataset from which the parameters are estimated. The model fitted by Hinkley et al. (2011), called MEEP, is:
where Wi is the replicative capacity (fitness) of sequence i, mj represents the main effect (ME) of the jth amino-acid variant and sij is the probability of that variant occurring in a randomly selected sequence from the population of sequence i. Similarly, ϵk represents the interaction epistatic effect (EP) of the kth combination of variants and sik is a variable that accounts for the presence or absence of that combination of variants in the sequence. The s parameters may be different from 0 or 1 because of population sequencing of the HIV viral sequences and the possible ambiguities caused by site-specific amino-acid polymorphism. I, the intercept, represents the log fitness of the reference sequence of the test vector (see details in Hinkley et al. 2011). In total, 1,859 alleles are present at the 404 amino-acid positions, with 1,090,889 possible interactions. Among these, we excluded nonindependent interactions between nonpolymorphic sites and those interactions present in less than 10 sequences, resulting in a net total of 556,125 epistatic effects. Amino-acid variants with less than ten copies in the whole sequence dataset were also excluded in Hinkley et al. (2011).
Bootstrapping of GKRR Estimates
To provide an estimate of the accuracy of the GKRR method to detect small effects, we bootstrapped the MEEP model by resampling the fitness of each viral sequence from the observed values, with replacement. We performed 1,000 bootstraps in the NODRUG environment. Because the bootstrap confidence intervals (CI) are strongly correlated among drug environments, we generated 400 bootstrap estimates in the EFV, 3TC, and LPV drug environments, hence bootstrapping one drug per drug class. The number of bootstraps is limited because of the extremely high computational demand of the procedure, and because little variation in confidence interval sizes is detected above 200 bootstrap replicates. Moreover, the per-mutation CI sizes among those three drug environments are highly correlated ( and 99% for CIs of main and epistatic effects, respectively). More variation in CIs exist among mutations within environments, with the most frequent mutations having the smallest CIs (, in NODRUG, EFV, 3TC, and LPV, respectively, all ). The size of the CI of a mutation thus depends on the amount of information available in the dataset instead of its effect size.
Randomization Tests
We assessed the significance of the observed distributions of pleiotropy and epistatic pleiotropy using different randomization tests. First, we tested for the significance of the distributions of and by randomizing the significant single and double mutation effects among the 16 environments. For this, we built a 1,859 × 16 matrix for the ME data and a 556,125 matrix for the EP data, with 1s and 0s indicating significant and nonsignificant effects, respectively. Each matrix was shuffled 10,000 times from which we calculated the mean PD distributions. Second, to test for the significance of the observed pattern of epistatic pleiotropy, we permuted the significant MEs and EPs within each environment to generate random expectations of repertoire composition while keeping the significance levels constant per environment for main and epistatic effects. This randomization scheme allows us to test for the null hypothesis of universal pleiotropy under which the epistatic pleiotropic effects (the private traits) would be caused by the failure of detecting the corresponding main effects in the interacting mutations. It thus tests whether the degree of nonadditive epistatic pleiotropy we observe is an artifact of the significance filtering we used. For this, we generated a null distribution of the average number of private traits per interaction by performing 10,000 permutations of the 1,859 main and 556,125 epistatic effects in each environment. A P value associated with our point estimate of privateness can be readily obtained by finding the empirical percentile from that bootstrapped distribution. Finally, we also test whether the additivity of the interaction departs from its null expectation under the same assumption.
Evolutionary Statistics
Autonomy
The autonomy of a set of traits provides a measure of the integration of the GP map: it represents the “proportion of evolvability that remains after conditioning on other traits” (p1207; Hansen and Houle 2008). GP maps with more integrated modules of traits that are genetically less related to other such modules will thus have higher autonomy. Corrected formula for autonomy is in Hansen and Houle (2009).
Effective dimensionality
The effective dimensionality measures the contrast between the first (λ1) and lower-rank eigenvalues (λi) of a covariance matrix and is , which can be interpreted as a weighted modularity measure representing independent modules with equal variance (Kirkpatrick 2009).
Random skewers
The random skewers approach measures the average vector correlation (average angle) of the selection response vectors of two covariance matrices submitted to the same set of random selection vectors (Cheverud 1996). We used 10,000 random selection vectors (random skewers) to provide an estimate of the similarity in the orientation of the covariance matrices in phenotype space.
The covariance matrices (M and G-matrices) were themselves generated by measuring all pairwise environment covariances of within environment genotypic values (G-matrices) or of all within environment significant mutational effects (M-matrices).
Parcellation
We computed the parcellation of the GP maps of the main () and epistatic () effects with the parcellation statistic of Mezey et al. (2000). Because the method requires a pre-defined set of modules, we first used the four modules that we found in the phenotypic SEQ matrix, excluding the NODRUG environment. The significance of the observed parcellation is evaluated against the parcellation of randomized sets of ME and EP within environments (see “Randomization Tests” section above).
To compare the parcellation of two networks of different sizes, we defined the following standardized parcellation index:
which is the difference of observed parcellation to the mean random parcellation in units of standard deviation.
All tests and analyses were performed with R v3.0.2 (R Core Team 2012). PCA and hierarchical cluster analysis were performed with prcomp and pvclust functions in R, respectively.
Supplementary Material
Supplementary figures S1–S7 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Acknowledgments
We wish to thank Mihaela Pavlicev, Mary Poss, Jobran Chebib, Roger Kouyos, and Jeremy Draghi for their helpful comments on previous versions of this article, and Louis du Plessis and Trevor Hinkley for their invaluable help with GKRR. The quality of the article was greatly improved after full peer-review at Axios Review (Vancouver, Canada) and comments of two anonymous reviewers. This work was supported by the Swiss National Science Foundation (grants PP00P3_144846/1 and PZ00P3_141987/1 to F.G.), and the ETH Zurich (Research Grant ETH-10 09-3 to R.P.) S.B. acknowledges support by the Swiss National Science Foundation.
References
- Ali A, Bandaranayake RM, Cai Y, King NM, Kolli M, Mittal S, Murzycki JF, Nalam MNL, Nalivaika EA, Özen A, et al. 2010. Molecular basis for drug resistance in HIV-1 protease. Viruses 2(11):2509–2535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armbruster WS, Pélabon C, Bolstad GH, Hansen TF. 2014. Integrated phenotypes: understanding trait covariation in plants and animals. Philos Trans R Soc B. 369(1649):10.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arts EJ, Hazuda DJ. 2012. HIV-1 antiretroviral drug therapy. Cold Spring Harb Perspect Med. 2(4):a007161.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayroles JF, Carbone MA, Stone EA, Jordan KW, Lyman RF, Magwire MM, Rollmann SM, Duncan LH, Lawrence F, Anholt RRH, Mackay TFC. 2009. Systems genetics of complex traits in drosophila melanogaster. Nat Genet. 41(3):299–307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azevedo L, Suriano G, van Asch B, Harding RM, Amorim A. 2006. Epistatic interactions: how strong in disease and evolution?. Trends Genet. 22:581–585. [DOI] [PubMed] [Google Scholar]
- Bartlett JA, Buda JJ, von Scheele B, Mauskopf JA, Davis EA, Elston R, King MS, Lanier ER. 2006. Minimizing resistance consequences after virologic failure on initial combination therapy: a systematic overview. J Acquir Immune Defic Syndr. 41(3):323–331. [DOI] [PubMed] [Google Scholar]
- Bennett DE, Camacho RJ, Otelea D, Kuritzkes DR, Fleury H, Kiuchi M, Heneine W, Kantor R, Jordan MR, Schapiro JM, et al. 2009. Drug resistance mutations for surveillance of transmitted HIV-1 drug-resistance: 2009 update. PLoS One 4(3):e4724.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonhoeffer S, Chappey C, Parkin NT, Whitcomb JM, Petropoulos CJ. 2004. Evidence for positive epistasis in HIV-1. Science s, 306(5701):1547–1550. [DOI] [PubMed] [Google Scholar]
- Camara MD, Pigliucci M. 1999. Mutational contributions to genetic variance-covariance matrices: an experimental approach using induced mutations in arabidopsis thaliana. Evolution 53(6):1692–1703. [DOI] [PubMed] [Google Scholar]
- Cheverud JM. 1996. Developmental integration and the evolution of pleiotropy. Am Zool. 36(1):44–50. [Google Scholar]
- Cheverud JM, Ehrich TH, Vaughn TT, Koreishi SF, Linsey RB, Pletscher LS. 2004. Pleiotropic effects on mandibular morphology ii: differential epistasis and genetic variation in morphological integration. J Exp Zoolog B Mol Dev Evol. 302B(5):424–435. [DOI] [PubMed] [Google Scholar]
- Cheverud JM, Routman EJ, Irschick DJ. 1997. Pleiotropic effects of individual gene loci on mandibular morphology. Evolution 51(6):2006–2016. [DOI] [PubMed] [Google Scholar]
- Chevin LM, Martin G, Lenormand T. 2010. Fisher’s model and the genomics of adaptation: restricted pleiotropy, heterogenous mutation, and parallel evolution. Evolution 64(11):3213–3231. [DOI] [PubMed] [Google Scholar]
- Cihlar T, Ray AS. 2010. Nucleoside and nucleotide HIV reverse transcriptase inhibitors: 25 years after zidovudine. Antiviral Res. 85(1):39–58. [DOI] [PubMed] [Google Scholar]
- Cordell HJ. 2009. Detecting gene-gene interactions that underlie human diseases. Nat Rev Genet. 10(6):392–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudley AM, Janse DM, Tanay A, Shamir R, Church GM. 2005. A global view of pleiotropy and phenotypically derived gene function in yeast. Mol Syst Biol.1:2005–0001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elena SF, Lenski RE. 1997. Test of synergistic interactions among deleterious mutations in bacteria. Nature 390(6658):395–398. [DOI] [PubMed] [Google Scholar]
- Estes S, Ajie BC, Lynch M, Phillips PC. 2005. Spontaneous mutational correlations for life-history, morphological and behavioral characters in caenorhabditis elegans. Genetics 170(2):645–653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falconer DS. 1952. The problem of environment and selection. Am Nat. 86(830):293–298. [Google Scholar]
- Franke J, Klozer A, de Visser JAGM, Krug J. 2011. Evolutionary accessibility of mutational pathways. PLoS Comp Biol. 7(8):e1002134.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giaever G, Chu AM, Ni L, Connelly C, Riles L, Veronneau S, Dow S, Lucau-Danila A, Anderson K, Andre B, et al. 2002. Functional profiling of the Saccharomyces cerevisiae genome. Nature 418(6896):387–391. [DOI] [PubMed] [Google Scholar]
- Griswold CK, Logsdon B, Gomulkiewicz R. 2007. Neutral evolution of multiple quantitative characters: a genealogical approach. Genetics 176(1):455–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillaume F, Otto SP. 2012. Gene functional trade-offs and the evolution of pleiotropy. Genetics 192:1389–1409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillaume F, Whitlock MC. 2007. Effects of migration on the genetic covariance matrix. Evolution 61(10):2398–2409. [DOI] [PubMed] [Google Scholar]
- Hallgrímsson B, Lieberman DE. 2008. Mouse models and the evolutionary developmental biology of the skull. Integr Comp Biol. 48(3):373–384. [DOI] [PubMed] [Google Scholar]
- Hammer S, Eron J, Reiss P, Schooley RT, Thompson MA, Walmsley S, Cahn P, Fisch MA, Gatell JM, Hirsch MS, et al. 2008. Antiretroviral treatment of adult HIV infection: 2008 recommendations of the International AIDS Society-USA panel. JAMA 300(5):555–570. [DOI] [PubMed] [Google Scholar]
- Hansen TF. 2006. The evolution of genetic architecture. Annu Rev Ecol Evol Syst. 37(1):123–157. [Google Scholar]
- Hansen TF, Houle D. 2008. Measuring and comparing evolvability and constraint in multivariate characters. J Evol Biol. 21(5):1201–1219. [DOI] [PubMed] [Google Scholar]
- Hansen TF, Houle D. 2009. Corrigendum. J Evol Biol. 22(4):913–915. [Google Scholar]
- Harrigan PR, Larder BA. 2002. Extent of cross-resistance between agents used to treat human immunodeficiency virus type 1 infection in clinically derived isolates. Antimicrob Agents Chemother. 46(3):909–912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill WG, Zhang XS. 2012. On the pleiotropic structure of the genotype-phenotype map and the evolvability of complex organisms. Genetics 190(3):1131–1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinkley T, Martins J, Chappey C, Haddad M, Stawiski E, Whitcomb JM, Petropoulos CJ, Bonhoeffer S. 2011. A systems analysis of mutational effects in HIV-1 protease and reverse transcriptase. Nat Genet. 43(5):487–490. [DOI] [PubMed] [Google Scholar]
- Houle D, Fierst J. 2013. Properties of spontaneous mutational variance and covariance for wing size and shape in Drosophila melanogaster. Evolution 67(4):1116–1130. [DOI] [PubMed] [Google Scholar]
- Jones AG, Arnold SJ, Burger R. 2003. Stability of the G-matrix in a population experiencing pleiotropic mutation, stabilizing selection, and genetic drift. Evolution 57(8):1747–1760. [DOI] [PubMed] [Google Scholar]
- Jones AG, Bürger R, Arnold SJ. 2014. Epistasis and natural selection shape the mutational architecture of complex traits. Nat Commun. 5:3709.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick M. 2009. Patterns of quantitative genetic variation in multiple dimensions. Genetica 136(2):271–284. [DOI] [PubMed] [Google Scholar]
- Lande R. 1979. Quantitative genetic analysis of multivariate evolution, applied to brain: body size allometry. Evolution 33(1):402–416. [DOI] [PubMed] [Google Scholar]
- Lande R. 1980. The genetic covariance between characters maintained by pleiotropic mutations. Genetics 94(1):203–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leder EH, McCairns RJS, Leinonen T, Cano JM, Viitaniemi HM, Nikinmaa M, Primmer CR, Merila J. 2015. The evolution and adaptive potential of transcriptional variation in sticklebacks–signatures of selection and widespread heritability. Mol Biol Evol. 32(3):674–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lourenço J, Galtier N, Glémin S. 2011. Complexity, pleiotropy, and the fitness effect of mutations. Evolution 65:1559–1571. [DOI] [PubMed] [Google Scholar]
- Mackay TFC, Stone EA, Ayroles JF. 2009. The genetics of quantitative traits: challenges and prospects. Nat Rev Genet. 10(8):565–577. [DOI] [PubMed] [Google Scholar]
- Martins J. a Z, Chappey C, Haddad M, Whitcomb JM, Stawiski E, Petropoulos CJ, Bonhoeffer S. 2010. Principal component analysis of general patterns of hiv-1 replicative fitness in different drug environments. Epidemics 2(2):85–91. [DOI] [PubMed] [Google Scholar]
- McGuigan K, Collet JM, McGraw EA, Ye YH, Allen SL, Chenoweth SF, Blows MW. 2014. The nature and extent of mutational pleiotropy in gene expression of male Drosophila serrata. Genetics 196(3):911–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mezey JG, Cheverud JM, Wagner GP. 2000. Is the genotype-phenotype map modular?: a statistical approach using mouse quantitative trait loci data. Genetics 156(1):305–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore JH. 2003. The ubiquitous nature of epistasis in determining susceptibility to common human diseases. Hum Hered. 56(1):73–82. [DOI] [PubMed] [Google Scholar]
- Ohya Y, Sese J, Yukawa M, Sano F, Nakatani Y, Saito TL, Saka A, Fukuda T, Ishihara S, Oka S, et al. 2005. High-dimensional and large-scale phenotyping of yeast mutants. Proc Natl Acad Sci U S A. 102(52):19015–19020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortlund EA, Bridgham JT, Redinbo MR, Thornton JW. 2007. Crystal structure of an ancient protein: evolution by conformational epistasis. Science 317(5844):1544–1548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostrowski EA, Rozen DE, Lenski RE. 2005. Pleiotropic effects of beneficial mutations in Escherichia coli. Evolution 59(11):2343–2352. [PubMed] [Google Scholar]
- Otto SP. 2004. Two steps forward, one step back: the pleiotropic effects of favoured alleles. Proc R Soc Lond B. 271:705–714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlicev M, Kenney-Hunt JP, Norgard EA, Roseman CC, Wolf JB, Cheverud JM. 2008. Genetic variation in pleiotropy: differential epistasis as a source of variation in the allometric relationship between long bone lengths and body weight. Evolution 62(1):199–213. [DOI] [PubMed] [Google Scholar]
- Pavlicev M, Norgard EA, Fawcett GL, Cheverud JM. 2011. Evolution of pleiotropy: epistatic interaction pattern supports a mechanistic model underlying variation in genotype-phenotype map. J Exp Zool B Mol Dev Evol. 316(5):371–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlicev M, Wagner GP. 2012. A model of developmental evolution: selection, pleiotropy and compensation. Trends Ecol Evol. 27(6):316–322. [DOI] [PubMed] [Google Scholar]
- Petropoulos CJ, Parkin NT, Limoli KL, Lie YS, Wrin T, Huang W, Tian H, Smith D, Winslow GA, Capon DJ, Whitcomb JM. 2000. A novel phenotypic drug susceptibility assay for human immunodeficiency virus type 1. Antimicrob Agents Chemother. 44(4):920–928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips PC. 2008. Epistasis–the essential role of gene interactions in the structure and evolution of genetic systems. Nat Rev Genet. 9(11):855–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pigliucci M. 2003. Phenotypic integration: studying the ecology and evolution of complex phenotypes. Ecol Lett. 6(3):265–272. [Google Scholar]
- Plomin R, Haworth CMA, Davis OSP. 2009. Common disorders are quantitative traits. Nat Rev Genet. 10(12):872–878. [DOI] [PubMed] [Google Scholar]
- Poelwijk FJ, Kiviet DJ, Weinreich DM, Tans SJ. 2007. Empirical fitness landscapes reveal accessible evolutionary paths. Nature 445(7126):383–386. [DOI] [PubMed] [Google Scholar]
- Polster R. (2013). On the nature of pleiotropy and its role for adaptation [PhD thesis]. ETH Zürich.
- R Core Team. (2012). R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing.
- Rhee SY, Gonzales MJ, Kantor R, Betts BJ, Ravela J, Shafer RW. 2003. Human immunodeficiency virus reverse transcriptase and protease sequence database. Nucleic Acids Res. 31(1):298–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roseman CC, Kenney-Hunt JP, Cheverud JM. 2009. Phenotypic integration without modularity: testing hypotheses about the distribution of pleiotropic quantitative trait loci in a continuous space. Evol Biol. 36(3):282–291. [Google Scholar]
- Rueffler C, Hermisson J, Wagner GP. 2012. Evolution of functional specialization and division of labor. Proc Natl Acad Sci U S A. 109(6):E326–E335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sönnichsen B, Koski LB, Walsh A, Marschall P, Neumann B, Brehm M, Alleaume AM, Artelt J, Bettencourt P, Cassin E, et al. 2005. Full-genome RNAi profiling of early embryogenesis in Caenorhabditis elegans. Nature 434(7032):462–469. [DOI] [PubMed] [Google Scholar]
- Via S, Lande R. 1985. Genotype-environment interaction and the evolution of phenotypic plasticity. Evolution 39(3):505–522. [DOI] [PubMed] [Google Scholar]
- Wagner GP, Altenberg L. 1996. Perspective: complex adaptations and the evolution of evolvability. Evolution 50(3):967–976. [DOI] [PubMed] [Google Scholar]
- Wagner GP, Pavlicev M, Cheverud JM. 2007. The road to modularity. Nat Rev Genet. 8(12):921–931. [DOI] [PubMed] [Google Scholar]
- Wagner GP, Zhang J. 2012. Universal pleiotropy is not a valid null hypothesis: reply to Hill and Zhang. Nat Rev Genet. 13(4):296–296. [DOI] [PubMed] [Google Scholar]
- Weinreich DM, Delaney NF, DePristo MA, Hartl DL. 2006. Darwinian evolution can follow only very few mutational paths to fitter proteins. Science 312(5770):111–114. [DOI] [PubMed] [Google Scholar]
- WHO, editor (2012). WHO HIV drug resistance report 2012. Switzerland (Geneva): World Health Organisation.
- Wittkop L, Günthard HF, de Wolf F, Dunn D, Cozzi-Lepri A, de Luca A, Kücherer C, Obel N, von Wyl V, Masquelier B, et al. 2011. Effect of transmitted drug resistance on virological and immunological response to initial combination antiretroviral therapy for HIV (EuroCoord-CHAIN joint project): a European multicohort study. Lancet Infect Dis. 11(5):363–371. [DOI] [PubMed] [Google Scholar]
- Wolf JB, Leamy LJ, Routman EJ, Cheverud JM. 2005. Epistatic pleiotropy and the genetic architecture of covariation within early and late-developing skull trait complexes in mice. Genetics 171(2):683–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf JB, Pomp D, Eisen EJ, Cheverud JM, Leamy LJ. 2006. The contribution of epistatic pleiotropy to the genetic architecture of covariation among polygenic traits in mice. Evol Dev. 8(5):468–476. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.