Detecting and segmenting cell nuclei in two-dimensional microscopy images

Abstract

Introduction:

Cell nuclei are important indicators of cellular processes and diseases. Segmentation is an essential stage in systems for quantitative analysis of nuclei extracted from microscopy images. Given the wide variety of nuclei appearance in different organs and staining procedures, a plethora of methods have been described in the literature to improve the segmentation accuracy and robustness.

Materials and Methods:

In this paper, we propose an unsupervised method for cell nuclei detection and segmentation in two-dimensional microscopy images. The nuclei in the image are detected automatically using a matching-based method. Next, edge maps are generated at multiple image blurring levels followed by edge selection performed in polar space. The nuclei contours are refined iteratively in the constructed edge pyramid. The validation study was conducted over two cell nuclei datasets with manual labeling, including 25 hematoxylin and eosin-stained liver histopathology images and 35 Papanicolaou-stained thyroid images.

Results:

The nuclei detection accuracy was measured by miss rate, and the segmentation accuracy was evaluated by two types of error metrics. Overall, the nuclei detection efficiency of the proposed method is similar to the supervised template matching method. In comparison to four existing state-of-the-art segmentation methods, the proposed method performed the best with average segmentation error 10.34% and 0.33 measured by area error rate and normalized sum of distances (×10).

Conclusion:

Quantitative analysis showed that the method is automatic and accurate when segmenting cell nuclei from microscopy images with noisy background and has the potential to be used in clinic settings.

INTRODUCTION

Cell nuclei in two-dimensional (2D) pathology images can yield quantitative information about the presence or absence of disease processes and also help evaluate disease progress.[1,2,3,4,5] Detecting and segmenting nuclei correctly with minimum human effort is important for cell nuclei analysis. Jung and Kim[6] showed that improved segmentation accuracy led to better classification performance using the unique classifier for thyroid follicular lesions. However, automatic nuclei segmentation in pathology images still remains a difficult problem due to the high variability in images caused by differences in slide preparation, image acquisition, and nuclei heterogeneity.[1,7]

Cell nuclei detection plays a critical role in the overall segmentation procedure, which requires a point per nucleus and close to nucleus center, referred to as seed. Many approaches have been described in the literature to locate cell nuclei in 2D microscopy images. The combination of finding peaks in the Euclidean distance map and watershed,[4] though often resulting in overseeding, can be applied to locate seeds. The circular-shaped nuclei can be effectively located using Hough transformation methods at the cost of expensive computation.[8] H-maxima/minima transform is a powerful approach to detect nuclei by finding the local maximums in images.[9] However, it often leads to overseeding due to its sensitivity to image textures. Recently, other nuclei detection methods have been proposed as well. The multiscale Laplacian-of-Gaussian (LoG) filtering constrained by the distance map-based adaptive scale selection can be used to detect cell nuclei.[10] This method improves seed accuracy but is sensitive to minor peaks in the distance map and thus leads to overseeding. Qi et al.[11] proposed a method based on single-path voting followed by mean-shift clustering to find seeds for touching and overlapping nuclei.

Speaking of segmentation methods more broadly, a wide range of methods has been described in the literature. Thresholding, morphological operation, watershed, region growing, active contour model, clustering, and graph cut are the cornerstones of the segmentation methods proposed in the literature. The simplest thresholding method followed by morphological operation[12] works well for objects with little intensity variations and high foreground/background contrast. Watershed is a nonparametric method widely applied in nuclei segmentation, with the disadvantage of over-segmentation.[13] Active contour models can be used to obtain a smooth contour by minimizing an energy function and can be utilized in pathology images where nuclei appear unclear. The well-known Chan and Vese model was used to obtain the outer contours of nuclei, followed by a watershed-like algorithm to separate the clustered nuclei.[14] Al-Kofahi et al.[10] utilized a graph-cut-based binarization to extract the foreground and then a second graph-cut-based algorithm to refine the initial contours obtained by constrained multiscale LoG filter, which was shown to perform well in pathology images with dense nuclei. Thévenaz et al.[15] proposed a method called Ovuscule which was a modified snake model taking the shape of an ellipse. Its evolution is driven by the combination of the integral of data over the inner ellipse and outer elliptical shell. More nuclei segmentation methods including active contour model, watershed-based method, and Markov random field are described in Irshad paper.[1] Here, we show a comparison between the method we propose and a few such modern methods.

In this paper, we describe an unsupervised nuclei segmentation method, which we call multiscale edge selection in polar space (MESPS). Specifically, a filter bank consisting of rings with various sizes is first constructed to locate nuclei by finding the local maximums in the response map. In the segmentation step, the nuclei contours are iteratively refined by selecting the correct edges in polar space at different smoothing levels. The produced final contour would attach tightly to the actual nucleus border. Figure 1 shows the overview of the proposed method. We believe the accurate nature of the segmentation procedure, simplicity of use, and computational efficiency are key advantages of our method as will be demonstrated.

Figure 1.

Overview of the nuclei detection and segmentation procedure. The nuclei seeds are firstly detected using a set of filters with different sizes. An edge pyramid is then constructed, where edge maps are generated using a set of smooth parameters. Edge selection is performed at each level and the nuclei contour evolves across the edge pyramid to delineate the spatial content of cell nuclei

MATERIALS AND METHODS

Case Selection

Tissue blocks and cytology slides were obtained from the archives of a local hospital (approved as an exempt protocol by the Institutional Review Board). Cases for analysis included liver resection specimens and cytology slides prepared from fine-needle aspiration biopsies of thyroid nodules.

Tissue Procurement and Processing

Liver tissues were procured at the time of a designated surgical procedure. All tissues were fixed in 10% neutral-buffered formalin and processed on a conventional tissue processor using a series of graded alcohols and xylenes before paraffin embedding. Tissue sections were cut at 5 μ thickness from the paraffin-embedded block and placed on conventional 25 mm × 75 mm × 1.0 mm Superfrost Plus microscope slides using Fisherbrand Superslip coverslips (50 mm × 24 mm × 0.17 mm; Fisher Scientific, Thermo Fisher Scientific, Inc., Waltham, MA, USA). All tissue sections for imaging were stained using conventional hematoxylin and eosin (H and E) protocol used in the histology laboratory. For the thyroid cytology preparations, aspirate smears were fixed in 95% ethanol and then stained with the Papanicolaou (Pap) staining technique. Briefly, the Pap stain uses hematoxylin, OG-6, and eosin azure (combination of eosin Y, light-green SF, and green FCF dyes) to stain cytological preparations. Nuclei stained with this technique have blue-green color and excellent chromatin detail that can be visualized by light microscopy.

Digital Image Acquisition

Whole slide digital images of the liver slides were acquired using an Omnyx VL4 digital whole slide scanner (Omnyx, LLC, Waterfront PI, Pittsburg, PA, USA) equipped with a ×60 dry objective. Images obtained had a resolution of 0.1375 μ/pixel and were saved in the proprietary format and then converted to lossless JPEG format. All thyroid cytology slide images were acquired using an Olympus BX51 microscope equipped with a ×100 UIS2 UPlanFl oil immersion objective (numerical aperture 1.30; Olympus America, Central Valley, PA, USA) and 2 megapixel SPOT Insight camera (Diagnostic Instruments, Sterling Heights, MI, USA). Image specifications were 24-bit RGB channels and 0.074 μ/pixel, 118 × 89 μm field of view.

Nuclei Detection

The basic idea of nuclei detection is to find local evidence for the presence or absence of a nucleus in the image. To that end, we construct a filter bank composed of rings of different sizes modeled by the function: r² ≤ x² + y² ≤ (r + ζ)², where r is the radius and ζ is the thickness. Given a certain dataset, prior information such as ζ, the size of the smallest and largest nuclei can be reasonably estimated; thus, the size range of the filters can be defined according to image resolution. We note that the shape of filters can be changed and modeled by different functions to adapt the nuclei appearance in different datasets. In our experiment, the sampled locations 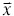=[x_i,y_i] can be obtained from a set of centered coordinates [x₁,…, x_{2r + 1}], −r −ζ ≤ x_i ≤ r + ζ

The filter image patch with size r denoted as f_r(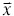) is convolved with a Gaussian function, which is meant to be an approximation of point spread function. Given an image I(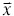), the likelihood of the pixel at 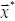being the center of an underlying nucleus is defined as follows:

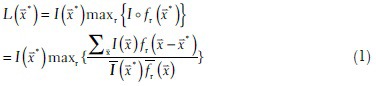
where ° denotes the normalized cross correlation (NCC) between the filter f_r(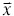) and the image I. 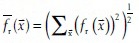and 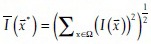with Ω being the neighborhood of pixel 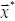of the same size as the filter f_r().

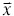The maximization procedure above is performed pixel by pixel searching for the filter f_r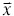 within the filter bank which best matches the appearance of the potential nucleus at location 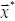. Pixels having ring-shaped surrounding pixels with similar radius as that of a filter will have strong responses and are likely to be nuclei centers. On the contrary, irrelevant tissue structures or noisy background tend to have weak responses. Thus, the method is able to yield size estimation for each nucleus by searching for the best-matched filters.

Here, we note that most nuclei take the shape of an ellipse and thus, theoretically, elliptical filters would generate stronger responses compared with ring-shaped filters. However, since more parameters (e.g., length of major and minor axis, rotation angle) would be required to control an ellipse, leading to a larger searching space when performing NCC operation, we use the ring-shaped filters instead. As we can see from the simulation experiment [Figure 2], ring-shaped filters are able to generate the strong responses when applied to detect both circular and elliptical nuclei in noisy background.

Figure 2.

Simulation for detecting both circular and elliptical nuclei with ring-shaped filters. (a) Constructed filter bank with filters of different sizes (magnified for viewing purpose). (b) Simulated circular nuclei. (c) Response map for (b). (d) Simulated elliptical nuclei. (e) Response map for (d)

To locate the cell nuclei, the standard K-means clustering method is applied to classify the responses into three classes based on the response intensity: (1) background; (2) weak responses from nonnuclei structures; (3) strong responses from potential nuclei. Using connected component analysis, nuclei seeds can be obtained by computing the mass center of each isolated pixel cluster classified as strong responses. Figure 3 shows the nuclei detection procedure applied to the real liver histopathology images.

Figure 3.

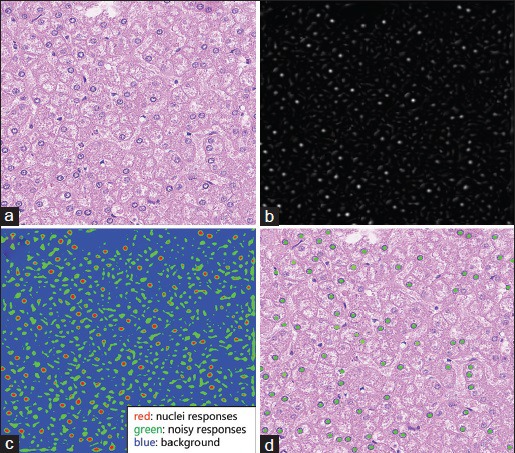
Nuclei detection on real nuclei image using the proposed method. Here, we adopted the hematoxylin channel extracted from the original image by color deconvolution. (a) Original image. (b) Response map. (c) K-means clustering results (in colors). (d) Detected nuclei seeds (green dots)

In practice, the false positive nuclei seeds can be filtered out by postprocessing operations, such as thresholding the area of isolated pixels clusters.

Nuclei Segmentation

With detected nuclei seeds, it is required that the subsequent segmentation algorithm delineate the nuclei contours efficiently and accurately with minimal manual intervention. Our goal is to segment nuclei correctly in the complex background (existence of a large variety of nuclei morphology, chromatin texture, staining procedure as well as tissue heterogeneity). As well known, edge detection[16,17,18] produces outlines at locations where large gradient exists, for example, nuclei borders and noisy background structures [Figure 4a]. To obtain the initial segmentation, a “blurred” version of the nuclei image is required, which describes the nuclei outlines and excludes noisy details hindering the delineation of nuclei contours. The multiscale strategy enables the nucleus contour to refine iteratively from the initial segmentation by changing the blur parameter σ smoothly. The proposed method is designed to discriminate the nuclei borders pixels from remaining “garbage pixels.”

Figure 4.

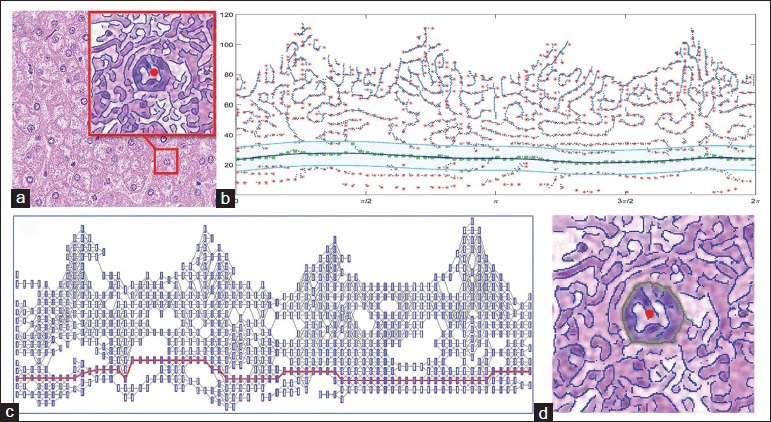
(a) Original image with a subwindow showing the edge map for one nucleus (detected by Canny edge detector, σ_i = 3) with the seed in the center (red dot). (b) Edge pixels are transformed into polar space with the nucleus seed being the origin. Red points are the locations with locally maximal number of pixels; green points show the edge pixels along the optimal path searched by Dijkstra's algorithm. The blue solid line is the fitted curve. In the cyan area, edge pixels from the i + 1^th level are chosen as candidates. (c) Constructed undirected graph with nodes being the red points in (b) and edge weights being the cost defined by the combination of distance and intensity metrics. Nodes marked as red constitute the optimal path. (d) Final contour (red), and optimal path (green) are shown in the image patch

Specifically, the input image is first convolved with the 2D Gaussian function 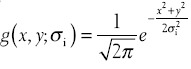with zero mean at multiple scales σ = [σ₀,…,σ_n−1], with σ₀ and σ_n−1 being the minimum and the maximum of σ, respectively. Next, an edge pyramid is constructed consisting of a set of edge maps generated by the edge detector (e.g., Canny detector), where the top level and the bottom level correspond to σ₀ and σ_n−1, respectively. We aim to select the correct edges in polar space starting from the bottom level and then take it as guidance for edge selection in the next higher level. The algorithm refines the contour iteratively and produces the final contour when edge selection is performed at the top level of the edge pyramid.

Edge selection

The first step is to select correct edges from the edge map obtained at the largest scale σ_n−1, where artifacts are the least prevalent. The size of the image patch for each nucleus can be determined adaptively according to the size estimation from nuclei detection step. In the nucleus edge map, edges can be classified into three categories: correct edges (forming the nucleus contour), edges inside the nucleus, and edges outside the nucleus.

One prominent feature to discriminate these three kinds of edges is that, intuitively, correct edge pixels on the nucleus counter often have smoother distance changes away from the seed in comparison to the drastic distance fluctuations of pixels on noisy edges inside or outside the nucleus. In addition, considering the intensity, edge pixels along the nucleus border have relatively consistent intensity compared with that of incorrect edge pixels. With these simple observations in mind, the solution of delineating nucleus contour becomes finding the path with the minimal transportation cost (nonzero) starting and ending at any chosen point on the nucleus border based on both distance and intensity metrics.

The polar coordinate system provides a natural space to search for the optimal path connecting the start point and the end point for each nucleus. Given the edge map E_σi detected at the i^th level, edge pixel =[x,y] in Cartesian coordinate can be transformed into polar space by 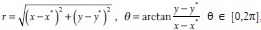, where 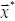= [x^*,y^*] is the coordinate of nucleus seed in the image patch. Figure 4b shows that the edge map in the subwindow of Figure 4a is transformed in polar space.

In the polar coordinate system, the transportation cost between any two neighbor edge pixels p_m = [r_m, θ] and p_n = [r_n, θ + Δθ] is defined as follows:

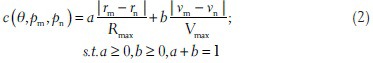
where v_m and v_n denote pixel intensities for p_m and p_n; Δθ is infinitesimal; a, b are the weights for the distance term and intensity term, respectively; R_max and V_max are the maximal distance difference and the maximal intensity difference, respectively, between p_m and p_n in the edge map, enabling both two metrics to have the same scale.

The optimal path Φ* can be found by minimizing the function defined as follows:

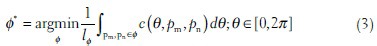
where l_Φ denotes the length for the path Φ.

In the discrete setting, the function above can be rewritten as follows:

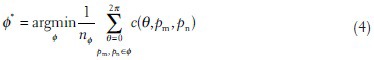
where n_Φ is the number of edge pixels along the path Φ.

Dijkstra's algorithm is an algorithm widely applied to find the shortest path between the source node and the terminal node in a graph, such as road networks and telephone network. It was first conceived in 1956 by Dijkstra.[19] In our case, Dijkstra's algorithm is suitable to solve the above minimization problem. We represent the edge pixels in polar space in the form of undirected graph G = [V, E] [Figure 4c], denote the edge pixels and the graph edges with weights c(θ, p_m, p_n) in E are only feasible for any two adjacent angle nodes p_m, p_n.

To make the algorithm robust against noisy edge pixels, the edge pixels are further represented/discretized by finding the locations with locally a maximal number of edge pixels for each angle in the polar space. A sliding window with width w and height h, moving along the distance direction for each θ, is constructed to capture and count the edge pixels locally. The number of edge pixels in the sliding window centered at [r_j, θ_i] is denoted as N (r_j, θ_i) and locations with locally maximal number of pixels at angle θ_i are denoted as 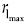(θ_i). These detected locations are the approximate representation of the original edge pixels in polar space [red dots in Figure 4b]. The benefit of discretizing edge pixels is that it helps reduce the number of possible paths between the source node and the terminal node. Thus, the computational cost is reduced dramatically when searching for the optimal path using Dijkstra's algorithm.

In practice, it is not easy to select the source node and terminal node along the nucleus border. In this paper, we propose that the source node and the terminal node can be chosen as edge pixels with the same distances away from the seed at angle 0 and 2π. However, there might be multiple source-terminal pairs in the graph, and thus multiple optimal paths are found by Dijkstra's algorithm. This is so especially when a small σ is applied, where many noisy edge pixels exist at the angle 0 and 2π. When noisy edge pixels are selected as the source or terminal node, the optimal path would be searched by Dijkstra's algorithm at the cost of passing through edges with large weights in the constructed graph. Thus, the real nucleus contour can be found by choosing the path with the minimal cost connecting source-terminal pairs.

One potential issue is that some detected edges may not be complete due to the weak gradient at the nucleus border and thus some pixels along the optimal path are not necessarily on the real nucleus contour. Here, we apply the RANSAC[20] algorithm and the spline curve fitting method to estimate the nucleus contour. Given the edge pixels on the optimal path, a subset of pixels is selected to generate a fitted curve model describing the rough shape of the optimal path. The points fit the estimated model well are called inliers and points with large errors are called outliers. Afterward, the model is refined using only the inliers. The step repeats for a fixed number of times, and the model with the maximal number of inliers is kept. The curve fitting step takes as input the pixels along the optimal path and outputs the final smooth contour C^k connecting the isolated and incomplete detected edges when performed at the k^th level of the edge pyramid.

Edge iteration

The smooth contour generated from the k^th level is taken as the initial nucleus border and helps guide the edge selection for the k + 1^th level. Specifically, at the k + 1^th level, edge pixels within the distance range [C^k − d, C^k + d] are chosen as edge candidates and edge pixels outside the range are discarded in the sense that a more refined contour at the k + 1^th level should be close to the contour obtained from the k^th level with a distance tolerance d. When the blur parameter σ is changed slightly, the edge locations change smoothly and would not shift too much. Therefore, for the k + 1^th level, the edge pixel locations at angle θ should be within the range [C^k(θ)−d, C^k(θ) + d]. With the set of edge candidates, the edge selection is performed as described above to generate a more accurate nucleus contour C^k+1.

As the contour is refined iteratively from the bottom level of the edge pyramid up to the top level, it gradually attaches to the real border of nucleus. Given the small blurring σ₀ at the top level, our algorithm can delineate the nucleus spatial extent precisely.

RESULTS

Before our algorithm is applied to pathology images, the nuclei channel should be extracted from RGB color space by color deconvolution[21] (e.g., extracting hematoxylin channel from H and E-stained images). After that, all image data are normalized to fit the intensity range [0, 1]. We demonstrate the proposed method on two real datasets including thyroid dataset (35 representative images, Pap-stained, 903 cell nuclei) and liver datasets (25 images, H and E-stained, 2145 cell nuclei).

In our experiment, the sliding window width w and height h were set as 15 degrees and 2 pixels, respectively, and were fixed for both two datasets. The only parameter to be changed differently for the two datasets is the maximal smooth level σ_max which was set to be 3 and 5 for the thyroid dataset and the liver dataset, respectively. The minimal smooth level σ_min is usually set to be 1 to capture the precise nucleus border.

For comparison, we choose the following state-of-the-art algorithms used for nuclei segmentation including the Ovuscule,[15] level set[22] and template matching.[23] Template matching has the ability of detecting nuclei in the image while level set and the Ovuscule need detected nuclei seeds for segmentation. In our experiment, level set and the Ovuscule adopted the seeds detected by MESPS for comparing the segmentation performance.

For qualitative comparison, sample segmentation results by approaches listed above are shown in Figure 5, where the rows from the top to the bottom correspond to the results from level set, the Ovuscule, template matching, and our method, respectively, and the columns from left to right correspond to sample images from liver dataset and thyroid dataset, respectively.

Figure 5.

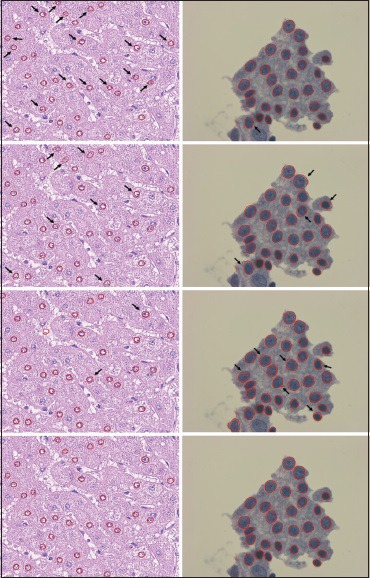
Segmentation results from two validation datasets. First column: liver dataset; second column: thyroid dataset. From the top row to the last row are the results by level set, the Ovuscule, template matching, and multiscale edge selection in polar space, respectively. Note that segmentation flaws are pointed out by black arrows

In addition, we evaluated the nuclei detection efficiency of template matching and MESPS using the miss rate (MR) defined as follows:

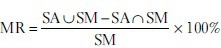
where SA are the seeds detected by the algorithms and SM are the seeds selected manually; SA∪SM and SA∩SM are the number of seeds in the union set and the intersection set of SA and SM, respectively.

The segmentation accuracy was measured by the area error rate (AER)[24] focusing on the number of incorrectly segmented pixels and the spatially-aware evaluation metric normalized sum of distances (NSD)[25] with the ground truth labeled manually. Quantitative analysis of nuclei detection and segmentation efficiency of different approaches is shown in Table 1.

Table 1.

Quantitative evaluation of different approaches on nuclei detection and segmentation efficiency

From the quantitative evaluation of different approaches, we note that the proposed method showed similar or superior performance compared with existing segmentation methods validated on two datasets. For the thyroid dataset, level set segmented nuclei with the highest accuracy with AER and NSD being 8.31% and 0.29, respectively. Our method generated similar results as that of level set, showing that MESPS has the nuclei segmentation ability comparable to the state-of-art method. Moreover, for the liver dataset in the complex setting (nonuniform illumination, noisy background, and nuclei heterogeneity), MESPS could still be able to find the nuclei borders accurately and perform the best compared with the listed approaches. Considering the comprehensive performance over the two validation datasets, MESPS archived the best segmentation accuracy with 10.34% AER and 0.33 NSD on average.

For the overall nuclei detection efficiency, both template matching and MESPS could detect most nuclei labeled manually with the similar MRs. However, we should be aware of the supervised fashion of template matching method that needs users to select a set of nuclei for training and then finds the templates that best match the testing nuclei from the constructed statistical model.

DISCUSSION AND CONCLUSION

This paper proposed an unsupervised method to detect and segment cell nuclei automatically from the 2D pathology images based on NCC and MESPS. The validation experiment showed that the method could segment the cell nuclei accurately when applied to real pathology images with different stainings (e.g., H and E, Pap staining) and image qualities (e.g., blurring, noise, texture heterogeneity).

There are several advantages of the method. First, it has the ability to locate nuclei borders accurately with certain robustness. The multiscale strategy ensures that the ill effects caused by noise, nonuniform intensity, etc., could be greatly reduced by smoothing. The small smooth level at the top of the edge pyramid helps the generated contour gradually cling to the real nucleus border at the pixel level. With the small step size of σ, the contour changes smoothly as it iterates from the bottom level up to the top level of the edge pyramid. Second, it is designed in an unsupervised way that does not need users to train a model used for segmentation. Once the parameters are set, the algorithm could detect and segment the cell nuclei in the dataset automatically. The performance of MESPS depends on the image gradient; thus, it is not sensitive to staining techniques or imaging modalities, which makes it useful and applicable to various datasets in clinic settings. Finally, the proposed algorithm is light weight, consisting of several basic but effective algorithms including NCC, edge detection, and Dijkstra's algorithm. The proposed framework is mathematically simpler than the mentioned state-of-the-art methods.

In addition, we proposed some ways to reduce the computational cost by reducing the number of both nodes and edges when Dijkstra's algorithm is applied. First, the edge pixels in polar space are represented by the points which have locally maximal number of pixels within a sliding window for each angle. This operation reduces the number of nodes greatly in the constructed undirected graph with the additional benefit of denoising. Moreover, edges between two nodes in the graph would be deleted if the distance difference is over a certain threshold, in the sense that pixels at adjacent angles on the nucleus contour should be near each other and the distance away from the nucleus center changes little. Each node only connects a few nodes at adjacent angles, which prominently cut down the number of possible paths between the source and the terminal nodes.

We should note that there are parameters introduced in our proposed method, including filter size, σ_min, σ_max, smooth step size, cost weights (a, b), and the threshold for edge deletion used to reduce computational cost. Here, the parameters to be set to adapt to various datasets are filter size and σ_max. As described in the previous section, the filter size depends on the image resolution as well as the cell nuclei type in study, whose size could be usually found in the literature. σ_max can be determined based on the image gradient in datasets. It is desired to keep the correct nuclei edge pixels in the edge map, at the same time, be able to filter out the noisy edges. In practice, the optimal σ_max can be set experimentally by randomly selecting a few sample images in the dataset and observing the edge maps so that the edge detector could describe the outlines of most nuclei. Our algorithm is not sensitive to other parameters and they were fixed when validated on two datasets. In our experiment, the values of σ_min, smooth step size, a, b, and the threshold were set to be 1, 0.5, 0.4, 0.6, and 20 pixels, respectively.

Besides the advantages mentioned above, the method also has some limitations that are noteworthy of discussion. First, the method is designed for segmenting convex-shaped cell nuclei. In the polar space, parts of the contour for nonconvex shape nucleus are mapped to multiple locations at the same angle, which violates our assumption that there is only one optimal location along the nucleus contour per angle. Even though most cell nuclei have the shape of sphere or ellipsoid, highly concave cell nuclei can be sometimes observed under microscopy due to the sectioning of nuclei at odd angles or tissue distortion in slides preparation procedure, or both. Second, the method could not handle overlapping cell nuclei even if the nuclei seeds are detected correctly. Because of the blurring of border in the overlapping area, the edge detector usually does not generate the edge pixels delineating the two nuclei. The method would treat the two nuclei as one and produce the outer border of them. However, we should note that (1) the ultimate goal of nuclei segmentation is for exploring the correlation between nuclei morphology and cellular/disease progress, (2) overlapping cell nuclei provides limited information for analysis due to the difficulty of recovering inherent information within the overlapping area. Therefore, with plenty of isolated cell nuclei available in the dataset, nuclei overlapping problem is negligible in nuclei based analysis.

The proposed method locates cell nuclei by measuring the matching degree between local image patches and the predefined nucleus-shaped filters. Afterward, the method transforms the object segmentation problem into a classic shortest path problem. The cost function is constructed considering both shape and intensity characteristics of nuclei borders. The accurate delineation of cell nuclei is based on the detected edge pixels on the border which can be correctly selected by the well-known Dijkstra's algorithm. The multiscale strategy enables the contour generated at each level evolves smoothly to the actual nuclei border. In the future, the method could be further automated by enabling the algorithm to select the optimal maximal smooth parameter based on image gradient statistics.

Financial Support and Sponsorship

NIH awards CA188938, GM090033, and PA State Health Department award 4100059192 supported the study.

Conflicts of Interest

There are no conflicts of interest.