Entropic stabilization of folded RNA in crowded solutions measured by SAXS

Abstract

Non-coding RNAs must fold into specific structures that are stabilized by metal ions and other co-solutes in the cell's interior. Large crowder molecules such as PEG stabilize a bacterial group I ribozyme so that the RNA folds in low Mg²⁺ concentrations typical of the cell's interior. To understand the thermodynamic origins of stabilization by crowder molecules, small angle X-ray scattering was used to measure the folding and helix assembly of a bacterial group I ribozyme at different temperatures and in different MgCl₂ and polyethylene glycol (PEG) concentrations. The resulting phase diagrams show that perturbations to folding by each variable do not overlap. A favorable enthalpy change drives the formation of compact, native-like structures, but requires Mg²⁺ ions at all temperatures studied (5–55°C). PEG reduces the entropic cost of helix assembly and increases correlations between RNA segments at all temperatures. The phase diagrams also revealed a semi-compact intermediate between the unfolded and folded ensemble that is locally more flexible than the unfolded state, as judged by SHAPE modification. These results suggest that environmental variables such as temperature and solute density will favor different types of RNA structures.

INTRODUCTION

Many RNAs must fold into specific three-dimensional RNA structures to act in gene expression and regulation. Therefore, the RNA folding process underpins many functions of a healthy cell. The formation of compactly folded RNA structures requires the condensation of positive counterions to screen the negative charge of the phosphodiester backbone (1–3). Many large RNAs, however, are unstable in physiological MgCl₂ concentrations in vitro, raising the question of how other solutes in the cell alter RNA folding thermodynamics. Here, we measure the temperature-dependence of folding of a bacterial group I ribozyme and find that the folding entropy becomes less unfavorable in crowded versus dilute solutions.

Predicting how co-solutes alter RNA thermodynamics remains challenging because solutes affect the RNA secondary and tertiary structure in different ways (4). Neutral solutes such as alcohols and sugars are reported to destabilize DNA and RNA secondary structure (5,6), by altering hydration or hydrogen bonding networks. These surface interactions are particularly important for folding of small nucleic acids (7,8) and for conformational changes requiring de-wetting of nucleobases, as in DNA quadruplexes (9). Because organic solutes also lower the dielectric constant of the solution (10), they can intensify electrostatic interactions such as ion condensation, and make folding more enthalpically favorable (11,12).

By contrast, excluded volume effects are expected to stabilize the RNA tertiary structure by favoring compact structures over extended ones. As co-solutes increase in size, the opportunities for direct surface interactions diminish while the resulting spatial confinement reduces their translational and configurational entropy (4,13,14). Using polyethylene glycol (PEG) as a synthetic crowder, we found that molecular crowding stabilizes the folded Azoarcus group I ribozyme (M_r = 67 kDa) by up to 6 k_BT, so that folding occurs in physiological Mg²⁺ concentrations (15). Several observations suggested this stabilization arises from excluded volume effects rather than surface interactions. First, stabilization of the folded RNA by PEG was not accounted for by changes to the activity of Mg²⁺ or water (15). Second, PEG and Ficoll, but not ethylene glycol and sucrose, favored the catalytically active form of the ribozyme (16). That molecular crowding stabilizes RNA tertiary structure was also in agreement with the increased cooperativity of thermal unfolding in tRNA (17) and improved docking of the hammerhead ribozyme (18).

Molecular crowding alters internal chain entropy as well as translational freedom. Simulations show that spatial confinement narrows the conformational space occupied by extended chains (19). The preferred polymer structures depend on the shape of the crowder, the solvent quality and temperature (20). In agreement with theory, solution X-ray scattering showed that PEG increases correlations between statistical segments of the unfolded Azoarcus ribozyme in low Mg²⁺ (21). That confinement favors intrachain interactions was demonstrated by recent single-molecule FRET experiments showing that PEG leads to faster docking of two helical domains of the hairpin ribozyme (18) and of a small RNA tetraloop with its helical receptor (22).

To better understand how crowders such as PEG stabilize folded RNA, we used small angle X-ray scattering (SAXS) to measure folding of the Azoarcus ribozyme in Mg²⁺ and PEG solutions at different temperatures. We directly demonstrate that PEG diminishes the unfavorable entropy change associated with folding, in good agreement with theoretical models and our earlier experimental results. We also find that temperature and crowders shift the RNA population from the unfolded state in low ionic strength to a flexible semi-compact intermediate that precedes folding to compact, native-like structures. The results show how the interplay of Mg²⁺ ions, temperature and spatial confinement shapes the phase diagram for the self-assembly of large RNA structures.

MATERIALS AND METHODS

RNA preparation

The Azoarcus ribozyme (195 nt) was transcribed in vitro from pAz-IVS digested with EarI and gel purified as previously described (21). The resultant RNA was at 5 mg/ml, as measured from UV absorption at 260 nm; the stock was incubated at 50°C for 5 min before use. RNA solutions for SAXS experiments were 0.4 mg/ml in 20 mM Tris-HCl (pH 7.5) in the stated PEG concentration. RNA solution was drawn through a 1 mm capillary tube at 37°C, passing through the X-ray beam for each measurement. The solution was kept flowing to minimize the effects of radiation damage to the RNA.

SAXS

SAXS measurements were performed using the BioCAT 18ID beamline at Argonne National Lab Advanced Photon Source. The wavelength was 1.033 Å (energy 12 keV) and measurements were made in the momentum transfer range of 0.006–0.34 Å⁻¹. SAXS data were radially averaged and corrected for background signal due to the buffer and PEG. The X-ray scattering contrast is proportional to the square of the difference in electron densities between scattering species. PEG and water have similar electron densities (0.60 and 0.56 moles electrons/cm³, respectively) compared to RNA (∼0.93 moles electrons/cm³). Although PEG contributed to the background scattering and thus increased the noise after background subtraction, the excess scattering from an RNA/water solution is ∼80 times higher than from a PEG/water solution, allowing measurement of the RNA structure without substantial interference from the PEG scattering.

The real space pair distribution functions of electron density, P(r), were calculated using GNOM as previously described (15), and used to determine the radius of gyration, R_g, of the RNA molecules. We use R_g as a single order parameter to define the global shape of the molecules. As contributions to P(r) come from a distribution of molecular sizes and shapes, however, R_g determined from P(r) also represents this distribution of structures. The values of R_g used in this paper were obtained from analysis of P(r), although similar values of R_g were obtained from Guinier plots. For the scattering curves, the error in the scattering intensity at each radially averaged Q was obtained from the counting statistics from the raw scattering image. The errors in R_g and other parameters were determined by propagating these measurement errors through the Guinier fits and P(r) calculations.

3-state model for RNA folding

We have previously fitted the change in R_g to a 2-state thermodynamic model, with a linear or logarithmic dependence of the R_g's for the unfolded RNA on salt concentration (21). In this paper, we fitted the SAXS folding data to a three-state model U ↔ I_U ↔ I_C (23) because the extra state is particularly apparent at high temperatures where the fully unfolded state U has an appreciably larger R_g than the semi-compact intermediate I_U. The compact, native-like intermediate I_C and the active native state N have similar R_g values and were treated as one folded state (24). This three-state model is a reasonable approximation of the equilibrium folding pathway detectable by SAXS, based on the concerted formation of tertiary interactions reported by hydroxyl radical footprinting (25,26). The equation used to fit the SAXS R_g data is:

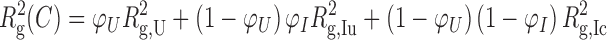(1)

in which R_g(C) is the radius of gyration as a function of Mg²⁺ concentration C; R_g,U is the radius of gyration of the RNA in its unfolded state; R_g,Iu is the radius of gyration of the RNA in the semi-compact I_U state; and R_g,Ic is the radius of gyration of the RNA in the folded I_C state. The equilibria between the unfolded and intermediate states, and the intermediate and folded states, are described by sequential 2-state Hill equations:

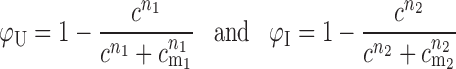(2)

In these equations, c_m1 and c_m2 are the [MgCl₂] midpoints of the U → I_U and I_U → I_C equilibria, respectively. The Hill coefficients n₁ and n₂ are equal to the gradient of each transition at its midpoint (the rate of change of ΔG with MgCl₂ concentration).

SHAPE

SHAPE experiments were carried out with N-methylisotoic anhydride (NMIA) as described previously (27,28). The peak heights were quantified using SAFA (29) to obtain the reactivity for each residue after subtracting the background signal in the absence of NMIA. To account for perturbations to ribose modification by MgCl₂ ions and PEG, we measured the NMIA modification of ATP in solutions with increasing PEG or MgCl₂ by separating unmodified ATP from 2′ O-acyl ATP on a 20% polyacrylamide denaturing gel. Higher MgCl₂ increased the amount of NMIA modification as shown in Supplementary Figure S1. Therefore, the modification levels at different MgCl₂ concentrations within a titration were adjusted using the adenosine triphosphate (ATP) standard curve to account for the presence of MgCl₂, and normalized to the maximum and minimum level of modification within that titration. PEG appeared to quench NMIA modification by 50–75%. Substantial variation in the normalized reactivities in different PEG solutions prevented us from quantitatively measuring the change in RNA reactivity due to the presence of PEG.

RESULTS

Ribozyme folding by SAXS

Solution scattering experiments on the Azoarcus group I ribozyme showed that the unfolded ribozyme in low ionic strength, U, goes through a concerted folding transition to a native-like intermediate, I_C, in the presence of cations such as Mg²⁺ (24,30). This folding transition in 0.3–0.7 mM MgCl₂ coincides with the assembly of core double helices (31) and is cooperative based on footprinting of individual interactions (25), double mutant cycles (23) and singular value decomposition of the scattering curves (32). An additional transition from the extended U state to a semi-compact intermediate, I_U, is also apparent below 0.2 mM MgCl₂ (23). As a result, R_g can be treated as an order parameter of the system and the reduction in R_g can be approximated by two phase transitions from U to I_U and I_U to I_C. Formation of native tertiary interactions (N) above 2 mM MgCl₂ causes only a small change in the scattering profile (24,30) and is neglected in our fits to the SAXS data.

Although cells contain particles of many sizes and shapes, excluded volume effects can be imitated by synthetic polymers such as PEG (14,33,34). PEG is advantageous for our experiments because of its low X-ray scattering contrast with water. Although PEG has been reported to interact directly with DNA quadruplexes (35), surface interactions appear to be greatly outweighed by excluded volume effects in our system (15,16). The R_g of linear polymers typically increases with increasing solvent quality and higher temperature. Here, we used SAXS to determine how these opposing effects of temperature and crowders influence the folding landscape of the ribozyme.

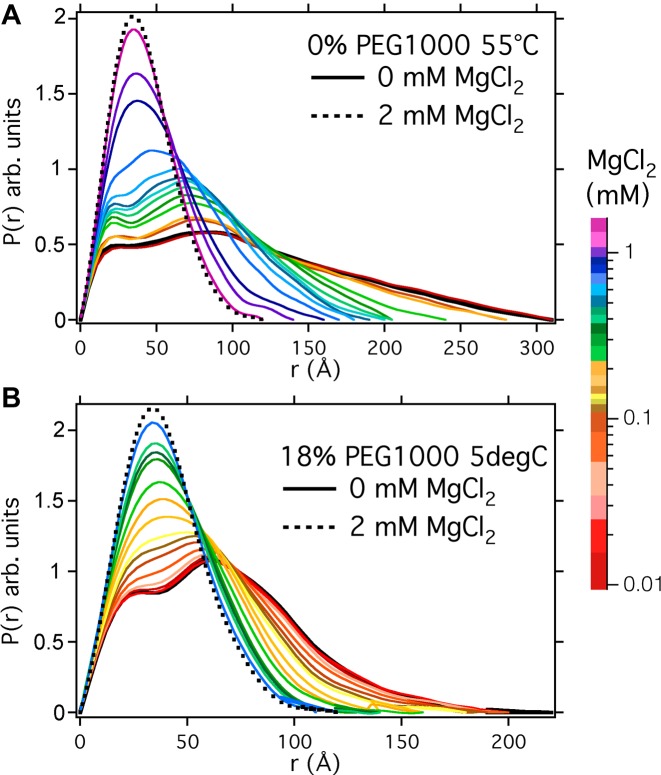
We measured the scattering functions of the Azoarcus ribozyme in 0–5 mM MgCl₂ and 0, 10% and 18% PEG 1000 MW, while varying the temperature from 5–55°C. Supplementary Figure S2 shows an example of the scattering data for RNA in buffer alone or in 18% PEG. The scattering functions were similar to those measured previously and can be inverted using a Fourier transform to calculate a density–density correlation probability function, P(r). Figure 1 compares the change in P(r) for MgCl₂ titrations in the absence of PEG at 55°C and with 18% PEG1000 at 5°C. These conditions give rise to the least compact and most tightly folded RNA conformations, respectively. (Additional data at 0%, 10% and 18% PEG at both 5°C and 55°C are shown in Supplementary Figure S3). The scattering functions of the folded RNA in 2 mM MgCl₂ were similar, as expected (dotted lines, Figure 1). By contrast, temperature and PEG substantially affected the structure of the unfolded ensemble in the absence of MgCl₂ (black lines, Figure 1). At 55°C in dilute buffer, the density–density correlations within a single RNA molecule, R_max, extend to 310 Å, whereas at 5°C in 18% PEG, R_max is 200 Å.

Figure 1.

Density-density probability distribution functions for Azoarcus ribozyme molecules stabilized at (A) 55°C and 0% PEG; and (B) 5°C and 18% PEG. The different colors indicate solutions containing a range of MgCl₂ concentrations indicated in the colored side bar. Scattering intensities after background subtraction are shown in Supplementary Figure S2. The probability distributions were calculated using GNOM (see Materials and Methods) and normalized to an equal area under the curve.

Temperature and Mg²⁺-dependent phase diagram for folding

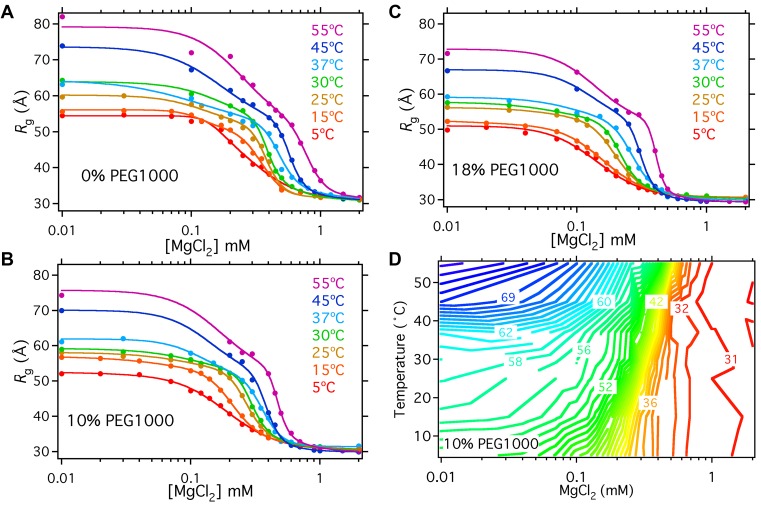
To identify the phase transitions for folding, we plotted the radius of gyration, R_g, as a function of MgCl₂ concentration in each PEG solution (Figure 2A–C). A contour plot of R_g as a function of temperature and MgCl₂ revealed distinct transitions between the folded I_C state in high MgCl₂, the semi-compact I_U state at low Mg²⁺ and low temperature, and an extended U state at low MgCl₂ and high temperature (Figure 2D shows data at 10% PEG; see Supplementary Figure S4 for corresponding plots at 0 and 18% PEG).

Figure 2.

Temperature and Mg²⁺ phase diagram for folding. (A–C) PEG stabilizes the folded RNA at 5–55°C. MgCl₂ titrations showing the decrease in R_g in MgCl₂ of the Azoarcus ribozyme at different temperatures. Folding in (A) 0% PEG1000; (B) 10% PEG1000; (C) 18% PEG1000. Solid lines represent fits to two sequential two-state cooperative folding transitions (Equations 1 and 2). Fitting constraints were imposed on the R_g of the unfolded intermediate, R_g,I, was constrained to have the same value at 5°C: R_g,I(0%) = R_g,I(10%) = R_g,I(18%), but this was allowed to vary as a global fitting parameter. The value of R_g,I(0%) at 15°C and 25°C was fixed at 50 Å, which gave the most stable fits. The typical s.d. was ± 1 Å for unfolded RNA and ± 0.15 Å for folded RNA. (D) Contour plot of the data in Figure 2B. The plateau of R_g values just above the main folding transition corresponds to I_U, approximately 51 Å.

Above 0.7 mM MgCl₂, the RNA is folded at all temperatures studied, consistent with the known thermal stability of this ribozyme (36). The main folding transition from I_U to I_C is temperature-dependent and cooperative with respect to MgCl₂ concentration, represented by closely spaced contour lines around 0.2 mM MgCl₂ at 5°C and 0.5 mM MgCl₂ at 55°C. PEG shifts the folding transition to lower MgCl₂ concentrations (15), and makes folding more cooperative, particularly at higher temperatures (Figure 2A–C). From the population of I_C at each temperature (Supplementary Figure S5), one can see that the melting temperature in 0.4 mM MgCl₂ without PEG is the same (36°C) as the melting temperature in 0.3 mM MgCl₂ and 10% PEG1000 (35°C). Nevertheless, titrations in 18% PEG (Figure 2c) showed that molecular crowding alone cannot drive the RNA into a compact state without sufficient cations to stabilize the folded structure, even at 5°C.

A plateau at MgCl₂ concentrations just below the folding transition corresponds to the semi-compact I_U state (R_g = 51 Å), which at 5°C is populated even without added Mg²⁺. Fits of the data to a three-state folding model yielded a constant value for R_g (I_U) = 51 ± 0.3 Å (Supplementary Figure S6), suggesting that it represents a distinct structural ensemble. Interestingly, I_U precedes the transition to the native-like I_C in all the conditions tested here. The transition between the semi-compact I_U state to the extended U state at low Mg²⁺ was most apparent at higher temperatures, at which base pairs begin to denature in the absence of Mg²⁺ (25). PEG counteracts this thermal expansion of the unfolded RNA, reducing the average R_g in low Mg²⁺ above 20°C.

Enthalpy of folding is nearly independent of Mg²⁺ and PEG

We next used the temperature-dependence of folding to evaluate how crowding perturbs the folding thermodynamics. The fits to individual MgCl₂ titrations in Figure 2A–C allowed us to determine the occupancy of the U, I_U and I_C RNA states at any given MgCl₂ concentration (Supplementary Table S1). We used these calculated occupancies to obtain the equilibrium constant of the main I_U to I_C folding transition. We compared the data in PEG and no PEG for MgCl₂ concentrations closest to the midpoints of the folding transitions to minimize errors from extrapolation of the slopes beyond the transition region.

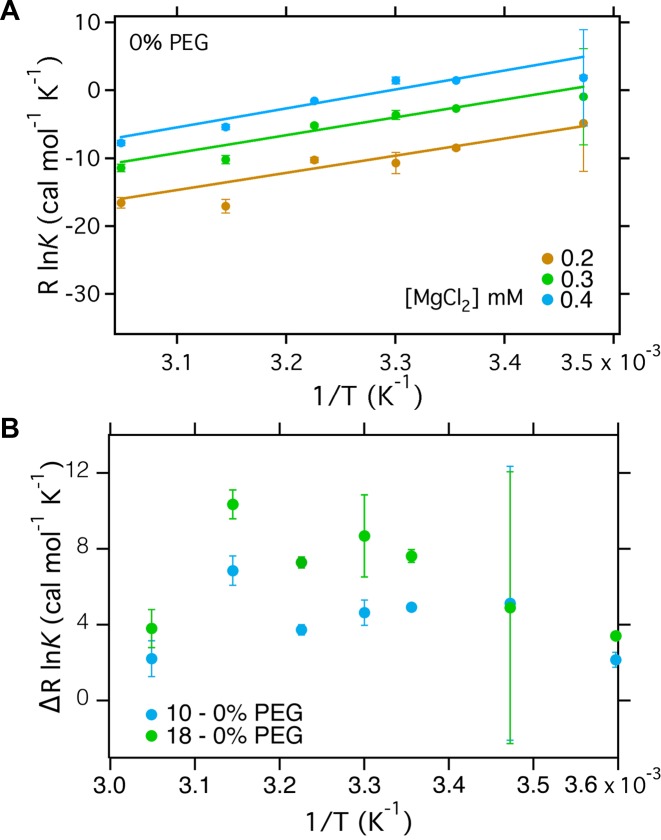
From the van't Hoff equation, RlnK = -ΔH°/T + ΔS°, we obtained the enthalpy and entropy change associated with folding in 0.2–0.4 mM Mg²⁺ (Figure 3A). In the absence of PEG, ΔH° for RNA folding is nearly constant between 5–55°C. The slopes of the van't Hoff plots were the same at each MgCl₂ concentration, within the error of the measurement (Supplementary Table S2). Constraining the slopes to be the same for all three salt concentrations yielded ΔH° = −27.6 ± 0.7 kcal mol⁻¹ within the range 0.2–0.4 mM MgCl₂ in the absence of PEG (Figure 3A and Table 1) and ΔH = −27.9 ± 1.3 kcal mol⁻¹ in 10% PEG (Supplementary Figure S7A and Table 1). The linear region is smaller in 18% PEG than in 0% and 10% PEG (Supplementary Figure S7B), making a comparison of the slopes far less reliable.

Figure 3.

Temperature-dependence of helix assembly. van't Hoff plots for the main I_U to I_C folding transition that involves assembly of core helices. The equilibrium constant at each temperature, PEG and MgCl₂ concentration was calculated using the occupancy of each state from the fits to the Hill equation from the SAXS data in Figure 2. (A) van't Hoff plot for folding in dilute buffer. ΔH of RNA folding is assumed to be constant and extracted from the gradient of the fits; ΔS is taken from the intercept. Fitting parameters are given in Table 1. See Supplementary Figure S7 for plots in 10% and 18% PEG. (B) RlnK for folding in 10% or 18% PEG versus dilute buffer. The weak temperature dependence is consistent with a small perturbation to ΔH° and larger perturbation to ΔS° in PEG.

Table 1. Entropy Change during RNA Folding.

PEG	ΔH° (kcal/mol)	ΔS° (cal/mol K)
0.2 mM MgCl2
0%	–27.6 ± 0.6	–101 ± 2
10%	–27.9 ± 1.3	–97 ± 4
18%	–22 ± 3	–74 ± 11
0.3 mM MgCl2
0%	–27.6 ± 0.6	–96 ± 2
10%	–27.9 ± 1.3	–92 ± 4
18%	–22 ± 3	–69 ± 11
0.4 mM MgCl2
0%	–27.6 ± 0.6	–92 ± 2
10%	–27.9 ± 1.3	–88 ± 4
18%	–22 ± 3	–65 ± 11

Entropy of folding

As expected, the main tertiary folding transition of the Azoarcus ribozyme from I_U to I_C is associated with a favorable enthalpy change and an unfavorable entropy change, based on a linear form of the van't Hoff equation (Table 1). The ΔS° of folding, however, was less unfavorable in the presence of PEG than in dilute solution. This observation is consistent with excluded volume theories suggesting that the energetic (ΔG) stabilization of folded macromolecules arises from reduced degrees of freedom in the unfolded state (13,14). Owing to the uncertainties in the van't Hoff fits, we also directly compared the effect of PEG on the folding equilibrium at each temperature (Figure 3B). The difference between RlnK in PEG and in dilute buffer, ΔRlnK, is roughly independent of temperature between 15–55°C within error, consistent with a small perturbation to ΔH°. Nevertheless, folding in PEG is always more favorable than folding in dilute buffer. The difference in the entropy changed associated with folding in PEG compared to dilute buffer ΔΔS = ΔS_PEG – ΔS_H2O ≈ 4 cal K⁻¹mol⁻¹ in 10% PEG and 27 cal K⁻¹mol⁻¹ in 18% PEG, corresponding to –TΔΔS ≈ –2.5 and –16.5 kcal/mol, respectively, at 37°C. Therefore, a smaller entropic penalty for folding in PEG solutions accounts for much of the observed stabilization of the folded RNA.

Coupled conformational change

Temperature-dependent coupled equilibria of single-stranded regions in the unfolded RNA ensemble have been associated with substantial changes in heat capacity, ΔC_p (37), although ΔC_p can be difficult to detect from folding equilibria owing to entropy–enthalpy compensation (38–40). A comparison of the folding phase diagrams in dilute buffer and in 18% PEG suggested that molecular crowding increases the overlap between changes in the ‘denatured’ ensemble (U→I_U) and the main I_U→I_C folding transition (Figure 2). This effect is more apparent at 45–55°C than 5°C, and may explain why the van't Hoff plots appear more curved in 18% PEG than in no PEG (Supplementary Figure S7).

To estimate how much PEG might alter ΔC_p for folding of the Azoarcus ribozyme, we also fit the folding equilibrium constants in 0.3 mM MgCl₂ to a non-linear van't Hoff equation that assumes a constant ΔC_p(Supplementary Figure S8). Although we cannot precisely determine ΔC_p given the narrow temperature range of our SAXS experiments, such fits yield an average ΔC_p ≈ –1.5 kcal/mol K that remains constant or increases with PEG content (Supplementary Table S2). Our estimates of ΔC_p are in the range of previous measurements on RNA helix junctions (37) but substantially larger than ΔC_p = 0.24 kcal/mol K for docking of an RNA tetraloop with its receptor (41). Using these estimates of ΔC_p to evaluate ΔS° at 30°C again shows that 18% PEG1000 reduces the entropic penalty for ribozyme folding by ∼20 cal/mol K (Supplementary Table S2).

Effect of PEG and temperature on RNA flexibility

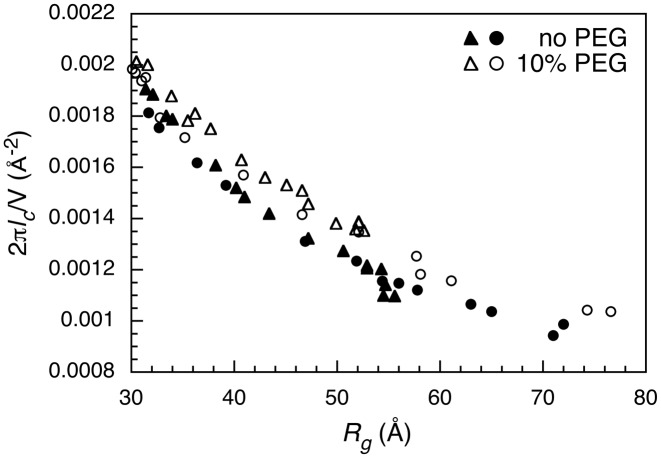
We next analyzed the RNA scattering intensity at higher momentum transfer to assess the flexibility of the ribozyme chain as it folds in MgCl₂. We calculated a correlation length, l_c, from the integral 2πl_c/V = ∫qI(q)dq / I(0) for MgCl₂ titrations at each temperature and PEG content. The correlation length is a measure of intra-chain correlations between different segments of the RNA, for a given particle volume V which is related to R_g (42). As shown in Figure 4 for scattering data at 5°C and 55°C, l_c increases as Mg²⁺ concentration rises and the RNA becomes more compact (lower R_g). PEG increases these intra-chain correlations in the Azoarcus ribozyme, particularly at length scales comparable to the size of a helical domain (50–100 Å), as we previously observed (21). We find here that this effect of PEG is surprisingly independent of temperature (Figure 4), consistent with a reduction in the entropy of the RNA chain.

Figure 4.

PEG stiffens correlations between RNA chain segments. Representative analysis of scattering curves at different Mg²⁺ content that lowers R_g. The correlation length l_c was obtained from 2πl_c/V = ∫qI(q)dq / I(0) (42) for q ≤ 0.2 for scattering data at 5°C (triangles) and 55°C (circles) in dilute solution (closed symbols) and in 10% PEG1000 (open symbols). A similar difference in l_c with and without PEG was observed at other temperatures.

Similarly, a comparison of the Porod exponent ν shows that the transition from the compact folded state I_c to the more extended unfolded state U is consistent with an increase in flexibility with the increase in R_g (Supplementary Figure S9). For the folded ribozyme in 2 mM MgCl₂, the value ν = 3 is typical of a compact polymer (43). This decreases to ν ≈ 1.3 in low Mg²⁺, indicating that RNA in the I_U and U states is closer to a rod than to a Gaussian chain (ν = 2). The chain crosses ν = 2 at about R_g ≈ 40–42 Å at all temperatures, although the RNA continues to expand at 55°C indicating a self-similarity of the chain conformation as the secondary structure begins to unfold between I_U and U.

Flexibility of core nucleotides

To obtain more information about the folding pathway at different temperatures, we probed the local structure of the RNA using SHAPE chemical modification under the same conditions used for SAXS (Materials and Methods). In this method, modification of the ribose 2′OH by NMIA reports on the local flexibility of the RNA backbone, or the presence of a reactive ribose conformation (44). The ribose modification pattern is read out by primer extension, as illustrated in Figure 5. As expected, nucleotides in hairpin loops at the exterior of the folded ribozyme 8a (nt 109 and nt 155) were strongly modified when the RNA was folded in 5 mM MgCl₂ (Figure 5), whereas nucleotides 116–127 in the core of the ribozyme became protected from modification.

Figure 5.

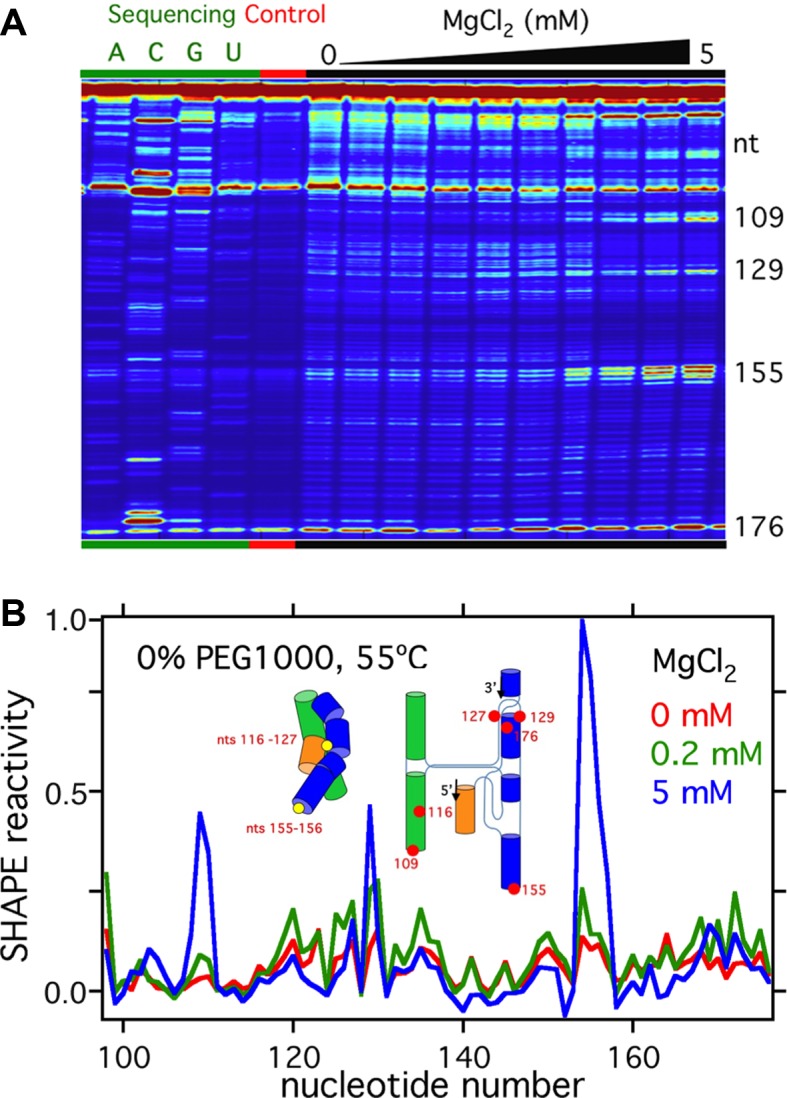
SHAPE experiments show changing nucleotide flexibility with MgCl₂. (A) Image of the sequencing data from SHAPE experiments. Higher intensity bands correspond to higher ribose 2′ O modifications. Following a band from left to right shows how the SHAPE reactivity of that nucleotide varies with increasing MgCl₂ concentration. These data are for RNA stabilized in 0% PEG at 55°C. The large peaks at the bottom and top of each lane correspond to un-extended primers and fully reverse-transcribed molecules, respectively. (B) Normalized SHAPE reactivity of each nucleotide in 0, 0.2 and 5 mM MgCl₂ in 0% PEG at 55°C. These reactivities are obtained by fitting the background-subtracted data down the corresponding lane in Figure 6A. Inset: Cartoon comparing the approximate locations of nts 155–156 and nts 116–127 (circles) in the Azoarcus ribozyme.

The extent of ribose modification was plotted as a function of Mg²⁺ concentration (Figure 6), after correcting for the intrinsic increase in NMIA reactivity with higher Mg²⁺ concentration (Materials and Methods and Supplementary Figure S1). Nucleotides in the peripheral hairpin loops, such as nt 155, became increasingly reactive with Mg²⁺ (Figure 6A and C). This likely reflects a change in solvation or backbone dynamics, because the extent of modification fails to reach a plateau by 5 mM MgCl₂, although the ribozyme is completely folded by 2 mM MgCl₂ (Figure 2A).

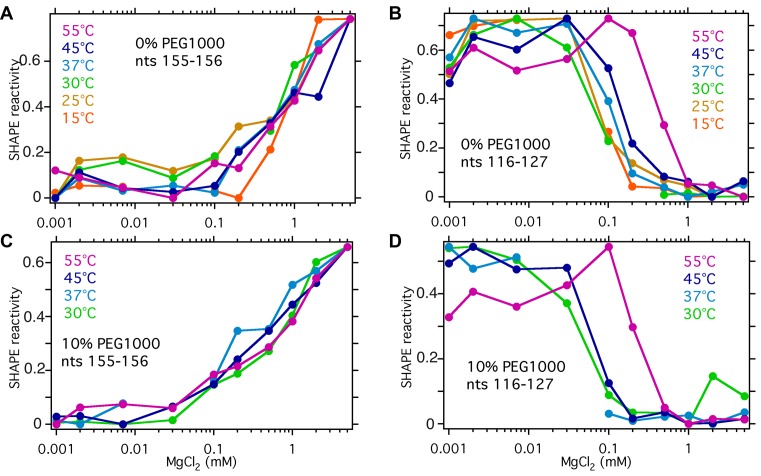
Figure 6.

Average SHAPE reactivities with MgCl₂ concentration. Relative reactivities for peripheral nucleotides (A and C) 155–156 and core nucleotides (B and D) 116–127 in 0% and 10% PEG. The reactivities are normalized to account for intrinsic differences in modification due to MgCl₂ and to the same minimum and maximum values for each trace. The relative reactivities in two trials at 55°C differed by 0.02 to 0.07 (S.D.), which is less than the differences from PEG or MgCl₂.

By contrast, core nt 116–127 exhibited two conformational transitions that correlated with global folding transitions observed by SAXS. First, the reactivity of core nucleotides sharply decreased between 0.2 and 2 mM MgCl₂, as the helices assemble into a native-like conformation (Figure 6B). Second, at 45°C and 55°C, the average SHAPE reactivity increased between 0 and 0.2 mM MgCl₂, the range over which the unfolded RNA converts to the I_U intermediate (Figure 6B). This increase in the apparent flexibility of the RNA backbone was unexpected, because the I_U state in 0.2 mM MgCl₂ is more compact than the U state in no MgCl₂ and the scattering correlations are similar. The addition of 10% PEG (Figure 6D) increased this difference, by stiffening the unfolded RNA (Figure 4) while simultaneously favoring compact structures (Figure 2).

DISCUSSION

The results of the SAXS and SHAPE experiments presented here illustrate how temperature, Mg²⁺ ions and crowder molecules influence tertiary folding of the Azoarcus ribozyme. Although these variables are linked—for example, thermal fluctuations in the solution oppose ion condensation around the RNA and the PEG co-solute alters the activity of water and ions—their effects on the RNA are observably distinct. This implies that different types of RNA interactions, such as base stacking or helix packing, will be advantageous under specific physiological conditions such as growth temperature, water content, polyamine concentration and metal ion homeostasis.

The secondary and tertiary structures of the Azoarcus ribozyme is unusually thermostable (36), owing to its GC-rich secondary structure and strong coupling between tertiary interactions (23), including two tetraloop-receptor interactions that are associated with a strongly favorable enthalpy change upon folding (41,45). Our SAXS experiments show that both Mg²⁺ ions and low temperature stabilize the ribozyme tertiary structure, as expected, with the midpoint for the I_U to I_C transition shifting to higher Mg²⁺ concentrations as the temperature rises. Further expansion of I_U to U at low Mg²⁺ and high temperature likely corresponds to some unraveling of the secondary structure that denatures at 53°C in the absence of Mg²⁺ (24). Assembly of the tertiary structure (I_C) in 0.3 mM MgCl₂ is stabilized by a favorable enthalpy change, ΔH° = -27.6 ± 2 kcal/mol at 30° (Table 1). Enthalpy-driven folding has been observed in other RNAs with abundant hydrogen bonding and base stacking interactions in the tertiary structure, such as the P4–P6 RNA (46), purine riboswitch (47), a 58-nt rRNA domain (48) and GAAA tetraloop-receptor motifs (45).

Although low temperature increases the stability of both secondary and tertiary RNA interactions, the assembly of compact tertiary structures is exquisitely sensitive to Mg²⁺ concentrations ([Mg²⁺]_1/2 = 0.3–0.8 mM) at all temperatures assayed (5–55°C). This strict requirement for counterions even in the presence of enthalpically favorable interactions such as base stacking (49,50) is congruent with the strong linkage between interhelical tertiary interactions and cation-dependent assembly of core helices in this RNA (23). Since Mg²⁺ ions stabilize the folded ribozyme more efficiently than Na⁺ and K⁺ (32,51), it will be of interest to know whether thermal denaturation of the ribozyme is broader in monovalent ions than in Mg²⁺ ions, as observed for tRNA (52).

Assembly of the core helices is accompanied by an unfavorable ΔS° = −91 ± 2 cal/mol•K (Table 1). When PEG1000 is added to the system, folding becomes more favorable at all temperatures between 5–55°C, implying a perturbation to the folding entropy ΔΔS ≈ 27 cal/mol K in 18% PEG. The smaller entropic penalty of folding in crowded solutions is consistent with simple excluded volume theories in which crowders reduce the translational freedom of other solutes (33). It is also consistent with our previous analysis of the solution scattering curves indicating that the unfolded RNA explores fewer conformations in crowded solutions, at the length scale of the folded ribozyme, resulting in a higher free energy for the unfolded state ensemble (21), and with increased RNA folding rates in PEG solutions as measured by smFRET (18,22). Our SAXS results show that PEG strengthens intra-RNA correlations at all of the temperatures tested, supporting the idea that molecular crowders restrict the conformational freedom of the RNA. Crowding also disfavors the extended U state compared to the semi-compact I_U state, particularly at high temperatures. This shift between U and I_U can be viewed as a temperature-dependent coupled equilibrium that changes the heat capacity of the RNA solution (Supplementary Figure S8).

A comparison of the SAXS and SHAPE data indicates that I_U in 0.2 mM MgCl₂ is more compact (smaller R_g) than the extended U state, yet the core residues are more amenable to SHAPE modification than they are in either U or I_C (Figure 6B). This apparent flexibility of the RNA backbone in the presence of Mg²⁺ agrees with recent quasi-elastic neutron scattering measurements showing greater ps-ns motions in folded tRNA (53), and the effects of charge screening by counterions on the flexibility of unfolded nucleic acids (53–55). Nevertheless, the X-ray scattering profiles of both U and I_U are characteristic of a rod network or stiff polymer (ν = 1.3). It remains to be understood how this flexibility on a nucleotide length-scale correlates with the rearrangements that allow an unfolded RNA to search for the native structure.

One interpretation of our data is that the flexible, semi-compact I_U state contains certain tertiary contacts, but not in sufficient number to fold the ribozyme completely, in agreement with recent simulations of the ribozyme folding pathway (56,57). In this scenario, the global structure of I_U is constrained to be smaller than the U state, but the increased MgCl₂ concentration allows more branched secondary structures and greater flexibility for those nucleotides not directly involved in the tertiary contacts, which will be most of them. This interpretation is supported by partial protection of core nucleotides from hydroxyl radical-dependent cleavage at very low Mg²⁺ concentrations (58). A second interpretation is that the intermediate state is a non-specific ‘electrostatically relaxed’ pre-folding state, as proposed for the Tetrahymena ribozyme based on time-resolved SAXS experiments (59). Regardless, our experimental phase diagrams show that the semi-compact I_U state borders the cooperative transition to the native-like I_C state in all conditions sampled here.

We note that a compact, yet flexible, state has been described by Tan and Chen (19) in simulations of two DNA helices tethered by a PEG linker with tune-able tertiary contact energies, in agreement with experimental SAXS data (54). With the tertiary contacts switched off, increasing Mg²⁺ or Na⁺ concentration stabilized an intermediate state that was more compact than randomly relaxed electrostatically neutral helices but less compact and more disordered than the folded state obtained when the tertiary contact between the helices was switched on. An intriguing possibility is that our I_U state is equivalent to their randomly relaxed state, in which double helices fluctuate about single-stranded RNA linkers. It will be interesting to learn in the future to what extent this ‘confinement’ effect arising from excluded volume alters RNA folding in more realistic solutions of mixed-sized solutes.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institute of Standards and Technology [70NANB10H257 to RMB]; National Institutes of Health [R01GM60819 to S.A.W.]; National Institutes of Health [RR-08630 to BioCAT]. Use of the Advanced Photon Source is supported by the U.S. Department of Energy, Basic Energy Sciences, Office of Science under contract No. W-31-109-ENG-38. The open access publication charge for this paper has been waived by Oxford University Press - NAR Editorial Board members are entitled to one free paper per year in recognition of their work on behalf of the journal.

Conflict of interest statement. None declared.