ABSTRACT
In animals, the ability to move has evolved as an important means of protection from predators and for enhancing nutrient uptake. In the animal kingdom, an individual's movements may become coordinated with those of other individuals that belong to the same group, which leads, for example, to the beautiful collective patterns that are observed in flocks of birds and schools of fish or in animal migration. Land plants, however, are fixed to the ground, which limits their movement and, apparently, their interactions and collective behaviors. We show that emergent maize plants grown in a group exhibit synchronized oscillatory motions that may be in-phase or anti-phase. These oscillations occur in short bursts and appear when the leaves rupture from the coleoptile tip. The appearance of these oscillations indicates an abrupt increase in the plant growth rate, which may be associated with a sudden change in the energy uptake for photosynthesis. Our results suggest that plant shoots behave as a complex network of biological oscillators, interacting through biophysical links, e.g. chemical substances or electric signals.
KEYWORDS: anti-phase synchronization, complex network, in-phase synchronization, oscillatory motion, plant shoots
Introduction
Plant motions are limited, except in organisms, such as green algae (Chlamydomonas reinhardtii), that use their flagella to move freely in the direction of a light source and can easily interact with other algae.1 Plants such as Mimosa pudica open and close their leaves following day/night cycles2 and respond to touch through immediate leaf closing, whereas carnivorous plants such as Dionaea muscipula trap insects3 and can control their bodies for well-defined purposes (i.e., protecting leaves and nutrient uptake). The mechanism underlying these plant motions is thought to be based on osmotic motors4,5 that are governed by endogenous biological clocks or purely mechanical clocks.6 On the other side the oscillatory movements and growth patterns (especially seen in climbing plants) called circumnutations (see review7), are a common feature of plants. The general mechanism of such movements is thought to be caused by differences in the rate of growth of the opposite sides of the growing stem, root, or shoot. It is worth to note, however, that there is a crucial difference between the oscillatory movements and the growth patterns, since in the former case the oscillations are dynamical in time and leave plant parts unchanged, while the latter case is static and thus modifies the aspect of plant bodies.
Studies on synchronization span many disciplines and are not limited to animal behavior. This phenomenon has been widely investigated in chemistry,8 physics,9 physiology,10,11 ecology12 and many other scientific areas. Recent discoveries on plant behavior 13 have shown that the roots of maize seedlings growing in a group may coordinate a plant's motion with that of its neighbors, resulting in swarm-like patterns similar to those observed in animal groups.14,15 Also, it was shown that the oscillatory circadian rhythms of stems and leaves may be synchronized.16 However, no other examples of coordinated plant behavior because of the presence of neighbors have been observed.
A well-known example of coordinated plant motion is that a sunflower continually and directly faces a light source during the day by the slow motion of the flower following the cyclic motion of the sun.17 For plant motion that is synchronized with the day/night cycle, as in sunflower motion, the collective motion of a group of plants growing together does not depend on whether other plants are in the vicinity but on the common external forcing by sunlight. It is difficult to ascertain whether plants coordinate their movements with each other in these cases. Straightforward evidence for mutual plant interactions should include correlated spontaneous movements that do not follow the day/night cycle and that preferably have much shorter rhythms than this cycle.
In this study, we show that the maize plant is an ideal candidate for investigating the mutual interactions between individuals grown in a group. We find that emergent maize shoots generate short-term oscillations with a much smaller period than circadian rhythms: thus, we eliminate external forcing (sunlight) as the principal cause of correlated collective motion. We show that correlated oscillations can have different characteristics, that is, they may be in-phase or anti-phase. Moreover, the synchronized states occur more frequently by decreasing the distance between the plants are separated, which indicates short-range interactions between neighboring individuals. Finally, we show that these oscillations begin with an abrupt change in the plant growth rate and cease before the rupture of the leaf from the coleoptile tip. We concentrate only on the dynamical aspects of plant behavior which does not change its morphology.
Materials and methods
Caryopses of Zea mays L. cv. Kubrick (SIS, Bergamo, Italy) were surface sterilized using a 10% (v/v) bleach solution for 15 min, rinsed thoroughly, and placed between damp paper towels in Petri dishes. The dishes were maintained in a vertical position, incubated at 26°C, and used after the primary root reached a length of approximately 1 cm (typically after 24 hours). Germinated seeds with equally long roots were then sowed in trays filled with sterilized soil. The tray dimensions were 25× 2 cm. The trays were placed in a plant growth chamber with constant fluorescent lighting (400−700 nm), at a constant temperature (25 ± 2°C), and water was provided every other day to maintain a constant level of moisture in the soil. A webcam (Microsoft LifeCam StudioTM) was positioned 45 cm in front of the tray to record the plant growth using time-lapse photography. Images (1920 × 1080 HD) were collected every 5 min after germination until the maize plant leaves were fully open. The images were processed using Tracker 4.0 software from the Open Source Physics collection, and the data were analyzed using routines written in MATLAB.
Results
Characteristics of growing plants
Plants were seeded at different distances from one another, ranging from 0.5 cm to 5 cm (Fig. 1a, b). The shoots initially grew upward, and only very-small-amplitude random fluctuations around the horizontal axis were observed. These fluctuations were produced by internal biological processes as well as measurement errors. Some plants of a certain height began to exhibit small-amplitude oscillations that increased to a maximum amplitude. We observed a decay in the amplitudes of the oscillations, which was clearly associated with an increase in the periods of the oscillations. The oscillations occurred in bursts of short duration. We noticed that the oscillation profiles of most plants that were grown alone were more similar to each other than those of plants that were grown in groups, showing that the presence of neighboring plants affected plant motions by deforming their trajectories. These abilities to deform their trajectories could allow plants to adjust their cycles. The appearance of oscillations marked an abrupt (discontinuous) increase in the growth rate and leaf deployment (Fig. 1c), indicating the role of these oscillations in the growth process. As the oscillations ceased, leaves emerged and the plants continued to grow in a constant and linear manner. When the plant growth slowed and the leaf opening was retarded or failed, the oscillatory movements of the shoots had low amplitudes or were absent.
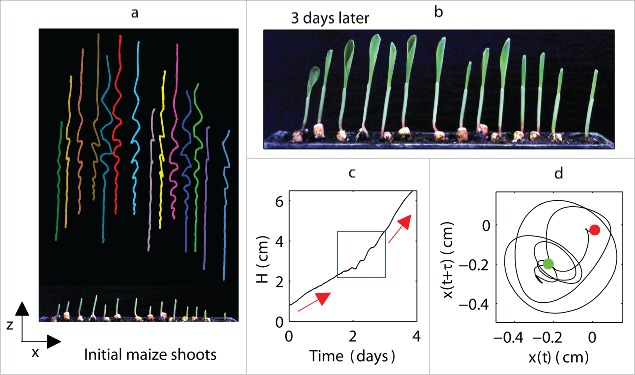
Figure 1.
Experiments performed on a group of maize plants. (a) Initial maize shoots and corresponding trajectories during the growth process; (b) maize shoots after 3 days: most shoots have open leaves; (c) plant height H as a function of time for a selected plant, where red arrows show changes in growth rate and blue rectangle marks the point at which oscillations appear; (d) x − y phase space reconstruction from the time series x(t), which describes the magnitude of the plant oscillations in the horizontal x direction: green point and red dot indicate beginning and end of oscillations, respectively; reconstruction shows rotational motion of the plant (i.e., plant motion is not unidirectional) around its axis in both x and y directions that could not be directly measured with the camera.
Living pendula
The observed oscillations were in the form of wavelets, showing that each plant could be considered to be a complex physical oscillator or pendulum. In the experiments, the oscillations were only measured in the x-axis direction because of the visual limitations for plants growing in a row. However, the plants could oscillate in 2 dimensions: from left to right (x-axis) and back and forth (y-axis). Some of the oscillations from left to right appeared to be weak if the primary component consisted of back-and-forth oscillations that could not be detected with a camera. This problem could be overcome using the embedding method18 from dynamical systems theory: the back-and-forth component was then reconstructed from the data for the oscillations from left to right, for which the component x(t+τ) could be interpreted as y(t) (Fig. 1d).
Oscillation bursts
The oscillations were characterized by a variable period, which, as previously mentioned, was short at the beginning of the burst and increased with time (Fig. 2a–b). The emergent oscillations were transitory, and the average duration of the entire burst was approximately 1.8 d and ranged from 0.25 to 3.75 d (Fig. 2c). We measured the extrema of the oscillations to describe the change in the period. The difference between consecutive maxima (or, equivalently, consecutive minima) provided information on the length of the characteristic time T of a cycle. This quantity is referred to as a characteristic time instead of a period because the oscillations were not periodic. This characteristic time was approximately T = 0.24 d on average and ranged from 0.08 to 0.72 d (Fig. 2d). Thus, the oscillations were ultradian rhythms because they changed approximately every 6 hours. This conclusion is significant because any observed correlations in the neighboring plant motions can be attributed solely to the mutual interactions between plants and not the external common forcing (i.e., sunlight).
Figure 2.
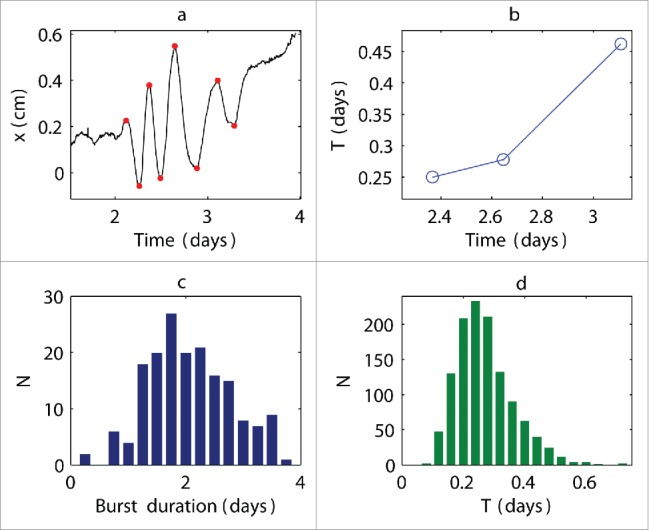
Characteristic time of oscillatory cycle and duration of bursts. (a) Example of movements of individual plants in the horizontal x direction; (b) corresponding characteristic elongation time T: red points in a show oscillation extrema used to calculate T values; T increased during oscillation bursts in all of the observed experiments, showing that this feature is universal for maize plants; (c) distribution of burst duration estimated from 18 experiments; (d) distribution of characteristic times T estimated from 18 experiments.
Synchronicity of cycles between neighboring plants
In observing the oscillations of neighboring plants, we noticed that the plant cycles were often synchronized (see Video S1). The synchronization took 2 different forms. The first form was an in-phase synchronization (Fig. 3a), i.e., the maxima of the cycles in one plant occurred at the same time as those for another plant. In contrast, the second form was an anti-phase synchronization (Fig. 3b), i.e., the maxima and minima of the cycles of different plants coincided with each other. An interesting phenomenon occurred when the plants were temporarily disturbed by an external, localized light source. The initial synchronized anti-phase state switched to a synchronized in-phase state (Fig. 3c). This observation provided further evidence that plants behave as mechanical oscillators and that the anti-phase and in-phase states are 2 possible correlated states that are selected based on the initial condition values.
Figure 3.
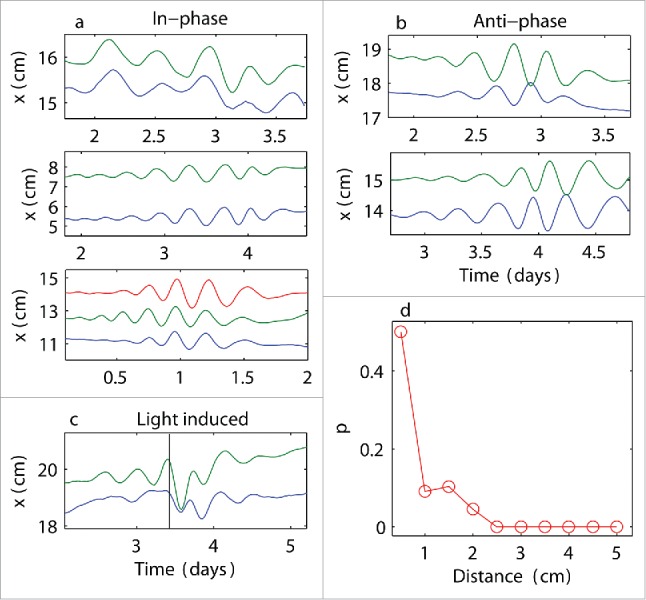
Synchronized states and distance dependence. Examples of synchronized dynamics between neighboring plants: (a) in-phase oscillations; (b) anti-phase oscillations; (c) in-phase synchronization induced by applying a light stimulus at the time indicated by the vertical black line: cycle resetting was observed; (d) probability p of observing coincident oscillations at the threshold k > 4 (i.e., at least 4 extrema coincided between neighboring plants) calculated at various distances between plants; higher probabilities at shorter distances suggest that plants coordinated their motions with their neighbors.
We estimated the degree of correlation between the neighboring plant oscillations by defining the probability of coincident oscillations as p = Mk/N, where Mkwas the number of plants that synchronized with their neighbors for at least k cycles. We used k > 4 to set a stronger standard for evidence of correlations between the oscillations. First, we selected all of the oscillation extrema (see the red points in Fig. 2a) and neglected the noisy low-amplitude fluctuations. We estimated the number of coincident extrema between 2 neighboring plants. Either in-phase or anti-phase synchronization was observed for these strong correlations. We then calculated the probability of coincident oscillations for plants located at various distances apart.
Statistical analyses of the data revealed that plants that were close to each other exhibited stronger correlations than plants that were separated by large distances (Fig. 3d). While the cycles of the plants were cycles, the corresponding amplitudes were rarely synchronized. We could not use the standard correlation function that is used to describe correlations between different signals because each plant oscillated differently in its growth direction (i.e., the oscillations were not exactly straight upward), and the oscillation amplitude and number also varied. However, we were able to use the maxima and minima to analyze the plant movements regardless of how diverse the individual plant motions were.
The plants began to oscillate around their horizontal axes at heights of approximately 2.8−3.8 cm (Fig. 4a). However, plant growth increased at similar times (Fig. 4b) as the mean maximum magnitudes of the oscillations occurred (Fig. 4c). This observation suggests that plants can synchronize both their cycles and growth speeds if their heights lie close enough.
Figure 4.
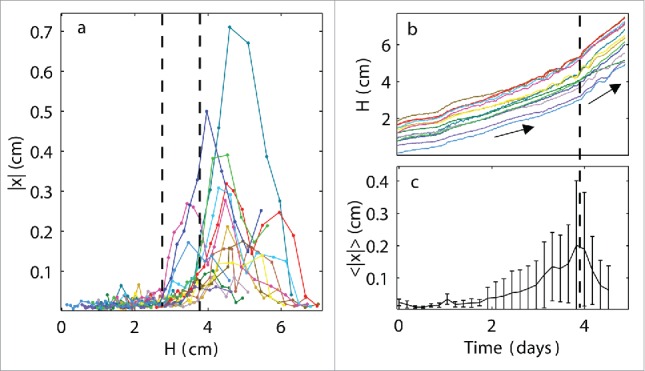
Increase in synchronized growth speed. (a) Oscillations in the horizontal direction |x| as a function of plant height H in a single experiment with 14 plants: vertical dashed lines indicate the range of H values over which the plants began to oscillate, demonstrating that the occurrence of oscillations was not strictly determined by the plant height; (b) heights H of all of the plants growing in a single experiment as a function of time; collective change in growth rate is indicated by a vertical dashed line; (c) mean oscillations in the horizontal direction<|x|> as a function of time averaged over all plants, where a maximum <|x|> appears as the collective plant growth increases.
Discussion
We demonstrated that maize oscillations have a characteristic time of approximately 6 hours, which enabled us to exclude the effect of an external common forcing (i.e., sunlight) as a cause of these correlated motions. Oscillatory bursts occurred at the moment the leaf was deployed, indicating an increase in the plant growth rate. During germination, heterotrophic plant growth (in which internal reserves accumulated in the seeds are used as energy sources) eventually transformed into photoautotrophic growth (during which chloroplast and leaf development occur), and photosynthesis became the main process by which the plant grew and developed. Thus, the oscillatory motions marked a transition in the type of energy uptake (seeds → photosynthesis). This observation indicated that the beginning of the photosynthetically active phase is closely related with the plant oscillatory behavior and motion. We observed little or no motion in plants that grew slowly or stopped growing during the experiments.
The synchronicity of the oscillation bursts was either anti-phase or in-phase. We applied external stimulation using a localized light source to show that these states were equivalent and depended on the initial conditions. Our data analyses showed that the probability of coincidence between the cycles was high at short distances and low at large distances, indicating mutual short-range interactions between plants. Huygens was the first to observe19 sympathy between clocks hanging on the same support frame, corresponding to the synchronization of the clock cycles. This behavior is a classic example in physics of synchronization through mutual interactions. In other systems, a wide variety of components may interact with each other.20 The interaction mechanism in plants remains unclear. However, we suggest that plants may interact through touch (electric field detection) or the release of chemical substances, as has been hypothesized for root swarming.13 For example, growing root apices are known to generate very characteristic electric fields around their apices21,22 which, if close enough, might interact and entrain with the adjacent ones. Interestingly, the root apex zone with the highest activity in this respect, the transition zone, is showing highly synchronous activities on cellular level.23 In order to understand the effects of such interactions, more studies are needed to determine whether the synchronization processes that enhance plant growth are casual or predetermined.
Supplementary Material
Disclosure of potential conflicts of interest
No potential conflicts of interest were disclosed.
Funding
S.M. and E.M. were supported by the Future and Emerging Technologies (FET) program within the 7th Framework Program for Research of the European Commission, under FET-Open grant number 293431 (PLANTOID). M.C. acknowledges Regione Toscana for financial support.
References
- [1].Furlan S, Comparini D, Ciszak M, Beccai L, Mancuso S, Mazzolai B. Origin of polar order in dense suspensions of phototactic micro-swimmers. PLoS ONE 2012; 7:e38895; PMID:22723904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Moran N. Rhythmic leaf movements: physiological and molecular aspects. In: Mancuso S, Shabala S (Eds.). Rhythms in Plants: Phenomenology, Mechanisms, and Adaptative Significance. Berlin-Heidelberg: Springer Verlag; 2007. [Google Scholar]
- [3].Forterre Y, Skotheim JM, Dumais J, Mahadevan L. How the Venus flytrap snaps. Nature 2005; 433:421-5; PMID:15674293; http://dx.doi.org/ 10.1038/nature03185 [DOI] [PubMed] [Google Scholar]
- [4].Satter RL, Galston AW. Mechanisms of control of leaf movements. Annu Rev Plant Physiol 1981; 32:83-110; http://dx.doi.org/ 10.1146/annurev.pp.32.060181.000503 [DOI] [Google Scholar]
- [5].Moran N. Osmoregulation of leaf motor cells. FEBS Lett 2007; 581:2337-47; PMID:17434488; http://dx.doi.org/ 10.1016/j.febslet.2007.04.002 [DOI] [PubMed] [Google Scholar]
- [6].James AB, Monreal JA, Nimmo GA, Kelly CL, Herzyk P, Jenkin GI, Nimmo HG. The circadian clock in Arabidopsis roots is a simplified slave version of the clock in shoots. Science 2008; 322:1832-5; PMID:19095940; http://dx.doi.org/ 10.1126/science.1161403 [DOI] [PubMed] [Google Scholar]
- [7].Stolarz M. Circumnutation as a visible plant action and reaction. Plant Signal Behav 2009; 4:380-7; PMID:19816110; http://dx.doi.org/ 10.4161/psb.4.5.8293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Kuramoto Y. Chemical Oscillations, Waves and Turbulence. Springer, Berlin, 1984. [Google Scholar]
- [9].Blekhman II. Synchronization in Science and Technology. Asme Press, New York, 1988. [Google Scholar]
- [10].Glass L. Synchronization and rhythmic processes in physiology. Nature 2001; 410:277-84; PMID:11258383; http://dx.doi.org/ 10.1038/35065745 [DOI] [PubMed] [Google Scholar]
- [11].Anderson PA, Pettijohn DE. Synchronization of division in Escherichia coli. Science 1960; 131:1098; PMID:13793437; http://dx.doi.org/ 10.1126/science.131.3407.1098 [DOI] [PubMed] [Google Scholar]
- [12].Blasius B, Huppert A, Stone L. Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 1999; 399:354-9; PMID:10360572; http://dx.doi.org/ 10.1038/20676 [DOI] [PubMed] [Google Scholar]
- [13].Ciszak M, Comparini D, Mazzolai B, Baluška F, Arecchi FT, Vicsek T, Mancuso S. Swarming behavior in plant roots. PLoS ONE 2012; 7:e29759; PMID:22272246; http://dx.doi.org/ 10.1371/journal.pone.0029759 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Krause J, Ruxton GD, Krause S. Swarm intelligence in animals and humans. Trends Ecol Evol 2010; 25:28-34; PMID:19735961; http://dx.doi.org/ 10.1016/j.tree.2009.06.016 [DOI] [PubMed] [Google Scholar]
- [15].Parrish JK, Edelstein-Keshet L. Complexity, pattern and evolutionary trade-offs in animal aggregation. Science 1999; 284:99-101; PMID:10102827; http://dx.doi.org/ 10.1126/science.284.5411.99 [DOI] [PubMed] [Google Scholar]
- [16].Spurny M. Synchronization of oscillatory rhythms of stems and leaves. Biol Plant 1976; 18:277-82; http://dx.doi.org/ 10.1007/BF02922373 [DOI] [Google Scholar]
- [17].Cerdá-Olmedo E, Corrochano LM. Genetics of Phycomyces and its responses to light. In: Häder DP, Lebert M (Eds.) Photomovement. Amsterdam: Elsevier Science; 2001. [Google Scholar]
- [18].Packard NH, Crutchfield JP, Farmer JD, Shaw RS. Geometry from a time series. Phys Rev Lett 1980; 45:712; http://dx.doi.org/ 10.1103/PhysRevLett.45.712 [DOI] [Google Scholar]
- [19].Huygens Ch. The Pendulum Clock. Iowa State University Press, Ames: 1986. [Google Scholar]
- [20].Pikovsky A, Rosenblum M, Kurths J. Synchronization: A Universal Concept in Nonlinear Sciences. Cambridge: Cambridge Univ. Press; 2003. [Google Scholar]
- [21].Collings DA, White RG, Overall RL. Ionic current changes associated with the gravity-induced bending response in roots of Zea mays L. Plant Physiol 1992; 100:1417-26; PMID:16653140; http://dx.doi.org/ 10.1104/pp.100.3.1417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Baluška F, Mancuso S. Ion channels in plants: from bioelectricity, via signaling, to behavioral actions. Plant Signal Behav 2013; 8:23009; PMID:23221742; http://dx.doi.org/ 10.4161/psb.23009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Baluška F, Mancuso S. Root apex transition zone as oscillatory zone. Front Plant Sci 2013; 4:354; PMID:24106493 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.