Finite Element Model of the Knee for Investigation of Injury Mechanisms: Development and Validation

Abstract

Multiple computational models have been developed to study knee biomechanics. However, the majority of these models are mainly validated against a limited range of loading conditions and/or do not include sufficient details of the critical anatomical structures within the joint. Due to the multifactorial dynamic nature of knee injuries, anatomic finite element (FE) models validated against multiple factors under a broad range of loading conditions are necessary. This study presents a validated FE model of the lower extremity with an anatomically accurate representation of the knee joint. The model was validated against tibiofemoral kinematics, ligaments strain/force, and articular cartilage pressure data measured directly from static, quasi-static, and dynamic cadaveric experiments. Strong correlations were observed between model predictions and experimental data (r > 0.8 and p < 0.0005 for all comparisons). FE predictions showed low deviations (root-mean-square (RMS) error) from average experimental data under all modes of static and quasi-static loading, falling within 2.5 deg of tibiofemoral rotation, 1% of anterior cruciate ligament (ACL) and medial collateral ligament (MCL) strains, 17 N of ACL load, and 1 mm of tibiofemoral center of pressure. Similarly, the FE model was able to accurately predict tibiofemoral kinematics and ACL and MCL strains during simulated bipedal landings (dynamic loading). In addition to minimal deviation from direct cadaveric measurements, all model predictions fell within 95% confidence intervals of the average experimental data. Agreement between model predictions and experimental data demonstrates the ability of the developed model to predict the kinematics of the human knee joint as well as the complex, nonuniform stress and strain fields that occur in biological soft tissue. Such a model will facilitate the in-depth understanding of a multitude of potential knee injury mechanisms with special emphasis on ACL injury.

Introduction

The knee is one of the most complex joints in the human body distinguished by its complex geometry and multibody articulations. Optimal joint stability and compliance during functional activities are provided through anatomical structures such as ligaments, menisci, and articular cartilage. However, abnormalities due to age, injury, disease, and other factors can affect biomechanical function of the knee joint. A thorough understanding of knee biomechanics may substantially contribute to the improvement of the current prevention and treatment strategies of knee disorders and injuries. The anterior cruciate ligament (ACL) plays a crucial role in maintaining knee stability in multiple planes. ACL injuries are exceedingly common and often devastating to adolescents and young adults [1,2]. The high frequency of ACL injury (more than 120,000 in the United States annually [3]), associated cost, and subsequent long-term disability have generated significant interest in the investigation of ACL injury mechanisms. Extensive efforts have served to investigate knee biomechanics with a primary emphasis on the ACL utilizing ex vivo techniques [4–11], clinical studies, and in vivo evaluations [2,12–18]. Although these controlled laboratory studies have substantially improved our understanding of knee biomechanics and injury, inherent limitations associated with the existing experimental methods make data interpretation and parametric analyses challenging. Alternatively, computational models have been used to investigate joint mechanics [19–41]. These models also serve to better characterize soft tissue (i.e., ligaments) function and yield information that is otherwise challenging or impossible to obtain experimentally. In particular, the use of finite element (FE) analysis has become progressively popular, as it allows for detailed analysis of the joint/tissue behavior under complex, clinically relevant loading conditions. Yet, the reliability of FE models strongly rely on (a) appropriate geometry reconstruction and assigned material properties, (b) simulated interactions, constraints, and boundary conditions, and (c) thorough validation against experimental data.

During the past three decades, a large number of knee FE models with varying degrees of complexity, accuracy, and functionality have been reported in the literature. A majority of these models are static or quasi-static in nature [20,24–26,28,29,31–33,37,38,40–42], typically focused on isolated tibiofemoral joint missing the patellofemoral interaction [22,25,26,37,38,40,41]. Further, a number of simplifying assumptions such as lack of anatomical representation of menisci [19,22,25,27,37,38,40,41], articular cartilage [19,22,37,38,41], and other connective tissue [26,31–33,37,38,40,41] are associated with some of the existing models. Also, in most cases, connective tissues are modeled by uniaxial discrete line elements (truss or spring elements) with simplified material properties [19,20,23–25,28]. Such an assumption of soft tissue geometry may be useful in the investigation of joint kinematics. However, this assumption is associated with shortcomings such as the inability to predict nonuniform 3-dimensional (3D) stresses and strains across the tissue [27,29,31,41]. Considering the fact that the accuracy in FE model predictions depends directly on assumptions made in the model, an anatomically accurate 3D representation coupled with realistic constitutive models is needed to simulate the complex nature of these structures [27,29,31,37,41]. Moreover, most existing knee FE models are validated against a limited number of experimentally measured parameters primarily under static and/or quasi-static loading conditions [25–28,31–33,37,38,40–42].

Due to the complex, multifactorial dynamic nature of knee injuries, FE models that include all key anatomic structures and are validated against multiple parameters under a range of loading conditions (static, quasi-static, and dynamic) are essential. Hence, this study aims to develop such a 3D FE model of the lower extremity with an anatomical representation of the knee joint for the evaluation of tibiofemoral biomechanics and injury mechanisms. We believe that such a model will provide deep insight into a multitude of potential knee injury mechanisms with special emphasis on ACL injury.

Materials and Methods

An anatomically accurate FE model of the lower extremity was developed based on the imaging data obtained from a healthy, skeletally mature young female athlete with no history of knee injury [43]. The model includes bony structures of the lower extremity in addition to soft tissue details of patellofemoral and tibiofemoral aspects of the knee joint. The model includes major ligaments, trans-knee muscles, articular cartilage, and menisci. Concurrently, a set of quasi-static and dynamic cadaveric experiments on fresh frozen lower limbs were conducted for model validation. Experimentally measured tibiofemoral kinematics, ACL and MCL strains along with tibiofemoral articular pressure distribution under various loading conditions, as well as published experimental data were used for FE model validation.

Model Development

Geometry and Mesh Generation.

Following IRB approval, computerized tomography (CT) and magnetic resonance imaging (MRI) scans of a young adult female athlete's lower limb (Age: 25 years, Height: 170 cm, Weight: 64.4 Kg) were used to capture bony and soft tissue geometry, respectively. Scans were obtained while the subject was supine with the leg in an unloaded neutral position. Acquired CT and MRI scans were coregistered using 3D-Slicer image processing software (Surgical Planning Laboratory, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA) [44] in order to align the final segmented 3D bone and soft tissue geometries. The coregistration process was conducted in all three orthogonal planes by rotation and translation of semitransparent MRI scans relative to the CT images until the corresponding structures were matched [45,46]. Subsequently, 3D geometry of the pelvis, leg (upper and lower), and foot segments were reconstructed from high resolution CT images (Toshiba Aquilion 64 CT Scanner, Zoetermeer, Netherlands) at intervals of 0.5 mm (512 × 512) in all three anatomical planes using Mimics software v13.1 (Materialise, Ann Arbor, MI). Sagittal, coronal, and axial MR images (GE Signa Excite HD 3.0 T, Waukesha, WI) of the left knee were used to generate the 3D geometry of the knee articular cartilage, menisci, and knee cruciate and collateral ligaments. These geometries were then converted into solid eight-node hexahedral elements using IA-FEMesh software (MIMIX, The University of Iowa, IA) [47]. Finally, meshed geometries were imported into the ABAQUS FE package v6.11 (SIMULIA, Providence, RI) to generate the FE model. Mesh convergence analyses on contact variables and ligament strain were conducted in order to identify the proper element size for simulated 3D soft tissue structures. To test for the convergence of the model and to assure that the model outputs are independent of mesh density, all the 3D structures except bones were meshed in multiple densities to generate a range of coarse to highly-refined models. The model’s output of peak stress under a constant compressive load for the articular cartilage and menisci and peak strain under a constant tensile load for both the cruciate and collateral ligaments were analyzed. The element size/mesh density for each individual structure was adopted based on the convergence tolerance of maximum 5% change in the model output (Table 1). A similar approach has been used by Donahue et al. for articular cartilage and menisci [26]. While cruciate and collateral ligaments, articular cartilage, and menisci were modeled as 3D structures, the rest of the simulated knee ligaments, joint capsule, and muscle tendons were modeled as uniaxial truss elements (Fig. 1). These structures were simplified as uniaxial representations in an effort to optimize the computational cost and overcome the technical challenges associated with anatomical simulation of all soft tissue structures. Whereas, the main weight bearing soft tissue constraints of the knee joint, which are at significantly higher risk of injury, were modeled as 3D anatomical structures to enhance model accuracy.

Table 1.

Mesh details of the simulated 3D components of the model

	Element
Model Component	Type	Average Size	Total No.
Pelvis	3D, Solid, Hexahedral, Rigid	6 mm × 6 mm	35,662
Femur	3D, Solid, Hexahedral, Deformable (distal)	3 mm × 3 mm	127,652
Patella	3D, Solid, Hexahedral, Deformable	2 mm × 2 mm	3568
Tibia	3D, Solid, Hexahedral, Deformable (proximal)	2.5 mm × 2.5 mm	30,738
Fibula	3D, Solid, Hexahedral, Rigid	2.5 mm × 3 mm	5472
Foot	3D, Solid, Hexahedral, Rigid	3 mm × 3 mm	43,993
Tibiofemoral Cartilage	3D, Solid, Hexahedral, Deformable	*2 mm × 2 mm	7852
Patellofemoral Cartilage	3D, Solid, Hexahedral, Deformable	*1 mm × 1 mm	912
Menisci	3D, Solid, Hexahedral, Deformable	*1.2 mm × 1.2 mm	8732
ACL	3D, Solid, Hexahedral, Deformable	*0.5 mm × 0.5 mm	2200
PCL	3D, Solid, Hexahedral, Deformable	*0.5 mm × 0.5 mm	2808
MCL	3D, Solid, Hexahedral, Deformable	*1 mm × 1 mm	3696
FCL	3D, Solid, Hexahedral, Deformable	*0.8 mm × 0.8 mm	1386

Note: *Determined using mesh convergence analysis.

Fig. 1.

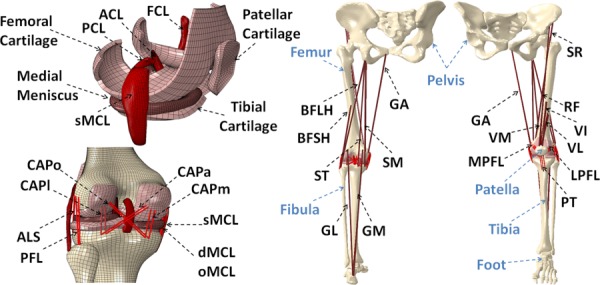
Developed FE model of lower extremity ACL: anterior cruciate ligament; PCL: posterior cruciate ligament; FCL: fibular collateral ligament; sMCL, dMCL and oMCL: superficial, deep and oblique bundles of medial collateral ligament; CAPm, CAPl, CAPo and CAPa: medial, lateral, oblique popliteal and arcuate popliteal bundles of posterior capsule; ALS: anterolateral structure; PFL: popliteofibular ligament; MPFL: medial patellofemoral ligament; LPFL: lateral patellofemoral ligament; PT: patellar tendon; VM: vastus medialis; RF: rectus femoris; VI: vastus intermidus; VL: vastus lateralis; BFLH: biceps femoris long head; BFSH: biceps femoris short head; SM: semimembranous; ST: semitendinosus; SR: sartorius; GA: gracilis; GM: gastrocnemius medial; GL: gastrocnemius lateral.

Material Properties.

Table 2 summarizes the material properties that were assigned to each structure. Bones were defined as linear elastic [48–52] with different moduli assigned to cortical and trabecular regions consistent with earlier FE studies of the human knee joint [23,26]. Further, the femoral and tibial cortical regions were defined as anisotropic with different material coefficients in radial, circumferential, and axial directions [35]. Considering substantially smaller loading time during quasi-static (i.e., walking) and dynamic (i.e., landing) tasks than the viscoelastic time constant for cartilage (1500 s) [53–55], cartilage was modeled as an isotropic linear elastic material [56]. Menisci were modeled as transversely isotropic linear elastic with different mechanical properties in circumferential, axial, and radial directions (Table 2) [57–59]. To better simulate the mechanical role of the menisci, the anterior and posterior horns of the medial and lateral menisci were attached to their anatomical insertion points across the tibial plateau. Horn-meniscus attachment was simulated with multiple linear elastic truss elements [26]. A similar approach has been employed in most previous FE studies of the human knee joint to simulate articular cartilage and menisci [23,25,26,28,32,33,40,42]. Finally, the external surface of the medial meniscus was attached to the opposing region of the superficial MCL [24].

Table 2.

Assigned material properties to the FE model components

Deformable Bony Components (Linear Elastic) [23,26]
Structure	Density (g/cm3)	Young’s Modulus (Mpa)	Poisson’s Ratio	Structure	Density (g/cm3)	Young’s Modulus (Mpa)	Poisson’s Ratio
Femoral Cortical Bone	2	*E1 = 12,000	υ12 = 0.38	Tibial Cortical Bone	2	*E1 = 6900	υ12 = 0.49
		*E2 = 13,400	υ13 = 0.22			*E2 = 8500	υ13 = 0.12
		*E3 = 20,000	υ23 = 0.24			*E3 = 18,400	υ23 = 0.14
Patellar Cortical Bone	2	15,000	0.3	Trabecular Bone	1.5	400	0.3

Articular Cartilage and Menisci (Linear Elastic)
Structure	Density (g/cm3)	Young's Modulus (MPa)	Poisson's Ratio	Structure	Density (g/cm3)	Young's Modulus (MPa)	Poisson's Ratio
Menisci	1.5 [23]	E1 = 20 [59] E2 = 120 [58] E3 = 20 [59]	υ12 = 0.3 [57] υ13 = 0.45 [57] υ23 = 0.3 [57]	Articular Cartilage	1 [23]	15 [56]	0.475 [56]
Horn-Meniscus Attachment		111 [26]

Knee Cruciate and Collateral Ligaments (Incompressible, anisotropic hyperelastic)
Structure	Density (g/cm3)	Constitutive Model	No. of Fiber Families	Structure	Density (g/cm3)	Constitutive Model	No. of Fiber Families
ACL	1 [42]	HGO	2 [64,65]	Superficial MCL	1 [42]	HGO	1
PCL	1 [42]	HGO	2 [64,65]	FCL	1 [42]	HGO	1

Uniaxial Nonlinear Elastic Components
Structure	Stiffness (N/mm)	Structure	Stiffness (N/mm)	Structure	Stiffness (N/mm)	Structure	Stiffness (N/mm)
Post. Capsule-Lateral (CAPl)	54.6 [19]	Post. Capsule-Arcuate (CAPa)	20.8 [19]	MCL-Deep Fibers (dMCL)	72.2 [19]	Medial Patello-femoral Lig (MPFL)	16 [73]
Post. Capsule-Medial (CAPm)	52.6 [19]	Patellar Tendon (PT)	300 [35]	MCL-Oblique Fibers (oMCL)	21.1 [19]	Lateral Patello-femoral Lig. (LPFL)	12 [73]
Post. Capsule-Oblique (CAPo)	21.4 [19]	Popliteofibular Ligament (PFL)	30.5 [22]	Anterolateral Structures (ALS)	76 [22]

Note: *Direction 1 is radial, direction 2 is circumferential, and direction 3 is axial (along the long axis of the bone).

Ligaments are dense connective tissues consisting of collagen fibers with a preferred orientation that are embedded in a compliant matrix of proteoglycans [60]. Thus, they can be simulated by a continuum model of fiber-reinforced composites at finite strains [27,29,31,61]. Knee cruciate and collateral ligaments were modeled as incompressible anisotropic hyperelastic structures using the Holzapfel–Gasser–Ogden (HGO) material model [62,63]. Briefly, isotropic noncollagenous ground matrix is modeled by the incompressible hyperelastic neo-Hookean component of the strain energy density (SED) function whereas the transversely isotropic fibrous component is modeled by the following function developed by Gasser et al. [62]

$$\overline{\Psi }(\overline{C},H_i)={\overline{\Psi }}_g(\overline{C})+\sum _{i=1,2}{\overline{\Psi }}_{\mathit{fi}}(\overline{C},H_i(a_{0i},\kappa ))$$

where ${\overline{\Psi }}_g$ and ${\overline{\Psi }}_{\mathit{fi}}$ are the respective isotropic and anisotropic components of the SED, $a_0$ is the mean orientation of the fibers, $H(a_0,\kappa )$ is the structure tensor, and $\kappa$ is the dispersion parameter for the fiber family. A statistical distribution function allows for a spatial distribution of the fiber orientation. Cruciate ligaments were modeled using two fiber families each in order to simulate bundles within ACL and posterior cruciate ligament (PCL) [64,65]. Both MCL (superficial bundle) and fibular collateral ligament (FCL) were modeled using one family of fibers. FE simulation of experimental uniaxial tensile tests along the longitudinal direction as per Butler et al. [66] for the ACL and PCL and Quapp and Weiss [67] for the MCL were used to derive a series of coefficients for the constitutive model using a curve fitting technique (Fig. 2). Coefficients for the FCL were assumed to be identical to those of the MCL [31,42]. All other simulated knee ligaments were modeled as nonlinear elastic, tension-only materials using truss elements with theoretically defined cross-sectional area (Fig. 1). The attachment site and material properties of each simulated ligament (except those simulated as 3D structures) were obtained from the literature [19,22,35,68–73]. Further, 12 uniaxial truss-connector elements were used to simulate trans-knee muscles (Fig. 1). The anatomical path (line of action) of each simulated muscle force at full extension was adopted from the literature [21,74,75]. In modeling knee ligaments, material properties were assumed to be constant over the entire length of the structure (from origin to insertion).

Fig. 2.

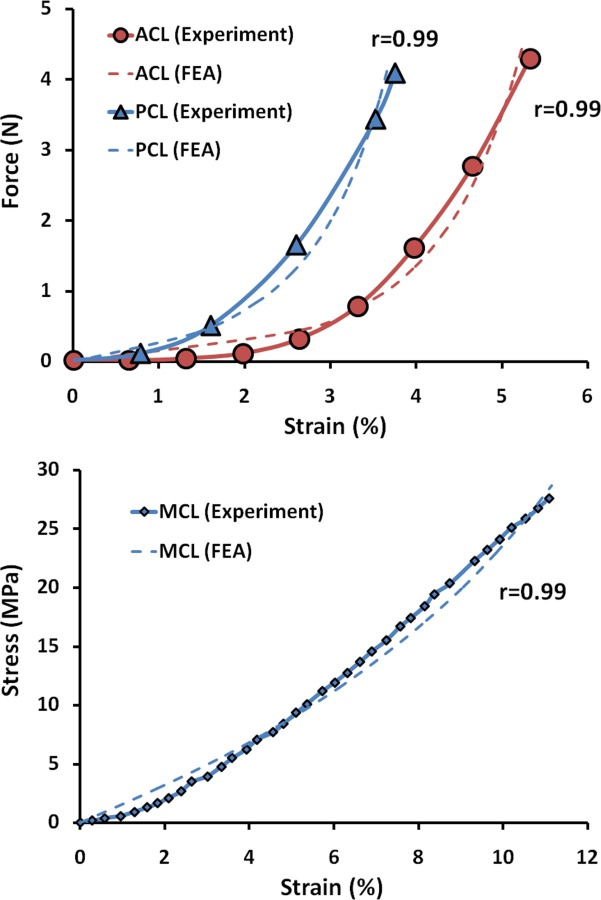
FE predictions versus experimental data of the uniaxial tension test for ACL and PCL (top) and MCL (bottom)

Constraints and Boundary Conditions.

Constraints, interactions, and boundary conditions were chosen in a way to assure an unconstrained, stable response of the knee joint (both the tibiofemoral and patellofemoral articulations) throughout the range of motion. To optimize computational expense without sacrificing model predictions, pelvis, proximal femur (from 10 cm above the joint line), distal tibia (from 10 cm below the joint line), fibula, and foot were modeled as rigid bodies while the remaining structures were considered deformable. A frictionless surface-to-surface tangential contact with nonlinear finite sliding property was used to simulate articular surfaces [24,26,31]. A set of primary and secondary contact surfaces were defined for each of the following 16 potential contact pairs including: femoral cartilage/tibial cartilage, femoral cartilage/menisci, menisci/tibial cartilage, femoral cartilage/patellar cartilage, knee cruciate and collateral ligaments/femur, knee cruciate and collateral ligaments/tibia, and ACL/PCL [24,26,31,32].

Since the current FE model was developed to investigate phenomena associated with knee biomechanics and relevant injuries, knee joint key soft tissue structures have been incorporated into the model. Both tibiofemoral and patellofemoral joints were simulated as six degree-of-freedom (DOF) joints with their motion defined by their surrounding soft tissue constraints and the topology of the articular surfaces. The hip and ankle joints were simulated in the model in order to create a more physiologically relevant biomechanical simulation of applied internal (muscle) and external loads. For this purpose, these joints were simplified as virtual ball-and-socket joints controlled by imported kinematic data, while optimizing for computational efficiency. The pelvis was fixed in all degrees of freedom during analysis. Joint kinematics were expressed using the nonorthogonal local coordinate systems proposed by Grood and Suntay [76]. Global 3D motion of the knee was characterized by six kinematics parameters: three translations and three rotations.

Cadaveric Experiments and FE Model Validation.

Sixteen fresh frozen human lower limbs (45 ± 7 years; 8 female and 8 male) were acquired and tested. Specimens were sectioned at the midfemoral shaft, potted, and all soft tissues up to 15 cm proximal to the joint line were dissected. Subsequently, the quadriceps and hamstrings tendons were isolated and clamped to allow for the application of simulated muscle loads. The remaining musculature along with the skin were maintained intact [9]. Both quasi-static and dynamic loading conditions were evaluated to simulate normal low-rate daily activities (such as walking) and high-rate dynamic activities (e.g., landing from a jump). Multiple combinations of single- and multi-axis loading conditions including anterior tibial shear, knee abduction, and internal tibial rotation as potential high risk loading factors for ACL injury were selected for model validation [9,77,78].

Quasi-Static Testing.

Specimens were tested using a custom designed passive 6-DOF force couple testing system [79–81]. Specimens were tested under five different loading conditions including: (1) 0–50 Nm of knee abduction (at 25 deg of flexion), (2) 0–50 Nm of knee abduction + 20 Nm of internal tibial rotation (at 25 deg of flexion), (3) baseline (no external load, 0–50 deg of flexion), (4) 15 Nm of internal tibial rotation (0–50 deg of flexion), and (5) 134 N of anterior tibial shear + 15 Nm of internal tibial rotation (0–50 deg of flexion) all under simulated muscle loads (quadriceps: 400 N and hamstrings: 200 N).

Dynamic Testing.

A custom designed drop-stand was used to simulate landing from a jump [9]. The impulsive ground reaction force during landing was simulated with the release of half body weight (350 N) from 30 cm onto the foot under 25 deg of knee flexion. Specimens were tested under axial impact with simulated muscle loads (quadriceps: 1200 N and hamstrings: 800 N) [77]. Tests were repeated with an additional 134 N anterior tibial shear force.

Instrumentation.

In both quasi-static and dynamic tests, ACL and MCL strains were calculated using Differential variable reluctance transducer (DVRT) displacement sensors (Microstrain, Williston, VT). A DVRT was arthroscopically placed on the ACL (anteromedial bundle), while three DVRTs (anterior/middle/posterior) were placed along the superficial MCL across the joint line [78]. Rigid body motion of the tibia and femur were collected by an Optotrak 3020 motion tracking system (Northern Digital, Waterloo, Ontario, Canada). A K-Scan sensor (Tekscan Inc., Boston, MA) was used to map the tibiofemoral articular pressure distribution. The sensor was arthroscopically placed into the medial and lateral compartments below the menisci [80,81]. Due to the low reliability of pressure sensors under high-rate conditions, experimental pressure mapping was only performed under quasi-static testing. Quasi-static data were collected at 100 Hz while the high-rate data were captured at 4 kHz.

Besides validation against the data collected from our own experiments, further validation was performed against static experimental data available in the literature [82]. Cadaveric measurements of ACL force (14 human cadaveric knee specimens) under isolated (100 N of anterior tibial shear) and combined (10 Nm knee abduction and 100 N anterior tibial shear) loading states conducted by Markolf et al. [82] were used for further validation. In order to simulate the experimental conditions, the femur and foot were constrained in all degrees of freedom with the hip and ankle joints in a neutral (initial) position while both tibiofemoral and patellofemoral joints were allowed unconstrained articulation.

Statistical Analysis.

Regression analyses were used to evaluate the ability of the FE model to predict experimentally measured tibiofemoral kinematics, ACL and MCL strains, and tibiofemoral articular pressure distribution (under static and quasi-static loading conditions). Pearson correlation coefficients along with p-values were calculated between model predictions and experimental data. Correlations were classified as poor (<0.4), good (0.4–0.74), and strong (≥0.75) [83]. Finally, 95% confidence intervals along with RMS errors were calculated in order to further investigate the accuracy of the model predictions with respect to direct experimental measurements.

Results

Validation Against Tibiofemoral Kinematics (Quasi-Static Loading).

The FE model closely reproduced experimentally measured kinematics in both the frontal and axial planes (Figs. 3 and 4). Strong correlations along with low RMS errors were observed between FE predictions and experimental measurements of tibial axial rotation (r > 0.8, p < 0.0005, RMSE ≤ 2.5 deg) and tibiofemoral frontal plane kinematics (r > 0.9, p < 0.0005, RMSE < 1.5 deg) under all modes of loading, Table 3. As shown in Figs. 3 and 4, all FE-predicted tibiofemoral kinematics were within the range of 95% confidence intervals of average experimental measurements. The model also replicated detailed tibiofemoral joint kinematics such as coupled motion and screw home mechanism as observed in cadaveric experiments. Figure 3 shows how the tibia internally rotates (experimental data: 2.4 deg ± 2.7 deg, FE model: 3.9 deg) during the early phase of flexion. This replicates the screw-home mechanism, as described by Freeman and Pinskerova [84]. Further, the effects of additional internal tibial rotation moment (20 Nm) on valgus rotation of the knee (experimental data: 7.4 deg ± 2.8 deg, FE model: 5.7 deg) was indicative of coupling between knee valgus and internal rotation of the tibia (Fig. 4).

Fig. 3.

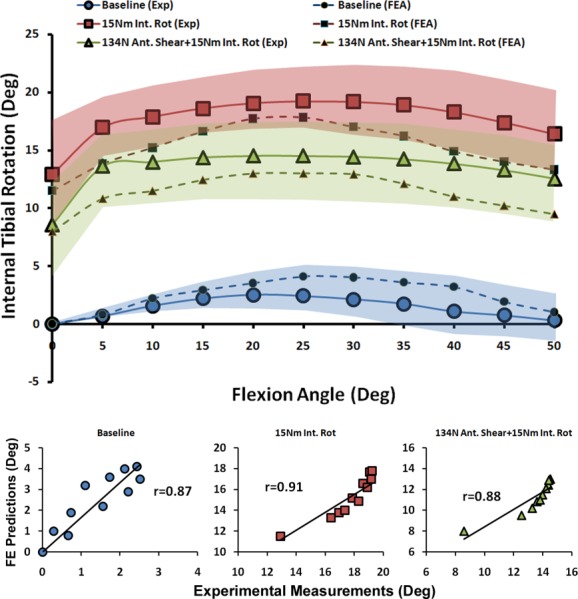
FE predictions versus experimental data for tibiofemoral axial plane kinematics under quasi-static loading conditions (shaded area represent experimental 95% confidence intervals)

Fig. 4.

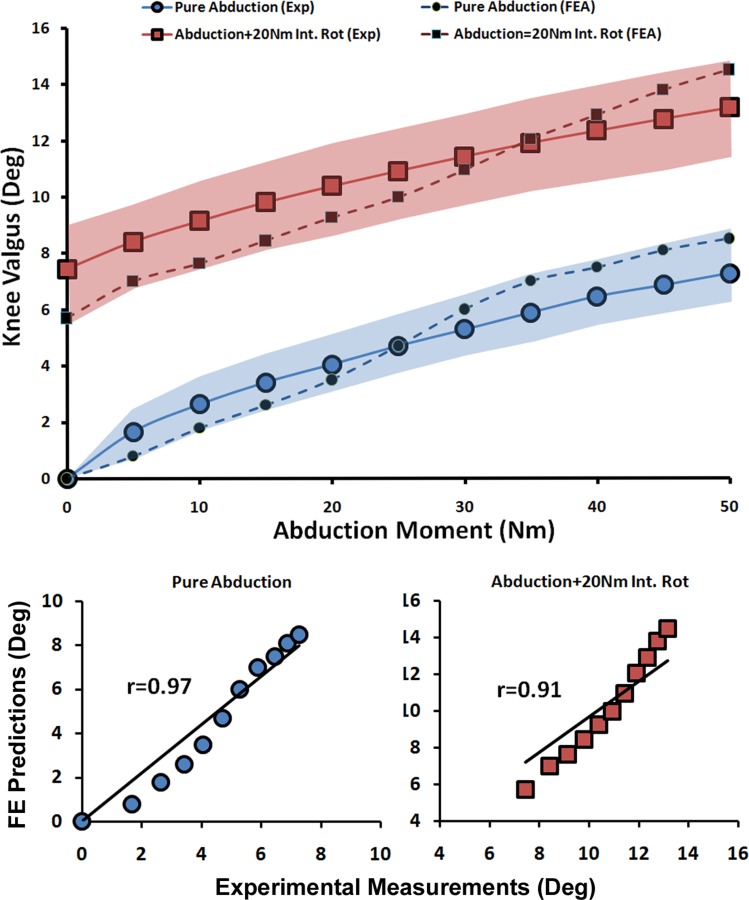
FE predictions versus experimental data for tibiofemoral frontal plane kinematics under quasi-static loading conditions (shaded area represent experimental 95% confidence intervals)

Table 3.

Correlations and RMS errors reported between FE predictions and experimental data

Validation		Model Vs. Experimental Data
Tested Parameter	Loading	r	p	RMSE
Tibiofemoral Axial Plane Kinematics	Baseline	0.87	<0.0005	1.3 deg
	15 Nm Int. Rot	0.91	<0.0005	2.5 deg
134 N Ant. Shear + 15 Nm Int. Rot	0.88	<0.0005	2.2 deg
Tibiofemoral Frontal plane kinematics	Pure Abduction	0.97	<0.0005	0.9 deg
Abduction + 20 Nm Int. Rot	0.91	<0.0005	1.2 deg
ACL Strain	15 Nm Int. Rot	0.89	<0.0005	0.5%
	134 N Ant. Shear + 15 Nm Int. Rot	0.93	<0.0005	0.5%
	Pure Abduction	0.87	<0.0005	0.7%
Abduction + 20 Nm Int. Rot	0.88	<0.0005	0.3%
ACL Force	100 N of Ant. Shear	0.93	<0.0005	15.4 N
100 N Ant. Shear + 10 Nm Abd.	0.94	<0.0005	16.7 N
MCL Strain	Pure Abduction	0.97	<0.0005	0.5%
Abduction + 20 Nm Int. Rot	0.98	<0.0005	0.7%
Medial COP A-P Translation	Baseline	0.98	<0.0005	0.6 mm
	15 Nm Int. Rot	0.97	<0.0005	0.4 mm
134 N Ant. Shear + 15 Nm Int. Rot	0.94	<0.0005	0.7 mm
Lateral COP A-P Translation	Baseline	0.94	<0.0005	0.4 mm
	15 Nm Int. Rot	0.98	<0.0005	0.5 mm
134 N Ant. Shear + 15 Nm Int. Rot	0.84	<0.0005	0.5 mm

Validation Against ACL and MCL Strains (Quasi-Static Loading).

As shown by both FE analyses and experimental data, the addition of anterior tibial shear force, knee abduction, and internal tibial rotation moments resulted in elevated ACL strain levels (Figs. 5 and 6). Furthermore, the knee abduction moment substantially increased MCL (superficial bundle) strain (Fig. 7). MCL strain was nonuniform with the lowest strains in the anterior and highest strains in the posterior region across the joint line. This is in agreement with findings of Gardiner and Weiss [27]. Similar trends were also observed in FE-predicted MCL strains of 1.9% for anterior (Exp: 2.6 ± 2.9%), 3.7% for middle (Exp: 2.9 ± 4.9%), and 5.8% for the posterior region of the superficial MCL (Exp: 6.1 ± 4.4%). Strong correlations along with low RMS errors were observed between FE predictions and experimental measures of ACL strain (r > 0.8, p < 0.0005; RMSE < 1%) and MCL strain (r > 0.9, p < 0.0005; RMSE < 1%) under all simulated loading conditions, Table 3. ACL strain data under baseline loading was not considered for validation due to the relatively unloaded ACL and associated error in strain measurement due to tissue buckling. Similarly, MCL strain data under baseline, internal rotation, and combined internal rotation with anterior shear were not considered for validation due to unloaded tissue. As demonstrated in Figs. 5, 6, and 7, all FE-predicted strain values were within the range of 95% confidence intervals of average experimental measurements.

Fig. 5.

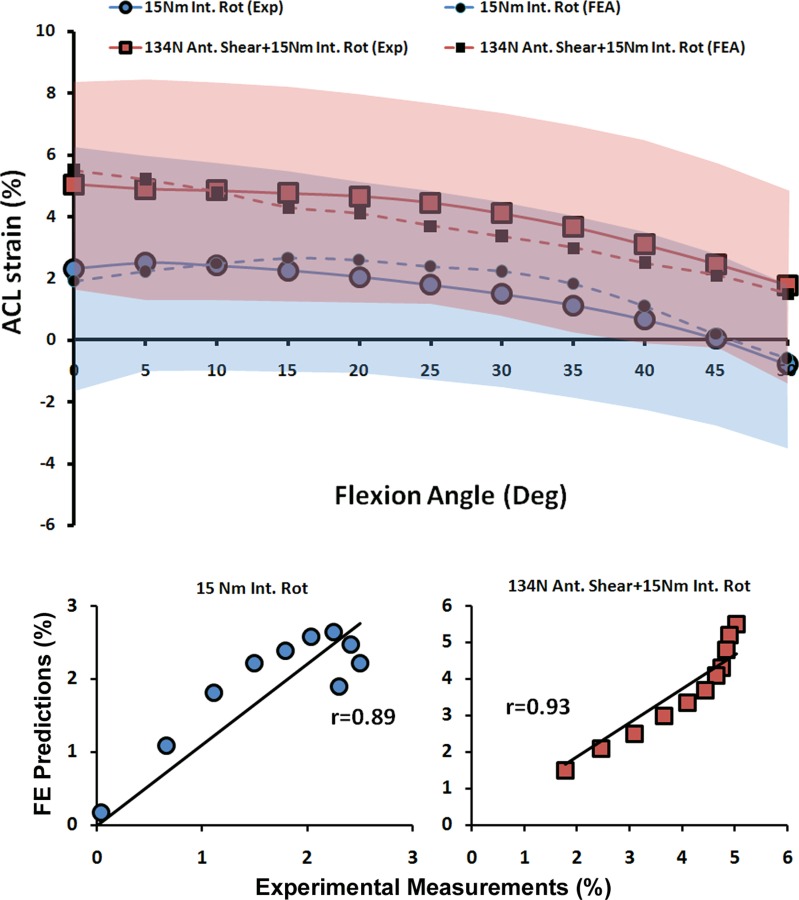
FE predictions versus experimental data for ACL strain under quasi-static isolated and combined internal rotation moments (shaded area represent experimental 95% confidence intervals)

Fig. 6.

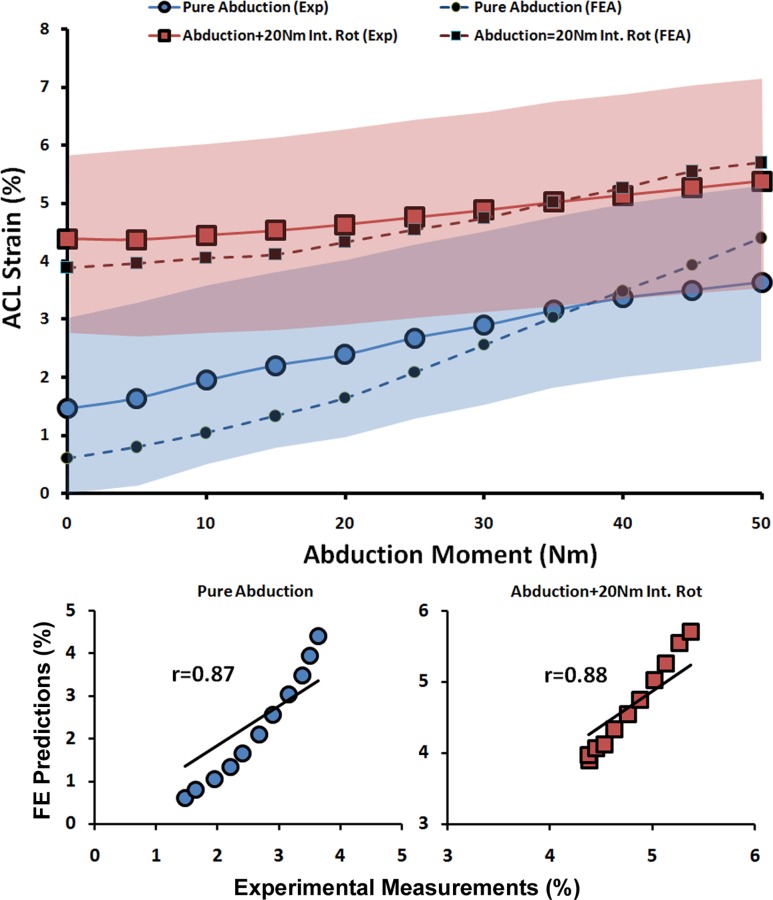
FE predictions versus experimental data for ACL strain under quasi-static isolated and combined abduction moments (shaded area represent experimental 95% confidence intervals)

Fig. 7.

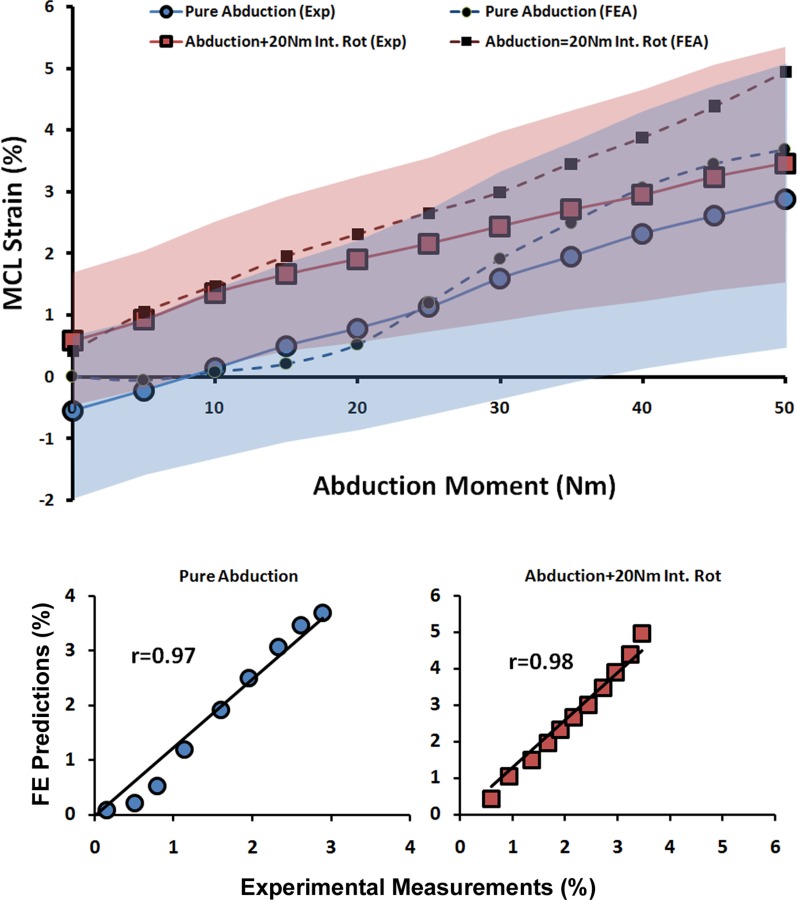
FE predictions versus experimental data for MCL strain under quasi-static isolated and combined internal rotation moments (shaded area represent experimental 95% confidence intervals)

Validation Against Tibiofemoral Articular Cartilage Pressure Distribution (Quasi-Static Loading).

FE predictions demonstrated trends similar to experimentally quantified tibiofemoral articular cartilage pressure data indicating anterior-posterior (A-P) translation of the center of pressure (COP) primarily under internal tibial rotation moments (Figs. 8 and 9). Strong correlations along with low RMS errors were observed between model-predicted COP A-P translation and experimental data across both medial (r > 0.9, p < 0.0005; RMSE < 1 mm) and lateral (r > 0.8, p < 0.0005; RMSE ≤ 0.5 mm) compartments for all simulations, Table 3. Further, as shown in Figs. 8 and 9, all FE-predictions were within the range of 95% confidence intervals of average experimental measurements. Additionally, the FE model resulted in similar articular cartilage pressure distribution as experimental data under all modes of tested loading conditions. Representative tibiofemoral articular cartilage pressure distributions for both FE model and experimental data are presented in Fig. 10.

Fig. 8.

FE predictions versus experimental data for medial compartment COP translation under quasi-static loading conditions (shaded area represent experimental 95% confidence intervals)

Fig. 9.

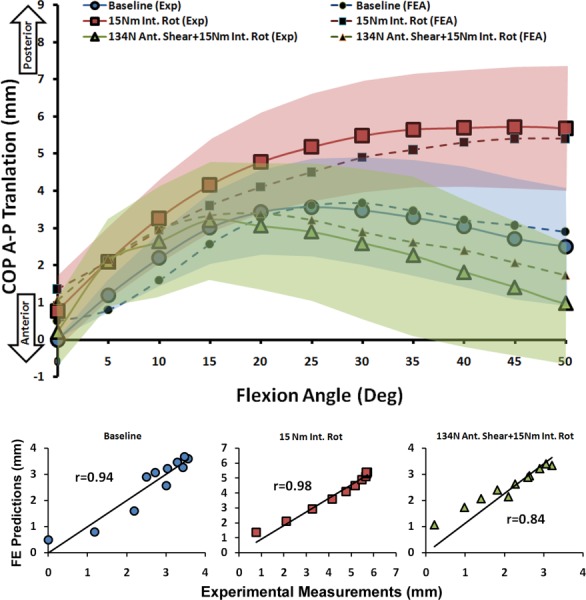
FE predictions versus experimental data for lateral compartment COP translation under quasi-static loading conditions (shaded area represent experimental 95% confidence intervals)

Fig. 10.

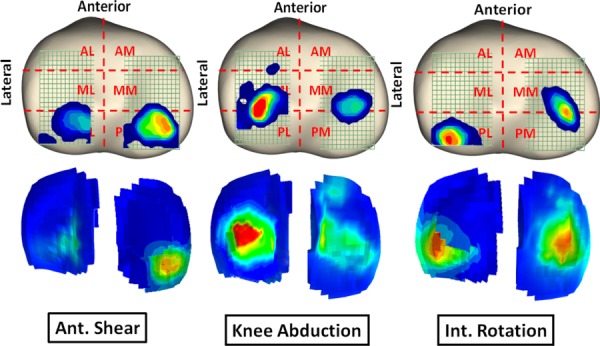
Pressure distribution across the tibial articular cartilage under functional loading conditions obtained experimentally (top) and predicted by the FE model (bottom)

Validation Against Tibiofemoral Kinematics and ACL/MCL Strains (Dynamic High-Rate Loading).

During simulated landings, initially applied force imbalance between the quadriceps and hamstrings muscle groups and externally applied anterior tibial shear force (simulating excessive quadriceps contraction or deceleration) increased anterior tibial translation and ACL strain (pre-impact). The pre-impact loading conditions did not change initial frontal and axial plane tibiofemoral alignment and resulted in an unloaded MCL. Similar trends as experimental data were observed in FE simulations (Table 4). Simulated bipedal landings resulted in an average axial impact load of 4108 ± 690 N (neutral landing) and 4015 ± 427 N (under additional 134 N of anterior shear force) over a period of 70 ms. Both model and cadaveric experiments showed that peak axial impact load (simulating ground reaction force) resulted in a substantial increase in anterior tibial translation, knee valgus, internal tibial rotation, ACL strain, and MCL strain (Table 4). Further, FE predictions during simulated dynamic landing resulted in similar trends as experimental data in both tissue strain and joint kinematics. Addition of a 134 N anterior shear force resulted in higher magnitudes of anterior tibial translation and ACL strain under both pre-impact and peak phases but did not result in a substantial change in tibiofemoral frontal and axial plane kinematics and MCL strain (Table 4).

Table 4.

FE model predictions and experimental data under simulated landing conditions

	No Ant. Shear				With Ant. Shear
	Pre-Impact		Peak		Pre-Impact		Peak
Parameter	*Exp.	FEM	*Exp.	FEM	*Exp.	FEM	*Exp.	FEM
ATT (mm)	3.7 ± 1.5	2.2	11 ± 2.8	8.6	6.5 ± 2.4	4.6	13.2 ± 3.9	11.2
Valgus (Deg)	0	0	1.2 ± 1.1	2.4	0.5 ± 0.9	0.1	3.7 ± 2.8	1.6
Int. Rot. (Deg)	0	0.1	2.8 ± 1.3	1.9	0.4 ± 0.8	0.2	1.9 ± 0.9	2.2
ACL (%)	2.1 ± 1.0	1.3	6.7 ± 1.8	5.2	4.7 ± 1.4	3.6	8.0 ± 1.2	7.1
MCL (%)	Unloaded		2.5 ± 3.1	1.5	1.1 ± 2.0	0.7	2.4 ± 2.1	1.2

Note: *Mean ± 95% confidence interval limits.

Validation Against ACL Force (static loading by Markolf et al.).

Both experimental and FE-predicted ACL forces demonstrated an increase in ACL force under applied isolated and combined loading states with maximum values at 30 deg of knee flexion angle [82]. Strong correlations with low RMS errors were observed between FE model prediction and cadaveric measurements of ACL force (r > 0.9, p < 0.0005, RMSE < 17 N) as shown in Table 3. Finally, all FE-predicted ACL forces were within the range of 95% confidence interval of average experimental measurements (Fig. 11).

Fig. 11.

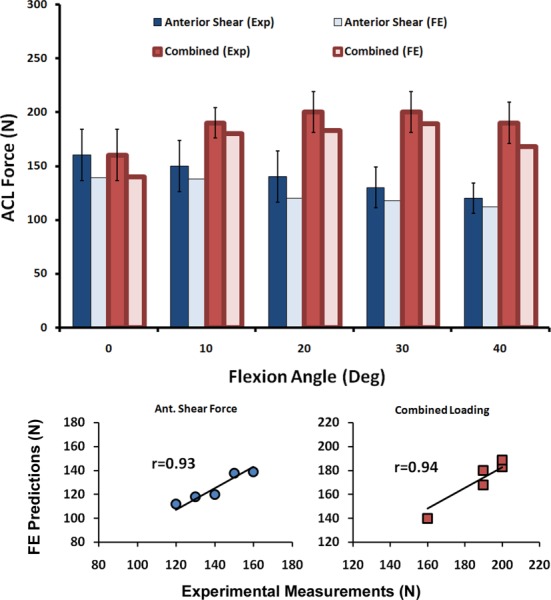
FE predictions versus experimental data for ACL force under simulated static loading conditions (error bars represent experimental 95% confidence intervals)

Discussion

Computational models, if properly validated, can serve as effective tools in parametric analyses, as well as population-based clinical studies. FE analysis is a powerful numerical technique that makes it feasible to investigate the biomechanical behavior of complex biological structures. Due to inherent challenges associated with experiments (in vivo and ex vivo) and the associated high cost and time, FE analysis has long been recognized and trusted as a reliable alternative method in the study of human joints. The primary advantage of these numerical approaches lies in precise control over boundary conditions, material properties, and structural alterations in parametric studies. Moreover, the ligament forces/strains, contact forces/areas, and stress/strain distribution across all soft and hard tissue structures are invaluable products of such model-based studies, which are challenging, if not impossible, to obtain experimentally. The purpose of this study was to develop and validate an anatomic FE model of the lower extremity with a detailed simulated knee joint comprising of all relevant hard and soft tissue structures in order to study knee biomechanics with the primary objective to investigate ACL injury mechanisms.

Accurate 3D geometry was modeled for all lower extremity bony and key soft tissue structures of the knee joint including cruciate and collateral ligaments, menisci, and articular cartilage. Remaining soft tissues of the knee joint, including joint capsule, tibiofemoral and patellofemoral ligaments, and trans-knee muscle-tendon units were incorporated into the FE model as uniaxial truss elements. Considering ligaments as primary constraints to define knee joint motion, FE predicted kinematics and resulting stress/strain distributions across knee structures may be highly dependent on the modeling technique and constitutive model chosen to simulate ligamentous structures [43].

Soft tissue structures such as ligaments undergo nonuniform deformation under functional loading conditions, while their regional contribution to overall joint stability differs with joint orientation [27,29,31]. Previously, 3D soft tissue models (i.e., ligaments, muscle) have demonstrated nonuniform stress/strain distributions that better represent physiologic tissue loading, while uniaxial truss element-based models implicitly assume uniform stress/strain distributions [27,29,31,85,86]. Anatomically accurate 3D representations of such structures coupled with structurally motivated constitutive models [62] facilitate implementation of realistic ligament mechanical properties such as finite deformation, anisotropy, and nonlinear incompressible fiber-reinforced structures. This approach also permits incorporation of realistic interactions between adjacent structures that may also result in a more realistic simulation of lines of action as varied with changes in joint orientation [29,31,85,86]. A recently developed constitutive material model [62] of soft tissue along with associated 3D geometry was used to simulate knee cruciate and collateral ligaments.

Although FE model solution convergence indicates model reliability, validation studies needed to be undertaken to ensure the validity of the model and the accuracy of the results. For this purpose, FE-model predictions of tibiofemoral kinematics, ligament strain and force, and tibiofemoral articular pressure distribution were compared with direct experimental measurements under both low-rate (static/quasi-static) and high-rate (dynamic) loading conditions. Due to the low reliability of pressure sensors under high-rate conditions, experimental pressure mapping was only performed under quasi-static testing.

The FE model was able to closely reproduce kinematics of the human knee joint measured during cadaveric experiments under a range of single- and multiplanar quasi-static loading conditions with strong correlation and minimal deviation. Further, similar trends as experimental data along with strong correlations and minimal deviation were observed between model predictions and experimental measurements of ACL strain and force, MCL strain, and tibiofemoral cartilage pressure distribution under multiple static and quasi-static loading conditions. FE predictions showed low deviations (RMS error) from average experimental data (static and quasi-static loading conditions), falling within 2.5 deg of tibiofemoral rotation, 1% of ACL and MCL strain, 17 N of ACL load, and 1 mm of tibiofemoral COP translation. Similarly, the FE model was able to accurately predict tibiofemoral kinematics and ACL and MCL strains during simulated bipedal landings. In addition to minimal deviation from direct cadaveric measurements, all model predictions fell within the 95% confidence intervals of average experimental data. This is believed to be very promising given the fact that subject-specific parameters were not taken into account. As a result, the developed model can be considered validated according to reported low RMS errors and strong correlations (r > 0.8 and p < 0.0005 for all comparisons) between FE and experimental data.

To the authors’ knowledge, this model is among the first knee FE models that not only incorporates anatomically accurate representation of the joint but is also validated against multiple parameters under static, quasi-static, and dynamic loading conditions. Various FE models of the knee joint have been previously developed by other investigators [19,20,22–33,37,38,40–42], but these models are mainly validated against a limited range of loading conditions [20,24–33,37,38,40–42] and/or do not include sufficient details for critical anatomical structures within the joint [19,22,25,26,31–33,37,38,40,41].

Earlier FE studies of the knee joint have simplified the joint with no representation of articular cartilage and/or menisci along with the simulation of knee ligaments as nonlinear elastic (springs) uniaxial elements without simulating patellofemoral articulation [2,87]. Later a variety of knee FE models that included both tibiofemoral and patellofemoral articulations were used to study knee joint biomechanics [23,24,28]. Similar to previous models, uniaxial elements with nonlinear elastic (spring) properties have been incorporated in these models in order to model knee ligaments and tendons. These models have also included a 3D representation of knee menisci as isotropic linear elastic materials [23,28] and isotropic composite [24] along with isotropic linear elastic articular cartilage [23,24,28]. Further improvements have been made in order to model menisci and articular cartilage as depth-dependent fiber oriented composite structures [36].

More recent studies have used a 2-dimensional (2D) or 3D representation of knee ligaments with various degrees of anatomical and constitutive model complexity [22,27,29,31,37,38,41,42]. Baldwin et al. developed a dynamic model of the knee joint consisting of tibiofemoral and patellofemoral articulations in addition to 2D representations of knee ligaments defined as fiber reinforced structures (membrane matrix with embedded nonlinear springs) [22]. However, due to the potential use of this model to study total joint replacement, menisci, articular cartilage, ACL, and PCL structures were not simulated. Song and colleagues have developed a 3D FE model of the tibiofemoral joint, which included 3D representation of the femur, tibia, and ACL (with distinct anteromedial and posterolateral bundles) defined as isotropic hyperelastic [37]. A similar approach has been used by Gardiner and Weiss in order to study MCL biomechanics under functional loading [27]. They have developed a novel material model based on strain energy density in order to simulate the MCL (superficial bundle) as transversely isotropic, incompressible hyperelastic with a composite structure [27]. Further, Limbert et al. have used a similar constitutive material model to study ACL biomechanics under passive tibial translation and flexion in a 3D FE model of an isolated ACL [29]. Others [42,88] have used similar constitutive modeling approaches with 3D simulations of key knee ligaments incorporated in 3D FE models of the knee joint. Although these models incorporate both tibiofemoral and patellofemoral articulation, cruciate and collateral ligaments, patellar tendon, menisci, and articular cartilage, they suffer from a lack of other ligamentous structures such as the posterior capsule, lateral and medial patellofemoral ligaments, deep MCL fibers, and anterolateral structures.

The current study aimed to combine the advantages of available knee FE models into an anatomic FE model of the lower extremity with sufficient details within the knee joint to study potential knee injury mechanisms with a specific focus on ACL injury. It is worthy of mention that this is the only knee FE model to date that has been validated against a combination of tibiofemoral kinematics, ACL and MCL strain/force, and tibiofemoral cartilage pressure distribution under both low-rate and high-rate loading conditions that the authors are aware of. Overall, the combination of detailed anatomic simulations of the joint and broad validation against direct experimental measures enhanced both model validity and accuracy in an effort to predict the complex physiologic behavior of knee joint structures. This model will also help to elucidate the importance of different loading factors on ACL biomechanics while serving as a powerful tool to investigate ACL injury mechanisms.

Despite the advantages of FE modeling, there are inherent limitations associated with computational modeling. First, as per the majority of previous FE models [23,26,28,31,40], articular cartilage has been represented as an isotropic linear elastic structure. However, previous experimental studies have shown that cartilage acts as a single-phase linear elastic material during short loading periods (less than 1500 s), as fluid flow within the tissue does not take place over short time intervals [53,54]. Although this may result in variations in FE-predicted stress across the cartilage, no alteration in joint kinematics and tissue stress/strain across other structures (i.e., ligaments) is expected. Further analyses are needed to quantify the effect of cartilage material properties in overall joint kinematics.

Second, subject-specific parameters (geometry and material properties) were not considered in the current model. Such an assumption may have resulted in the observed slight deviation in model predictions from average experimental findings. This is mainly associated with interspecimen variability in both anatomy and tissue properties between tested specimens and the subject upon which the FE model was based. However, this resulted in minimal errors in the results as demonstrated by small RMS errors between model predictions and experimental data, and strong correlations between the two that were observed. Further, there are technical challenges associated with large scale subject-specific modeling especially in tissue mechanical properties in addition to time constraints. Parametric and sensitivity analyses are being conducted to examine the sensitivity of model predictions to those parameters.

Finally, the experimentally reported tissue strain values were based on the regional measurements of DVRT displacement transducers. While DVRTs only reports tissue elongation and not the actual tissue force, the choice of using these sensors was based on acquisition of in situ tissue mechanical response in a minimally invasive matter with minimum tissue disruption. Previous studies have demonstrated that these regional measurements are valid representations of overall tissue behavior [89]. Care was taken to understand these limitations during the interpretation of our findings and model validation process.

Despite these limitations, the agreement between model predictions and experimental data demonstrates the ability of the developed model to predict the complex, nonuniform stress and strain fields that occur in biological soft tissues and the kinematics of the human knee joint. Future work will involve development of systematic approaches in order to customize the current model to be able to account for variation in individuals’ anatomy to enhance the accuracy of model’s predictions [90]. Additionally, in vivo biomechanical data from different individuals can be used as an input to the current validated FE model, which may be used in the clinical evaluation of various risk factors associated with ACL injury.